Similar presentations:
Простейшие движения твердого тела
1.
Простейшие движения твердого тела.2.
Простейшие движения твердого тела.К простейшим движения твердого тела относятся поступательное
движение и вращательное движение вокруг неподвижной оси.
В кинематике твердого тела при различных видах его движений
интересуются
кинематическими характеристиками
движения твердого тела в целом
и движения отдельных его точек .
3.
Поступательное движение твердого тела.Поступательным называется такое движение твердого тела,
при котором любая прямая, проведенная в этом теле,
перемещается, оставаясь параллельной самой себе.
При поступательном движении тела траектории его точек
могут быть любыми кривыми линиями.
4.
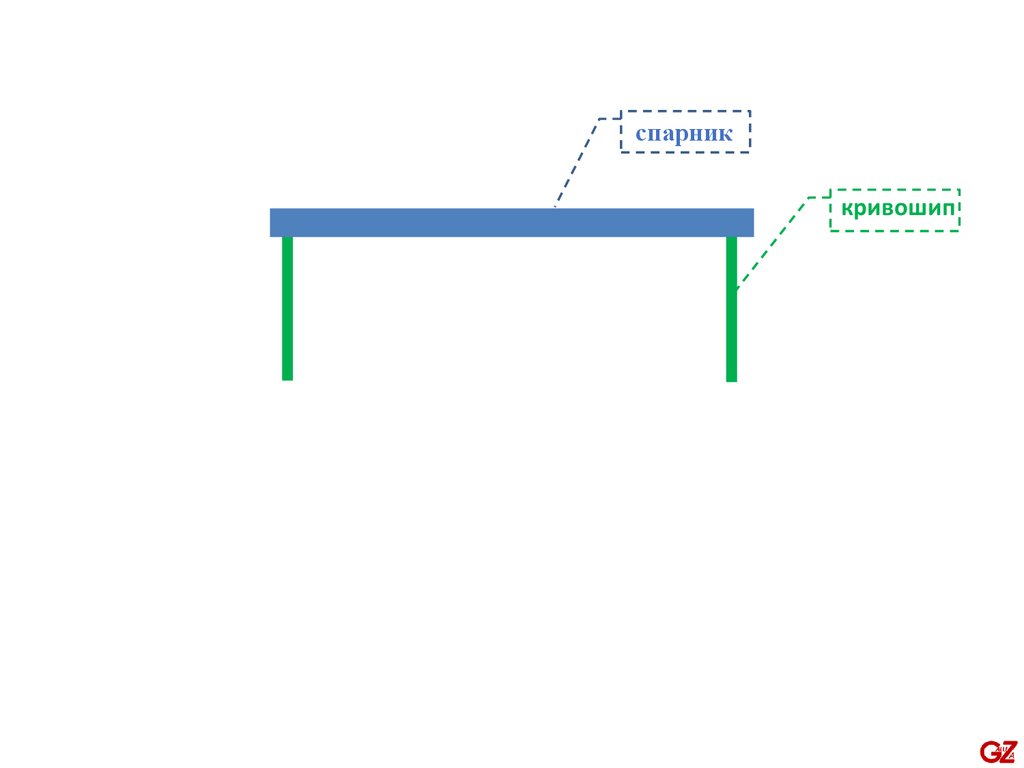
кривошип5.
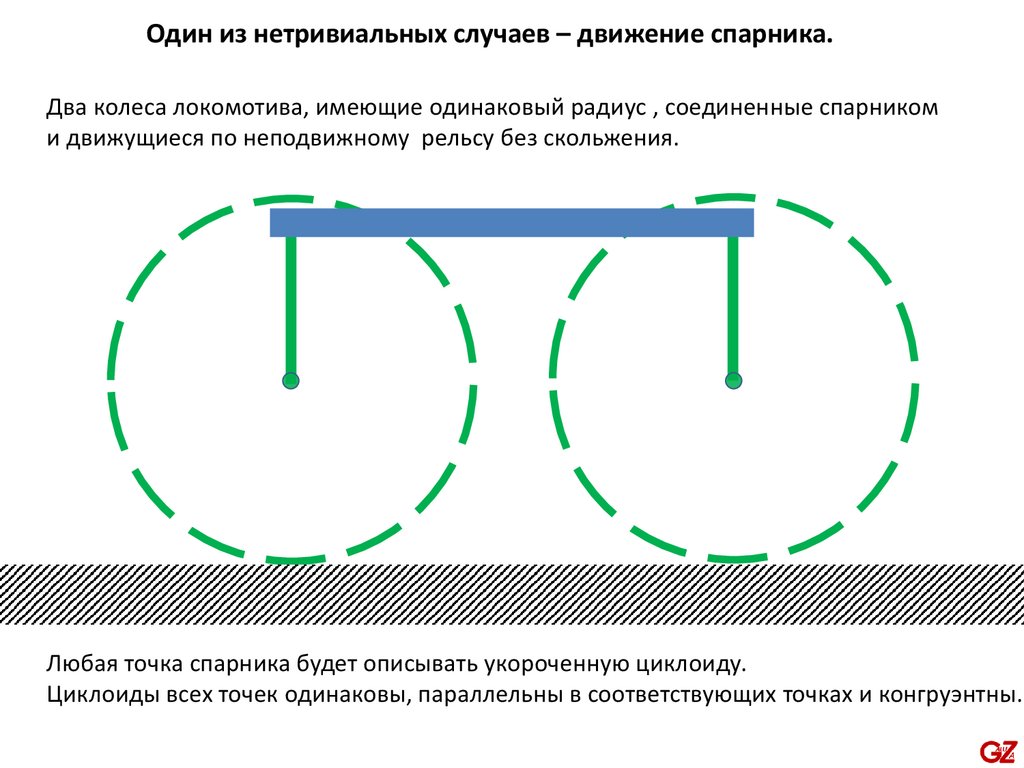
Один из нетривиальных случаев – движение спарника.Два колеса локомотива, имеющие одинаковый радиус , соединенные спарником
и движущиеся по неподвижному рельсу без скольжения.
111111
111111
Любая точка спарника будет описывать укороченную циклоиду.
Циклоиды всех точек одинаковы, параллельны в соответствующих точках и конгруэнтны.
6.
спарниккривошип
1
111111
1
1
111111
1
7.
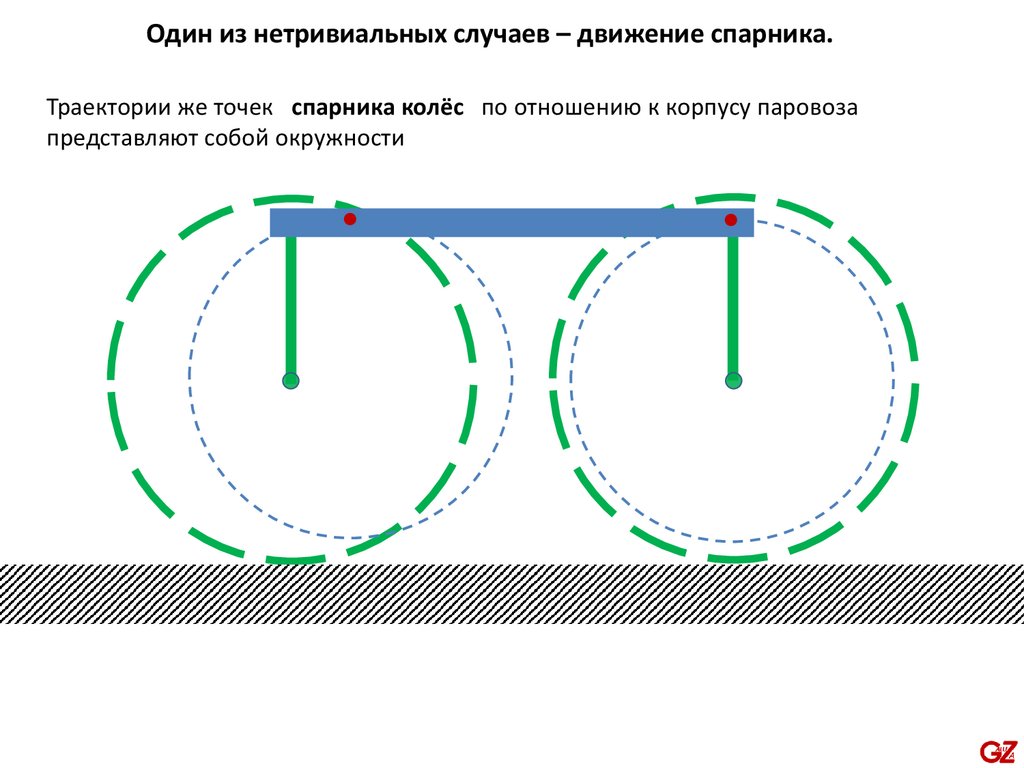
Один из нетривиальных случаев – движение спарника.Траектории же точек спарника колёс по отношению к корпусу паровоза
представляют собой окружности
111111
111111
8.
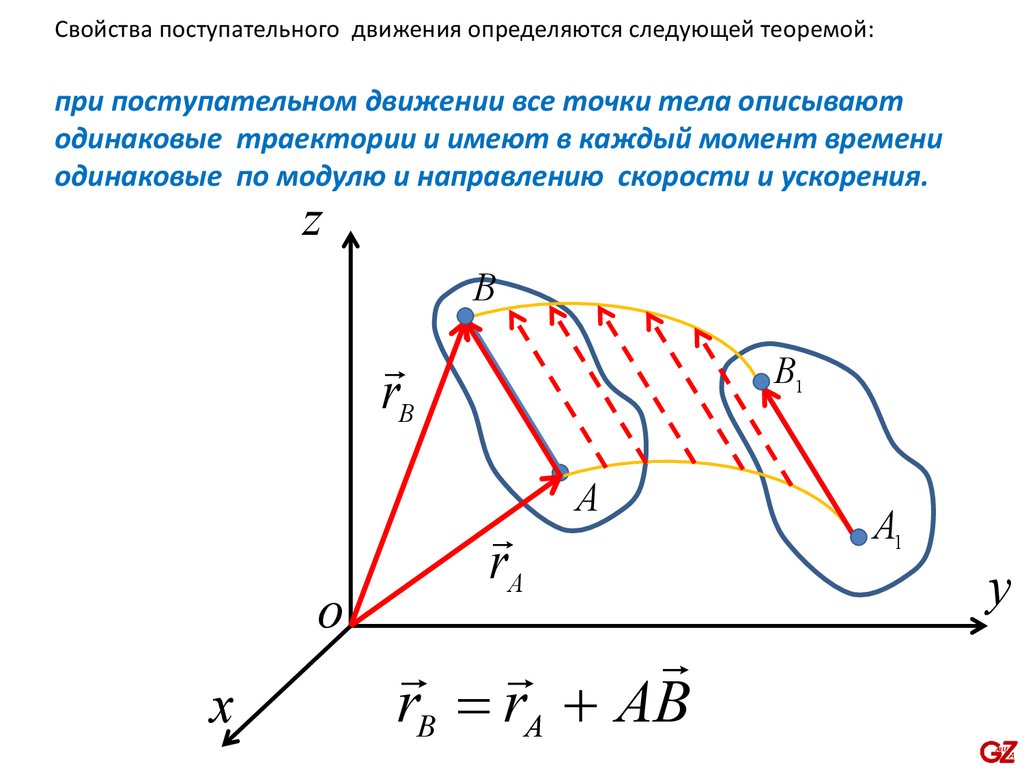
Свойства поступательного движения определяются следующей теоремой:при поступательном движении все точки тела описывают
одинаковые траектории и имеют в каждый момент времени
одинаковые по модулю и направлению скорости и ускорения.
z
B
rB
о
x
B1
rA
A
rB = rA + AB
A1
y
9.
Длина АВ постоянна, как расстояние между точками твердого тела,а направление AB остается неизменным, так как тело
движется поступательно. Таким образом вектор AB во все
время движения остается постоянным ( AB = const ) .
Траектория точки В получается из траектории точки А параллельным
смещением всех ее точек на постоянный вектор
.
траектории точек А и В действительно будут одинаковыми
(при наложении совпадающими) кривыми.
rB = rA + AB
Для нахождения скоростей точек А и В дифференцируем обе части равенства.
10.
Тогда получим :drB drA d ( AB)
=
+
dt
dt
dt
Производная от постоянного вектора AB равна нулю.
rA и rB дают скорости точек А и В.
V A = VB
Производные от векторов
Скорости точек А и В тела в любой момент времени одинаковы и по модулю
и по направлению.
dV A dVB
=
dt
dt
или
.
a A = aB
Ускорения точек А и В тела в любой момент времени тоже одинаковы
и по модулю и по направлению.
11.
Так как точки А и В выбраны произвольно, то следует, что у всех точектела их траектории, а также скорости и ускорения в любой момент
времени одинаковы.
Из теоремы следует, что поступательное движение твердого тела вполне
определяется движением какой-нибудь одной его точки.
Уравнения поступательного движения тела имеют вид
x А = x A (t ), y А = y A (t ) , z А = z A (t ) .
При
поступательном движении общую для всех точек тела скорость
V называют скоростью поступательного движения тела,
а ускорение
a - ускорением поступательного движения.
12.
оерд го
т
е
тв
. Вращ
а
л
жение
ви
т
а
ное
ь
л
е
д
13.
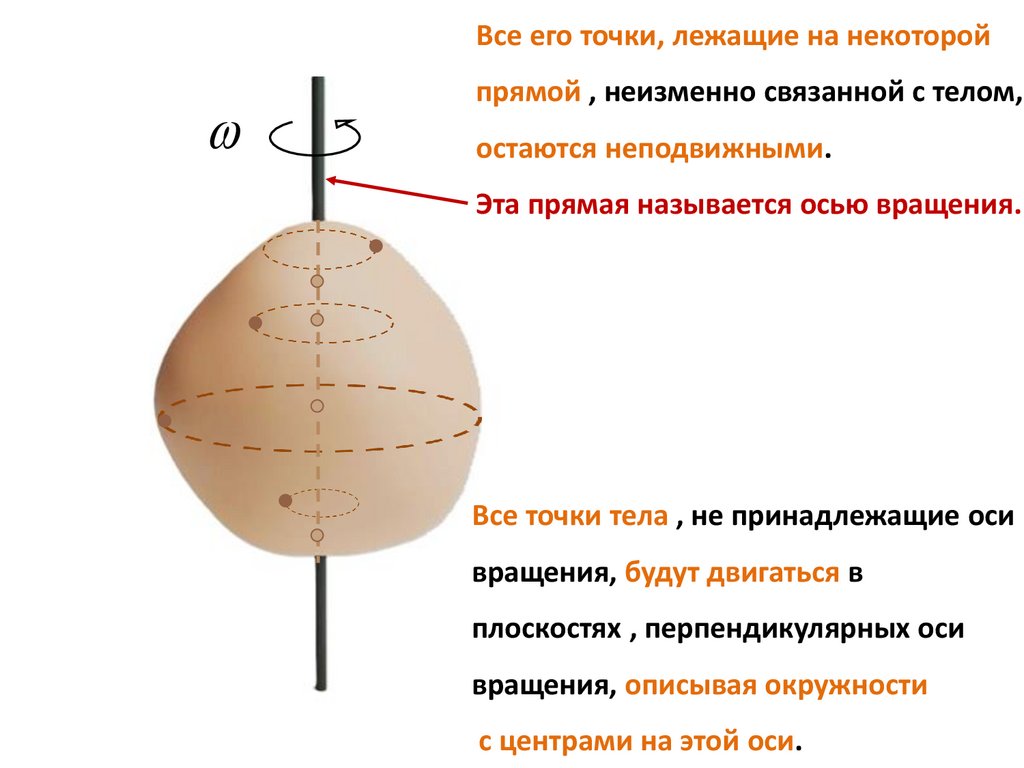
Вращательным движением называют такое движение твердого тела,при котором все его точки, лежащие на некоторой прямой , неизменно
связанной с телом, остаются неподвижными.
Эта прямая называется осью вращения.
Все точки тела , не принадлежащие оси вращения, будут двигаться в
плоскостях , перпендикулярных оси вращения, описывая окружности
с центрами на этой оси.
14.
Все его точки, лежащие на некоторойпрямой , неизменно связанной с телом,
остаются неподвижными.
Эта прямая называется осью вращения.
Все точки тела , не принадлежащие оси
вращения, будут двигаться в
плоскостях , перпендикулярных оси
вращения, описывая окружности
с центрами на этой оси.
15.
16.
zНеподвижная
Н
плоскость
Подвижная
плоскость
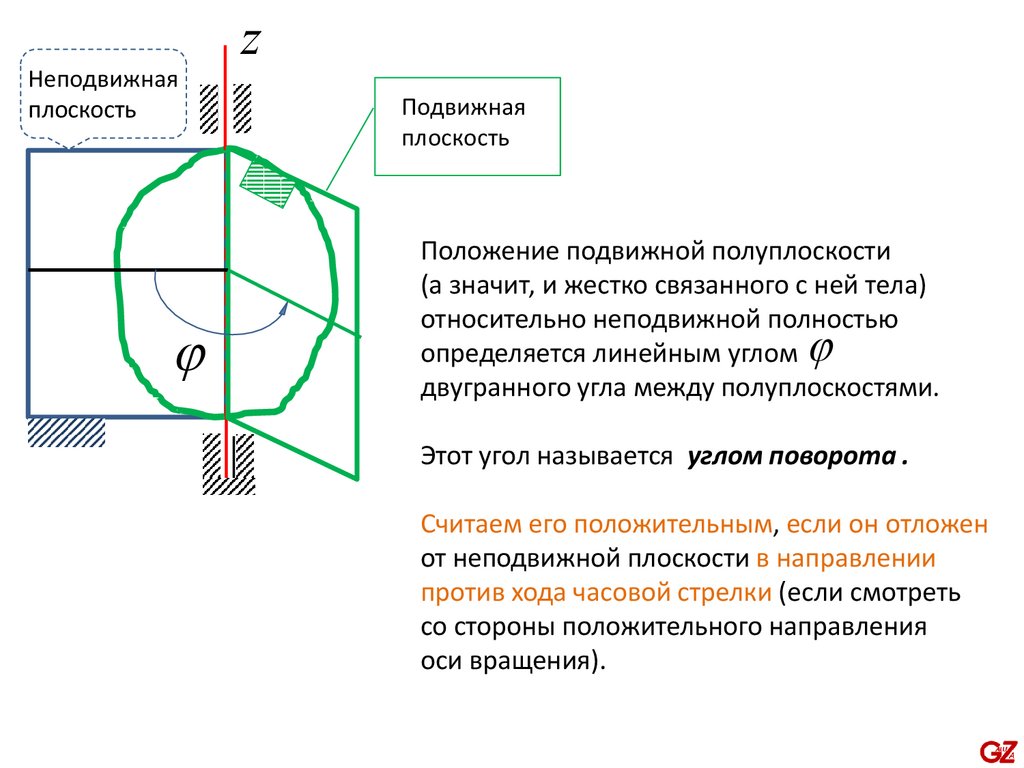
Положение подвижной полуплоскости
(а значит, и жестко связанного с ней тела)
относительно неподвижной полностью
определяется линейным углом
двугранного угла между полуплоскостями.
Этот угол называется углом поворота .
Считаем его положительным, если он отложен
от неподвижной плоскости в направлении
против хода часовой стрелки (если смотреть
со стороны положительного направления
оси вращения).
17.
НеподвижнаяН
плоскость
z
Подвижная
плоскость
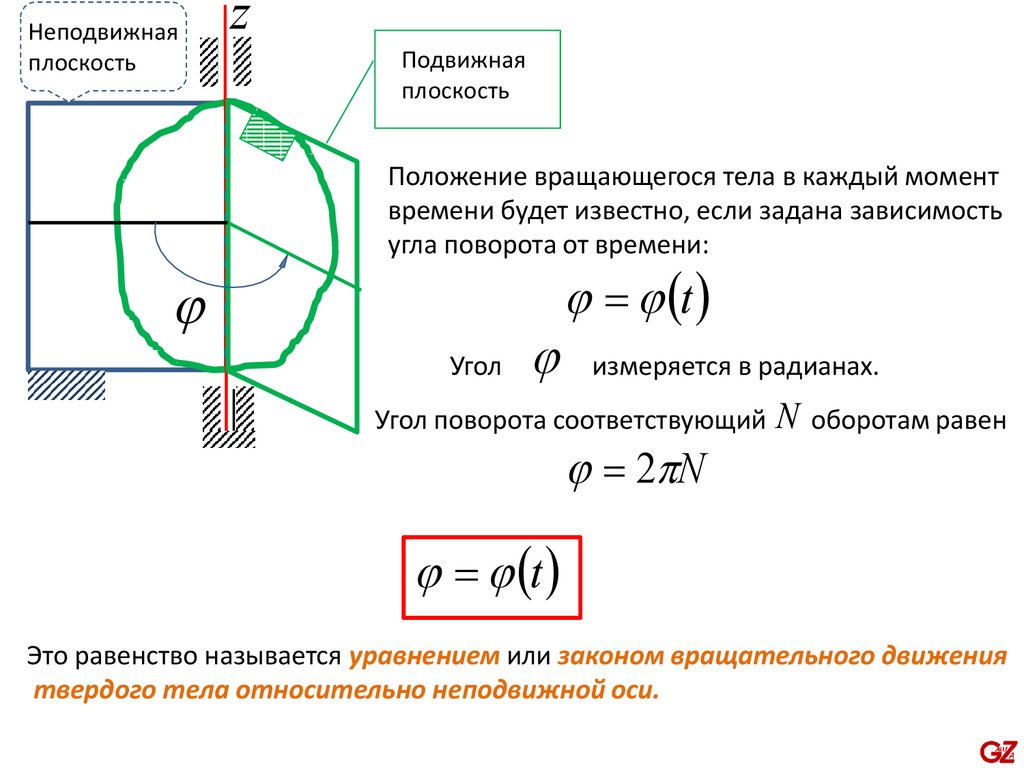
Положение вращающегося тела в каждый момент
времени будет известно, если задана зависимость
угла поворота от времени:
= (t )
Угол
измеряется в радианах.
Угол поворота соответствующий N оборотам равен
= 2 N
= (t )
Это равенство называется уравнением или законом вращательного движения
твердого тела относительно неподвижной оси.
18.
Угловая скорость и угловое ускорение.За малый промежуток времени t угол поворота изменится на величину .
Средней угловой скоростью тела за время t называется отношение ср =
.
t
Средняя угловая скорость характеризует быстроту изменения угла поворота
приблизительно, так как она зависит от t .
t , которая равна
Вместо нее используют угловую скорость в момент
предельному значению
при
.
ср
t → 0
d
= lim
=
=
dt
t → 0 t
Угловая скорость равна первой производной по времени от угла поворота.
d
=
=
dt
19.
d=
=
dt
Угловая скорость характеризует кинематическую меру изменения угла
времени.
Знак производной показывает направление вращения:
во
При
0 вращение происходит против хода часовой стрелки;
при
0 - по ходу часовой стрелки.
Угловая скорость измеряется в радианах в секунду -
рад
с
или
с −1 .
В технике угловую скорость часто задают числом nоборотов в минуту.
рад
Связь между в
с
и
nв
об
мин
2 n n
=
=
60 30
определяется формулой.
20.
За малый промежуток времениприращение
за время t
t угловая скорость тела получила
; тогда средним угловым ускорением тела
называется отношение
Предел этого отношения при
t → 0
ср =
t
.
называется угловым ускорением тела
t или просто угловым ускорением :
d
= lim
=
=
dt
t → 0 t
в данный момент времени
d d 2
=
= 2
dt dt
Угловое ускорение тела равно первой производной
по времени от угловой скорости тела или второй
производной по времени от угла поворота тела.
21.
d d=
= 2
dt dt
2
Если 0 , то изменение угловой скорости происходит в направлении
против хода часовой стрелки,
Если 0 ,то - по ходу часовой стрелки.
На рисунках угловая скорость и угловое ускорение изображают в виде
круговых стрелок
и
.
Круговая стрелка для
показывает направление изменение угла поворота,
а круговая для
показывает направление изменения угловой скорости.
Когда направления
и
совпадают ,и, следовательно
и
имеют одинаковые знаки, вращение называется ускоренным, в противном
случае замедленным.
Единицей измерения углового ускорения является
рад
с2
или
с −2 .
22.
Угловая скорость и угловое ускорение могут быть представлены ввиде векторов
и
.
Вектором угловой скорости назовем вектор, модуль которого равен
абсолютной величине производной угла поворота по времени
d и направлен по оси вращения так, чтобы смотря ему навстречу
=
dt
видеть вращение тела происходящим против хода часовой стрелки.
z
d
=k
= k ,
dt
где
алгебраическая величина угловой cкорости
или проекция вектора скорости на ось OZ.
k
y
x
Направление вращения указанное стрелкой будем считать
положительным, вектор
направлен вверх, это
скользящий вектор.
23.
Вектор углового ускорения определяется по формулеd
=k
= k , где алгебраическая величина углового
ускорения, либо проекция вектора на ось OZ.
dt
Векторы и k совпадают, если 0 .
Вектор характеризует изменение угловой скорости по величине и направлению.
24.
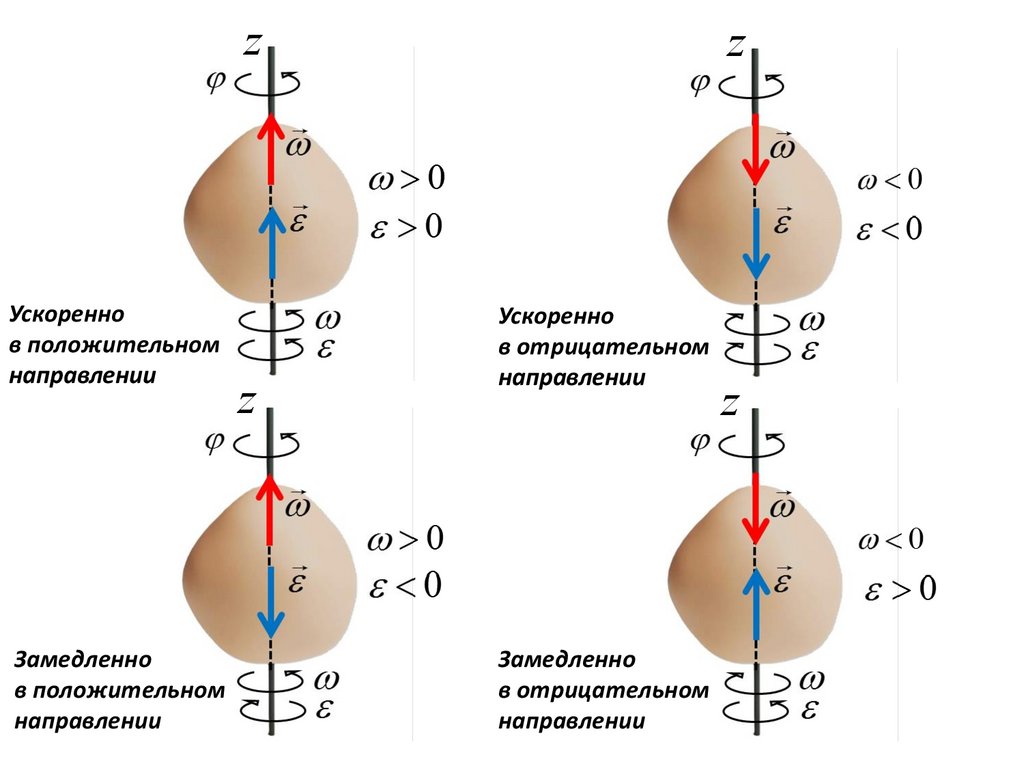
zУскоренно
в положительном
направлении
Замедленно
в положительном
направлении
z
z
Ускоренно
в отрицательном
направлении
Замедленно
в отрицательном
направлении
z
25.
Ускореннов положительном
направлении
26.
Замедленнов положительном
направлении
27.
Ускореннов отрицательном
направлении
28.
Замедленнов отрицательном
направлении
29.
30.
Равнопеременное и равномерное вращение.Вращение называется равнопеременным, если угловое ускорение тела
в процессе движения остается постоянным, т. е.
d
= ; d = dt ;
dt
= 0 + t
= const .
t
0
0
d = dt ;
Закон изменения угловой скорости
при равнопеременном вращении.
31.
td
= ; d = dt ; d = dt ;
0
0
dt
t
0
0
d = ( 0 + t ) dt
t2
= 0 + 0 t +
2
Закон равнопеременного вращения.
В случае равномерного вращения угловая скорость постоянна по модулю
и направлению.
= 0 + 0 t
Закон равномерного вращения.
32.
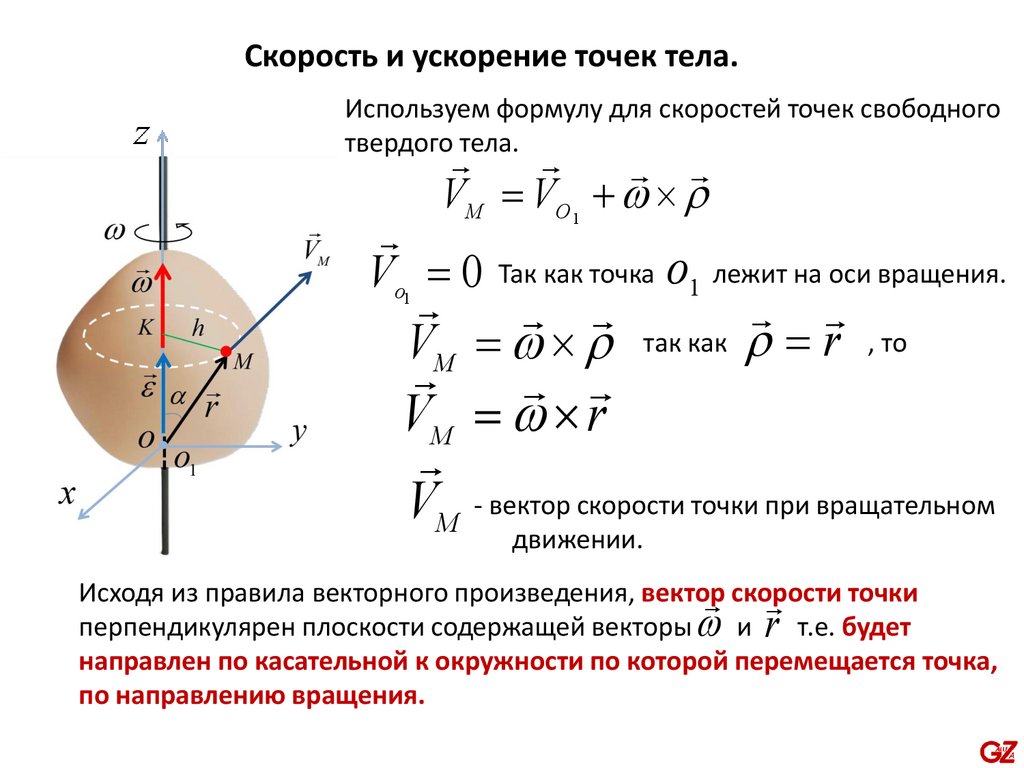
Скорость и ускорение точек тела.Используем формулу для скоростей точек свободного
твердого тела.
VМ = VO +
Vo = 0 Так как точка о1 лежит на оси вращения.
1
так как , то
=r
VМ =
1
VМ = r
VМ - вектор скорости точки при вращательном
движении.
Исходя из правила векторного произведения, вектор
точки
скорости
перпендикулярен плоскости содержащей векторы и r т.е. будет
направлен по касательной к окружности по которой перемещается точка,
по направлению вращения.
33.
Учитывая, чтоh = r sin .
VМ = r sin ( , r ) = h
Модуль скорости любой точки вращающегося тела
равен произведению модуля угловой скорости
этого тела на расстояние h от точки до оси вращения.
V = h
о
V Так как модуль скорости пропорционален
расстоянию h , то эпюра скоростей
M
имеет вид.
34.
Определение ускорения точки вращающегося твердого тела.dV
d d dr
a=
= ( r ) =
r +
dt dt
dt
dt
= r + V
- вращательная составляющая ускорения.
a = r
a направлен по касательной к окружности, по которой перемещается
точка и совпадает с вектором скорости при ускоренном движении.
a = rsin ( , r ) = h
- модуль вращательного ускорения равен произведению модуля углового
ускорения на расстояние
h.
35.
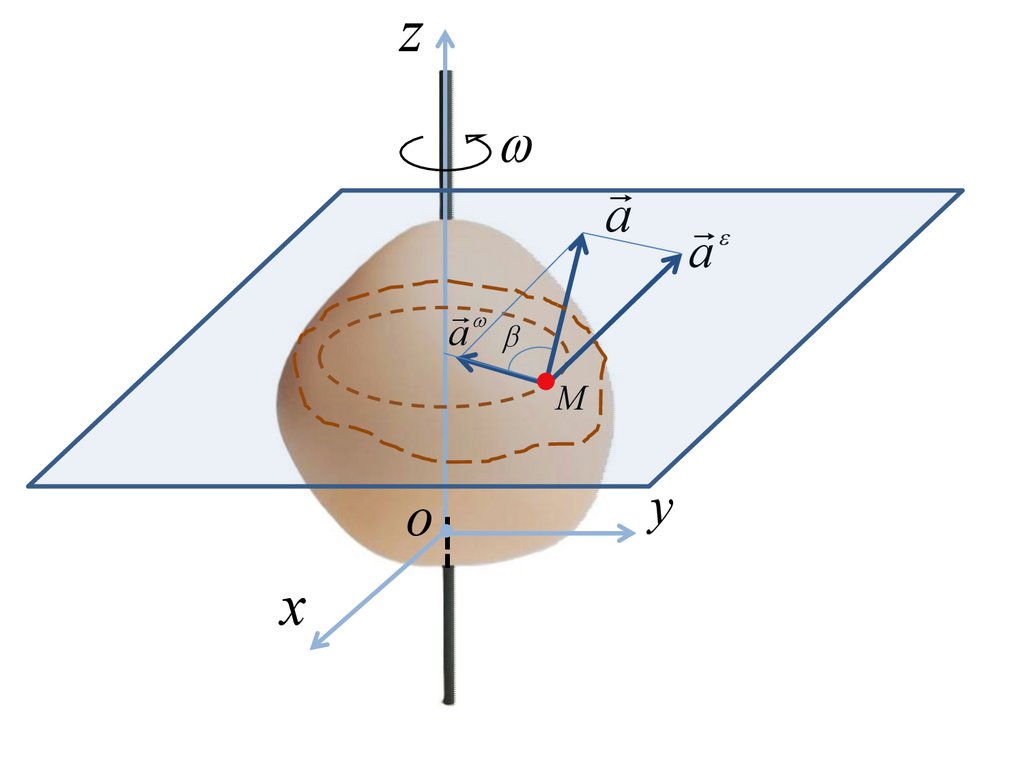
- осестремительная составляющая ускорения.a = V
Вектор a всегда направлен по радиусу вращения к центру вращения или
по главной нормали к траектории точки.
a = ( r )
a = V sin 90 = V = h = h
0
2
a = h - модуль осестремительного ускорения.
2
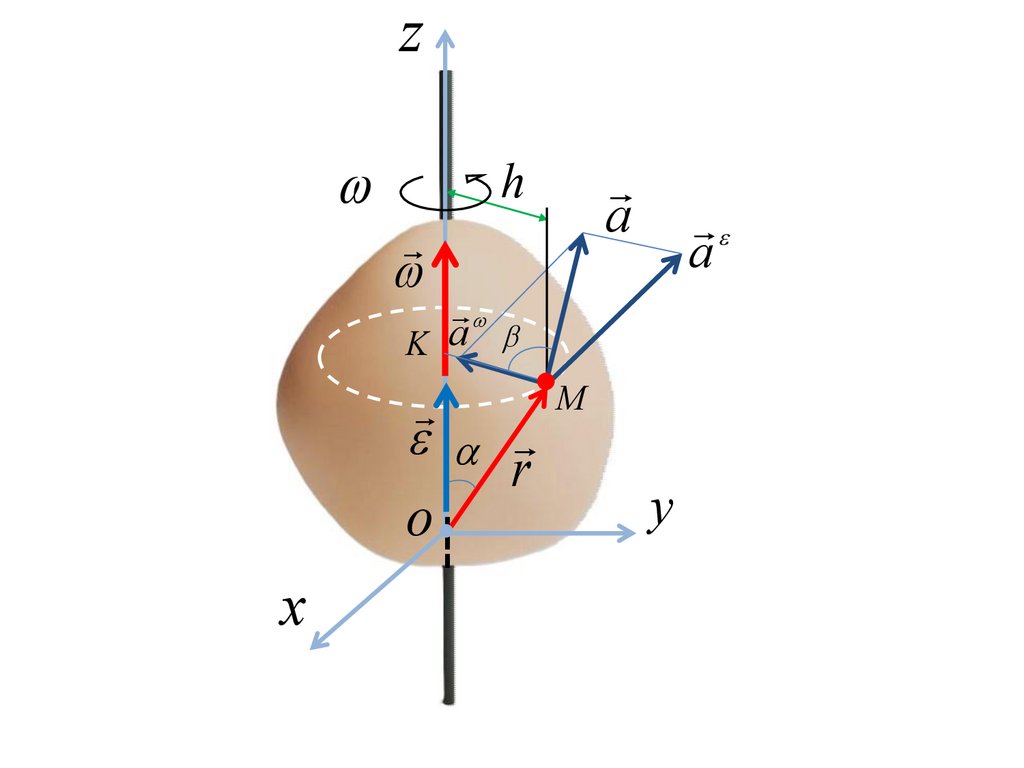
полного ускорения точки равен геометрической
Вектор
вращательной и осестремительной составляющих
a = a + a сумме
ускорения.
36.
Модуль полного ускорения точки определяется по формулеa= a +a
2
2
или
a = h + h = h +
2
2
4
2
2
4
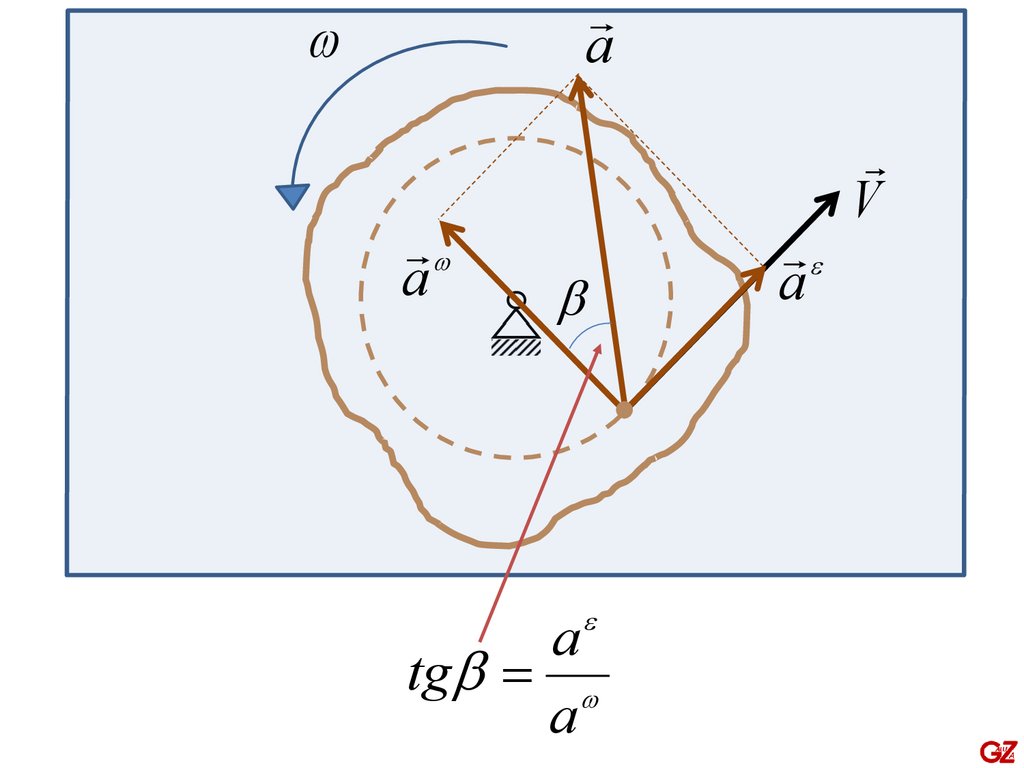
Направление полного ускорения определяется по тангенсу угла ,
который полное ускорение образует с осестремительным ускорением.
a
tg =
a
Тангенс угла не зависит от положения точки.
37.
zh
a
a
K a
M
о
x
r
y
38.
za
a
a
M
о
x
y
39.
aa
a
tg =
a
a
V
40.
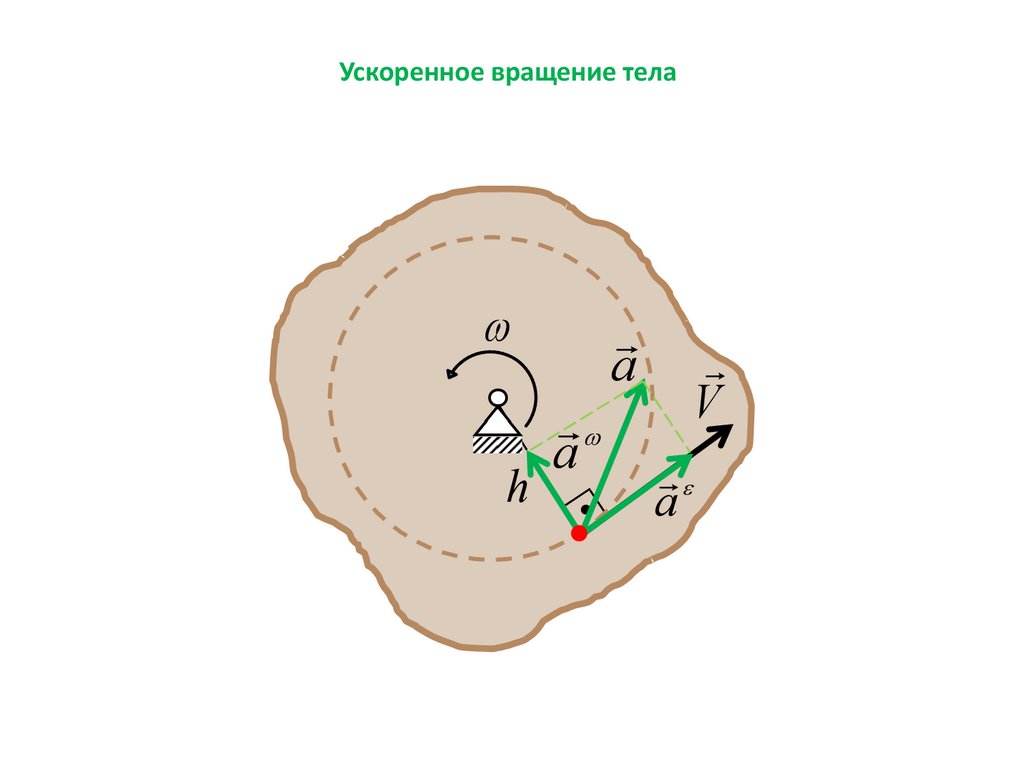
Ускоренное вращение телаh
a
a
V
a
41.
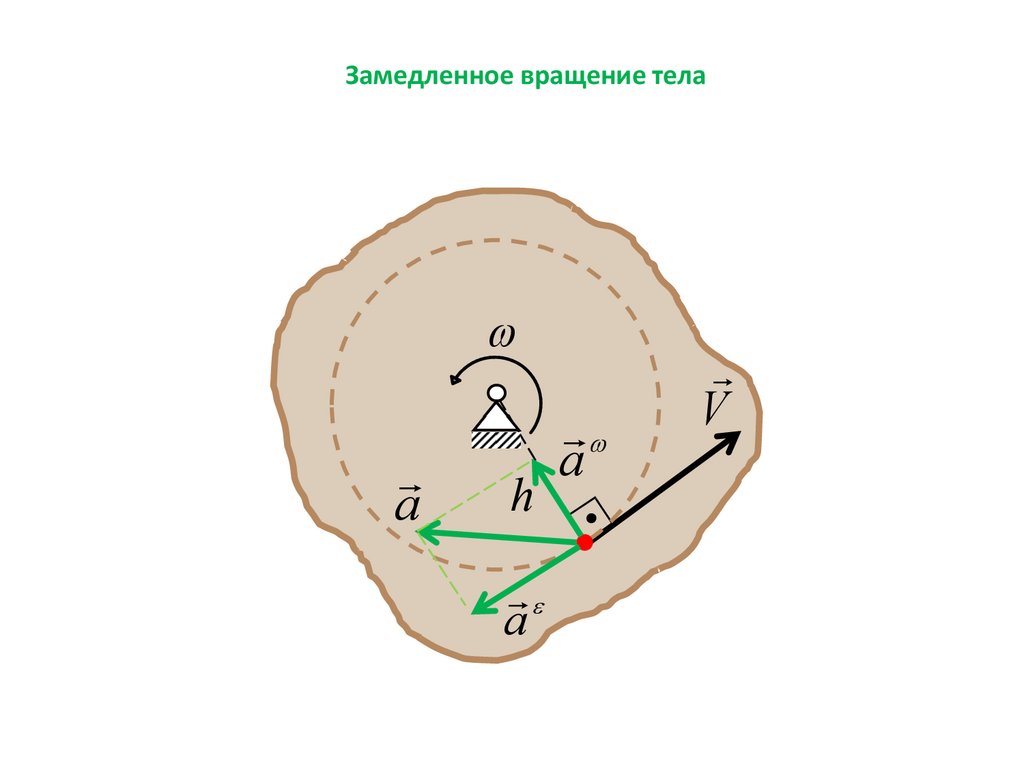
Замедленное вращение телаa
h
a
a
V
42.
Передачи вращательного движения.43.
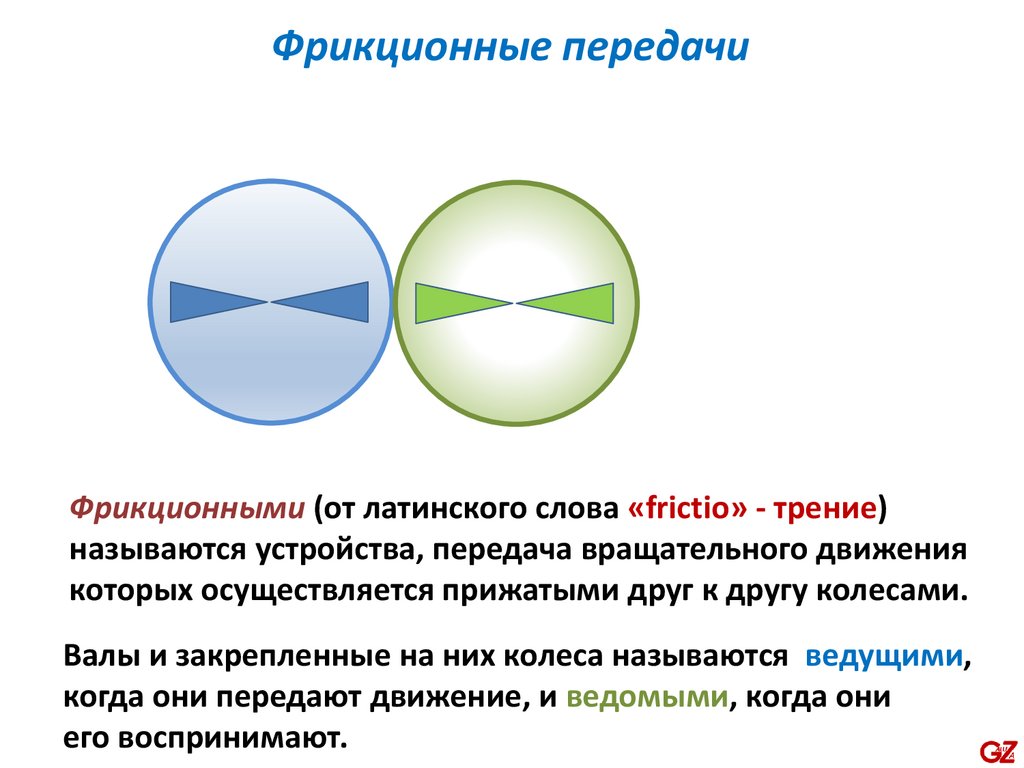
Фрикционные передачиФрикционными (от латинского слова «frictio» - трение)
называются устройства, передача вращательного движения
которых осуществляется прижатыми друг к другу колесами.
Валы и закрепленные на них колеса называются ведущими,
когда они передают движение, и ведомыми, когда они
его воспринимают.
44.
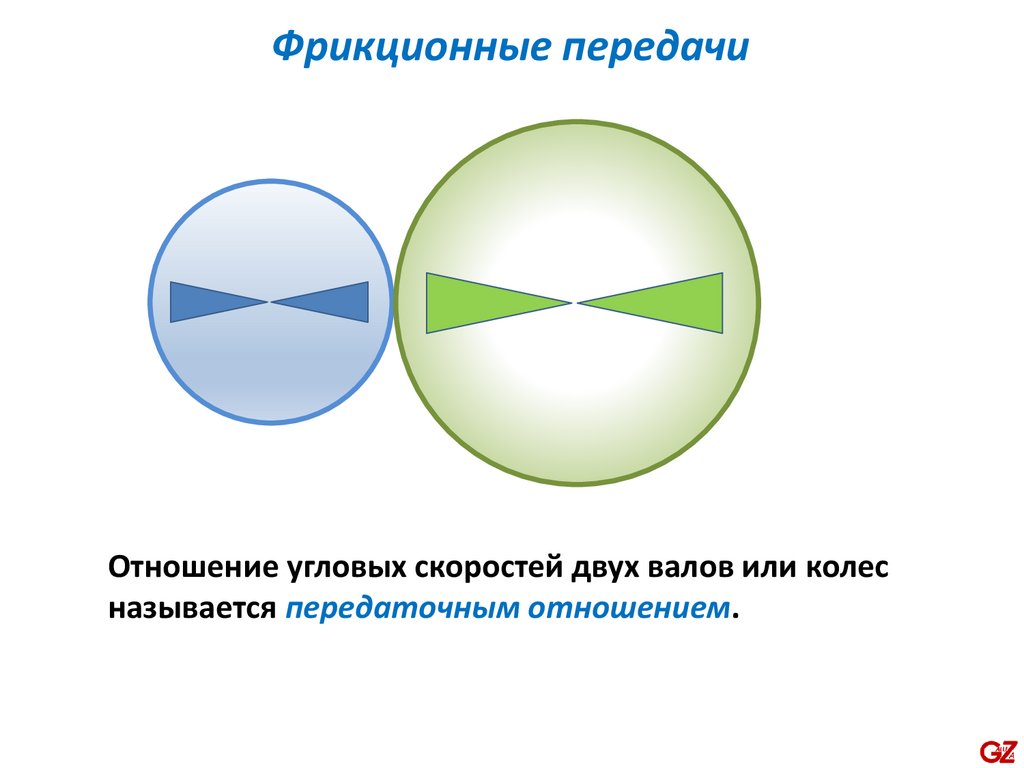
Фрикционные передачиОтношение угловых скоростей двух валов или колес
называется передаточным отношением.
45.
Ременные передачи.Открытая передача.
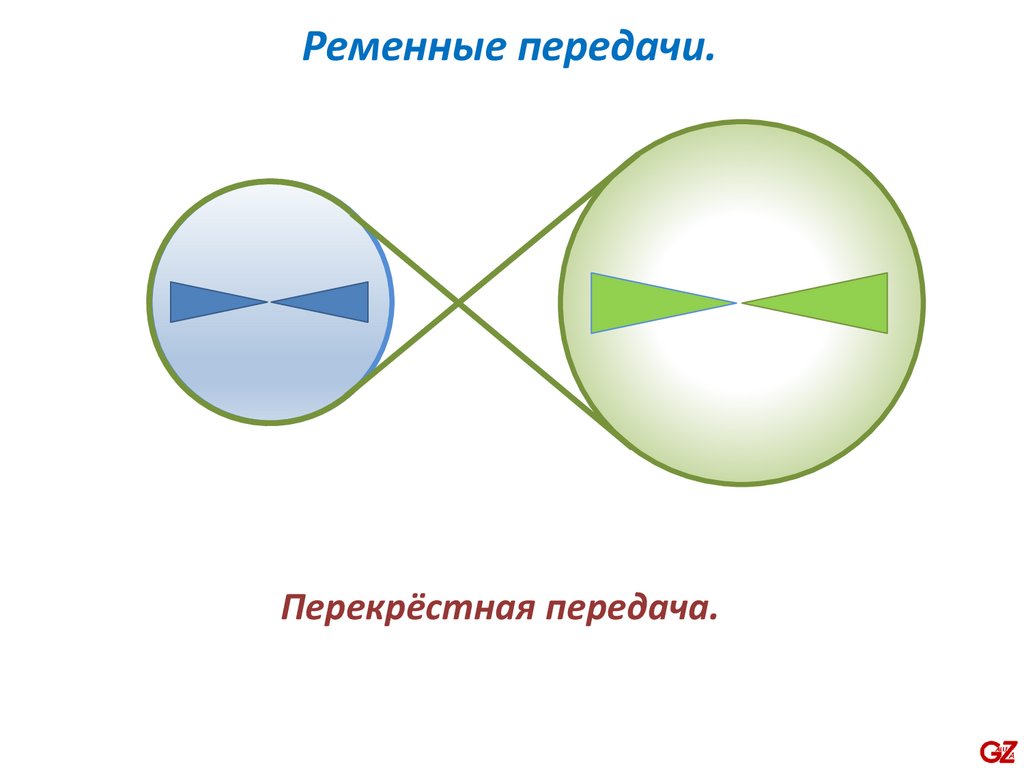
46.
Ременные передачи.Перекрёстная передача.
47.
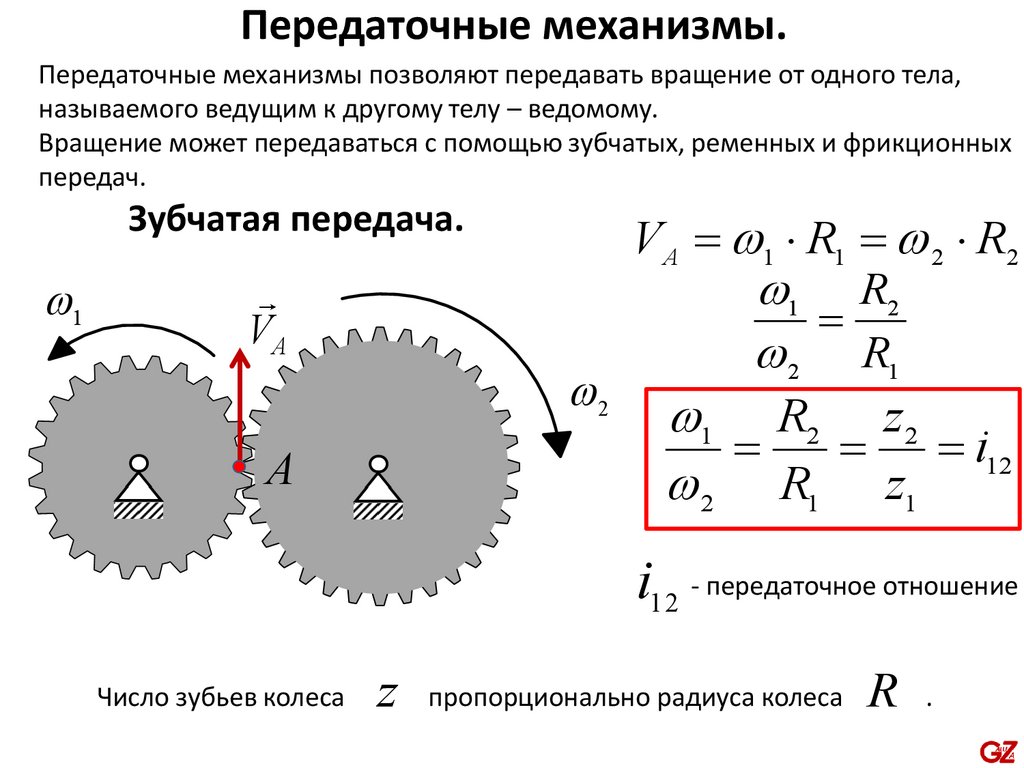
Передаточные механизмы.Передаточные механизмы позволяют передавать вращение от одного тела,
называемого ведущим к другому телу – ведомому.
Вращение может передаваться с помощью зубчатых, ременных и фрикционных
передач.
Зубчатая передача.
1
VA
A
V A = 1 R1 = 2 R2
1 R2
=
2 R1
2
1 R2 z 2
=
= = i12
2 R1 z1
i1 2 - передаточное отношение
Число зубьев колеса
z пропорционально радиуса колеса R .
48.
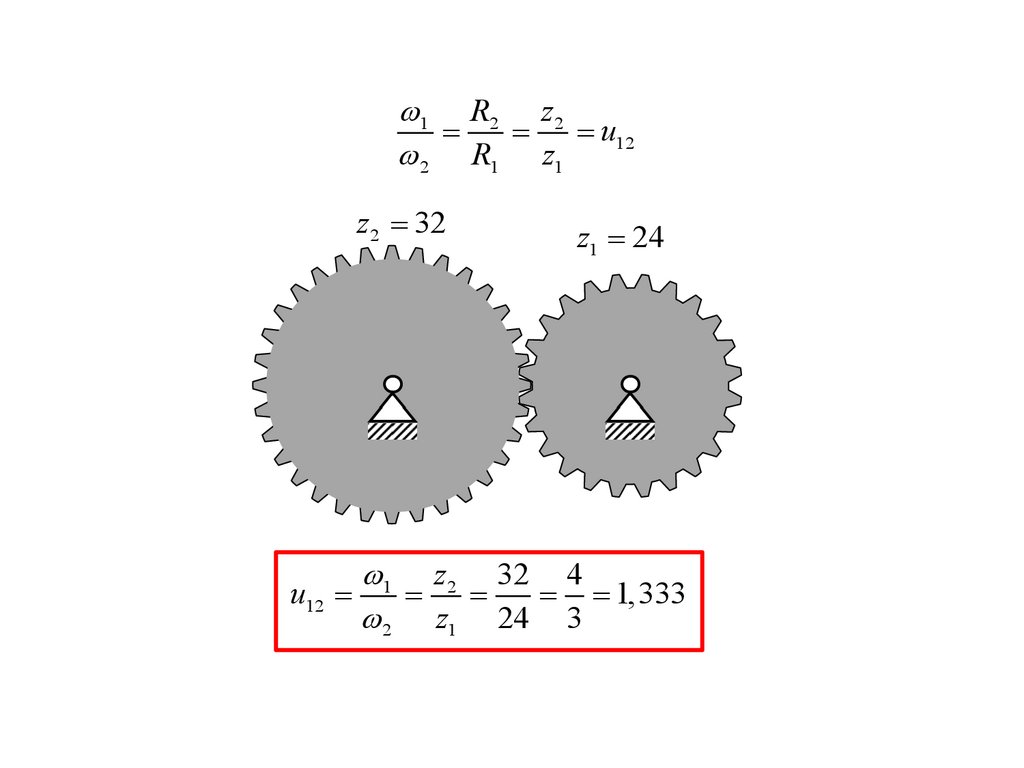
1 R2 z2=
=
= u12
2 R1 z1
z2 = 32
z1 = 24
1 z2 32 4
u12 =
=
=
= = 1,333
2 z1 24 3
49.
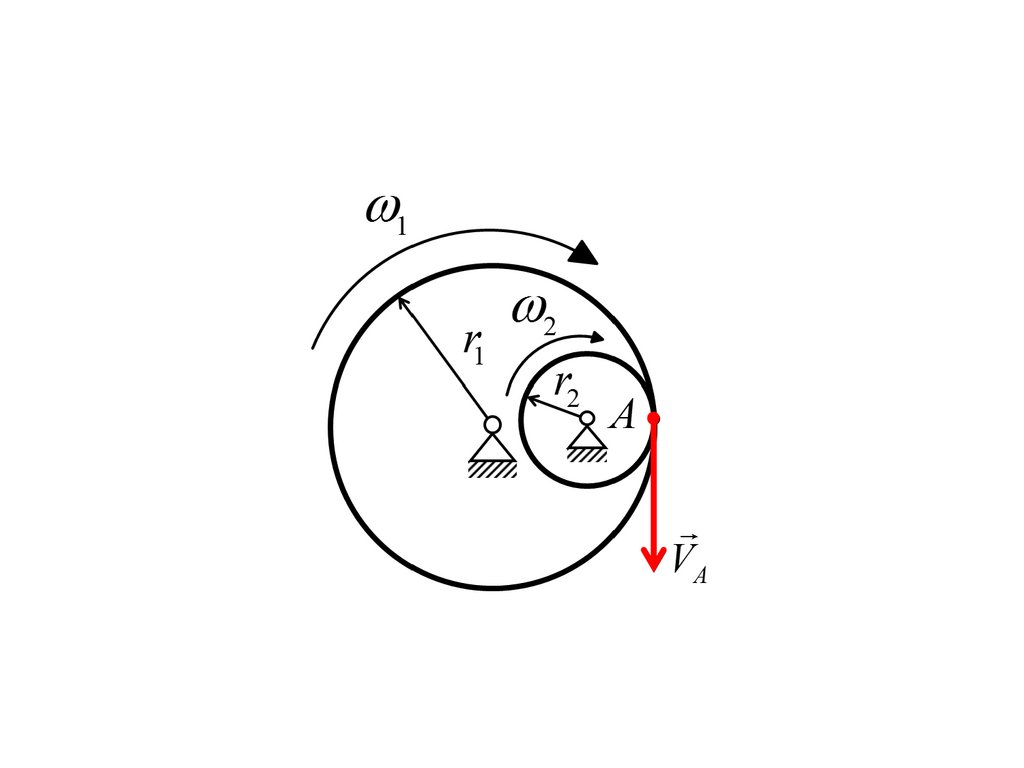
1r1
VA
2
r2
A
VA = 1 r1 = 2 r2
1 , 2
r1 , r2
z1 , z2
d1 , d 2
1 r2 z2 d 2
= =
=
= i12 .
2 r1 z1 d1
1 r2 z2
= =
= i12
2 r1 z1
Число зубьев колеса
z пропорционально радиуса колеса r .
50.
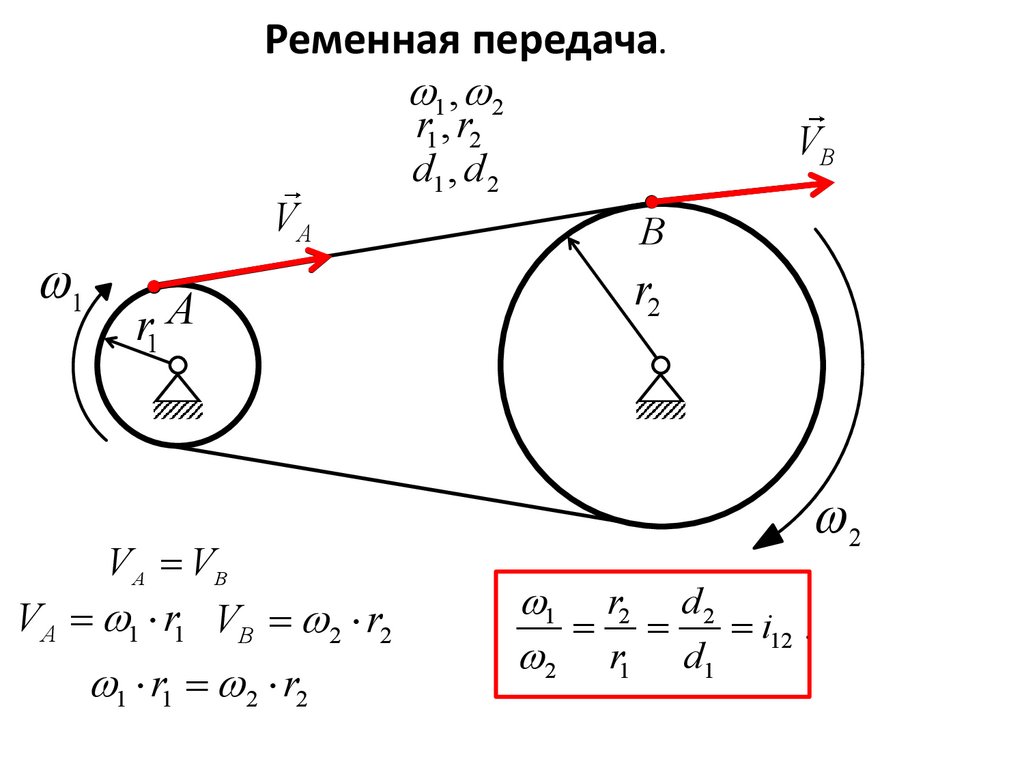
51.
Ременная передача.1 , 2
r1 , r2
d1 , d 2
1
VA
rA
VВ
B
r2
1
V A = VB
VA = 1 r1 VB = 2 r2
1 r1 = 2 r2
2
1 r2 d 2
= =
= i12 .
2 r1 d1
52.
Фрикционная передача.1
2
1 R2
=
= i1 2
2 R1
Если оси ведущего и ведомого валов пересекаются, то вращение можно
передать с помощью фрикционной передачи.
53.
Спасибоза
внимание !
































 physics
physics








