Similar presentations:
Основнi спiввiдношення мiж тригонометричними функцiями одного аргумента
1. ОСНОВНI СПIВВIДНОШЕННЯ МIЖ ТРИГОНОМЕТРИЧНИМИ ФУНКЦIЯМИ ОДНОГО АРГУМЕНТА
2. Виконання усних вправ
1. Знайдiть значення виразу:2
3
б) 1 ;
5
25
а) 1
;
169
в ) 1 0,6 .
2
3. 2. Виразiть змiнну a iз формули:
ab
а) ab 1; б ) c; в) d ;
b
a
2
2
г ) a b 1;
1
д) 1 a 2 ;
c
2
1
е) 1 b 2 .
a
2
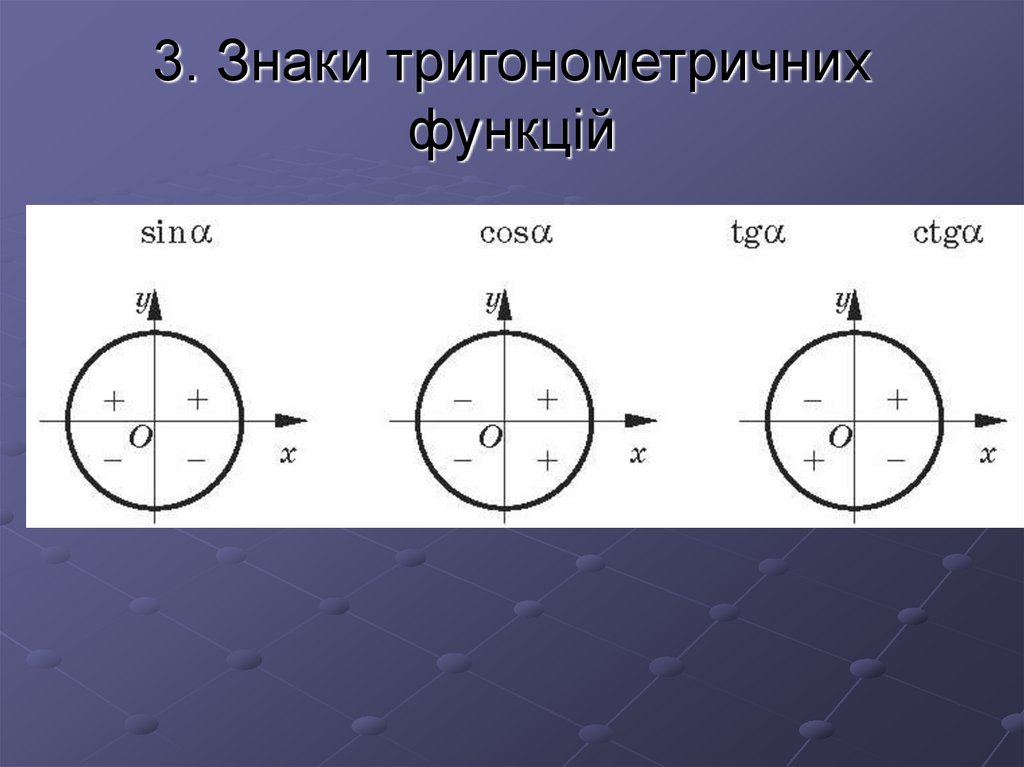
4. 3. Знаки тригонометричних функцій
5.
4. Виконайте дiї:а) a b ;
б ) m n .
2
2
5. Подайте у виглядi квадрата:
а ) b 2bc c ;
2
2
б ) p 2 pq q .
2
2
6. 6. Спростiть вираз:
а) x y x y ;б ) t 1 1 t ;
в) a b a b .
2
2
7. Спiввiдношення мiж тригонометричними функцiями одного аргумента
sin cos 12
2
sin
tg
cos
cos
ctg
sin
1
2
1 tg
2
cos
1
2
tg ctg 1
1 ctg
2
sin
8.
ЕйлерЛеонард
(1707– 1783)
видатний
математик
XVIII
сторіччя
9. Виконання усних вправ
1. Виразiть: а ) cos через sin ;б ) ctg через tg ; в) sin через tg i cos ;
г ) cos через sin i tg .
2
2
2. Знайдiть значення виразу:
19
19
а ) sin 625 cos 625 ; б ) tg
сtg
.
3
3
1
3. Вiдомо, що cos .
3
Знайдiть значення виразу 1 tg 2 .
2
2
10. 4. Обчислiть значення виразу
1 ctg ,2
якщо вiдомо, що
sin 0,5.
5. Порiвняйте:
2
2
а) sin cos
і 0,4;
3
3
б ) tg140 ctg140 і 1,2.
6. Знайдiть ctg x, якщо tg x дорівнює
1
1,1 , 4,5.
3


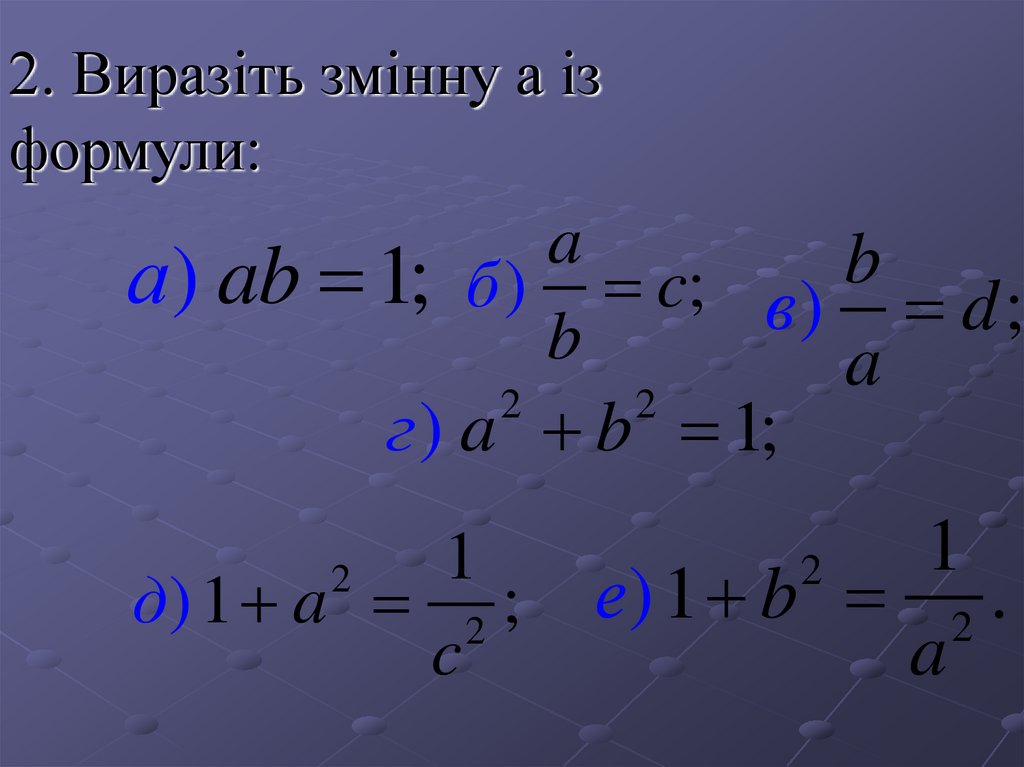







 mathematics
mathematics








