Similar presentations:
Визначення вихідних інструментальних поверхонь
1. Визначення вихідних інструментальних поверхонь
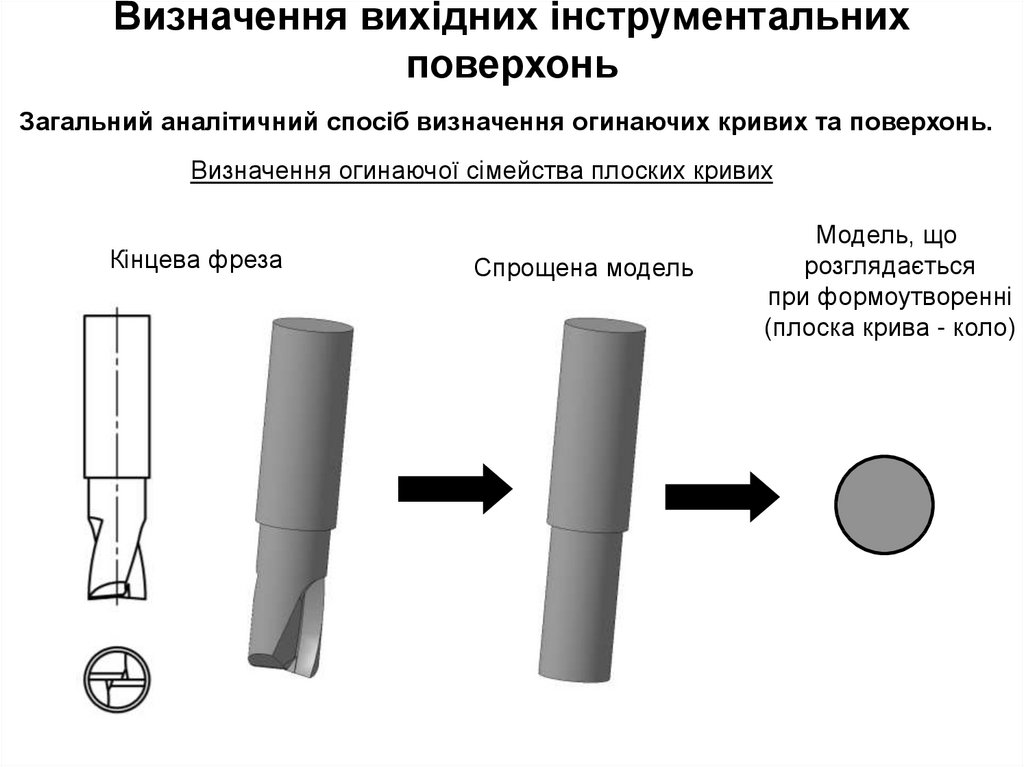
Загальний аналітичний спосіб визначення огинаючих кривих та поверхонь.Визначення огинаючої сімейства плоских кривих
Кінцева фреза
Спрощена модель
Модель, що
розглядається
при формоутворенні
(плоска крива - коло)
2.
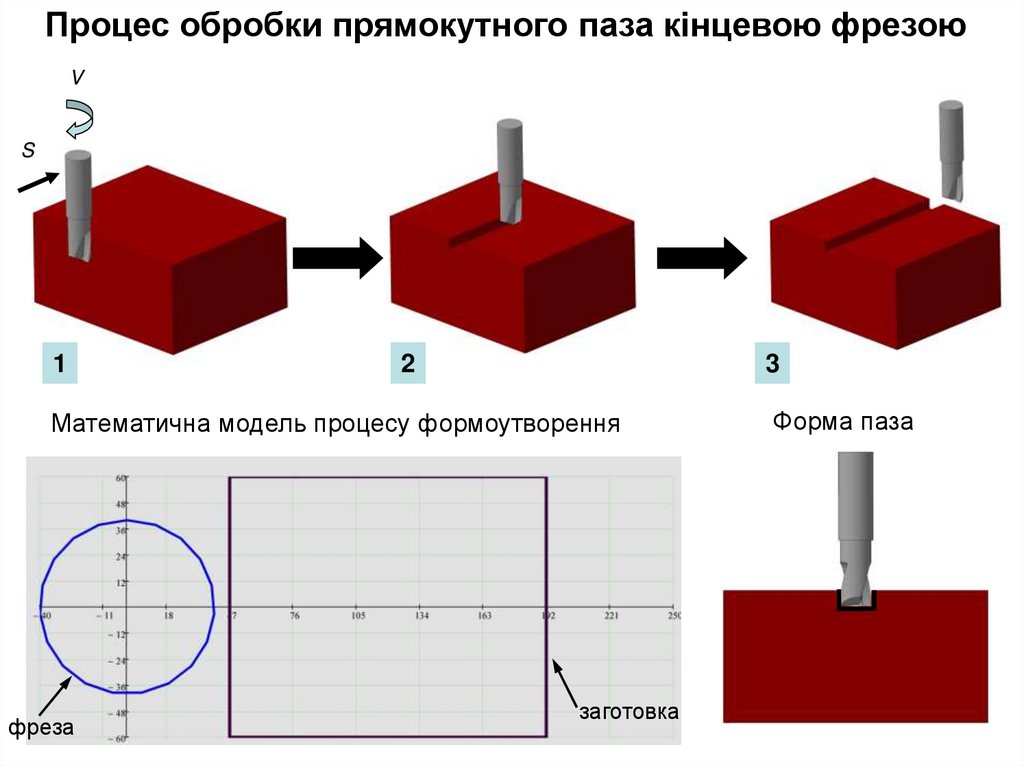
Процес обробки прямокутного паза кінцевою фрезоюV
S
1
2
3
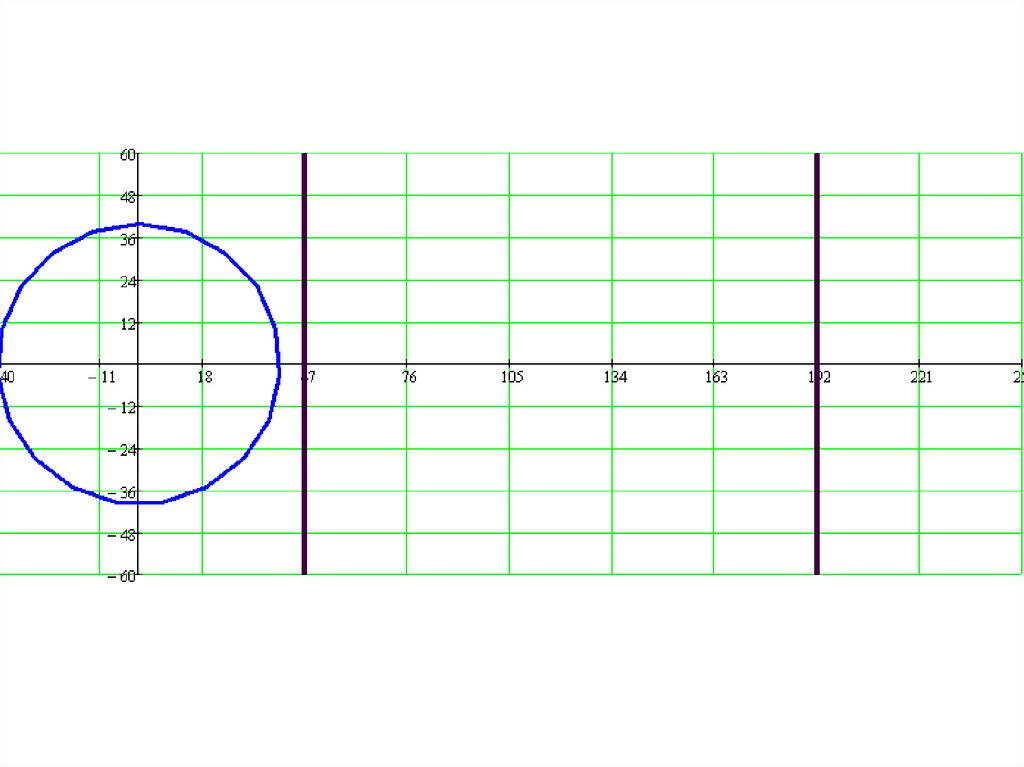
Математична модель процесу формоутворення
фреза
заготовка
Форма паза
3.
4.
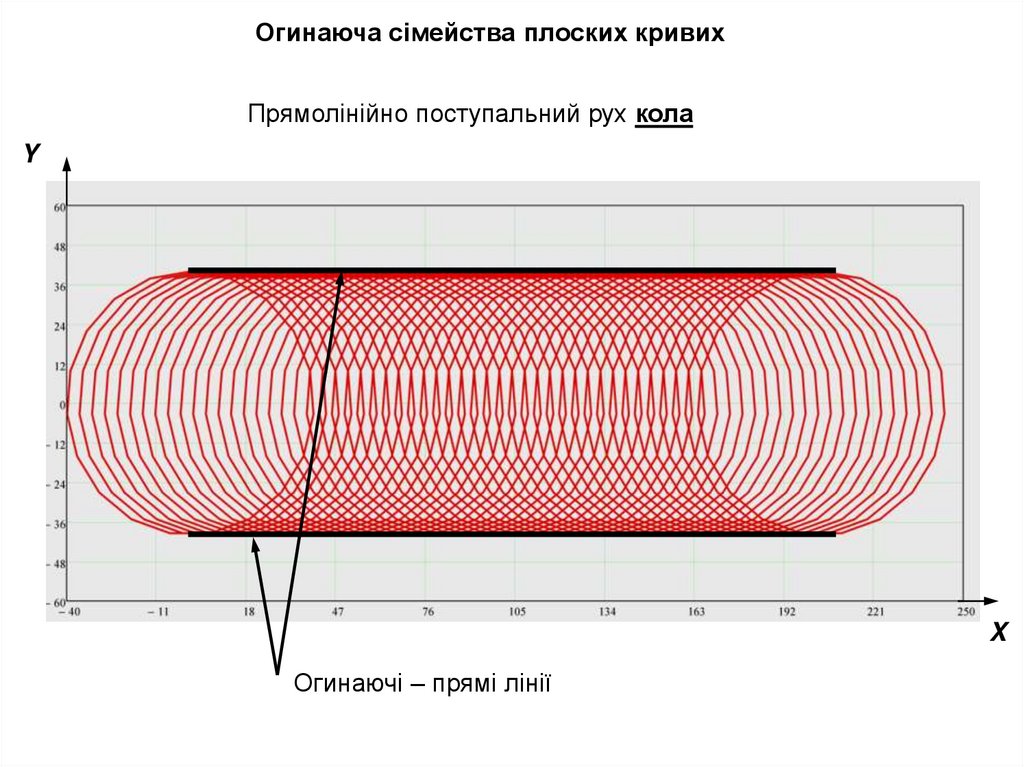
Огинаюча сімейства плоских кривихПрямолінійно поступальний рух кола
Y
X
Огинаючі – прямі лінії
5.
Сімейство кривих, яке залежить від параметру t:f ( x, y , t ) 0
Огинаюча сімейства кривих, яке залежить від параметру t:
f ( x, y , t ) 0
f ( x, y, t )
0
t
Приклад 1. Огинаюча сімейства кіл:
( x t )2 y 2 R2
Система рівнянь для визначення огинаючої:
( x t ) 2 y 2 R 2
x t y R
2( x t ) 0
6.
Сімейство кривих (задано параметричними рівняннями),яке залежить від параметру t :
x f1 (t , c); y f 2 (t , c)
Огинаюча сімейства кривих, яке залежить від параметру t:
x f1 (t , c );
y f 2 (t , c);
x
t
x
c
y
t 0
y
c
7.
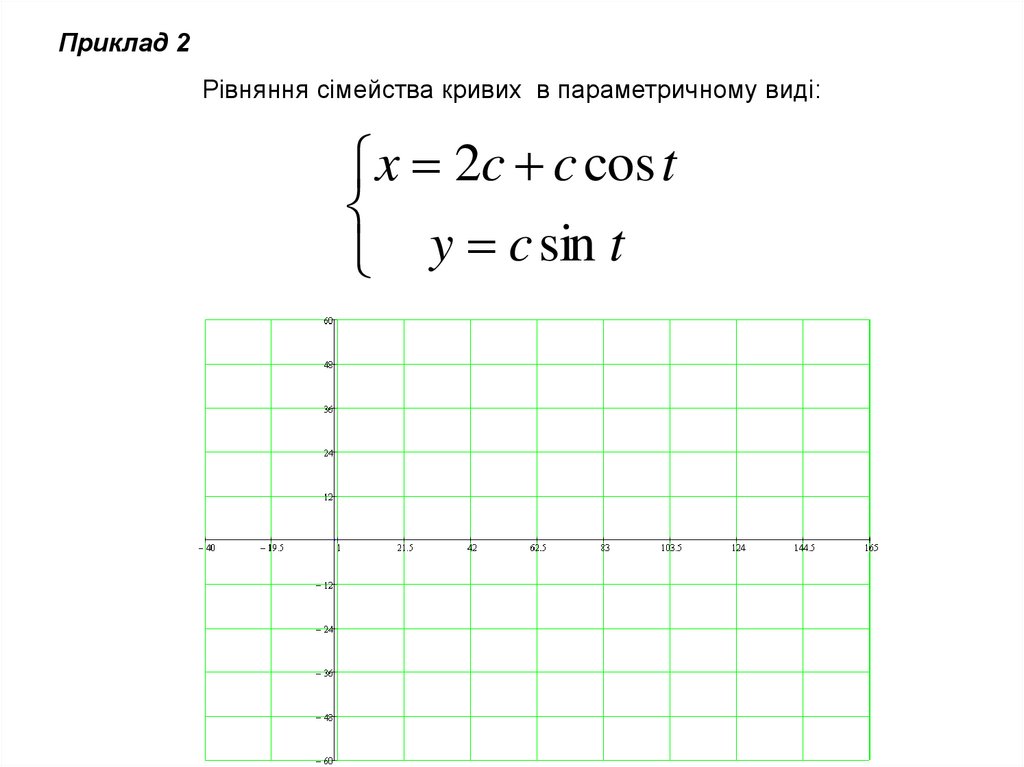
Приклад 2Рівняння сімейства кривих в параметричному виді:
x 2c c cos t
y c sin t
8.
x y (2c c cos t ) (c sin t )c sin t c cos t
t t
t
t
0
x y (2c c cos t ) (c sin t ) 2 cos t sin t
c c
c
c
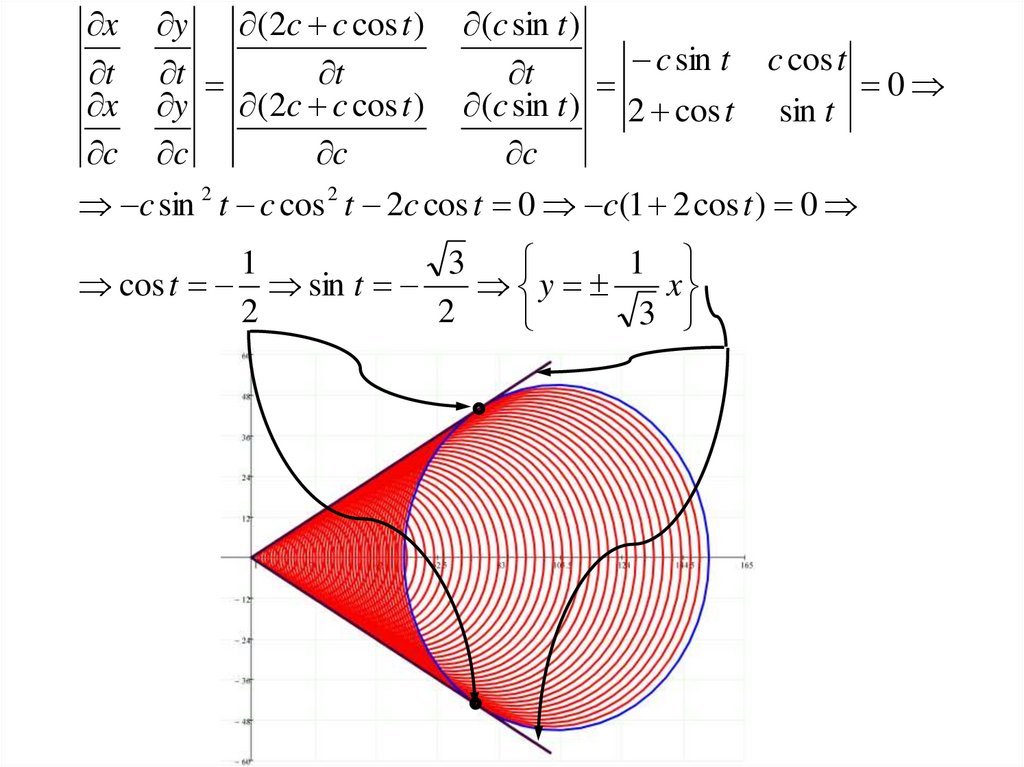
c sin 2 t c cos 2 t 2c cos t 0 c(1 2 cos t ) 0
1
3
1
cos t sin t
y
x
2
2
3
9.
10.
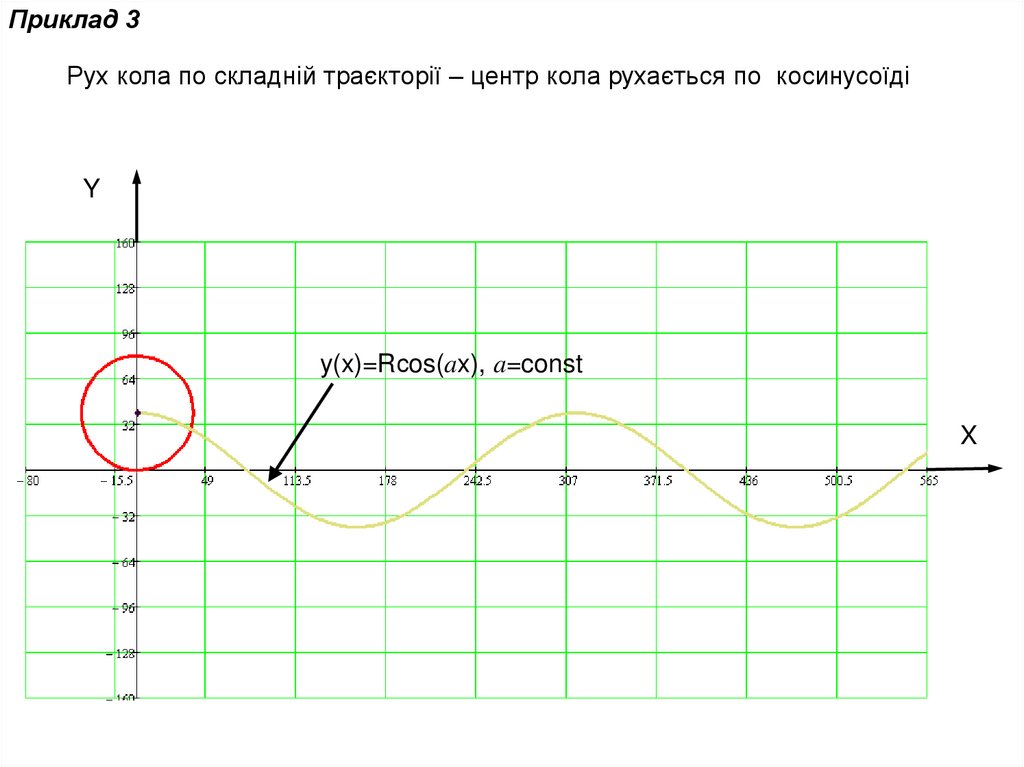
Приклад 3Рух кола по складній траєкторії – центр кола рухається по косинусоїді
Y
y(x)=Rсos(ax), a=const
X
11.
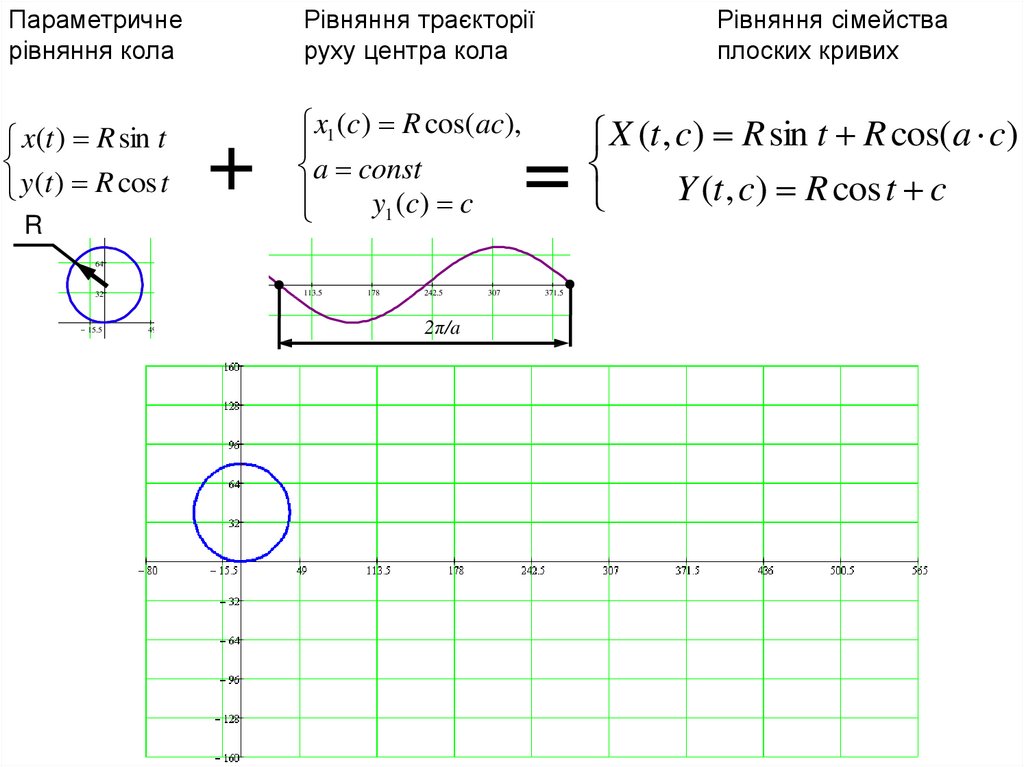
Параметричнерівняння кола
x(t ) R sin t
y (t ) R cos t
Рівняння траєкторії
руху центра кола
160
160
128
160
160
R
+
64
=
X (t , c) R sin t R cos( a c)
Y (t , c) R cos t c
96
32
64
yr21
yr71
32
yr61
r31
80
15.5
r21
r41
96
128
x1 (c) R cos( ac),
a const
y1 (c) c
Рівняння сімейства
плоских кривих
49
113.5
178
242.5
32
80
15.5
49
r51
113.5
178
242.5
307
371.5
2π/a
307
371.5
436
436
500.5
500.5
565
565
64
32
96
64
128
96
160
160
128
80
160
xr21 xr71 xr61
565
160
80
xr31 xr21 xr41 xr51
565
12.
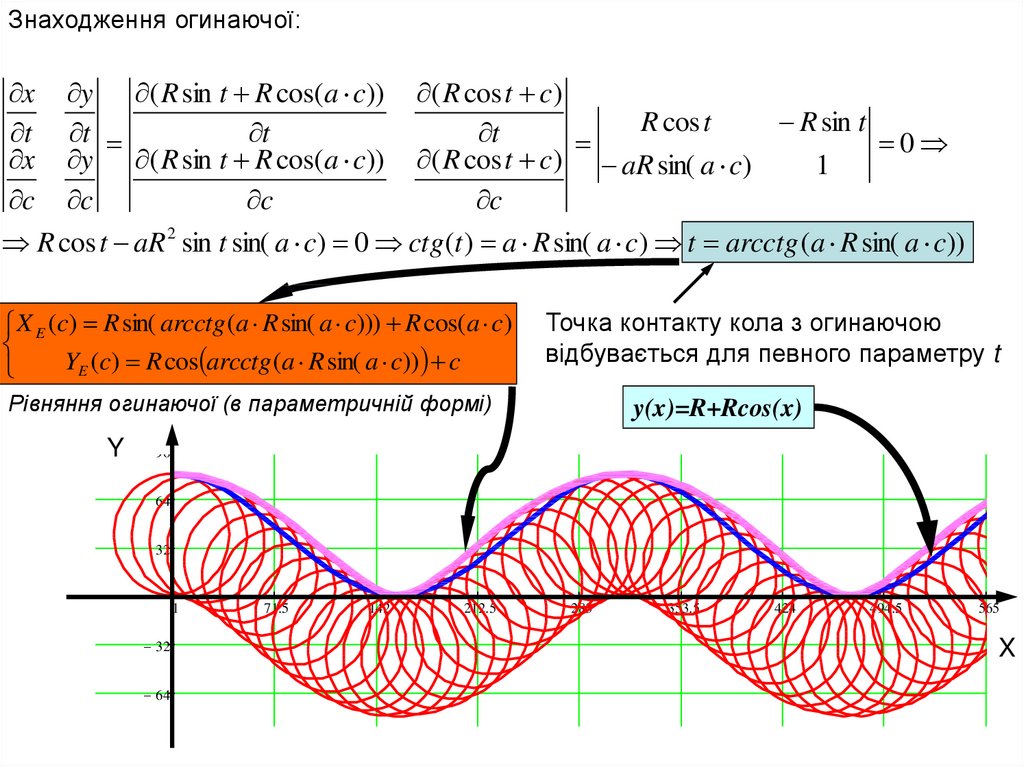
Знаходження огинаючої:x y ( R sin t R cos( a c)) ( R cos t c)
R cos t
R sin t
t t
t
t
0
x y ( R sin t R cos( a c)) ( R cos t c) aR sin( a c)
1
c c
c
c
R cos t aR 2 sin t sin( a c) 0 ctg (t ) a R sin( a c) t arcctg (a R sin( a c))
X E (c) R sin( arcctg (a R sin( a c))) R cos(a c)
160
YE (c) R
cos arcctg (a R sin( a c)) c
Точка контакту кола з огинаючою
відбувається для певного параметру t
128
Рівняння огинаючої
(в параметричній формі)
Y
y(x)=R+Rcos(x)
96
64
32
69.5
1
32
64
96
71.5
142
212.5
283
353.5
424
494.5
565
X
13.
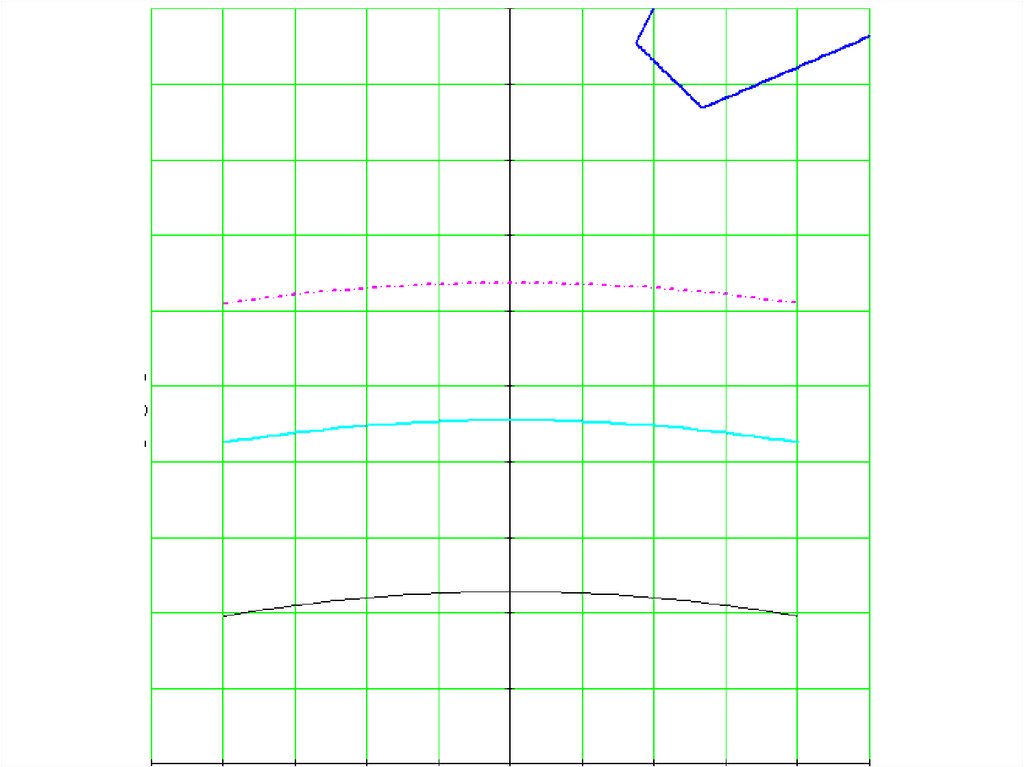
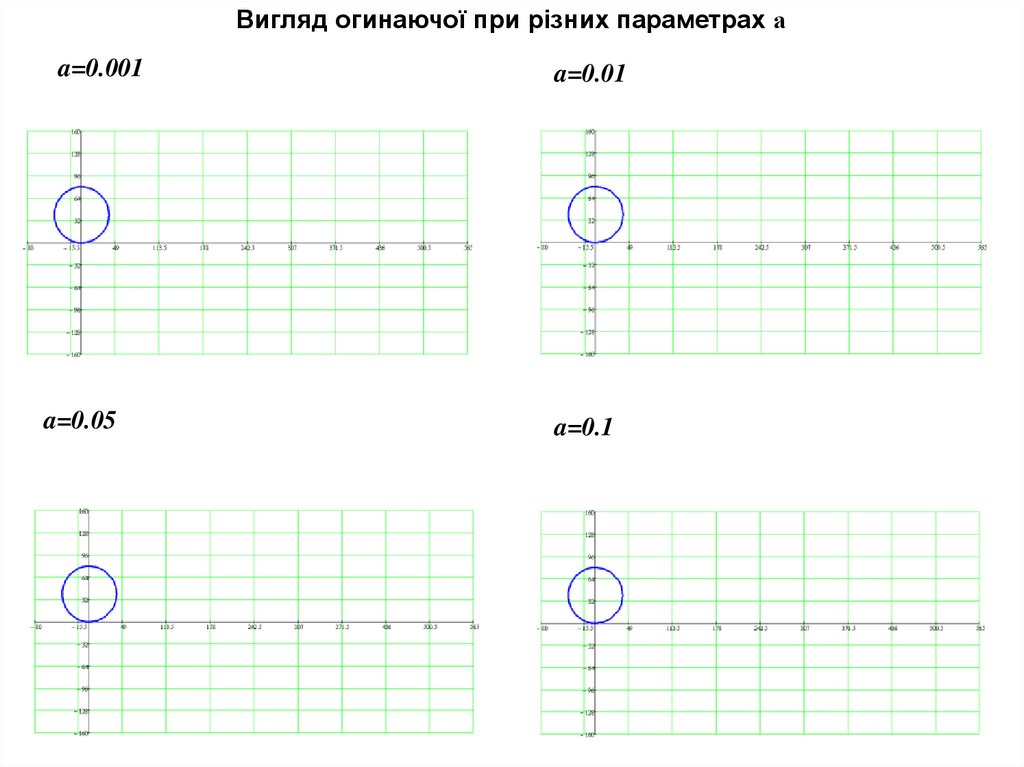
Вигляд огинаючої при різних параметрах аa=0.001
a=0.05
a=0.01
a=0.1
14.
Визначення огинаючої сімейства поверхоньСімейство поверхонь, яке залежить від параметру t:
f ( x, y , z , t ) 0
Огинаюча сімейства поверхонь, яке залежить від параметру t:
f ( x, y , z , t ) 0
f ( x, y, z, t )
0
t
f ( x, y, z , t )
0
t
Рівняння визначає характеристику –
лінію контакту поверхні з огинаючою
15.
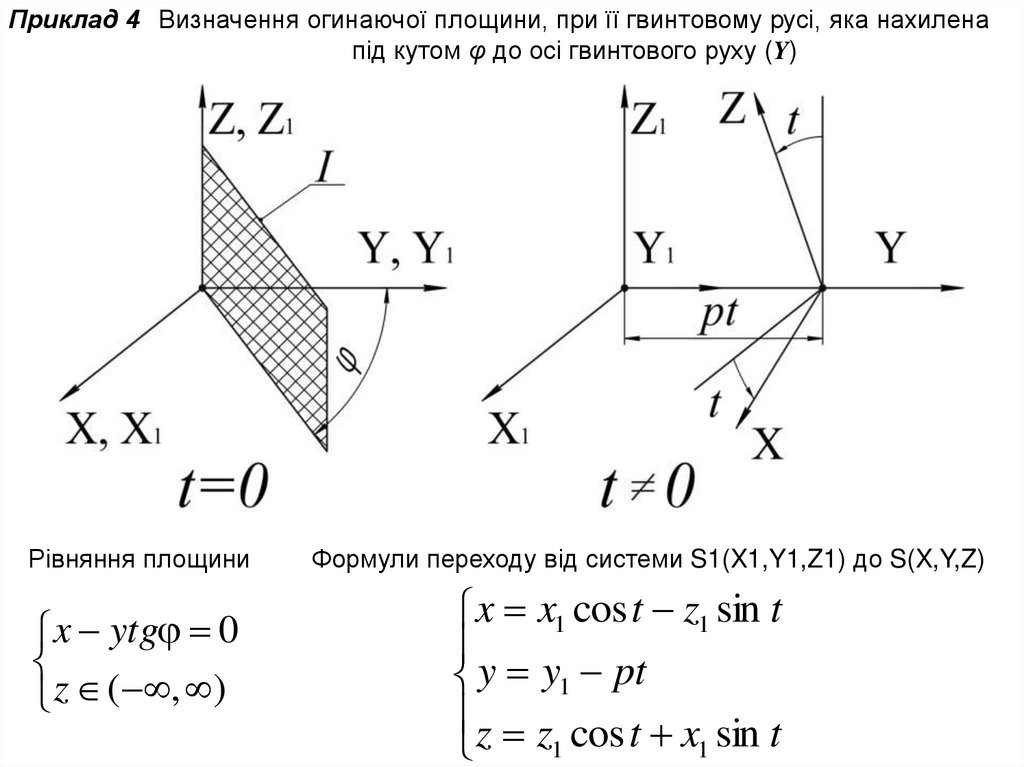
Приклад 4 Визначення огинаючої площини, при її гвинтовому русі, яка нахиленапід кутом φ до осі гвинтового руху (Y)
Рівняння площини
x ytg 0
z ( , )
Формули переходу від системи S1(X1,Y1,Z1) до S(X,Y,Z)
x x1 cos t z1 sin t
y y1 pt
z z cos t x sin t
1
1
16.
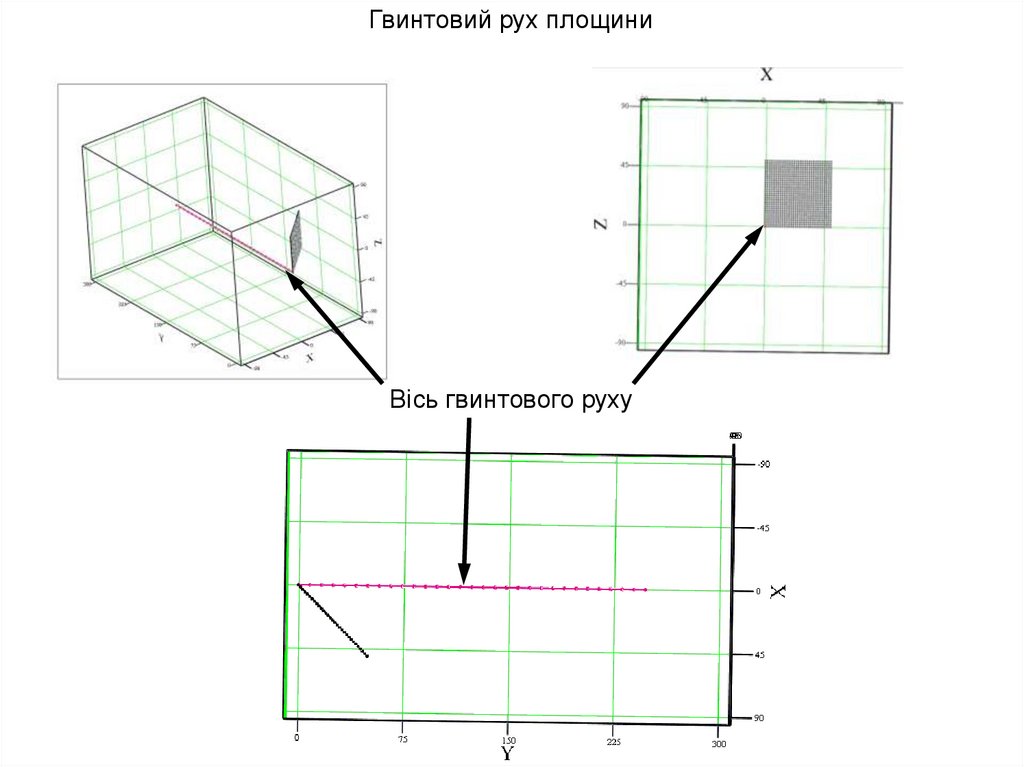
Гвинтовий рух площиниВісь гвинтового руху
17.
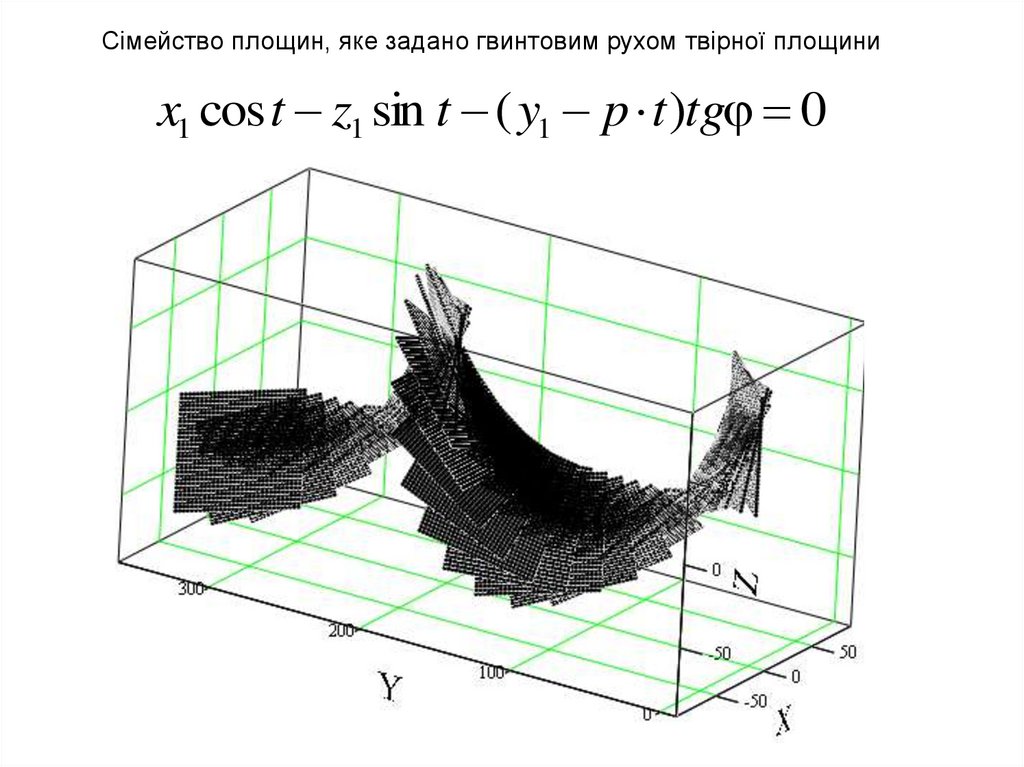
Сімейство площин, яке задано гвинтовим рухом твірної площиниx1 cos t z1 sin t ( y1 p t )tg 0
18.
f ( x, y, z , t )0
t
( x1 cos t z1 sin t ( y1 p t )tg )
0
t
Огинаюча визначиться системою рівнянь
f ( x, y, z , t ) x1 cos t z1 sin t ( y1 p t )tg 0
f ( x, y, z , t )
x1 sin t z1 cos t p tg 0
t
Торцевий переріз огинаючої площиною Y1=0
x1 cos t z1 sin t p t tg 0
x1 sin t z1 cos t p tg 0
z1 ptg cos t ptg t sin t
x1 ptg sin t ptg t cos t
rB ptg
sin t cos t
cos t sin t
- параметричне рівняння евольвенти
- радіус основного кола
19.
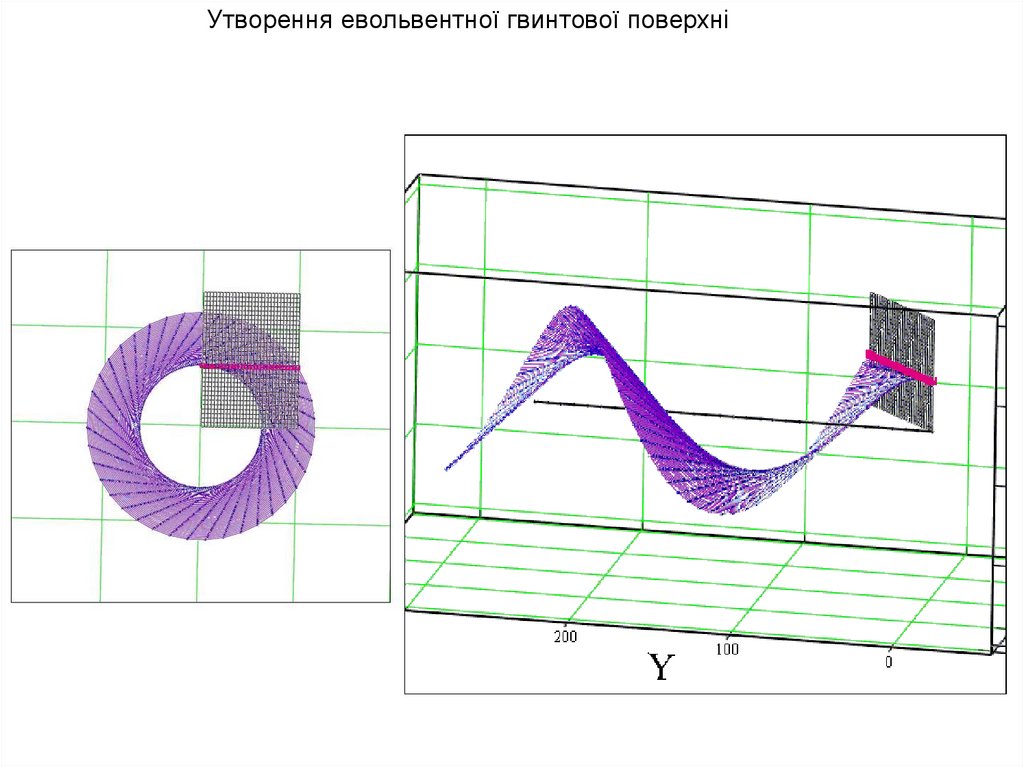
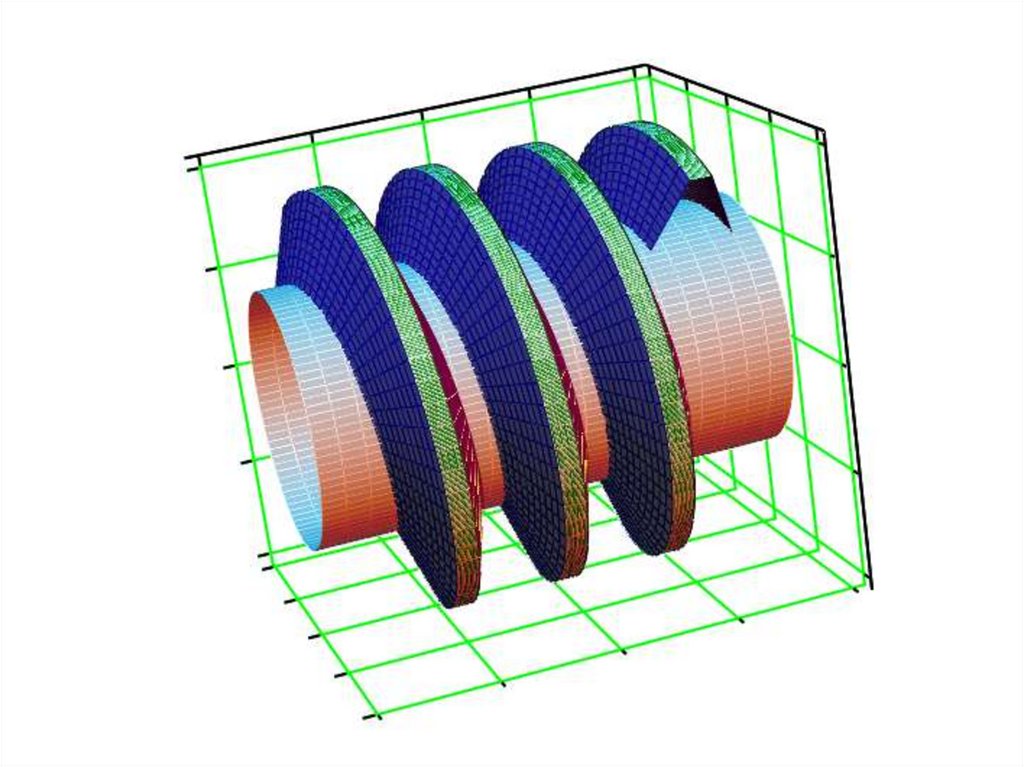
Утворення евольвентної гвинтової поверхні20.
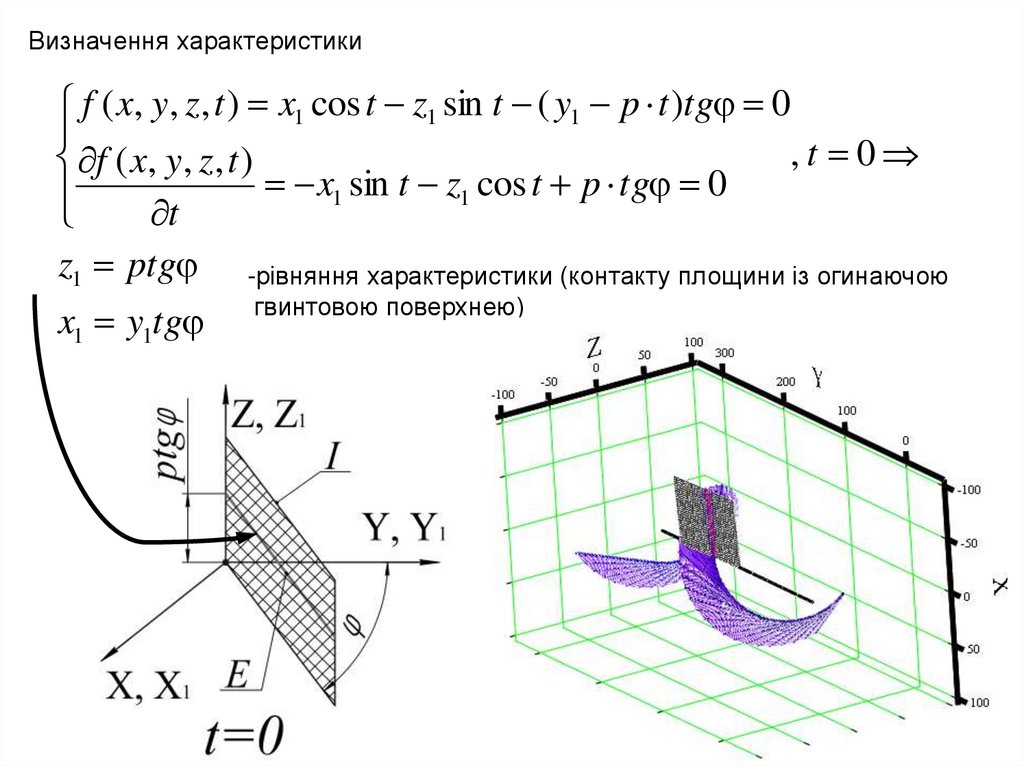
Визначення характеристикиf ( x, y, z , t ) x1 cos t z1 sin t ( y1 p t )tg 0
,t 0
f ( x, y, z , t )
x1 sin t z1 cos t p tg 0
t
z1 ptg -рівняння характеристики (контакту площини із огинаючою
x1 y1tg
гвинтовою поверхнею)
21.
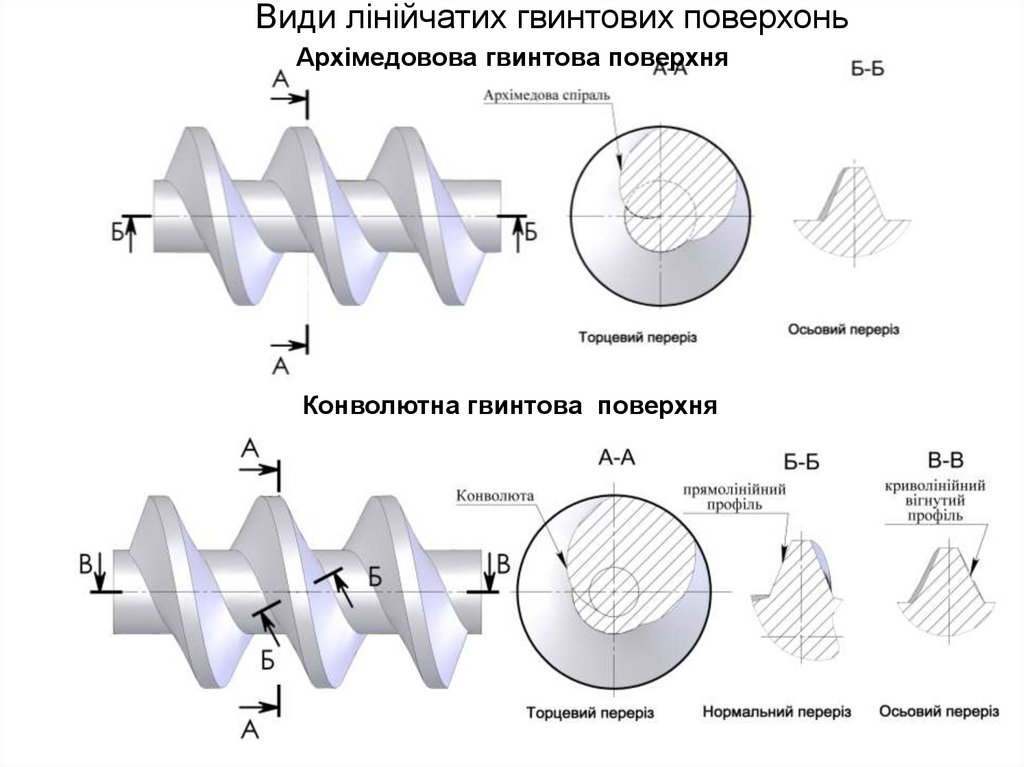
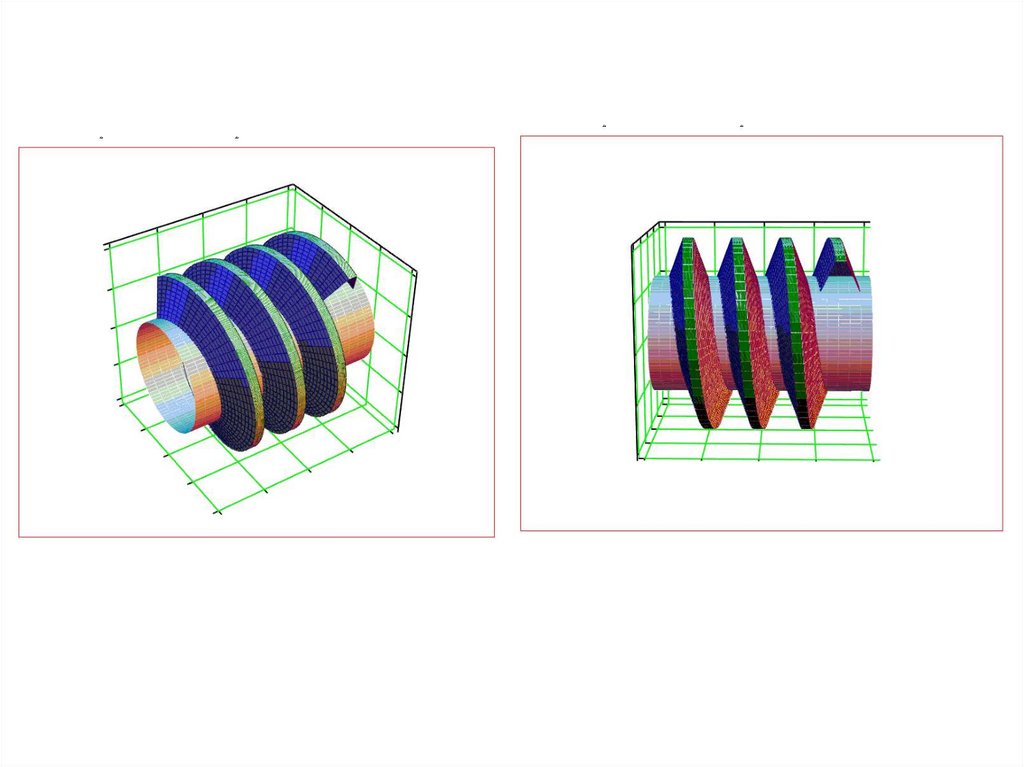
Види лінійчатих гвинтових поверхоньАрхімедовова гвинтова поверхня
Конволютна гвинтова поверхня
22.
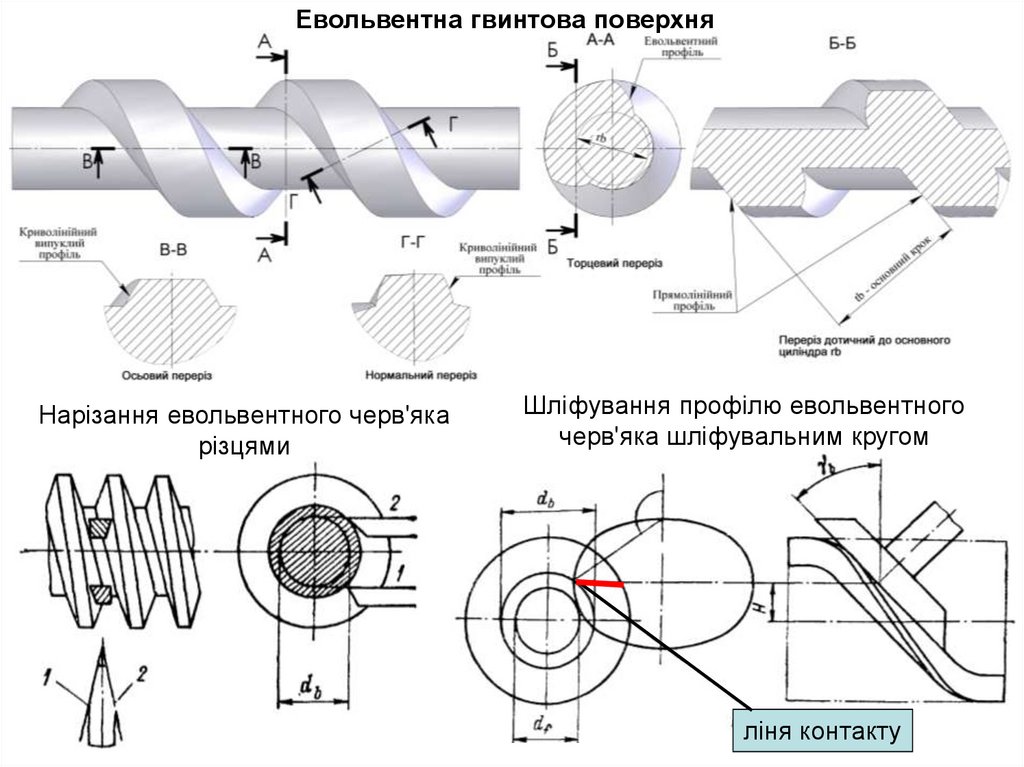
Евольвентна гвинтова поверхняНарізання евольвентного черв'яка
різцями
Шліфування профілю евольвентного
черв'яка шліфувальним кругом
ліня контакту
23.
Сімейство поверхонь (задано параметричними рівняннями),яке залежить від параметру с :
x f1 (t , u, c);
y f 2 (t , u, c); z f 3 (t , u, c)
Огинаюча сімейства поверхонь, яке залежить від параметру с:
x f1 (t , u , c);
y f 2 (t , u , c);
z f 3 (t , u , c);
x
t
x
u
x
c
y
t
y
u
y
c
z
t
z
0
u
z
c
24.
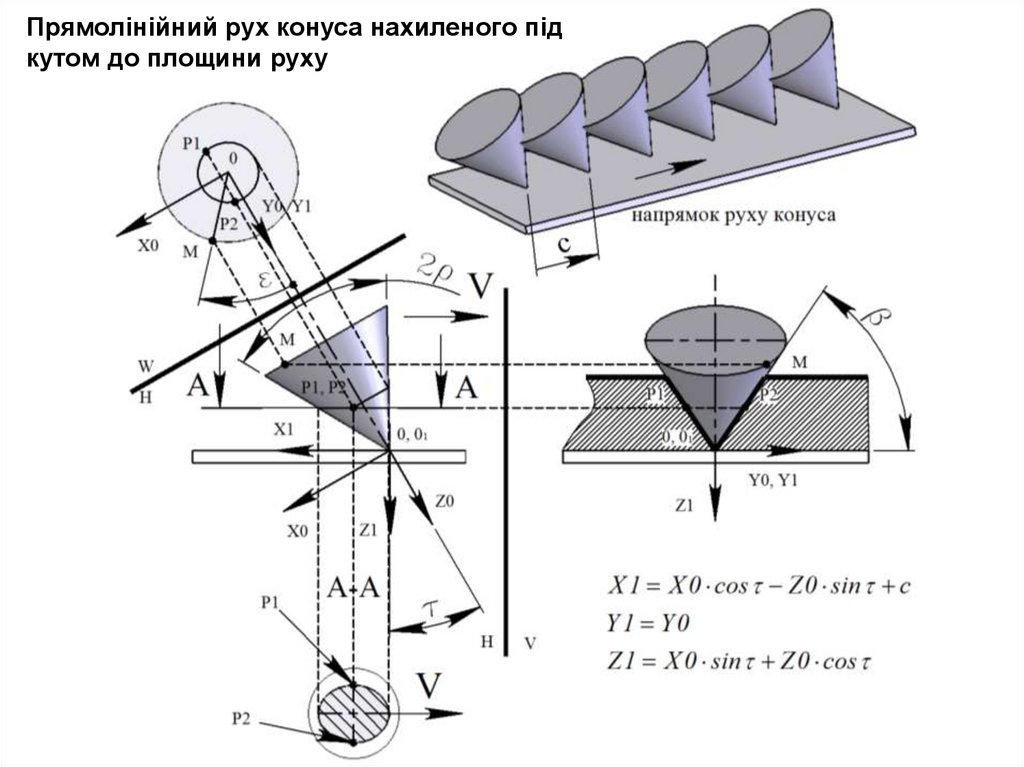
Прямолінійний рух конуса нахиленого підкутом до площини руху
25.
Рівняння поверхні конуса в системі S(X0,Y0,Z0) заданих в параметричній форміx0 (l , ) l sin
y0 (l , ) l cos
z0 (l ) lctg
Рівняння сімейств поверхонь конусів в системі S1(X1,Y1,Z1)
x1 l sin cos lctg sin c
y1 l cos
z1 l sin sin lctg cos
Визначення огинаючої до сімейства поверхонь конусів в системі S1(X1,Y1,Z1)
x1
c
x1
l
x1
y1 z1
c c
y1 z1
0 l cos 2 sin l sin 2 sin l sin ctg cos 0
l
l
y1 z1
sin tg tg
26.
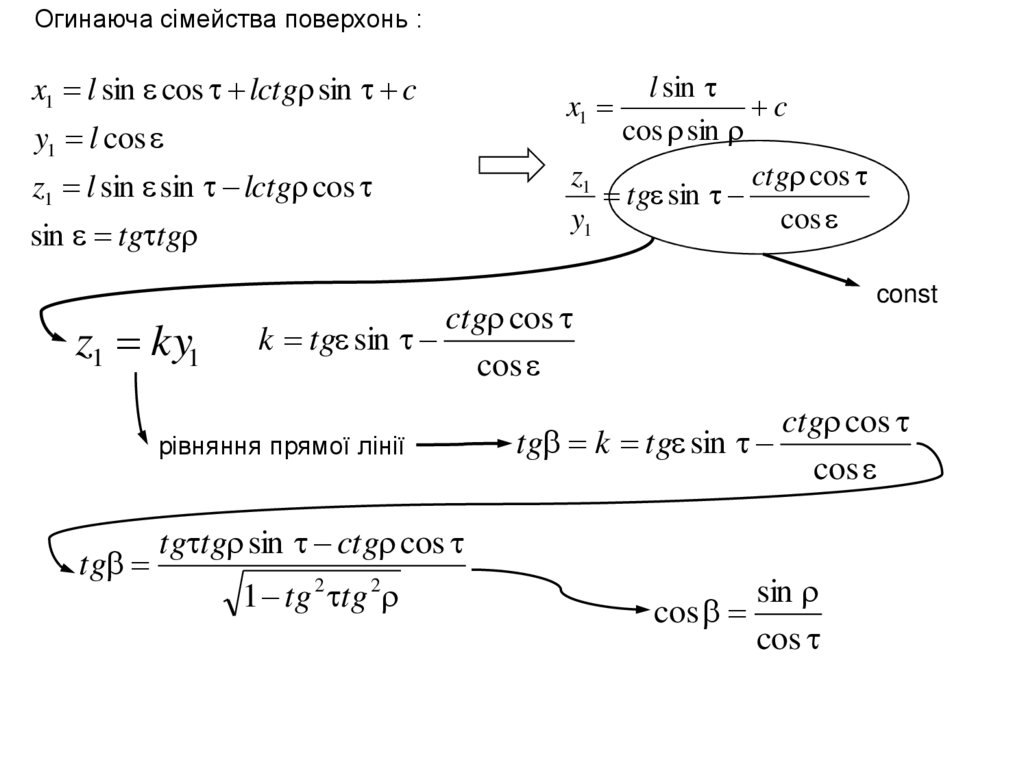
Огинаюча сімейства поверхонь :x1 l sin cos lctg sin c
y1 l cos
z1 l sin sin lctg cos
sin tg tg
z1 ky1
const
ctg cos
k tg sin
cos
рівняння прямої лінії
tg
l sin
c
cos sin
z1
ctg cos
tg sin
y1
cos
x1
ctg cos
tg k tg sin
cos
tg tg sin ctg cos
1 tg 2 tg 2
sin
cos
cos
27.
Графічне визначення огинаючихВизначення огинаючої при обертанні площини І навколо похилої осі O
28.
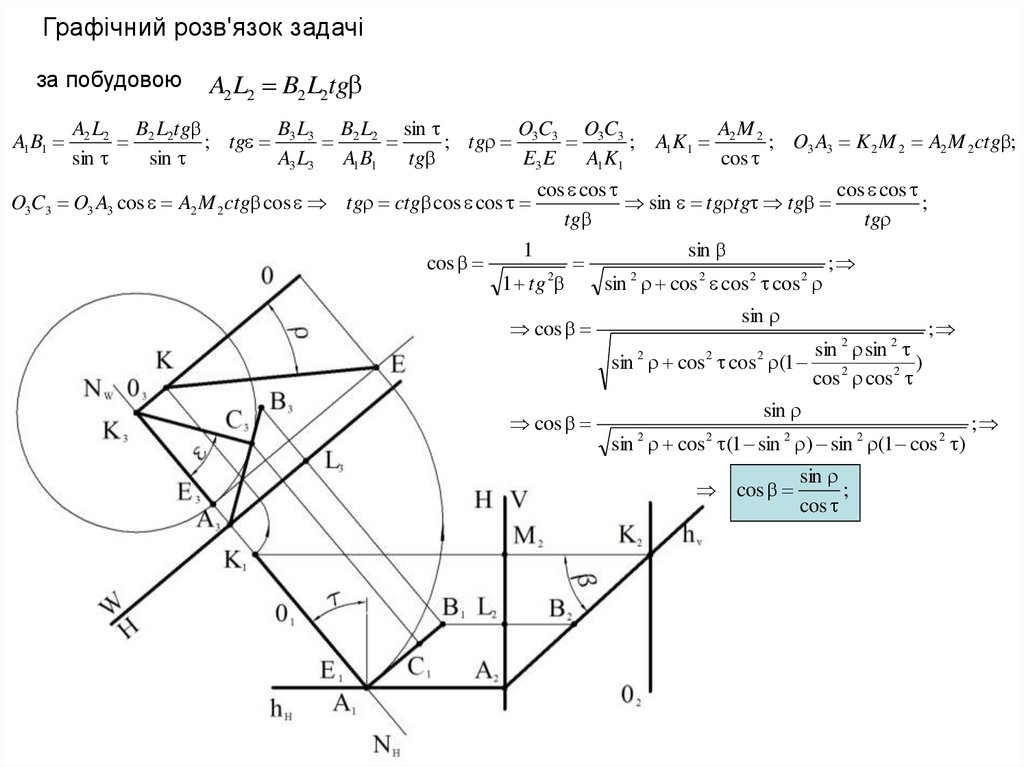
Графічний розв'язок задачіза побудовою
A1 B1
A2 L2 B2 L2tg
BL
OC
OC
A2 L2 B2 L2tg
BL
sin
; tg 3 3 2 2
; tg 3 3 3 3 ;
sin
sin
A3 L3 A1 B1
tg
E3 E
A1 K1
A1 K1
A2 M 2
; O3 A3 K 2 M 2 A2 M 2 ctg ;
cos
cos cos
cos cos
sin tg tg tg
;
tg
tg
1
sin
cos
;
2
2
2
2
2
1 tg
sin cos cos cos
O3C3 O3 A3 cos A2 M 2 ctg cos tg ctg cos cos
cos
cos
sin
sin 2 sin 2
sin 2 cos 2 cos 2 (1
)
cos 2 cos 2
;
sin
sin cos (1 sin ) sin (1 cos )
2
2
2
cos
2
sin
;
cos
2
;
29.
Кінематичний метод визначення огинаючої сімействаповерхонь
N V 0
- рівняння контакту
30.
Властивість загальних нормалей31.
N V N V 1 N V 2 0 N V 1 0;r
tg
p
V B V A [ BA]
tg i
ri
p
- комплекс променів гвинта
N V 2 0;
V
p ; V V 1 V 2;
V2 Vtg
l
ptg
32.
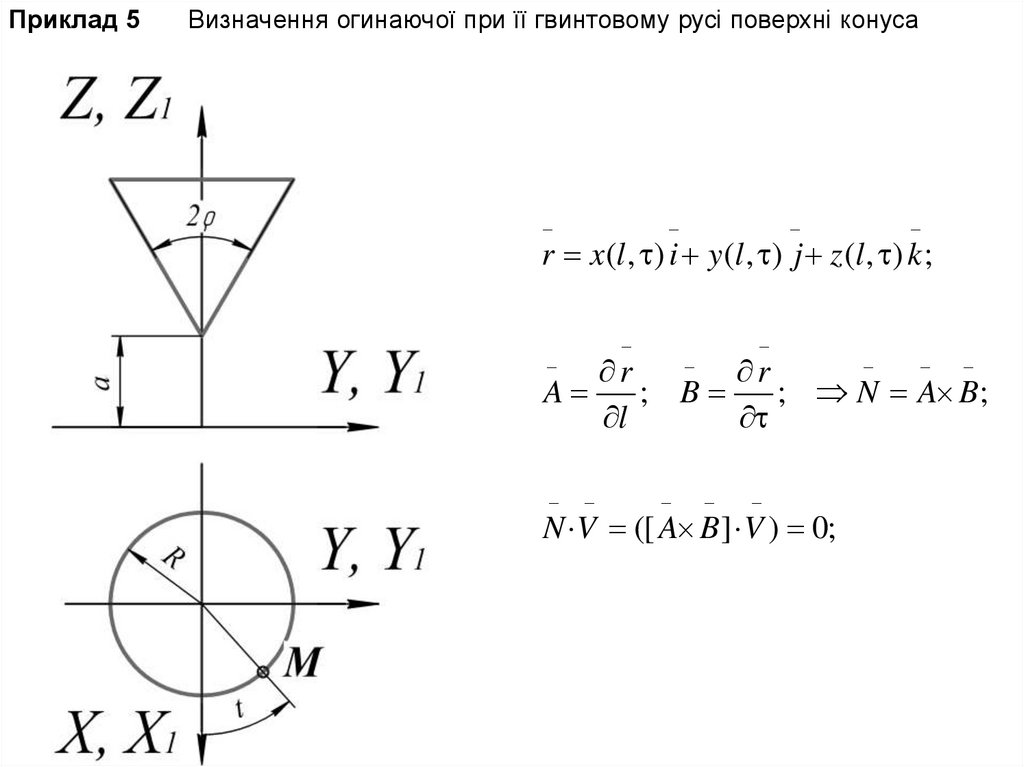
Приклад 5Визначення огинаючої при її гвинтовому русі поверхні конуса
r x(l , ) i y (l , ) j z (l , ) k ;
r
r
A
; B
; N A B;
l
N V ([ A B ] V ) 0;
33.
Рівняння поверхні конуса таДотичних до цієї поверхні;
Вектор швидкості при
гвинтовому русі;
r l cos i l sin j (lctg a) k ;
r
A
cos i sin j ctg k ;
l
r
B
l sin i l cos j;
V V p V ;
V p p j;
V r ; j;
34.
Вектор швидкості при гвинтовому русіV p j
i
j
k
0
0
;
l cos l sin lctg a
V (lctg a ) i p j l cos k ;
Рівняння контакту
l sin
l cos
0
N V ([ A B ] V ) 0
cos
sin
ctg 0
(lctg a )
p l cos
l 2 sin 2 cos p l sin ctg l 2 cos 2 cos l (lctg a )ctg cos 0
(/ lctg )
tg
l
a
;
p sin cos p
35.
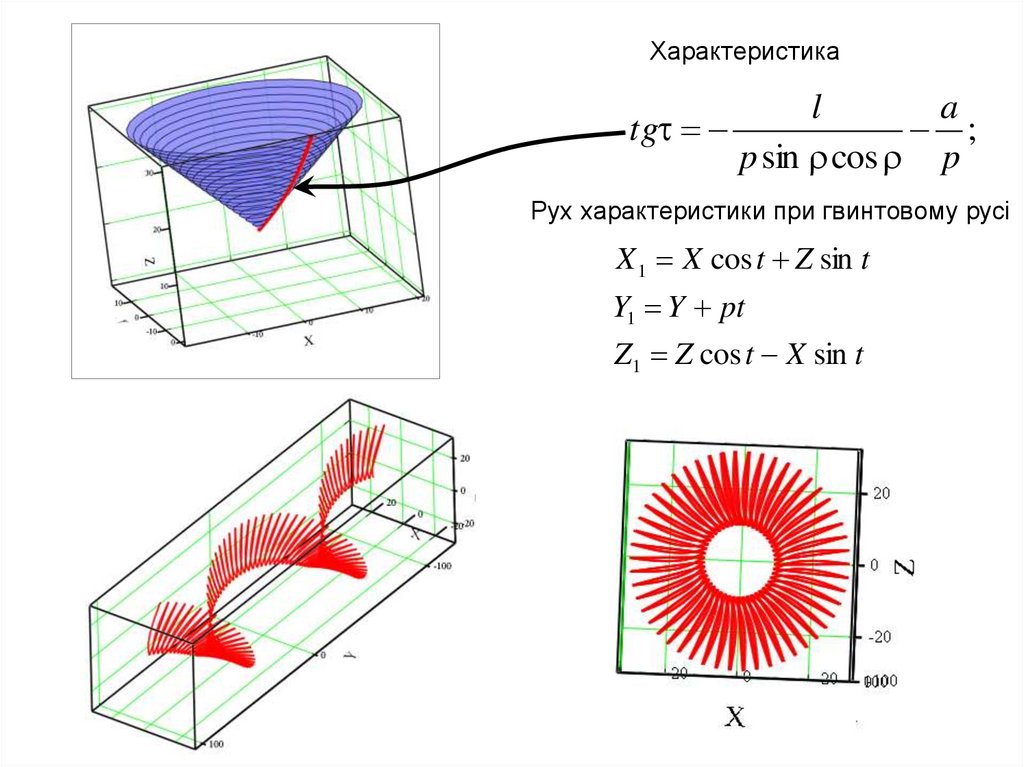
Характеристикаl
a
tg
;
p sin cos p
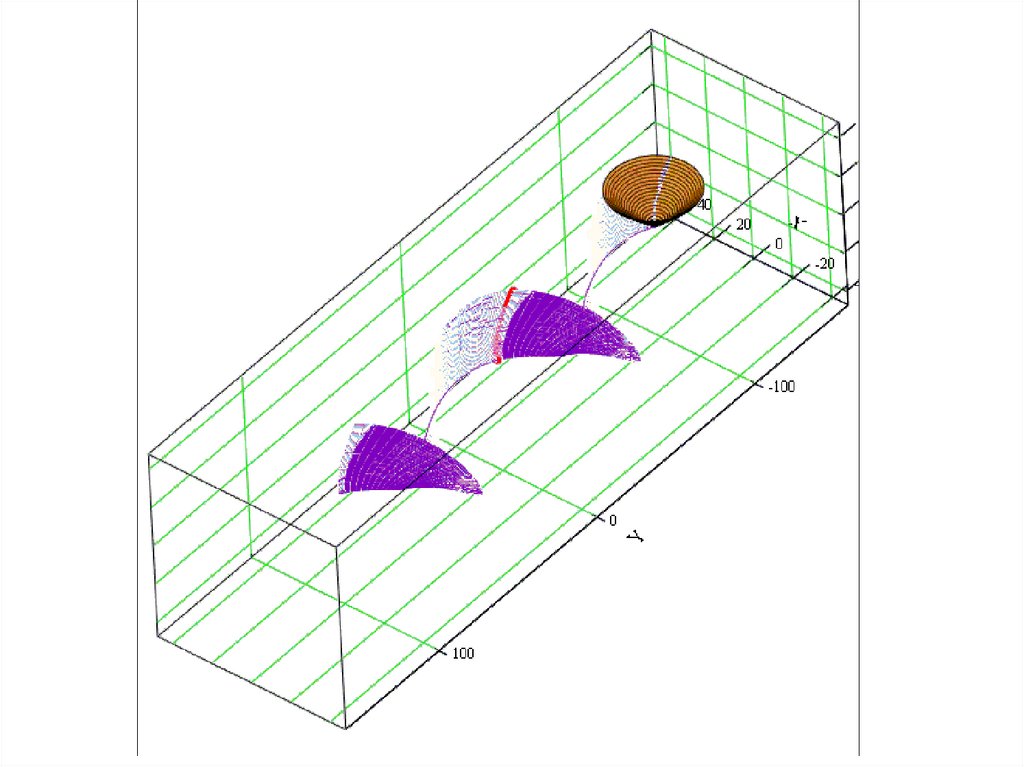
Рух характеристики при гвинтовому русі
X 1 X cos t Z sin t
Y1 Y pt
Z1 Z cos t X sin t
S2 ( xe1 ye1 ze1)
36.
37.
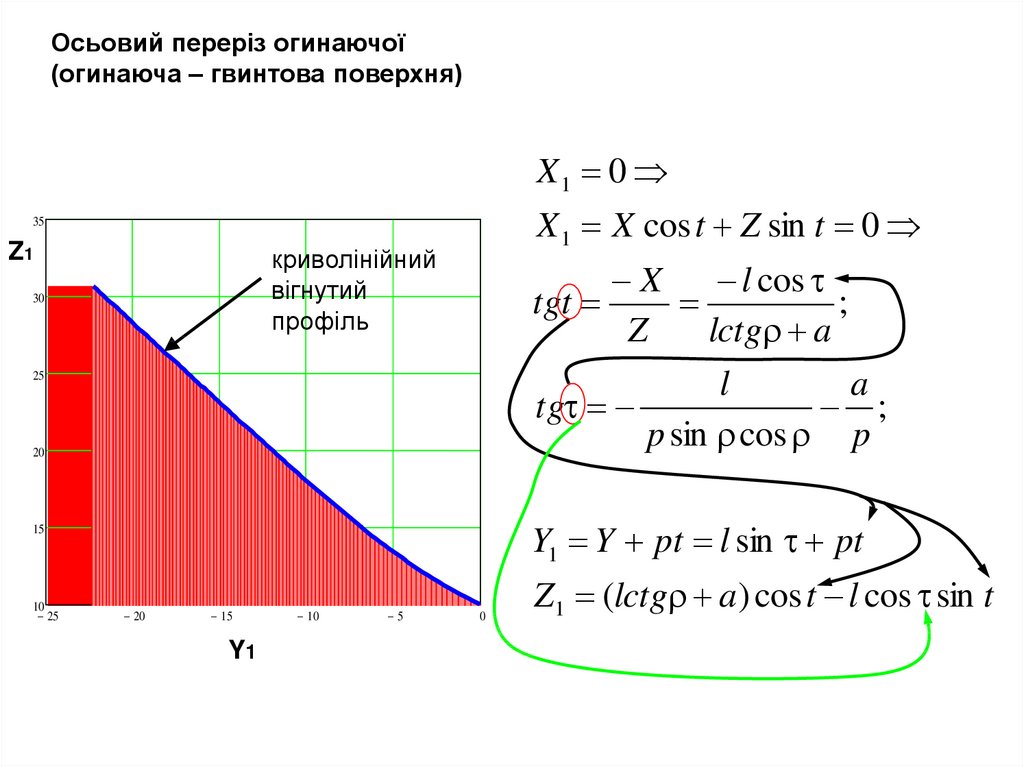
Осьовий переріз огинаючої(огинаюча – гвинтова поверхня)
X1 0
X 1 X cos t Z sin t 0
35
35
Z1
криволінійний
вігнутий
профіль
30
X
l cos
tgt
;
Z
lctg a
l
a
tg
;
p sin cos p
25
ZOS
ZOS
20
Y1 Y pt l sin pt
15
10
10
25
25
20
15
10
YOS
Y1
5
0
0
Z1 (lctg a ) cos t l cos sin t
38.
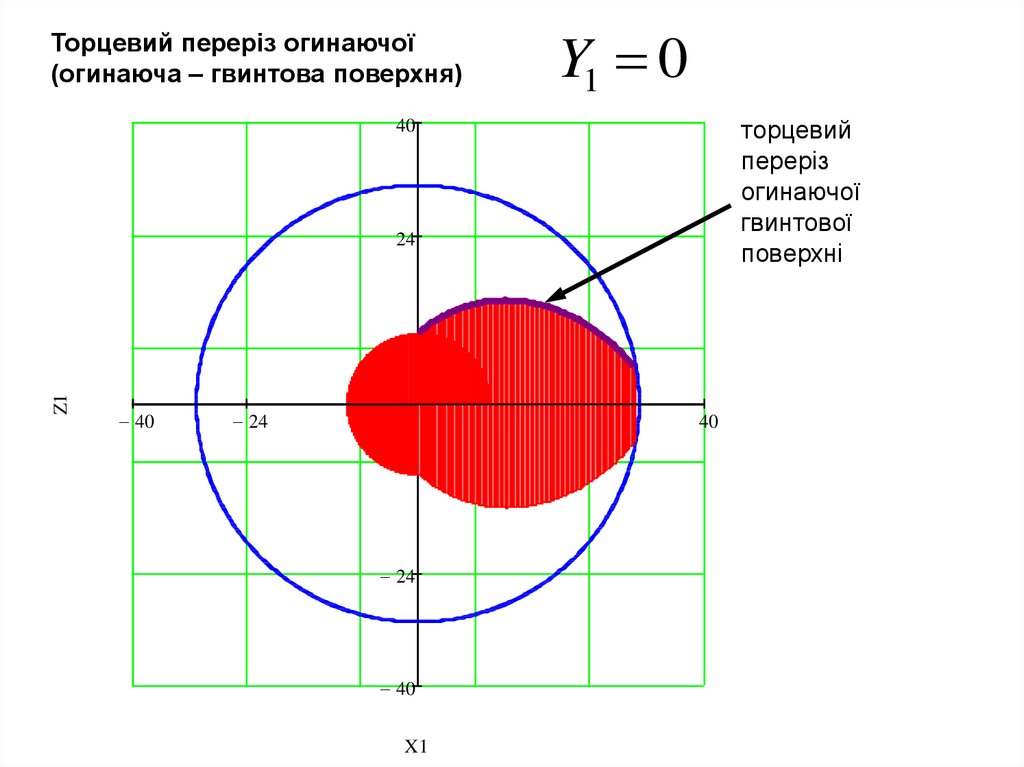
Y1 0Торцевий переріз огинаючої
(огинаюча – гвинтова поверхня)
торцевий
переріз
огинаючої
гвинтової
поверхні
40
24
Z1
8
40
24
8
8
8
24
40
X1
24
40













 mathematics
mathematics








