Similar presentations:
Рівняння математичної фізики
1. Рівняння математичної фізики
2.
• Лекція 1Основні поняття математичної фізики.
Диференціальні рівняння
з частинними похідними
3.
• 1.1. Предмет математичної фізики.Диференціальні рівняння
з частинними похідними
4.
• Диференціальним рівнянням з частиннимипохідними відносно невідомої функції
U U ( x1, x2 , xn )
називається рівняння, що зв’язує незалежні змінні
x1, x2 , xn ,
шукану функцію U та її частинні похідні. Найвищий
порядок частинної похідної, що входить в рівняння,
називається порядком диференціального рівняння.
5.
2U 2U2 f ( x1 , x2 )
2
x1
x2
– диференціальне рівняння з частинними похідними
2-го порядку для функції U(x1, x2).
Функція називається розв'язком диференціального
рівняння з частинними похідними, якщо в результаті
підстановки її в рівняння воно перетвориться в
тотожність.
6.
Приклад 1.1. Знайти функцію U = U(x, y), яка єрозв’язком диференціального рівняння
.
2U
f (x , y ).
2
x
a)
2U
0;
2
x
b)
2U
1;
2
x
c)
2U
x;
2
x
d)
2U
y;
2
x
e)
f)
2U
xy ;
2
x
2U
sin( xy ).
2
x
7.
Приклад 1.1а. Знайти функцію U = U(x, y), яка є.
U
0.
2
x
2
розв’язком диференціального рівняння
U
dx 0 dx ;
2
x
2
U
x 2 dx 0dx ;
U
C 1 y ;
x
2
U
x dx C 1 y dx ;
U x ,y C 1 y x C 2 y .
8.
Приклад 1.1b. Знайти функцію U = U(x, y), яка є.
U
1.
2
x
2
розв’язком диференціального рівняння
U
dx 1 dx ;
2
x
2
U
x 2 dx dx ;
U
x C 1 y ;
x
2
U
x dx x C 1 y dx ;
2
x
U x , y
C 1 y x C 2 y .
2
9.
Приклад 1.1c. Знайти функцію U = U(x, y), яка є.
U
x.
2
x
2
розв’язком диференціального рівняння
U
dx x dx ;
2
x
2
U
x 2 dx xdx ;
2
U x
C 1 y ;
x
2
2
U
x
x dx 2 C 1 y dx ;
2
x3
U x , y C 1 y x C 2 y .
6
10.
Приклад 1.1d. Знайти функцію U = U(x, y), яка є.
U
y.
2
x
2
розв’язком диференціального рівняння
U
dx ydx ;
2
x
2
U
x 2 dx ydx ;
U
xy C 1 y ;
x
2
U
x dx xy C 1 y dx ;
2
xy
U x , y
C 1 y x C 2 y .
2
11.
Приклад 1.1e. Знайти функцію U = U(x, y), яка є.
U
xy .
2
x
2
розв’язком диференціального рівняння
U
dx xydx ;
2
x
2
U
x 2 dx y xdx ;
2
U x y
C 1 y ;
x
2
x 2y
U
x dx 2 C 1 y dx ;
2
x 3y
U x , y
C 1 y x C 2 y .
6
12.
Приклад 1.1f. Знайти функцію U = U(x, y), яка є.
U
розв’язком диференціального рівняння
sin( xy ).
2
x
2
U
dx sin( xy )dx ;
2
x
2
U
x 2 dx sin( xy )dx ; U
1
x dx y cos xy C 1 y dx ;
U
1
cos(xy ) C 1 y ;
x
y
1
U x , y 2 sin xy C 1 y x C 2 y .
y
2
13.
Диференціальне рівняння з частинними похідниминазивається лінійним, якщо шукана функція і всі її
частинні похідні входять в рівняння лінійно.
Загальний вигляд рівнянь математичної фізики
для функції
U U x, y
є наступним:
"
"
AU xx
2BU xy
CU "yy DU x' EU y' FU f x, y ,
де A, B, C, D, E, F – сталі,
а права частина – задана функція від x, y.
14.
• 1.2. Зведення до канонічного видудиференціального рівняння другого
порядку
15.
""
AU xx
2BU xy
CU "yy F x, y,U ,U x' ,U y' 0,
де A, B, C – сталі,
F – неперервна функція.
(1.1)
16.
• Л. Ейлер довів, що будь-яке диференціальнерівняння виду (1.1) за допомогою заміни
незалежних змінних x і y можна привести до
одного з трьох видів (типів), відомих як
гіперболічний, параболічний та еліптичний
(по аналогії з теорією кривих другого порядку в
курсі аналітичної геометрії).
17.
Введемо нові змінні( x, y), ( x, y).
'
x
'
x
'
y
'
y
U x' U ' 'x U ' 'x ;
U y' U ' 'y U ' 'y .
0.
(1.2)
18.
AU 2BU"
xx
"
xy
CU F x, y,U ,U ,U
"
yy
'
x
'
y
0,
AU 2B U C U F , ,U ,U ,U 0,
"
де
"
"
'
'
(1.1)
(1.3)
2B C ,
C A 2B C ,
B A B C .
A A
' 2
x
' 2
x
'
x
'
x
' 2
y
' '
x y
'
x
'
x
' 2
y
'
y
'
y
'
y
'
x
'
y
'
y
Спробуємо вибрати функції ξ = ξ(x, y) і η = η(x, y)
так, щоб деякі із коефіцієнтів A , C , B
стали рівними нулю.
19.
C 0.A 0,
Az
' 2
x
z
A
z
'
x
'
y
2Bz z C z
'
x
2
'
y
z x'
2 B
z'
y
' 2
y
0.
C 0,
(1.4)
ax 2 bx c 0,
D b2 4ac .
ax bx c 0,
2
2
D b
ac .
4 2
20.
C 0.A 0,
Az
' 2
x
z
A
z
'
x
'
y
2Bz z C z
'
x
2
'
y
z x'
2 B
z'
y
' 2
y
0.
(1.4)
C 0,
z x'
B B 2 AC
,
'
A
zy
(1.5)
z x'
B B 2 AC
.
'
A
zy
(1.6)
21.
Криву z(x, y) = const, що є розв’язком рівняння (1.4)будемо називати характеристичною кривою, а саме
рівняння (1.4) − рівнянням характеристик.
З умови z(x, y) = const випливає, що
z'x dx+ z'y dy = 0.
z'y dy = − z'x dx.
'
z
dy
x' .
dx
zy
22.
zA
z
'
x
'
y
2
z x'
2 B
z'
y
C 0,
2
dy
dy
A 2 B C 0.
dx
dx
dy
B B AC B B AC
,
dx
A
A
2
2
dy
B B 2 AC B B 2 AC
.
dx
A
A
23.
Ady BB AC dx 0.
Ady B B 2 AC dx 0;
2
(1.7)
(1.8)
Нехай
( x, y ) C1
( x, y) C2
(1.9)
− загальні інтеграли рівнянь (1.7) і (1.8).
Тоді ці функції і будуть розв'язками рівнянь (1.5) і (1.6).
Криві (1.9) називаються характеристиками
рівняння (1.1).
24.
А(dy)² − 2Bdxdy + C(dx)² = 0.(1.10)
D = В² − АС.
A B
2
AC B .
B C
D.
1) Нехай у розглядуваній області ∆ < 0
(D = В² −АС > 0) − рівняння гіперболічного типу
(можна вважати, що або A 0, або C 0).
(ε > 1);
(D > 0).
25.
,( x, y ).
( x, y );
A С 0,
(1.11)
B 0.
Розділивши рівняння (1.3) почленно на 2В, одержимо
канонічний вид рівняння гіперболічного типу:
AU 2B U C U F , ,U ,U ,U 0,
"
"
"
'
"
U
Ф1 , ,U ,U ' ,U '
'
(1.3)
26.
При A = C = 0 рівняння (1.1) належитьгіперболічному типу і вже має канонічний вид.
;
.
"
"
U
U
, ,U ,U ' ,U ' .
Це другий канонічний вид рівняння гіперболічному
типу.
27.
2) Нехай ∆ = 0 (D = В² − АС = 0) – рівнянняпараболічного типу.
(ε = 1);
(D = 0).
Нехай A 0.
У цьому випадку загальні інтеграли (1.9) дійсні
і співпадають.
Рівняння (1.5) і (1.6) також співпадають і
набувають вигляду
Az x' Bz 'y 0.
28.
Не важко бачити, що будь-який розв’язокz C x, y
цього рівняння в силу
B 2 AC 0
задовольняє також рівняння:
A 'x B 'y 0.
Врахувавши це, маємо ξ= φ(x, y), а за η(x, y),
візьмемо будь-яку двічі неперервнодиференційовну
функцію, для якої якобіан
'x
'x
'y
0.
'
y
29.
Тоді А 0. Враховуючи, що D = 0 (а це означає щоD B 2 A C 0), отримаємо, що B 0 , а коефіцієнт C
1
'
' 2
C 0 набуває виду C A A x B y .
Одержимо канонічне рівняння параболічного типу:
"
U
2 , ,U ,U ' ,U ' .
Зауважимо, якщо A 0 , а C 0 , то отримали б
"
аналогічне канонічне рівняння для U
.
30.
3) Нехай ∆ > 0 (D = В² − АС < 0) − рівнянняеліптичного типу.
(ε < 1);
(D < 0).
Тут загальні інтеграли (1.9) є комплексними
величинами.
Нехай φ(x, y) ≡ φ1(x, y) + іφ2(x, y) = С1 − один із
загальних інтегралів (1.9); другий загальний
інтеграл буде комплексно спряженим з даним.
31.
Покладемо в (1.2):ξ = φ1(x, y), η = φ2(x, y).
Доводиться, що A C , B 0 . Очевидно, що A 0.
Отримаємо рівняння еліптичного виду:
"
''
U
U
3 , ,U ,U ' ,U ' .
32.
"U
Ф1 , ,U ,U ' ,U '
"
"
U
U
1 , ,U ,U ' ,U '
канонічні рівняння гіперболічного типу;
U
"
"
'
'
U
,
,
U
,
U
,
U
2 , ,U ,U ,U
2
канонічні рівняння параболічного типу;
U U
"
'
''
'
, ,U ,U ,U
3
'
'
канонічне рівняння еліптичного типу;
A(dy )2 2 Bdxdy C (dx)2 0
характеристичне рівняння.
33.
Приклад 1.2. Знайти загальний розв’язок рівняння,звівши його до канонічного виду
2u
2u
2u
5
6 2 0.
2
x
x y
y
A 1; 2 B 5; C 6.
1
5
2
5
2 6 25 1 0.
4
4
6
Отже, задане рівняння гіперболічного типу.
34.
Запишемо рівняння характеристикdy 5dxdy 6 dx
2
y ' 5 y ' 6 0.
2
2
0;
k y .
k 2 5k 6 0.
a 1; b 5; c 6.
D 5 4 1 6 25 24 1.
2
k1, 2
5 1
; k1 2, k2 3.
2
y1 2, y2 3.
35.
y 2;y 3;
y 2 x C1;
y 3x C2 ;
y 2 x C1;
y 3x C2 ;
x, y y 2x.
x, y y 3x.
Введемо заміну змінних
( x, y );
( x, y ),
y 2 x;
y 3x.
36.
2u0;
u
0d C ( );
u C( )d C1 ( ) C2 ( ),
де C1(ξ) і C2(η) – довільні двічі диференційовані
в розглядуваній області функції.
u C1 y 2 x C2 y 3x .
37.
Приклад 1.3. Знайти загальний розв’язок рівняння,звівши його до канонічного виду
2u
2u
2u
8
16 2 0.
2
x
x y
y
A 1; 2 B 8; C 16.
1 4
16 16 0.
4 16
Отже, задане рівняння параболічного типу.
38.
dy2
8dxdy 16 dx 0.
2
y 2 8 y 16 0.
k y .
k 2 8k 16 0.
a 1; b 8; c 16.
D 8 4 1 16 64 64 0.
2
8 0
k
4.
2
y 4.
39.
y 4 x C;y 4 x C;
x, y y 4x.
Введемо заміну змінних:
x, y y 4 x.
За другу нову змінну візьмемо, наприклад,
'x
'
x
'y 4 1
4 4 8 0.
'
y
4 1
y 4x.
40.
u0;
2
2
u
0dη C1 ξ ;
η
u C1 d C1 C2 ;
u x 4 y C1 y 4 x C2 y 4 x .
Це і буде загальним розв’язком заданого рівняння.
41.
Приклад 1.4. Звести до канонічного виду рівняння2u
2u
2u
6
25 2 0.
2
x
x y
y
A 1; 2 B 6; C 25.
1 3
25 9 16 0.
3 25
Отже, задане рівняння еліптичного типу.
42.
dy 2 6dxdy 25 dx 2 0.y
2
k y .
6 y 25 0.
k 6k 25 0.
2
a 1; b 6; c 25.
D 6 4 1 25 36 100 64.
2
D 64 8i.
6 8i
k
3 4i.
2
3, 4.
43.
y 1 3 4i;y 2 3 4i;
y 3 4i x C1;
y 3 4i x C2 ;
C1 y 3x 4ix;
C2 y 3x 4ix;
C1, 2 y 3x 4ix.
1 x, y y 3x;
2 x, y 4x.
44.
Для рівняння гіперболічного типу0 D 0 k1, k2
U C1 y k1x C2 y k2x
Для рівняння параболічного типу
0 D 0 k1
U y k1x C1 y k1x C2 y k1x
Для рівняння еліптичного типу
0 D 0 k1,2 i
y x xi C1,2
45.
• Лекція 2Поздовжні коливання стержня
2.1. Поздовжні коливання стержня.
Виведення хвильового рівняння
46.
Розглянемо задачу про поздовжні коливання, яківиникають у стержні під час його розтягу або
стиску внаслідок прикладених зусиль.
При виведенні рівняння, яке описує такі
коливання, зробимо ряд припущень відносно
геометричного та фізичного станів стержня.
Нехай стержень, як тіло циліндричної або
призматичної форми, буде задовольняти
наступним умовам:
47.
1) стержень прямолінійний завдовжки l;2) поперечний переріз є сталим, тобто його
площа S = const;
3) стержень однорідний, тобто густина ρ = const;
4) стержень пружний, тобто мова йде про пружні
коливання, коли має місце закон Гука і немає
залишкових деформацій (σ = Eε , де σ – нормальне
напруження, ε – відносна поздовжня деформація,
Е – модуль Юнга, E = const);
48.
МатеріалАлюміній
Бронза
Вольфрам
Латунь
Мідь
Нікель
Олово
Свинець
Срібло
Сірий чавун
Сталь
Скло
Цинк
Хром
Модуль Юнга E, гПа
70
75-125
350
95
110
210
35
18
80
110
200-210
50-90
120
300
49.
1 паскаль (Па) ≡ 1 Н/м² ≡ 1 Дж/м³ ≡ 1 кг/(м·с²).Для орієнтації: Звичайний атмосферний тиск
дорівнює приблизно 105 Паскалів, або, звучніше,
1000 гектопаскалів.
Гектопаскаль, гПа, що дорівнює 100 Па,
традиційно використовується для вимірювання
атмосферного тиску.
Одиниця названа на честь французького фізика
Блеза Паскаля.
50.
5) стержень ізотропний, тобто властивості матеріалу,з якого виготовлено стержень, у всіх напрямках
однакові;
6) коливання малі;
7) зовнішні сили, якщо вони є, діють вздовж осі
стержня;
8) в результаті коливань поперечні перерізи
залишаються перпендикулярними до осі стержня.
51.
Розглянемо стержень, вздовж осі якого спрямуємовісь Ox (рис. 2.1). Виділимо довільний елемент
стержня [ x1, x2].
N
0
x1
x2
l
x
Рис. 2.1. – Стержень з виділеним довільним елементом [ x1, x2]
Прикладемо до стержня деяку осьову, наприклад,
розтягуючу силу N, під дією якої поперечні перерізи
стержня змістяться, кожний на свою величину.
52.
Припустимо, що в деякий момент часу, якийприймаємо за початковий (t = 0), силу знято.
Тоді у стержні виникають поздовжні коливання,
оскільки, будучи пружним, він намагається
повернутися у свій початковий стан.
53.
Нехай у результаті коливань кожний переріз xв момент часу t зміститься на деяку величину U(x, t).
Тоді переріз x1, зміститься на величину U(x1, t),
а x2 – на U(x2, t), а виділений елемент [ x1, x2]
займе положення [x1 + U(x1, t); x2 + U(x2, t)],
і видовжиться на величину
x2 U ( x2 , t ) x1 U ( x1, t ) ( x2 x1) U ( x2 , t ) U ( x1, t ).
Це є абсолютним видовженням.
54.
Позначимо початкову довжину виділеного елементачерез x = x2 – x1 і знайдемо відносну деформацію ε,
як границю відношення абсолютного видовження до
довжини елемента, коли ця довжина прямує до нуля:
U ( x2 , t ) U ( x1, t )
U U ( x, t )
lim
lim
.
x 0
x 0 x
x2 x1
x
55.
Для виведення рівняння, яке описує коливальнийпроцес скористаємося другим законом Ньютона, згідно
якого сума всіх діючих на рухомий об’єкт сил дорівнює
добутку маси на прискорення. Розглянемо сили, які
можуть діяти на виділений елемент [x1, x2]:
1) Внутрішні сили N(x, t), які згідно із законом Гука для
будь-якого перерізу x і будь-якого часу t
U ( x, t )
N ( x, t ) ES
.
x
(2.1)
56.
Отже, у перерізі x1 діє сила N(x1, t), а у перерізіx2 – сила N(x2, t). Таким чином, на виділений елемент
діє внутрішня сила
U ( x2 , t ) U ( x1 , t )
N ( x2 , t ) N ( x1 , t ) ES
x
x
U x, t
U x, t
ES
dx.
dx ES
2
x x
x
x1
x1
x2
x2
2
(2.2)
57.
2) Зовнішні сили, які за нашим припущенням діютьвздовж осі стержня. Позначимо через f(x, t) величину
цієї сили, віднесену до одиниці об’єму (інтенсивність
зовнішніх сил). Тоді на елементарний об’єм dV = Sdx
діє сила f(x, t)dV, а на виділений елемент [x1, x2]
x2
Sf x, t dx.
x1
(2.3)
58.
3) Сила інерції, яка діє на елементарний об’єм dV,дорівнює
U ( x, t )
U ( x, t )
dm
S
dx.
2
2
t
t
2
2
(2.4)
А для виділеного елемента [x1, x2] ця сила дорівнює
2U x , t
x S t 2 dx .
1
x2
(2.5)
59.
Згідно із другим законом Ньютона маємо:U
2U
x ES x 2 dx x Sf x ,t dx x S t 2 dx ;
1
1
1
x2
2
x2
x2
U
U
x ES x 2 dx x Sf x ,t dx x S t 2 dx 0;
1
1
1
x2
2
x2
x2
2
2U
2U
x S t 2 ES x 2 Sf s ,t dx 0;
1
2U
2U
S 2 ES
Sf (x , t ) 0;
2
t
x
x2
2U E 2U 1
f x , t .
2
2
t
x
(2.6)
: S
60.
Введемо позначенняE
a2;
Тоді
1
f ( x, t ) F ( x, t ).
2
2U
U
2
a
F ( x, t )
2
2
t
x
0 x l,
t 0 .
(2.7)
Одержане рівняння називається хвильовим рівнянням,
яке описує поздовжні коливання у стержні.
F ( x, t ) – характеризує наявність зовнішніх сил.
61.
Якщо F(x, t) = 0, то хвильове рівнянняU
2 U
a
2
t
x 2
2
2
0 x l,
t 0 .
(2.8)
Якщо стержень розташований вертикально вздовж осі,
напрямленої донизу, то хвильове рівняння для важкого
стержня:
2
2U
U
2
a
g
2
2
t
x
0 x l,
t 0 .
(2.9)
62.
2.2. Постановка задачіматематичної фізики
про поздовжні коливання стержня
63.
Для повного визначення поздовжніх коливань стержняодного хвильового рівняння недостатньо. Із фізичних
міркувань випливає, що для того, щоб однозначно
описати коливальний процес необхідно додатково
задати величини зміщення U перерізів стержня і
швидкості U в початковий момент часу (початкові
t
умови) і режим на кінцях стержня (крайові умови).
64.
Отже, постановка задачі про поздовжні коливаннястержня складається з хвильового рівняння
(диференціального рівняння 2-го порядку для функції
двох змінних x і t) та двох початкових і двох крайових
умов.
65.
Початкові умови (П.У.) характеризують стан стержня впочатковий момент часу t = 0:
П.У.
U (x ,0) (x );
U (x ,0) (x ).
t
(2.10)
Крайові умови (К.У.) показують, що відбувається на
кінцях стержня під час коливань.
66.
Розглянемо різні види граничних умов:1) Нехай один кінець стержня закріплений жорстко,
а другий – вільний (рис. 2.2).
Якщо вважати, що нерухомим кінцем стержня є x = 0,
а вільним x = l, то:
0
l
x
Рис. 2.2 – Стержень, один з кінців якого
закріплений, а другий – вільний
67.
К.У.U (0, t ) 0;
U (l , t ) 0.
x
(2.11)
Дійсно так, бо для закріпленого кінця характерним є
те, що зміщення його весь час дорівнює нулю, а для
вільного кінця – те, що у перерізі x = l пружна сила
N = 0. Отже,
U l , t
ES
0.
x
Звідси
U (l , t )
0.
x
68.
2) Нехай один кінець стержня закріплений жорстко, а довільного кінця (x = l) прикладено силу P (рис. 2.3). Тоді
маємо:
P
0
l
x
Рис. 2.3. – Один кінець стержня жорстко закріплений, а на
другий – діє сила Р
К.У.
U (0, t ) 0;
U (l , t ) P
.
ES
x
(2.12)
69.
3) Нехай обидва кінці стержня жорстко закріплені(рис. 2.4). Тоді:
0
l
x
Рис. 2.4. – Обидва кінці стержня жорстко закріплені
К.У.
U (0, t ) 0;
U (l , t ) 0.
(2.13)
70.
4) Нехай один кінець стержня (x = 0) жорсткозакріплений, а на другому кінці (x = l) має місце в’язкий
опір з коефіцієнтом в’язкості μ (рис. 2.5).
0
l
x
Рис. 25. – На правому кінці стержня має місце в’язкий опір
К.У.
U (0, t ) 0;
U (l , t )
U (l , t )
0.
ES x t
(2.14)
71.
5) Нехай один кінець стержня (x = 0) жорстко закріплено,а до другого (x = l) приєднано вантаж маси М (рис.2.6).
0
Тоді на цьому кінці виникає сила
інерції, яка дорівнює добутку маси
вантажу на прискорення руху.
Записуючи умову рівноваги на кінці
x = l маємо:
U (0, t ) 0;
(2.15)
К.У. U (l , t )
2U (l , t )
ES x M t 2 0.
l
M
x
Рис. 2.6. – Один кінець стержня жорстко
закріплено, а до іншого приєднано вантаж маси М
72.
6) Нехай один кінець стержня (x = 0) жорсткозакріплено, а другий (x = l) – пружно: до цього кінця
прикріплено пружину з жорсткістю с (рис. 2.7).
Оскільки вважається, що сила натягу пружини прямо
пропорційна зміщенню, то, записуючи умову рівноваги
на кінці x = l маємо:
0
l
x
Рис. 2.7. – Один кінець стержня закріплено
жорстко, а другий – пружно
К.У.
U 0, t 0;
U l , t
ES x cU l , t 0.
(2.16)
73.
• Лекція 3Поперечні коливання струни
3.1. Поперечні коливання скінченної струни.
Виведення хвильового рівняння
74.
Розглянемо туго натягнуту струну із закріпленимикінцями. Якщо вивести її із стану рівноваги, то
почнуться коливання струни. При вивченні цього
коливального процесу зробимо ряд припущень щодо
геометричного і фізичного стану струни:
75.
1) струна скінченна завдовжки l;2) діаметр поперечного перерізу d набагато менший за
довжину струни l, тобто ним можна знехтувати і
вважати, що є тільки один характерний розмір –
довжина;
3) струна однорідна, тобто лінійна густина;
4) струна пружна, тобто має місце закон Гука;
76.
5) коливання поперечні, тобто всі точки струнирухаються перпендикулярно до її положення
рівноваги, причому у будь-який момент струна
лежить в одній площині;
6) коливання малі, тобто малі відхилення точок струни
від положення рівноваги;
7) зовнішні сили неперервно розподілені вздовж
струни і діють перпендикулярно до положення
рівноваги струни;
8) сила натягу струни у всіх точках є величиною
сталою (T = const) і напрямленою по дотичній до
струни.
77.
Виведемо рівняння поперечних коливань струни.Введемо систему координат xOu, у якій струну
розмістимо на осі Ox.
T
u
M2
1
0
T
M1
x1
2
1
x2
l
Рис. 3.1 – Нескінченно малий елемент струни М1, М2,
спроектований на інтервалі [x1, x2]
x
78.
Вважаємо, що кінці струни (x = 0 та x = l) закріпленінерухомо.
Якщо струну вивести із положення рівноваги
(відтягнути, або ударити по ній), то кожна її точка
переміститься на деяку величину U = U(x, t).
Розглянемо нескінченно малий елемент струни М1М2,
який проектується на інтервал [x1, x2].
На цей елемент діють сили натягу T, які замінюють
відкинуті частини струни (рис. 3.1). Знайдемо проекції
сил на вісь Ou:
T sin 1 T sin 2 T sin 2 sin 1 .
(3.1)
79.
;Оскільки коливання малі, то кути α1 та α2 теж малі,
тому
U x1 , t
sin 1 tg 1
;
x
U x2 , t
sin 2 tg 2
.
x
Тоді сила натягу струни
U x2 , t U x1 , t
T sin 2 sin 1 T
x
x
x2
2U
T 2 dx.
x
x1
(3.2)
80.
Сила натягу належить до внутрішніх сил.Припустимо, що на одиницю довжини струни діє
зовнішня сила з інтенсивністю f(x, t).
Елементарна сила, що діє на елементарну довжину
струни з проекцією dx дорівнює f(x, t)dx, а на
виділений елемент M1M2:
x2
f x, t dx.
x1
81.
Зовнішня сила вважається додатною, якщо вона дієвгору, і від’ємною, якщо – вниз.
Тепер, згідно другого закону Ньютона (сума всіх
діючих на рухомий об’єкт сил дорівнює добутку його
маси на прискорення), маємо:
U
U
x t 2 dx x T x 2 dx x f x ,t dx
1
1
1
x2
2
x2
2
x2
або
2
2U
U
x t 2 T x 2 f x ,t dx 0.
1
x2
82.
За основною лемою математичної фізики маємо:2U
2U
2 T
f x , t 0,
2
,
t
x
або, поділивши на ρ
.
2
2
U T U 1
;
(3.3)
f
x
,
t
.
t 2 x 2
Введемо такі позначення:
T
2
1
a
.
f x , t F x , t ,
Тоді отримаємо хвильове рівняння для поперечних
коливань струни:
2
2U
U
2
a
F x , t
2
2
t
x
0 x l ,
.
t 0 . (3.4)
83.
Зазначимо, що U(x, t) – розв’язок цього рівняння,що визначає положення будь-якої точки струни x у
будь-який момент часу t, тобто визначає форму струни.
Знайдемо вільний член F(x, t), пов’язаний з
наявністю зовнішніх сил, у випадку важкої струни.
Середня інтенсивність сили тяжіння для елемента x:
P
f x, t
.
x
84.
Інтенсивність в точці x струниg x
P
f x, t lim
lim
g .
x 0 x
x 0 x
Тоді F(x, t) –g, а хвильове рівняння набуває вигляду:
2
2U
U
2
a
g
2
2
t
x
0 x l,
t 0 . (3.5)
85.
Якщо F(x, t) = 0, то коливання називаютьсявільними, а якщо F(x, t) 0, то – вимушеними.
З фізичної точки зору коефіцієнт a – це швидкість
розповсюдження поперечної хвилі, що підтверджується
його розмірністю:
2
2
T
H
кг
м
м
2
a
2
2 .
кг / м с кг с
м
Отже, а .
с
86.
3.2. Постановка задачі про поперечніколивання скінченної струни
Формулювання задачі про поперечні коливання
струни включає хвильове рівняння, початкові та
крайові умови. Початкові умови задають початкову
форму струни і початкові швидкості точок струни, а
крайові умови відображають закріплення кінців
струни.
87.
Отже, загальна постановка задачі має вигляд:2
2U
U
2
a
F( x, t ),
2
2
t
x
U (x ,0) (x );
П.У.
U (x ,0)
(x ),
t
T
a ,
2
0 x l,
К.У. U (0, t ) 0;
U (l , t ) 0.
t 0 .
(3.6)
Задача полягає у знаходженні функції U(x, t)
класу C2, яка описує поперечні коливання струни.
88.
3.3. Постановка задачі про поперечніколивання нескінченної струни
Розглянемо дуже довгу струну, настільки довгу, що
на коливання, які виникають в її середній частині,
кінці впливати практично не будуть. Таким чином,
на відміну від попередніх задач, у постановці
задачі про поперечні коливання нескінченної
струни крайові умови виключаються.
89.
Постановка задачі про поперечні коливаннянескінченної струни складається з диференціального
рівняння, яке описує коливальний процес, і
початкових умов, які задають початкову форму
струни і початкові швидкості точок струни.
При розгляді вільних коливань постановка задачі буде
наступною:
2
2U
U
2
a
,
2
2
t
x
T
a ,
2
x ,
t 0 .
90.
U x ,0 x ;П.У. U x ,0
x .
t
(3.7)
Функції φ(x) та ψ(x) задано на всій числовій осі,
x ; .
Така задача ще називається задачею Коші. Її розв’язком
є функція U(x, t) класу C2, яка в указаній області
задовольняє хвильове рівняння і обидві початкові
умови.
91.
Зауваження1) Хвильове рівняння характеризує не тільки процеси
поздовжніх коливань стержня і поперечних коливань
струни. Воно є універсальною математичною
моделлю для всіх коливальних процесів різної
фізичної природи. Так, хвильове рівняння описує
електричні коливання, крутильні коливання валу,
акустичні коливання пружного газу тощо.
92.
2) Також хвильове рівняння можна поширити наколивальні процеси, які відбуваються не лише в
одновимірному просторі, як у випадках зі стержнем
чи струною, але й у двовимірному та тривимірному
просторі. Так, хвильове рівняння, що моделює вільні
поперечні коливання плоскої мембрани у формі
області D , має вигляд:
2
2
2U
U
U
2
a 2 2 ,
2
t
y
x
x, y D,
t 0
(3.8)
93.
А тривимірна модель коливального процесу вдеякій просторовій області V має такий вигляд:
2
2
2
2U
U
U
U
2
a 2 2 2 ,
2
t
y
z
x
x, y, z V ,
t 0 .
(3.9)
Таке рівняння описує, наприклад, закон
поширення світлових та електромагнітних хвиль у
просторі. Фізичний зміст сталої а у хвильовому
рівнянні – це швидкість розповсюдження хвиль у
відповідних хвильових процесах.
94.
• Лекція 4Методи розв’язування задач
про коливання струни
4.1. Поперечні коливання нескінченної струни
95.
Перш ніж розв’язувати задачу про коливаннязакріпленої струни, розглянемо більш просту
задачу про коливання нескінченної струни.
Метод Д’Аламбера (для розв’язування задачі про
вільні поперечні коливання нескінченої струни).
96.
Розглянемо вільні поперечні коливаннянескінченної струни в наступній постановці:
2
2U
U
2
a
,
2
2
t
x
П.У.
T
a ,
2
U x ,0 x ;
U x ,0
x ,
t
x ,
t 0 .
(4.1)
де функції φ(x) і ψ (x) задані на всій числовій осі.
97.
Задача полягає у знаходженні функції U(x, t), якавизначає переміщення будь-якої точки х у будь-який
момент часу t.
1
0
2
a
0.
2
0 a
(рівняння гіперболічного типу)
Згідно з методом характеристик запишемо рівняння:
(dx) 2 a 2 (dt ) 2 або
dx adt.
98.
Отже, отримали два звичайних диференціальнихрівняння. Проінтегруємо кожне з них:
dx a dt;
dx a dt;
x at C1;
x at C2 ;
x at C1.
x at C2 .
Тепер введемо нові змінні:
x at , x at.
99.
Звідси2U
0
– хвильове рівняння у канонічному виді.
Проінтегрувавши його спочатку по ξ, потім по η,
отримаємо розв’язок:
U ( , ) C1 C2
або:
U ( x, t ) C1 ( x at ) C2 ( x at )
це загальний розв’язок хвильового рівняння, де
C1 ( x at )
C2 ( x at )
довільні двічі диференційовні функції.
(4.2)
100.
Щоб їх знайти, використаємо початкові умови:U ( x,0) C1 ( x a 0) C2 ( x a 0) C1 ( x) C2 ( x);
U ( x,0)
C1 ( x a 0)
C2 ( x a 0)
a
a
aC1 ( x) aC2 ( x).
t
t
t
П.У.
U (x ,0) C 1 (x ) C 2 (x ) (x );
U (x ,0)
aC 1 (x ) aC 2 (x ) (x ).
t
101.
Після інтегрування другого рівняння у межах від 0 до х,отримаємо систему:
C 1 (x ) C 2 (x ) (x );
x
1
C 1 (x ) C 2 (x ) a (x )dx С ,
0
де
C С1 0 С2 0 const .
102.
Розв’язавши систему рівнянь, знайдемо шуканіфункції:
x
1
1
С
C2 ( x ) ( x )
( x )dx ,
2
2a 0
2
x
1
1
С
C1 ( x ) ( x )
( x )dx .
2
2a 0
2
Щоб отримати функції C1(x – at) та C2(x + at),
достатньо замість аргумента х підставити відповідні
аргументи x – at та x + at.
103.
Отже, розв’язок задачі U(x, t):U ( x, t ) C1 ( x at ) C2 ( x at )
1
1
( x at )
2
2a
x at
1
1
0 ( x)dx 2 ( x at ) 2a
x at
( x at ) ( x at ) 1
( x )dx.
2
2a x at
x at
( x)dx
0
104.
Таким чином, для задачі про поперечні коливаннянескінченної струни розв’язок за методом
Д’Аламбера має вигляд:
x at x at 1
U x, t
x dx.
2
2a x at
x at
(4.3)
Формула (4.3) називається розв’язком
Д’Алембера задачі Коші для рівняння коливань
нескінченної струни.
105.
Для задачі про поперечні коливання нескінченноїструни розв’язок за методом Д’Аламбера має вигляд:
2
2U
U
2
a
,
2
2
t
x
П.У.
T
a ,
2
x ,
U x ,0 x ;
U x ,0
x ,
t
t 0 .
(4.1)
x at x at 1
U x, t
x dx.
2
2a x at
x at
(4.3)
106.
Приклад 4.1. Знайти розв’язок задачіматематичної фізики у такій постановці:
2
2U
U
2
a
,
2
2
t
x
П.У.
T
a ,
2
U (x ,0) x 2 ;
U (x ,0)
1.
t
x ,
t 0 .
107.
За умовою задачі функції( x) x 2 ,
( x ) 1.
За методом Д’Аламбера маємо:
( x at )2 ( x at )2
U ( x, t )
2
x at
x at
1
1
2
2 2
2
2 2
1
dx
x
a
t
x
x
a
t t.
2a x at
2a x at
Відповідь:
U ( x, t ) x 2 a 2 t 2 t.
108.
4.2. Поперечні коливання скінченної струниМетод Фур’є (для розв’язування задачі про вільні
поперечні коливання скінченної струни).
Розглянемо струну завдовжки l із закріпленими
кінцями. Ця задача має таку постановку:
2
2U
U
2
a
,
2
2
t
x
T
a ,
2
0 x l,
t 0 .
109.
U x ,0 x ;П.У. U x ,0
x ,
t
U 0, t 0 ;
К.У.
U l , t 0 .
(4.4)
Згідно з методом Фур’є (його ще називають методом
відокремлення змінних) розв’язок шукаємо у вигляді:
U ( x, t ) X ( x ) T (t ).
(4.5)
110.
Функція (4.5) має задовольняти хвильове рівнянняі початкові та крайові умови.
Підставимо її в рівняння.
Для цього знайдемо відповідні похідні:
U
X ( x) T (t ),
x
2U
X ' ' ( x) T (t ),
2
x
U
X ( x) T (t ),
t
2U
X ( x) T (t ).
2
t
111.
Підкладаючи знайдені вирази у хвильове рівняння,отримаємо:
X ( x ) T ' ' (t ) a 2 X ( x ) T (t ) |: a 2 X ( x ) T ( x ) ,
T (t ) X ( x )
c const .
2
a T (t ) X ( x )
Або:
X ( x ) c X ( x ) 0;
T (t ) ca 2T (t ) 0.
(I)
(II)
112.
Таким чином, кожному значенню n = 1, 2, 3, ...будуть відповідати розв’язки:
n x
n at
n at
U n ( x, t ) X n x Tn t Bn sin
Dn sin
Cn cos
l
l
l
Внесемо множник Bn у дужки та введемо такі
позначення:
Bn Сn an
Bn Dn bn .
113.
Тодіn at
n at n x
U n ( x, t ) an cos
bn sin
.
sin
l
l
l
(4.8)
Розв’язки Un(x, t) називають власними функціями
задачі, а відповідні їм коливання струни – власними
(або вільними) коливаннями.
Числа
λn називають власними числами.
114.
За допомогою функцій (4.8) побудуємо розв’язок,який би задовольняв початкові умови задачі. Для
цього візьмемо суму розв’язків (4.8), яка завдяки
лінійності та однорідності хвильового рівняння
також буде його розв’язком:
U ( x , t ) U n ( x , t )
n 1
n at
n at
n x
an cos
bn sin
.
sin
l
l
l
n 1
(4.9)
115.
Вважатимемо, що цей ряд збіжний, і його можнапочленно диференціювати по аргументу t.
Підберемо коефіцієнти an та bn так, щоб функція
U(x, t) задовольняла початкові умови:
П.У.
U (x ,0) (x );
U (x ,0)
(x ).
t
116.
Таким чином, розв’язок задачі про поперечні коливанняскінченної струни з закріпленими кінцями має
вигляд:
n at
n at
n x
U ( x, t ) a n cos
bn sin
,
sin
l
l
l
n 1
де
2
n x
an ( x ) sin
dx,
l 0
l
l
2
n x
bn
( x ) sin
dx.
n a 0
l
l
(4.12)
117.
Розв’язок задачі про поперечні коливання скінченноїструни з закріпленими кінцями має вигляд:
U x ,0 x ;
П.У. U x ,0
x ,
t
U 0, t 0 ;
К.У.
U l , t 0 .
(4.4)
n at
n at
n x
U ( x, t ) a n cos
bn sin
,
sin
l
l
l
n 1
2
n x
an ( x ) sin
dx,
l 0
l
l
2
n x
bn
( x ) sin
dx.
n a 0
l
l
(4.12)
118.
4.3*. Фізичний зміст розв’язку задачі пропоперечні коливання
Щоб з’ясувати фізичний зміст розв’язку (4.12),
проаналізуємо власні функції (4.8):
n at
n at n x
U n (x , t ) an cos
bn sin
.
sin
l
l
l
119.
Очевидно, що у всіх точках струни відбуваютьсягармонічні коливання з тою самою частотою
n а
l
і фазою φn
an
tg n .
bn
Амплітуда коливань залежить від абсциси точки
струни і дорівнює:
n x
An a b sin
.
l
2
n
2
n
120.
При такому коливанні всі точки струни одночаснодосягають свого максимального відхилення в ту чи
іншу сторону та одночасно проходять положення
рівноваги.
Такі коливання називаються стоячими хвилями на
відміну від коливань безмежної струни, які
називаються біжучими хвилями.
121.
Якщо зафіксувати n (нехай n = 1), то можнапоказати різні форми струни у різні моменти часу
(рис. 4.2).
При цьому кінці струни завжди залишаються
нерухомими, а найбільшого відхилення функція
досягає тільки в точці x = l/2 (у будь-який момент
часу).
122.
uA1
0
l
2
l
Рис. 4.2. – Форми струни у різні моменти часу при n = 1
x
123.
При n = 2 нерухомих точок вже буде три: кінці x1, x5,струни і середня точка x3, а найбільшого відхилення
функція досягає в точках x2, x4 (рис. 4.3).
u
A2
0
l
4
l
2
3l
4
l
x
x1 0
l
x2
4
l
x3
2
3l
x4
4
x5 l
Рис. 4.3. – Форми струни у різні моменти часу при n = 2
124.
Взагалі нерухомих точок стояча хвиля буде матистільки, скільки коренів має рівняння
n x
sin
0
l
в інтервалі [0;l].
Отже, таких точок буде (n + 1) з абсцисами х = 0;
l
2l
n 1 l
x ; x ;...;
; l.
n
n
n
Ці точки називаються вузлами стоячої хвилі.
125.
Всередині між ними будуть точки, в якихвідхилення будуть максимальними.
При цьому частоти коливань
n а
n
l
називаються власними частотами струни.
Найменша із частот буде при n = 1:
а T
1
.
l
l
126.
Коли струна коливається, з’являється звук, висотаякого буде зростати разом з частотою коливань.
При цьому найнижчий (основний) тон буде
відповідати власній частоті 1.
Звук буде тим вищим, чим більше натягнута струна
і чим вона коротша, та легша (тобто, чим більша
сила натягу струни Т і чим менші довжина l та
густина ρ).
127.
Решту тонів називають обертонами, абогармоніками. Таким чином, функція U(x, t), яка є
розв’язком задачі про поперечні коливання
скінченної струни являє собою суму окремих
гармонік (при n = 1, 2, ... ), які накладаючись одна на
одну створюють досить складний коливальний
процес.
128.
4.4*. Вимушені коливання струниЗадача про вимушені коливання скінченної струни
довжини l зводиться до інтегрування неоднорідного
диференціального рівняння:
2
T
2U
U
2
2
a
F x, t , a ,
2
2
t
x
0 x l,
t 0 .
(4.13)
129.
при заданих додаткових умовах:U x ,0 x ;
П.У. U x ,0
x ,
t
U 0, t 0;
К.У.
U l , t 0.
Тут функція F(x, t) є заданою у всій
розглядуваній області.
130.
Як і при розв’язуванні звичайних неодноріднихдиференціальних рівнянь, розв’язок рівняння (4.13)
можна шукати як суму двох функцій:
U (x , t ) v (x , t ) w (x , t ),
(4.14)
131.
перша з яких задовольняє однорідне рівняння2
2v
v
2
a
,
2
2
t
x
0 x l,
t 0
при умовах:
П.У.
v (x ,0) (x );
v (x ,0)
t (x ),
v (0, t ) 0;
К.У.
v (l , t ) 0,
(4.15)
132.
а друга функція w(x, t) задовольняє неодноріднерівняння
2
2w
w
2
a
F (x , t ),
2
2
t
x
0 x l,
t 0
при однорідних умовах
w (x ,0) 0;
П.У.
w (x ,0)
0,
t
w (0, t ) 0;
К.У.
w (l , t ) 0.
(4.16)
133.
Функція v(x, t) описує вільні коливання струни,зумовлені наявністю початкових відхилень та
початкових швидкостей точок струни.
Метод відшукання цієї функції нами вже з’ясовано
раніше.
134.
Одержали лінійне диференціальне рівняннядругого порядку із спеціальною правою частиною.
Розв’язок шукаємо у вигляді:
m (t ) m (t ) m (t ),
де m (t ) – загальний розв’язок відповідного однорідного
рівняння:
(2m 1)2 2a 2
m (t )
m (t ) 0.
2
l
135.
Розв’язування задачіпро поздовжні коливання стержня
136.
5.1. Метод Фур’є для розв’язування задачіпро поздовжні коливання стержня
Враховуючи, що метод Фур’є застосовують при
однорідних крайових умовах, розглянемо задачу про
вільні коливання стержня, один кінець якого (x = 0)
жорстко закріплений, а другий (x = l) вільний.
Ця задача має наступну постановку:
2
2U
U
2
a
,
2
2
t
x
E
a ,
0 x l,
2
U x ,0 x ;
П.У. U x ,0
x ,
t
К.У.
t 0 .
U 0, t 0;
U l , t
x 0.
(5.1)
137.
Припустимо, що функції φ(x) та ψ(x) можнарозкласти в ряд Фур’є по синусах кратних дуг
на (0; l).
За методом Фур’є ненульові розв’язки хвильового
рівняння, які задовольняють однорідні крайові
умови (5.1), шукаємо у вигляді
U(x, t) = X(x)·T(t).
138.
Таким чином, розв’язок задачі про поздовжніколивання стержня, один кінець якого жорстко
закріплений, а другий вільний, має вигляд:
( 2n 1) at
( 2n 1) at
( 2n 1) x
U ( x, t ) an cos
bn sin
sin
,
2l
2l
2l
n 0
де
l
2
(2n 1) x
an ( x ) sin
dx,
l 0
2l
l
4
(2n 1) x
bn
( x ) sin
dx.
(2n 1) a 0
2l
(5.11)
139.
Розв’язок задачі про поздовжні коливання стержня,один кінець якого жорстко закріплений,
а другий вільний.
2
2U
U
2
a
,
2
2
t
x
E
a ,
0 x l,
2
U x ,0 x ;
U x ,0
x ,
П.У.
t
К.У.
t 0 .
U 0, t 0;
U l , t
x 0.
(5.1)
( 2n 1) at
( 2n 1) at
( 2n 1) x
U ( x, t ) an cos
bn sin
sin
,
2l
2l
2l
n 0
l
2
(2n 1) x
an ( x ) sin
dx,
l 0
2l
bn
(5.11)
l
4
(2n 1) x
( x ) sin
dx.
(2n 1) a 0
2l
140.
Розповсюдження тепла6.1. Задача про розповсюдження тепла.
Рівняння теплопровідності
Розглянемо задачу про розповсюдження тепла в
нерівномірно нагрітому тілі V, обмеженому
поверхнею S.
У цьому випадку виникають теплові потоки від
ділянок з вищою температурою до ділянок з
нижчою.
Тобто відбувається перерозподіл тепла.
141.
За величину, що характеризує даний процес,візьмемо функцію
U = U(x, y, z, t),
яка визначає температуру в будь-якій точці M(x,y,z)
у будь-який момент часу t.
142.
При побудові математичної моделі зробимо наступніприпущення стосовно фізичних властивостей тіла:
1) тіло однорідне;
2) ізотропне;
3) у тілі відбувається механічний перенос тепла від
більш нагрітих ділянок до менш нагрітих;
4) усе тепло йде на зміну температури тіла;
5) властивості тіла від температури не залежать.
143.
Щоб вивести рівняння теплопровідностідостатньо скласти рівняння теплового балансу, яке
запишемо так:
Q Q1 Q2
(6.1)
144.
Визначимо всі складові цього рівняння.1) Q1 – це кількість тепла, що проходить через
поверхню σ за деякий час ∆t.
Для визначення Q1 скористаємося експериментальним
законом Фур’є, згідно з яким елементарна кількість
тепла dQ1, що проходить через елементарну частину
поверхні dσ у напрямку внутрішньої нормалі n
до неї за одиницю часу, дорівнюватиме
U
dQ1 k
d ,
n
де k – коефіцієнт внутрішньої теплопровідності, k > 0,
розмірність
Дж
м К с .
145.
Вважаємо, що коефіцієнт k не залежить віднапряму нормалі.
Щоб визначити всю кількість тепла, що
проходить через поверхню σ за час ∆t, достатньо
вираз, що визначає елементарну кількість тепла dQ1,
проінтегрувати по цій поверхні і домножити на ∆t:
U
Q1 t k
d .
n
146.
Нехай векториU U U
grad U
,
,
,
x y z
n cos , cos , cos ,
тоді
U U
U
U
cos
cos
cos grad U n.
n
x
y
z
Тоді
Q1 t k grad U nd .
147.
Використовуючи формулу Остроградського повідношенню до вибраного елемента ω з внутрішньою
нормаллю до поверхні σ, маємо
P Q R
d P cos Q cos R cos d .
x y z
Звідси
Q1 t k div grad U d .
(6.2)
148.
2) Q2 – це кількість тепла, що виділяється(поглинається) джерелами (якщо вони є),
розподіленими в об’ємі ω за деяким законом.
Позначимо через f(M, t) питому потужність джерела
в точці M(x,y,z) у момент часу t (аналог інтенсивності
зовнішніх сил в задачах на коливання).
Тоді елементарна кількість тепла за одиницю часу буде
dQ2 f M , t d .
Вся кількість тепла за час ∆t:
Q2 t f ( M , t )d .
(6.3)
149.
3) Q – уся кількість тепла, що йде на змінутемператури в будь-якій точці М за деякий час ∆t, може
бути визначена за законом Ньютона, згідно якого
елементарна кількість тепла dQ прямо пропорційна
зміні температури ∆U за час ∆t і масі елементарної
частини ρdω та дорівнюватиме
dQ = C ∆Uρdω,
де С – питома теплоємність матеріалу тіла, розмірність
Дж
кг К .
Звідси
Q C Ud
(6.4)
150.
враховуючи рівності (6.1) – (6.4), запишеморівняння теплового балансу
C Ud t k div grad U d t f M , t d ,
або
С U t k div grad U t f M , t d 0.
(6.5)
Згідно з основною лемою математичної фізики,
якщо підінтегральна функція неперервна та інтеграл
по довільній області ω дорівнює нулю, то і сама
функція також дорівнює нулю.
Отже,
С U t k div(grad U ) t f ( M , t ) 0.
151.
Поділимо на Cρ∆t і перейдемо до границі при t 0 :U
k
1
lim t C div(grad U ) C f ( M , t )
t 0
або
U
a 2 div(grad U ) F ( M , t ),
t
де
k
;
a
C
2
1
F(M ,t)
f ( M , t ).
C
Якщо врахувати, що
U U U 2U 2U 2U
div(grad U )
.
2
2
2
x x y y z z x
z
y
152.
то отримаємо2
2
2
U
U
U
U
2
a 2
2 F ( M , t ).
2
t
z
y
x
(6.6)
Це тривимірна модель розповсюдження тепла у тілі
V, або просторове рівняння теплопровідності. Тут М
– точка M(x,y,z).
Очевидно, що двовимірна модель буде мати вигляд:
2
2
U
U
U
2
a 2
F ( M , t ),
2
t
y
x
(6.7)
153.
яка описує розповсюдження тепла в дуже тонкій(плоскій) пластині . Тут М – точка M(x,y).
І одновимірна модель:
2
U
2 U
a
F ( M , t ).
2
t
x
(6.8)
Це рівняння теплопровідності для прямолінійного
тонкого стержня (один характерний розмір –
довжина). Тут М – точка з однією координатою x.
Саме з цим рівнянням ми і будемо далі працювати.
Зауважимо, що в силу зроблених нами припущень
величини k, C, ρ сталі. Також вважаємо, що бічна
поверхня стержня теплоізольована.
154.
Проаналізуємо рівняння теплопровідності (6.8):2
U
2 U
a
F ( x, t ),
2
t
x
k
;
a
C
2
1
F ( x, t )
f ( x, t ).
C
Тут x – просторова координата,
t – час,
U(x,t) – температура в точці з координатою х
в момент часу t.
155.
Якщо зафіксувати x = x0, то отримаємо U(x0, t) –закон, за яким змінюється температура в точці x0.
Якщо зафіксувати час t = t0, то отримаємо U(x, t0) –
розподіл температур у стержні в момент часу t0.
Вільний член F(x,t) характеризує наявність джерел
тепла в стержні.
Якщо їх нема, то F(x,t) = 0 і рівняння теплопровідності
набуває простого вигляду
2
U
2 U
a
,
2
t
x
k
.
a
C
2
(6.9)
156.
6.2. Постановка задачі теплопровідностіІз фізичних міркувань випливає, що для
однозначного визначення температури в стержні
довжиною l, крім рівняння теплопровідності,
необхідно задати додаткові три умови, які
складаються з однієї початкової і двох крайових.
157.
Початкова умова для рівняння теплопровідностізадає розподіл температур у всіх точках стержня
в деякий момент часу, який приймаємо за початковий
(t = 0).
Початковий розподіл температур має вигляд:
П.У. U(x,0) = U|t = 0 = φ(х),
де φ(х) – задана функція для всіх x [0; l].
(6.10)
158.
Крайові умови мають виконуватись там, дестержень може мати теплообмін з навколишнім
середовищем, тобто на торцях стержня.
Нехай стержень лежить на осі Ох і один його кінець
збігається з початком координат (x = 0), а другий має
абсцису x = l.
Крайові умови відображають тепловий режим на
кінцях стержня і можуть задаватися по-різному.
Розглянемо деякі з них.
159.
Нехай на кінцях стержня підтримується сталатемпература – U0 на кінці x = 0 і Ul на кінці x = l.
К.У.
де U0, Ul
U 0, t U x 0 U 0 ,
U l , t U x l U l ,
– задані числа (можуть бути і нулі).
(6.11)
160.
Запишемо загальніші крайові умови. Використовуючизакон Ньютона, запишемо тепловий потік Р, що
проходить через одиницю площі за одиницю часу
пропорційно зміні температури на торці стержня:
P h U U ,
(6.12)
де h – коефіцієнт зовнішньої теплопровідності або
коефіцієнт теплообміну, U – температура на кінці
стержня, U* – температура навколишнього
середовища поблизу цього кінця.
161.
При цьому потік вважається додатним, якщо U > U*тобто іде процес охолодження стержня.
Отже, функція U – спадна.
А згідно з законом Фур’є цей самий потік
пропорційний швидкості зміни температури
в напрямку нормалі до торця:
U
P k
.
n
(6.13)
162.
Оскільки вектор нормалі паралельний до осі Ох,то для правого кінця потік буде:
a на лівому:
U
P k
,
x
U
P k
.
x
Тепер запишемо умови на лівому і правому кінцях
стержня:
К.У.
U (0, t )
k
h
U
(
0
,
t
)
U
0
0 ,
x
k U l , t hl U L, t U l .
x
(6.14)
163.
Тут U 0 , U l – задані температури навколишньогосередовища поблизу відповідних кінців.
Оскільки кінці стержня можуть знаходитися в різних
середовищах, то сталі h0, hl взято різними.
Розглянемо окремі випадки:
1) Нехай коефіцієнт теплообміну h = 0, тоді крайова
умова
К.У.
U
0
x
означає, що кінець стержня теплоізольований.
(6.15)
164.
2) Нехай значення коефіцієнт теплообміну h дужевелике. Тоді, наприклад, для лівого кінця маємо:
k U (0, t )
U (0, t ) U 0
h0
x
(6.16)
і, переходячи до границі при h0 ,
отримаємо крайову умову
К.У.
U 0, t U 0 ,
(6.17)
що означає вільний теплообмін з навколишнім
середовищем на кінці х = 0.
Фактично, це те саме, що розглядалося в першому типі
крайових умов.
165.
3) На кінці стержня, не уточнюючи на якому,задається потік, як функція часу
U
f (t ).
x
(6.18)
166.
6.3. Метод Фур’є для розв’язування задачітеплопровідності
Розглянемо задачу теплопровідності у скінченному
стержні довжиною l.
Нехай його кінці відповідають точкам х = 0 та х = l
на осі Ох.
Враховуючи специфіку метода Фур’є, розглянемо ряд
задач з однорідними крайовими умовами.
167.
1) Знайти розподіл температур в стержні, на кінцяхякого весь час підтримується нульова температура,
а початковий розподіл задається функцією φ(x).
Поставимо задачу:
2
U
2 U
a
,
2
t
x
k
,
a
C
2
0 x l ,
t 0 .
168.
П.У. U x,0 x ,К.У.
U (0, t ) 0;
U (l , t ) 0.
(6.19)
Для неперервності U(х; t) в точках (0; 0) і (l; 0)
необхідно вимагати, щоб φ(0) = φ(l) = 0.
Також припускаємо, що функцію φ(x) можна
розкласти по синусах кратних дуг на проміжку [0; l].
Згідно методу Фур’є ненульові розв’язки рівняння, що
задовольняють умови (6.19), шукаємо у вигляді
добутку двох функцій:
U ( x, t ) X ( x) T (t ).
169.
Підставляючи цю функцію у рівняннятеплопровідності, отримаємо:
X ( x) T (t ) a2 X ( x) T (t ),
або
T (t )
X ( x )
2
const 0.
2
a T (t ) X ( x )
170.
Останній факт було досліджено при розв’язуваннізадач про коливання.
Таким чином, рівняння теплопровідності
розпадається на два звичайних диференціальних
рівняння:
X ( x) 2 X ( x) 0
(I)
T (t ) 2 a 2 T (t ).
(II)
171.
Таким чином, розв’язок задачі про поширеннятепла у стержні, на кінцях якого підтримується
нульова температура, а початковий розподіл
температур задається функцією φ(x) шукається за
формулами (6.22), (6.23).
n a 2 n x
sin
U ( x, t ) an exp
t
.
l
n 1
l
2
n x
an ( x ) sin
dx.
l 0
l
(6.22)
l
(6.23)
172.
Зауваження1) Розглянемо випадок, коли на кінцях стержня
задається ненульова температура.
Тоді задача має наступну постановку:
2
U
2 U
a
,
2
t
x
k
,
a
C
2
П.У. U x,0 x ;
0 x l ,
U (0, t ) U 0 ;
К.У.
U (l , t ) U l .
t 0 .
(6.24)
Тут U0 та Ul – сталі температури відповідно на
кінцях х = 0 та x = l.
173.
У цій задачі з неоднорідними крайовими умовамидостатньо зробити підстановку:
l x
x
U ( x, t ) V x, t
U0 Ul ,
l
l
(6.25)
яка зведе її до попередньої задачі відносно функції
V(x, t).
Цю процедуру пропонується виконати студентам
самостійно.
174.
2) Знайти розподіл температур в стержні, на одномукінці якого весь час підтримується нульова
температура, а другий кінець теплоізольвано при
довільній початковій умові.
Поставимо задачу:
2
U
U
2
a
,
2
t
x
П.У. U(x,0) = φ(x),
k
,
a
C
2
0 x l ,
U (0, t ) 0;
К.У. U (l , t )
x 0.
t 0 .
(6.26)
175.
Зазначимо, що тут не суттєво, який кінецьтеплоізольовано. Як бачимо, крайові умови однорідні.
Розв’яжемо цю задачу за методом Фур’є, згідно якого
U ( x, t ) X ( x) T (t ).
розв’язок якого X x A cos x B sin x.
Розпишемо крайові умови:
A 0,
B cos l 0.
(6.27)
176.
Очевидно, що B 0, 0, тоді cos l 0.Звідси
Отже,
2n 1
n
, n 0,1, 2, ...
2l
X n ( x ) Bn
2n 1 x
sin
2l
(6.28)
Розв’яжемо друге рівняння для функції T(t), що
одержується з рівняння теплопровідності:
T (t ) 2 a2 T (t ).
(2n 1) a 2
.
Tn (t ) Cn exp
t
2
l
(6.29)
177.
Отже, маємоU n ( x, t ) X n ( x) Tn (t )
і розв’язок даної задачі шукаємо у вигляді:
U ( x, t ) U n x, t .
n 0
Поклавши
an Bn Cn ,
остаточно будемо мати:
2n 1 a 2
2n 1 x
U ( x, t ) an exp
t sin
.
2l
2l
n 0
(6.30)
178.
Коефіцієнти визначаються із початкової умови, як упопередній задачі:
2
2n 1 x
an ( x ) sin
dx.
l 0
2l
l
(6.31)
Отже, формули (6.30) і (6.31) дають розв’язок даної
задачі.
179.
3) Розв’язати задачу про поширення тепла в стержні,на одному кінці якого стала температура U0, а
другий – теплоізольований.
Поставимо задачу:
2
U
U
2
a
,
2
t
x
k
,
a
C
2
П.У. U(x,0) = φ(x),
0 x l ,
U (0, t ) U 0 ;
К.У. U (l , t )
x 0.
t 0
(6.32)
180.
За методом Фур’є крайові умови мають бутинульовими. Тому проведемо заміну
U ( x, t ) V ( x, t ) U 0.
181.
За методом Фур’є отримаємо(2n 1) a 2 2n 1 x
V ( x, t ) an exp
t sin
,
2l
2l
n 0
2
2n 1 x
dx.
де an ( x ) U 0 sin
l 0
2l
l
Отже, остаточно маємо:
U ( x, t ) V ( x, t ) U 0 .
(6.34)
182.
1а) Розподіл температур в стержні:на кінцях стержня задається нульова температура.
2
U
U
2
a
,
2
t
x
П.У.
k
,
a
C
0 x l ,
2
U x,0 x ;
К.У.
U (0, t ) 0;
U (l , t ) 0.
n a 2 n x
sin
U ( x, t ) an exp
t
.
l
n 1
l
t 0 .
(6.19)
2
n x
an ( x ) sin
dx.
l 0
l
(6.22)
l
(6.23)
183.
1б) Розподіл температур в стержні:на кінцях стержня задається ненульова температура.
2
U
U
2
a
,
2
t
x
П.У.
U x,0 x ;
k
,
a
C
0 x l ,
2
К.У.
U (0, t ) U 0 ;
U (l , t ) U l .
t 0 .
(6.24)
n a 2 n x
sin
V ( x, t ) an exp
t
.
l
n 1
l
(6.22)
2
n x
an ( x ) sin
dx.
l 0
l
(6.23)
l
l x
x
U ( x, t ) V x, t
U0 Ul ,
l
l
(6.25)
184.
2) Розподіл температур в стержні:на одному кінці - нульова температура,
а другий кінець теплоізольвано.
2
U
2 U
a
,
2
t
x
k
,
a
C
2
П.У. U(x,0) = φ(x),
0 x l ,
U (0, t ) 0;
К.У. U (l , t )
x 0.
2n 1 a 2
2n 1 x
U ( x, t ) an exp
t sin
.
2
l
2l
n 0
t 0 .
(6.26)
2
2n 1 x
an ( x ) sin
dx.
l 0
2l
(6.30)
l
(6.31)
185.
3) Задача про поширення тепла в стержні:на одному кінці якого стала температура U0,
а другий – теплоізольований.
2
U
U
2
a
,
2
t
x
k
,
a
C
2
П.У. U(x,0) = φ(x),
0 x l ,
К.У.
t 0
U (0, t ) U 0 ;
U (l , t )
x 0.
(2n 1) a 2 2n 1 x
V ( x, t ) an exp
t sin
,
2l
2l
n 0
(6.32)
2
2n 1 x
an ( x ) U 0 sin
dx.
l 0
2l
(6.34)
l
U ( x, t ) V ( x, t ) U 0 .
186.
6.4. Стаціонарні процеси. Рівняння ЛапласаСтаціонарні процеси моделюються диференціальними
рівняннями з частинними похідними еліптичного типу.
Це процеси різної фізичної природи: коливання
(механічні, звукові, електромагнітні); теплопровідність,
дифузія тощо.
Найпростішим рівнянням такого типу є рівняння
2
2
2
U
U
U
2
U U
f x, y, z ,
2
2
2
x
z
y
яке називається рівнянням Пуассона.
(6.35)
187.
Функція U(x, y, z) двічі диференційована,а функція
f x, y , z – задана в деякій просторовій області V.
Відповідне однорідне рівняння
2
2
2
U U U
U U
0
2
2
2
x
z
y
2
називається рівнянням Лапласа.
(6.36)
188.
Наприклад, таким рівнянням описується стаціонарнийрозподіл температури у тривимірному тілі.
Дійсно, якщо температура U = U(x, y, z, t) не залежить
від часу t, то
U
0
t
і рівняння теплопровідності зводиться до рівняння
Лапласа.
189.
Зауважимо, що у двовимірному випадку рівнянняЛапласа (6.36) набуває вигляду:
2
U
U
U
0,
2
2
x
y
2
2
а в одновимірному:
d U 0.
2
dx
Функцію U називають гармонічною в області V якщо
вона неперервна у ній разом зі своїми похідними
першого та другого порядків і задовольняє рівняння
Лапласа.
190.
У кожній задачі математичної фізики, пов’язаній зрівнянням Лапласа, шуканий розв’язок виділяється
із множини усіх гармонічних функцій за допомогою
додаткової умови, якою є крайова умова.
Завдяки стаціонарності процесу початкова умова
у цих задачах відсутня.
Залежно від способу задання крайової умови
виділяють три крайові задачі:
– задачу Діріхле (першу крайову задачу);
– задачу Неймана (другу крайову задачу);
– мішану (третю крайову задачу).
191.
– задача Діріхле (перша крайова задача):на границі S підтримується певна температура;
– задача Неймана (друга крайова задача):
через границю S надходить певний тепловий потік;
– мішана (третя крайова задача):
на границі S має місце теплообмін із зовнішнім
середовищем, температура якого відома.
192.
6.5. Задача ДіріхлеЦя задача (перша крайова задача) у просторі
формулюється так: знайти функцію U(x, y, z), яка
задовольняє всередині замкненої поверхні S рівняння
Лапласа
U 0
та набуває у кожній точці М поверхні S заданих
значень:
К.У.
U S (M ).
(6.37)
Очевидним можна вважати той факт, що задача Діріхле
завжди має розв’язок.
193.
Дійсно, якщо, наприклад, кожна точка на поверхні тілапостійно підтримується при певній заданій температурі
(яка може бути різною у різних точках поверхні), то у
кожній точці тіла встановиться своя температура, яка і
дає розв’язок задачі Діріхле при заданих крайових
умовах.
Також очевидно, що цей розв’язок буде єдиним.
194.
Аналогічно формулюється задача Діріхле удвовимірному випадку: знайти функцію U(x, y), яка
задовольняє всередині замкненої кривої Г рівняння
Лапласа
U 0
та набуває у кожній точці М кривої Г заданих значень:
К.У.
U Γ (M ).
(6.38)
195.
Зазначимо, що задача Діріхле розв’язується дужепросто в одновимірному випадку, коли розглядається,
наприклад, стаціонарний розподіл температури у
тонкому стержні довжини l з теплоізольованою
бічною поверхнею.
Тоді задача Діріхле ставиться так: знайти функцію
U(x) яка задовольняє рівняння Лапласа для усіх
x 0; l
і набуває на кінцях стержня заданих значень:
К.У. U x x U 0 , U x x Ul .
0
l
(6.39)
196.
Задача Діріхле у цьому випадку має розв’язокUl U0
U
x U0.
l
(6.40)
197.
6.6. Задача НейманаЗадача Неймана (друга крайова задача) формулюється
так: знайти функцію U(x, y, z), яка задовольняє
всередині замкненої поверхні S рівняння Лапласа та її
похідна по напрямку зовнішньої нормалі
U
n
у кожній точці М поверхні S набуває заданих значень:
К.У.
U
n
М .
S
(6.41)
198.
Нагадуємо, що похіднаU
n
пов’язана з потоком тепла через поверхню S.
Аналогічно формулюється задача Неймана для
двовимірного та одновимірного випадків.
199.
6.7. Мішана задачаМішана задача (третя крайова задача) формулюється
так: знайти функцію U(x, y, z),
яка задовольняє всередині замкненої поверхні
рівняння Лапласа, а у кожній точці М поверхні
виконується умова:
К.У.
U
М U S М ,
n S
(6.42)
де функції φ(M), ψ(M) є заданими.
Цю задачу ще називають задачею з косою похідною.
200.
6.8. Рівняння Лапласа в циліндричних координатахНехай U(x, y, z) – гармонічна в деякій області V
функція трьох змінних.
Тоді для неї рівняння Лапласа має вигляд:
2
2
U
U
U
0.
2
2
2
x
z
y
2
(6.43)
Введемо у розгляд циліндричні координати (r, φ, z),
які пов’язані з декартовими координатами
формулами
201.
x r cos ,y r sin ,
z z,
0 r ,
0 2 ,
z .
(6.44)
Звідси зворотній зв’язок:
r x y ,
2
2
y
tg ,
x
z z.
(6.45)
202.
Щоб записати рівняння Лапласа в циліндричнихкоординатах, знайдемо відповідні частинні похідні
функції U(x, y, z), використовуючи формули
диференціювання складеної функції декількох
змінних:
отримаємо:
2U 1 U 1 2U 2U
2
2 0.
2
2
r
r r r
z
(6.46)
Це і є рівняння Лапласа в циліндричних координатах.
203.
Якщо функція U не залежить від z, а лише від x та y,то рівняння Лапласа буде мати вигляд
2U 1 U 1 2U
2
0,
2
2
r
r r r
(6.47)
де r та φ – полярні координати на площині.
Знайдене рівняння є рівнянням Лапласа в полярних
координатах.
204.
Приклад 6.3. Знайдемо розв’язок рівнянняЛапласа в області D, що обмежена двома колами:
Г1 : x 2 y 2 R12
Г 2 : x 2 y 2 R22 ,
якщо значення шуканої функції на колах:
К.У.
U Г R U1 ,
1
де U1 та U2 – сталі.
U
Г R2
U2,
205.
Це може бути, наприклад, задача про стаціонарнийрозподіл температури у кільці між двома колами,
якщо на самих колах температура задана.
Розв’язуємо задачу у полярних координатах.
Очевидно, шукана функція U не залежить від кута φ.
Тоді рівняння Лапласа набуває простішого вигляду:
206.
2U 1 U0.
2
r r
r
Це звичайне диференціальне рівняння другого
порядку, яке допускає пониження порядку.
Інтегруючи його, знайдемо
U С1 ln r C2 .
Визначимо C1 та C2 із крайових умов:
U 1 C 1 ln R1 C 2 ;
U 2 C 1 ln R 2 C 2 ,
207.
звідсиU 2 U1
С1
;
R2
ln
R1
ln R1
C 2 U 1 U 2 U 1
.
R2
ln
R1
Остаточно отримаємо:
r
ln
U U 1 U 2 U 1 R 1 .
R2
ln
R1
208.
6.9. Задача Діріхле для кругаНехай на площині хOу є круг радіуса R з центром в
початку координат. на його колі задана деяка функція
f(φ), де φ – полярний кут.
Треба знайти функцію U = U(r, φ), неперервну у крузі,
яка задовольняє всередині круга рівнянню Лапласа.
Постановка задачі в полярних координатах має вигляд:
2U 1 U 1 2U
2
0,
2
2
r
r r r
К.У.
U R f .
0 r R, 0 2
209.
Припустимо, що f(φ) можна розкласти в ряд Фур’єна [0; 2π].
Перепишемо рівняння Лапласа, домноживши його
на r2 :
2
2
U
U
U
2
r
r
2 0.
2
r
r
Будемо шукати розв’язок за методом Фур’є, подаючи
функцію у вигляді добутку двох функцій, кожна з
яких залежить від однієї змінної:
U (r, ) R(r ) ( ).
(6.48)
210.
Тоді( ) А cos В sin .
n ( ) Аn cos n Вn sin n ,
(6.49)
n 0, 1, 2,...
Розв’язок Коефіцієнти An та Bn залишились
невизначеними. Розглянемо рівняння (ІІ):
r 2 R" (r ) rR ' (r) n2 R(r) 0.
Розв’язок цього рівняння будемо шукати у вигляді
R(r) = rα , де α – невідомий параметр.
Отже,
Rn ( r ) r n .
211.
U ( r, ) r n An cos n Bn sin n .(6.51)
Завдяки лінійності та однорідності рівняння Лапласа
сума частинних розв’язків:
U ( r, ) U n r, r n ( An cos n Bn sin n )
n 0
n 0
(6.52)
буде також розв’язком рівняння Лапласа.
Для знаходження коефіцієнтів An та Bn використаємо
крайову умову:
U
Γ R
f An R n cos n Bn R n sin n .
n 0
212.
A0 nU (r , )
r ( An cos n Bn sin n )
2 n 1
1
An
R n
1
Bn
R n
2
f ( ) cos n d ,
0
(6.53)
2
f ( ) sin n d .
0
Таким чином, розв’язком задачі Діріхле у крузі радіуса R
є функція (6.52) з коефіцієнтами (6.53).
213.
A0 nf ( )
R ( An cos n Bn sin n )
2 n 1
1
R2 r 2
U (r , )
f (t ) 2
dt.
2
2
R 2Rr cos(t ) r
(6.53а)
Отримали розв’язок задачі Діріхле для круга.
Інтеграл в (6.53а) називається інтегралом Пуасона.
214.
Лекція 7. Елементи операційного числення7.1. Застосування операційного числення
при розв’язуванні диференціальних рівнянь
з частинними похідними
Ефективним способом розв’язування диференціальних
рівнянь з частинними похідними є використання
операційних методів, зокрема, перетворення Лапласа.
Природно сподіватися, що застосування цього методу
для розв’язання таких рівнянь приведе до переведення
однієї зі змінних у просторі оригіналів до параметра у
просторі зображень.
215.
Так, якщо в розглядуваному рівнянні невідомою єфункція двох змінних, то застосування операційного
методу до однієї зі змінних приведе до звичайного
диференціального рівняння зображення відносно другої
змінної.
Щоб знайти зображення, отримане рівняння можна
розв’язувати з використанням теорії диференційних
рівнянь або знову застосувати перетворення Лапласа та
одержати скінченне зображувальне рівняння щодо
другого параметра.
Далі застосовуємо обернене перетворення Лапласа
один раз у першому випадку та двічі у другому і
отримаємо в просторі оригіналів шукану функцію [5].
216.
Відомості про операційне численняОзначення 7.1 Оригіналом називається така функція
f (t) дійсного аргументу t, яка задовольняє наступні
три умови:
1) f (t) – однозначна, неперервна або кусковонеперервна разом зі своїми похідними n-го порядку
при t ≥ 0;
2) | f (t ) | росте не швидше, ніж деяка показникова
функція, тобто існують такі сталі додатні числа M і α0,
які не залежать від t і при яких f (t ) M e t
для всіх t ≥ 0;
0
3)
f (t) ≡ 0 при t < 0.
217.
Означення 7.2 Зображенням функції-оригінала f (t)називається функція F(p) комплексної змінної
p = σ + i , яка визначається інтегралом Лапласа:
F ( p ) e pt f (t )dt .
(7.1)
0
Інтеграл Лапласа (7.1) називають перетворенням
Лапласа функції f (t). Відповідність між зображенням і
оригіналом будемо позначати так:
F ( p)
f (t ) , або
f (t )
F ( p ).
Іноді використовують таке позначення: F (p) = L[f (t)],
де символ L означає перетворення Лапласа.
218.
Властивості зображень1) Властивість лінійності
Якщо
f (t ) C1 f1 (t ) C2 f 2 (t ) і при цьому
f1 ( t )
F1 ( p)
f (t )
F (p ) C 1F1 (p ) C 2F2 (p ).
то
f 2 (t )
F2 ( p),
2) Властивість подібності
Якщо f (t ) – оригінал і f (t ) F ( p ) , то при
0
f ( t )
1 p
також оригінал і f ( t ) F .
219.
3) Властивість зміщенняЯкщо оригінал f (t ) F ( p ) , то для довільної сталої α
має місце відповідність:
.
e t f (t ) F ( p ).
4) Властивість запізнення
Якщо оригінал f (t )
F ( p)
і
0 , то
f (t ) e p F ( p ).
220.
5) Властивість диференціювання оригіналаНехай f(t) – оригінал, функція f(t) неперервна і
f (t )
F (p ).
Якщо існує похідна f (t), яка є теж оригіналом, то
f (t ) pF ( p ) f ( 0).
Зокрема, якщо f (0) 0, то диференціювання
оригіналу зводиться до множення зображення на р.
f (n ) (t ) p n F ( p ).
Зауважимо, що ця властивість широко використовується
при розв’язуванні лінійних диференціальних рівнянь із
сталими коефіцієнтами та їх систем.
221.
6) Властивість диференціювання зображенняЯкщо оригінал f (t )
також оригінал і
n
t
f t ,
,
то
F ( p)
n N,
1 n t n f (t ) F n ( p).
7) Властивість інтегрування зображення
Якщо оригінал f (t)
збігається, то
F ( p)
і інтеграл
.
f (t )
F (z )dz .
t
p
F ( z)dz
p
222.
7.2 Зображення згорткиНехай маємо дві функції f(t) , φ(t), t .
Згорткою цих функцій називається інтеграл
f (t ) ( )d
(якщо він існує). Цей інтеграл є функцією від t і
позначається f * φ.
Якщо f(t) і φ(t), є оригіналами, то із означення
оригінала випливає, що
f *
f (t ) ( )d .
Неважко переконатися, що f * φ = φ * f .
223.
Таблиця зображень і оригіналівОригінал
№
f (t )
Зображення
F ( p) e pt f (t )dt
0
1
1
1
p
2
e t
1
p
3
e t
1
p
224.
№Оригінал
Зображення
f (t )
F ( p) e pt f (t )dt
0
4
5
6
7
sin t
p 2 2
cos t
p
p 2 2
sh t
p 2 2
ch t
p
p 2 2
225.
№Оригінал
Зображення
f (t )
F ( p) e pt f (t )dt
0
8
9
e
e
sin t
p 2 2
cos t
p
p 2 2
t
t
t
10
11
n
n
t e
t
n!
p n 1
n!
p n 1
226.
№Оригінал
Зображення
f (t )
F ( p) e pt f (t )dt
0
12
13
14
15
t sin t
t cos t
t sh t
t ch t
p
2 p
2 2
2
p 2 2
p
2
p
2 2
2 p
2
2 2
p 2 2
p
2
2 2
227.
№Оригінал
Зображення
f (t )
F ( p) e pt f (t )dt
0
16
f ( t )
1 p
F
17
e t f (t )
F ( p )
18
f (t a )
e ap F ( p)
19
f (t )
pF ( p ) f (0)
f (t )
p 2 F ( p) pf (0) f (0)
20
228.
7.3 Схема побудови розв’язку диференційногорівняння з частинними похідними
Наведемо схему побудови розв’язку диференційного
рівняння з частинними похідними, де шукана функція
U(x, t) залежить лише від двох змінних x і t.
Нехай вона задовольняє рівняння:
2U
U
2U
U
a 2 b
cU a1 2 b1
f ( x, t ) 0,
x
x
t
t
(7.2)
де a, b, c, a1, b1 – неперервні функції від x, задані на
проміжку 0 ≤ x ≤ l. Нехай треба знайти розв’язок
рівняння (7.2) U(x, t) для напівнескінченної смуги:
0 ≤ x ≤ l, 0 ≤ t < + , що задовольняє задані додаткові
умови
229.
U (x ,0) (x );П.У. U (x , t )
(x ),
t
t 0
U (0, t ) g (t );
U (x , t )
К.У. U (x , t )
U (l , t ),
x
t x l
де , , – сталі.
(7.3)
230.
Задача (7.2) – (7.3) нестаціонарна, оскільки шуканийрозв’язок істотно залежить від початкових умов і
описує так званий неусталений перехідний режим
фізичного процесу.
Застосуємо перетворення Лапласа до функції U(x, t) за
змінною t.
Вважаємо, що функції U(x, t),
є оригіналами.
U ( x , t )
x
і
2U ( x, t )
x 2
231.
Позначивши зображення шуканої функції через U ( x, p ),запишемо наступні співвідношення:
U ( x, t ) U ( x, p );
U ( x, t ) dU
;
x
dx
Тут p розглядається як параметр.
2U ( x, t ) d 2U
.
2
2
x
dx
232.
Для знаходження зображень частинних похідних по tзастосуємо теорему про диференціювання оригіналу.
Одержимо
U (x , t )
pU (x , p ) (x );
t
2U (x , t ) 2
p U (x , p ) p (x ) (x ).
2
t
233.
Вважатимемо, що g(t) – оригінал, тоді крайові умовиу просторі зображень матимуть вигляд
U (x , p ) G ( p );
x 0
dU
pU (x ) U (x , p ) x l ,
dx
x l
де g (t ) G ( p ).
(7.4)
234.
Таким чином, вважаючи, що f(x, t) є оригіналом,операційний метод приводить розв’язання
поставленої нестаціонарної задачі (7.2) – (7.3) до
розв’язання звичайного диференціального рівняння
другого порядку
d 2U
dU
a 2 b
AU B F ( x, p) 0
dx
dx
з крайовими умовами (7.4), де
B a1 p ( x) a1 ( x) b1 ( x);
A c a1 p 2 b1 p;
f ( x, t ) F ( x, p ); p – комплексний параметр.
(7.5)
235.
Приклад 7.1 Кінці струни x = 0 і x = l закріпленіжорстко.
x
Початкове відхилення задано рівністю U ( x,0) A sin ,
l
початкова швидкість рівна нулю.
Знайти відхилення U(x, t) при t > 0.
Задача зводиться до розв’язання диференційного
рівняння:
2U 1 2U
2 2 0,
2
x
a t
236.
яке задовольняє задані додаткові умовиx
U (x ,0) A sin l ;
П.У.
U x ,0 0,
t
U (0, t ) 0;
К.У.
U (l , t ) 0.
237.
Застосуємо перетворення Лапласа до функції U(x, t)за змінною t .
Позначивши зображення шуканої функції через U ( x, p ),
запишемо наступні співвідношення:
U ( x, t ) U ( x, p ),
U ( x, t ) dU
,
x
dx
U ( x, t )
x
pU ( x, p ) A sin
,
t
l
2U ( x, t ) 2
x
p U ( x, p) pA sin .
2
t
l
2U ( x, t ) d 2U
,
2
2
x
dx
238.
Тоді на основі цих співвідношень та сформульованоїзадачі з додатковими умовами, одержимо у просторі
зображень наступну задачу
d 2U p 2
p
x
2 U 2 A sin
2
dx
a
a
l
К.У.
U (x , p ) 0;
x 0
U (x , p ) x l 0.
(7.6)
239.
Розв’язок лінійного неоднорідного диференціальногорівняння другого порядку шукаємо у вигляді:
U ( x, p ) U 0 ( x, p ) U ( x, p ),
де
U 0 ( x, p )
– загальний розв’язок відповідного
однорідного рівняння
d 2U 0 p 2
2 U 0 0.
2
dx
a
2
p
Характеристичне рівняння k 2 2 0.
a
p
Звідси k1,2 .
a
240.
Тоді загальний розв’язок однорідного рівняння будеU 0 ( x, p) C1e
px
a
C2e
px
a
.
px
px
U 0 (x , p ) C 1 exp
C 2 exp
.
a
a
Частинний розв’язок неоднорідного рівняння U ( x, p)
знайдемо у вигляді
x
U ( x, p ) B sin
.
l
Для знаходження невідомої сталої B підставимо
частинний розв’язок у (7.6) та отримаємо рівняння
2 p 2 x
p
x
B 2 2 sin
2 A sin .
a
l
a
l
l
241.
ЗвідсиAp
B
.
2 2
a
2
p 2
l
Тоді
Ap
x
U ( x, p )
sin .
2 2
a
l
2
p 2
l
242.
Загальний розв’язок рівняння буде мати вигляд:U ( x, p) C1e
px
a
C2e
px
a
Ap
x
sin
2 2
a
l
2
p 2
l
Ap
x
px
px
U (x , p ) C 1 exp
sin
.
C 2 exp
2 2
l
a
a p2 a
l2
Підставляючи розв’язок у крайові умови, знайдемо
невідомі константи
U (x , p ) 0;
C 1 0;
x 0
C 2 0.
U (x , p ) x l 0.
243.
Отже, оригіналом дляU ( x, p )
з врахуванням формули оберненого перетворення
p
p
2
cos
2 2
a
at
l
l2
буде функція
at
x
U ( x, t ) A cos
sin
,
l
l
яка є розв’язком поставленої задачі.
244.
Приклад 7.2 Знайти розв’язок рівняннятеплопровідності
2
U
U
2
a
,
2
t
x
який задовольняє початковим і крайовим умовам
n x
U ( x,0) A sin
;
l
0 x l , U (0, t ) 0, U (l , t ) 0.
Задача зводиться до розв’язання диференційного
рівняння
2U 1 U
2
0,
2
x
a t
245.
яке задовольняє задані додаткові умовиП.У.
К.У.
n x
U (x ,0) A sin
,
l
U (0, t ) 0;
U (l , t ) 0.
246.
Застосуємо перетворення Лапласа до функції U(x, t)за змінною t. Позначивши зображення шуканої функції
через
U ( x, p ),
запишемо наступні співвідношення:
U ( x, t ) U ( x, p ),
U ( x, t ) dU
,
x
dx
U ( x, t )
n x
pU ( x, p ) A sin
.
t
l
2U ( x, t ) d 2U
,
2
2
x
dx
247.
Вихідне рівняння після підстановки отриманихформул та крайові умови у просторі зображень
набудуть вигляду
d 2U
p
A
n x
2 U 2 sin
.
2
dx
a
a
l
К.У.
U (x , p ) 0;
x 0
U (x , p ) x l 0.
248.
Розв’язок отриманого лінійного неоднорідногодиференціального рівняння другого порядку
шукатимемо у вигляді:
U ( x, p ) U 0 ( x, p ) U ( x, p ),
де U 0 ( x, p ) – загальний розв’язок відповідного
однорідного рівняння:
d 2U 0 p
2 U 0 0,
2
dx
a
характеристичне рівняння:
Звідси
k1, 2
p
.
a
p
k 2 0.
a
2
249.
Тоді загальний розв’язок однорідного рівняння будеU0 ( x, p) C1e
px
a
C2e
px
a
.
px
px
C 2 exp
.
U 0 (x , p ) C 1 exp
a
a
Частинний розв’язок неоднорідного рівняння U ( x, p)
знайдемо у вигляді
n x
U ( x, p ) B sin
.
l
250.
Для знаходження невідомої сталої підставимочастинний розв’язок у (7.6) та отримаємо рівняння
n 2 2 p n x
1
n x
B 2 2 sin
2 A sin
.
a
l
a
l
l
Звідси
Тоді,
A
B
.
2 2 2
na
p
l2
A
n x
U ( x, p )
sin
.
2 2 2
na
l
p
l2
251.
Загальний розв’язок рівняння буде мати вигляд:U ( x, p ) C1e
px
a
C2e
px
a
A
n x
sin
2 2 2
na
l
p
l2
px
px
A
n x
U (x , p ) C 1 exp
C 2 exp
sin
.
2 2 2
na
a
l
a
p
l2
Підставляючи розв’язок у крайові умови, знайдемо
невідомі константи
U (x , p ) 0;
x 0
U (x , p ) x l 0.
C 1 0;
C 2 0.
252.
Отже, оригіналом дляU ( x, p )
з врахуванням формули оберненого перетворення
1
e
2 2 2
n a
p
l2
n 2a 2 2
l2
t
2 2 2
1
n
a
exp
t
2 2 2
2
na
l
p
l2
буде функція
U ( x, t ) Ae
n 2 a 2 2
t
2
l
n x
sin
,
l
яка і буде розв’язком поставленої задачі.
253.
Перелік використаних джерел1. Араманович И.Г. Уравнения математической
физики / И.Г. Араманович, В.И. Левин. – М.: Наука,
1964. – 286 с.
2. Владимиров В.С. Уравнения математической физики
/ В.С. Владимиров. – М. : Наука, 1967. – 436 с.
3. Кальницкий Л.А. Специальный курс высшей
математики / Л.А. Кальницкий, Д.А. Добротин, В.Ф.
Жевержеев. – М.: Высшая школа, 1976. – 389 с.
4. Кошляков Н.С. Уравнения в частных производных
математической физики / Н.С. Кошляков, Э.Б. Глинер,
М.М. Смирнов. – М.: Высшая школа, 1970. – 710 с.
254.
5. Краснов М.Л. Функции комплексного переменного.Операционное исчисление. Теория устойчивости /
М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. – М.:
Наука, 1971. – 256 с.
6. Полянин А.Д. Справочник по линейным
уравнениям математической физики / А.Д. Полянин. –
М.: физматлит, 2001. – 576 с.
7. Смирнов М.М. Задачи по уравнениям
математической физики / М.М. Смирнов. – М.: Наука,
1975. – 126 с.
8. Чинаев П.И. Высшая математика. Специальные
главы / П.И. Чинаев, А.А. Черенков, Н.А. Минин,
А.Ю. Перевозников. – К.: Вища школа, 1977. – 368 с.


















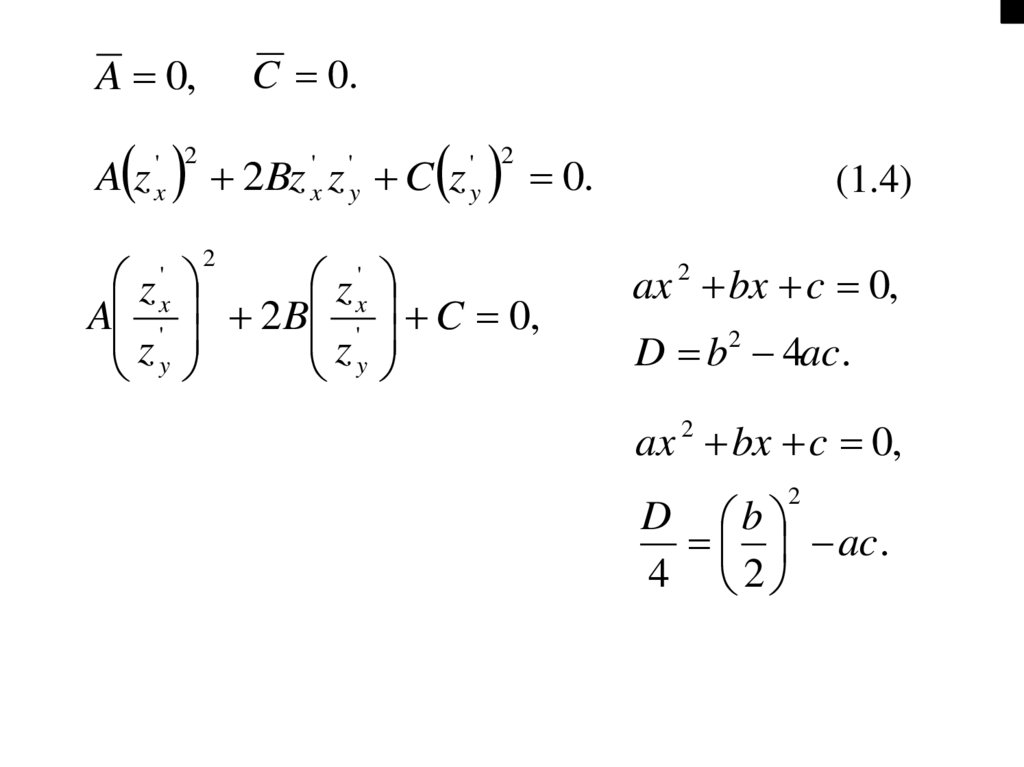


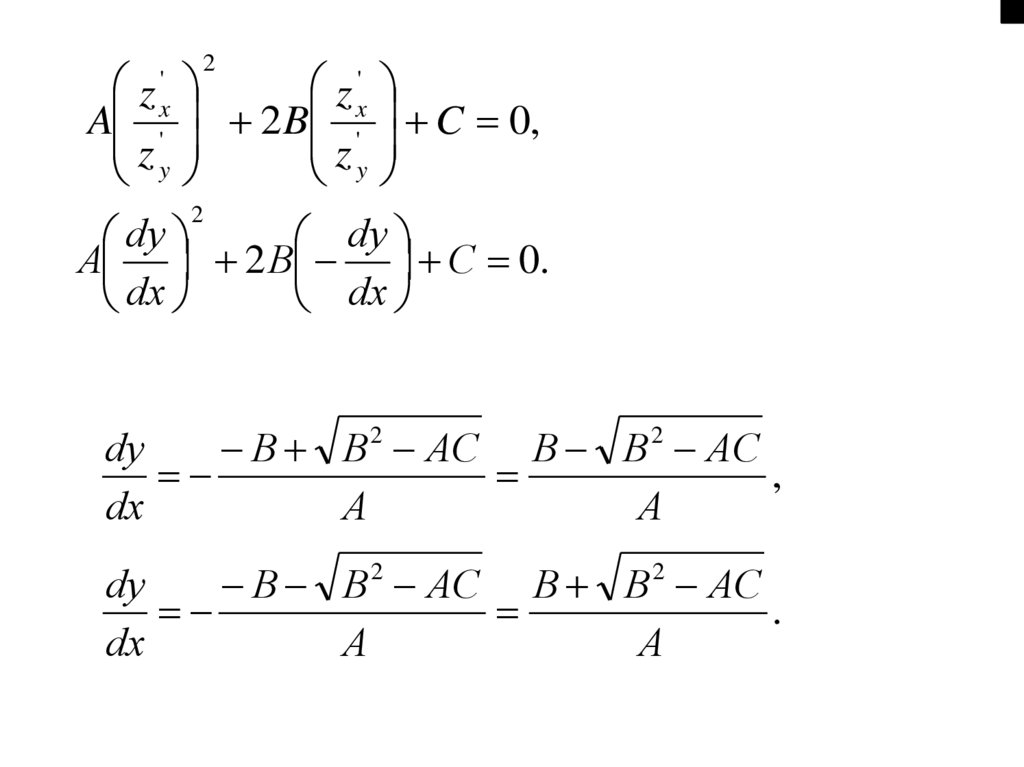















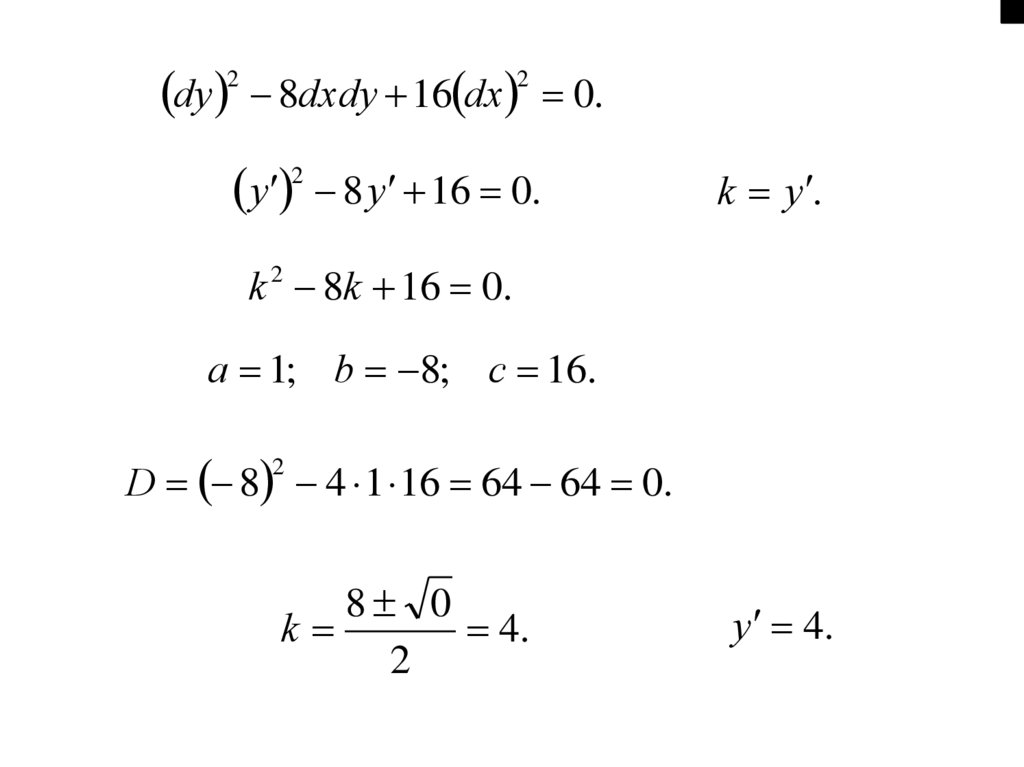
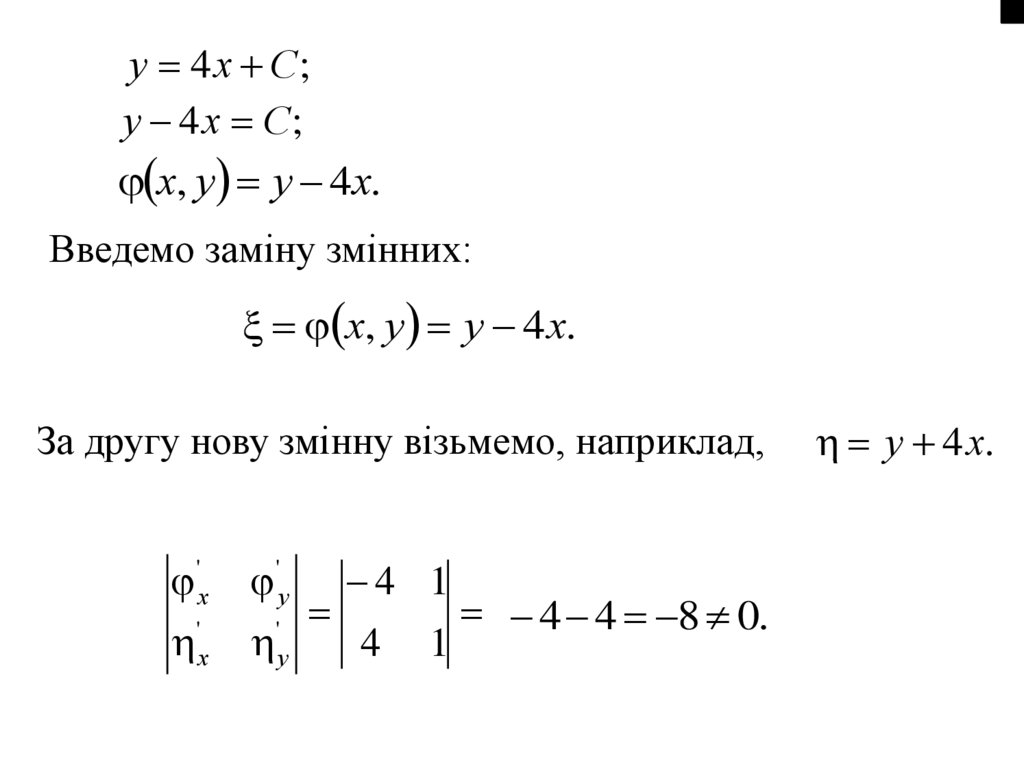


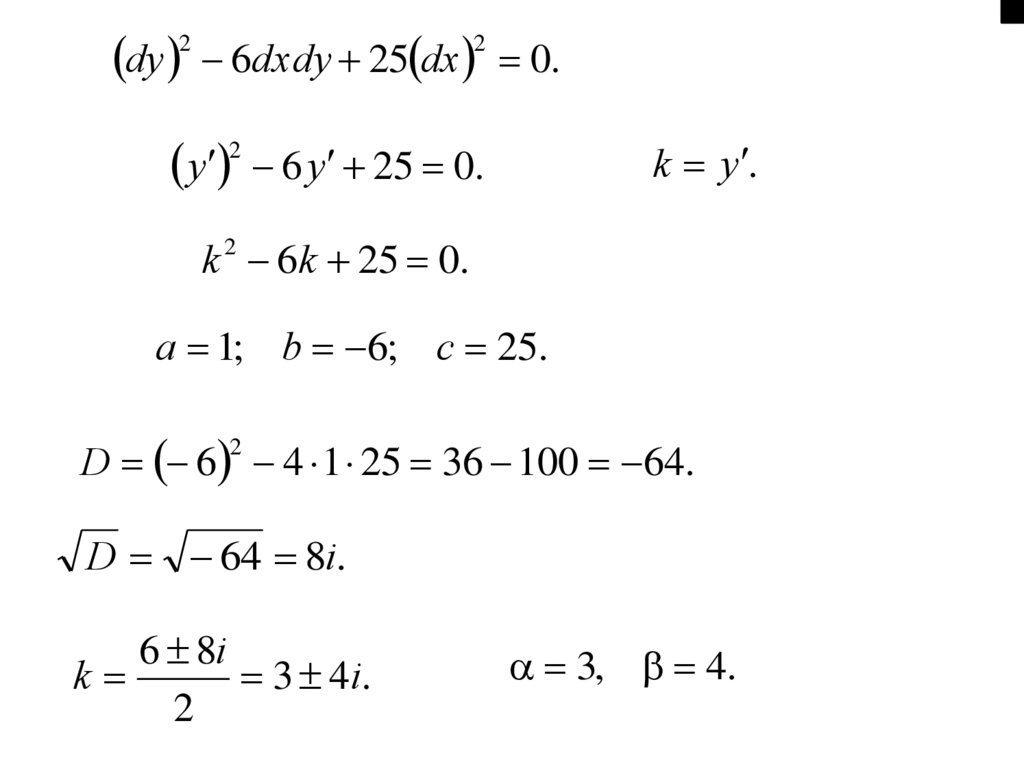
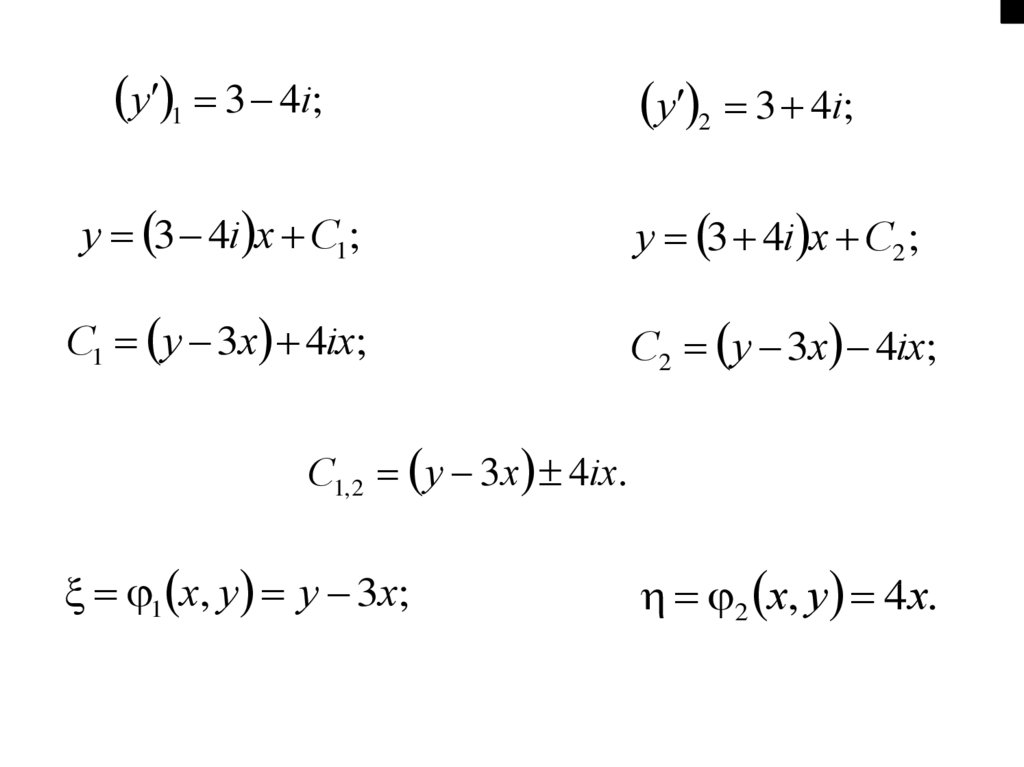
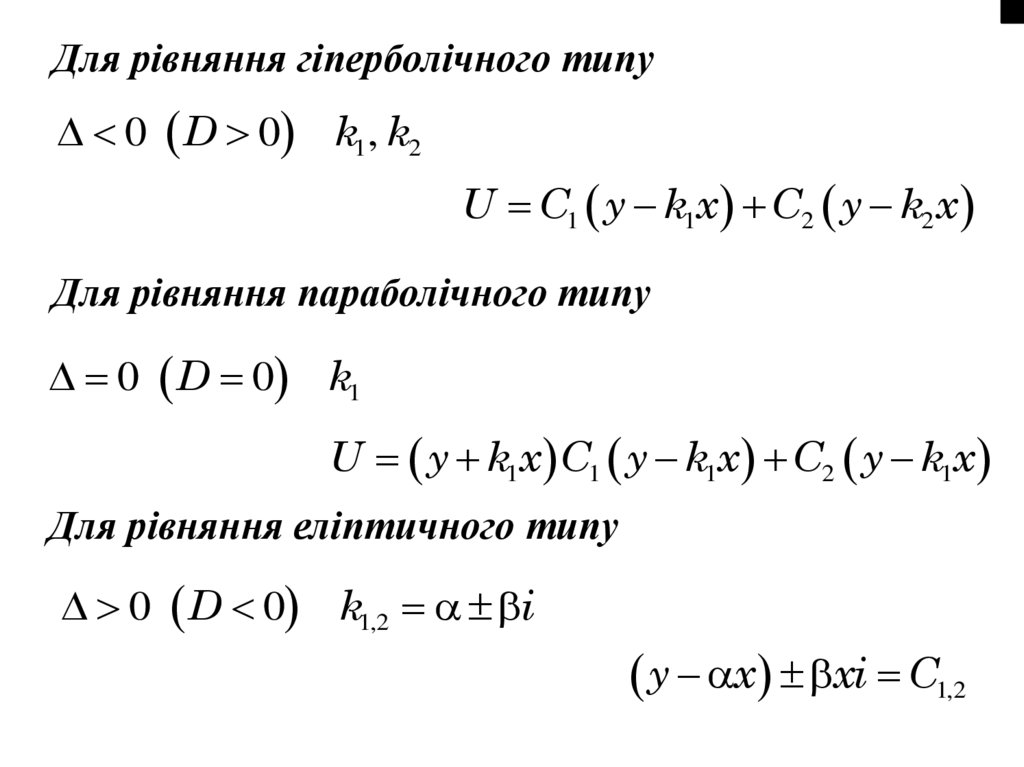



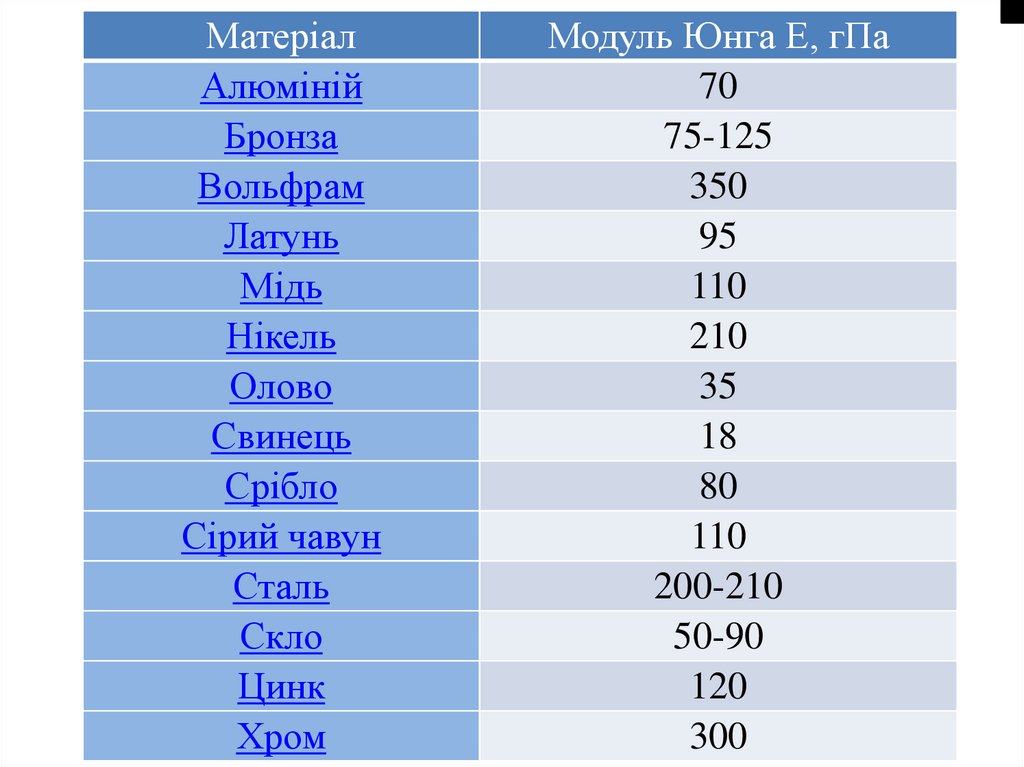


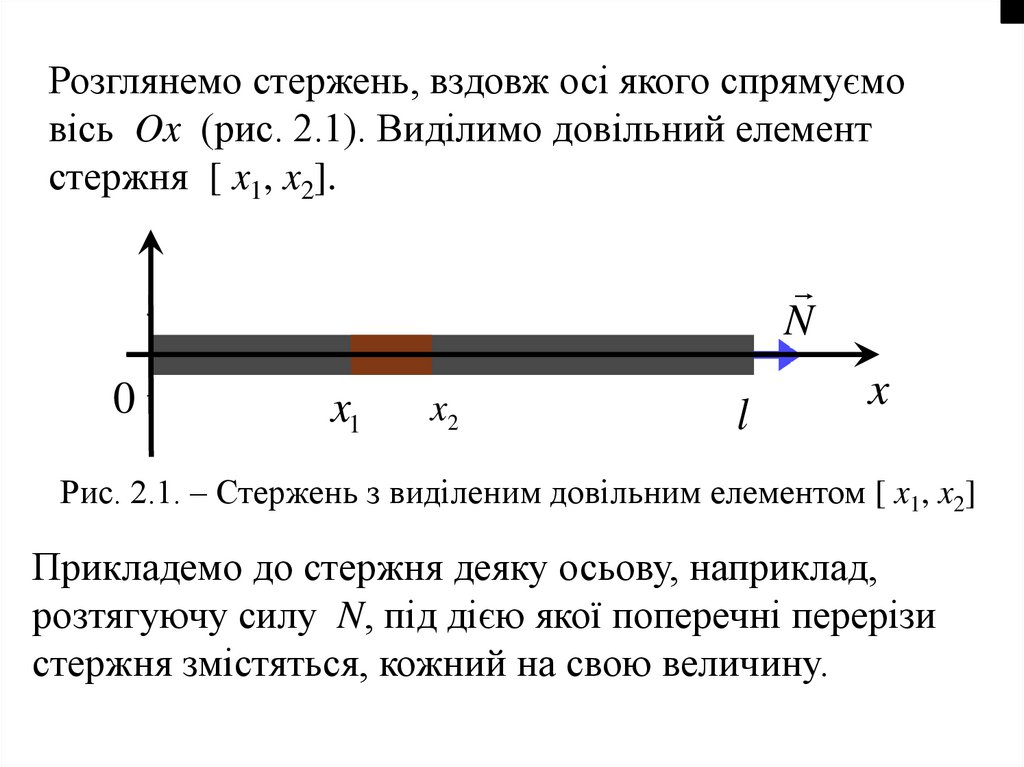














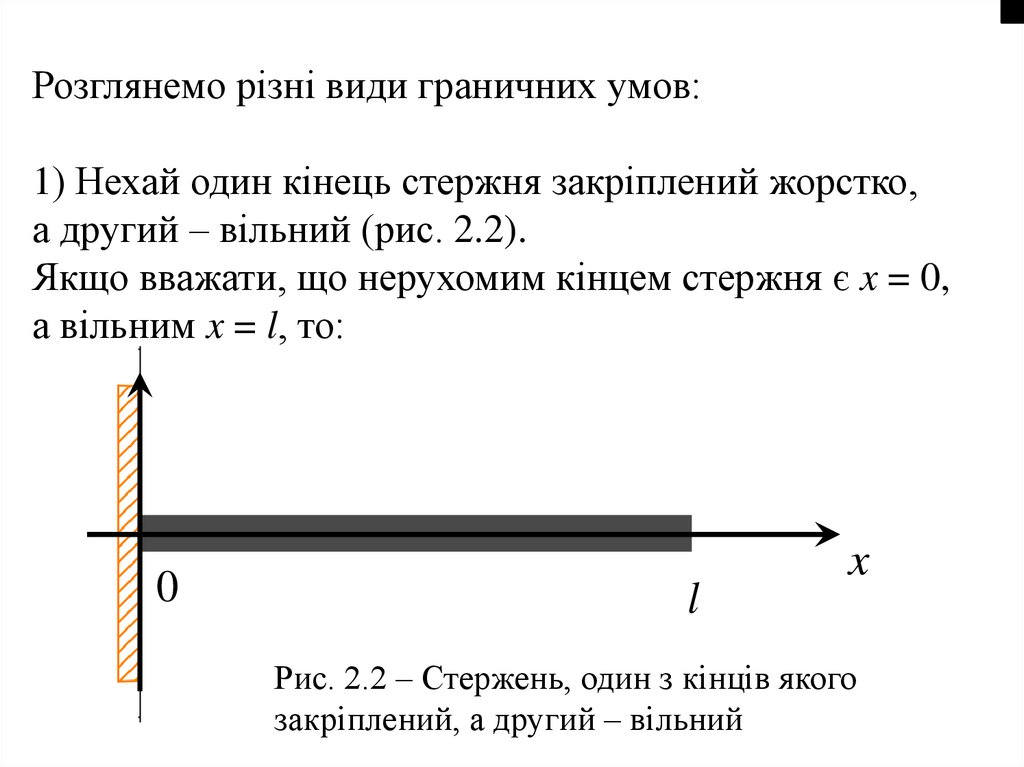

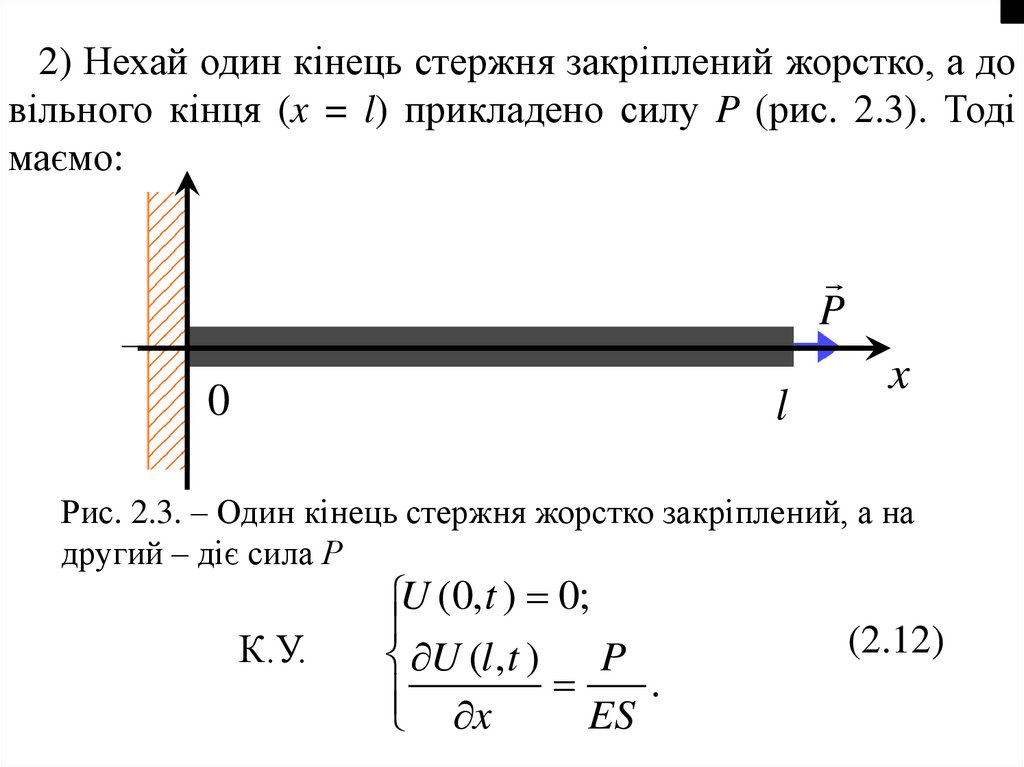
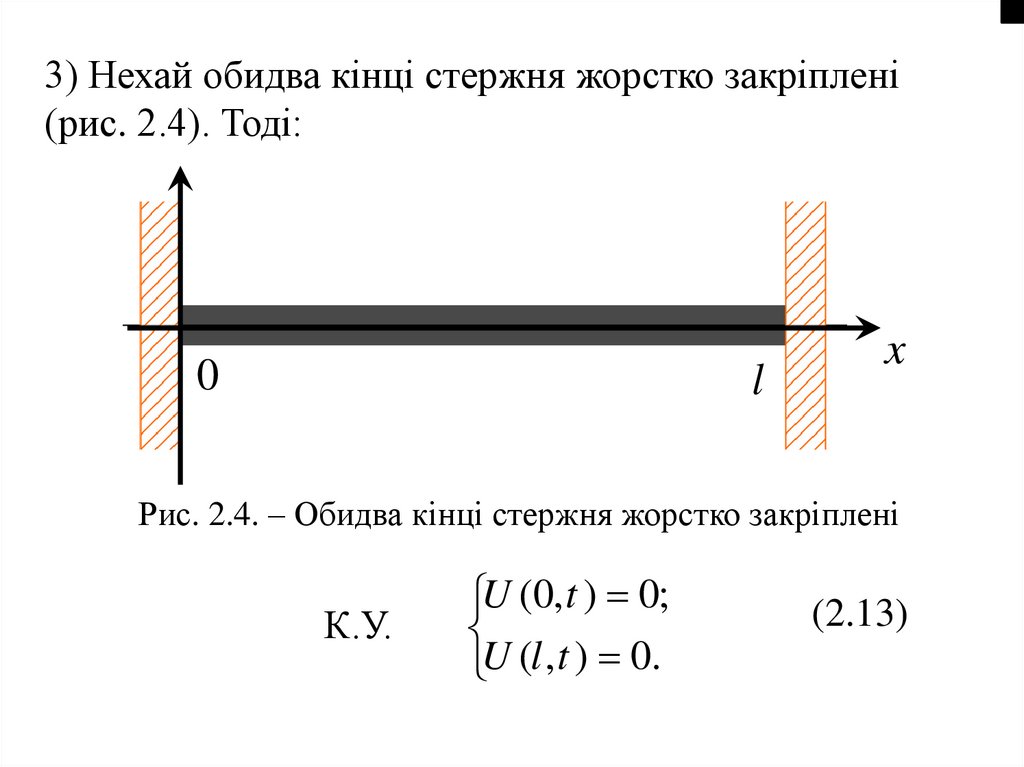
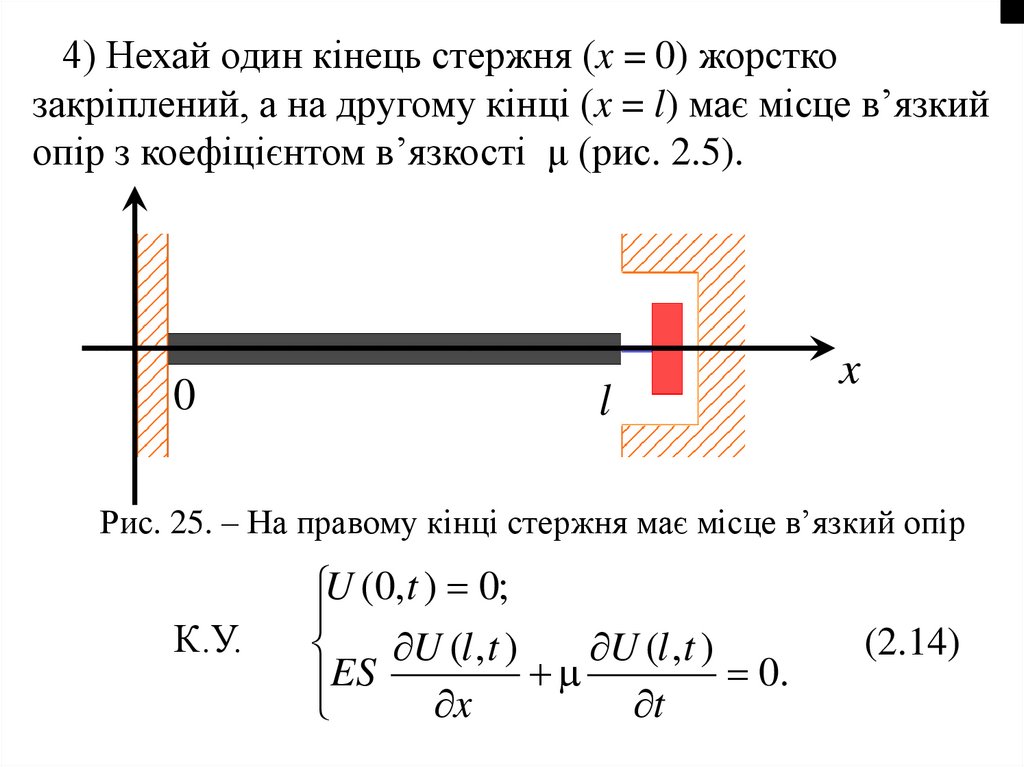






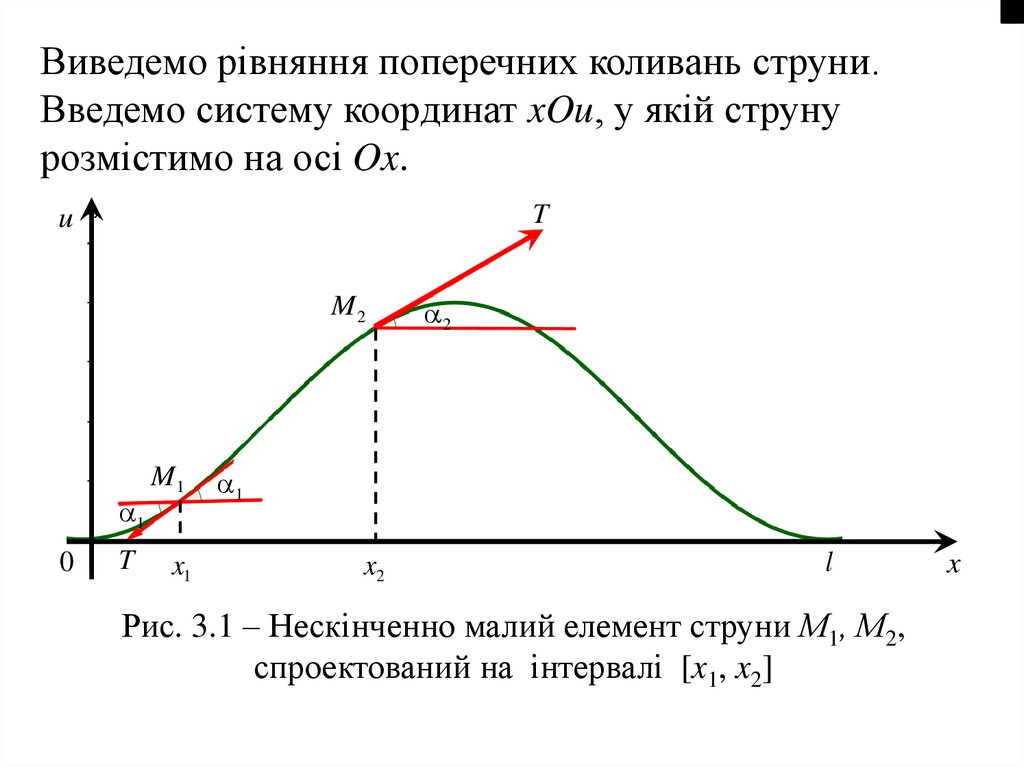

























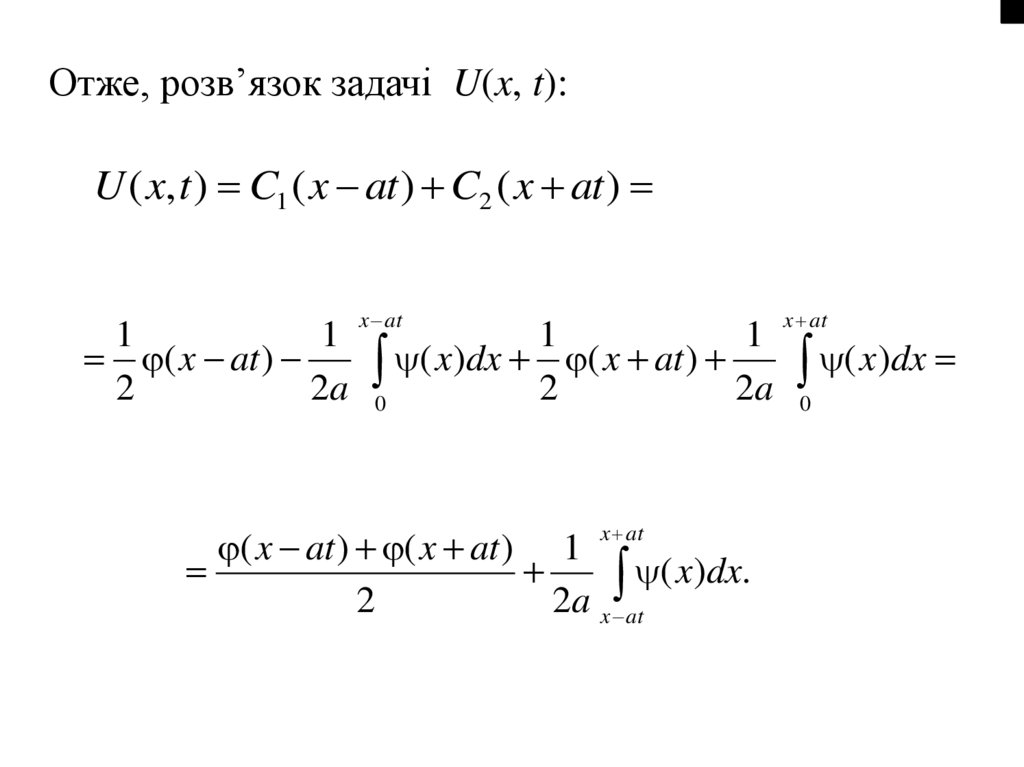


















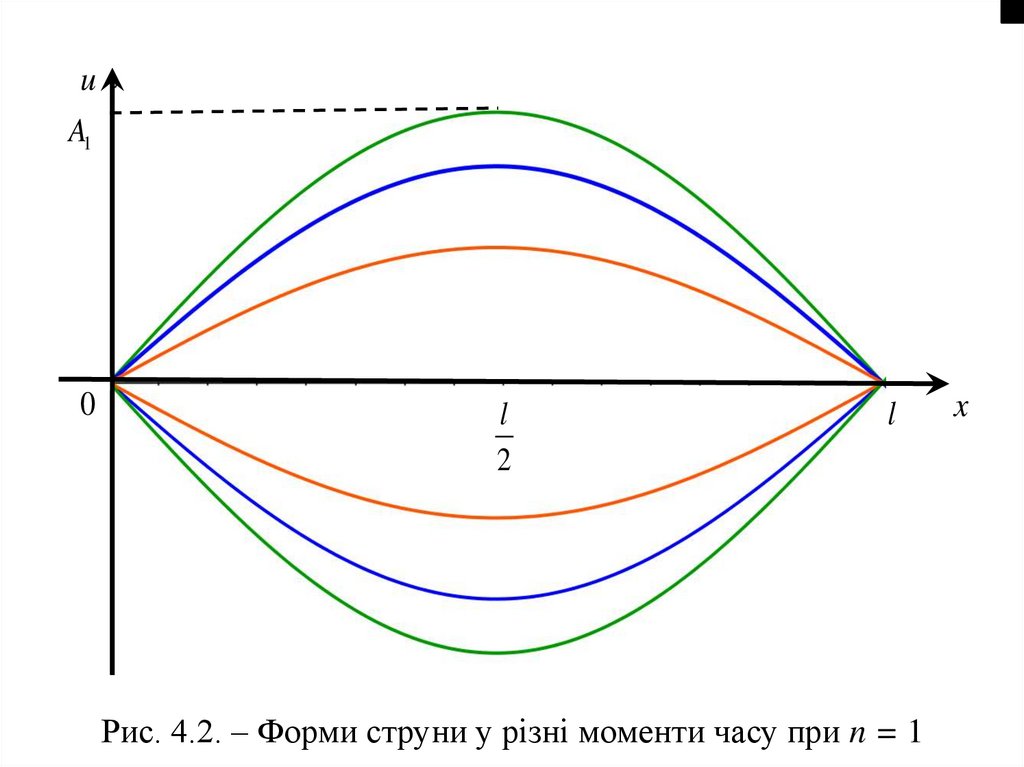
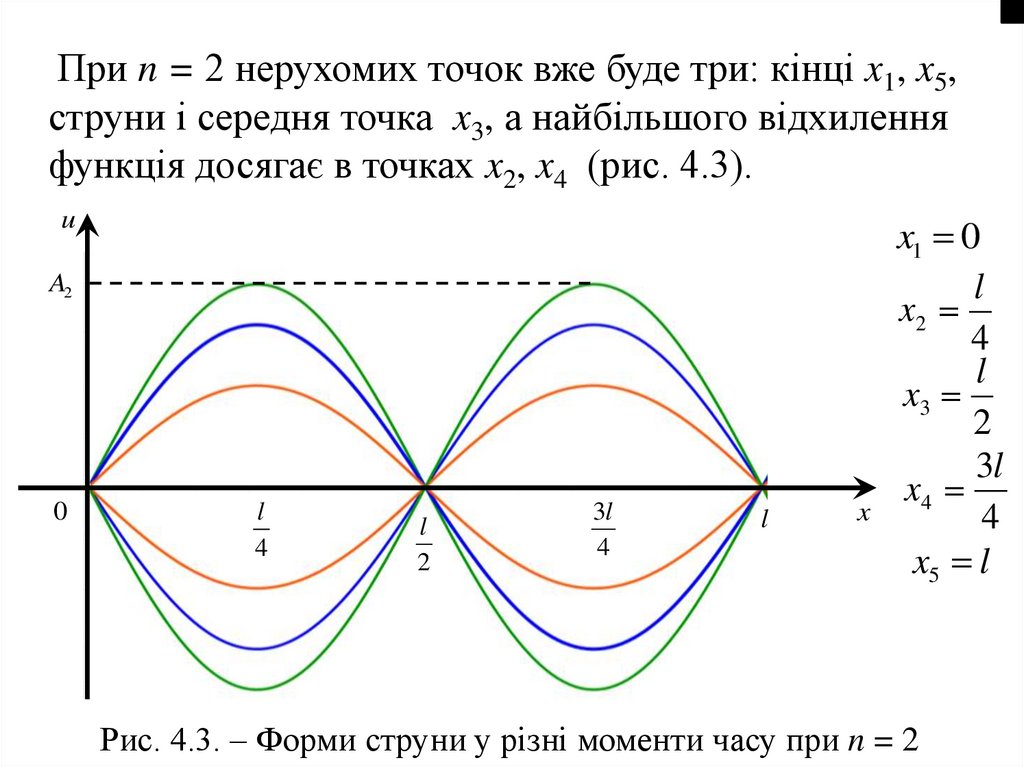




































































































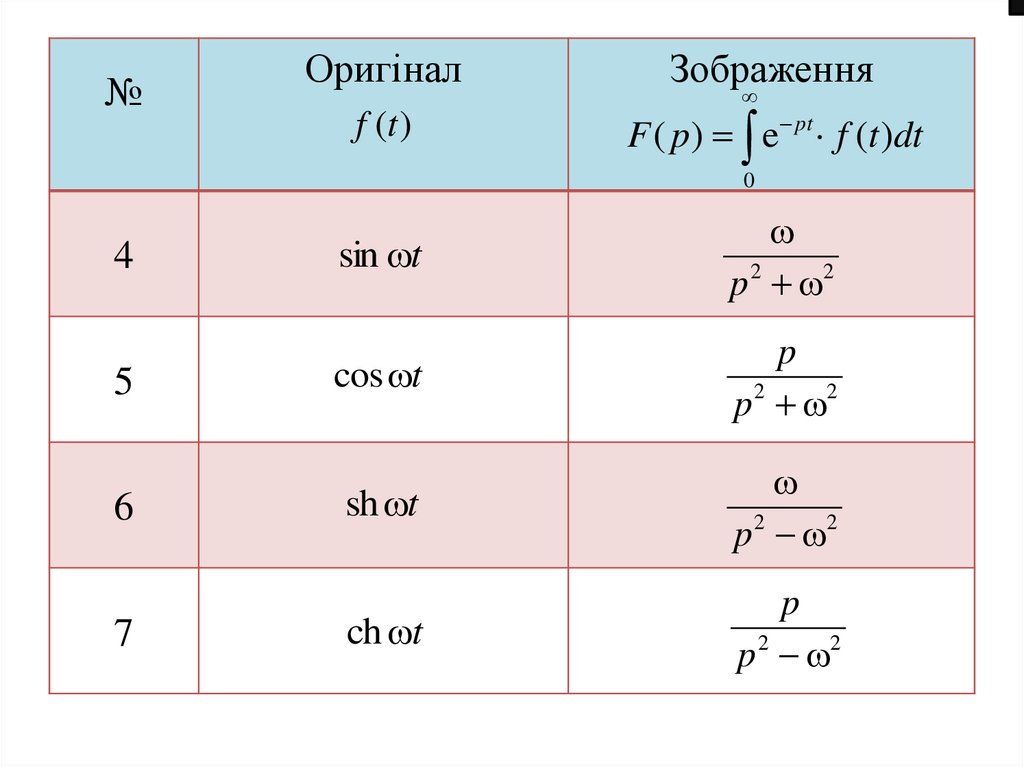

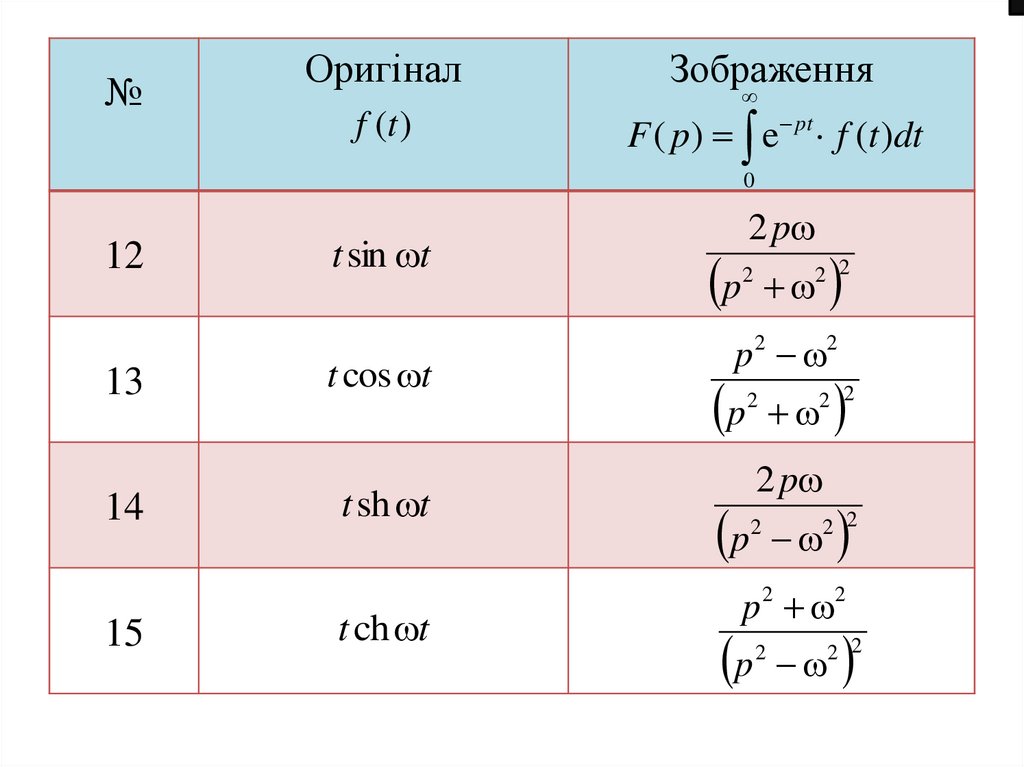
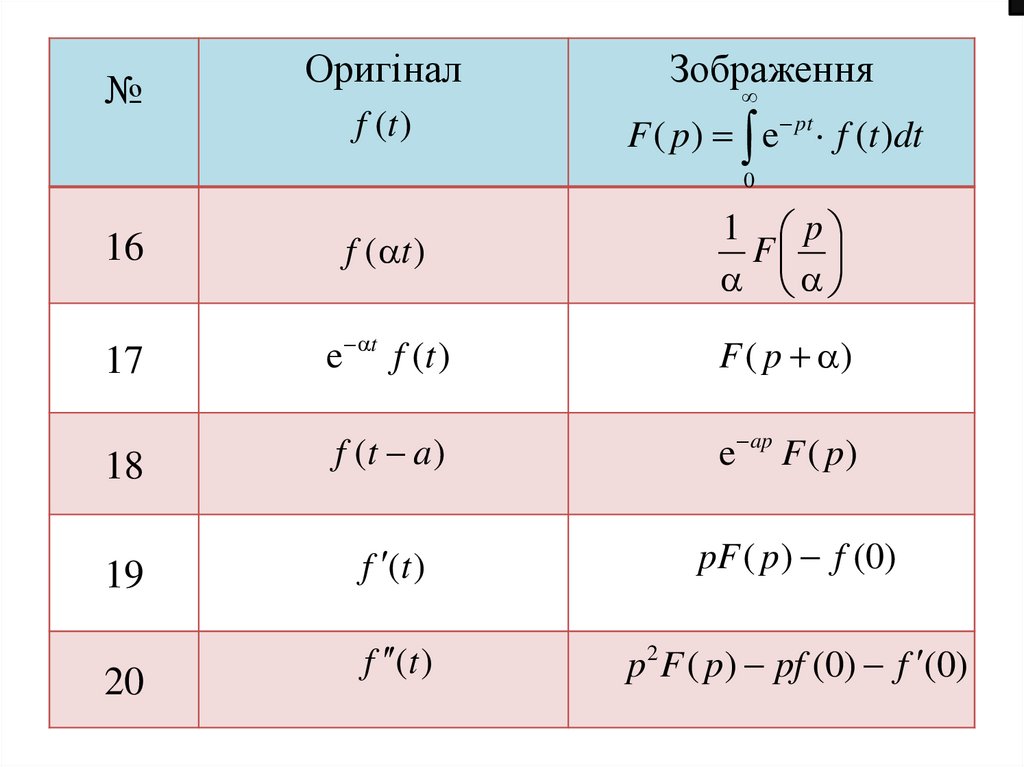

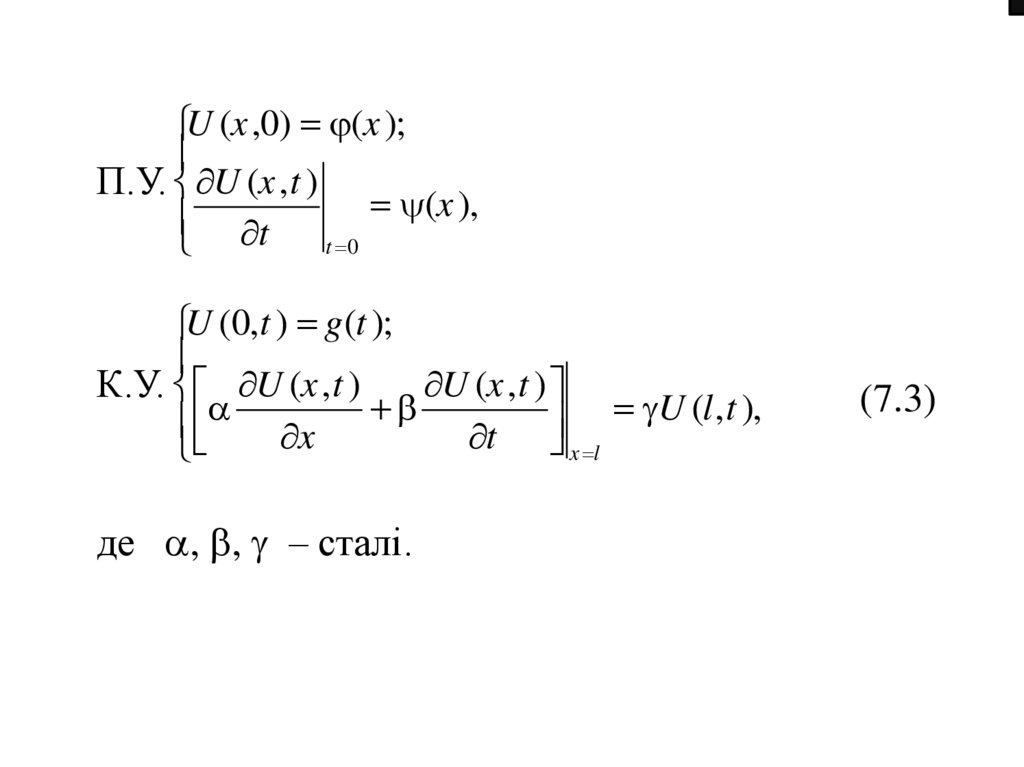

























 mathematics
mathematics








