Similar presentations:
Елементи прямокутного трикутника
1.
Геометрія 8 класПідготувала: Голуб Г.С.,
учитель математики
Соколовобалківської загальноосвітньої школи І-ІІІ ст.
Новосанжарської районної ради Полтавської області
2.
Елементи прямокутноготрикутника
В
∆АВС- прямокутний
АВ = с - гіпотенуза
ВС = а і АС = b - катети
α - гострий кут
ВС - протилежний катет куту α
і АС - прилеглий катет
c
а
α
А
90°
b
C
3.
Означення синуса, косинуса і тангенсагострого кута прямокутного трикутника
4.
Історія математикиВидатний індійський астроном і математик
АРІАБХАТА
Пам'ятник Аріабхаті на
території університету в Пуне
5.
Історія математикиАбу Абдаллах Мухаммад ібн
Джабір ібн Сінан ал-Баттані
Абу-л-Вафа Мухаммад ібн Мухаммад
ібн Яхья ібн Исмаіл ібн ал-Аббас алБузджані
видатний середньовічний астроном і
математик
арабский астроном і математик з
Хорасана
6.
Практична роботаВисновок
7.
Побудова кута за його тригонометричнимифункціями
3
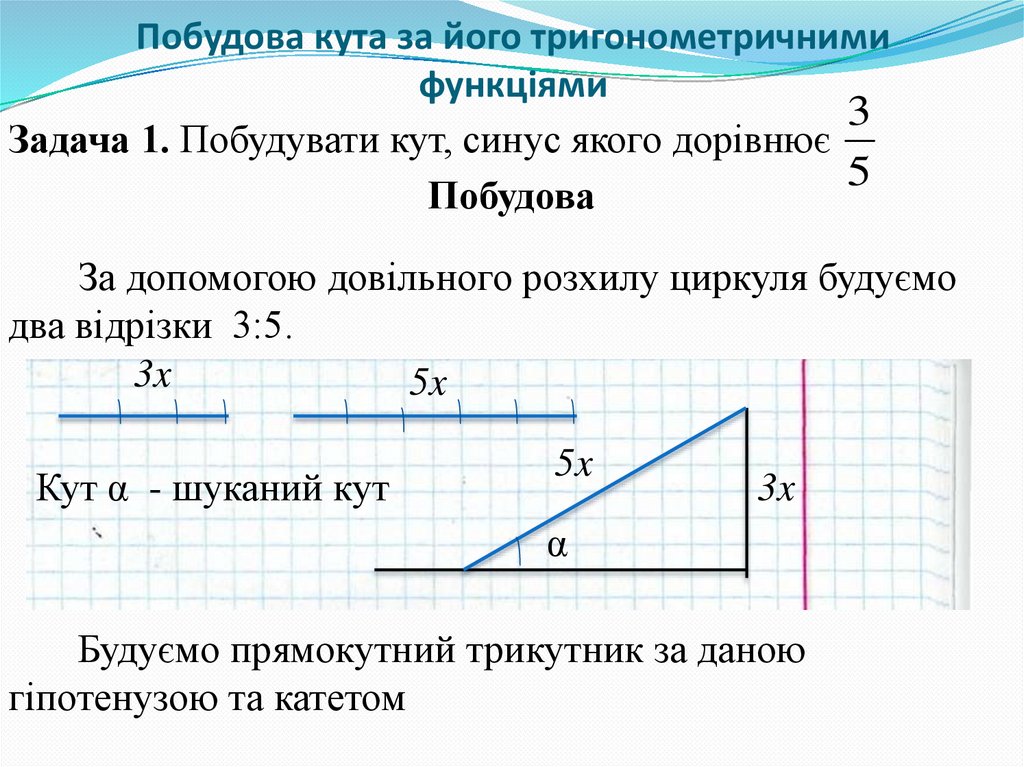
Задача 1. Побудувати кут, синус якого дорівнює
5
Побудова
За допомогою довільного розхилу циркуля будуємо
два відрізки 3:5.
3x
5x
Кут α - шуканий кут
5x
3x
α
Будуємо прямокутний трикутник за даною
гіпотенузою та катетом
8.
Побудова кута за його тригонометричнимифункціями
2
Задача 1. Побудувати кут, косинус якого дорівнює
3
Побудова
За допомогою довільного розхилу циркуля будуємо
два відрізки 2:3.
2x
3x
Кут α - шуканий кут
3x
α 2x
Будуємо прямокутний трикутник за даною
гіпотенузою та катетом
9.
Побудова кута за його тригонометричнимифункціями
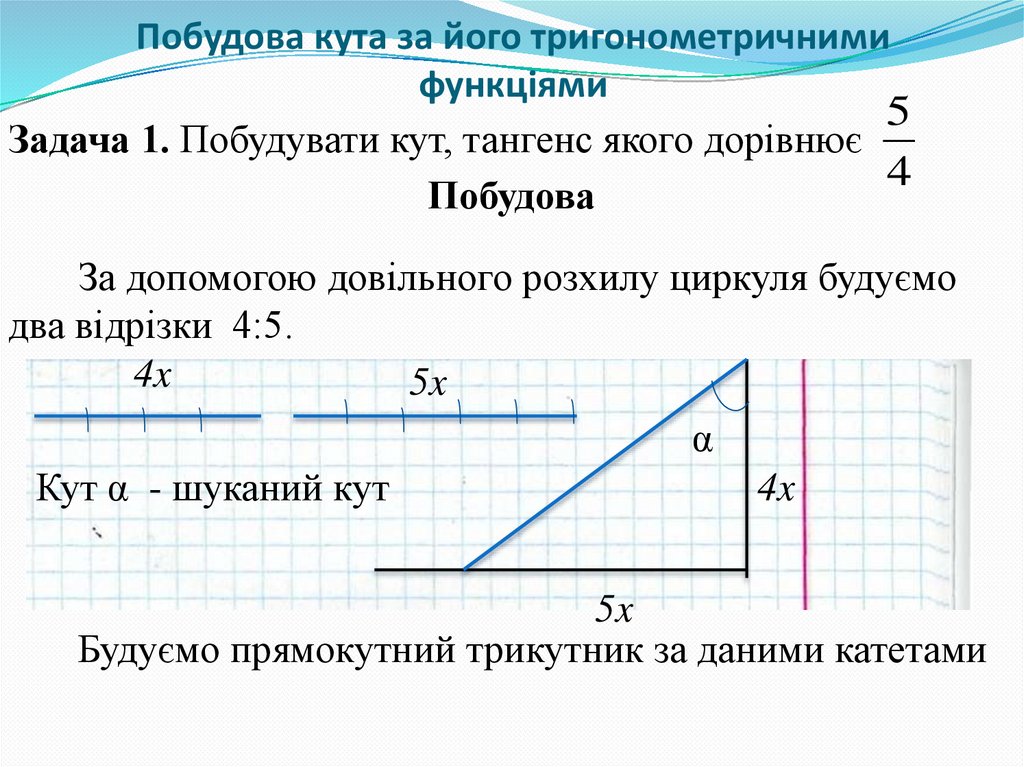
5
Задача 1. Побудувати кут, тангенс якого дорівнює
4
Побудова
За допомогою довільного розхилу циркуля будуємо
два відрізки 4:5.
4x
5x
α
Кут α - шуканий кут
4x
5x
Будуємо прямокутний трикутник за даними катетами
10.
Розмірковуємо1. Чи правильна нерівність sinα > 1? Відповідь
пояснити.
2. Чи правильна нерівність cosα > 1? Відповідь
пояснити.
3. Чи правильна нерівність tgα > 1? Відповідь
пояснити.
Висновок
Значення sinα , cosα не може бути більше одиниці,
тому, що катет завжди менший від гіпотенузи.
Значення tgα , сtgα може бути більше одиниці і менше
одиниці, тому, що катети можуть бути і менше і більше
один одного.
11.
Розв'язування вправ усно12.
Розв'язування вправ усно13.
Розв'язування вправ усно14.
Розв'язування вправ самостійноПеревірка
У ∆АВС
BC
AB
BC
sin
; cos
; tg
.
AC
AC
AB
У ∆BDA
BD
AD
sin
; cos
; tg BD .
AB
AB
AD
15.
Розв'язування вправ самостійно+
+
+
+
+
+
16.
Розв'язування вправРозв'язання
BC
8
sin
; sin
0,5;
AВ
17
AС
cos
;
AВ
15
cos
0,9;
17
BC
tg
,
AС
8
tg
0,5.
15
17.
Розв'язування вправРозв'язання
ABC DBC .
DC
tg DBC
, tg DBC 1,5 0,5;
BС
3
АC
tg АBC
,
D
BС
4
tg АBC 1,3.
3
C
tg АBC tg DBC .
А
В
18.
Розв'язування вправРозв'язання
4,1
sin 35
0,5616;
7,3
6
cos 40
0,8219;
7,3
4,1
tg
0,6833.
6
19.
Розв'язування вправДано: ∆АВС , С 90 , АС=24см, ВС=7см
Знайти: 1) cos A.
24 см
АС Розв'язання
А
cos A
.
АВ
2
2
2
За теоремою Піфагора AВ АС BC .
AВ 24 7 546 49 25(см).
24
cos A 0,96.
25
C
2
2
7 см
В
20.
Розв'язування вправРозв'язання
За теоремою Піфагора AВ
2
АС BC . А
2
ВС 15 9 (15 9)(15 9)
6 24 6 6 4 6 2 12(см).
АС cos A 9 3 0,6.
cos A
,
15 5
АВ
BС
12 4
sin A
, sin A 0,8.
АВ
15 5
2
2
2
9 см
C
В
21.
ВикористаноПідручник Геометрія 8 клас/
М.І.Бурда, Н.А.Тарасенкова/Київ, Зодіак-Еко, 2008



















 mathematics
mathematics








