Similar presentations:
Співвідношення між сторонами і кутами прямого трикутника
1.
2.
Дайте означення синуса, косинуса ітангенса гострого кута прямокутного
трикутника.
Доведіть основну тригонометричну
тотожність.
Доведіть формули доповнення.
Назвіть значення тригонометричних
функцій кутів 30°, 45°, 60°.
3.
tg 603
3
0
cos 30
2
2
2
1
1
1 1
sin30 tg 45
2
2
0
0
2 3 sin60 tg30
0
0
3
3
3
3
2 1
2 3
2 3
2 3
3
3
2
3
3 3
2
4.
Катет, протилежнийдо кута α, дорівнює:
α
с
в
а
добутку гіпотенузи на sin α
а = c·sin α
добутку прилеглого катета на tg α
a = b·tg α
5.
Катет, прилеглийдо кута α, дорівнює:
α
с
в
β
а
добутку гіпотенузи на cos α
а = c·cosα
відношенню протилежного катета
до tg α
a
b
tg
6.
αГіпотенуза дорівнює:
с
в
а
β
відношенню протилежного катета
a
до sinα
c
sin
відношенню прилеглого катета
до cosα
b
c
cos
7.
Шуканасторона
Протилежний
катет
Прилеглий
катет
Гіпотенуза
Спосіб знаходження
Катет, протилежний до кута α,
дорівнює:
• добутку гіпотенузи на sin α;
• добутку прилеглого катета на tg α
Катет, прилеглий до кута a, дорівнює:
• добутку гіпотенузи на cos α;
• відношенню протилежного катета до
tg α
Гіпотенуза дорівнює:
•відношенню протилежного катета до
sin α
•відношенню прилеглого катета до cos α
Формула
а = c· sin α
a = b· tg α
b = c ·cos α
b
a
tg
a
sin
b
c
cos
c
8.
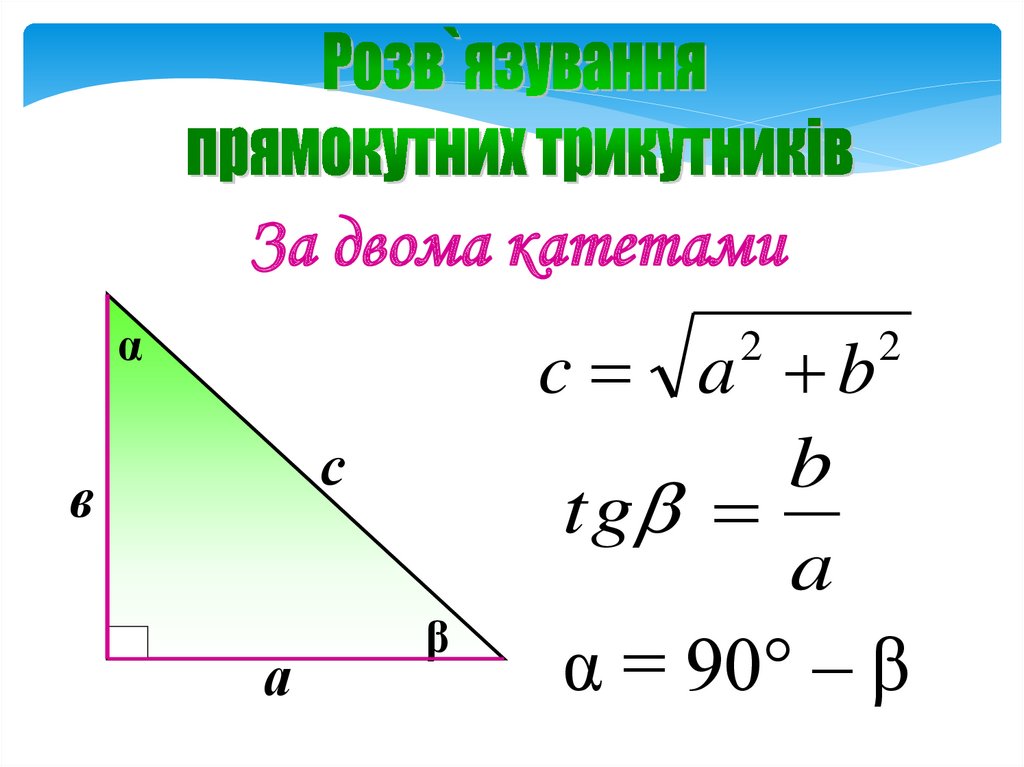
За двома катетамиα
c a b
b
tg
a
α = 90° – β
2
с
в
а
β
2
9.
За гіпотенузою і гострим кутомα
а = c sin α
с
в
b = c cosα
а
β
β = 90° – α
10.
За гіпотенузою і катетомα
b c a
2
с
в
а
2
a
cos
c
β
α = 90° – β
11.
За катетом і гострим кутомa
c
sin
α
с
в
а
b = c·cos α
β
β = 90° – α
12.
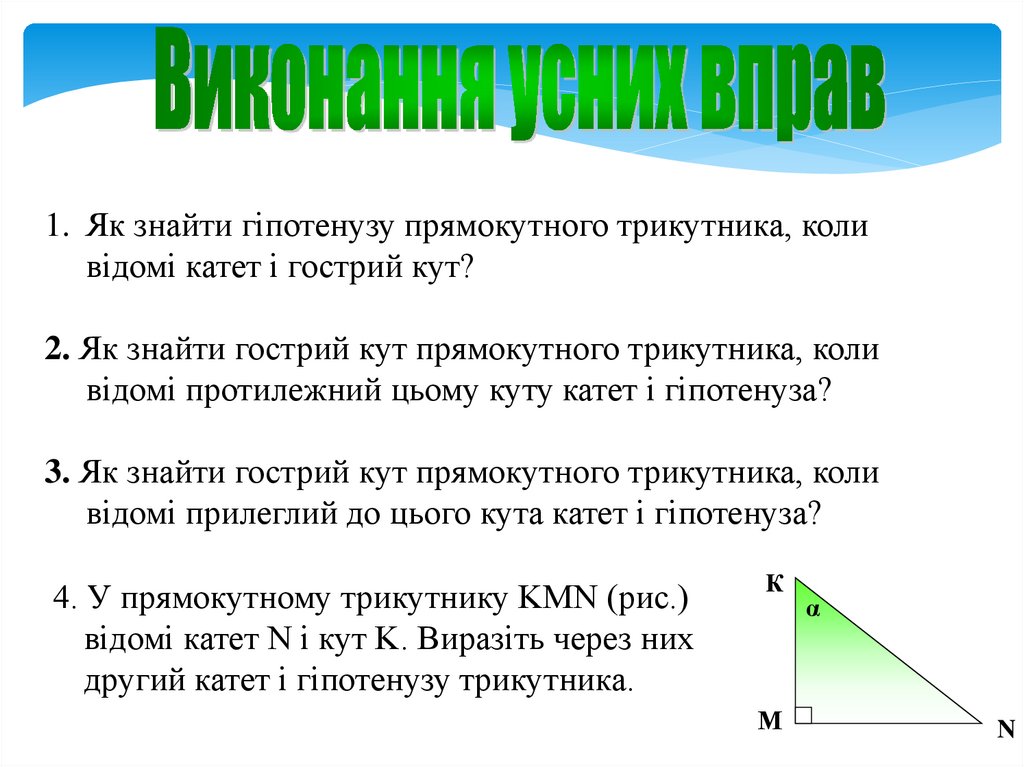
1. Як знайти гіпотенузу прямокутного трикутника, коливідомі катет і гострий кут?
2. Як знайти гострий кут прямокутного трикутника, коли
відомі протилежний цьому куту катет і гіпотенуза?
3. Як знайти гострий кут прямокутного трикутника, коли
відомі прилеглий до цього кута катет і гіпотенуза?
4. У прямокутному трикутнику KMN (рис.)
відомі катет N і кут K. Виразіть через них
другий катет і гіпотенузу трикутника.
К
М
α
N
13.
У прямокутному трикутнику катетзавдовжки 7 см є прилеглим до кута 60°.
Знайдіть гіпотенузу трикутника.
Дано:
К
∆КМР, <М=90°, КМ=7 см, <К=60°
60°
Знайти: КР
Розв`язування:
7
ÊÌ
М
Р
1
ÊÐ
7: 7 2 14ñì
2
cos600
Відповідь: 14 см
14.
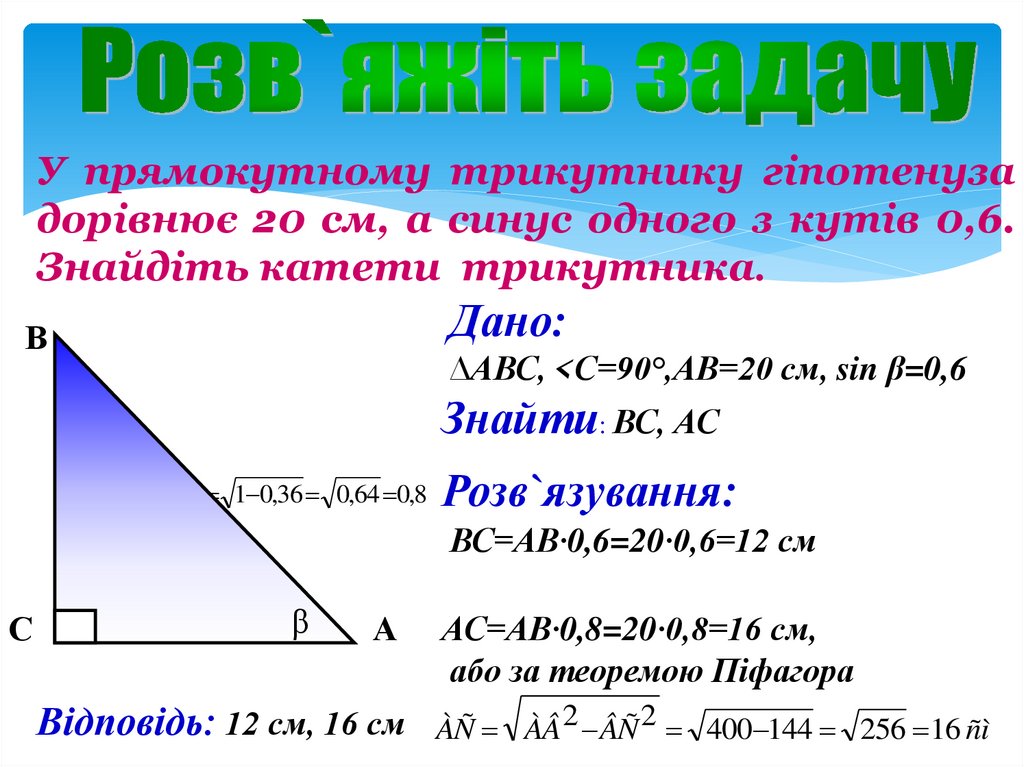
У прямокутному трикутнику гіпотенузадорівнює 20 см, а синус одного з кутів 0,6.
Знайдіть катети трикутника.
Дано:
В
∆АВС, <С=90°,АВ=20 см, sin β=0,6
Знайти: ВС, АС
cosA 1 0,36 0,64 0,8
Розв`язування:
ВС=АВ·0,6=20·0,6=12 см
С
β
А
Відповідь: 12 см, 16 см
АС=АВ·0,8=20·0,8=16 см,
або за теоремою Піфагора
ÀÑ ÀÂ 2 ÂÑ 2 400 144 256 16 ñì
15.
Розв`язати№ 721, 722, 734
Підручника “Геометрія, 8”
А.П. Єршова,
В.В. Головобородько,
О.Ф. Крижанівський,
С.В. Єршов
16.
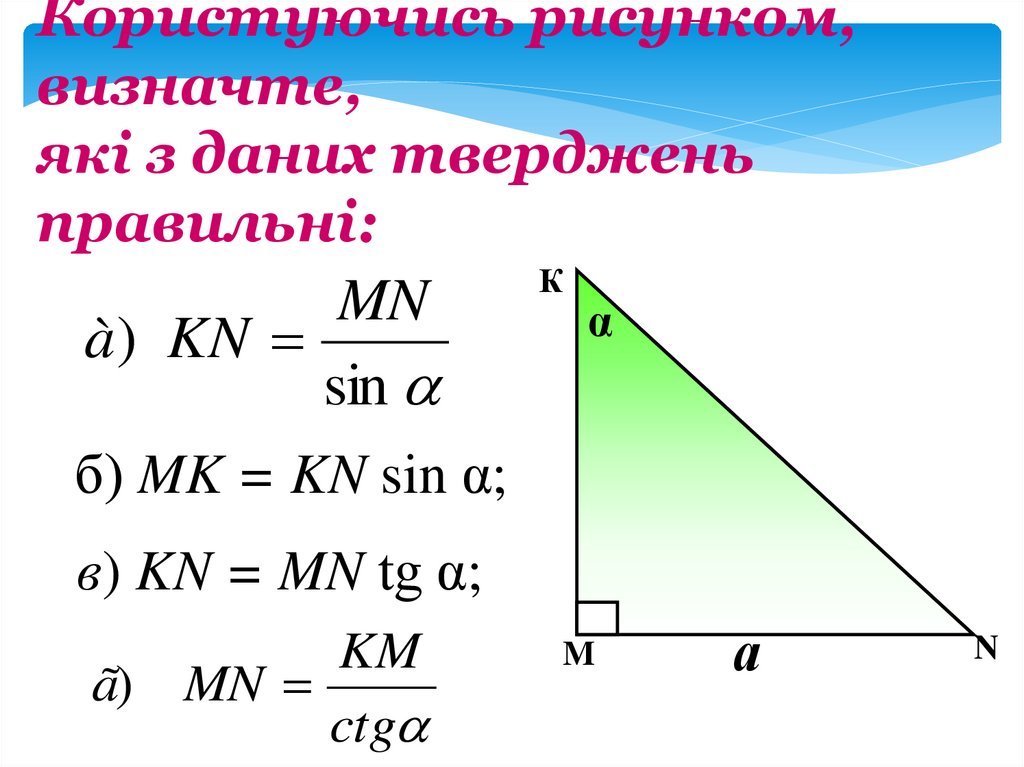
Користуючись рисунком,визначте,
які з даних тверджень
правильні:
К
MN
α
à) KN
sin
б) MK = KN sin α;
в) KN = MN tg α;
KM
ã) MN
ctg
M
а
N












 mathematics
mathematics








