Теорема Піфагора. Розв’язування задач

1.

2. Мета уроку:

• Узагальнити та систематизувати знання
учнів; показати різні способи доведення
теореми Піфагора; вдосконалювати
вміння та навички учнів застосовувати
теорему Піфагора при розв’язуванні
задач.
• Розвивати логічне мислення,
стимулювати пізнавальну діяльність
учнів.

3.

теоретичного матеріалу

4.

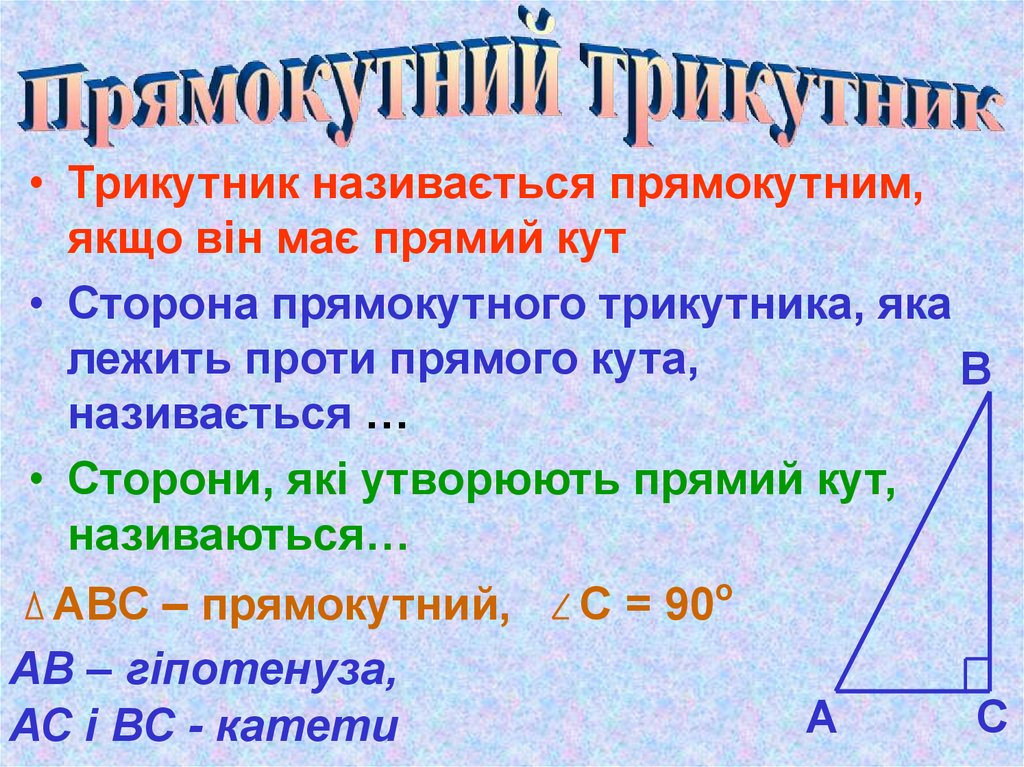
• Трикутник називається прямокутним,
якщо він має прямий кут
• Сторона прямокутного трикутника, яка
лежить проти прямого кута,
В
називається …
• Сторони, які утворюють прямий кут,
називаються…
АВС – прямокутний,
АВ – гіпотенуза,
АС і ВС - катети
С = 90о
А
С

5.

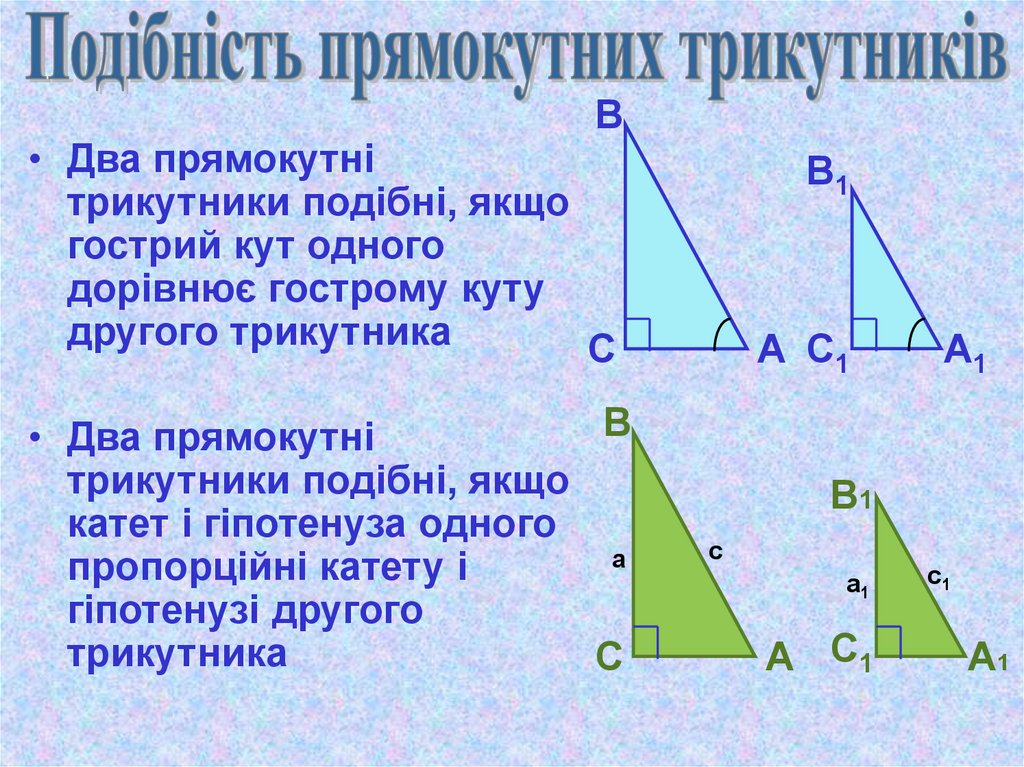
В
• Два прямокутні
трикутники подібні, якщо
гострий кут одного
дорівнює гострому куту
другого трикутника
С
В
• Два прямокутні
трикутники подібні, якщо
катет і гіпотенуза одного
а
пропорційні катету і
гіпотенузі другого
трикутника
С
В1
А С1
А1
В1
с
а1
А С1
с1
А1

6.

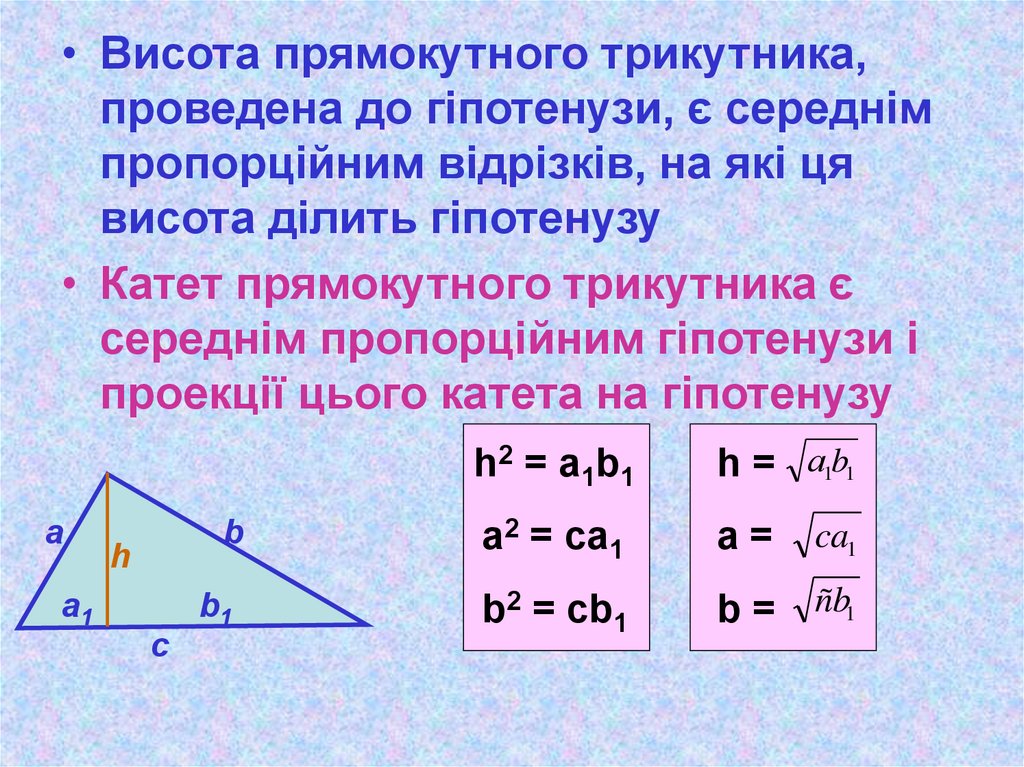
• Висота прямокутного трикутника,
проведена до гіпотенузи, є середнім
пропорційним відрізків, на які ця
висота ділить гіпотенузу
• Катет прямокутного трикутника є
середнім пропорційним гіпотенузи і
проекції цього катета на гіпотенузу
а
h
а1
c
h2 = a1b1
h = а1b1
b
a2 = ca1
a=
b1
b2 = cb1
b = ñb1
ca1

7.

• Косинусом гострого кута прямокутного
трикутника називається відношення
прилеглого катета до гіпотенузи
• Синусом гострого кута прямокутного
трикутника називається відношення
протилежного катета до гіпотенузи
• Тангенсом гострого кута прямокутного
трикутника називається відношення
протилежного катета до прилеглого
катета
с
b
cos
c
a
sin
c
a
tg
b
а
α
b

8. Основні тригонометричні тотожності

sin cos 1
2
sin
tg
cos
2
cos
ctg
sin
tg ctg 1
1
1 tg
2
cos
2
1
1 ctg 2
sin
2

9.

• У прямокутному трикутнику
квадрат гіпотенузи дорівнює сумі
квадратів катетів
В
2
2
АВ = АС + ВС
а
с
2
2
с =α +b
С
2
b
А
2

10.

• В прямокутному трикутнику будь-який з
катетів менший за гіпотенузу
• Cos α < 1 для будь-якого гострого кута α
• Коли з даної точки до прямої проведено
перпендикуляр і похилі, то будь-яка
похила більша від перпендикуляра,
рівні похилі мають рівні проекції, з двох
похилих більша та, у якої проекція
більша

11. Теорема, обернена до теореми Піфагора

• Якщо в трикутнику квадрат
сторони дорівнює сумі квадратів
двох інших сторін, то цей
трикутник прямокутний
В
Якщо АВ2 = АС2+ ВС2 , то АВС –
прямокутний трикутник з прямим кутом С
С
А

12.

• Піфагор – можливо найбільш
знаменитий учений за всю історію
людства.
• Він був не лише вченим і
засновником першої наукової
школи.
• Ця унікальна людина була і
“володарем дум”, проповідником
власної “піфагорійської” етики

13.

І не знатність, не
багатство, а ясний
розум і чиста
совість цінувалися
в піфагорійському
братерстві над усе

14.

• Твори велике, не обіцяючи великого.
• Не заплющуй очей, коли хочеш спати,
не проаналізувавши всіх своїх
учинків за минулий день.
• Тимчасова невдача краще
тимчасової удачі.

15.

• Лише неблагородна людина здатна
в очі хвалити, а поза очі
злословити.
• Не роби нічого ганебного ні в
присутності інших, ні таємно.
Першим твоїм законом має бути
повага до себе самого.

16.

• Роби лиш те, що в майбутньому
не засмутить тебе.
• Не давай дурневі в руки меч, а
нечесним – владу.
• Нічому не дивуйся

17.

• Живи з людьми так, щоб твої друзі
не стали недругами, а недруги стали
друзями
• Не зневажай здоров’ям свого тіла.
Доставляй йому вчасно їжу і питво, і
вправи, без яких воно бідує
• Усе впорядковується відповідно до
чисел

18.

19.

С
А
b
а
b1
a1
Н
c
b2 =cb1
а2 = са1
a2 + b2 = ca1 + cb1 = c(a1 + b1) = c2
Отже,
c2 = a2 + b2
В

20.

С
А
AC
AD AC
AB
AC AB
Тоді одержимо
AD AB AC 2
BD BC
BC
BD
cos B
cos B
BC AB
AB
BC
cos A
AD
AC
В
D
cos A
Тоді одержимо
Додавши рівності, матимемо:
BD AB BC 2
AC 2 BC 2 AD AB BD AB AB AD BD AB AB AB 2

21.

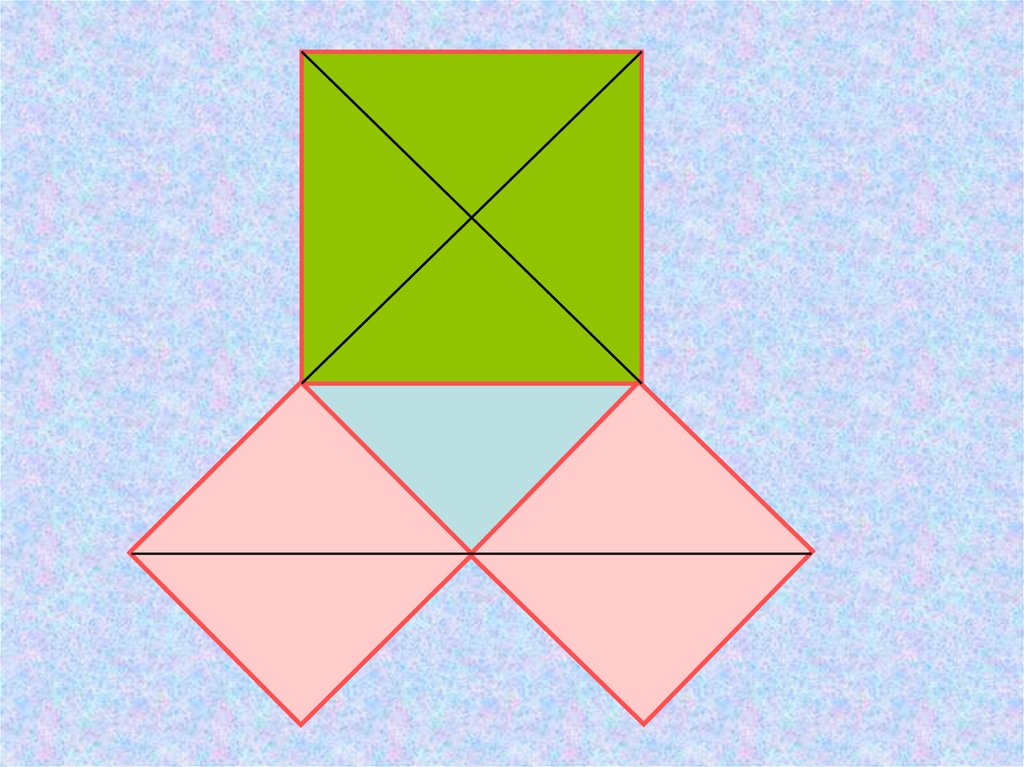
Класичне формулювання теореми Піфагора
Якщо сторони прямокутного трикутника є сторонами
квадратів, то площа квадрата, побудованого на
гіпотенузі, дорівнює сумі площ квадратів, побудованих
на катетах.
b
b
a
c
b
a
a
2
2
2
c =a +b

22.

a
b
a
c
b
c
c
b
c
a
1
2
2
4 ab c a b
2
a
b
2ab c a 2ab b
2
c a b
2
2
2
2
2

23.

с
а
с
b
с
( a – b )2
а
b
с
1
2
с 4 ав а в 2ав а 2 2ав в 2 а 2 в 2
2
2

24.

25.

a
b
a
b
b-a
c
b
a
c
b
1
1
2
а в 8 ав в а 4 ав с 2
2
2
2
a
1
2
4 ав в а с 2
2

26.

1. Якщо катети прямокутного трикутника
дорівнюють 1см і 3см, то гіпотенуза
дорівнює…
А) 4см; Б) 10см;
В) 10 см; Г) 2 2 см
2. Якщо гіпотенуза прямокутного
трикутника дорівнює 15см, а один з
катетів – 9см, то другий катет
дорівнює…
А) 6см; Б)12см;
В) 24см; Г) 3 34 см

27.

3. Якщо сторони прямокутника
дорівнюють 8см і 6см, то діагональ
цього прямокутника дорівнює…
А) 14см; Б) 28см; В)10см; Г) 7см
4. Якщо діагоналі ромба дорівнюють
16см і 12см, то сторона цього ромба
дорівнює…
А) 28см; Б) 20см;
В) 15см; Г)10см

28.

5. Якщо основа рівнобедреного
трикутника дорівнює 30см, а
висота, проведена до неї, - 8см, то
бічна сторона трикутника
дорівнює…
А) 34см; Б) 22см; В) 19см; Г) 17см
6. Якщо сторона ромба дорівнює
13см, а одна з діагоналей – 24см,
то друга діагональ дорівнює…
А) 5см; Б)2,5см; В) 10см; Г)37см

29.

7. Якщо бічна сторона рівнобедреного
трикутника дорівнює 5см, а основа –
6см, то висота, проведена до основи,
дорівнює…
А) 4см; Б) 8см; В)11см; Г) 30см
8. Більша основа прямокутної трапеції
дорівнює 10см, а менша – 6см.
Знайти більшу бічну сторону
трапеції, якщо менша дорівнює 3см
А) 10см; Б) 12см; В) 5см; Г) 4см

30.

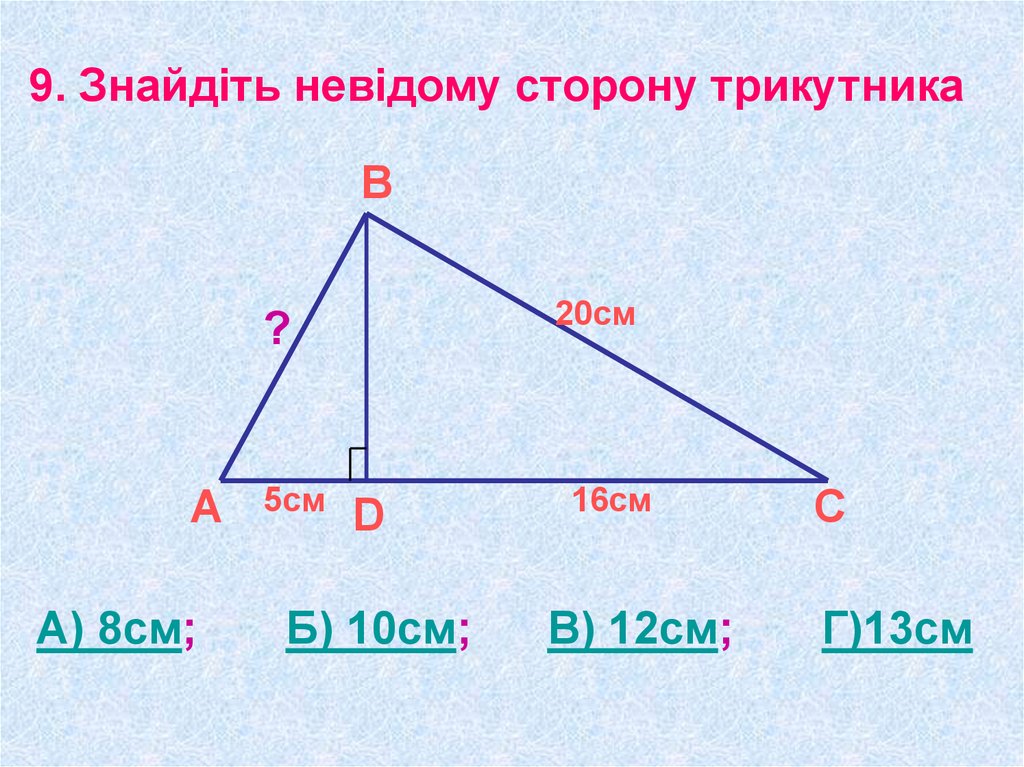
9. Знайдіть невідому сторону трикутника
В
А
А) 8см;
?
20см
5см
16см
С
В) 12см;
Г)13см
D
Б) 10см;

31.

• У рівнобічній трапеції основи
дорівнюють 7см і 13см, а висота
дорівнює 4см. Знайдіть бічну
сторону трапеції
В
?
А
7см
С
4см
M
13см
К
D

32.

• Основа AD рівнобічної трапеції ABCD
ділиться висотою ВЕ на відрізки
довжиною 5см і 16см, а довжина бічної
сторони трапеції 13см. Знайти діагоналі
трапеції
В
С
13см
?
А 5см E
16см
D

33.

• Дано прямокутну трапецію, у якої
бічні сторони дорівнюють 17см і
15см, а менша основа – 9см. Знайти
середню лінію трапеції.
В
С
9см
17см
15см
Q
А
?
P
М
D

34.

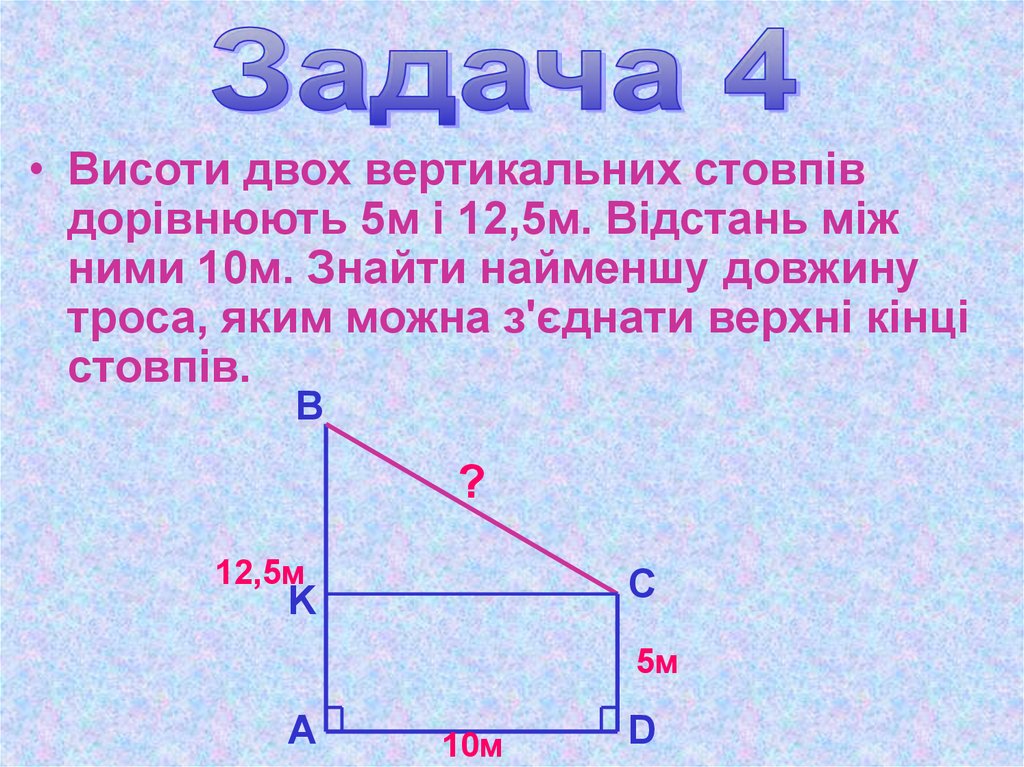
• Висоти двох вертикальних стовпів
дорівнюють 5м і 12,5м. Відстань між
ними 10м. Знайти найменшу довжину
троса, яким можна з'єднати верхні кінці
стовпів.
В
?
12,5м
С
K
5м
А
10м
D

35.

Завдання додому :
• Повторити теорему Піфагора
• Розв’язати задачу
• ** Знайти медіану рівнобедреного
трикутника, проведену до бічної
сторони, якщо бічна сторона і
основа трикутника дорівнюють
відповідно 30см і 48см
В
30см
30см
?
А
48см
С