Теорема косинусів (9 клас)

1.

Теорема
косинусів
Геометрія, 9 клас

2. Перевірка домашнього завдання

б ) cos(90 ) sin( 180 ) sin sin 2 sin
г)ctg(90 - ) - tg(180 - ) tg tg 2 tg
1
б )5 sin30 ctg135 5 1 2,5 1 1,5
2
1
г )3 cos 60 tg 45 tg 60 3 1 3 1,5 3
2

3. Перевірка домашнього завдання

1
Дано : 90 180 ; sin
3
Знайти : cos , tg , ctg
Розв’язання
sin 2 cos 2 1 cos 2 1 sin 2
2
1 8
8
2 2
1
2
cos 1 1
; cos
9 9
9
3
3
2 2
Так як 90 180 то cos
3
sin 1 2 2
1
tg
:
cos 3
3
2 2
1
ctg
2 2
tg

4. Актуалізація опорних знань

• Які види трикутників ви знаєте?
• Який трикутник називається
прямокутним?
• Як називаються сторони прямокутного
трикутника?
• Яка відома теорема виражає зв’язок між
сторонами прямокутного трикутника?

5. Теорема Піфагора

c a b
2
с
а
2
2
b
Квадрат гіпотенузи дорівнює
сумі квадратів катетів

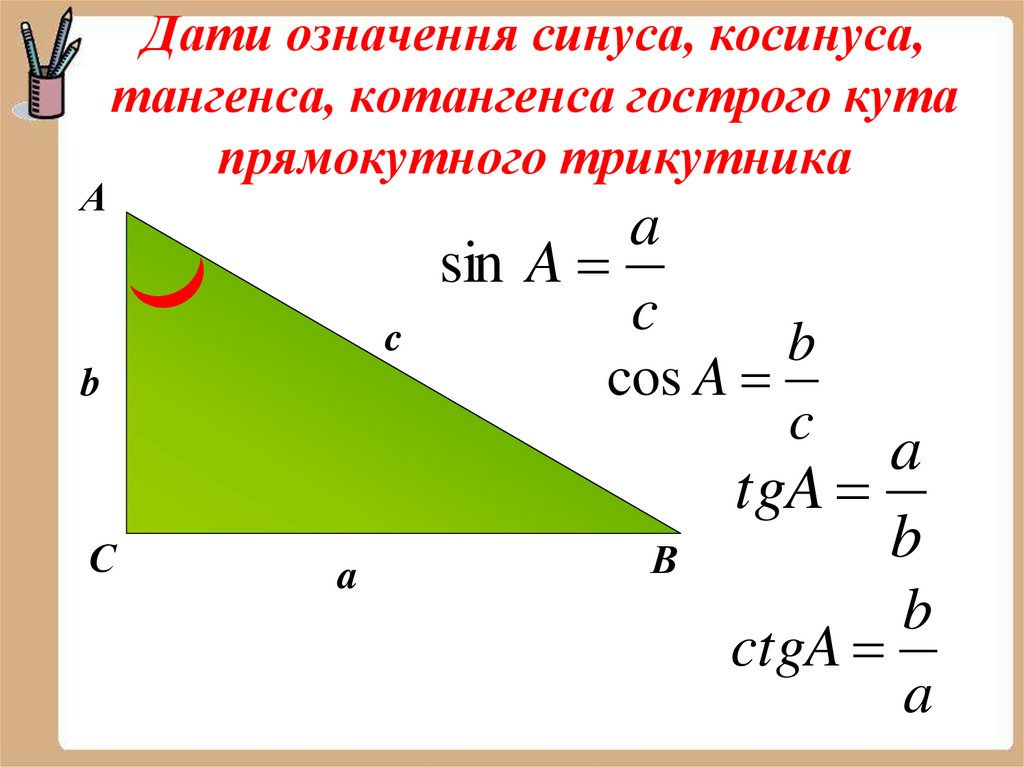
6. Дати означення синуса, косинуса, тангенса, котангенса гострого кута прямокутного трикутника

А
Дати означення синуса, косинуса,
тангенса, котангенса гострого кута
прямокутного трикутника
a
sin A
c
c
b
cos A
c
b
С
a
В
a
tgA
b
b
ctgA
a

7. Залежність між сторонами і кутами у прямокутному трикутнику

a c sin A
А
c
b c cos A
b
С
a
a b tgA
В
b a ctgA

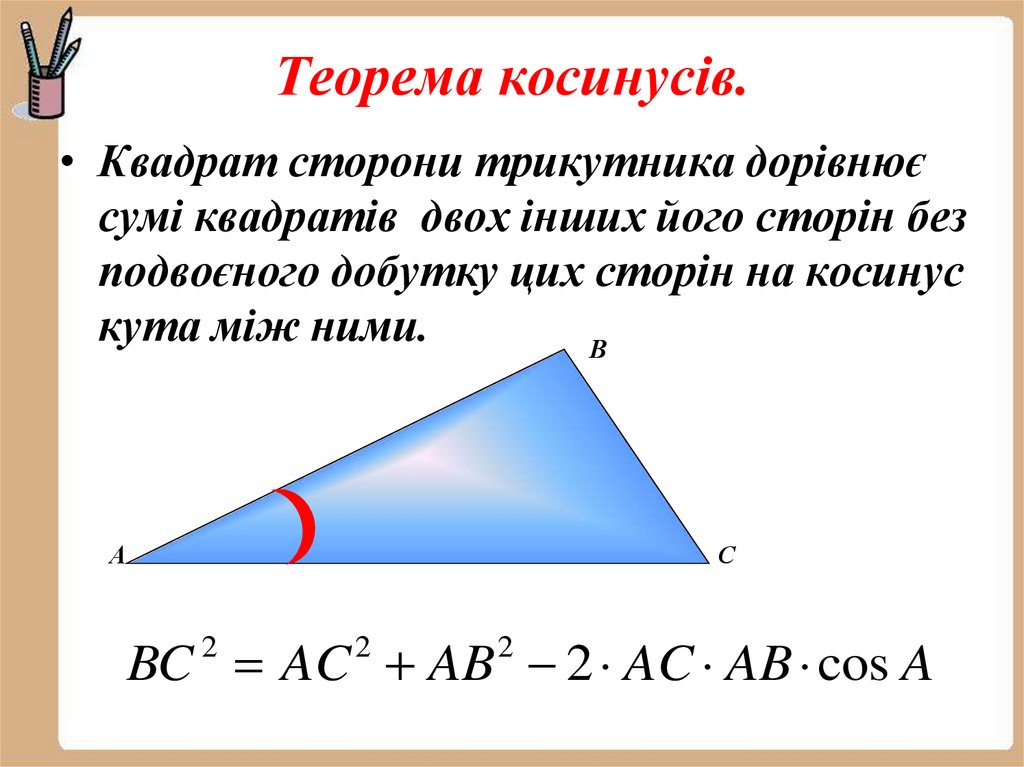
8. Теорема косинусів.

• Квадрат сторони трикутника дорівнює
сумі квадратів двох інших його сторін без
подвоєного добутку цих сторін на косинус
кута між ними.
В
А
С
BC AC AB 2 AC AB cos A
2
2
2

9. Історична довідка

• Теорема косинусів була доведена,
звичайно,геометрично ще в “Началах”
Евкліда.
• Словесно теорема косинусів була вперше
сформульована французьким
математиком Франсуа Вієтом в XVI
столітті.
• Сучасний вид теорема косинусів приймає
в 1801 році у французького математика
Лазара Карно.

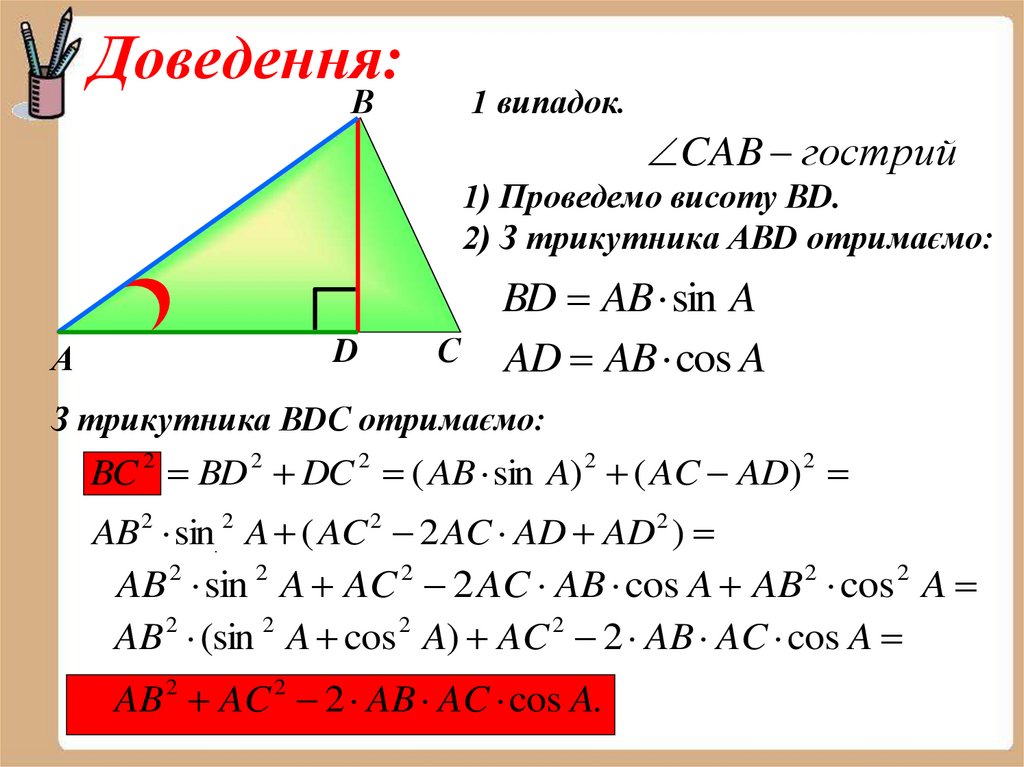
10. Доведення:

В
1 випадок.
CAB гострий
1) Проведемо висоту ВD.
2) З трикутника АВD отримаємо:
А
D
С
BD AB sin A
AD AB cos A
З трикутника ВDС отримаємо:
BC 2 BD 2 DC 2 ( AB sin A) 2 ( AC AD) 2
AB 2 sin. 2 A ( AC 2 2 AC AD AD 2 )
AB 2 sin 2 A AC 2 2 AC AB cos A AB 2 cos 2 A
AB 2 (sin 2 A cos 2 A) AC 2 2 AB AC cos A
AB 2 AC 2 2 AB AC cos A.

11. Доведення:

В
2 випадок. CAB тупий
1) Проведемо висоту ВD.
2) З трикутника АВD отримаємо:
BD AB sin BAD
AB sin( 180 BAC ) AB sin BAC
А
D
З трикутника ВDC:
AD AB cos BAD
С AB cos(180 BAC )
AB cos BAC
BC 2 BD 2 DC 2 ( AB sin BAC ) 2 ( AC AD) 2
AB 2 sin 2 BAC ( AC AB cos BAC ) 2
AB 2 sin 2 BAC AC 2 2 AC AB cos BAC AB 2 cos 2 BAC
AB2 (sin 2 BAC cos 2 BAC ) AC 2 2 AB AC cos BAC
AB 2 AC 2 2 AB AC cos BAC .

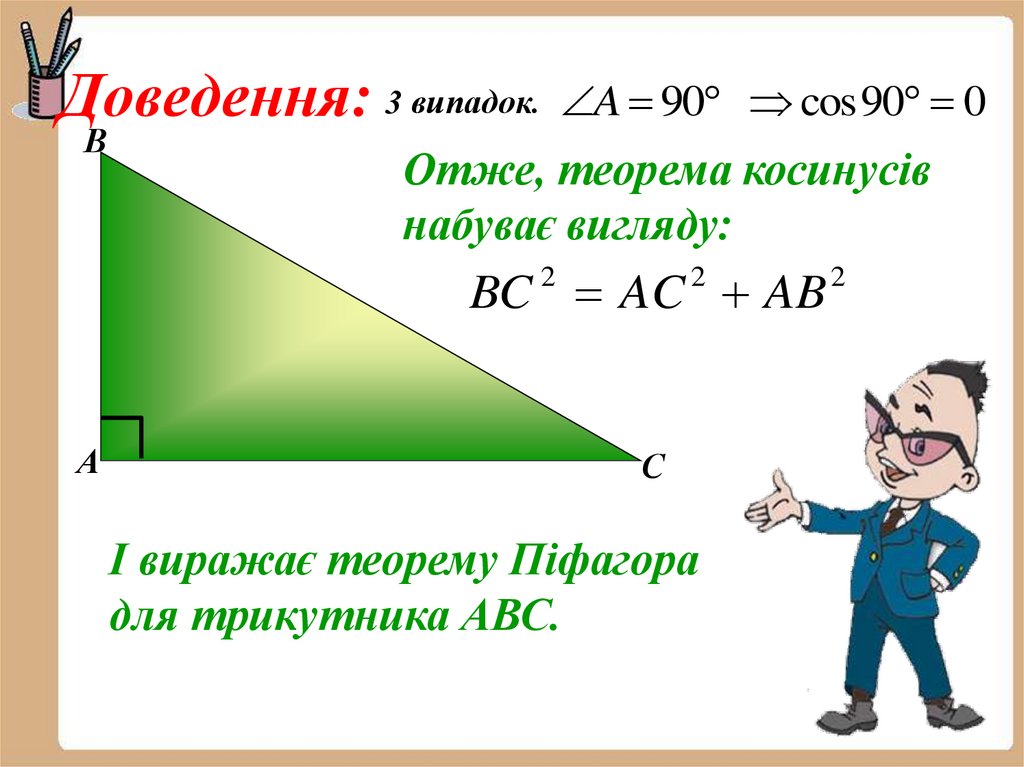
12. Доведення:

3 випадок. A 90 cos 90 0
В
Отже, теорема косинусів
набуває вигляду:
BC AC AB
2
А
2
С
І виражає теорему Піфагора
для трикутника АВС.
2

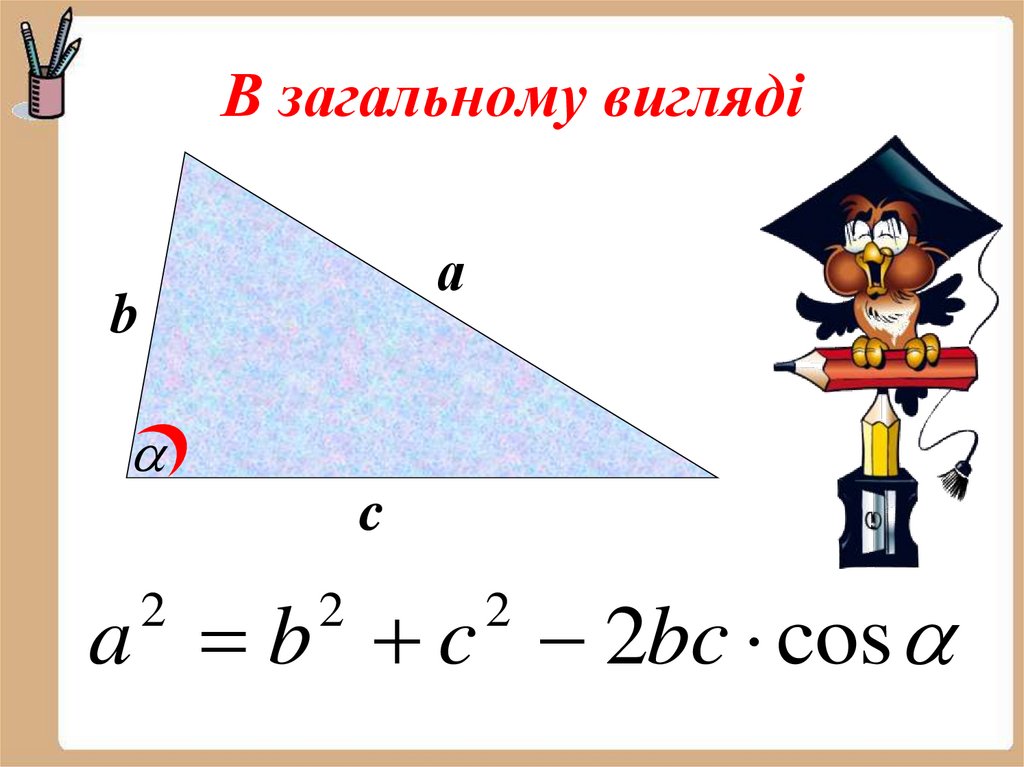
13. В загальному вигляді

а
b
c
a b c 2bc cos
2
2
2

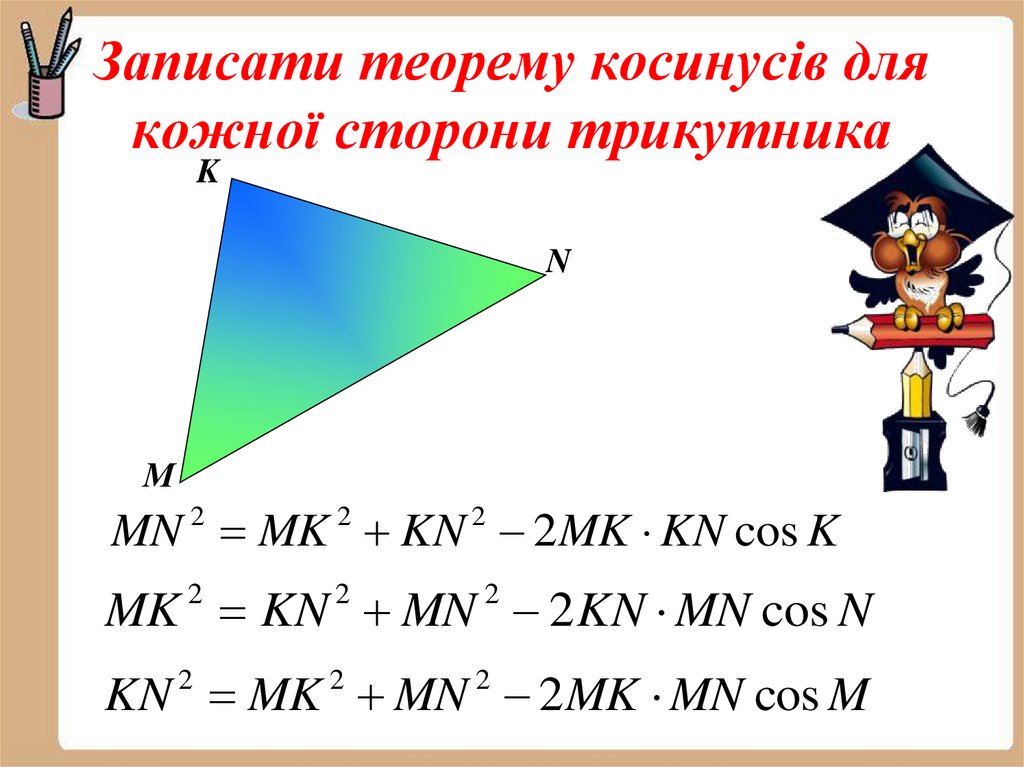
14. Записати теорему косинусів для кожної сторони трикутника

K
N
М
MN 2 MK 2 KN 2 2MK KN cos K
MK 2 KN 2 MN 2 2 KN MN cos N
KN MK MN 2MK MN cos M
2
2
2

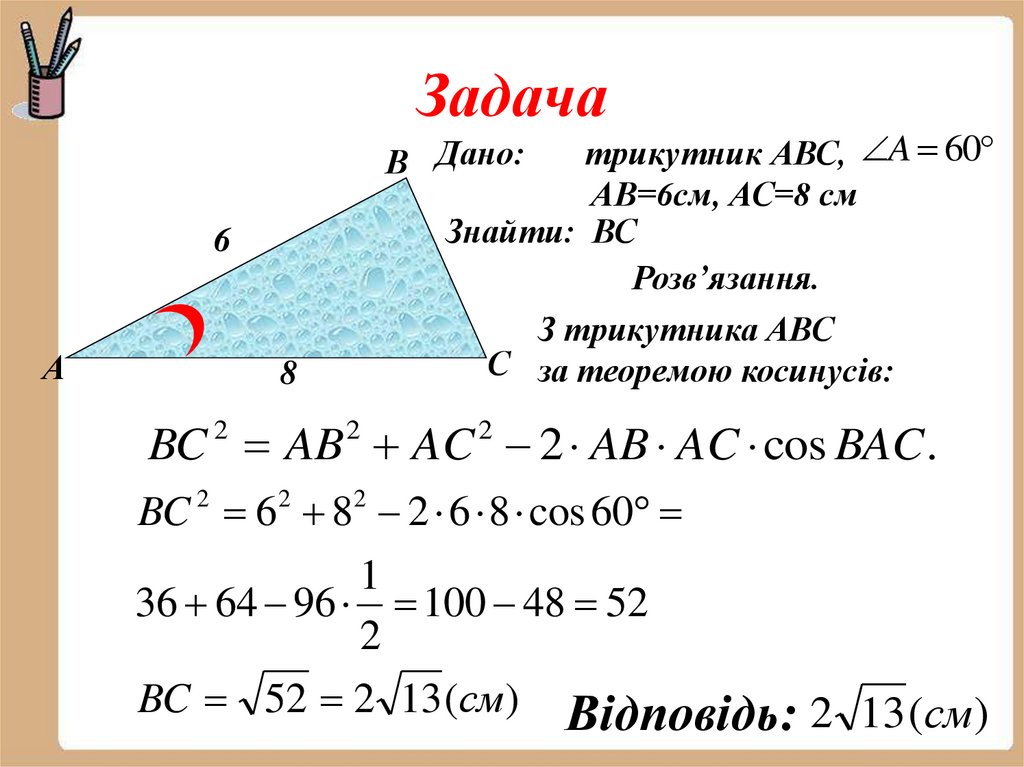
15. Задача

трикутник АВС, A 60
АВ=6см, АС=8 см
Знайти: ВС
Розв’язання.
В Дано:
6
А
8
З трикутника АВС
С за теоремою косинусів:
BC 2 AB 2 AC 2 2 AB AC cos BAC .
BC 2 6 2 82 2 6 8 cos 60
1
36 64 96 100 48 52
2
BC 52 2 13 (см) Відповідь: 2 13 (см)

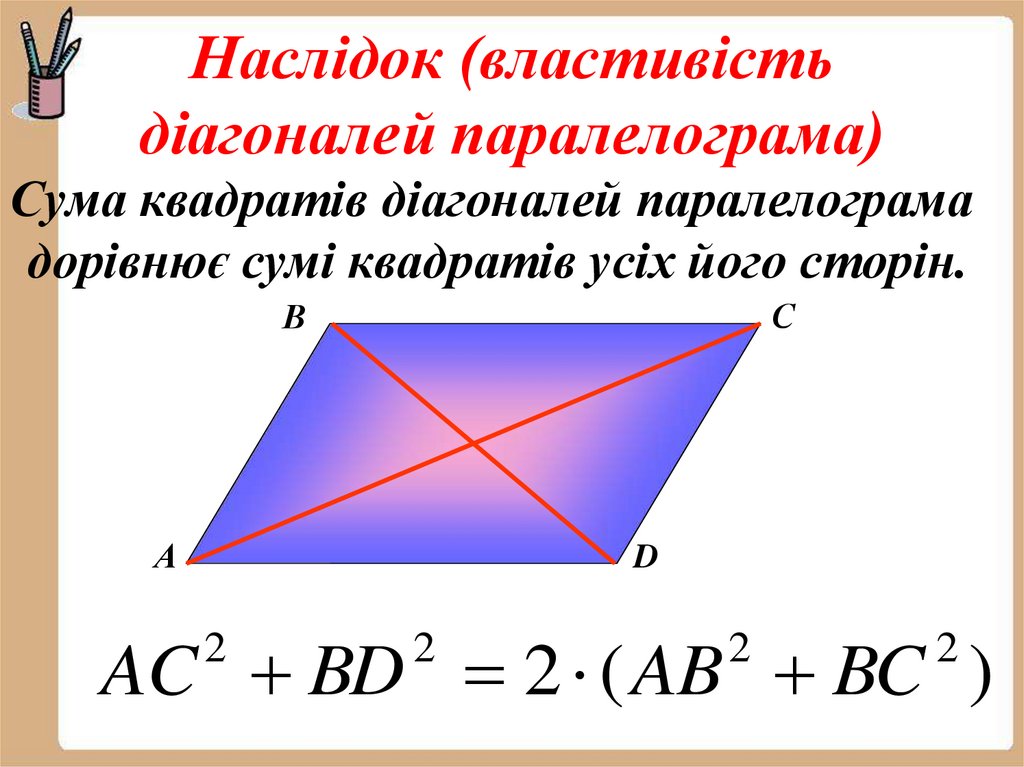
16. Наслідок (властивість діагоналей паралелограма)

Сума квадратів діагоналей паралелограма
дорівнює сумі квадратів усіх його сторін.
С
В
А
D
AC BD 2 ( AB BC )
2
2
2
2

17. Доведення:

В
а
Доведення:
b
С
а
Нехай АВ=СD= а;
АD=ВС= b.
A
B 180
D
А
b
З трикутника АВD за теоремою косинусів:
BD 2 a 2 b 2 2ab cos
З трикутника АВС за теоремою косинусів:
AC 2 a 2 b 2 2ab cos(180 ) a 2 b 2 2ab cos
AC 2 BD 2
a 2 b 2 2ab cos a 2 b 2 2ab cos 2 (a 2 b 2 )

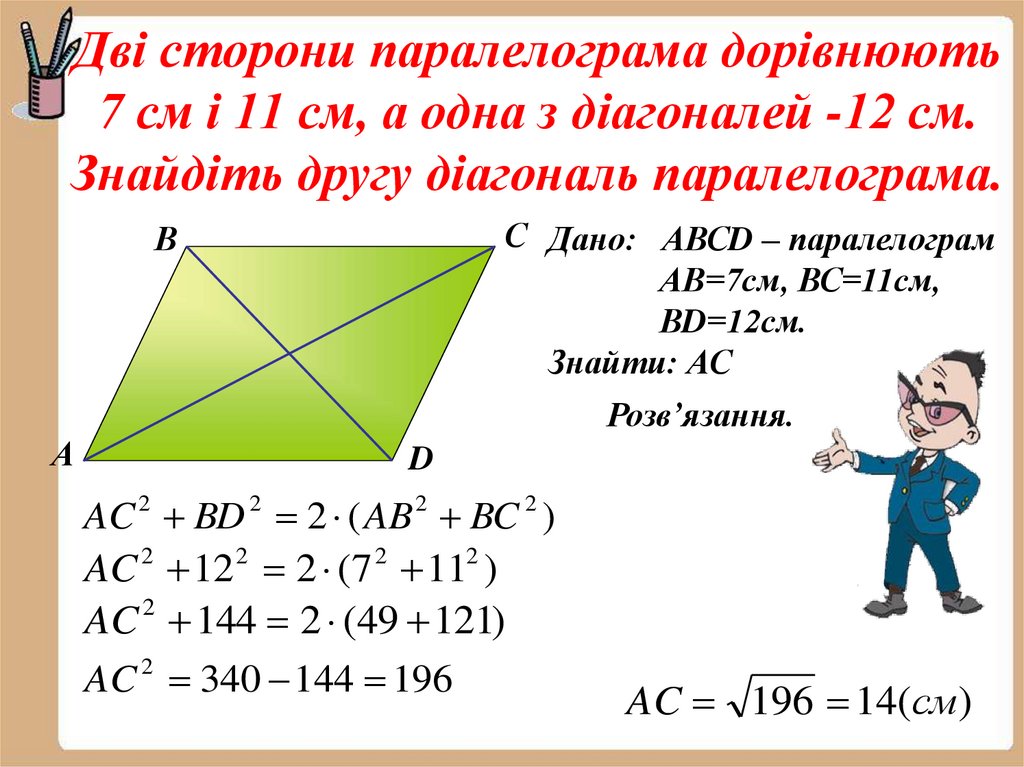
18. Дві сторони паралелограма дорівнюють 7 см і 11 см, а одна з діагоналей -12 см. Знайдіть другу діагональ паралелограма.

С Дано: АВСD – паралелограм
АВ=7см, ВС=11см,
ВD=12см.
Знайти: АС
В
Розв’язання.
А
D
AC 2 BD 2 2 ( AB 2 BC 2 )
2
2
2
2
AC 12 2 (7 11 )
AC 2 144 2 (49 121)
AC 2 340 144 196
AC 196 14(см)

19. Домашнє завдання:

20.

• За що ти можеш себе сьогодні
ПОХВАЛИТИ?
• Що тобі ВДАЛОСЯ сьогодні на
уроці?
• Над чим ще потрібно
ПОПРАЦЮВАТИ?
• Навіщо нам був потрібний цей урок?