Similar presentations:
Тетраэдр. Понятие тетраэдра
1. Тетраэдр
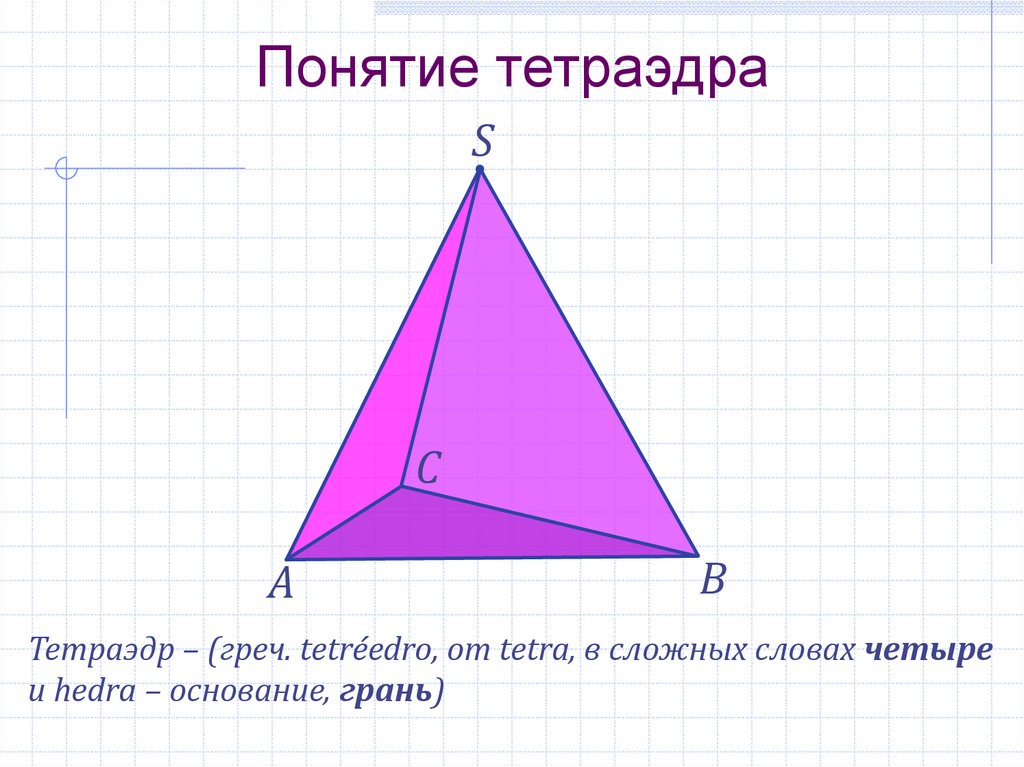
2. Понятие тетраэдра
SС
А
В
Тетраэдр – (греч. tetréedro, от tetra, в сложных словах четыре
и hedra – основание, грань)
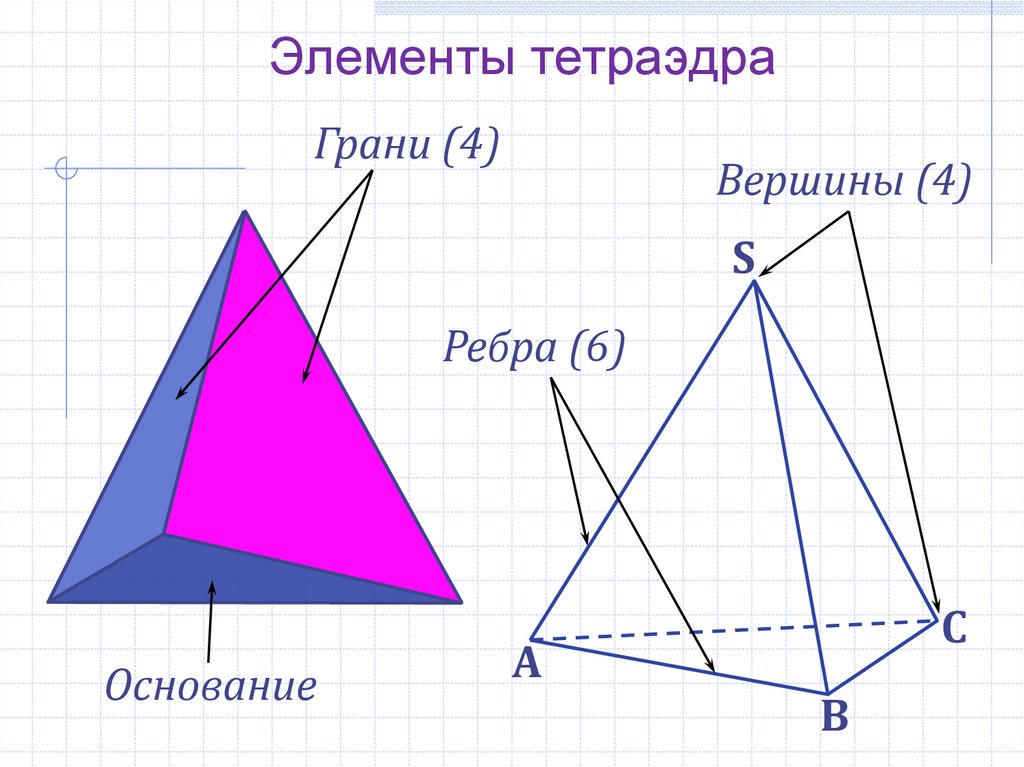
3. Элементы тетраэдра
Грани (4)Вершины (4)
S
Ребра (6)
Основание
А
С
В
4.
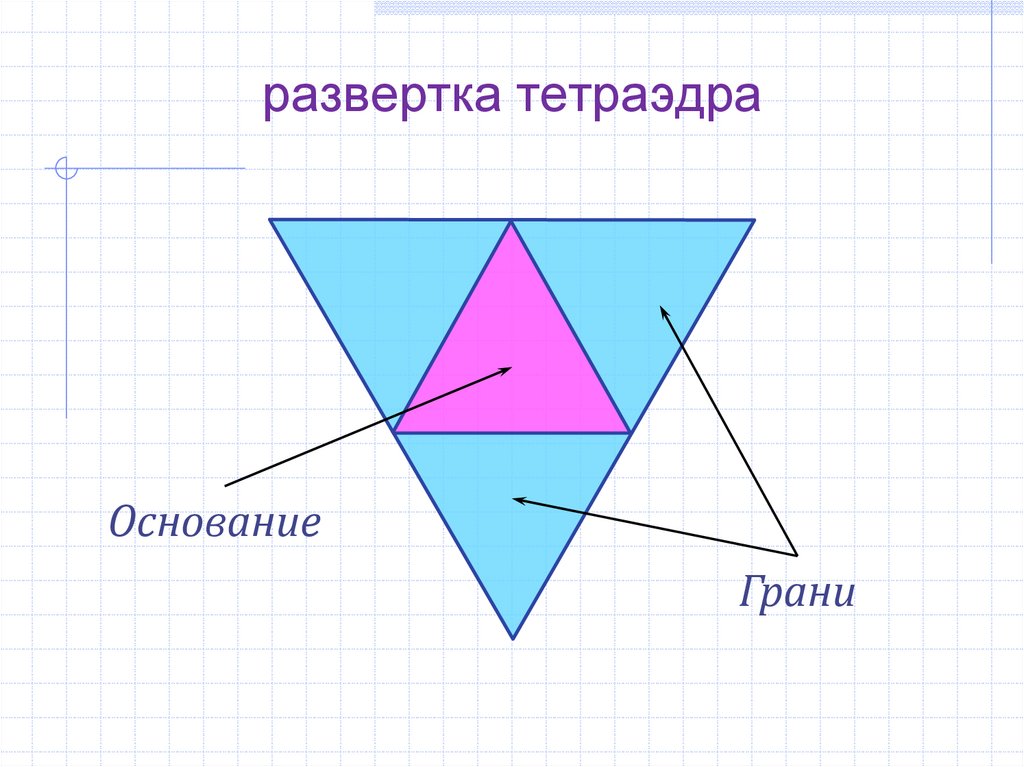
развертка тетраэдраОснование
Грани
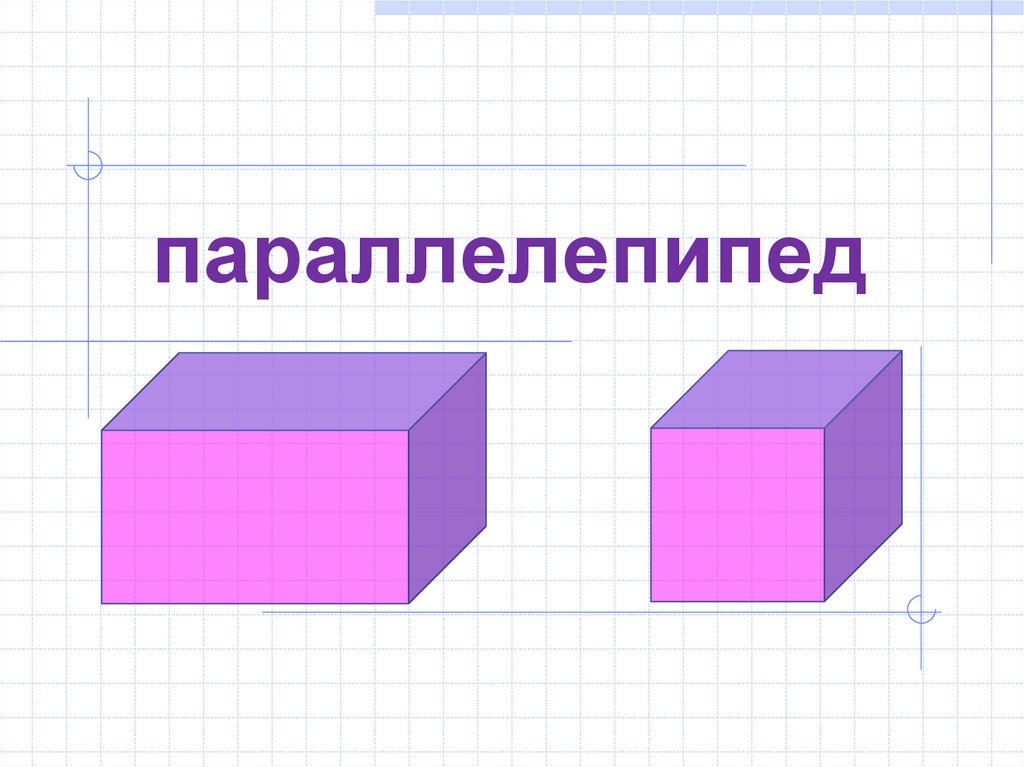
5. параллелепипед
6.
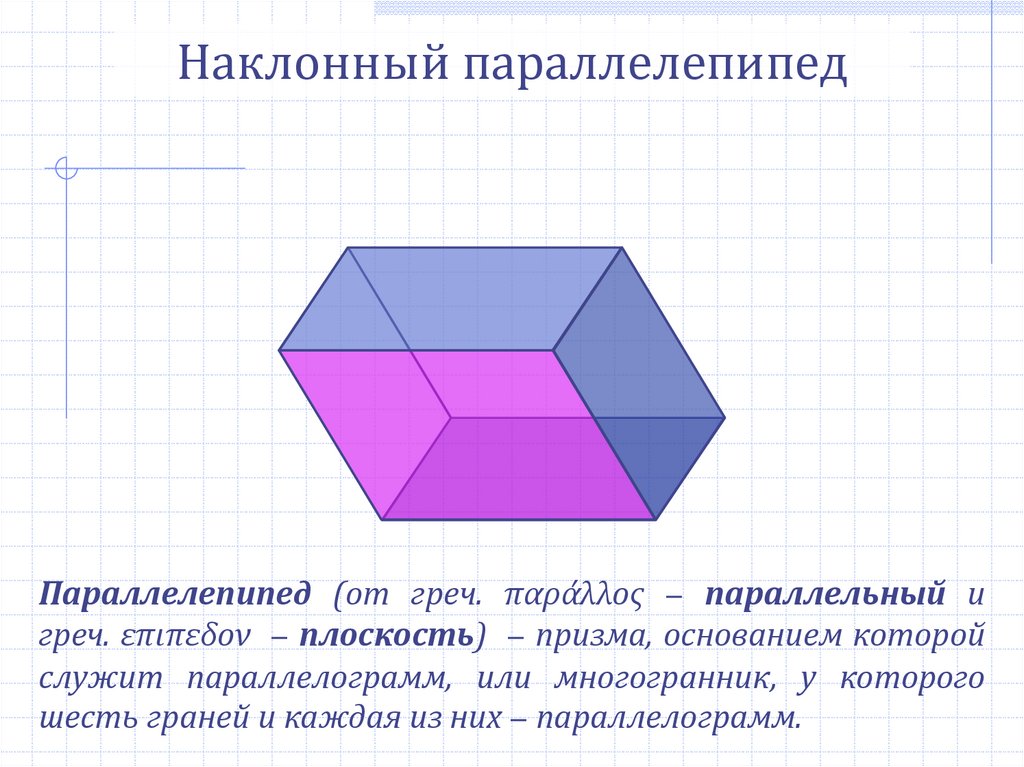
Наклонный параллелепипедПараллелепипед (от греч. παράλλος − параллельный и
греч. επιπεδον − плоскость) − призма, основанием которой
служит параллелограмм, или многогранник, у которого
шесть граней и каждая из них − параллелограмм.
7.
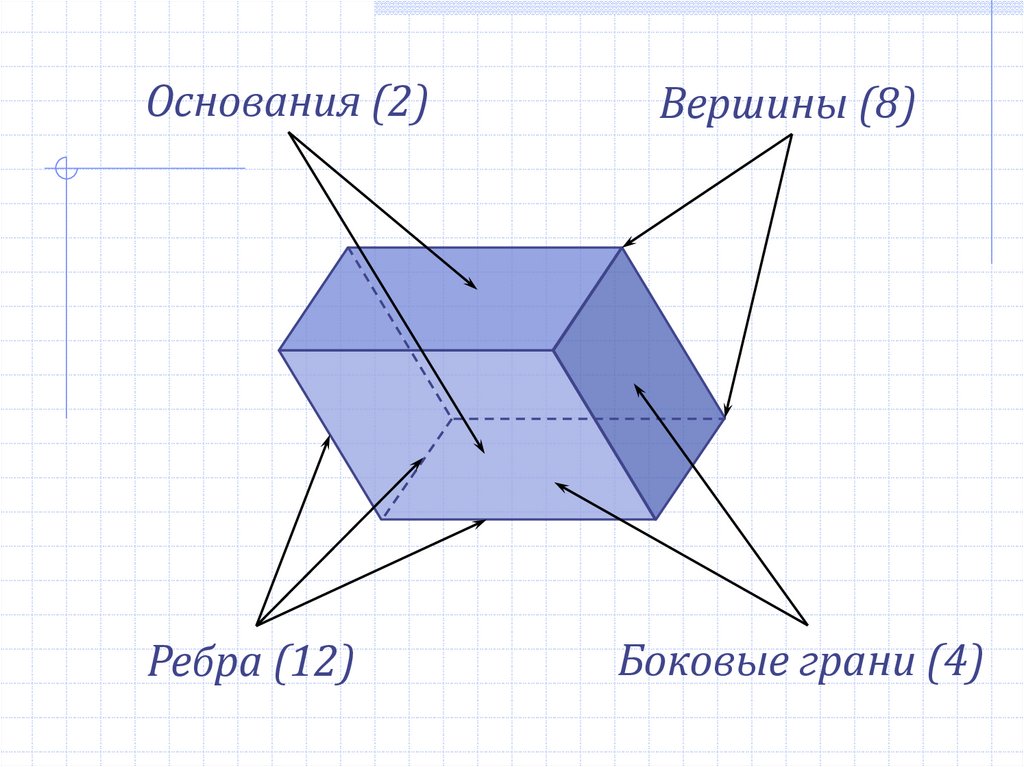
Основания (2)Ребра (12)
Вершины (8)
Боковые грани (4)
8.
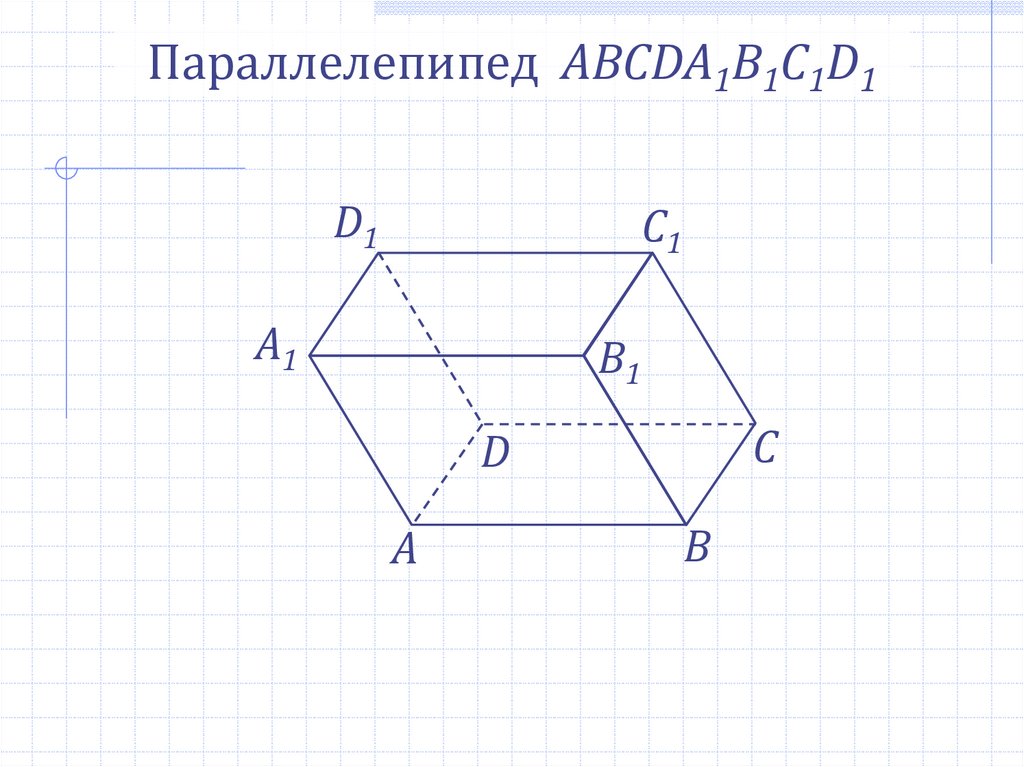
Параллелепипед ABCDA1B1C1D1D1
C1
А1
B1
С
D
А
В
9.
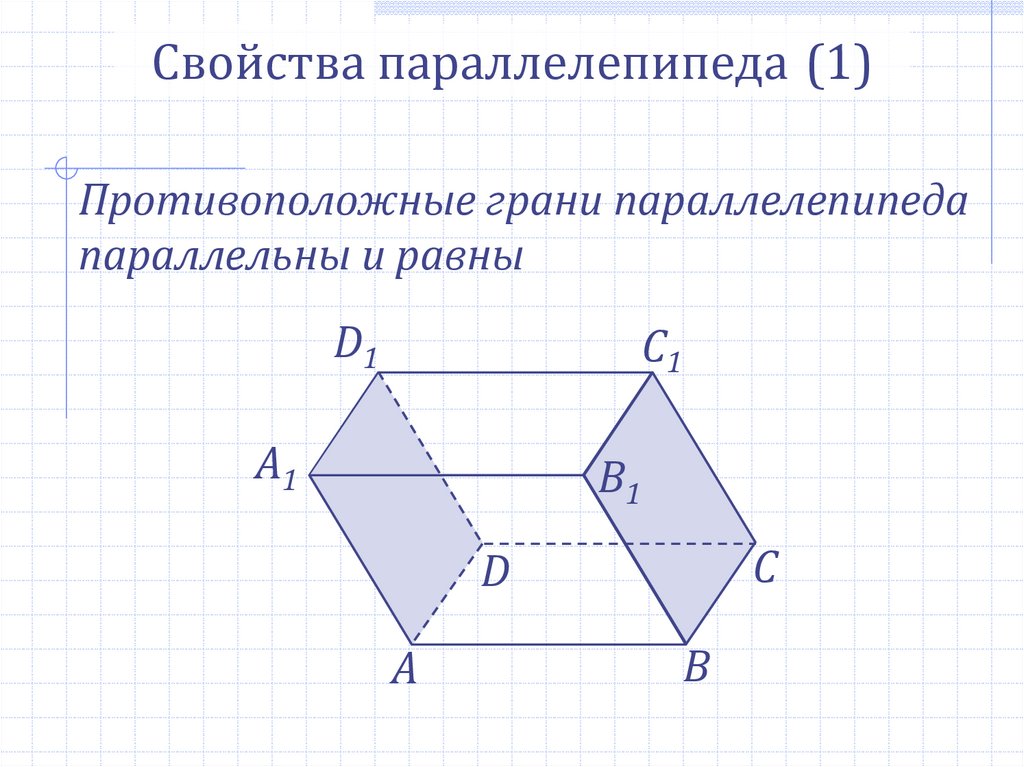
Свойства параллелепипеда (1)Противоположные грани параллелепипеда
параллельны и равны
D1
C1
А1
B1
С
D
А
В
10.
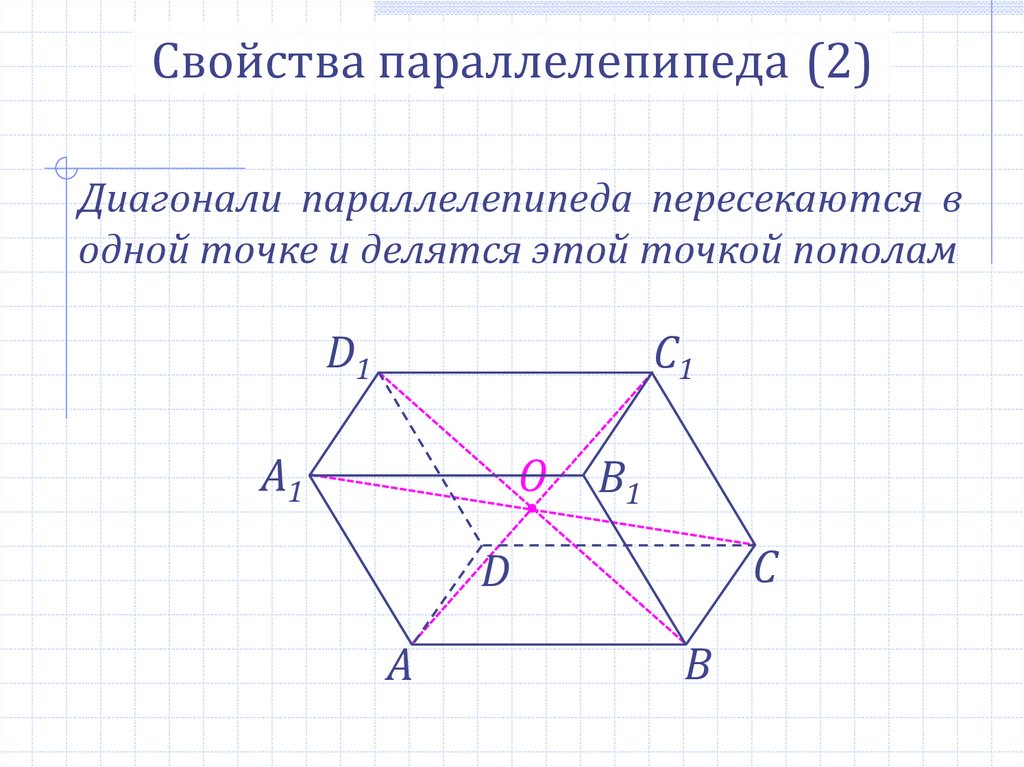
Свойства параллелепипеда (2)Диагонали параллелепипеда пересекаются в
одной точке и делятся этой точкой пополам
D1
C1
А1
О
B1
С
D
А
В
11.
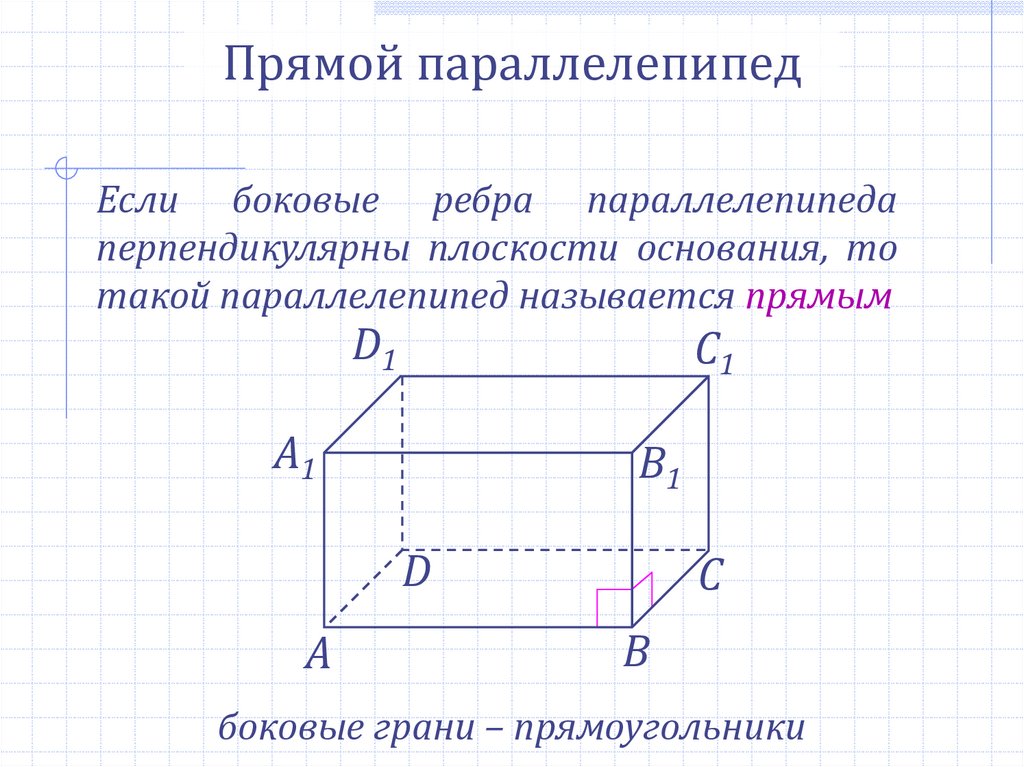
Прямой параллелепипедЕсли боковые ребра параллелепипеда
перпендикулярны плоскости основания, то
такой параллелепипед называется прямым
D1
C1
А1
B1
D
А
С
В
боковые грани – прямоугольники
12.
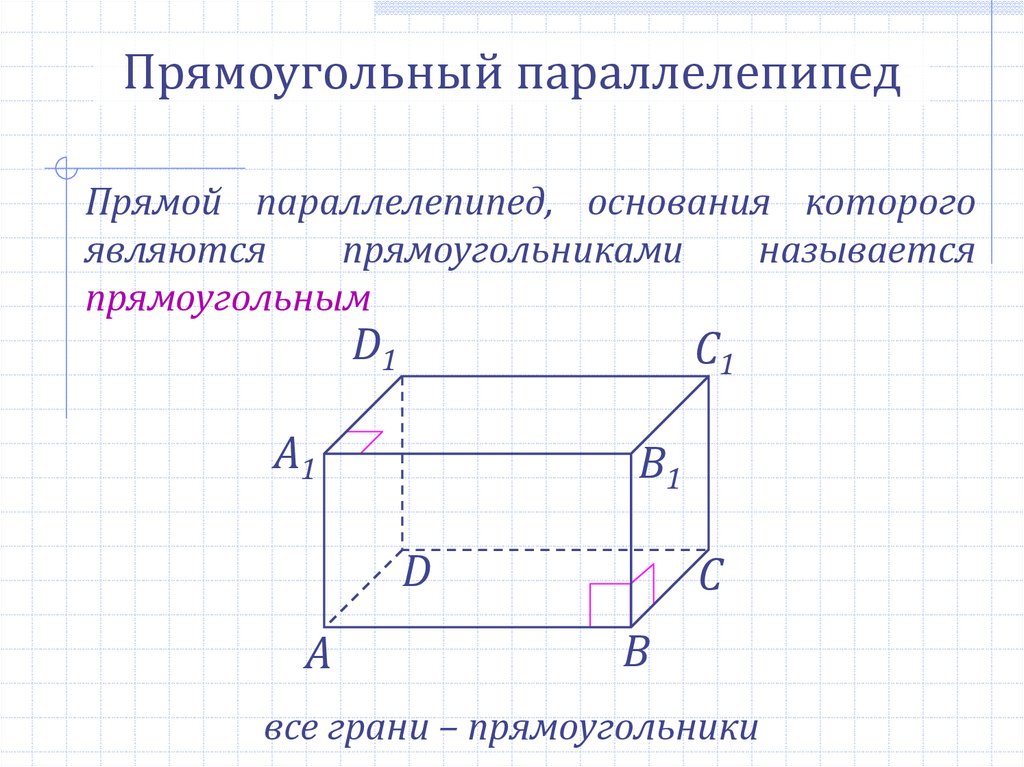
Прямоугольный параллелепипедПрямой параллелепипед, основания которого
являются
прямоугольниками
называется
прямоугольным
D1
C1
А1
B1
D
А
С
В
все грани – прямоугольники
13.
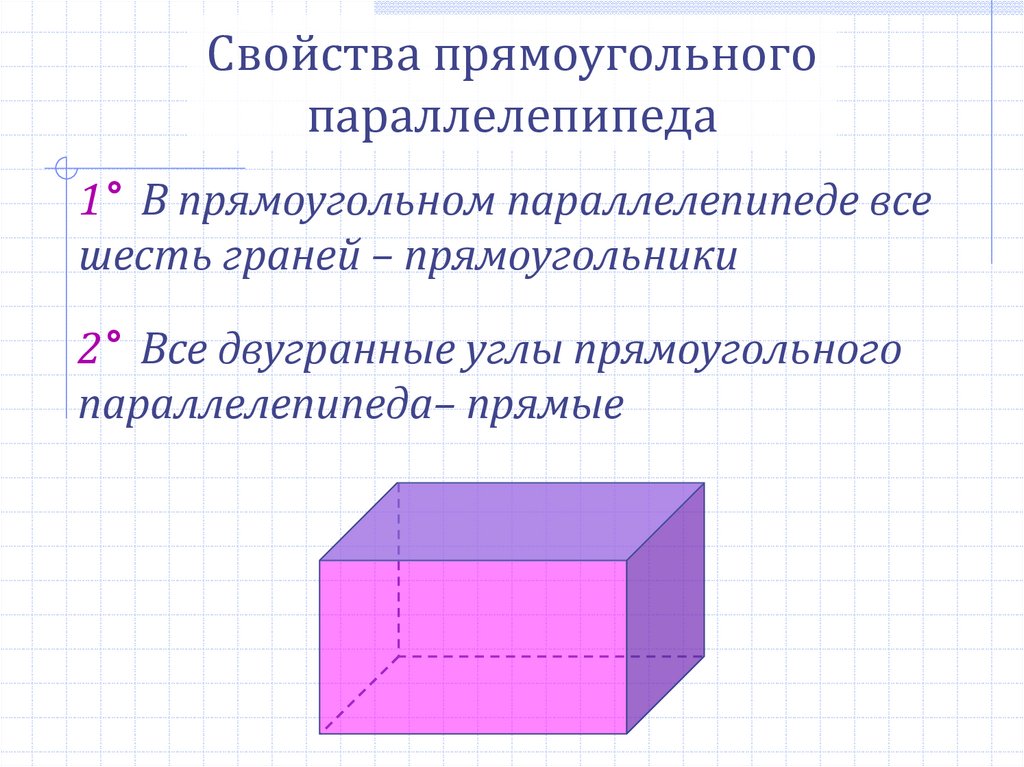
Свойства прямоугольногопараллелепипеда
1° В прямоугольном параллелепипеде все
шесть граней – прямоугольники
2° Все двугранные углы прямоугольного
параллелепипеда– прямые
14.
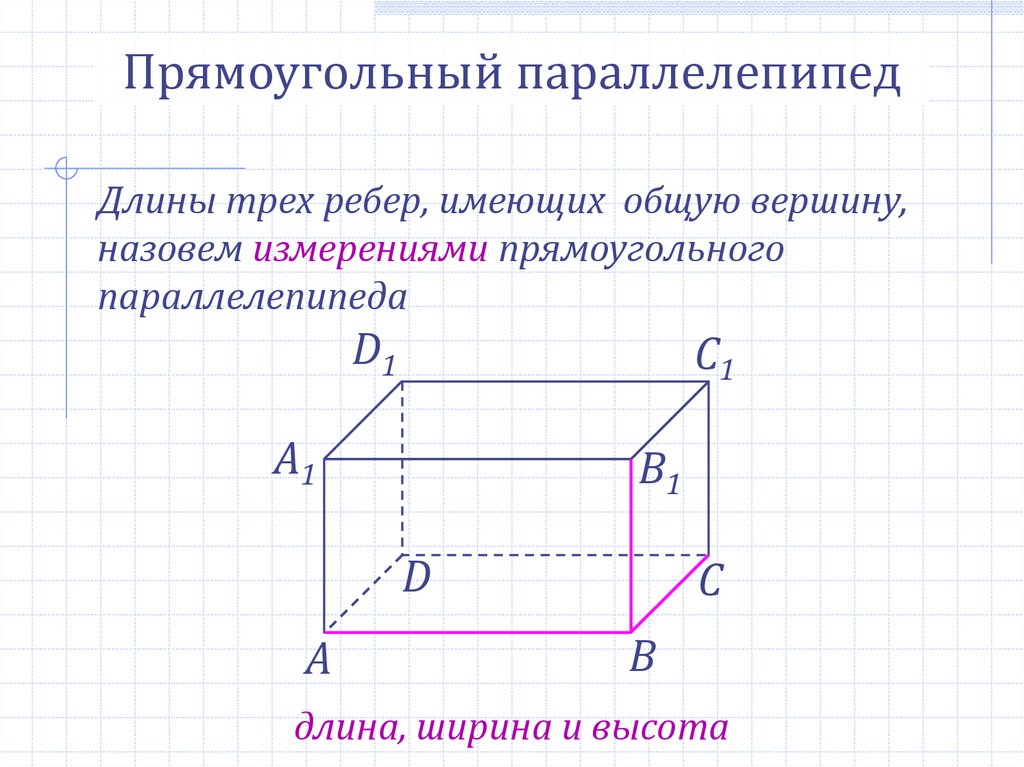
Прямоугольный параллелепипедДлины трех ребер, имеющих общую вершину,
назовем измерениями прямоугольного
параллелепипеда
D1
C1
А1
B1
D
А
С
В
длина, ширина и высота
15.
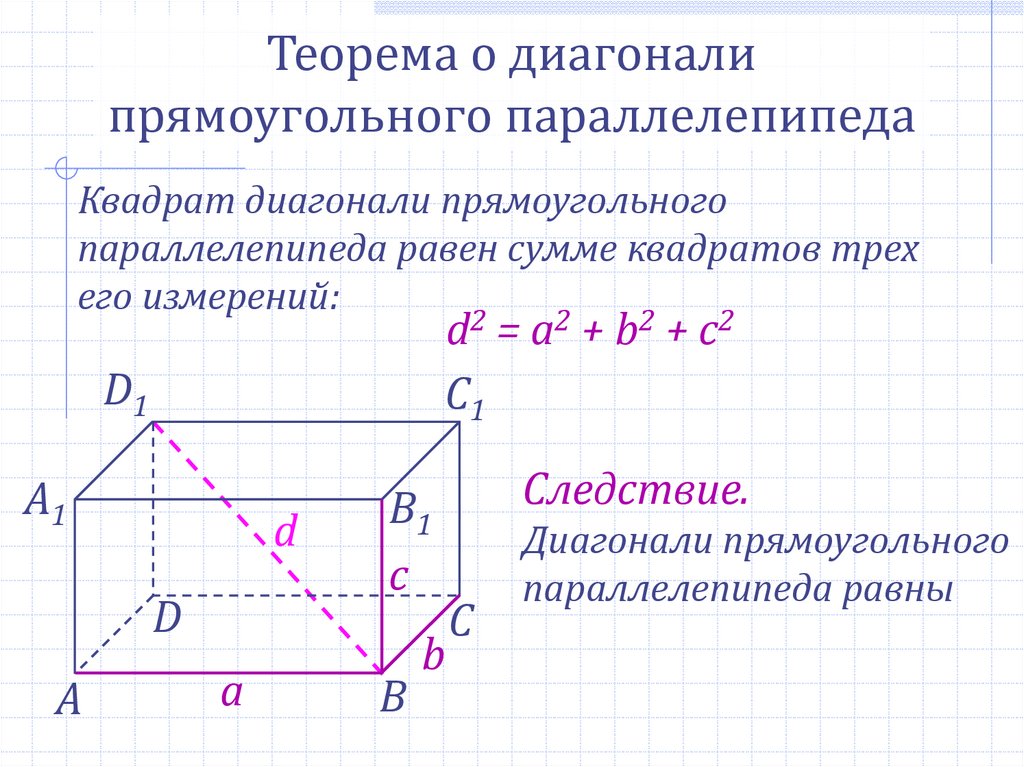
Теорема о диагоналипрямоугольного параллелепипеда
Квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов трех
его измерений:
d2 = a2 + b2 + c2
C1
D1
А1
d
D
А
a
B1
c
В
b
Следствие.
С
Диагонали прямоугольного
параллелепипеда равны
16.
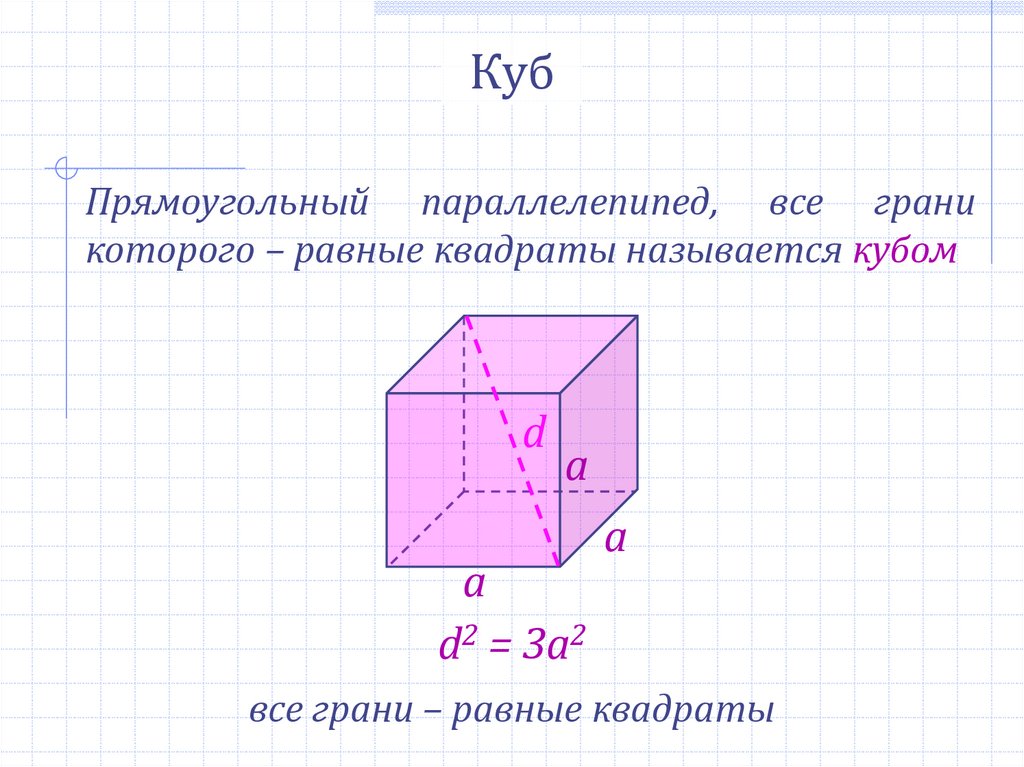
КубПрямоугольный параллелепипед, все грани
которого – равные квадраты называется кубом
d
a
a
a
d2 = 3a2
все грани – равные квадраты
 mathematics
mathematics








