Similar presentations:
Прямая в пространстве и её основные уравнения
1. Прямая в пространстве и её основные уравнения
Рассмотрим прямую l впрямоугольной декартовой
системе координат. Положение
прямой в пространстве вполне
определяется точкой M 0 ( x0 , y 0 , z 0 ) l
и направляющим вектором
s (m, n, p) || l
1
2.
Возьмем любую точку M ( x, y, z ) lи построим вектор M 0 M || s ,
из условия коллинеарности этих
векторов получим канонические
уравнения прямой в
пространстве:
x x0 y y 0 z z 0
m
n
p
2
3.
Обозначим коэффициентпропорциональности через
параметр t и выразим через t
переменные x, y, z. Приходим к
параметрическим уравнениям
прямой в пространстве:
x x 0 mt ,
y y 0 nt,
z z pt,
0
3
4.
Уравнение прямой, проходящейчерез две точки M1(x1, y1, z1) и
M2(x2, y2, z2) , имеет вид:
x x1
y y1
z z1
.
x 2 x1 y 2 y1 z 2 z 1
4
5.
Рассмотрим две плоскости P1 :A1x + B1y + C1z+ D1 = 0 и
P2 : A2x + B2y + C2z+ D2 = 0. Если
эти плоскости не параллельны,
то они пересекаются по прямой,
задаваемой системой
уравнений:
5
6.
A1 x B1 y C1 z D1 0,A
x
B
y
C
z
D
0
.
2
2
2
2
Эта система называется общим
уравнением прямой в
пространстве.
6
7.
Угол φ междупрямыми l1 и l2
равен углу между
их направляющими
s1 ( m1 , n1 , p1 ) s 2 (m 2 , n 2 , p 2 )
векторами
s1 s 2
mи
1 m 2 n1 n 2 p1 p 2
cos
2
2
2
2
2
2
| s1 || s 2 |
m1 n1 p1 m 2 n 2 p 2
7
8.
Угол ψ междуx x0 y y 0 z z 0
прямой
m
n
p
и плоскостью Ax + By
+ Cz + D = 0
определяется
| Am Bn Cp | по
sinформуле
2
2
2
2
2
2
A B C m n p
8
9.
Пример.Составить
канонические и
параметрические
уравнения
прямой,
проходящей через
точки M 1(3; 2; -1) и M 2(4; 2;
1).
9
10.
Решение.Подставляем в
формулу
координаты точек
M1x(3; 2;3-1) иyM 2(4;
2 2; 1):z 1
4 3
2 2
1 1
10
11.
илиx 3 y 2 z 1
1
0
2
– канонические
уравнения прямой
(нуль
в
s (1, 0, 2)
знаменателе
означает, что
направляющий
вектор
11
12.
Запишемпараметрические
уравнения
y
2
x
3
z
1
прямой
:
t
1
0
2
x 3 t,
y 2 0, z 1 2t ,
x 3 t,
y 2, z 1 2t
12
13. Прямая на плоскости и её основные уравнения
Уравнение прямойс угловым
коэффициентом
k
y kx b
имеет вид
y y 0 k ( x x0 )
или
13
14.
где k = tg α – угловойкоэффициент
прямой, b –
величина
отрезка,
отсекаемого этой
прямой на оси Oy, (x0,
y0) – точка, лежащая
на прямой.
14
15.
Кроме того,прямую l на
плоскости можно
задатьnвектором
( A, B) l
нормали
M
(
x
,
y
)
l
0 0
0
и точкой
15
16.
Получим триуравнения,
аналогичные
уравнениям для
A( x x 0 ) B( y: y 0 ) 0
плоскости
– уравнение
прямой, заданной
16
17.
Ax By C 0– общее уравнение
прямой;
x y
1
a b
– уравнение
прямой в
17
18.
Прямая l наплоскости также
определяется
s
(
m
,
n
)
||
l
направляющим
вектором
M
(
x
,
y
)
l
0 0
0
и точкой
18
19.
Получим еще 3уравнения,
аналогичные
уравнениям
x x0 в y y 0
прямой
пространстве:
m
n
19
20.
–x x0 mt ,
y y 0 nt
параметрические
x
x
y
y
1
1
уравнения
прямой
x ; x
y y
2
1
2
1
– уравнение
прямой,
20
21.
Угол между двумяпрямыми,
заданными
y k1 x b1
уравнениями:
l1: y k x b и
2
2
l2:
k 2 k1
tg найти по
можно
1 k1 k 2
формуле
21
22.
при этомl1 l 2
т.е. ,
k1k 2 1,
1
k1
k2
l1 || l2 k1 k2 .
22
23.
Расстояние d отточки M 1(x1, y1) до
прямой Ax + By + C = 0
вычисляется по
формуле
d
| Ax1 By1 C |
2
A B
2
23
24.
Пример. Записатьуравнения
прямых,
проходящих через
точку M (– 2, 1)
параллельно и
перпендикулярно
прямой
3x – 4y + 12 = 0.
24
25.
Решение.Перепишем общее
уравнение прямой
3x – 4y + 12 = 0, выразив
из него
переменную y:
3
l: y x 3
4
25
26.
Получилиуравнение прямой
с угловым
коэффициентом
k=
l1 || l
3/4. Запишем
уравнение прямой
и проходящей
через точку
3 M (– 2, 1).
k1 k для
Поскольку
4
параллельных
26
27.
то3
y 1 ( x 2)
4
или
4 y 4 3 x 6,
3x 4 y 10 0.
27
28.
Составимпрямой
lуравнение
l
2
, проходящей
через точку
M (–
2,1). Так как
угловые
коэффициенты
1
4
k2
перпендикулярны
k связаны
3
х прямых
соотношением
28
29.
4y 1 ( x 2)
3
или
3 y 3 4 x 8,
4 x 3 y 5 0.
29







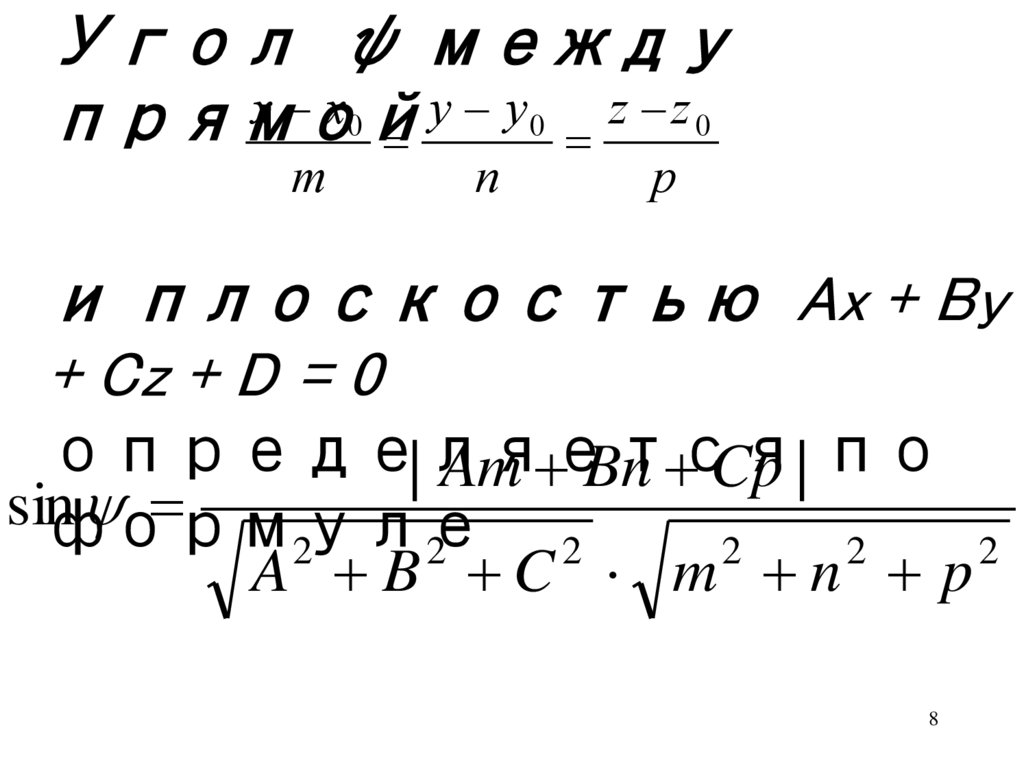



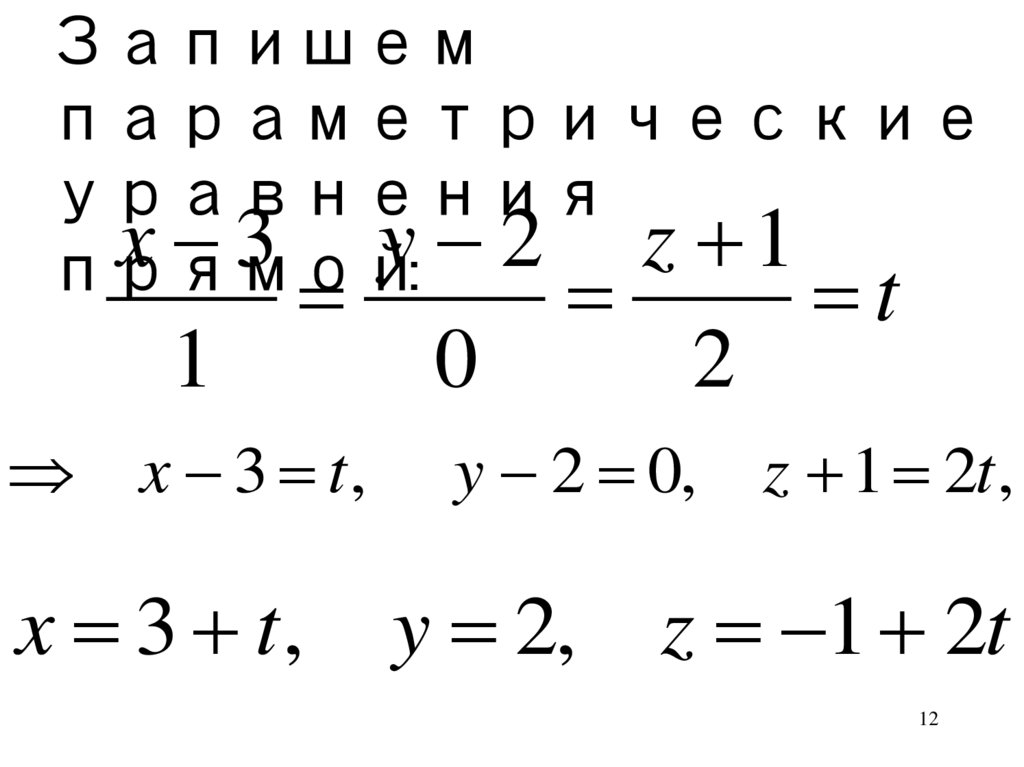




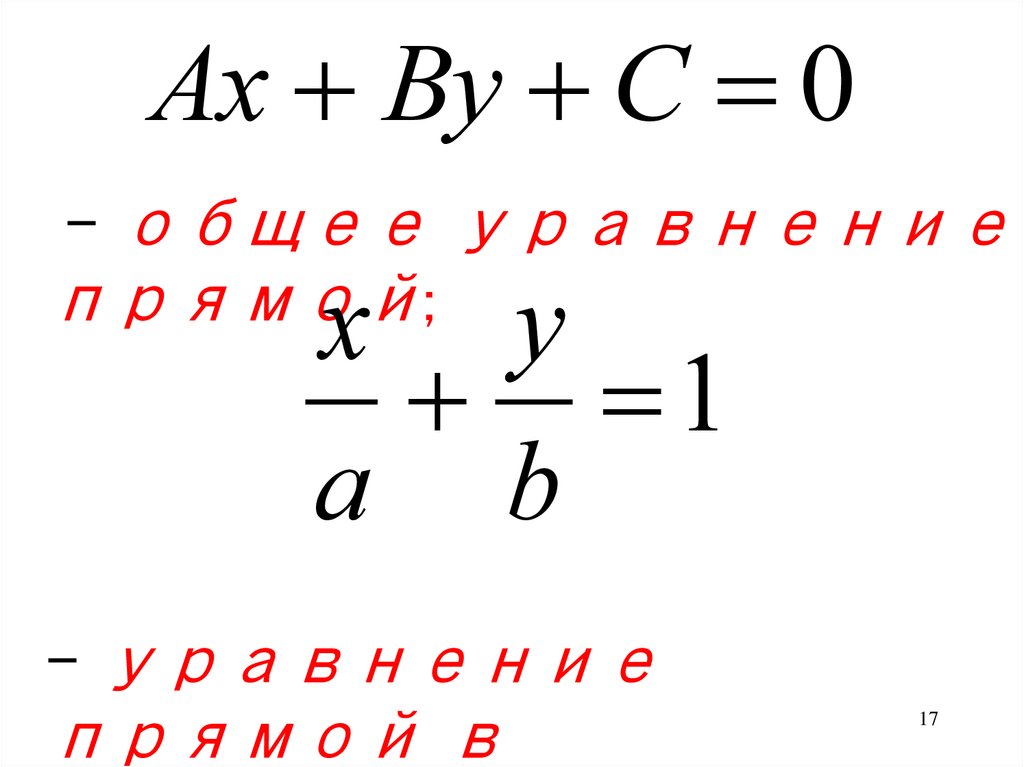


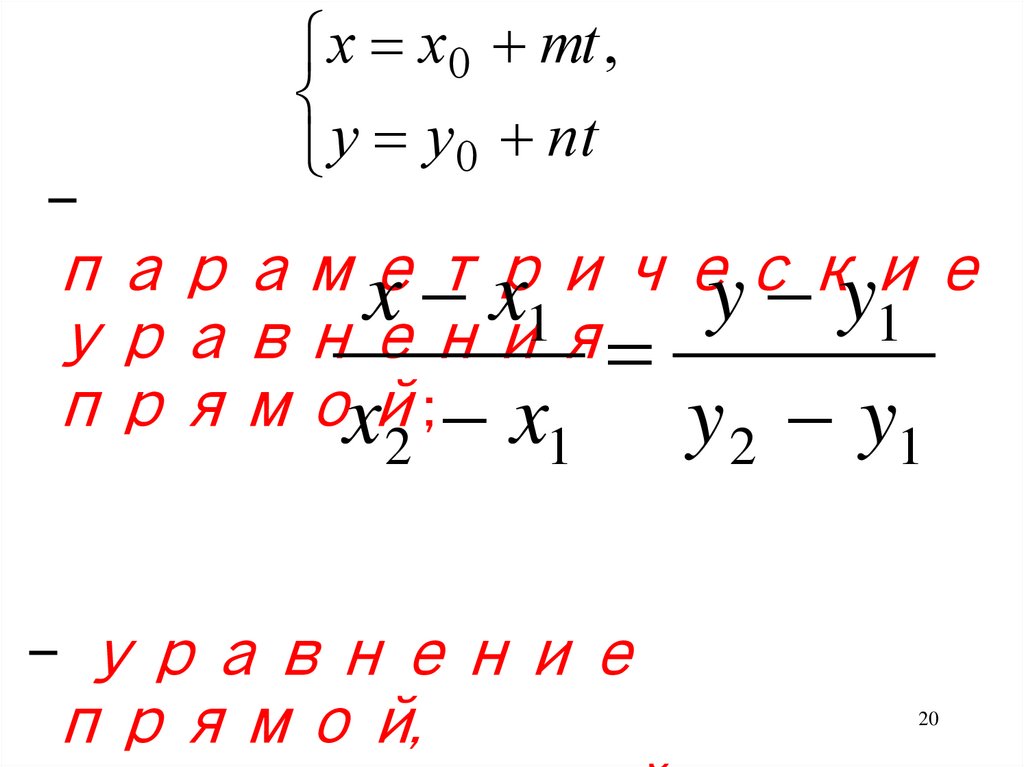
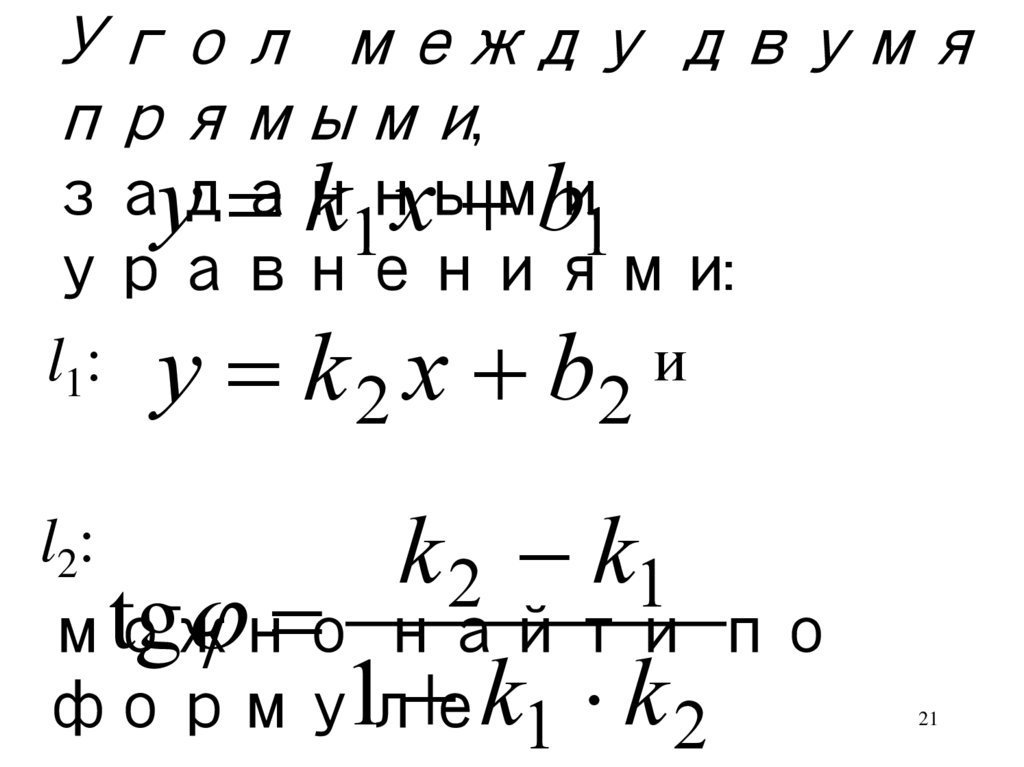
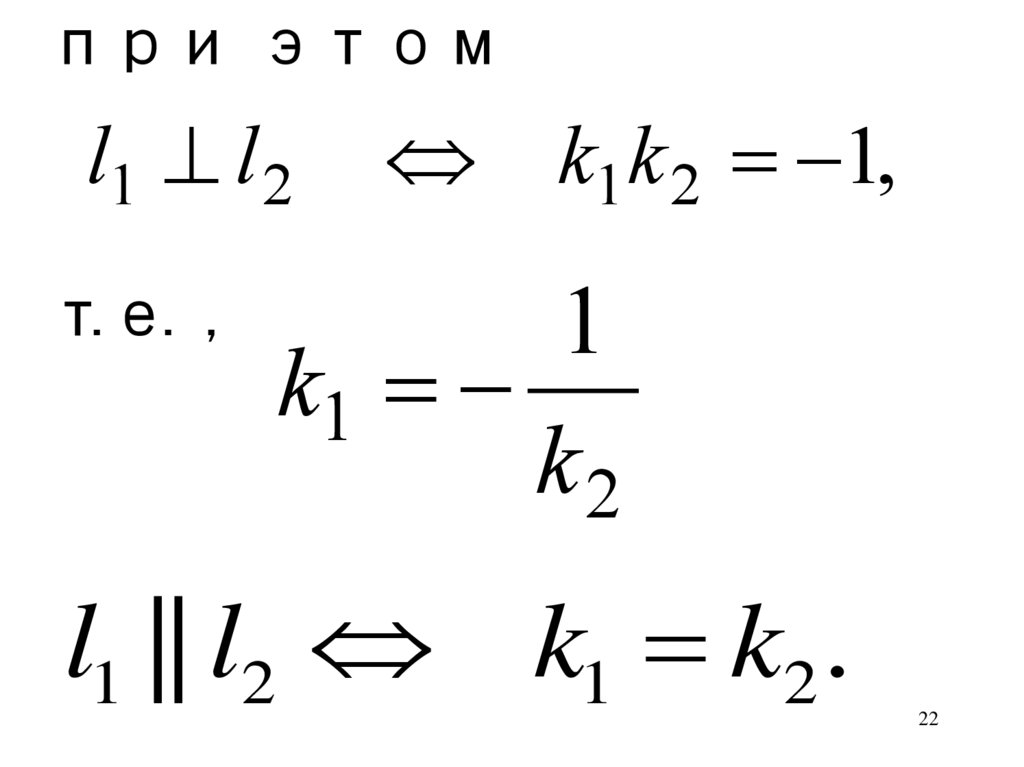
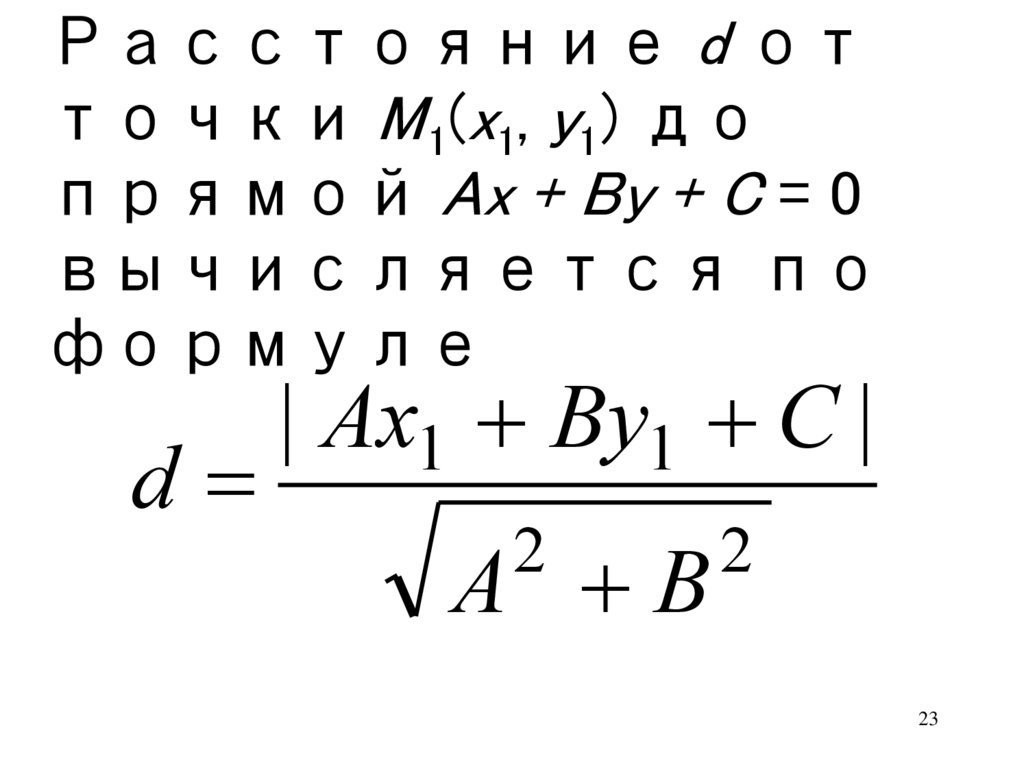

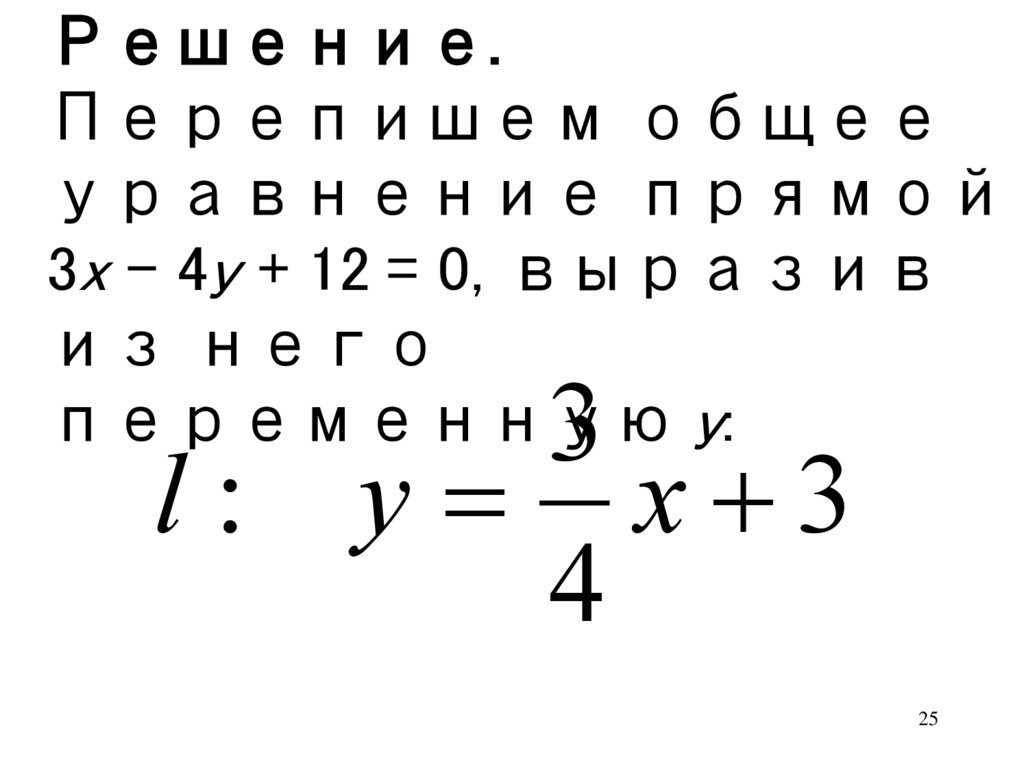

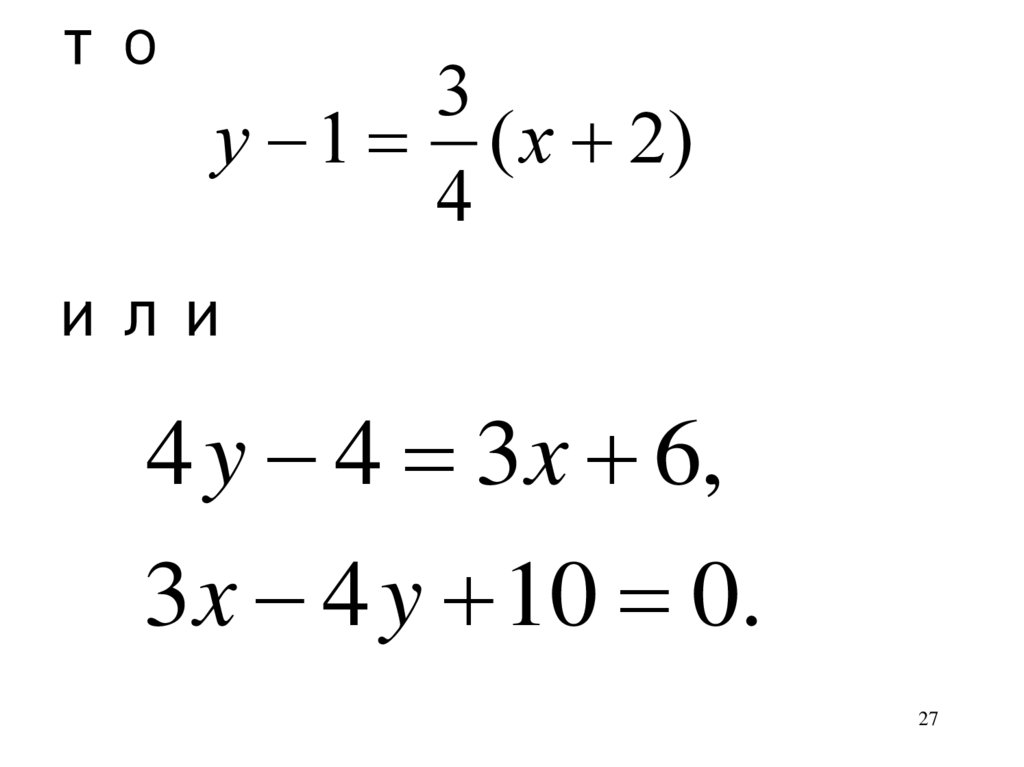

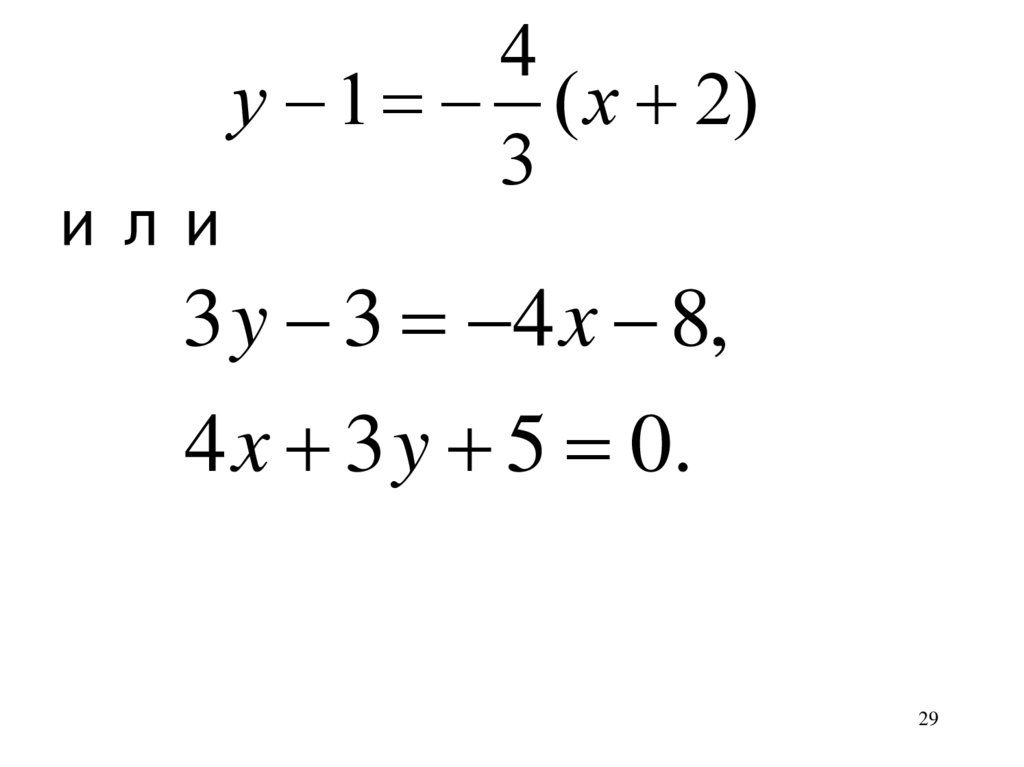
 mathematics
mathematics








