Similar presentations:
Прямая в пространстве. Уравнение прямой
1. Прямая в пространстве
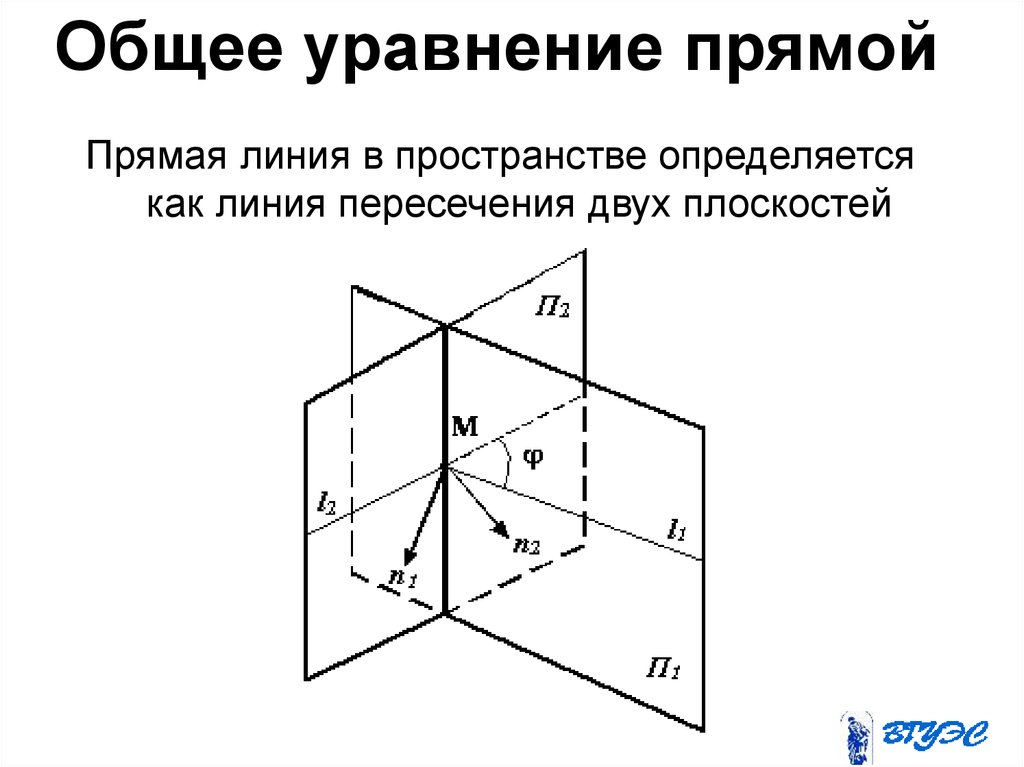
2. Общее уравнение прямой
Прямая линия в пространстве определяетсякак линия пересечения двух плоскостей
3.
A1 x B1 y C1 z D1 0,A2 x B2 y C 2 z D2 0,
n1 A1 , B1 , C1 , n2 A2 , B2 , C2
n1 l; n2 l; S || l n1 S , n2 S
S n1 n2
4.
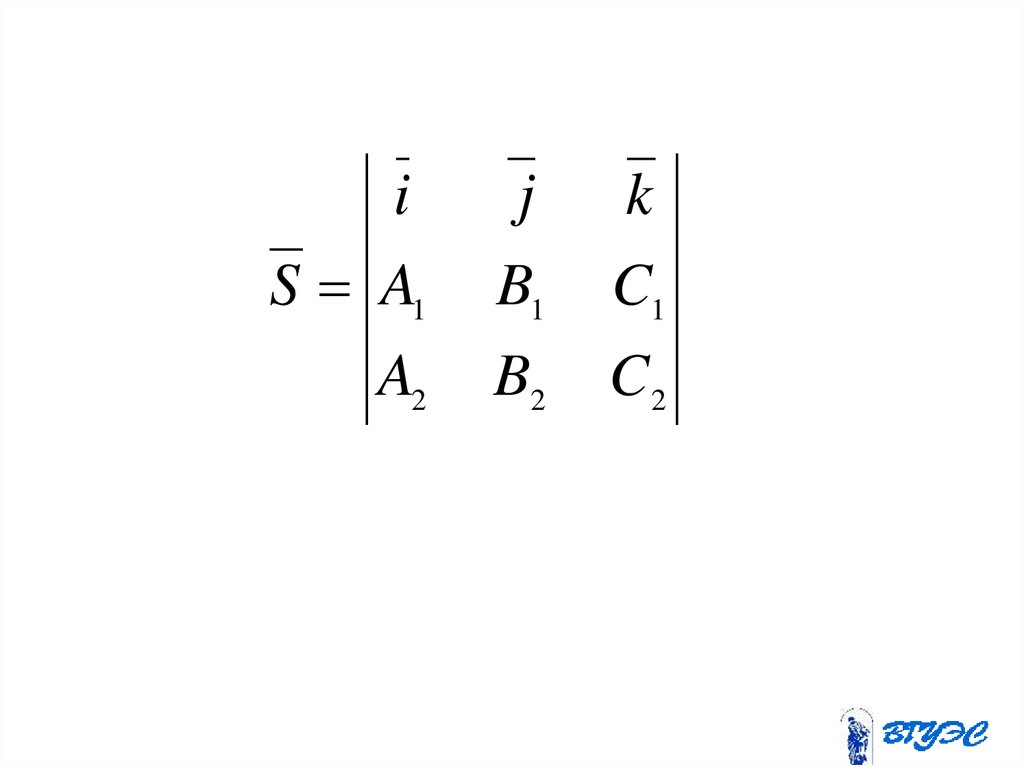
ij
k
S A1
B1
C1
A2
B2
C2
5. Канонические уравнения прямой
• Уравнение прямой, проходящей череззаданную точку параллельно заданному
вектору
х хо у у о z z о
m
p
q
6. Параметрические уравнения
х mt xo ,y pt yo ,
z qt zo
7. Уравнение прямой, проходящей через две точки
x xy y
z z
x x y y z z
1
2
1
1
2
1
1
2
1
8. Угол между прямыми
S1 S 2cos
а1 а2
m1m2 p1 p2 q1q2
.
2
2
2
2
2
2
m1 p1 q1 m2 p2 q2
9. Параллельность прямых
Еслито
,
1 2
m1 p1 q1
S1 S2 .
m2 p2 q2
10. Перпендикулярность прямых
Если 1 2 тоS1 S2 S1 S2 0
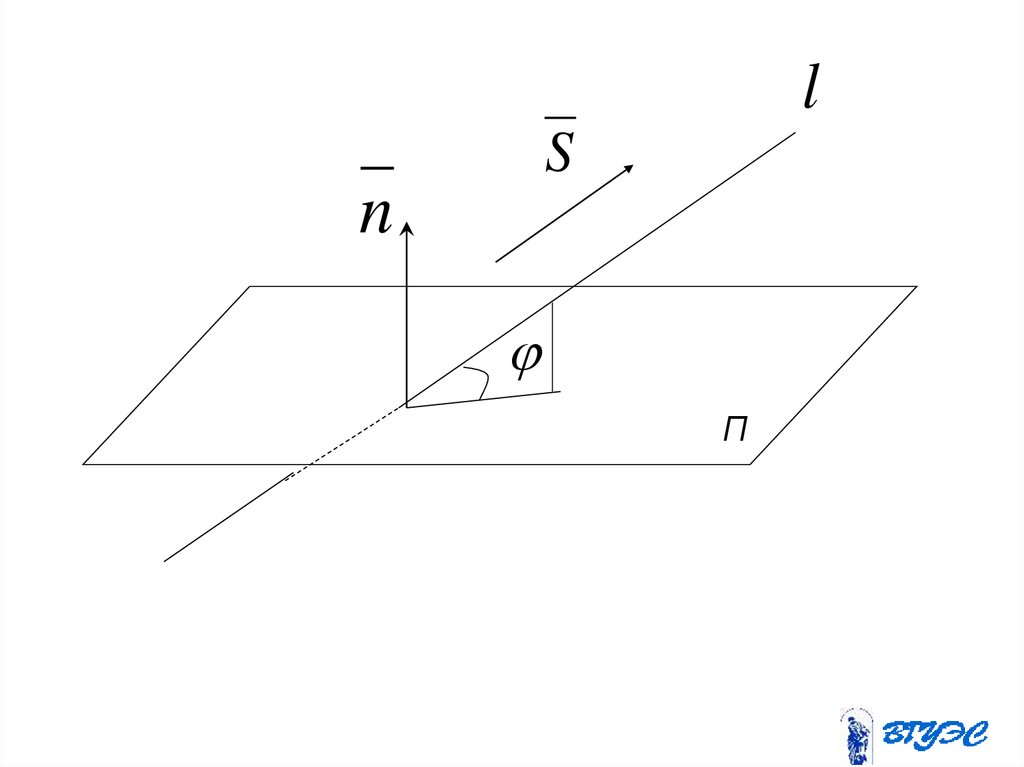
11. Угол между прямой и плоскостью
12.
lS
n
П
13.
Углом между прямой и плоскостьюназывается угол между прямой и ее
ортогональной проекцией на плоскость
sin
n S
n S
Am Bp Cq
A B C m p q
2
2
2
2
2
.
2
14. Условие параллельности прямой и плоскости
ЕслиП ,то
n S
Аm Вp Сq 0
15. Условие перпендикулярности прямой и плоскости
ЕслиП ,
то
n || S
А B С
m p q

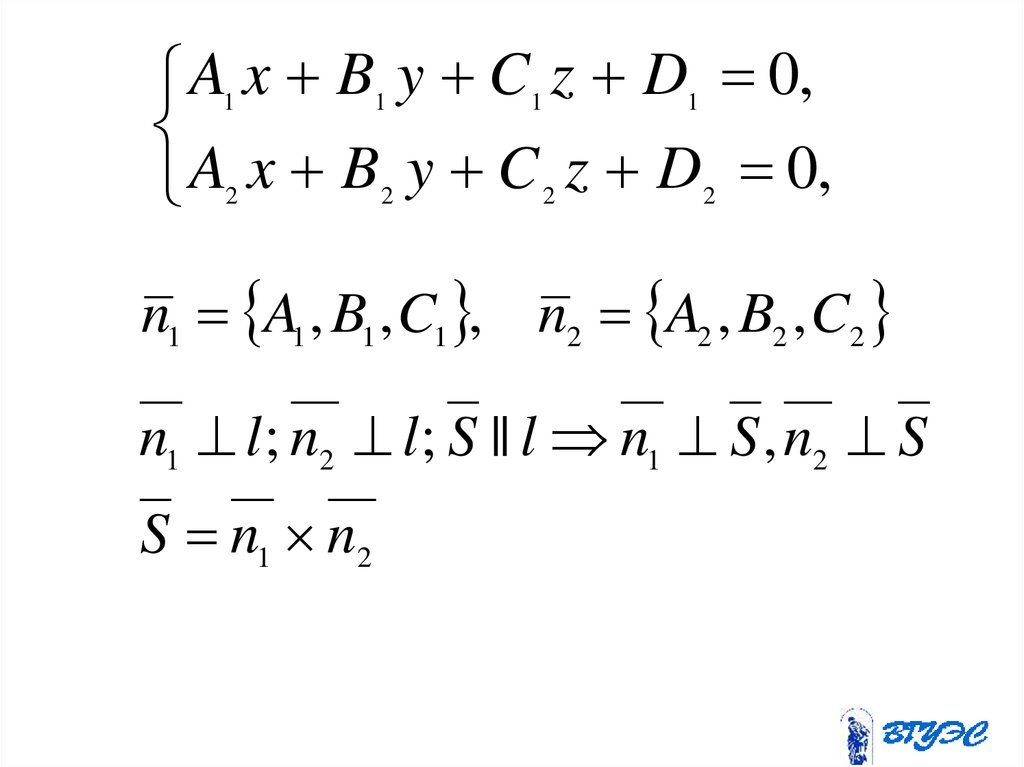










 mathematics
mathematics








