Lecture-8

1.

Digital Logic Design
Lecture – 8:
Arithmetic circuits: binary addition, half
adders, full adders, binary subtraction…
Konakbayev Olzhas, senior-lecturer,

2.

Lecture base
Digital Electronics: Principles & Applications, 9th edition by Roger
Tokheim & Patrick E. Hoppe:
• Chapter 10
2

3.

Introduction 1
• Binary Addition
• Half & Full Adders
• 3-Bit Adders
• Binary Subtraction
• Parallel Subtractors
3

4.

Introduction 2
• IC Adders
• Binary Multiplication
• 2s Complement Notation
• 2s Complement Adding/Subtracting
4

5.

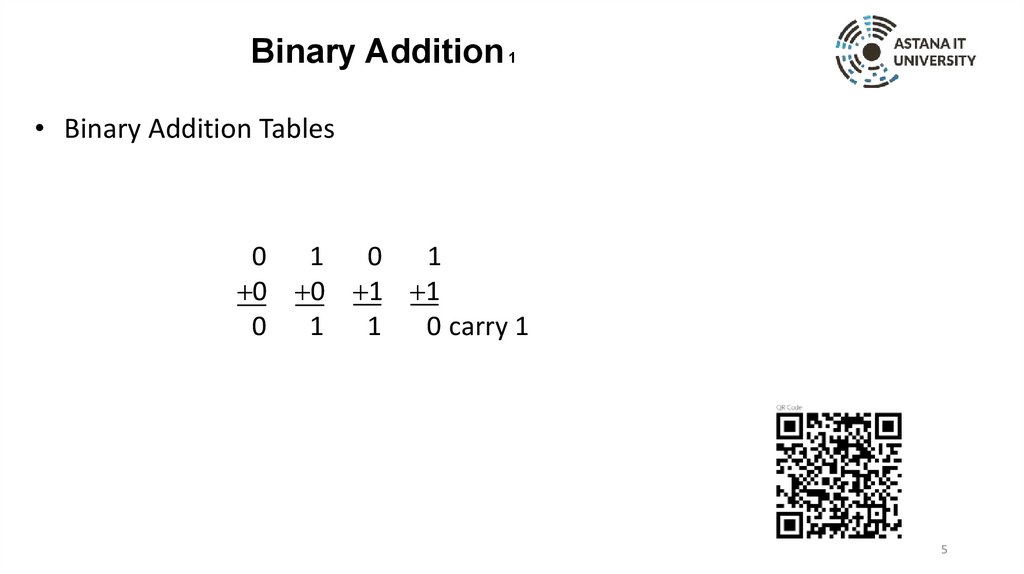
Binary Addition 1
• Binary Addition Tables
0 1 0
1
0 0 1 1
0 1 1
0 carry 1
5

6.

Binary Addition 2
• Binary Addition Examples
6

7.

Binary Addition 3
• Binary Addition Practice
1 0 1 0
0 1 0 1
7

8.

Binary Addition 4
• Binary Addition Practice
1 0 1 0
0 1 0 1
1 1 1 1
check
10
5
15
8

9.

Binary Addition 5
• Binary Addition Practice
1 0 1 1
0 1 0 1
9

10.

Binary Addition 6
• Binary Addition Practice
carry bits 1 1 1 1
1 0 1 1
0 1 0 1
1 0 0 0 0
check
11
5
16
10

11.

Binary Addition 7
• Binary Addition Practice
1 0 1 1 0 1 1 1
0 1 0 1 1 1 0 0
1 0 0 0 1 0 0 1 1
11

12.

Binary Addition 8
• Binary Addition Practice
carry bits 1 1 1 1 1 1
1 0 1 1 0 1 1 1
0 1 0 1 1 1 0 0
1 0 0 0 1 0 0 1 1
check
183
92
275
12

13.

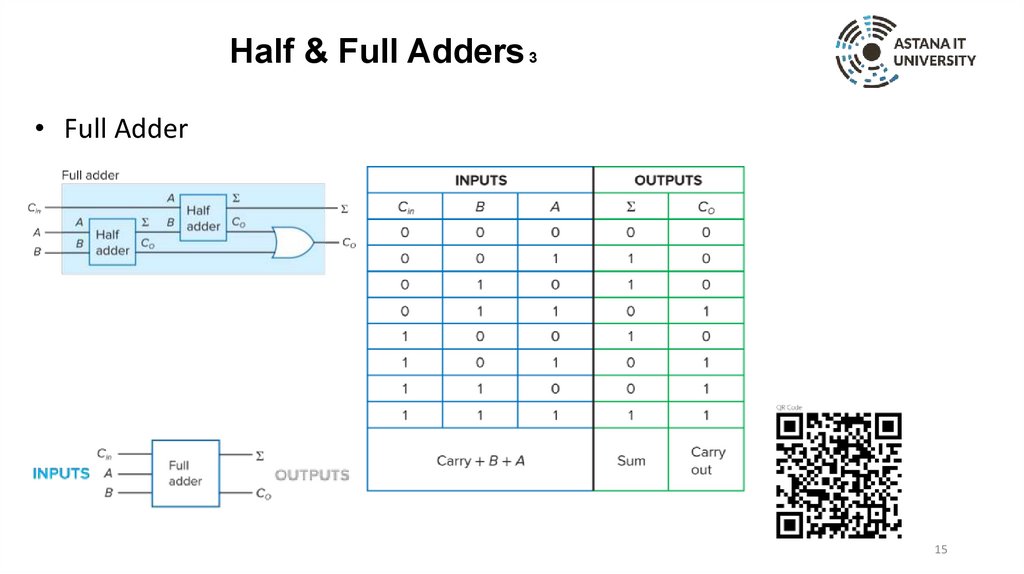
Half & Full Adders 1
• Half Adder
• Two input bits
• Sum bit out
• Carry bit out
• Full Adder
• Two input bits plus a
carry bit in
• Sum bit out
• Carry bit out
13

14.

Half & Full Adders 2
• Half Adder
14

15.

Half & Full Adders 3
• Full Adder
15

16.

Half & Full Adders 4
• Full Adder
16

17.

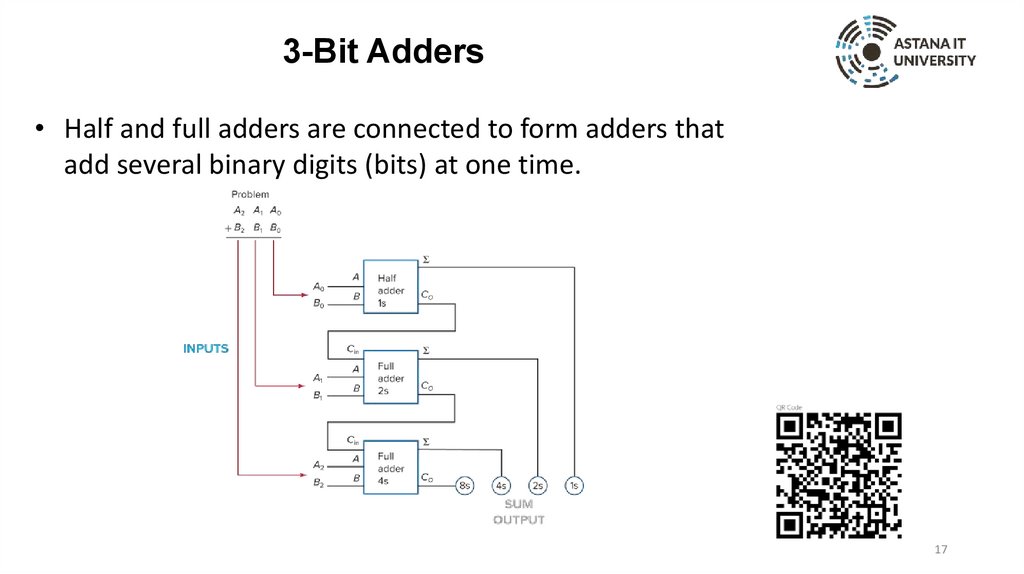
3-Bit Adders
• Half and full adders are connected to form adders that
add several binary digits (bits) at one time.
17

18.

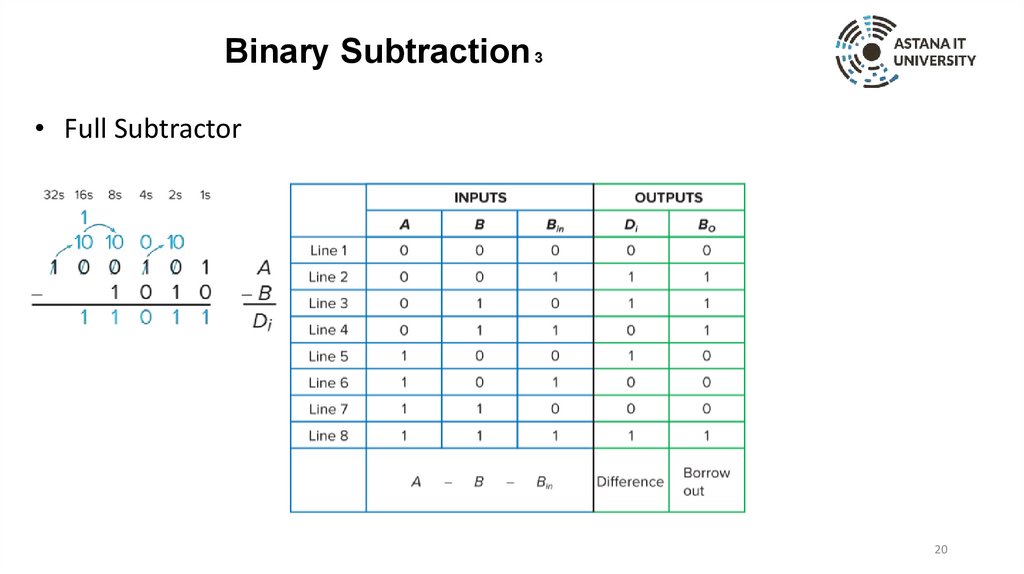
Binary Subtraction 1
• Binary subtractors are very similar to binary adders.
• Instead of a carry out, there is a borrow.
18

19.

Binary Subtraction 2
• Half subtractor
19

20.

Binary Subtraction 3
• Full Subtractor
20

21.

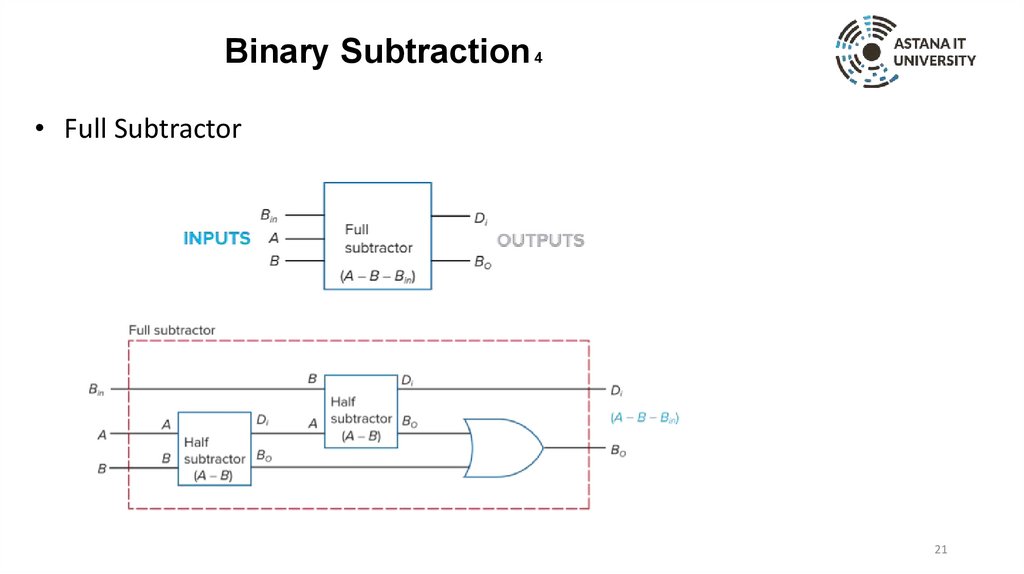
Binary Subtraction 4
• Full Subtractor
21

22.

Binary Subtraction 5
• Binary Subtraction Practice
1 0 1 1
0 1 0 1
22

23.

Binary Subtraction 6
• Binary Subtraction Practice
borrow bits
10
1 0 1 1
0 1 0 1
0 1 1 0
check
11
5
6
23

24.

Binary Subtraction 7
• Binary Subtraction Practice
1 0 1 1 0 1 1 1
0 1 0 1 1 1 0 0
24

25.

Binary Subtraction 8
• Binary Subtraction Practice
borrow bits
10 10 10
1 0 1 1 0 1 1 1
0 1 0 1 1 1 0 0
0 1 0 1 1 0 1 1
check
183
92
91
25

26.

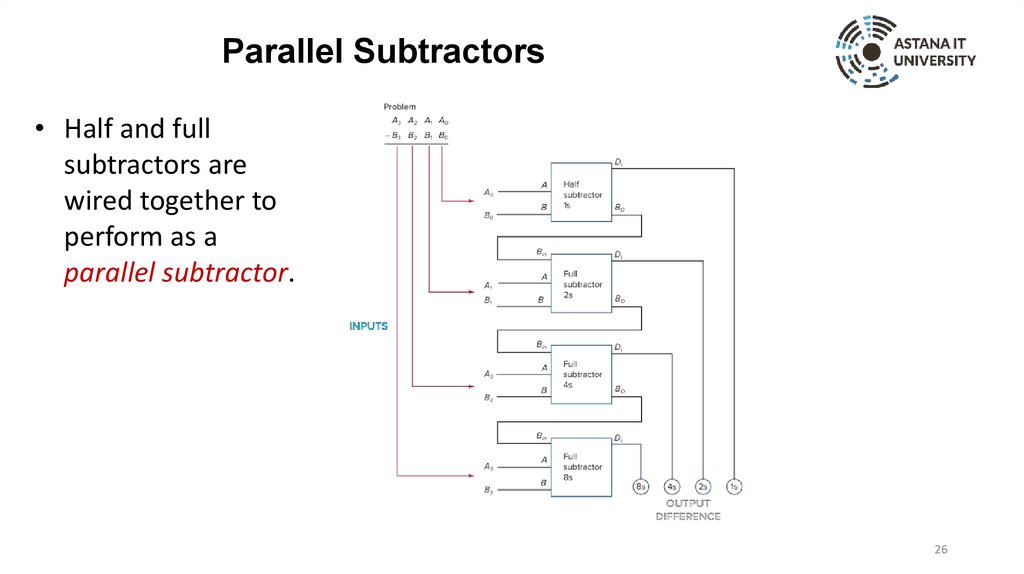
Parallel Subtractors
• Half and full
subtractors are
wired together to
perform as a
parallel subtractor.
26

27.

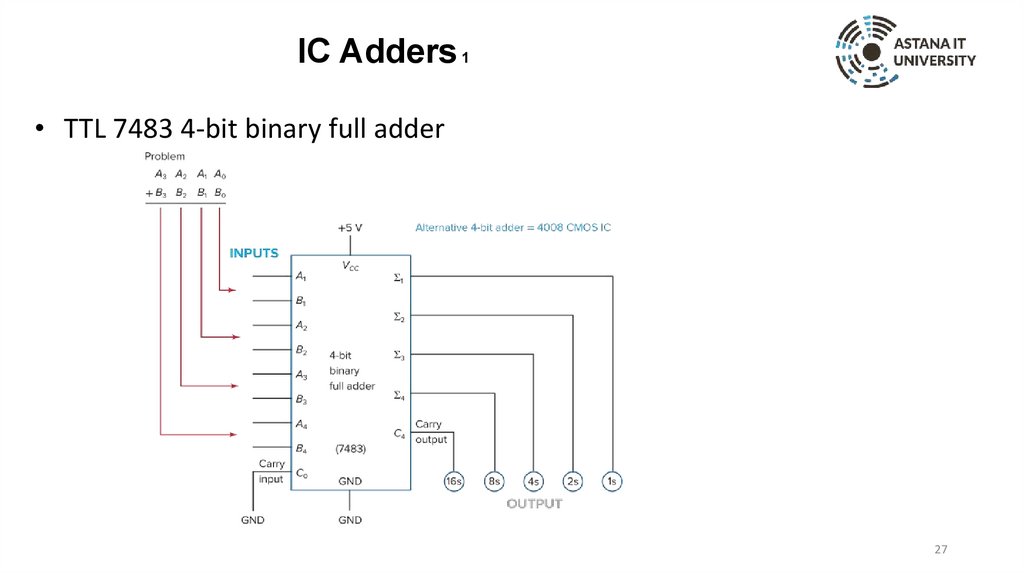
IC Adders 1
• TTL 7483 4-bit binary full adder
27

28.

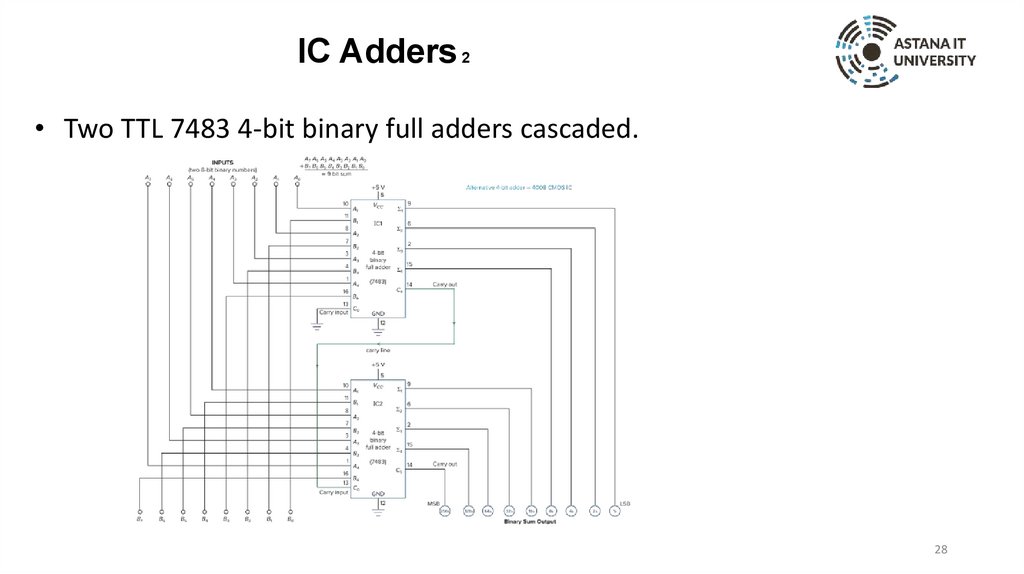
IC Adders 2
• Two TTL 7483 4-bit binary full adders cascaded.
28

29.

Binary Multiplication 1
• Multiplication can be thought of as repeated addition.
29

30.

Binary Multiplication 2
• Multiplication is the sum of partial products.
216
540
756
30

31.

Binary Multiplication 3
• Rules for Multiplication
• Example
31

32.

Binary Multiplication 4
• Example
32

33.

2s Complement Notation 1
• Sign Bit
• Positive number, sign bit = 0
• Negative number, sign bit = 1
• The 2s complement of a positive number is the same
as binary: +7 (decimal) = 0111 (2s complement) = 0111
(binary).
33

34.

2s Complement Notation 2
• The 2s complement of a negative number is found by
first taking the 1s complement and then adding 1.
• Convert the decimal number to its binary equivalent.
• Convert the binary number to its 1s complement by
changing all 1s to 0s and all 0s to 1s.
• Add 1 to the 1s complement number, using regular binary
addition.
34

35.

2s Complement Notation 3
35

36.

2s Complement Notation 4
• Example: Convert 410 to its 2s complement.
36

37.

2s Complement Notation 5
• Converting from 2s complement to binary.
37

38.

2s Complement Adding/Subtracting 1
• The 2s complement is useful in the addition of signed
numbers.
( 4)
( 3)
710
0100
0011
0111 (2s complement SUM)
38

39.

2s Complement Adding/Subtracting 2
• The 2s complement is useful in the addition of signed
numbers.
( 1)
( 2)
310
1111
1110
11101 (2s complement SUM)
Discard
39

40.

2s Complement Adding/Subtracting 3
• The 2s complement is useful in the addition of signed
numbers.
( 1)
( 3)
210
0001
1101
1110 (2s complement SUM)
40

41.

2s Complement Adding/Subtracting 4
• The 2s complement is useful in the addition of signed
numbers.
( 5)
( 4)
110
0101
1100
10001 (2s complement SUM)
Discard
41

42.

2s Complement Adding/Subtracting 5
• The 2s complement is useful in the addition of signed
numbers.
( 50)
( 30)
8010
1 1 0 0 1 1 1 0 2s
1 1 1 0 0 0 1 0 2s
11011 0 0 0 0
Negative
sign
0 1 0 0 1 1 1 1 1s
1
0 1 0 1 0 0 0 0 2s
8010
42

43.

2s Complement Adding/Subtracting 6
• The 2s complement is useful in the subtraction of
signed numbers.
( 7) Form 2s comp. 0111
( 3)
1101
410 and ADD 1 0100 (2s comp. Difference)
Discard
43

44.

2s Complement Adding/Subtracting 7
• The 2s complement is useful in the subtraction of
signed numbers.
( 8) Form 2s comp. 1000
( 3)
0011
510 and ADD
1011 (2s comp. Difference)
44

45.

2s Complement Adding/Subtracting 8
• The 2s complement is useful in the subtraction of
signed numbers.
( 3) Form 2s comp.
0011
( 3)
0011
610 and ADD
0110 (2s comp. Difference)
45

46.

2s Complement Adding/Subtracting 9
• The 2s complement is useful in the subtraction of
signed numbers.
( 4) Form 2s comp. 1100
( 2)
1110
610 and ADD 1 1010 (2s comp. Difference)
Discard
46

47.

Review 1
• Add the following binary numbers.
1011
0111
47

48.

Review 2
• Add the following binary numbers.
1011
0111
10010
48

49.

Review 3
• Add the following binary numbers.
10111101
01110 011
49

50.

Review 4
• Add the following binary numbers.
10111101
01110 011
10 0110 0 0 0
50

51.

Review 5
• Draw a block diagram of a half adder.
• Draw a block diagram of a full adder.
51

52.

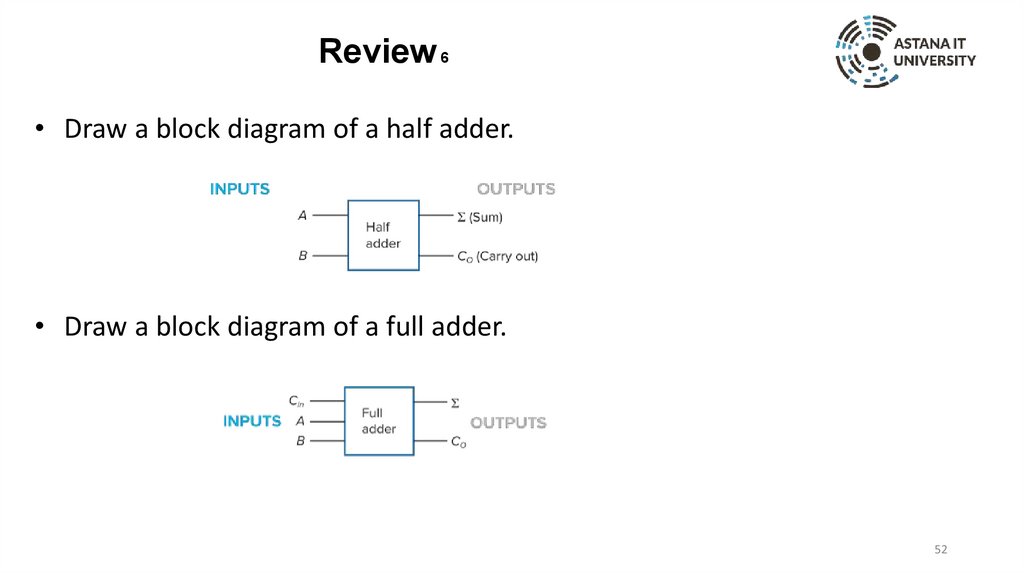
Review 6
• Draw a block diagram of a half adder.
• Draw a block diagram of a full adder.
52

53.

Review 9
• Complete the following binary subtraction.
10101010
01010110
53

54.

Review 10
• Complete the following binary subtraction.
Borrow
10 10 10
10101010
01010110
01010100
54

55.

Review 17
• Complete the following binary multiplication.
111
101
55

56.

Review 18
• Complete the following binary multiplication.
111
101
111
000
111
10 0 011
56

57.

Review 13
• Draw a block diagram of a half subtractor.
• Draw a block diagram of a full subtractor.
57
57

58.

Review 14
• Draw a block diagram of a half subtractor.
• Draw a block diagram of a full subtractor.
58

59.

Thank you!
59