Summaator Adder

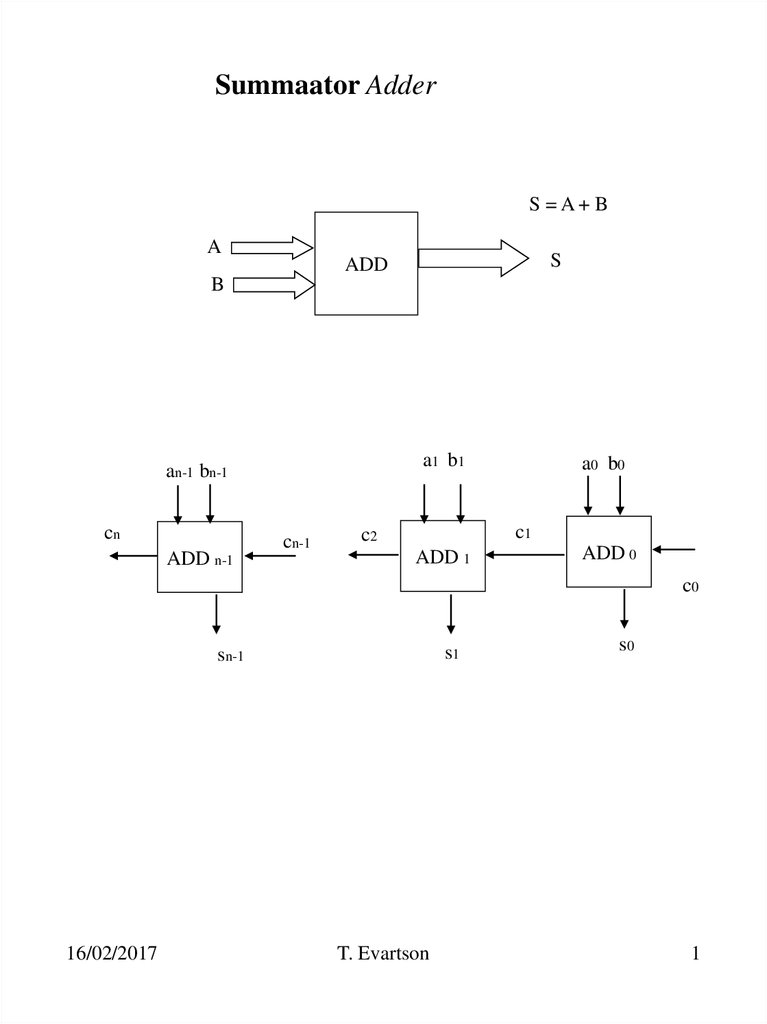
1. Summaator Adder

S =A+ B
A
S
ADD
B
a1 b 1
an-1 bn-1
cn
ADD n-1
cn-1
a0 b 0
c1
c2
ADD 1
ADD 0
c0
s1
sn-1
16/02/2017
T. Evartson
s0
1

2. Täissummaator Full adder

ai
0
0
0
0
1
1
1
1
ai
bi
0
0
1
1
0
0
1
1
ci
0
1
0
1
0
1
0
1
si
0
1
1
0
1
0
0
1
ci+1
0
0
0
1
0
1
1
1
+
bi
+
ci
si
&
&
1
ci+1
&
16/02/2017
T. Evartson
2

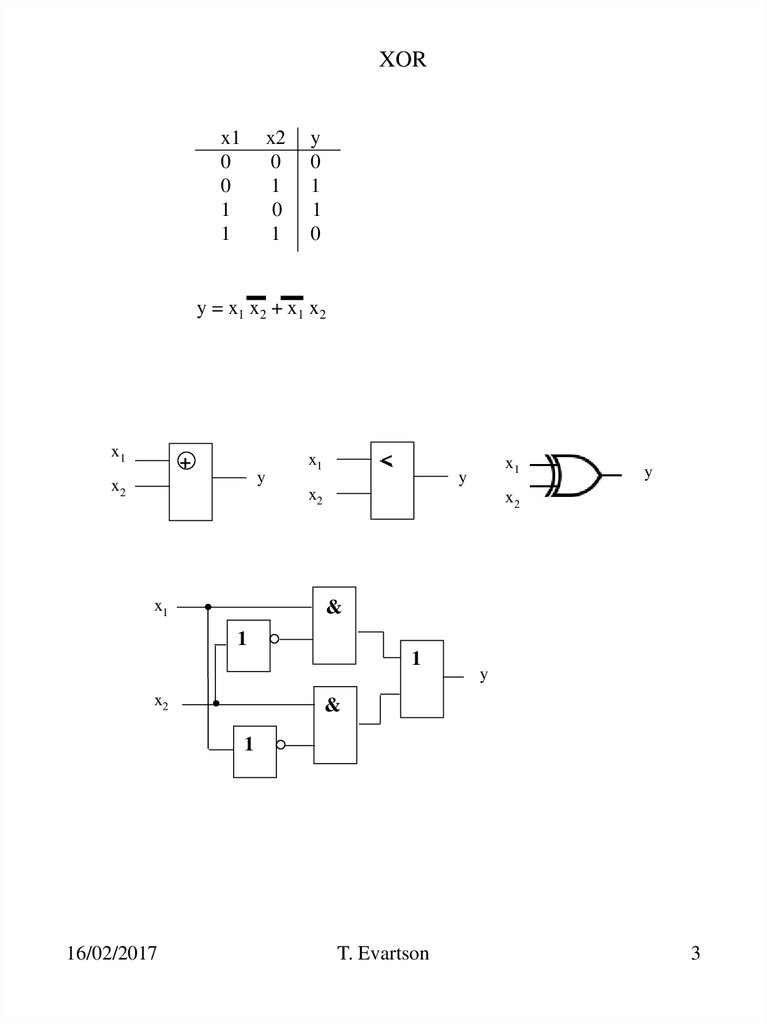
3. XOR

x1
0
0
1
1
x2
0
1
0
1
y
0
1
1
0
y = x 1 x 2 + x1 x 2
x1
+
y
x2
<
x1
x1
y
x2
x1
y
x2
&
1
1
x2
y
&
1
16/02/2017
T. Evartson
3

4.

16/02/2017
T. Evartson
4

5.

16/02/2017
T. Evartson
5

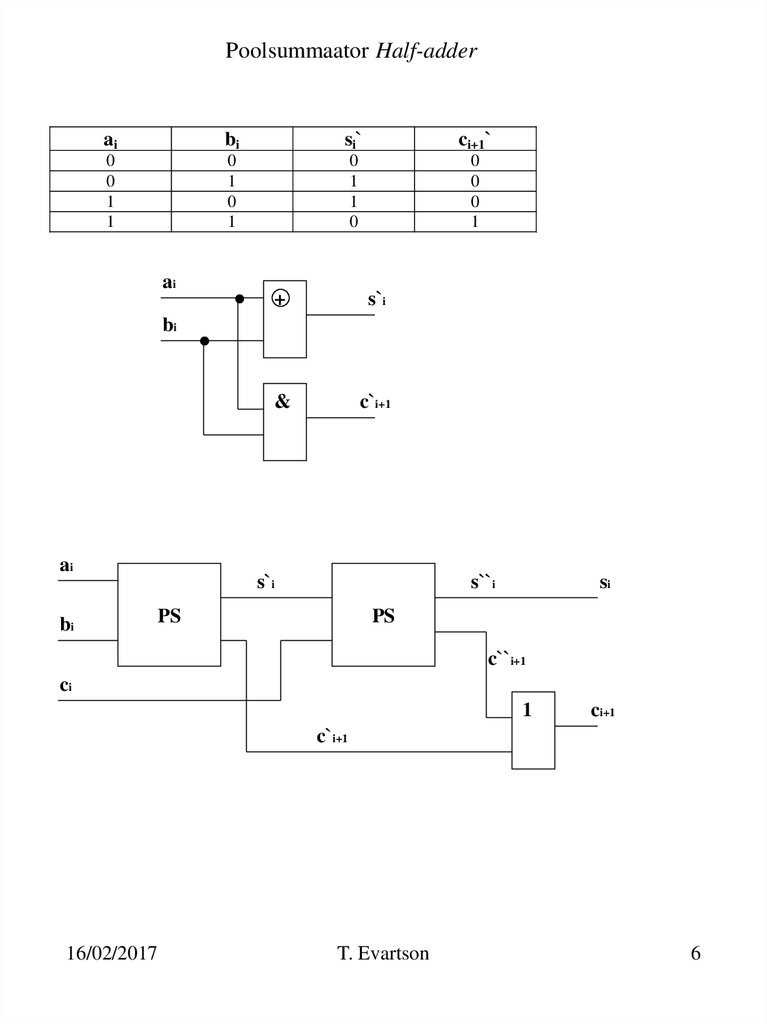
6. Poolsummaator Half-adder

ai
bi
s i`
ci+1`
0
0
1
1
0
1
0
1
0
1
1
0
0
0
0
1
ai
+
s`i
&
c`i+1
bi
ai
bi
s`i
s``i
PS
si
PS
c``i+1
ci
1
ci+1
c`i+1
16/02/2017
T. Evartson
6

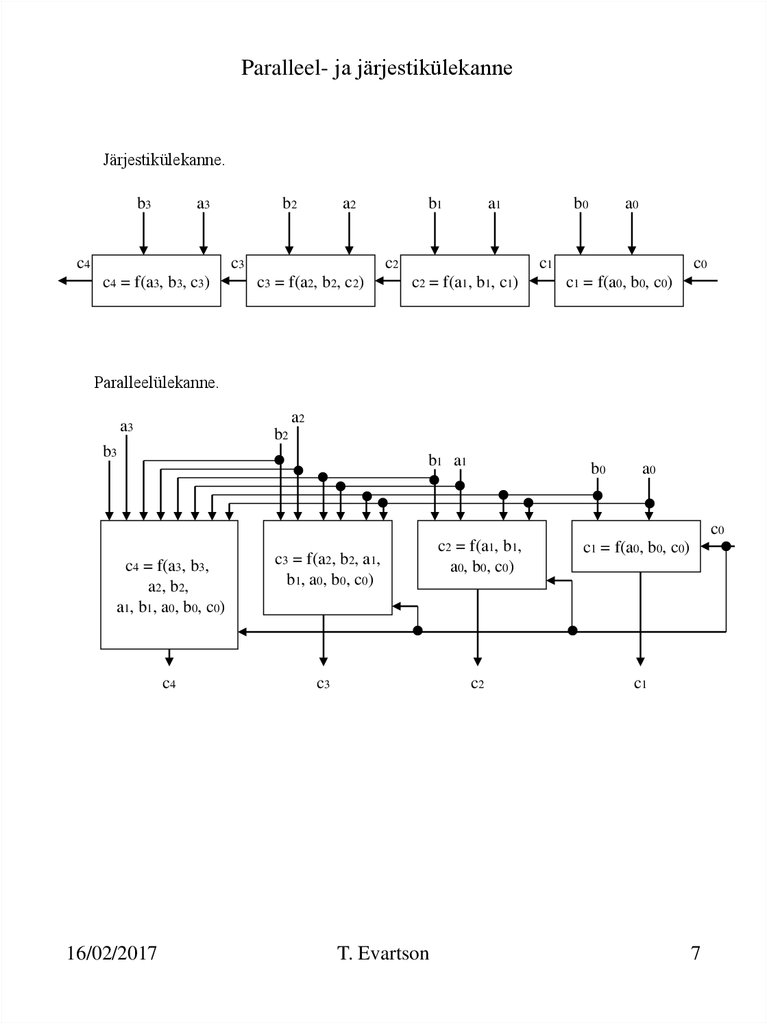
7. Paralleel- ja järjestikülekanne

Järjestikülekanne.
b3
a3
c4
b2
a2
c3
c4 = f(a3, b3, c3)
b1
a1
c2
c3 = f(a2, b2, c2)
b0
a0
c1
c2 = f(a1, b1, c1)
c0
c1 = f(a0, b0, c0)
Paralleelülekanne.
a2
a3
b2
b3
b1 a1
b0
a0
c0
c4 = f(a3, b3,
a2, b2,
a1, b1, a0, b0, c0)
c3 = f(a2, b2, a1,
b1, a0, b0, c0)
c4
c3
16/02/2017
T. Evartson
c2 = f(a1, b1,
a0, b0, c0)
c1 = f(a0, b0, c0)
c2
c1
7

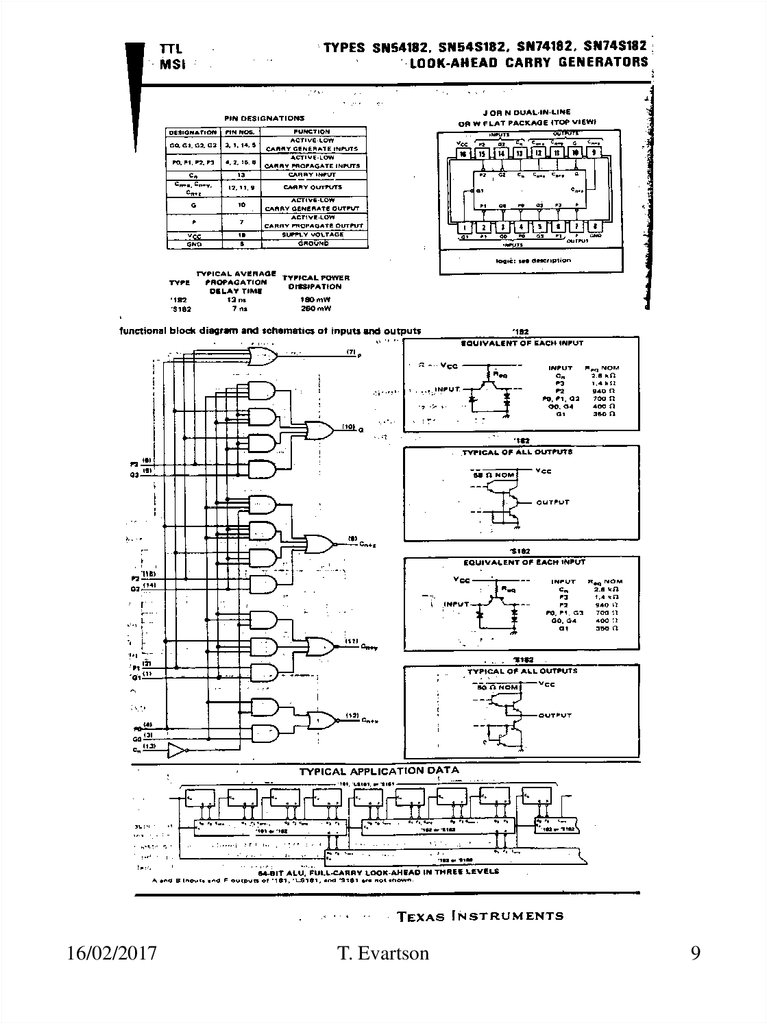
8. Kiire ülekanne Look-Ahead Carry Generator

Liitmis blokk (LB)
bi
&
1
ai
ci
+
+
gi
pi
si
P
G
Kiire ülekannde skeem
c4
p3 g3
p2 g2
b3 a3
LB3
s3
16/02/2017
p1 g1
b2 a2
c3
c0
LB2
b1 a1
c2
s2
T. Evartson
p0 g0
LB1
b0 a0
c1
s1
LB0
s0
8

9.

16/02/2017
T. Evartson
9

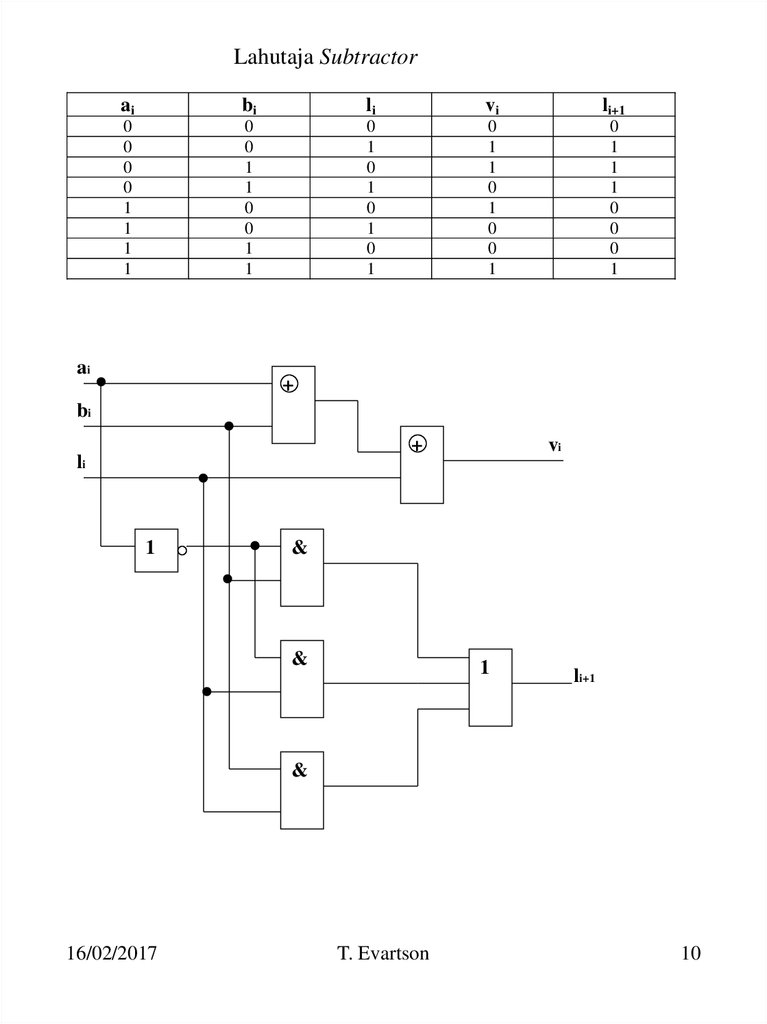
10. Lahutaja Subtractor

ai
bi
li
vi
li+1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
0
1
0
0
1
0
1
1
1
0
0
0
1
ai
+
bi
+
li
1
vi
&
&
1
li+1
&
16/02/2017
T. Evartson
10

11. Summaator-lahutaja I Adder-Subtractor I

ai
+
bi
+
ci/li
+
m
m=1 > m=0 > +
si/vi
&
&
1
ci+1/li+1
&
16/02/2017
T. Evartson
11

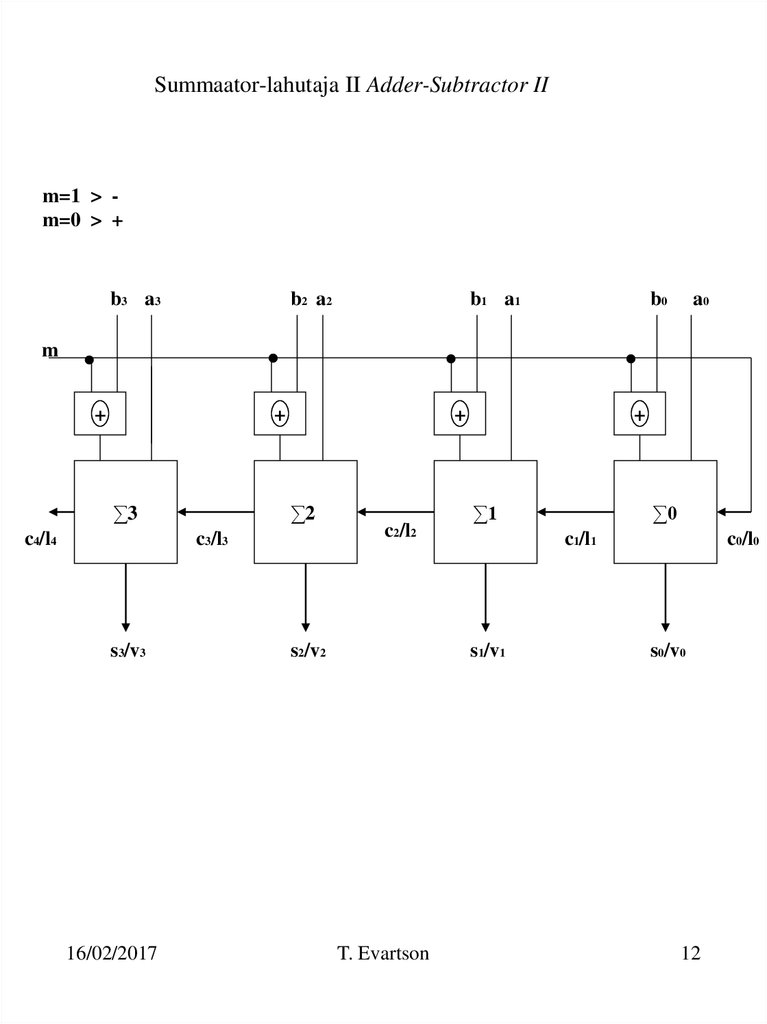
12. Summaator-lahutaja II Adder-Subtractor II

m=1 > m=0 > +
b3 a3
b2 a2
b1 a1
b0
a0
m
+
+
∑3
c4/l4
+
∑2
c3/l3
s3/v3
16/02/2017
c2/l2
s2/v2
+
∑1
c1/l1
s1/v1
T. Evartson
∑0
c0/l0
s0/v0
12