(3.1) 6_Delta-function (2)

1.

Дельта-функция Дирака
«Грубое» определение
0, x a
x a
, x a
Аккуратное определение
x2
a
x
dx f x x a f a , a x , x
1
x1
2

2.

Представление в виде интеграла Фурье
Преобразование Фурье
f k dx f ( x) e ikx
Обратное преобразование Фурье
dk
f (k ) eikx
2
f x
Подставить первое равенство во второе?

3.

Результат
dk ik ( x x )
dk ikx
ikx
f x
e dx f ( x ) e dx f ( x )
e
2
2
Чему равна функция в квадратных скобках?

4.

Интегральное представление дельта-функции
dk ik ( x x )
x x
e
2
Другое возможное представление дельта-функции
dk ik ( x x )
dk ik ( x x )
sin A( x x )
e
2 e
2
( x x ) A
A
A
A

5.

Первообразная для дельта-функции
x
dx x ?

6.

Первообразная для дельта-функции
0, x 0
dx x 1, x 0
x
Ступенчатая функция (функция Хэвисайда)
0, x 0
( x)
,
1, x 0
d ( x)
( x)
dx
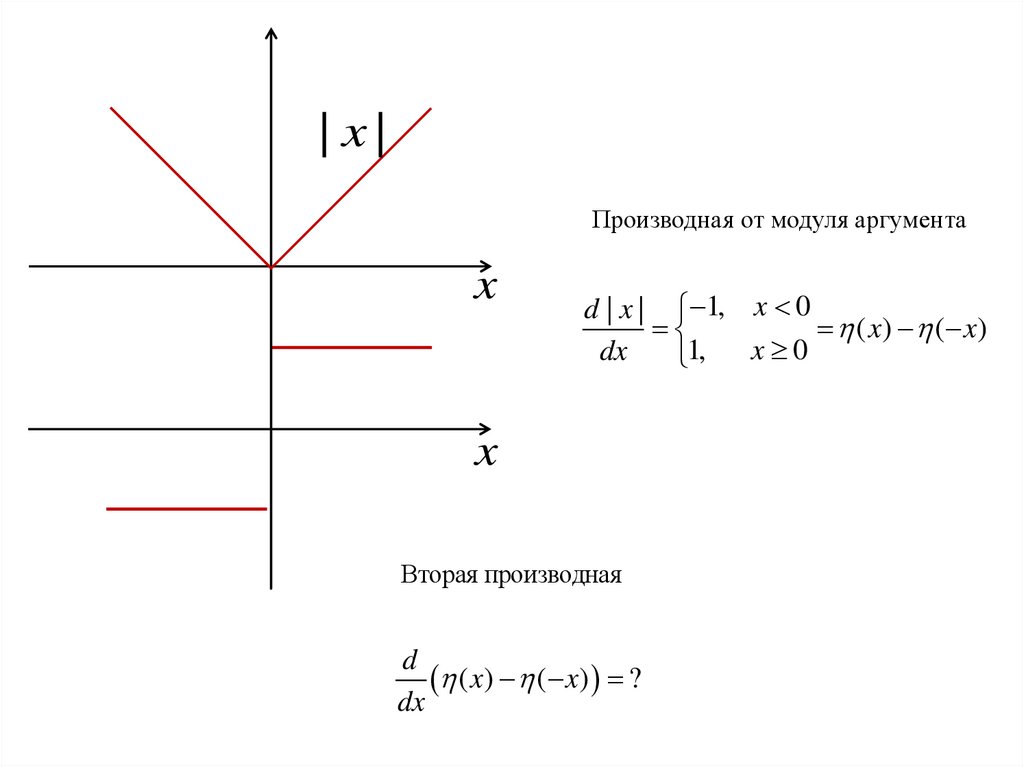
Найти вторую производную от модуля аргумента
d2 | x |
?
2
dx

7.

Производная от модуля аргумента (второй способ)
| x | x ( x) x ( x)
d | x|
( x) x ( x) ( x) x ( x)
dx
Свойство дельта-функции
f x, x ( x x ) f x, x ( x x ) f x , x ( x x ) x ( x) 0
Результат
d | x|
( x) ( x)
dx

8.

| x|
Производная от модуля аргумента
x
d | x | 1, x 0
( x) ( x)
x 0
dx
1,
x
Вторая производная
d
( x) ( x) ?
dx

9.

Вторая производная от модуля аргумента
d
( x) ( x) ( x) ( x) 2 ( x)
dx
Задача
d 2 e |x|
?
2
dx

10.

Решение
d e |x|
d | x|
e |x|
e |x| ( x) ( x)
dx
dx
d 2 e |x|
d |x|
d e |x|
| x|
e
(
x
)
(
x
)
(
x
)
(
x
)
2e
( x)
2
dx
dx
dx
Или
d 2 e |x|
d |x|
2
|x|
| x|
e
(
x
)
(
x
)
e
(
x
)
(
x
)
2
(
x
)
e
2 ( x)
2
dx
dx
Задача
dx f x b x a ?

11.

Решение
1
1
dx
f
x
b
x
a
d
f
ab
f a
b
b
b
Или
b x a x a
1
b
Задача
2
2
dx
f
x
x
a
?

12.

Решение
2
2
dx
f
x
x
a
?
Эвристические соображения: ответ должен
содержать f a
a
x
a
Разобьём интеграл на два и воспользуемся заменой переменной
2
2
dx
f
x
x
a
a
a
a
a
2
2
2
2
dx
f
x
x
a
dx
f
x
x
a
Первое слагаемое справа
a
a
2
2
dx
f
x
x
a
dx
f
x
x
a
2
2
a
a
Или
2
2
dx f x x a
a 2
a 2
1
d
1
d
2
f
a
f
2 a2
2 a2
a
2

13.

Решение
2
2
dx
f
x
x
a
1
f a f a
2a
Или
1
x a x a x a
2a
2
2
Общая формула
f ( x)
n
x xn
df ( x) / dx x x
n
,
f ( xn ) 0

14.

Трёхмерная дельта-функция
r a x ax y a y z az
Пример использования дельта-функции
Плотность точечного заряда, расположенного в начале координат?

15.

Плотность точечного заряда, расположенного в начале координат
r q r
Найти результат дифференцирования
1
?
r
Указание: воспользоваться уравнением для потенциала точечного заряда

16.

Потенциал точечного заряда
(r )
q
r
Уравнение Пуассона для потенциала
(r ) 4 (r )

17.

Результат дифференцирования
1
4 r
r