Первообразная и интеграл

1.

Первообразная и интеграл
F x первообразная для f x на
если F ' x f x на а; b
а; b
y
f x непрерывна и неотрицательна на
f x 0
y f x
Общий вид первообразных
F(x) + C – всевозможные
первообразные f(x) на (а;b)
Основное
свойство
a
первообразных
Совокупность всех возможных первообразных
данной функции - неопределённый интеграл
подынтегральная функция
f x dx F x C
0
x0 x1 x2
c0 c1 c2
n 1
x cx
1) Af x dx A f x dx
2) f x g x dx f x dx g x dx
1
3) f kx b dx F kx b C
k
x a
x b криво
линейная
y f x трапеция
b y 0
n
n 1
S n f ci x;
i 0
lim S n S
n
подынтегральное выражение
Правила интегрирования
n 1
Операция нахождения
S кр .тр. S
Интегральная сумма
S lim S n , если f x 0
n
S n , если f x 0
S lim
n
lim S n интегрирование f(x) на [ a ; b ]
n
b
lim S n f x dx
n
a; b
a
определённый
интеграл f(x) по dx
от a до b
Геометрический смысл определённого интеграла
b
S f x dx, если f x 0
ab
S f x dx, если f x 0
a
b
S f x dx
a

2.

Математический
анализ
Дифференциальное
исчисление
Интегральное
исчисление

3.

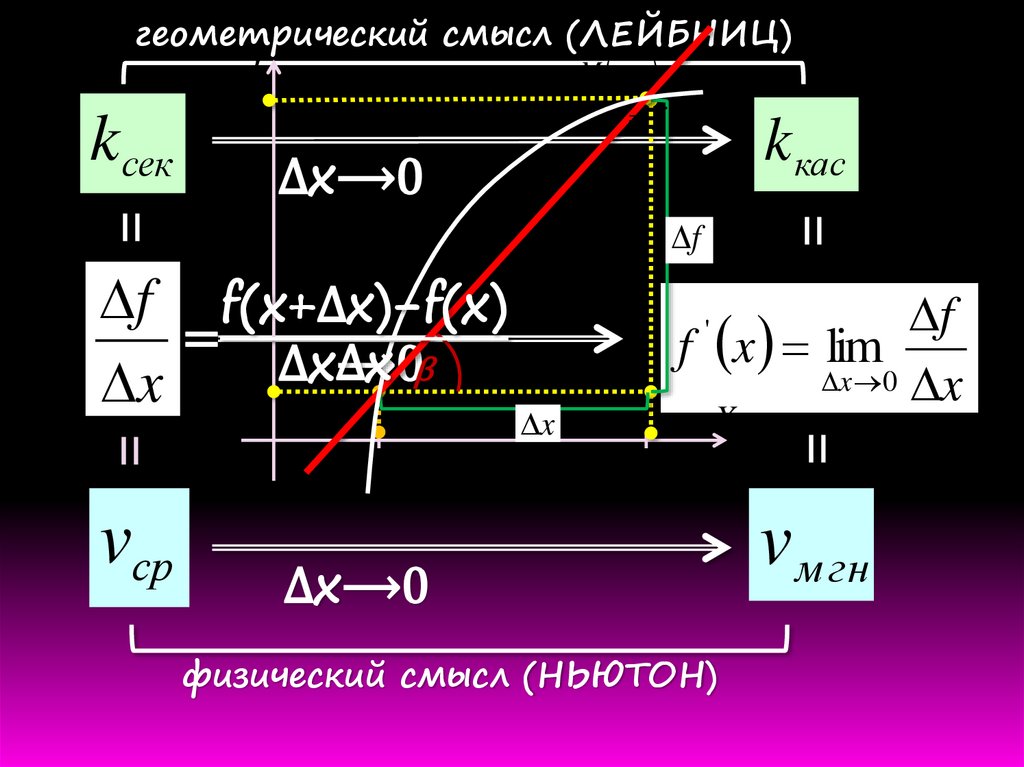
геометрический смысл (ЛЕЙБНИЦ)
Y
M x; y
kсек
y f (x)
k кас
∆x⟶0
f f(x+∆x)−f(x)
=
∆x
∆x⟶0
β
x
f
f x lim
x 0 x
'
x
X
x0 x
∆x⟶0
физический смысл (НЬЮТОН)
=
=
vср
x0
=
=
f
v м гн

4.

1.
ТАБЛИЦА ПРОИЗВОДНЫХ
C R, C const
r '
r R
x
C
'
sin x
'
e
x '
a
x '
cos x
a 0, a 1
'
tgx
x n, n Z
2
ctgx '
x n, n Z
ln x
x 0
log a x
x 0, a 0, a 1
x
x 0
1
x
arcsin x '
x 1
arccos x '
'
'
'
arctgx
'
'
'
x 0
arcctgx
'
x 1

5.

Физический смысл производной
(Ньютон)
S(t)=f(t)
закон
движения
v(t)=S’(t)
закон
мгновенной
скорости

6.

Известно: снаряд летит
со скоростью v(t)=-2t+20
Каков закон движения
снаряда S(t)?

7.

Постановка задачи в общем виде
Проблема:
Мы “потеряли” функции (y=F(x)),
производная которой известна,
т.е. F’(x)=f(x)
Цель:
восстановить саму функцию
y=F(x) по её производной(y=f(x))
d
e
f
F(x)-первообразная f(x) на
(a;b), если F’(x)=f(x) на (a;b)

8.

d
e
f
F(x)-первообразная f(x) на
(a;b), если F’(x)=f(x) на (a;b)
Проверьте, является ли F(x)-первообразная для f(x)
f(x)
F(x)
2
5x + x
1
15x +
2 x
x
x2 +3
3
Ln(x +3)
2

9.

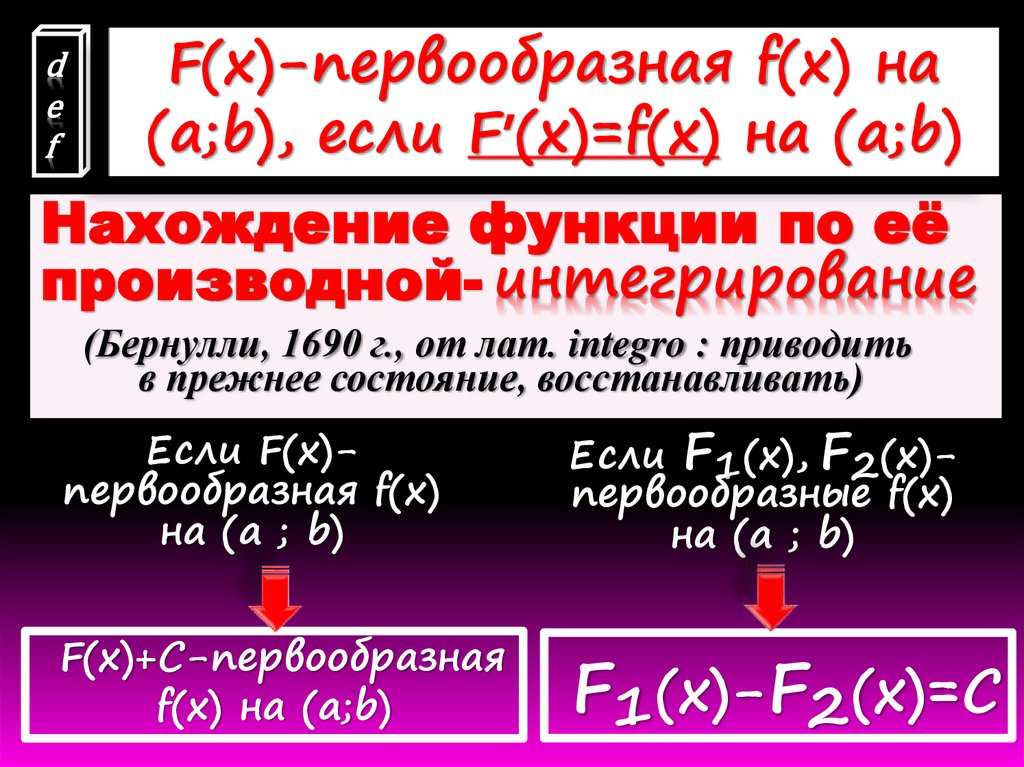
d
e
f
F(x)-первообразная f(x) на
(a;b), если F’(x)=f(x) на (a;b)
Нахождение функции по её
производной- интегрирование
(Бернулли, 1690 г., от лат. integro : приводить
в прежнее состояние, восстанавливать)
Если F(x)первообразная f(x)
на (a ; b)
Если F1 (x), F2 (x)первообразные f(x)
на (a ; b)
F(x)+C-первообразная
f(x) на (a;b)
F1 (x)-F2 (x)=C

10.

d
e
f
F(x)-первообразная f(x) на
(a;b), F’(x)=f(x) на (a;b)
Общий вид первообразных
F(x) + C – все возможные
первообразные f(x) на (а;b)
Основное
свойство
первообразных
Геометрический смысл :
всевозможные кривые, полученные
параллельным переносом графика
функции y=F(x)

11.

2.Найдите F(x)+C-общий вид первообразной
функции f(x), ответив на вопрос:
производная какой функции есть f(x)?
f(x)
0
1
2x
cosx
sinx
F(x)+С

12.

3. Таблица первообразных
f x
0
x
f x
k
r 1
r
F x C
1
x
cos x
sin x
x
a
x
1
cos 2 x
1
1 x2
1
sin 2 x
e
1
1 x2
F x C

13.

? Общий вид первообразной
Основное свойство
?
первообразных
интегрирование
Геометрический смысл
? первообразной
общего вида
Первообразная

14.

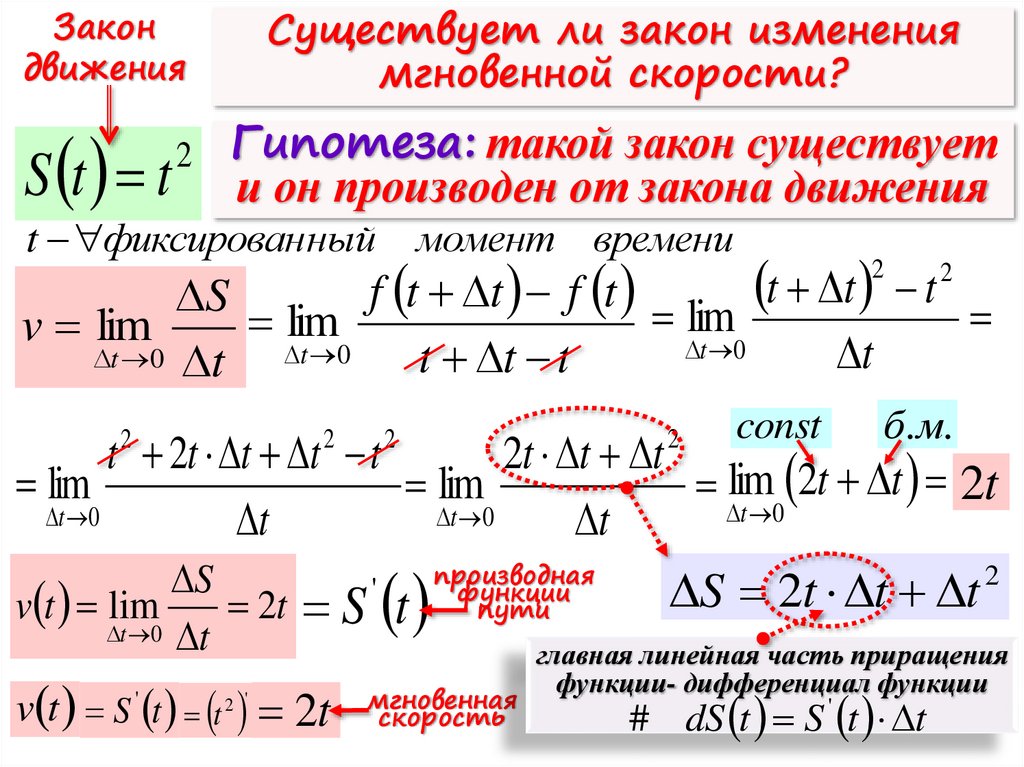
Закон
движения
Существует ли закон изменения
мгновенной скорости?
S t t
Гипотеза: такой закон существует
и он производен от закона движения
2
t фиксированный момент времени
t t t
f t t f t
S
lim
lim
v lim
t 0
t 0
t 0 t
t
t t t
2
const
2
б.м.
t 2t t t t
2t t t
lim
lim
lim 2t t 2t
t 0
t 0
t 0
t
t
2
2
2
2
производная
2
S
'
функции
S 2t t t
v t lim
2t S t
пути
t 0 t
главная линейная часть приращения
v t S t t 2t
'
2 '
мгновенная
скорость
функции- дифференциал функции
# dS t S ' t t

15.

f
v lim
f ' x f f ' x x x
x 0 x
главная линейная часть приращения
функции- дифференциал функции
'
# df x f x x
f ( x) x dx x x dx x
'
df x f x dx
'
#
df
f x
dx
'
б.м.

16.

d
e
f
F(x)-первообразная f(x) на
(a;b), если F ’(x)=f(x) на (a;b)
Общий вид первообразных
F(x) + C – все возможные
первообразные f(x) на (а;b)
Основное
свойство
первообразных
Совокупность всех возможных
первообразных данной функциинеопределённый интеграл
f
x
dx
F
x
C
подынтегральная
функция
f x dx
подынтегральное
выражение

17.

интегрируем
(восстанавливаем)
функцию F(x)
F’(x)=f(x)
f x
dx
по f(x) её
производной
полученной
дифференцированием
по переменной x
f
x
dx
F
x
dx
dF
x
'
d F x C F x C
Интегрирование и дифференцирование–
взаимно обратные операции

18.

Правила интегрирования
F x некоторая первообразная f x
№1. Докажите, что
1
f
kx
b
dx
F
kx
b
C
k

19.

Найдите неопределённый интеграл:
1
dx
x
dx
3
cos
3
x
dx
1
sin
x
dx
3

20.

Правила интегрирования
F x некоторая первообразная f x
№2. Докажите, что
Af
x
dx
A
f
x
dx
Константа
выносится за знак
интеграла!

21.

Правила интегрирования
'
'
F x f x , G x g x
№3. Докажите, что
f x g x dx f x dx g x dx

22.

Правила интегрирования
'
'
F1 x f1 x , F2 f 2 x
№4.Докажите, что
A f x A f x dx A f x dx A f x dx
1 1
2
2
1
1
2
2

23.

ДЗ на 13.12.23г

24.

До ма ш не е
задани е
№1

25.

6.8. Найдите неопределённый интеграл:
1) 3x 5 dx;
x2 x 1
2) dx;
7 3 5
1
3) 2 x dx;
x
4) x 3 x dx;
5) x 2 3 x 4 x dx;
6)
x 0, 25 x x 0, 25
dx;
x x
2
cos x
7)
dx;
2
cos x
5

26.

27.

В-5
Диагностическая работа-0

28.

В-11
Диагностическая работа