Similar presentations:
Неопределенный интеграл
1.
Неопределенный интеграл2.
ПервообразнаяФункция F(x) называется первообразной для функции
f(x), если F’(x)=f(x) или dF(x)=f(x)dx.
1)
2)
3)
4)
Свойства первообразной:
Если функция F(x) – первообразная для функции f(x),
то множество всех первообразных функции f(x)
задаются формулой F(x)+C, C .
Первообразная суммы функций равна сумме
первообразных.
Постоянный множитель можно вынести за знак
первообразной.
Если F(x) – первообразная для f(x), а k и b –
постоянные (k≠0), то первообразная для f(k·x+b) есть:
3.
Неопределенный интегралМножество всех первообразных функции называется ее
неопределенным интегралом:
Операция нахождения первообразных функции
называется интегрированием. Интегрирование –
операция, обратная дифференцированию (нахождению
производной).
4.
Свойства неопределенного интеграла1) Производная от неопределенного интеграла равна
подынтегральной функции:
2) Дифференциал от неопределенного интеграла равен
подынтегральному выражению:
3) Интеграл от дифференциала первообразной равен
самой первообразной и дополнительному слагаемому C:
5.
Свойства неопределенного интеграла4) Постоянный множитель можно выносить за знак
неопределенного интеграла:
5) Интеграл от алгебраической суммы конечного числа
функций равен алгебраической сумме интегралов от
слагаемых:
6.
Первообразные элементарных функций7.
Методы интегрирования1) Метод непосредственного интегрирования (с
помощью таблицы первообразных).
2) Метод замены переменной (метод подстановки):
3) Метод интегрирования по частям:
8.
Определенный интеграл9.
Криволинейная трапецияПусть на отрезке [a,b] задана
непрерывная функция y=f(x).
Фигура, ограниченная
графиком функции y=f(x),
осью OX и вертикальными
прямыми x=a и x=b (a<b),
называется криволинейной
трапецией.
10.
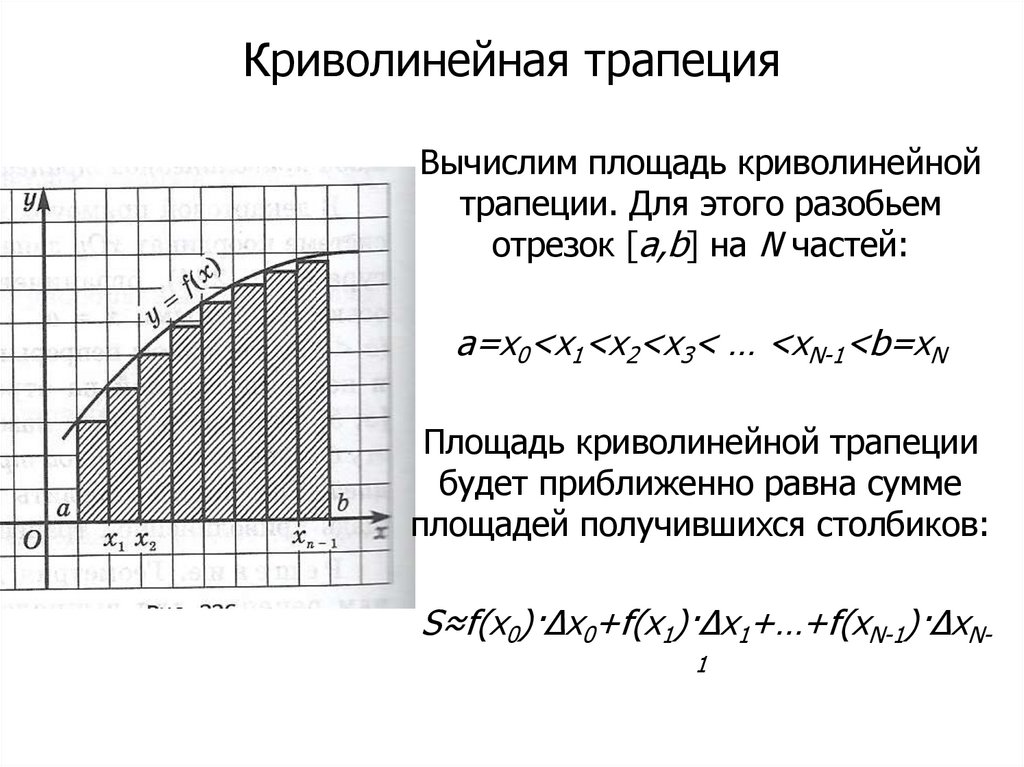
Криволинейная трапецияВычислим площадь криволинейной
трапеции. Для этого разобьем
отрезок [a,b] на N частей:
a=x0<x1<x2<x3< … <xN-1<b=xN
Площадь криволинейной трапеции
будет приближенно равна сумме
площадей получившихся столбиков:
S≈f(x0)·Δx0+f(x1)·Δx1+…+f(xN-1)·ΔxN1
11.
Определенный интегралSN=f(x0)·Δx0+f(x1)·Δx1+…+f(xN-1)·ΔxN-1
Выражение SN называется интегральной суммой.
Определенным интегралом от функции f(x) на
отрезке [a,b] называется предел интегральной суммы
при длине сегмента, стремящемся к нулю:
b
f ( xn ) xn
x 0
S f ( x)dx lim S n lim
a
x 0
N 1
n 0
12.
Формула Ньютона-ЛейбницаГеометрический смысл определенного интеграла –
площадь криволинейной трапеции под графиком
функции f(x).
Для
вычисления
определенного
интеграла
используется формула Ньютона-Лейбница:
b
f ( x)dx
b
F ( x) a
F (b) F (a )
a
где F(x) – первообразная функции f(x).
13.
Свойства определенного интегралаb
1.
a
dx b a
2.
a
a
3.
f ( x)dx 0
b
a
a
b
f ( x)dx f ( x)dx
14.
Свойства определенного интеграла4. Аддитивность
c
a
b
b
c
a
f ( x)dx f ( x)dx f ( x)dx, (a c b)
5. Линейность
b
b
b
a
a
a
(c1 f ( x) c2 g ( x))dx c1 f ( x)dx c2 g ( x)dx,
(c1 , c2 const)
15.
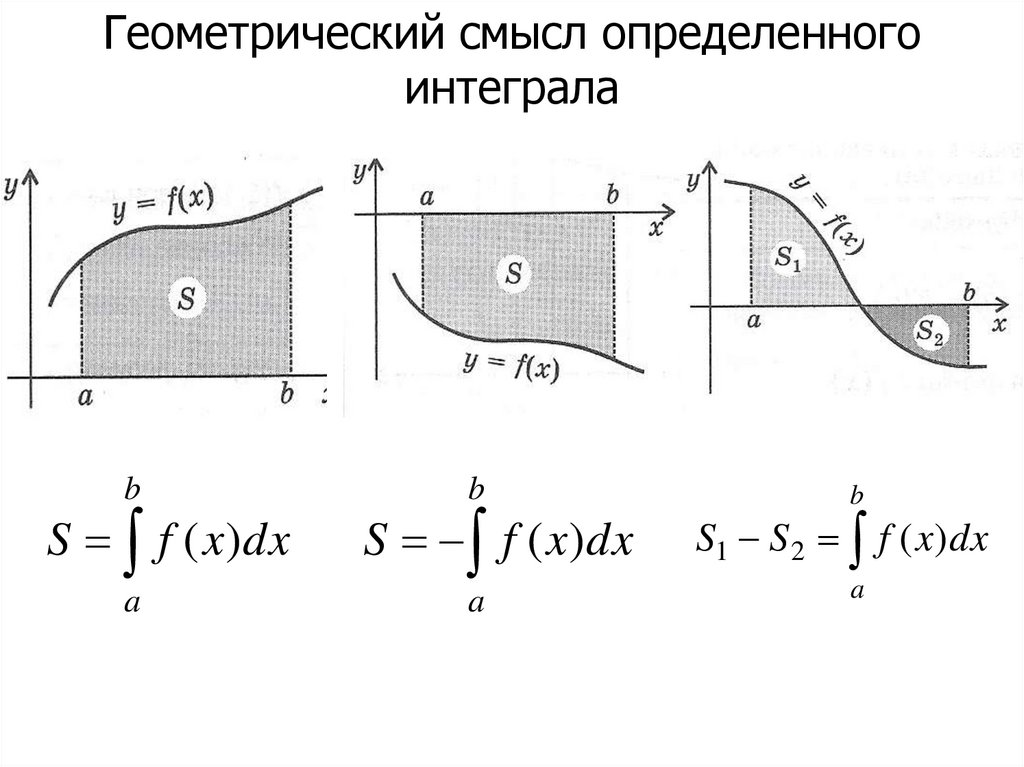
Геометрический смысл определенногоинтеграла
b
S f ( x) dx
a
b
S f ( x)dx
a
b
S1 S 2 f ( x)dx
a
16.
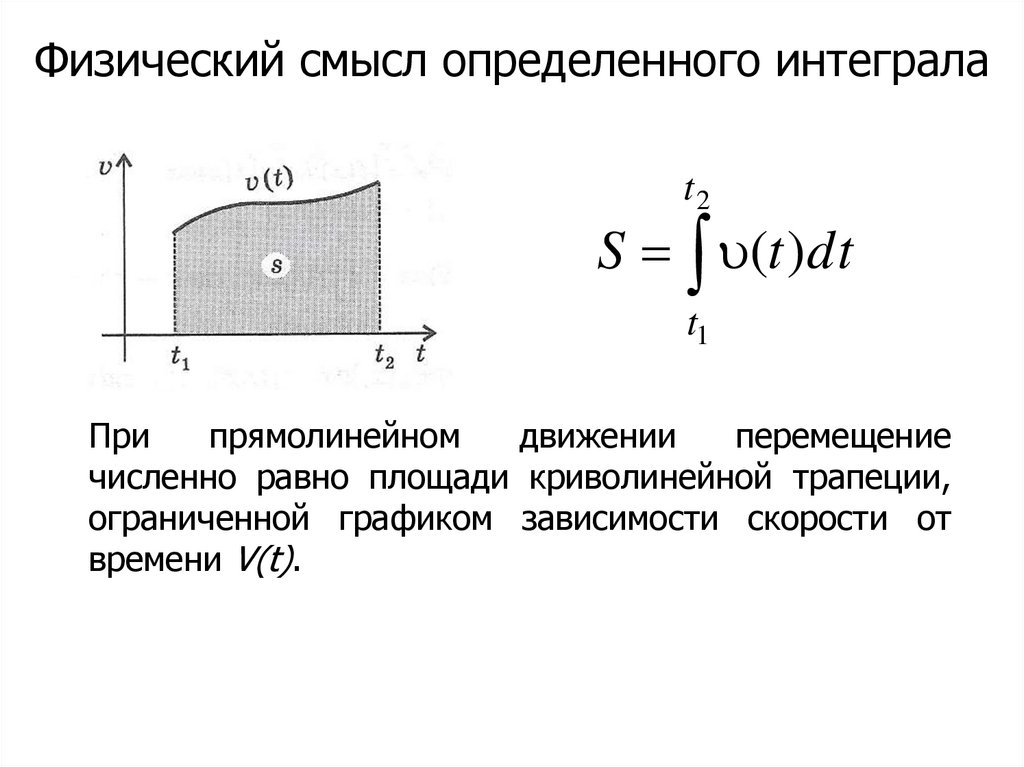
Физический смысл определенного интегралаt2
S (t )dt
t1
При
прямолинейном
движении
перемещение
численно равно площади криволинейной трапеции,
ограниченной графиком зависимости скорости от
времени V(t).
17.
Вычисление площадей и объемов фигурb
S ( f ( x) g ( x))dx
a
b
V
2
a
f ( x)dx
18.
Вычисление определенного интеграла1. Замена переменной:
b
a
f ( x)dx f ( g (t )) g (t )dt
g ( ) a, g ( ) b
19.
Вычисление определенного интеграла1
Пример:
S
1 x 2 dx
1
Замена: x cos t , 0,
1 x 2 1 cos2 t sin 2 t sin t , dx d (cos t ) sin t dt
0
0
1 cos 2t
S sin t ( sin t )dt sin t dt sin t dt
dt
2
0
0
2
2
1
cos 2t
t
1
1
1
dt
dt
cos 2t d (2t ) 0 sin 2 sin 0
2
2
20 40
2
4
4
2
0
0
20.
Вычисление определенного интеграла2. Интегрирование по частям:
b
u ( x) dv( x)
b
u ( x) v( x) a
a
b
v( x)du( x)
a
Пример:
0
0
0
S x sin x dx x d ( cos x) x cos x cos xdx
0 sin x 0
0

















 mathematics
mathematics








