Лекция_2_Общие_теоремы_динамики

1.

К.т.н., доцент Музалевская А.А.
Курс лекций по теоретической
механике. Часть 2.
R
G
N
Лекция №2
Динамика
механической системы
и твердого тела

2.

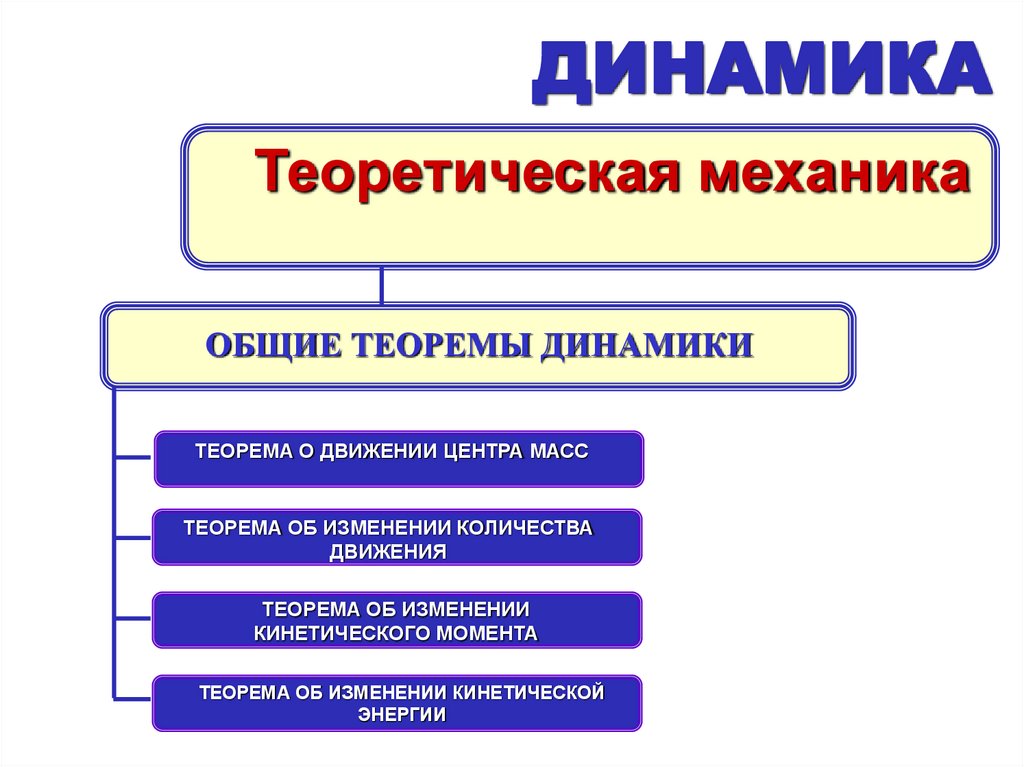
ДИНАМИКА
Теоретическая механика
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ

3.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
ЛЕКЦИЯ 2 план:
1. Количество движения.
2. Импульс силы.
3. Теорема об изменении количества
движения
4. Закон сохранения количества
движения.

4.

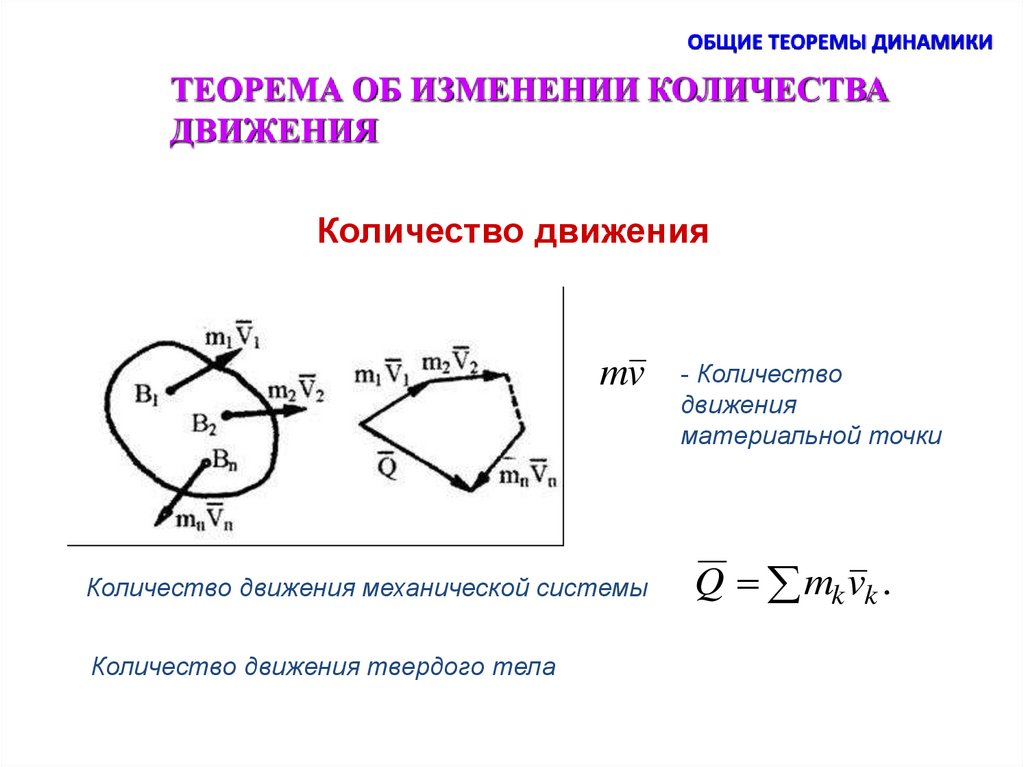
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Количество движения
mv
Q МvС
Количество движения механической системы
Количество движения твердого тела
- Количество
движения
материальной точки
Q mk vk .

5.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Импульс силы
dS Fdt
Элементарный импульс силы:
Импульс силы за конечный промежуток времени t1:
t1
S F dt.
0
Проекции импульса на координатные оси
t1
t1
t1
S у Fу dt .
S x Fx dt.
S z Fz dt.
0
0
0
Единицей измерения импульса силы в системе СИ является 1
кг м/с = 1 Н/с.

6.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Дифференциальное уравнение движения точки
t1
d ( mv )
Fk .
dt
mv mv0 Fk dt .
0
mv mv0 Sk
Теорема об изменении количества
движения материальной точки
mv1x mv0 x Skx ,
mv1 y mv0 y Sky ,
mv1z mv0 z Skz.

7.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
mk a k Fke Fki
Для всех точек механической системы
d m v dQ .
m
a
k k
k k
dt
dt
=0
Теорема об изменении количества движения системы:
dQ
Fke .
dt
t1
Q1 Q0
0
Fke dt
dQ y
dQx
dQz
e
e
Fkx ,
Fkze .
Fky ,
dt
dt
dt
Q1 Q0
e
Sk
e
Q1x Qox S kx
e
Q1 y Qoy S ky
e
Q1z Qoz S kz

8.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА
ДВИЖЕНИЯ
Закон сохранения количества
движения
1.
2.
Fke 0.
Fkхe 0.
dQ
Fke 0
dt
dQx
e
Fkx
0
dt
Q const
Qх const

9.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
ЛЕКЦИЯ План:
1. Осевые моменты инерции тела.
2. Момент количества движения
материальной точки.
3. Теорема об изменении момента
количества движения точки

10.

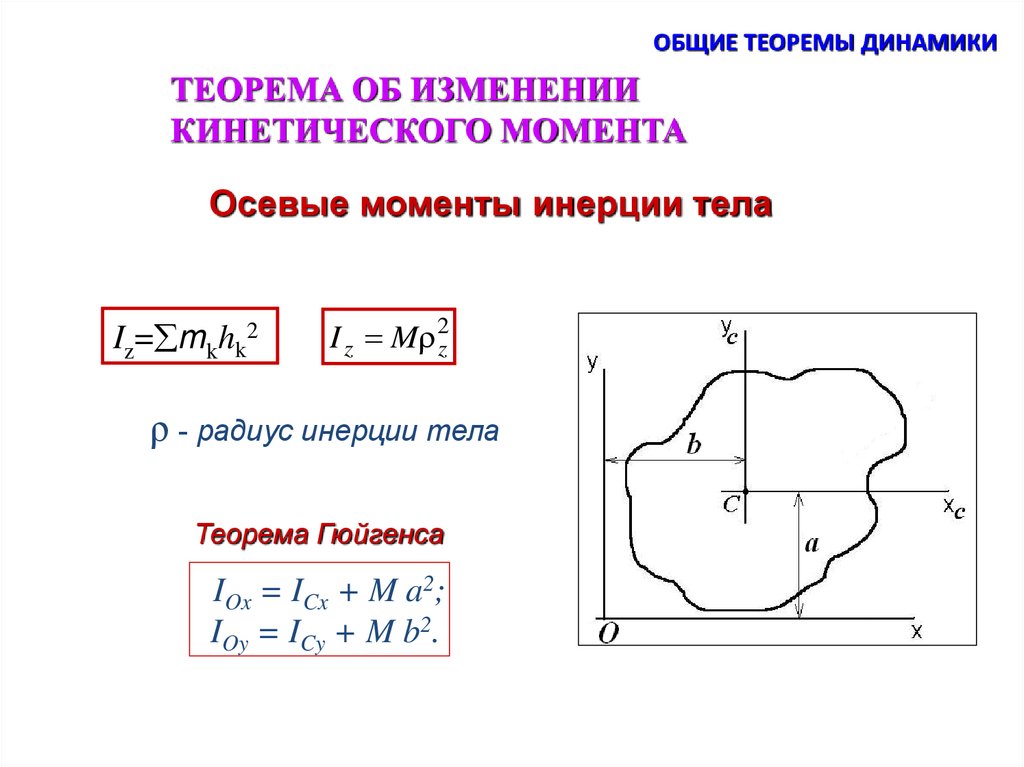
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Осевые моменты инерции тела
Iz= mkhk2
I z M 2z
ρ - радиус инерции тела
Теорема Гюйгенса
IOx = ICx + M a2;
IOy = ICy + M b2.

11.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Момент количества движения
материальной точки
m0 mv r mv
m0 mv mvh
mz mv m0 mv z
m0 mv cos
γ

12.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Теорема об изменении
момента количества движения точки
d r mv dr mv r m dv v mv r ma .
dt
dt
dt
v mv 0
d
r mv r F
dt
d
m0 (mv ) m0 ( F )
dt
или

13.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
ЛЕКЦИЯ План:
1. Теорема об изменении кинетического
момента.
2. Дифференциальное уравнение вращения
твёрдого тела

14.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Кинетический момент системы
К 0 m0 (mk vk )
К х mх (mk vk )
К у mу (mk vk )
К z mz (mk vk )
Кинетический момент вращающегося
тела
mz mk vk mk vk hk
К z mz (mk vk )
К z mk vk hk mk hk2
К z I z

15.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
Если рассмотреть одну точку системы:
d [m (m v )] m ( F e ) m ( F i ) ,
0
k k
0 k
0 k
dt
для всех точек системы:
=0
d [ m ( m v )] m ( F e ) m ( F i ).
0 k k
0 k 0 k
dt
dK 0
m0 ( Fke )
dt
Теорема об изменении кинетического
момента механической системы
dK x
mx ( Fke )
dt
dK y
my ( Fke )
dt
dK z
mz ( Fke )
dt

16.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОГО МОМЕНТА
следствия из теоремы:
dK 0
m0 ( Fke )
dt
dK z
mz ( Fke )
dt
1. Если сумма моментов всех внешних сил, действующих на
систему, относительно центра О равна нулю
m0 ( Fke ) 0
то
K0 const
2. Если сумма моментов всех внешних сил, действующих на
систему, относительно некоторой неподвижной оси равна нулю
mz ( Fke ) 0
то
Kz = const

17.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
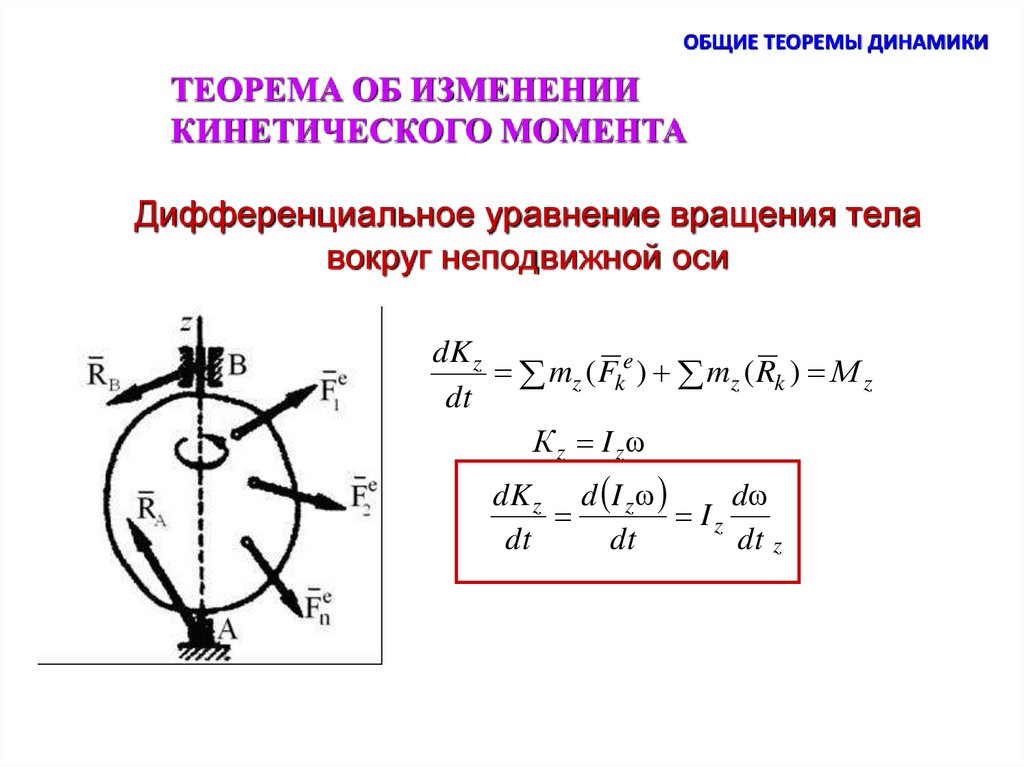
КИНЕТИЧЕСКОГО МОМЕНТА
Дифференциальное уравнение вращения тела
вокруг неподвижной оси
d
d 2
Iz
Iz 2 М z
dt
dt
dK z
mz ( Fke ) mz ( Rk ) М z
dt
К z I z
dK z d I z
d
Iz
dt
dt
dt z

18.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
ЛЕКЦИЯ план:
1. Работа силы и мощность
2. Кинетическая энергия.
3. Теорема об изменении кинетической
энергии

19.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ
Работа силы. Мощность
Элементарная работа силы
dA = F ds, где F = F cos ,
dA = Fds cos .
Работа силы на конечном перемещении
1. ( F const)
( M1 )
A( M 0 M1 ) F ds
(M 0 )
2. ( F const)
A( M 0 M1 ) F s1 Fs1cos

20.

Работа силы. Мощность
• Элементарная работа A – скалярная
величина и алгебраическая:
– если < /2; A > 0,
– если > /2; A < 0,
– если = /2, A = 0, т.е. при условии, что сила
F перпендикулярна перемещению dr и
скорости v тела.

21.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
Если вектор силы спроецировать на оси координат
( M1 )
A( M 0 M1 ) ( Fx dx Fy dy Fz dz)
(M 0 )
Единицей измерения работы в системе СИ является - 1 джоуль
(1 Дж = 1H м = 1 кг м2 /с2).
Мощность - это величина, определяющая работу, совершаемую
силой в единицу времени.
N = dA/dt = F ds/dt = F v.
Единицей измерения мощности в системе СИ является ватт
(1 Вт = 1Дж/с). В технике - 1 л.с. = 736 Вт.

22.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Примеры вычисления работы
Работа силы тяжести
z1
A( M 0 M1 ) ( P)dz P( z0 z1 )
z0
z0 - z1 = h
A( M 0 M1 ) Р h
Работа силы тяжести не зависит от формы траектории точки её
приложения. Силы, обладающие таким свойством, называются
потенциальными силами.

23.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
Работа силы упругости
F = cλ = c x и Fx = -cx.
x1
c
A( M 0 M1 ) ( cx)dx ( x02 x12 ).
2
x0
с 2
A( M 0 M1 ) ( 0 21 ) ,
2

24.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы. Мощность
Работа силы, приложенной к вращающемуся телу
dA F ds
где
ds = h dφ
dA = F h dφ.
F h = mz( F ) = Mz
dA = Mz dφ
1
A M z d или
0
A = ± Mz ∙ φ.

25.

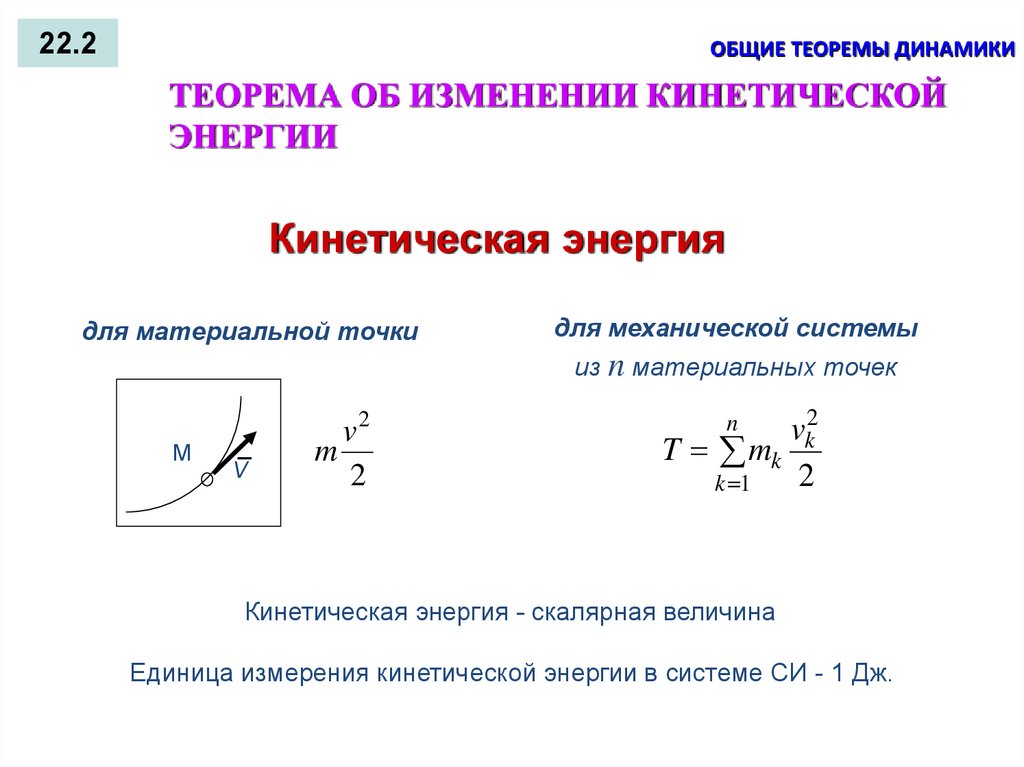
22.2
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ
Кинетическая энергия
для материальной точки
для механической системы
из n материальных точек
M
V
v2
m
2
vk2
T mk
2
k 1
n
Кинетическая энергия - скалярная величина
Единица измерения кинетической энергии в системе СИ - 1 Дж.

26.

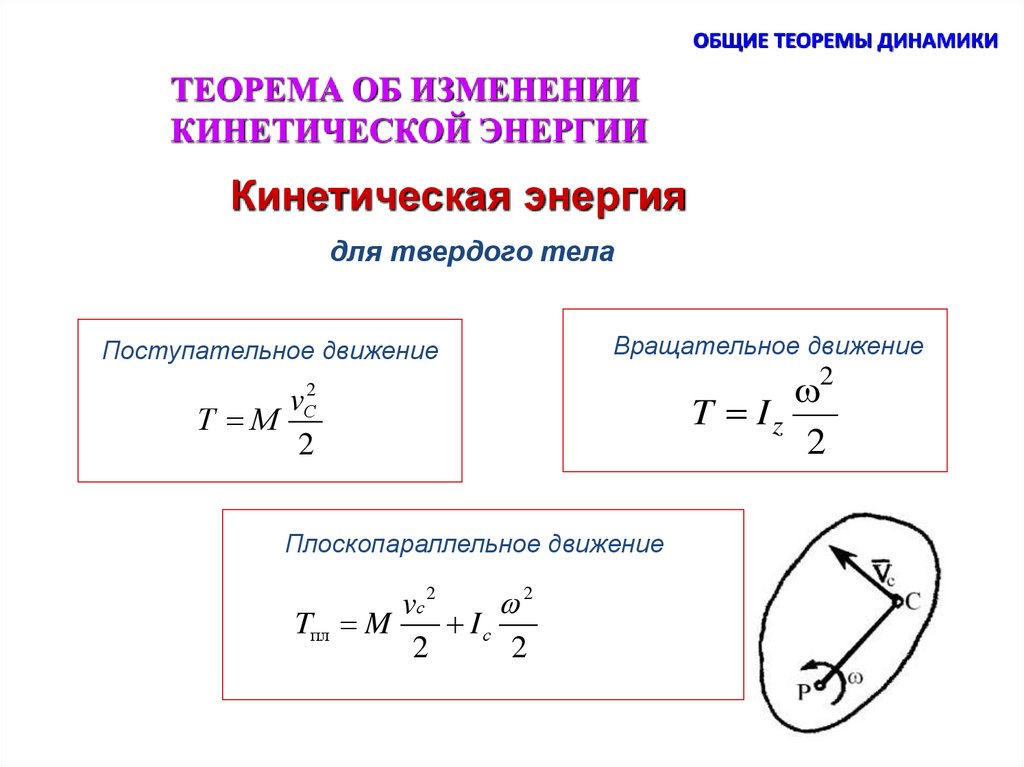
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Кинетическая энергия
для твердого тела
Поступательное движение
vС2
Т М
2
Вращательное движение
2
Плоскопараллельное движение
vс 2
2
Tпл M
Iс
2
2
T Iz
2

27.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим материальную точку с массой m
ma = Fk .
M
a
dv dv ds
dv
v
dt ds dt
ds
V
mv
mv 2
d(
) dAk
2
теорема об изменении
кинетической энергии точки
в дифференциальной форме
dv
Fk
ds
mvdv dAk
mv12 mv02
А(М0М1 )
2
2
теорема об изменении
кинетической энергии точки
в конечном виде

28.

ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим материальную точку механической системы с массой mk
d(
mk v 2k
2
) dAek dAik
Для всей механической системы
d (
mk v 2k
2
) dAek dAik
dT dAek dAik
T Т 0 Aek Aik
теорема об изменении
кинетической энергии системы
в дифференциальной форме
теорема об изменении
кинетической энергии системы
в интегральной форме

29.

ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ
ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ
T T0 A A
e
i
Изменение кинетической энергии системы точек на
некотором перемещении равно сумме работ внешних и
внутренних сил системы на этом же перемещении
A 0
i
T T0 A
e
Изменение кинетической энергии системы точек на
некотором перемещении равно сумме работ
10
внешних
Теорема
об изменении сил системы на этом же перемещении

30.

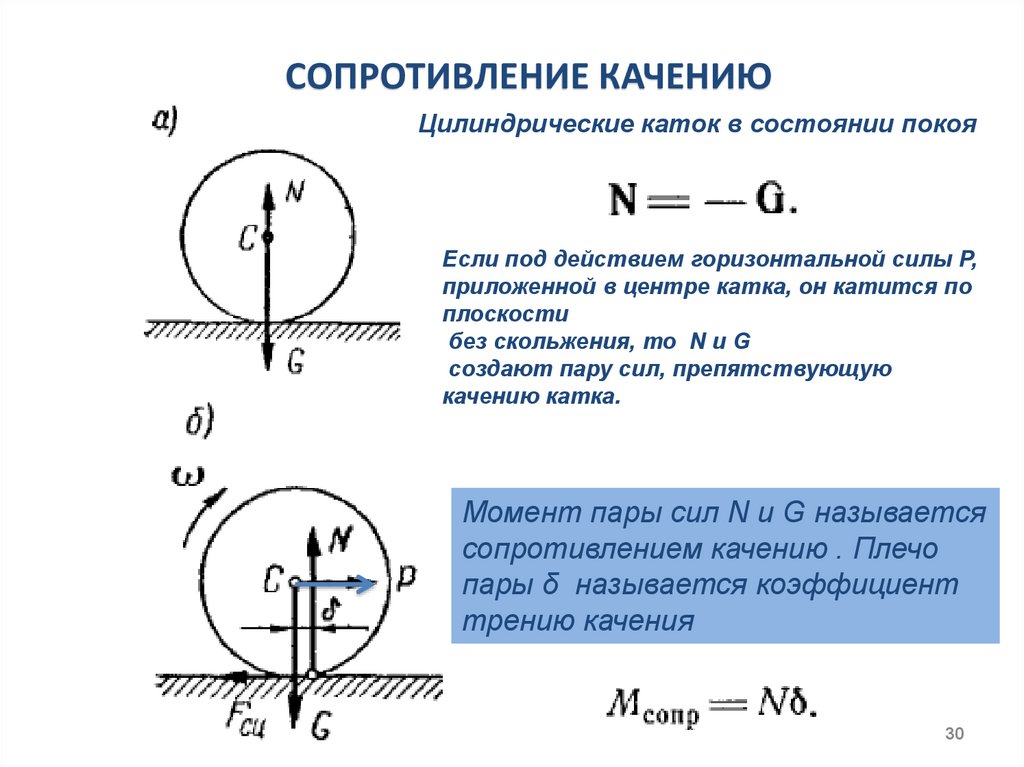
СОПРОТИВЛЕНИЕ КАЧЕНИЮ
Цилиндрические каток в состоянии покоя
Если под действием горизонтальной силы P,
приложенной в центре катка, он катится по
плоскости
без скольжения, то N и G
создают пару сил, препятствующую
качению катка.
Момент пары сил N и G называется
сопротивлением качению . Плечо
пары δ называется коэффициент
трению качения
30

31.

КОЭФФИЦИЕНТ ТРЕНИЯ КАЧЕНИЯ
Коэффициент трения качения выражается в линейных единицах.
Значение коэффициента трения качения для некоторых
материалов в таблице:
31

32.

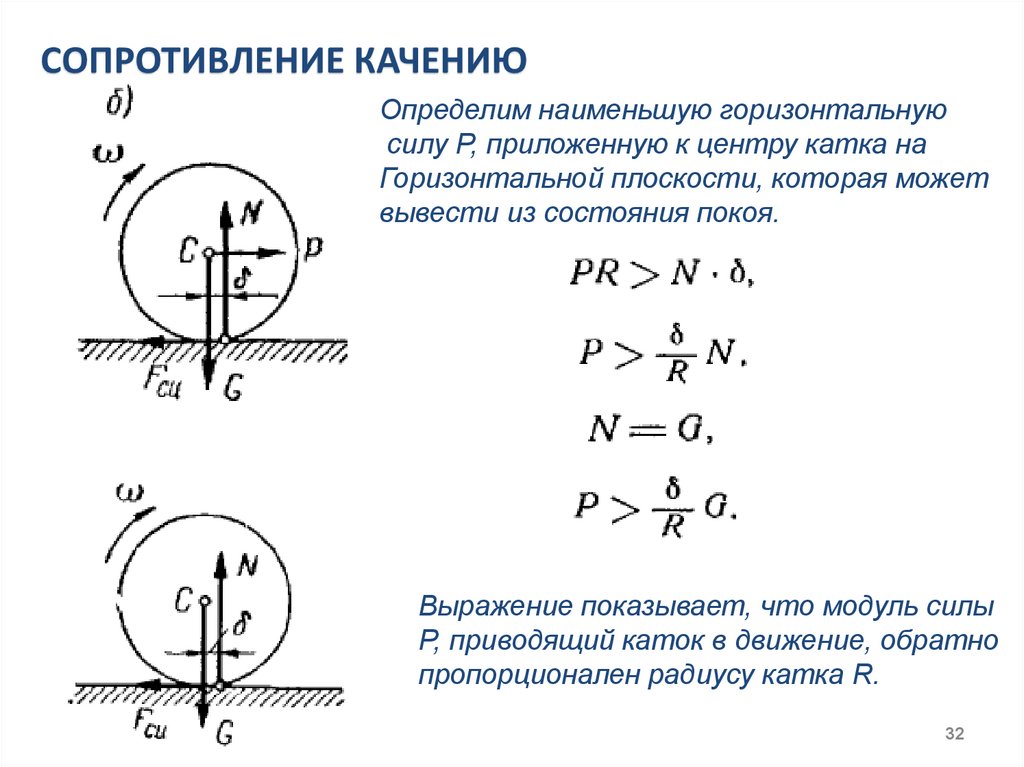
СОПРОТИВЛЕНИЕ КАЧЕНИЮ
Определим наименьшую горизонтальную
силу P, приложенную к центру катка на
Горизонтальной плоскости, которая может
вывести из состояния покоя.
Выражение показывает, что модуль силы
P, приводящий каток в движение, обратно
пропорционален радиусу катка R.
32