Similar presentations:
Динамика механической системы
1. Динамика механической системы
Механической системойназывается такая
совокупность
материальных точек
или тел,
в которой положение или
движение каждой точки
(или тела)
зависит от положения и
движения всех
остальных
Силы,
действующие на
точки
или тела системы,
разделяются,
на внешние
и
внутренние
2. Свойства внутренних сил (на основании 3-го закона динамики):
1.Геометрическая сумма (главный вектор) всех
внутренних сил системы равняется нулю.
2. Сумма моментов (главный момент) всех
внутренних сил системы относительно любого
центра или оси равняется нулю
3.
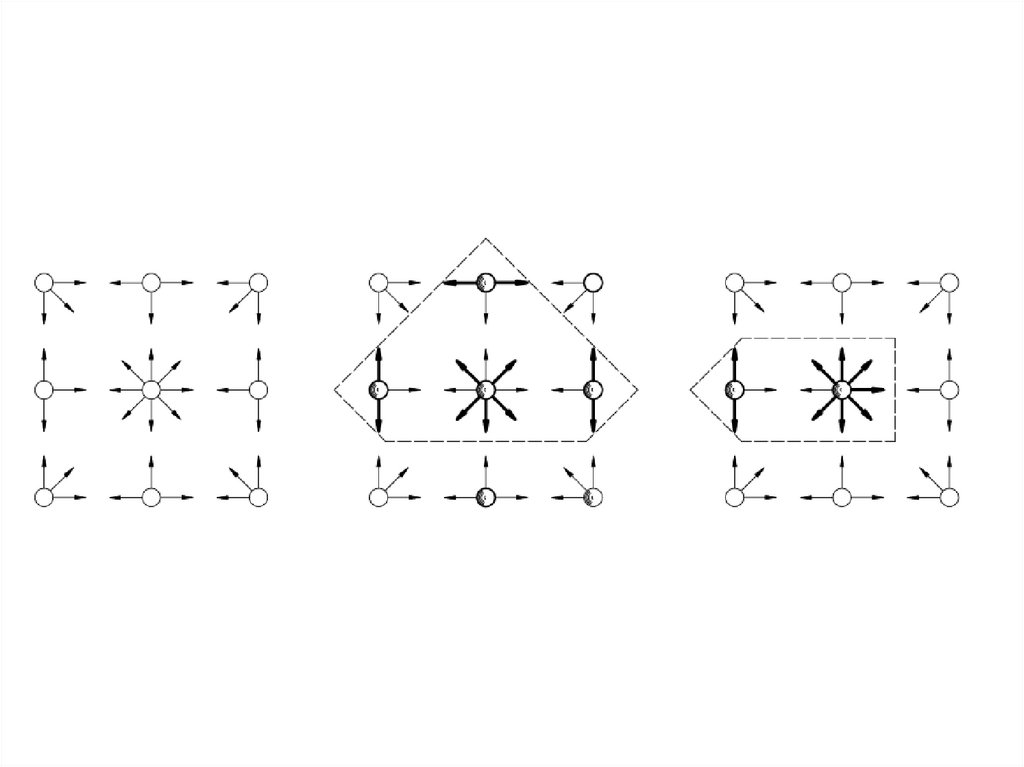
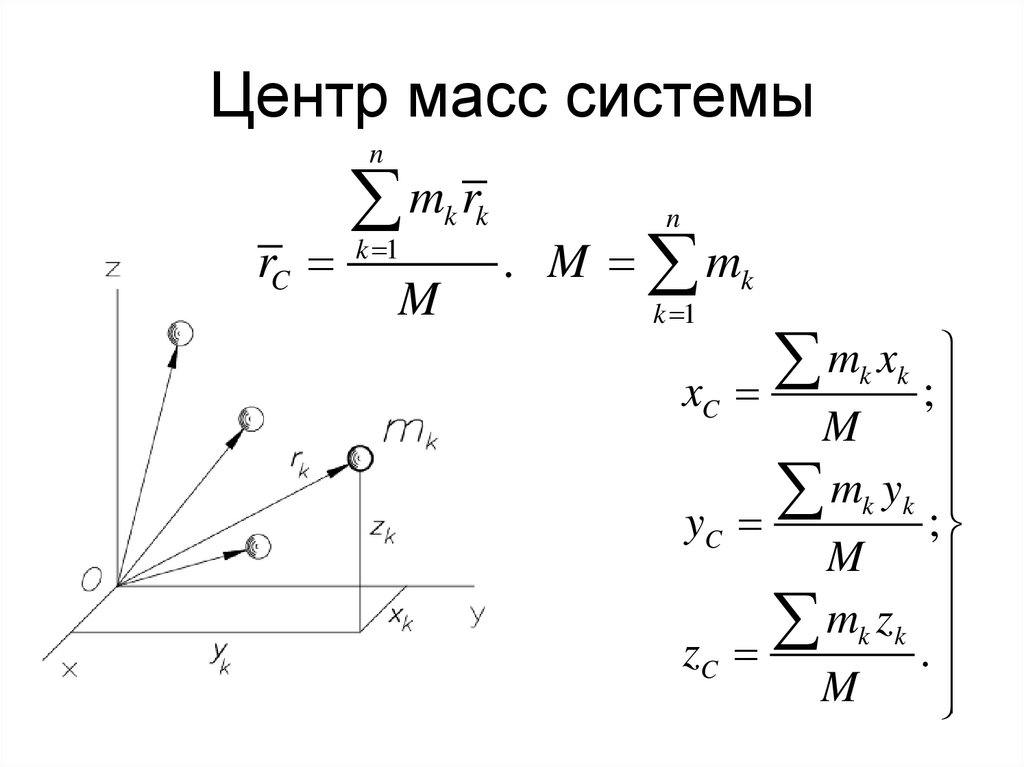
4. Центр масс системы
nrC
m r
k 1
M
k k
n
. M mk
k 1
mx
xC
;
M
mk yk
yC
;
M
mk zk
zC
.
M
k
k
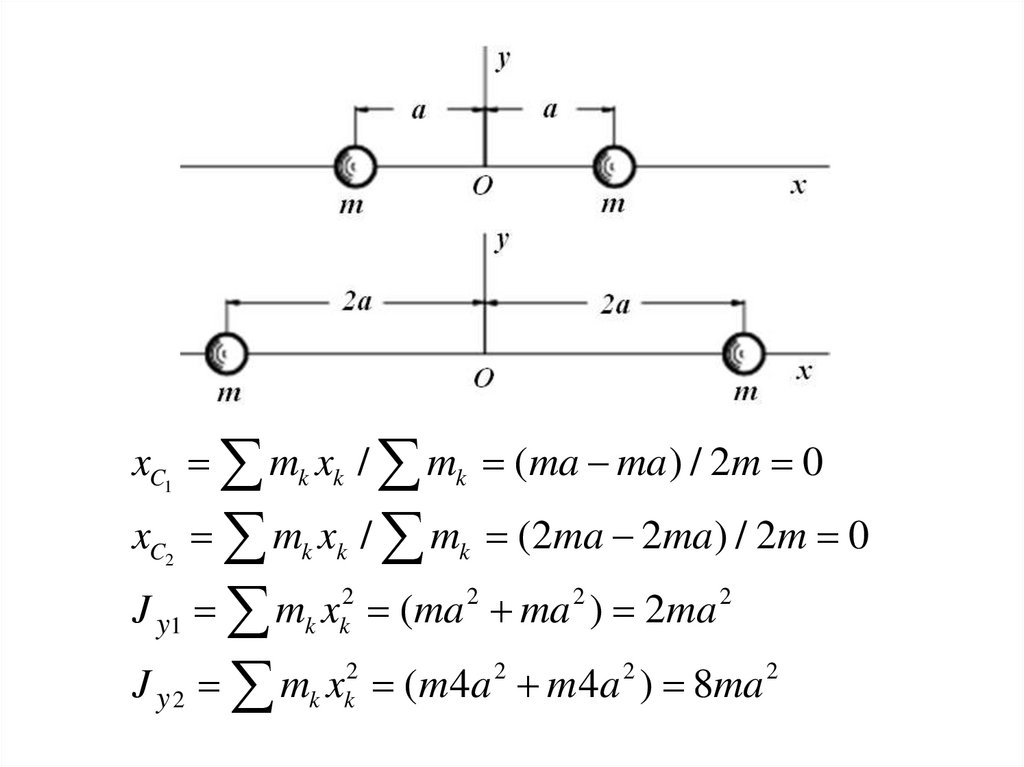
5.
xC1 mk xk / mk (ma ma ) / 2m 0xC2 mk xk / mk (2ma 2ma ) / 2m 0
J y1 mk xk2 (ma 2 ma 2 ) 2ma 2
J y 2 mk xk2 (m 4a 2 m 4a 2 ) 8ma 2
6.
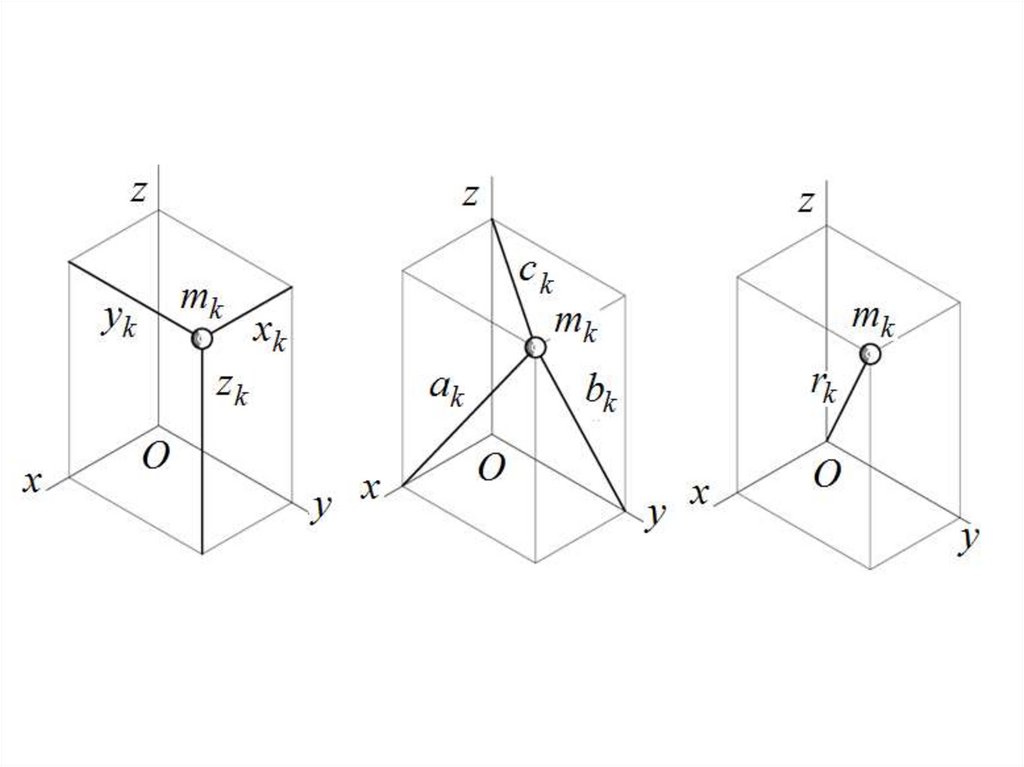
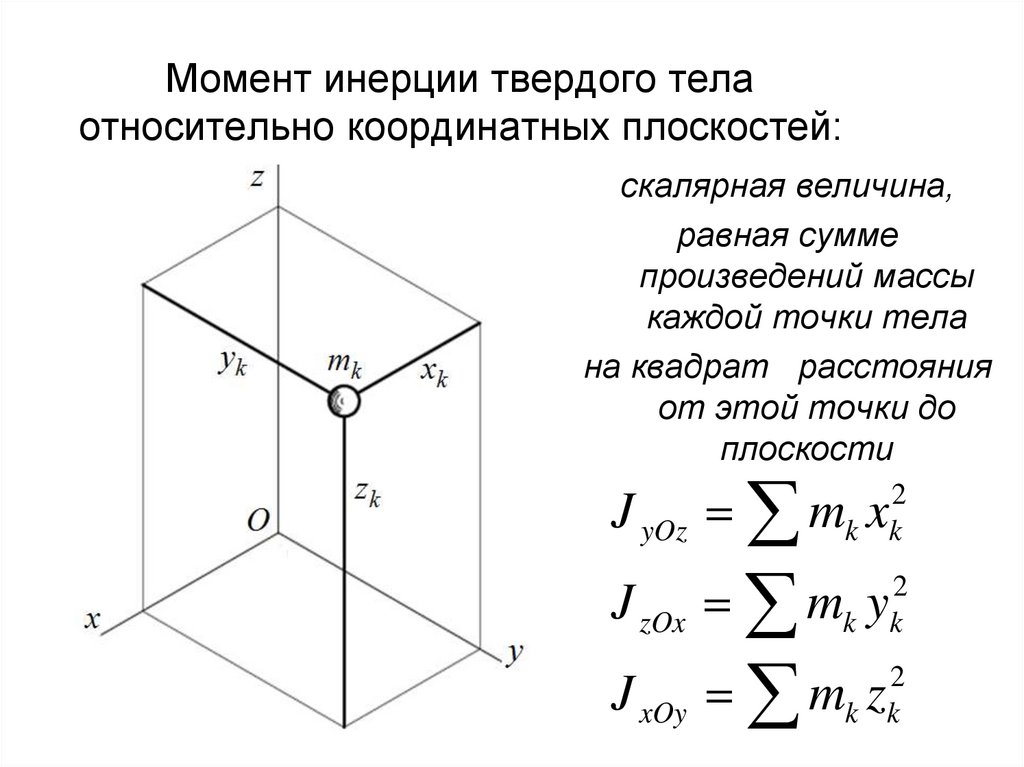
7. Момент инерции твердого тела относительно координатных плоскостей:
скалярная величина,равная сумме
произведений массы
каждой точки тела
на квадрат расстояния
от этой точки до
плоскости
J yOz mk x
2
k
J zOx mk y
J xOy m z
2
k
2
k k
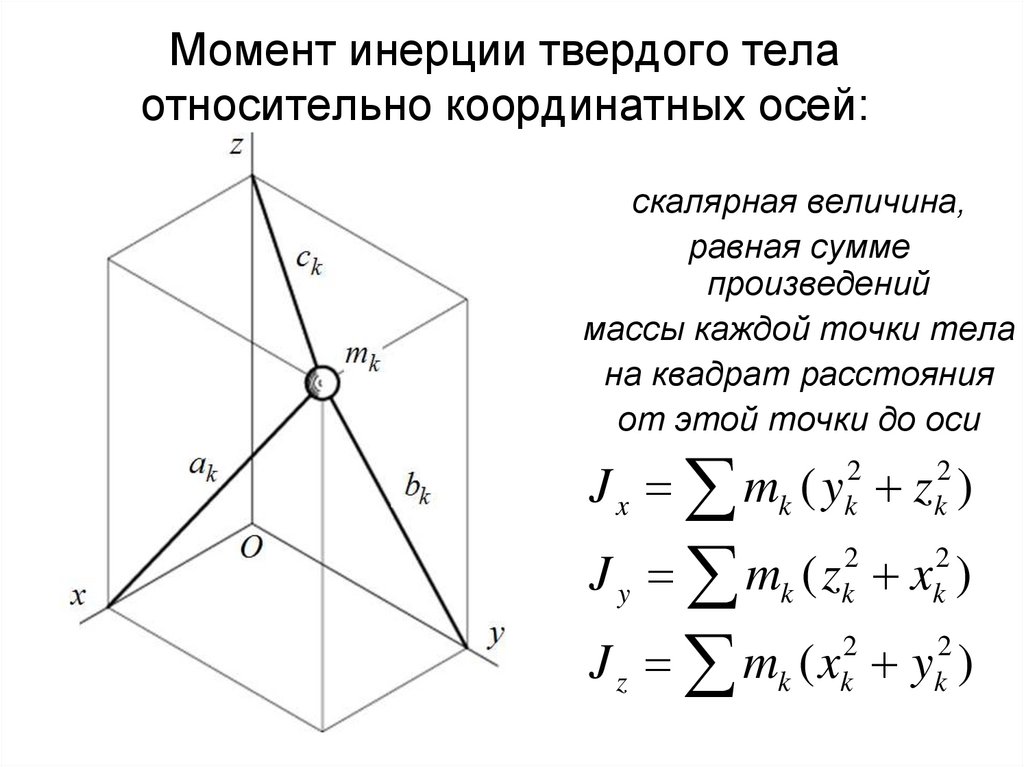
8. Момент инерции твердого тела относительно координатных осей:
скалярная величина,равная сумме
произведений
массы каждой точки тела
на квадрат расстояния
от этой точки до оси
J x mk ( y z )
2
k
2
k
J y mk ( z x )
2
k
2
k
J z mk ( x y )
2
k
2
k
9. Момент инерции твердого тела относительно полюса (полярный момент инерции):
скалярная величина, равнаясумме произведений
массы каждой точки тела
на квадрат расстояния
от точки до этого
полюса
JO m r
2
k k
10. Зависимости между моментами инерции твердого тела
JO mk ( xk2 yk2 zk2 ) J yOz J yOz J xOy(1)
J x J y J z 2 mk ( xk2 yk2 zk2 ) 2 J O ,
откуда J O 1 ( J x J y J z )
2
J x J zOx J xOy ;
J y J yOz J xOy ;
J z J yOz J zOx .
(3)
(2)
11. Радиус инерции
J z mi2
z
где m - масса тела;
iz - радиус
инерции тела
относительно оси z.
12. ТЕОРЕМА О МОМЕНТАХ ИНЕРЦИИ ТВЕРДОГО ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ (теорема Гюйгенса-Штайнера)
«Момент инерции твердого телаотносительно некоторой оси
равен моменту инерции тела
относительно параллельной оси,
проходящей через его центр масс,
сложенному с произведением
массы тела
на квадрат расстояния
между осями»
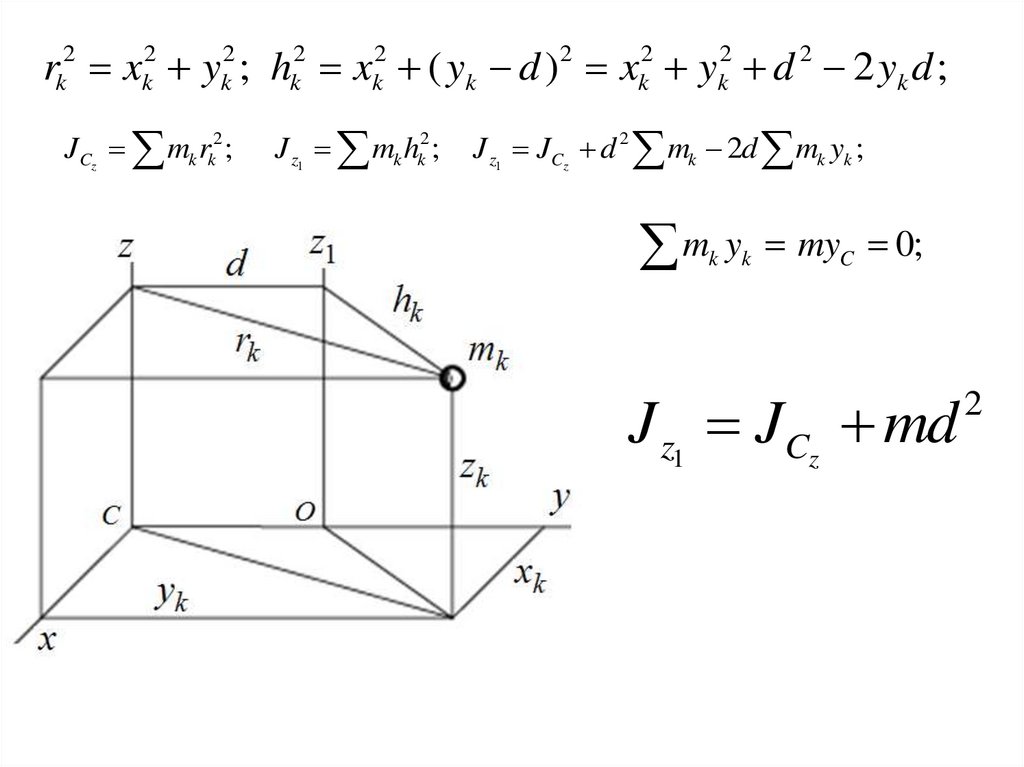
13.
rk2 xk2 yk2 ; hk2 xk2 ( yk d )2 xk2 yk2 d 2 2 yk d ;JCz mk rk2 ;
J z1 mk hk2 ;
J z1 JCz d 2 mk 2d mk yk ;
m y
k
k
myC 0;
J z1 JCz md
2
14.
Из совокупностипараллельных осей,
ось,
проходящая
через
центр масс тела,
характеризуется
наименьшим
моментом инерции
Так как
J O 1 ( J x J y J z ),
2
следовательно,
центр масс тела
является полюсом,
относительно
которого полярный
момент инерции тела
имеет наименьшее
возможное значение
15. Дифференциальные уравнения движения системы в векторной форме
m1a1 F F ;.......................
e
i
mn an Fn Fn .
e
1
i
1
16. Теорема о движении центра масс
ei
m
a
F
F
k k k k;
2
m r
(1)
k k
2
d rk
d rC
mk dt 2 M dt 2 ;
m a
k k
MaC ;
(3)
(4)
MaC F ;
e
k
(5)
MrC ;
(2)
17.
«Произведение массы системына ускорение ее центра масс
равно
геометрической сумме
всех действующих на систему внешних сил»
d xC
e
M
Fkx ;
2
dt
2
d yC
e
M
Fky ;
2
dt
2
d zC
e
M
Fkz .
2
dt
2
18. Закон сохранения движения центра масс
Следствие 1:Пусть сумма внешних сил, действующих на систему, равна нулю.
Тогда
MaC F 0,
e
k
тогда
или
aC 0
vC const
19.
Если сумма всех внешних сил,действующих на систему,
равна нулю,
то центр масс этой системы
движется с постоянной по модулю и направлению
скоростью,
т.е. равномерно и прямолинейно.
В частности, если вначале центр масс был в
покое, то он и останется в покое.
20.
Действие внутренних силдвижение центра масс системы
изменить
не может
21.
Следствие 2Пусть сумма проекций внешних сил, действующих на
систему, на какую-нибудь ось (например, ось Ох) равна
нулю
d 2 xC
dxC
0;
vCx const
2
dt
dt
Следовательно,
если сумма проекций всех действующих внешних сил на
какую-нибудь ось равна нулю,
то проекция скорости центра масс системы
на эту ось
есть величина постоянная
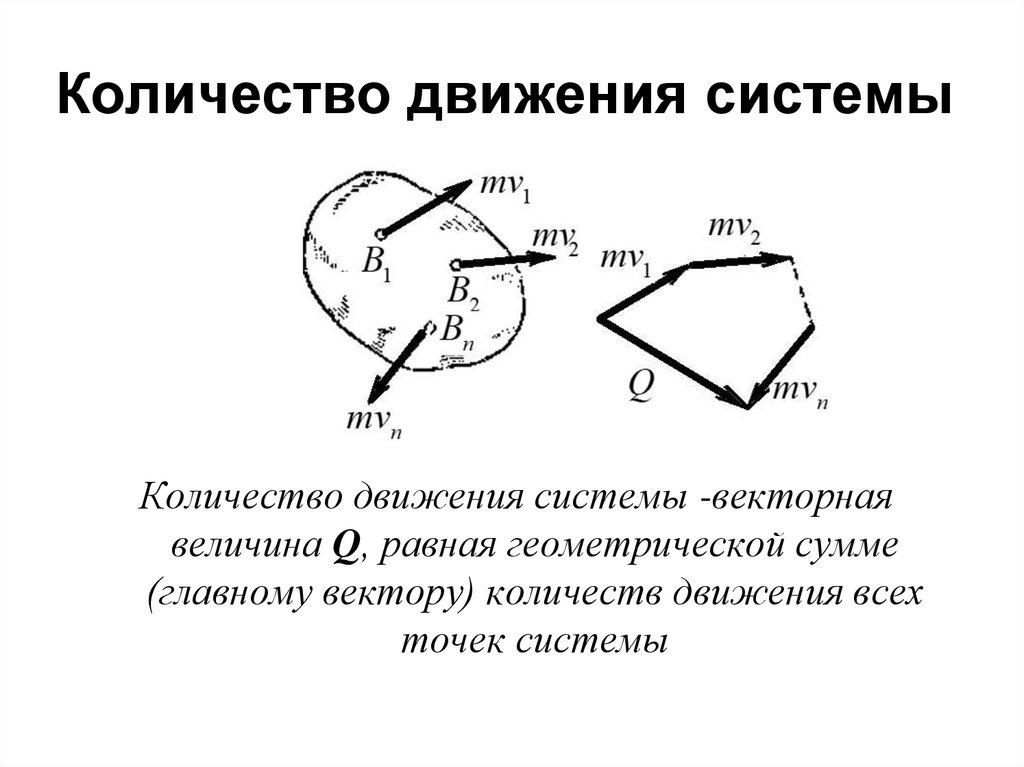
22. Количество движения системы
Количество движения системы -векторнаявеличина Q, равная геометрической сумме
(главному вектору) количеств движения всех
точек системы
23.
m rk k
MrC ;
drk
drC
mk dt M dt ;
m v
k k
MvC .
Q MvC .
Количество движения системы
равно произведению массы всей системы
на скорость ее центра масс
24.
Теорема об изменении количества движения системы вдифференциальной форме:
«Производная по времени от количества движения
системы равна геометрической сумме всех действующих
на систему внешних сил»
m a F F ;
k
k
e
k
i
k
d
dQ
mk ak dt ( mk vk ) dt ;
dQ
e
Fk
dt
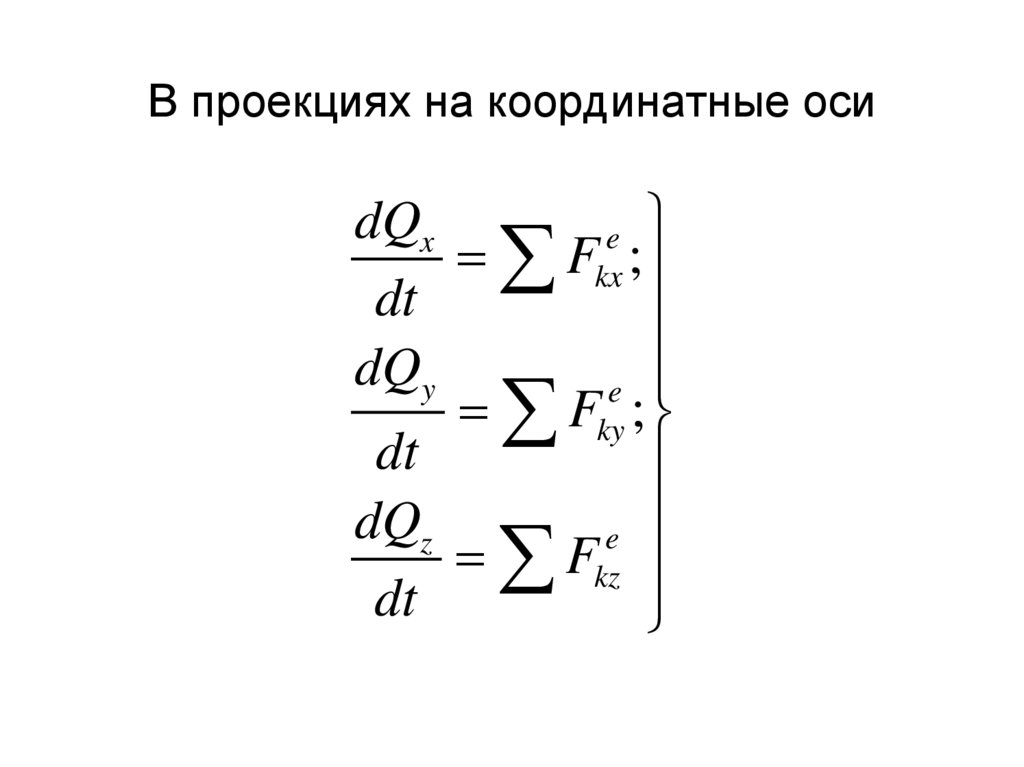
25. В проекциях на координатные оси
dQxe
Fkx ;
dt
dQy
e
Fky ;
dt
dQz
e
Fkz
dt
26.
Теорема об изменении количества движения системыв интегральной форме:
«Изменение количества движения системы за
некоторый промежуток времени равно сумме
импульсов действующих на систему внешних сил за
тот же промежуток времени»
dQ
Fke ;
dt
t1
Q1 Q0 Fke dt ;
0
Q1 Q0 Ske .
27. В проекциях на координатные оси
Q1x Q0 x S ;e
Q1 y Q0 y S ky ;
e
Q1z Q0 z S kz .
e
kx
28.
Из теоремы об изменении количества движениясистемы можно получить следующие важные
следствия:
1) Если сумма всех внешних сил, действующих на
систему, равна нулю, то вектор количества
движения системы будет постоянен по модулю и
направлению.
2) Если сумма проекций всех действующих
внешних сил на какую-нибудь ось равна нулю, то
проекция количества движения системы на эту ось
есть величина постоянная.
Эти результаты и выражают закон сохранения
количества движения системы.
Из них следует, что внутренние силы изменить
суммарное количество движения системы не могут.
29.
Главным моментом количеств движения системы(кинетическим моментом,
моментом количеств движения)
относительно данного центра О называется
величина Lо, равная геометрической сумме
моментов количеств движения всех точек системы
относительно этого центра:
LO M O (mk vk )
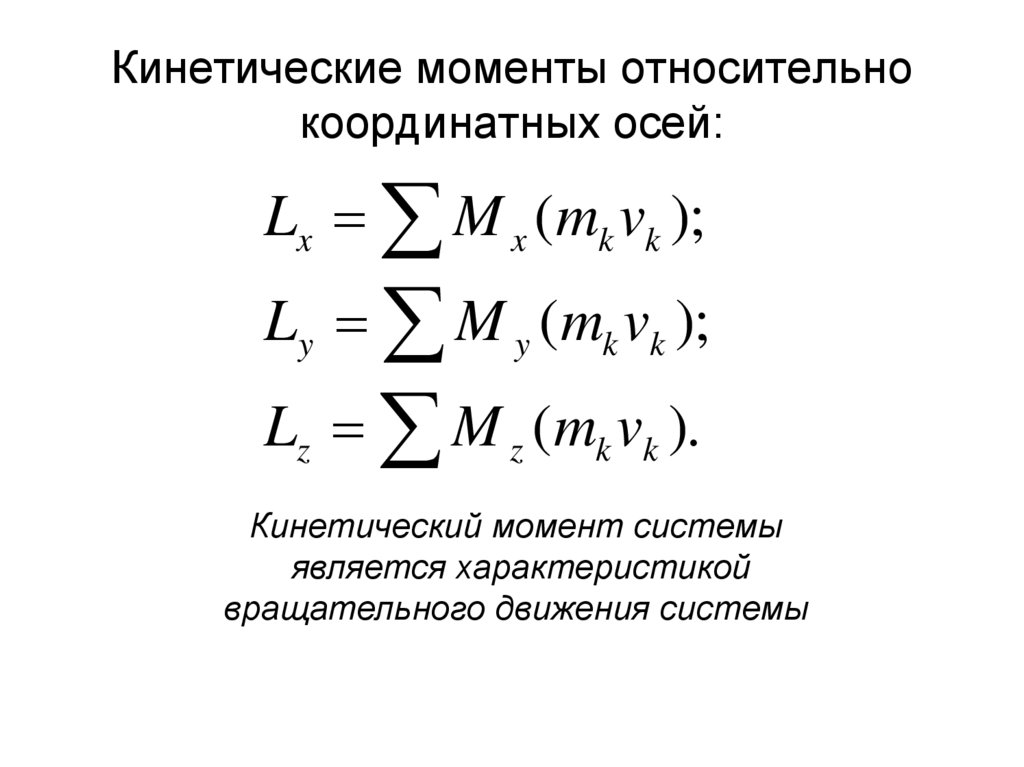
30. Кинетические моменты относительно координатных осей:
Lx M x (mk vk );Ly M y (mk vk );
Lz M z (mk vk ).
Кинетический момент системы
является характеристикой
вращательного движения системы
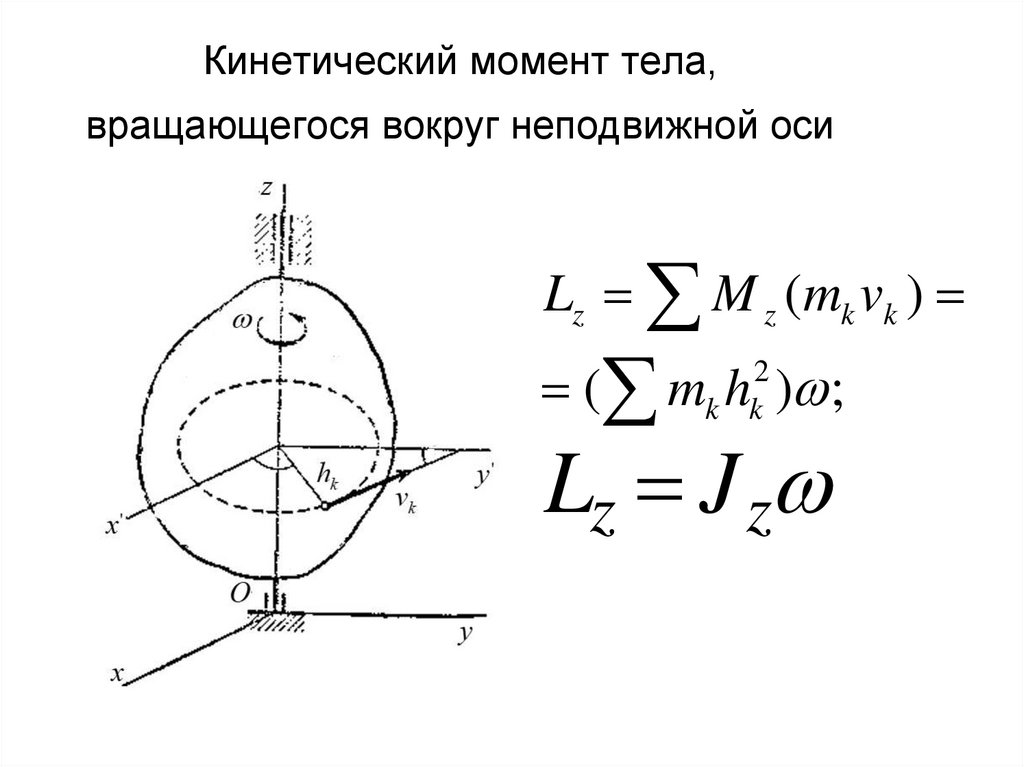
31. Кинетический момент тела, вращающегося вокруг неподвижной оси
Lz M z ( mk vk )( m h ) ;
2
k k
Lz J z
32. Теорема об изменении кинетического момента системы
d[ M O (mk vk )] M O ( Fke ) M O ( Fki );
dt
d
[ M O (mk vk )] M O ( Fke ) M O ( Fki );
dt
dLO
M O ( Fke ).
dt
«Производная по времени от кинетического момента
системы относительно некоторого неподвижного центра,
равна сумме моментов всех внешних сил системы
относительно того же центра»
33. Проектируя обе части равенства на неподвижные оси, получим:
dLxe
M x ( Fk );
dt
dLy
e
M y ( Fk );
dt
dLz
e
M z ( Fk ).
dt
34. Закон сохранения кинетического момента количеств движения
1. Если сумма моментовотносительно данного
центра
всех приложенных к системе
внешних сил равна нулю,
то кинетический момент
системы
относительно этого
центра
будет численно и по
направлению постоянен
2. Если сумма моментов
всех действующих на
систему внешних сил
относительно какойнибудь оси равна нулю,
то кинетический момент
системы
относительно этой оси
будет величиной
постоянной
35. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ –
скалярная величинаmv 2
T
,
2
равная половине произведения массы точки на
квадрат ее скорости.
В системе СИ единица измерения
кг м / сек н м джоуль
2
2
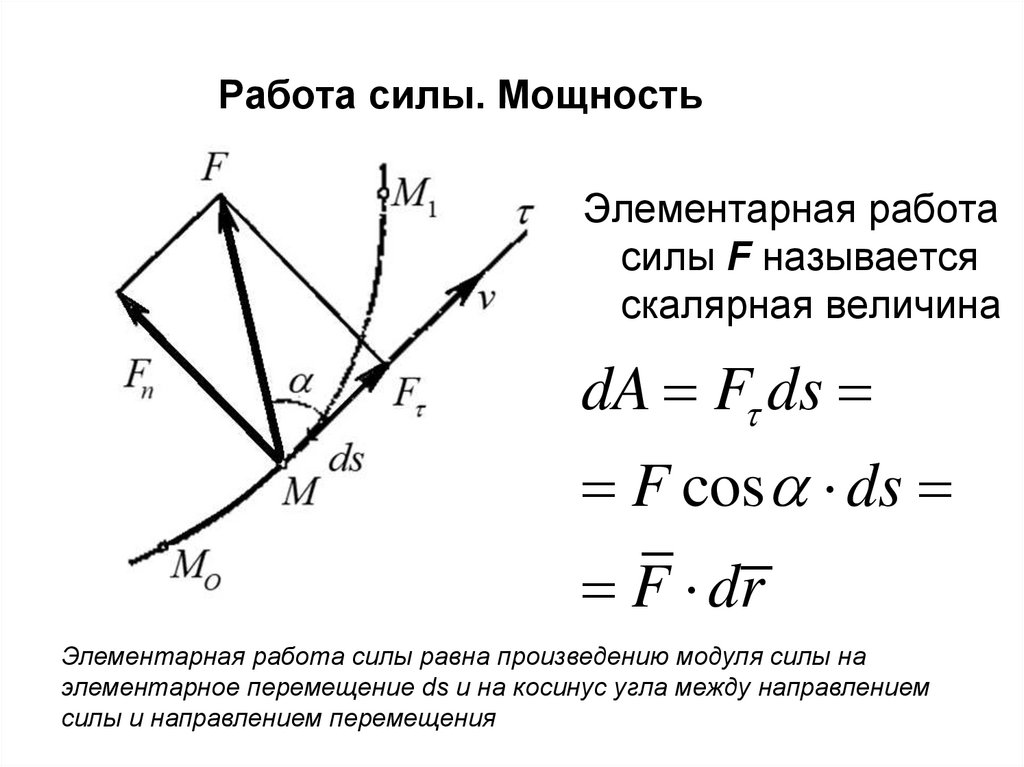
36. Работа силы. Мощность
Элементарная работасилы F называется
скалярная величина
dA F ds
F cos ds
F dr
Элементарная работа силы равна произведению модуля силы на
элементарное перемещение ds и на косинус угла между направлением
силы и направлением перемещения
37.
38. Аналитическое выражение элементарной работы
dA F dr ( Fx i Fy j Fz k ) (dx i dy j dz k )Так как i j i k j k 0,
а i i j j k k 1,
то dA Fx dx Fy dy Fz dz
39.
Работа силы на любом конечном перемещениивычисляется как интегральная сумма
соответствующих элементарных работ
и будет равна:
A( M 0 M1 )
( M1 )
(M0 )
F ds
( M1 )
( Fx dx Fy dy Fz dz )
( M0 )
Работа силы на любом перемещении М0М1
равна взятому вдоль этого перемещения
интегралу
от элементарной работы
Единицей измерения работы в системе СИ является джоуль
(1 дж=1Нм)
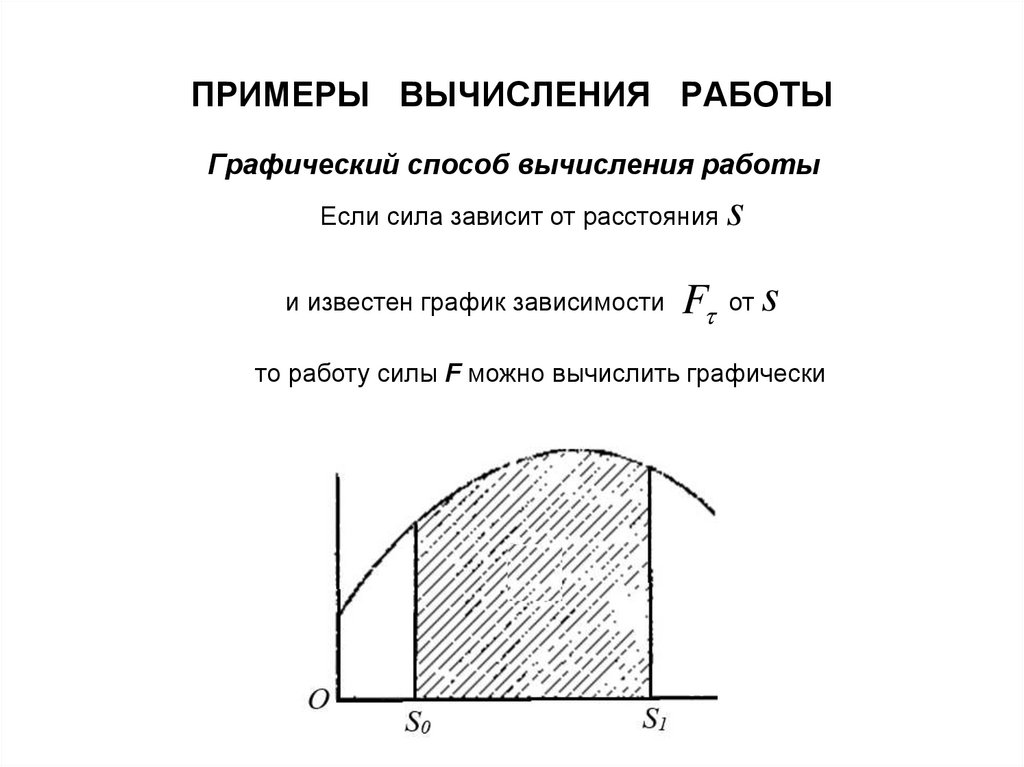
40. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
Графический способ вычисления работыЕсли сила зависит от расстояния
и известен график зависимости
F
s
от
s
то работу силы F можно вычислить графически
41. Работа силы тяжести
A( M 0 M1 )( M1 )
z1
( P)dz P dz P ( z0 z1 ) Ph.
(M0 )
A( M 0 M1 ) Ph
z0
42.
Работа силы тяжести не зависитот вида той траектории,
по которой перемещается точка ее
приложения.
Силы, обладающие таким свойством,
называются потенциальными
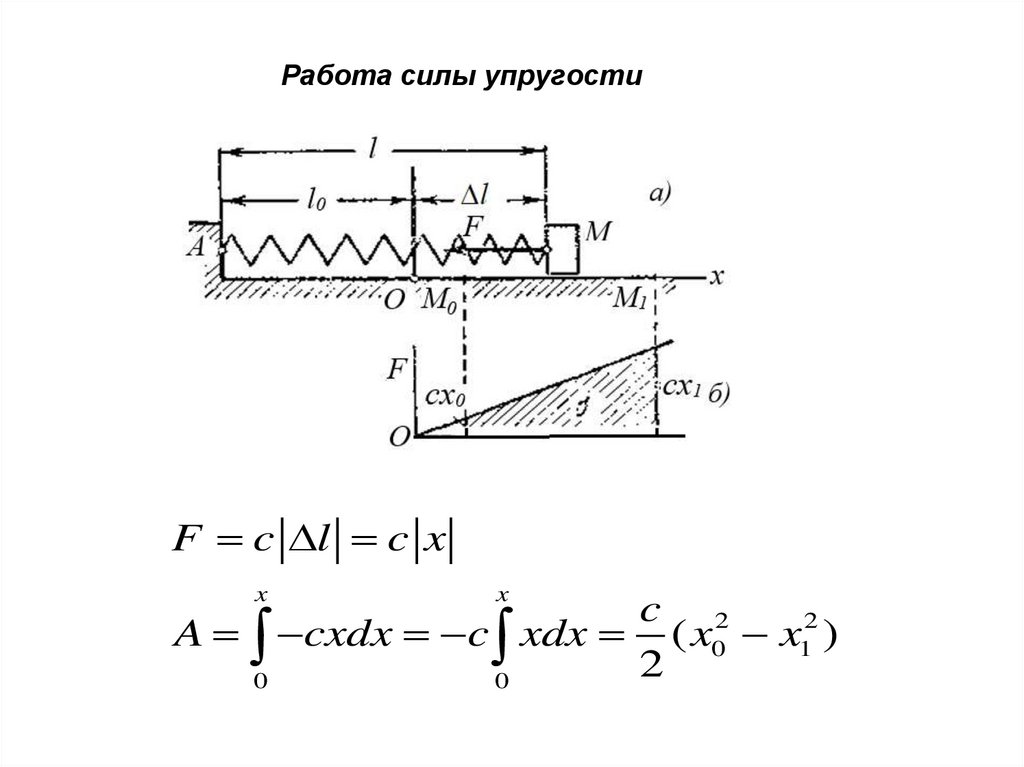
43. Работа силы упругости
F c l c xx
x
c 2
A cxdx c xdx ( x0 x12 )
2
0
0
44.
Работа силы упругости равнаполовине произведения коэффициента жесткости
на разность квадратов
начального и конечного удлинений (или сжатии)
пружины
45. Работа силы трения
A( M 0 M1 )( M1 )
(M0 )
Fтр ds
( M1 )
f N ds
(M0 )
Работа силы трения при скольжении
всегда отрицательна.
Величина этой работы зависит от длины дуги М0М1 ,
следовательно,
сила трения является
силой непотенциальной
46. Мощность
Мощность - величина, определяющаяработу, совершаемую силой в
единицу времени.
W dA
dt
F ds
dt
F v
Единицей измерения мощности в системе СИ является
ватт (1вт=1 дж/сек), а в системе МкГС—1 кГм/сек.
В технике за единицу мощности часто принимается 1
лошадиная сила, равная 75 кГм/сек или 736 вт.
47. Теорема об изменении кинетической энергии точки
ma Fia dv
dt
dv
ds
ds
dt
dv
dv
mv
Fi ; mvdv Fi ds;
ds
2
mv
d(
) Fi ds
2
ds
v
48.
21
2
0
mv
mv
A( M 0 M1 )
2
2
Изменение кинетической энергии точки при
некотором ее перемещении
равно алгебраической сумме работ
всех действующих на точку сил
на том же перемещении
49.
Кинетическая энергия системы –скалярная величина Е,
равная арифметической сумме кинетических
энергий всех точек системы
2
k k
mv
E
2
50. Поступательное движение
Eпост2
i C
mv
1
1
2
2
( mi )vC MvC
2
2
2
Кинетическая энергия тела
при поступательном движении
равна
половине произведения массы тела
на квадрат скорости центра масс
51. Вращательное движение
mvmi (hi )
Eвр
2
2
1
1
2
2
2
( mi hi ) J z
2
2
2
i i
2
Кинетическая энергия тела
при вращательном движении
равна половине произведения
момента инерции тела относительно оси
вращения на квадрат его угловой скорости
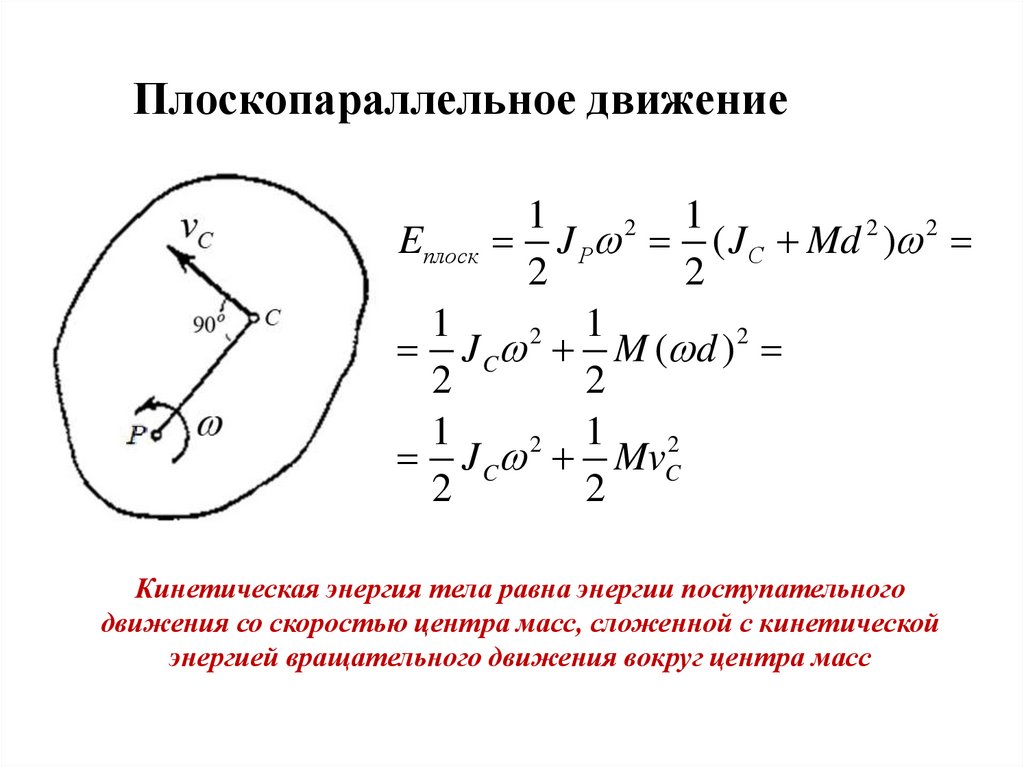
52. Плоскопараллельное движение
11
2
Eплоск J P ( J C Md 2 ) 2
2
2
1
1
2
J C M ( d ) 2
2
2
1
1
2
J C MvC2
2
2
Кинетическая энергия тела равна энергии поступательного
движения со скоростью центра масс, сложенной с кинетической
энергией вращательного движения вокруг центра масс
53. Некоторые случаи вычисления работы
Работа сил тяжести,действующих на систему,
вычисляется как работа их
равнодействующей G
на перемещении центра тяжести
(или центра масс) системы
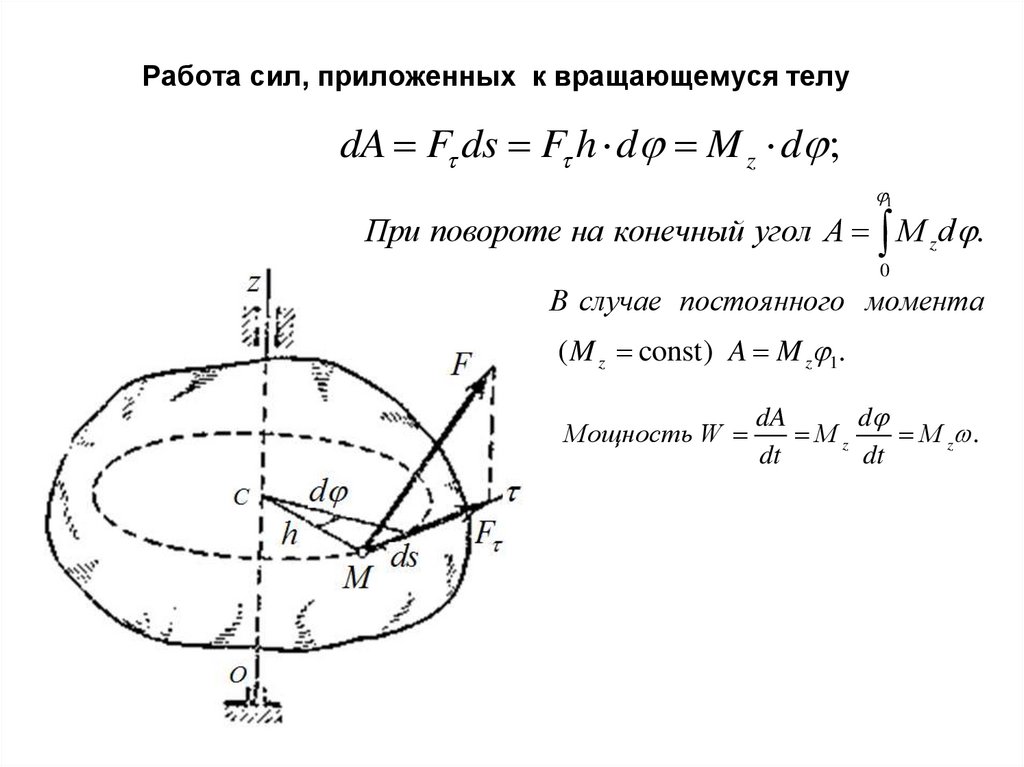
54. Работа сил, приложенных к вращающемуся телу
dA F ds F h d M z d ;1
При повороте на конечный угол A M z d .
0
В случае постоянного момента
( M z const) A M z 1.
Мощность W
dA
d
Mz
M z .
dt
dt
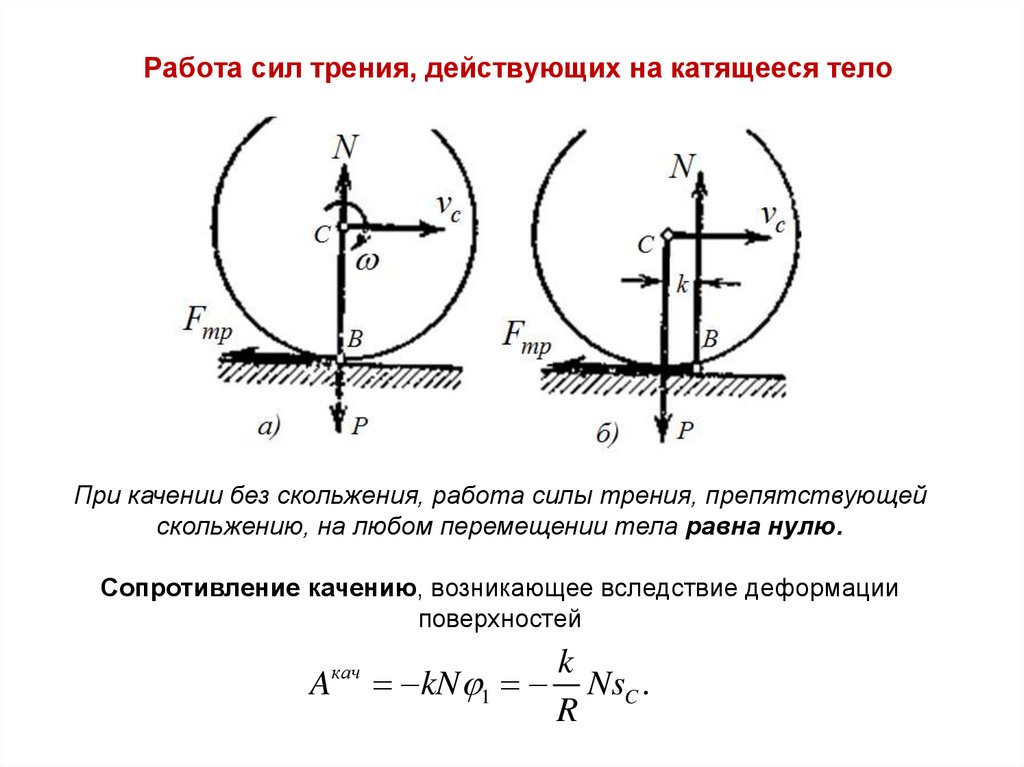
55. Работа сил трения, действующих на катящееся тело
При качении без скольжения, работа силы трения, препятствующейскольжению, на любом перемещении тела равна нулю.
Сопротивление качению, возникающее вследствие деформации
поверхностей
Aкач kN 1
k
NsC .
R
56. Теорема об изменении кинетической энергии системы
mi vi2Для каждой из точек системы d (
) dAie dAi j ;
2
Складывая почленно, получим
mi vi2
d (
) dAie dAi j или dE dAie dAi j .
2
Проинтегрировав обе части этого равенства
в пределах, соответствующих перемещению
системы из некоторого начального положения
E1 E0 Aie Ai j .
57.
Изменениекинетической энергии системы при
некотором ее перемещении равно
сумме работ
на этом перемещении
всех приложенных к системе
внешних
и
внутренних сил
58. Принцип Даламбера:
«Если к заданным (активным) силам,действующим на точку, и реакциям
наложенных связей
присоединить силу инерции,
то получится уравновешенная система сил»
ma P N ; P N ma 0;
Pi Ni Фi 0
ma Ф;









































 physics
physics








