ПЗ Геометрический смысл дифференциала

1.

ДИФФЕРЕНЦИАЛ
ФУНКЦИИ

2.

Продифференцируйте функции
• f(x)=4x²-6x³+9x⁵-2x+3
• f(x)= (x²-6x³)∙sinx
• f(x)=3x²/cosx
• f(x)=(5х-4)∙lnx
• f(x)=6х∙6x

3.

Ответить на вопросы
• 1. Дайте определение производной
• 2. Геометрический смысл
производной
• 3. Физический смысл производной

4.

Дифференциал функции
• Главная часть приращения функции,
линейная относительно приращения
независимой переменной, называется
дифференциалом
функции
и
обозначается знаком
dy
dy=f´(x)dx

5.

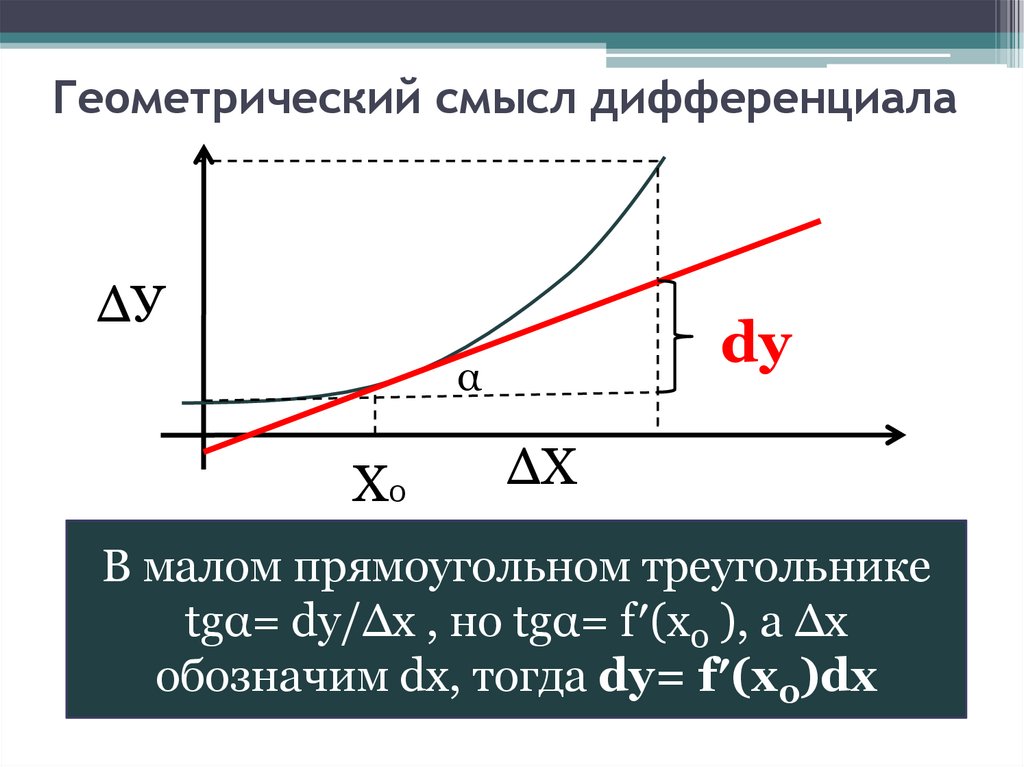
Геометрический смысл дифференциала
∆У
dу
α
Х0
∆Х
В малом прямоугольном треугольнике
tgα= dy/∆x , но tgα= f′(x0 ), а ∆х
обозначим dx, тогда dy= f′(x0)dx

6.

Геометрический смысл
дифференциала
Геометрически дифференциал функции
y=f(x) в точке х равен приращению ординаты
касательной к графику этой функции в этой
точке, когда х получит приращение ∆x.

7.

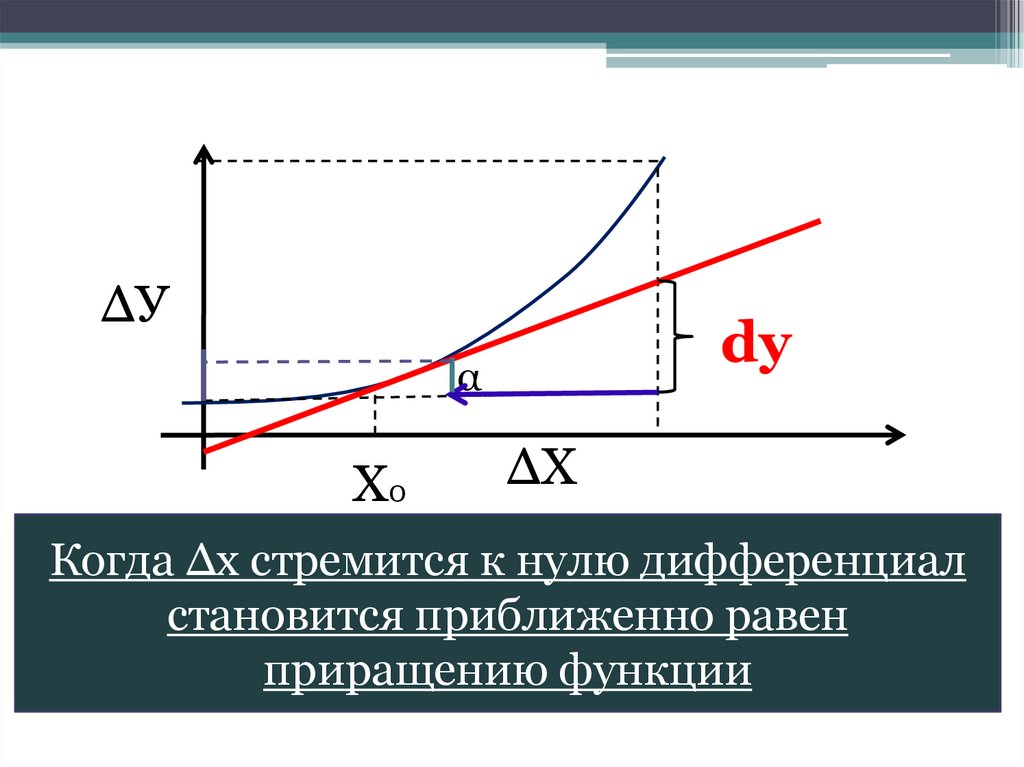
∆У
dу
α
Х0
∆Х
Когда ∆x стремится к нулю дифференциал
становится приближенно равен
приращению функции

8.

Самостоятельная работа
В-1
В-2
1.Продифференцируйте функции
f(x)=5x²-7x³+3x⁵-2x+1
f(x)=3x²+6x³-4x⁵-3x-9
2.Найдите дифференциал функции
f(x) =tgх
f(x) =ctgx
3.Найдите дифференциал функции в точке х0
f(x) =2х²сosx, х0=π
f(x) =х³sinx, х0=π/2