Дифференциал функции

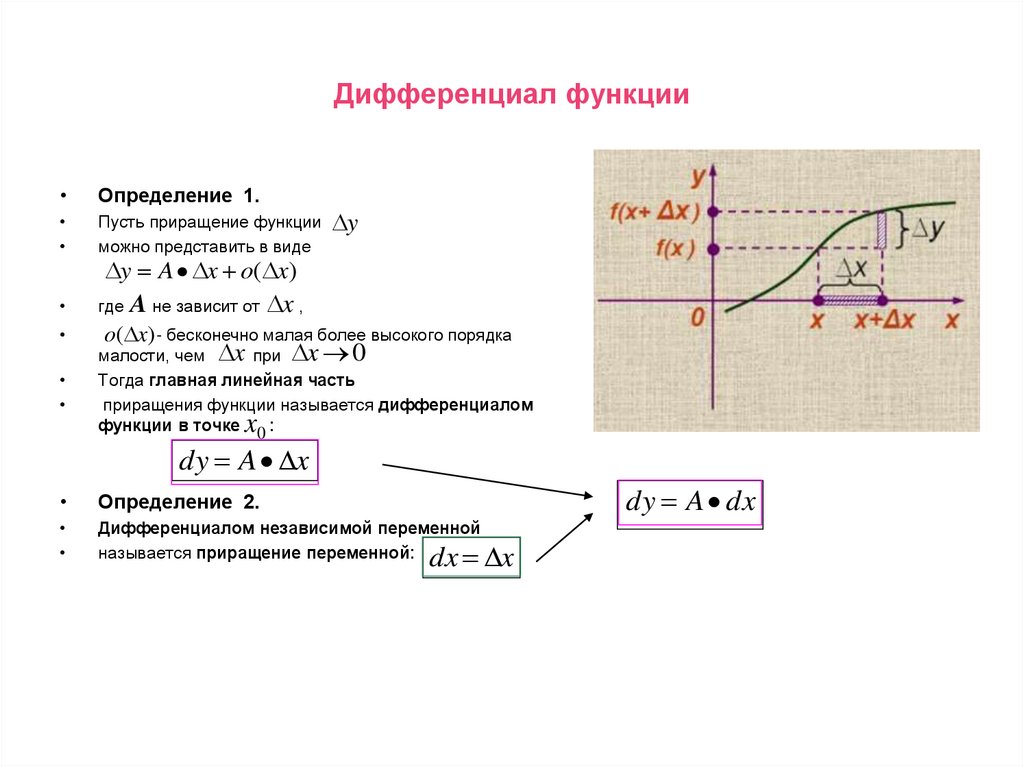
1. Дифференциал функции

Определение 1.
Пусть приращение функции y
можно представить в виде
y A x o( x)
где A не зависит от x ,
o( x)- бесконечно малая более высокого порядка
малости, чем x при x 0
Тогда главная линейная часть
приращения функции называется дифференциалом
функции в точке 0 :
Определение 2.
Дифференциалом независимой переменной
называется приращение переменной:
x
dy A x
dy A dx
dx x

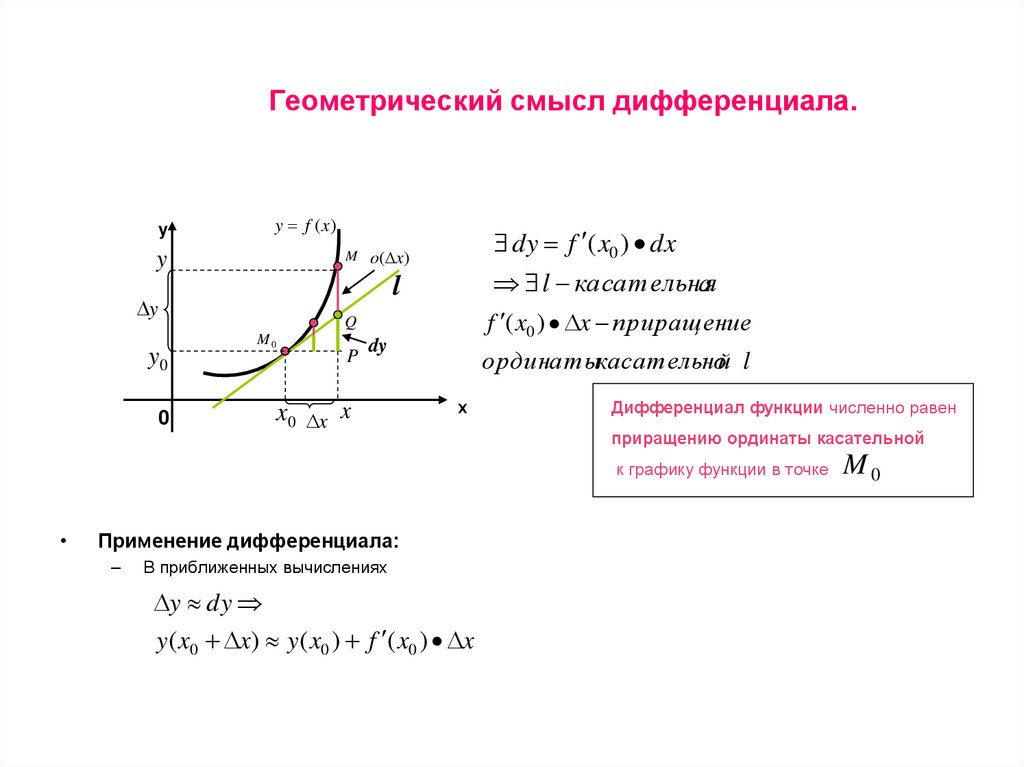
2. Геометрический смысл дифференциала.

y
y f (x)
dy f ( x0 ) dx
M o( x)
y
l касательная
l
y
f ( x0 ) x приращение
Q
y0
0
M0
P
dy
x0 x x
ординатыкасательной l
х
Дифференциал функции численно равен
приращению ординаты касательной
к графику функции в точке
Применение дифференциала:
–
В приближенных вычислениях
y dy
y ( x0 x) y( x0 ) f ( x0 ) x
M0

3.

4. Пусть y = f(x) определена и непрерывна в точке

x x 0 ,
Если полное приращение функции в этой точке можно представить в виде
y A x o( x),
то функция y = f(x) называется дифференцируемой при x x 0 ,
а выражение
A x dy.
Здесь o( x ) - бесконечно малая величина при x 0 более высокого
порядка, чем x.

5. Необходимое и достаточное условие дифференцируемости функции

Для того, чтобы функция
y f ( x ) в точке x 0 была дифференцируемой
необходимо и достаточно, чтобы для нее в этой точке существовала конечная
производная y ' f ( x 0 ). При выполнении этого условия равенство
y A x o( x) имеет место при значении постоянной
A y' f ' ( x 0 ) :
y y' x o( x).
Доказательство.
Необходимость. Выполняется y A x o( x). Разделим на x :
y
o ( x )
A
.
x
x
y
o( x )
A lim
,
x 0 x
x 0 x
lim
x 0
y
y'.
x 0 x
A lim

6. Достаточность.

По условию существует производная
Тогда
y
y' o( x )
x
y' f ' ( x 0 ) :
y
y' ,
x 0 x
lim
и
y y' x o( x).
Приращение функции записано в таком виде, следовательно, функция
дифференцируема.

7. Свойства дифференциала.

y f ( x) и y g ( x)
Пусть функции
дифференцируемые.
Тогда:
1.
d ( f g ) df dg ;
2. d ( f g ) (df ) g f (dg) ;
3.
4. Инвариантность формы дифференциала.
Пусть функция
Функция u g (x) дифференцируемая.
Тогда
f
(df ) g f (dg)
d( )
;
2
g
g
y f (u )
дифференцируемая;
dy f (u ) du f ( g ( x)) dx
du g ( x) dx
f (u ) g ( x)
Форма дифференциала функции
не зависит от того, является ли ее
аргумент независимой переменной или
функцией от новой переменной.

8. Таблица дифференциалов основных элементарных функций.

1.
d (C ) 0
2.
d ( x n ) nxn 1dx
3.
d (a x ) a x ln a dx
4.
d (e x ) e x dx
5.
1
d (loga x)
dx
6.
1 x ln a
d (ln x) dx
x
7.
d (sin x) cos x dx
8.
d (cosx) sin x dx
9.
1
d (tgx)
dx
2
cos x
10.
1
d (ctgx) 2 dx
sin x
11.
12.
13.
14.
d (arcsin x)
1
dx
1 x
1
d (arccosx)
dx
2
1 x
1
d (arctgx)
dx
1 x2
1
d (arcctgx)
dx
2
1 x
2

9. Функции двух переменных

• Функцией двух переменных называется
закон, по которому каждой паре
значений независимых переменных
(аргументов) из области определения
соответствует значение зависимой
переменной (функции).

10. Данную функцию обозначают следующим образом: Z = f(x; y)

• Поскольку упорядоченная пара
значений «икс» и «игрек» определяет
точку на плоскости, то функцию также
записывают через z = f(M), где M –
точка плоскости с координатами x,y.
Такое обозначение широко
используется в некоторых практических
заданиях.

11. Область определения

• Областью определения функции двух
переменных называется множество
всех пар (x;y), для которых существует
значение z.
• Графически область определения
представляет собой всю плоскость
либо её часть.

12. Пример

• Найти область определения функции
z
x y 1
x
• Решение: подкоренное выражение должно быть
неотрицательным: x y 1 0
• и знаменатель не может равняться нулю: x 0 .
• Таким образом, область определения задаётся
системой x y 1 0
.
x 0
• Со вторым условием системы тоже всё просто:
уравнение задаёт ось ординат, и коль скоро , то её
следует исключить из области определения.

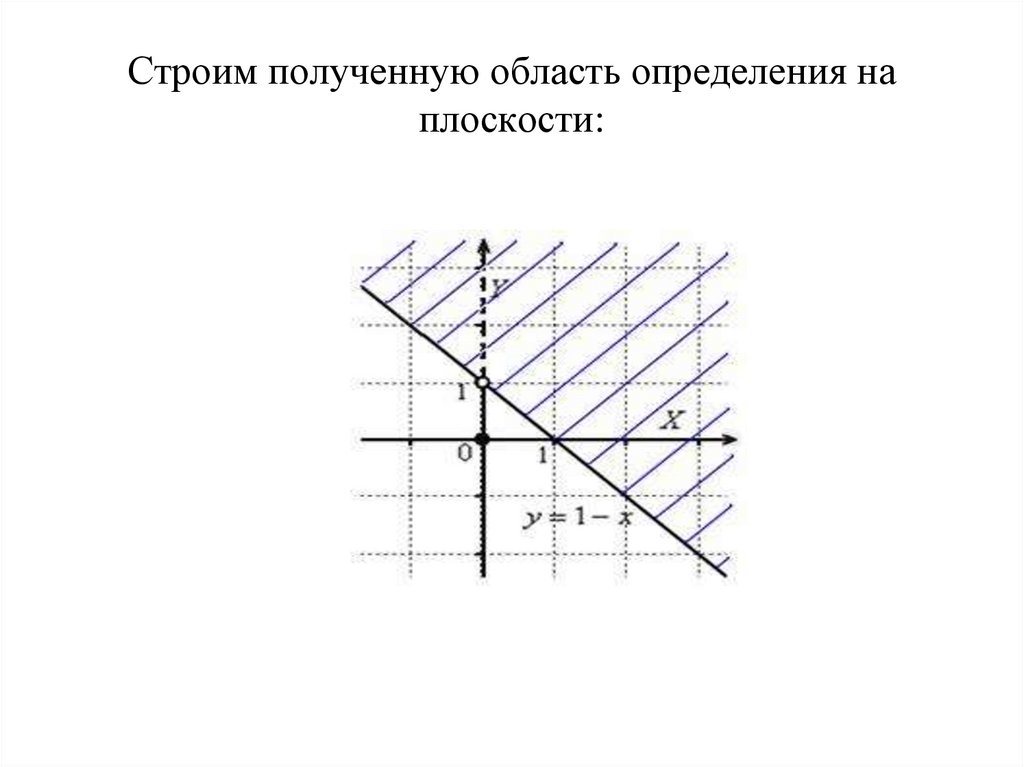
13. Построение области определения

• Строим прямую x + y - 1 = 0 и определяем
полуплоскость, которая соответствует
неравенству x y 1 0 .
• Поскольку неравенство нестрогое, то сама
прямая также будет являться решением.
• Второе условие системы: уравнение x = 0
задаёт ось ординат, и так как x 0
• , то эту ось следует исключить из области
определения.
x 0

14. Строим полученную область определения на плоскости:

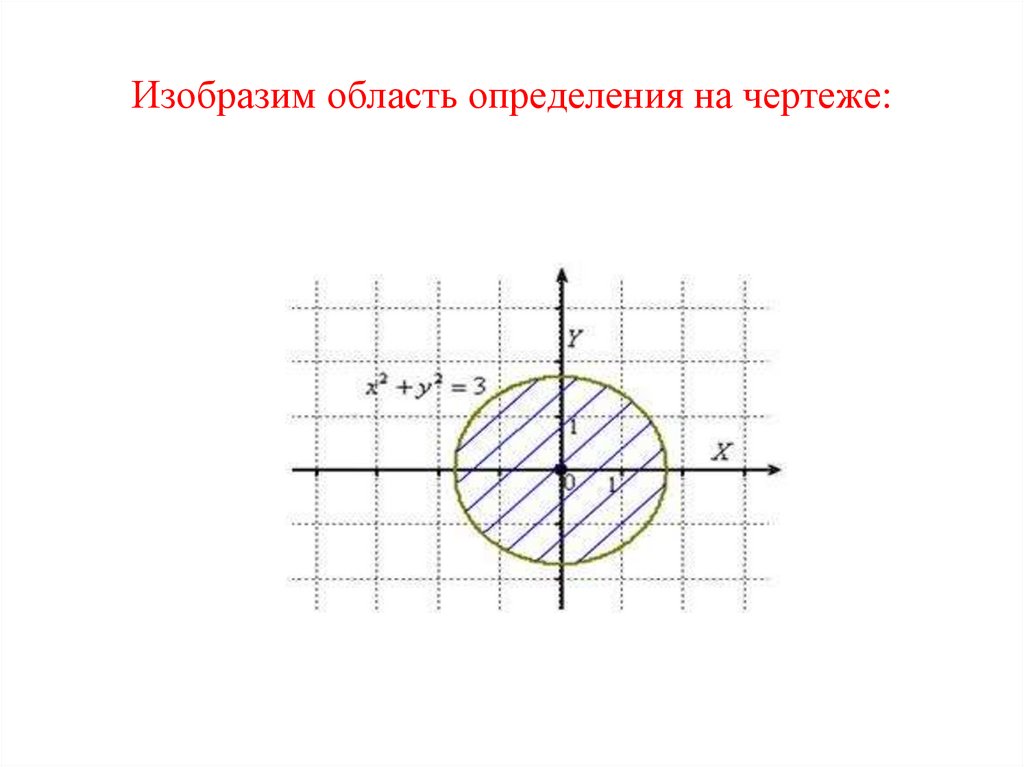
15. Пример

Найти область определения функции
z 3 x2 y 2
Решение:
Подкоренное выражение должно быть
неотрицательным: 3 x2 y 2 0
или x 2 y 2 3
Это круг радиуса 3 с центром в начале координат.
Изобразим область определения на чертеже:

16. Изобразим область определения на чертеже:

17.

18. Имеем дело с областями , ограниченными линиями.

Линия, ограничивающая данную область,
называется границей области.
Точки области, не лежащие на границе,
называются внутренними точками области.
Область, состоящая из одних внутренних
точек, называется открытой.

19. Если же к области относятся и точки границы, то область называется замкнутой.

• Связной называется область, любые две точки
которой можно соединить линией, целиком
лежащей в этой области.

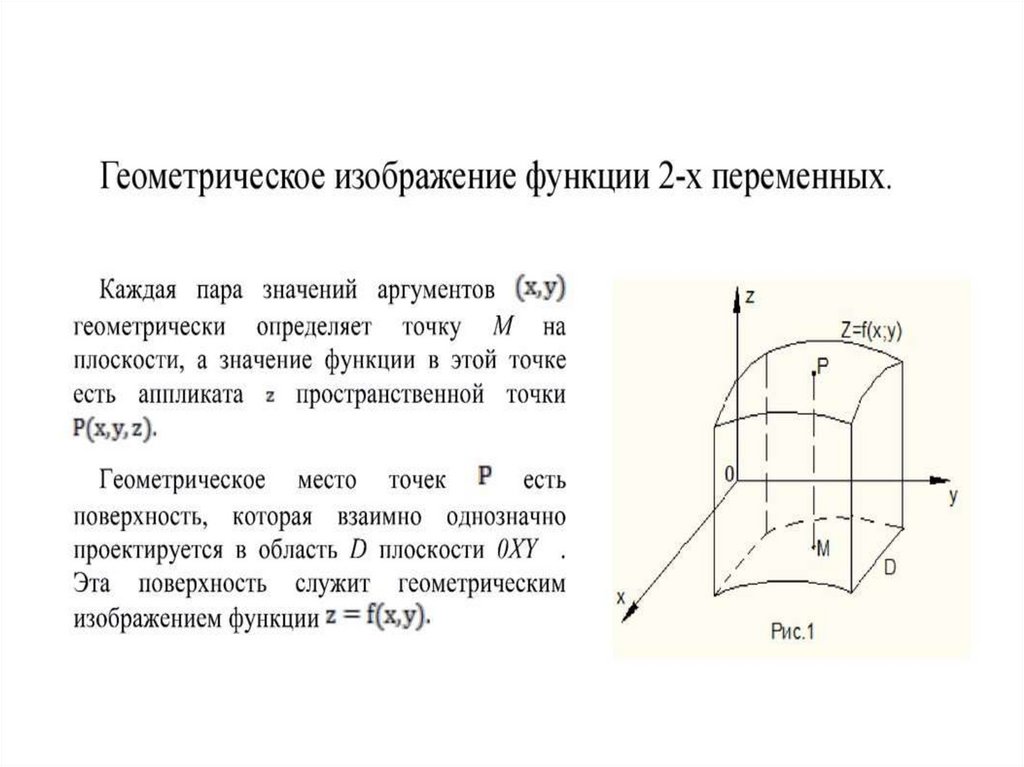
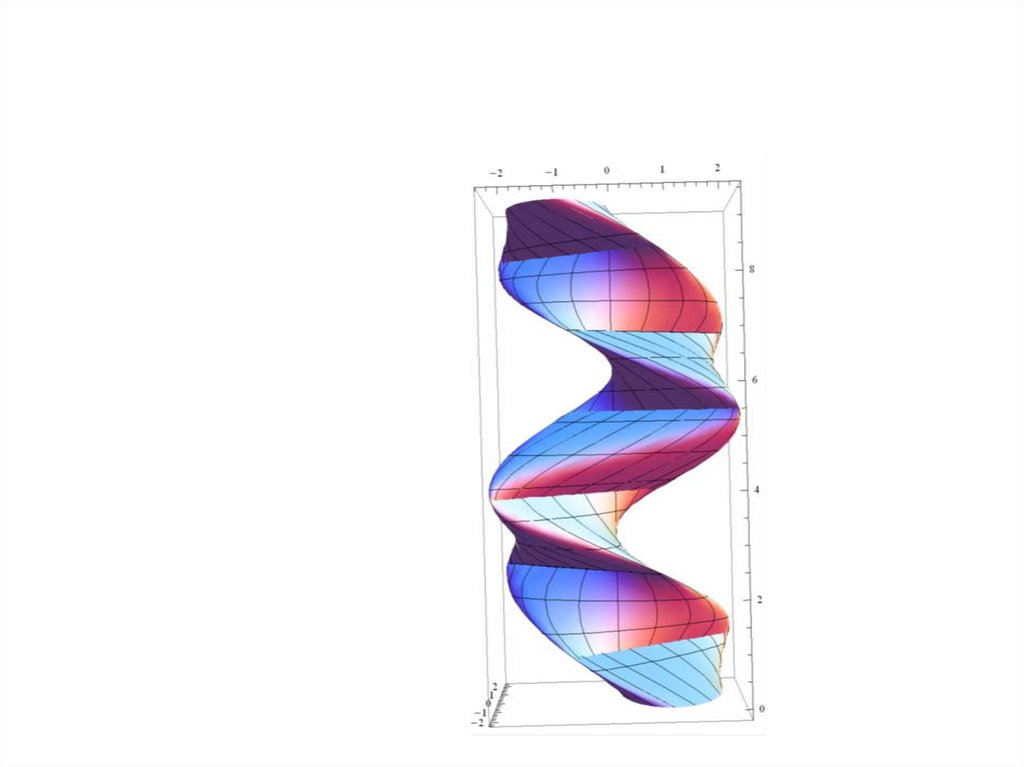
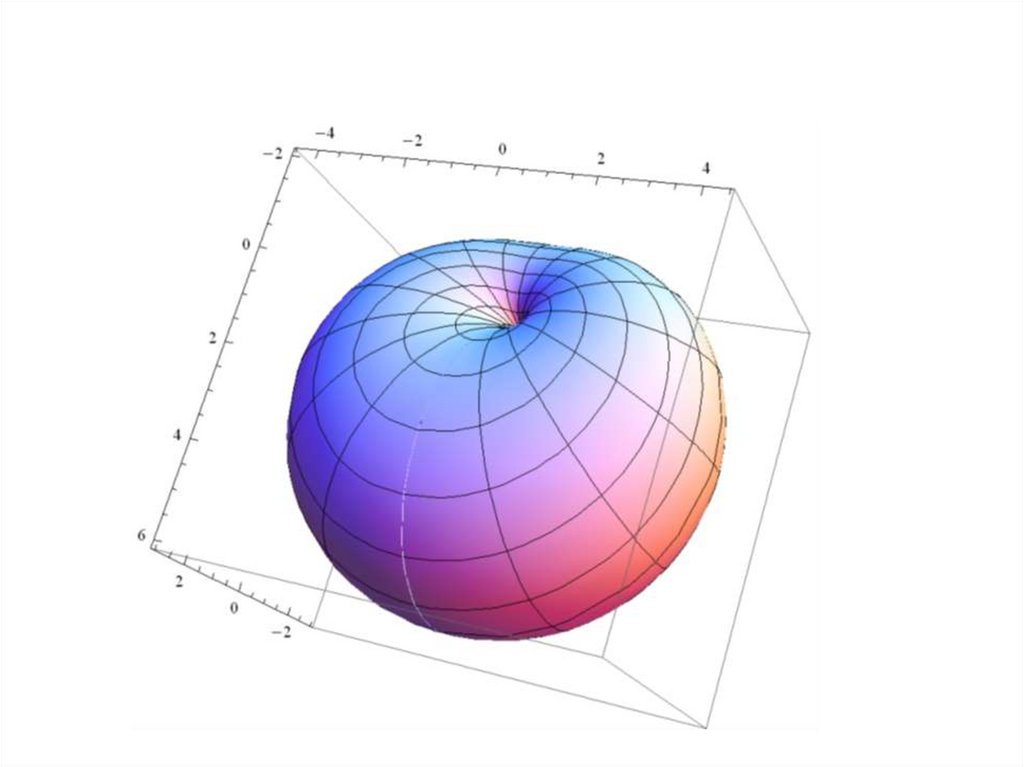
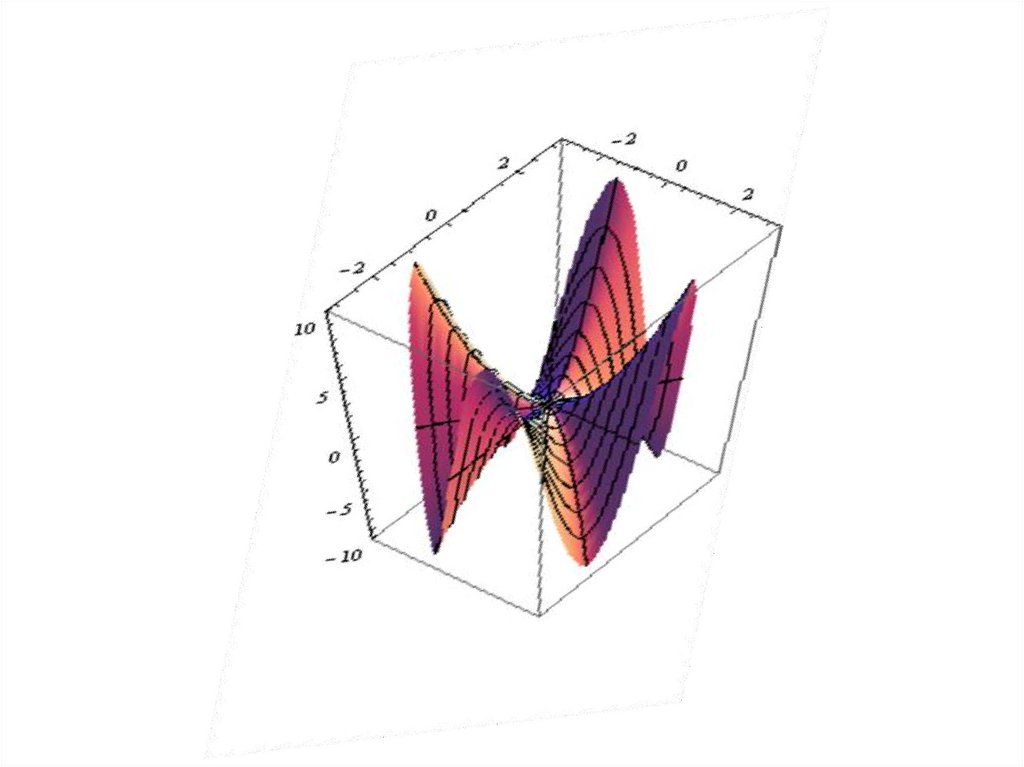
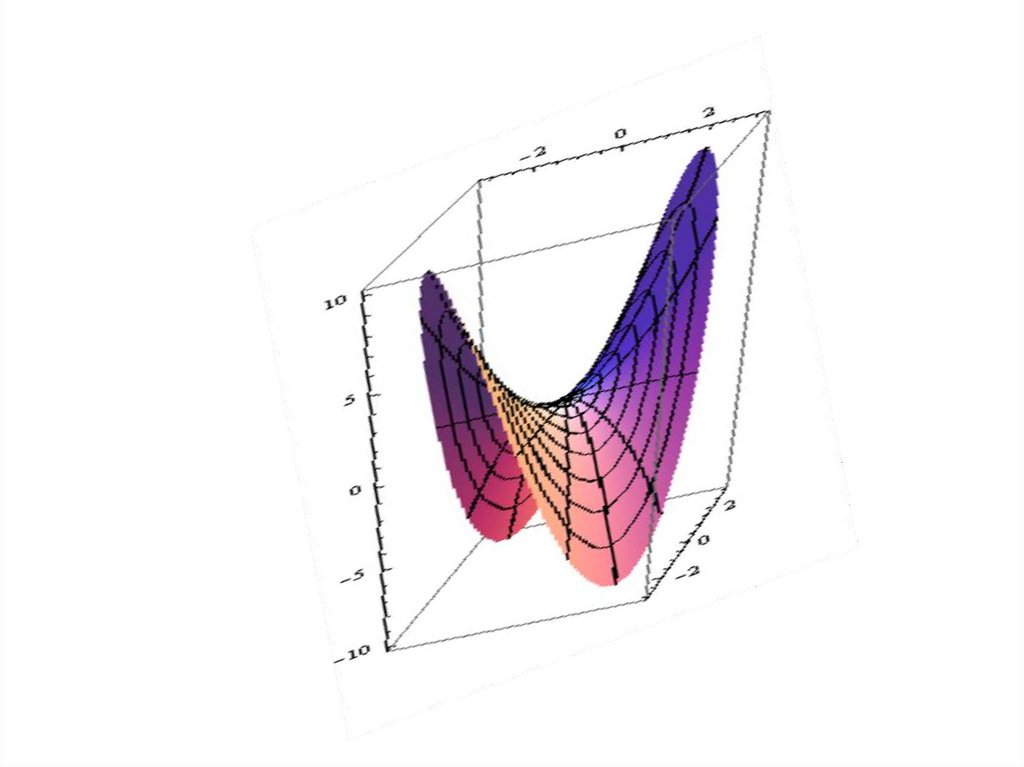
20. Геометрическое изображение функции двух переменных.

• Графиком функции z = f(x; y) является
поверхность с уравнением z = f(x; y).

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

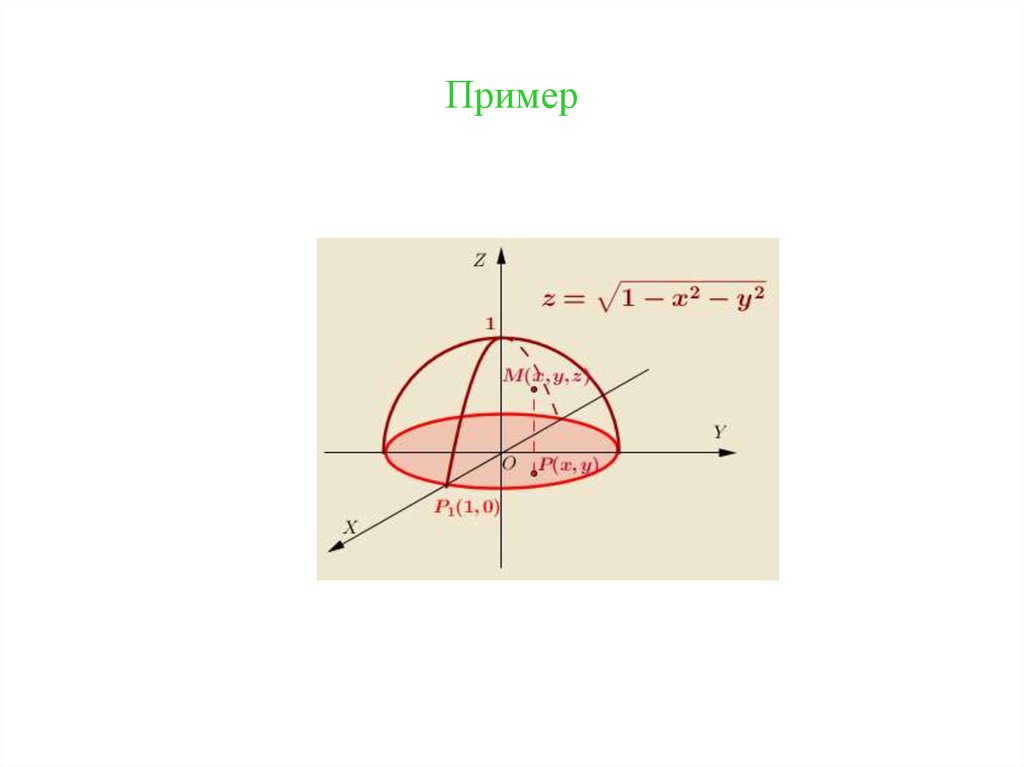
32. Пример

33.

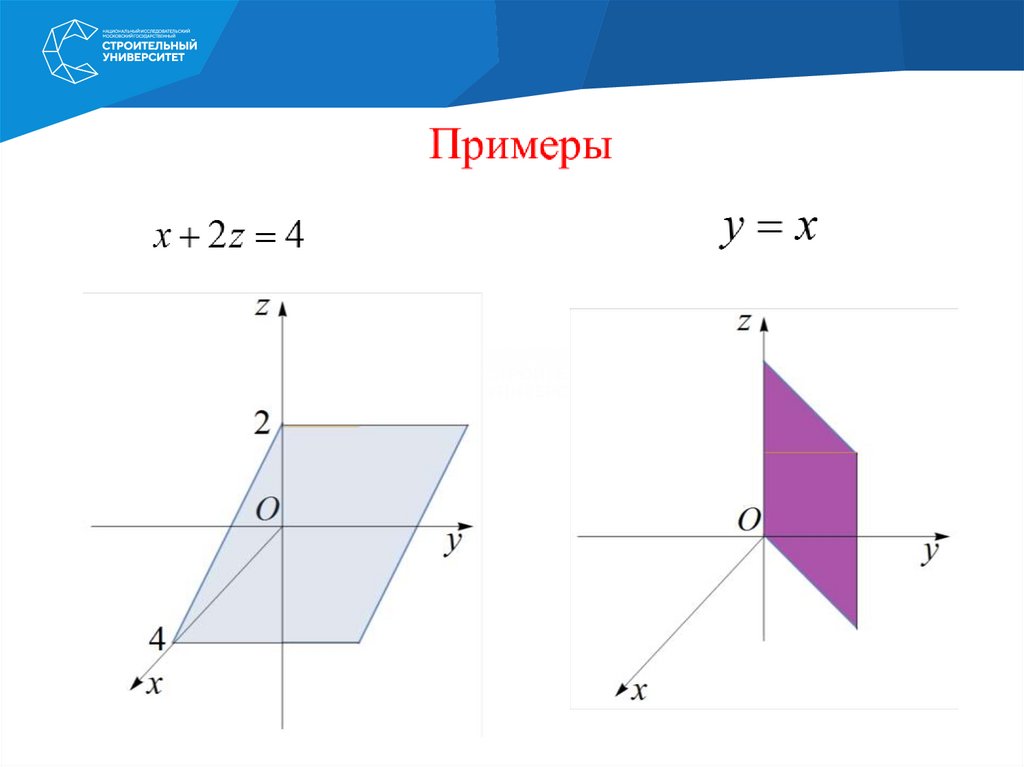
34. Построить самостоятельно:

Плоскость: z = 1 – x
Полусфера:
z 4 x2 y2

35. Ограниченность функции двух переменных

• Функция z = f(x;y) называется
ограниченной, если существуют такие
числа M и N, что
M f ( x; y) N
Например, z sin( x 2 2 y )

36.

37.

38.

39. Частные приращения функции двух переменных

• Частным приращением по x функции z = f(x; y) в
точке ( x0 ; y0 ) называется разность
x z f ( x0 x; y0 ) f ( x0 ; y0 ) ,
• то есть приращение функции, полученное за счет
приращения x при y - const.

40.

Частным приращением по y функции
z = f(x; y) в точке ( x0 ; y0 ) называется разность
y z f ( x0 ; y0 y ) f ( x0 ; y0 ),
то есть приращение функции, полученное за
счет приращения y при x - const.

41. Полное приращение функции z = f(x;y)

Полным приращением функции z = f(x;y) в
точке ( x0 ; y0 ) называется разность
z f ( x0 x; y0 y ) f ( x0 ; y0 )

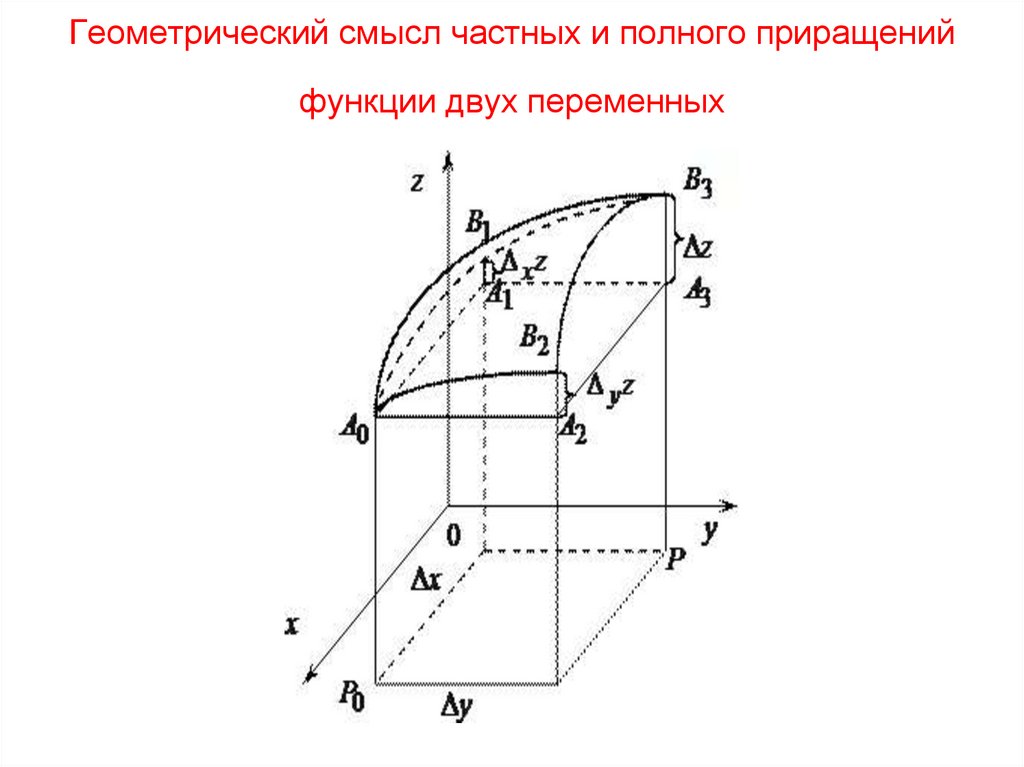
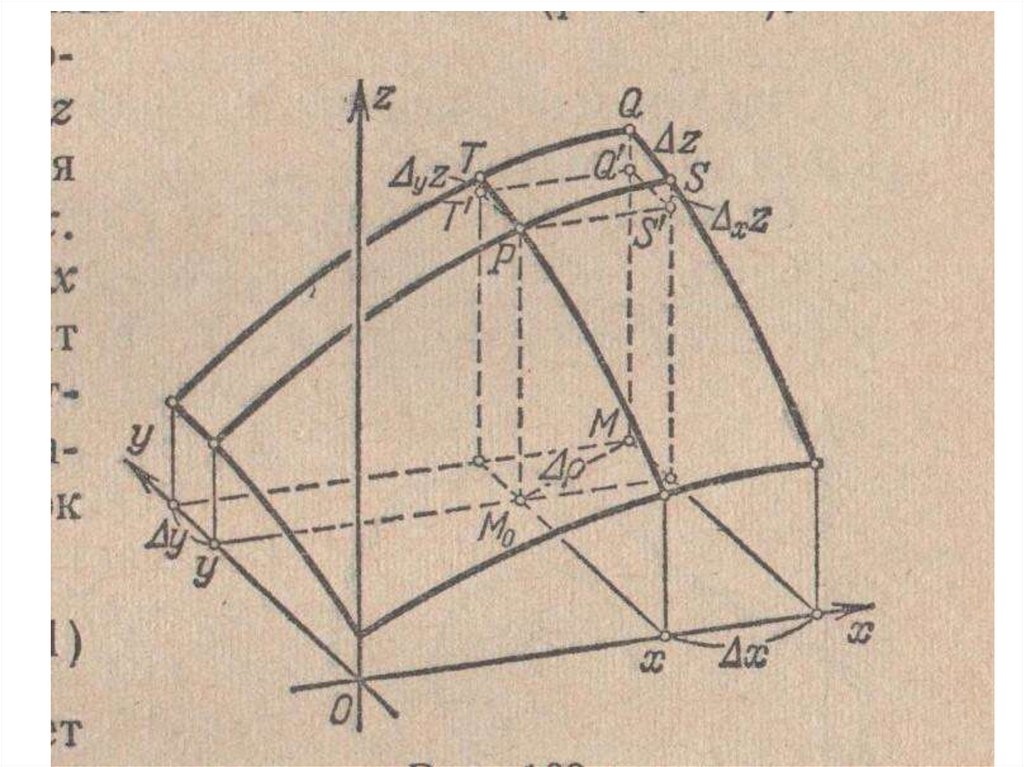
42. Геометрический смысл частных и полного приращений функции двух переменных

43.

44. Непрерывность функции в точке.

• Функция z f (M ) называется непрерывной в точке M 0 ,
если
1). функция определена в точке
и некоторой ее
окрестности;
2). существует lim f (M ) ;
M M 0
3). lim f (M ) f (M 0 ) .
M M 0

45. Второе определение непрерывности функции z =f(x; y) в точке

Пусть функция z = f(x; y) непрерывна в точке M 0 ( x0 ; y0 )
(по первому определению).
lim f ( x0 x; y0 y ) f ( x0 ; y0 )
Тогда x x0 x, y y0 y ,
x 0
y 0
или
lim [f ( x0 x; y0 y ) f ( x0 ; y0 )]=0 .
x 0
y 0
Но f ( x0 x; y0 y ) f ( x0 ; y0 ) z - полное приращение
функции.
Пусть ( x )2 ( y )2 , при x 0 и y 0, 0 , тогда получим
lim z = 0
0

46.

47. Частные производные функции двух переменных z = f (x; y)

Частной производной функции z = f(x; y) по x
называется
x z
f ( x0 x; y0 ) f ( x0 ; y0 )
lim
x 0 x
x 0
x
z x lim
(y - const)
z
Другое обозначение: x
Частной производной функции z = f(x; y) по y
называется
z y lim
yz
y 0 y
( x - const)
f ( x0 ; y0 y ) f ( x0 ; y0 )
y 0
y
lim
z
Другое обозначение: y

48. Пример

Найти частные производные:
z 3x 2 y 5x y 2 xy 4 x y 5
4
3
2
z
12 x3 10 xy 2 y 2 4
x
(y = const)
z
6 y 2 5 x 2 4 xy 1
y
(x = const)
2

49. Пример

Найти частные производные:
z e2 x 5 ysin (4 - 2 x+5y2 )
2 x 5 y
2
2 x 5 y
2
zx e
2 sin(4 - 2 x+5y ) e
cos(4 - 2 x+5y ) ( 2)
(y = const)
2 x 5 y
2
2 x 5 y
2
zy e
5 sin(4 - 2 x+5y ) e
cos(4 - 2 x+5y ) (10y)
(x = const)

50. Геометрический смысл частных производных

Пусть y y0 const . Это плоскость, параллельная
координатной плоскости Oxz. В пересечении с
поверхностью z = f(x; y) получим линию.
Угол - угол, образованной касательной к этой
линии и положительным направлением оси Ox.
Касательная проведена в точке P0 ( x0 ; y0 ;z0 ), где
z0 f ( x0 ; y0 ).

51. Аналогично,

Пусть x x0 const . Это плоскость,
параллельная координатной плоскости Oyz. В
пересечении с поверхностью z = f(x; y)
получим линию.
Угол - угол, образованной касательной к
этой линии и положительным направлением
оси Oy.
Касательная проведена в той же точке.

52.

53. Физический смысл частных производных

Частная производная
- это скорость
изменения z относительно переменной x в точке
P0 ( x0 ; y0 ).
Частная производная z y ( x0 ; y0 ) - это скорость
изменения z относительно переменной y в той же
точке.

54.

55.

56. Или: функция называется дифференцируемой в точке, если

ее полное приращение можно представить в виде
z A x B y 1 x 2 y ,
где
1 0 и 2 0 при x 0, y 0

57. Полный дифференциал:

dz A x B y
Что представляют собой A и B ?

58. Связь между дифференцируемостью и существованием частных производных функции двух переменных

Если функция z = f(x; y) имеет в точке M(x; y) дифференциал
, то в этой точке существуют и обе
частные производные z и z , причем
x
y
z
z
A
, B
.
x
y

59. Доказательство

Дадим приращение x величине x, а y оставляем
постоянным ( y 0 ),
Тогда dz A x ,
x z dz o( ) A x o( | x| ) ,
так как | x|.
x z
o( | x | )
lim
lim A
A
x 0 x
x 0
x
z
Это значит, существует x A.
Аналогично,
z
B.
y

60.

61. Теорема

z z
и
Если в точке (x; y) частные производные
x y
существуют и непрерывны, то в этой точке
функция имеет дифференциал.

62. Теорема. Связь между дифференцируемостью и непрерывностью функции в точке.

Если функция z = f(x; y) дифференцируема в точке (x; y), то она
непрерывна в этой точке.
Доказательство.
По условию функция дифференцируема, это значит ее полное
приращение можно представить в виде:
z z x x z y y 1 x 2 y
тогда
lim z 0
x 0
y 0

63. Частные производные высших порядков

Частными производными второго порядка функции z = f (x,y)
называются частные производные от частных производных
первого порядка.
2 z z
z xx ( z x ) x
2
x
x x
z xy ( z x ) y
2 z
z
x y y x
z yx ( z y ) x
2 z
z
y x x y
z yy ( z y ) y
2 z
z
y 2 y y

64. Теорема

Пусть функция z = f(x; y) в некоторой окрестности
точки (x; y) имеет смешанные производные z xy и z yx ,
причем они непрерывны в этой точке. Тогда в этой
точке смешанные производные равны между собой:
z xy z yx

65. Пример

Найти частные производные второго порядка
z 3x4 y3 xy x2 y5 4x 7 y 10
z x 12x3 y 2xy5 4, z y 3 y 2 x 5x2 y 4 7
z xx ( z x )x 36 x 2 2 y 5 , z xy ( z x ) y 1 10 xy 4 ,
z yx ( z y )x 1 10 xy 4 , z yy ( z y ) y 6 y 20 x 2 y 3

66.

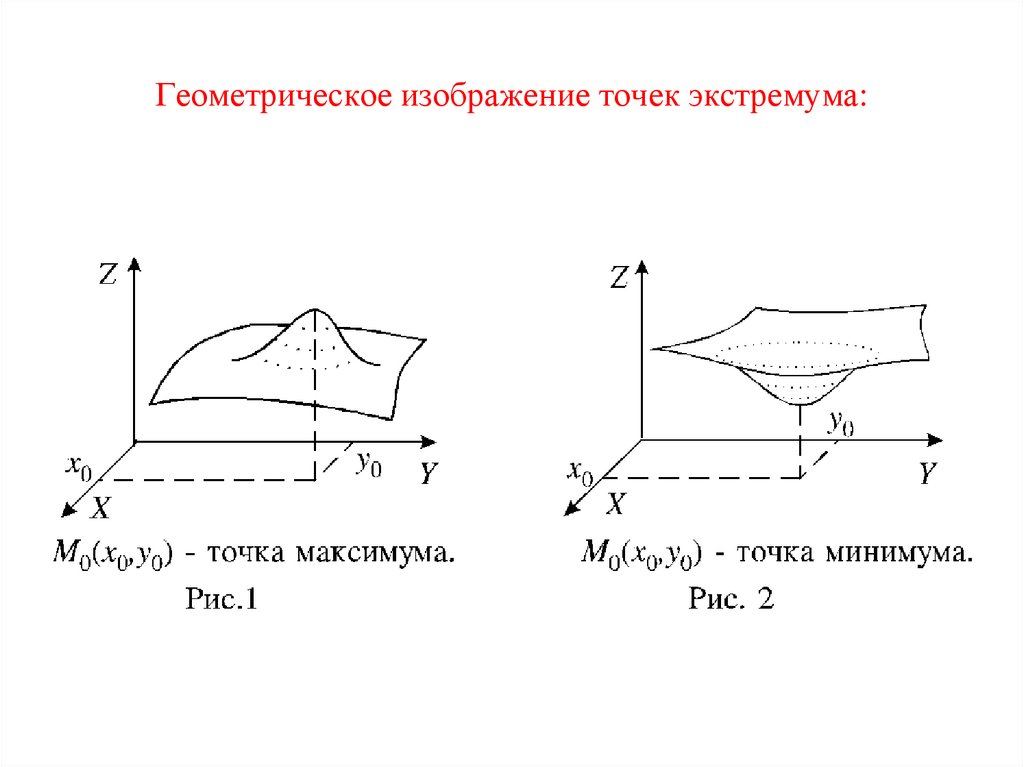
67. Геометрическое изображение точек экстремума:

68.

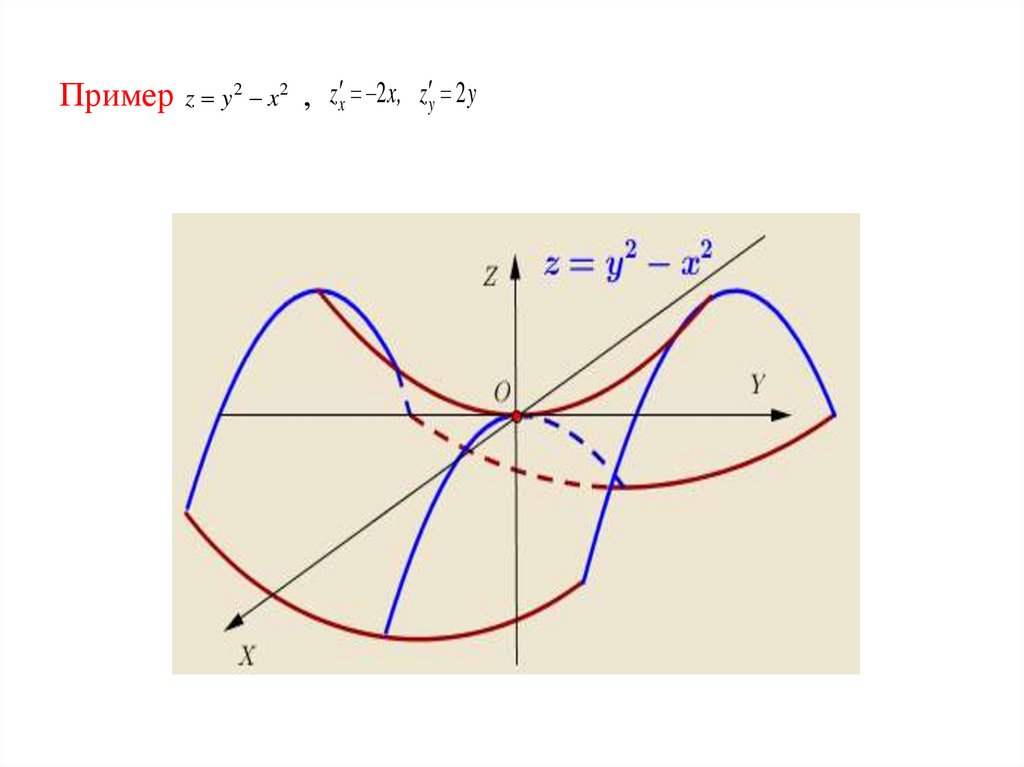
69. Пример ,

Пример z y 2 x2 , z x 2x, z y 2 y

70.

71. Пример

Исследовать на экстремум функцию
z x3 8 y3 6 xy 1