Полный дифференциал функции нескольких переменных

1. Полный дифференциал функции нескольких переменных

Лекция 2

2. Полное приращение функции 2-х переменных

Если обеим переменным дать
приращение, то функция получит
полное приращение
z f ( x x, y y ) f ( x, y )

3. Определение дифференцируемой функции

Функция z f ( x, y ) называется
дифференцируемой в точке М(х,у), если ее
полное приращение можно представить в виде
z A x B y o( ) ,
где Δx и Δy -произвольные приращения аргументов
х и у в некоторой окрестности точки М(х,у), А и В –
постоянные, независящие от Δx и Δy
, o(ρ)-
бесконечно малая более высокого порядка, чем
x 2 y 2 -расстояние между М(х,у) и
M1 ( x x, y y)

4. Определение дифференциала

Главная линейная относительно Δx и
Δy часть полного приращения функции
z f ( x, y ) называется полным
дифференциалом этой функции и
обозначается dz или df(x,y) .
Таким образом, dz A x B y .

5. Формула для вычисления дифференциала

Если функция z f ( x, y )
дифференцируема в точке М(х,у),то она
имеет в этой точке частные
производные f x ( x, y ) и f y ( x, y ) ,
причем f x ( x, y ) =А, а f y ( x, y ) =В .
Так что, z f x x,y x f y x,y y 0 ρ
dz f x ( x, y ) x f y ( x, y ) y .
Если положить x dx, y dy ,то
dz f x ( x, y )dx f y ( x, y )dy

6.

При малых
z dz , то есть
f x x, y y f x,y f x x,y x f y x,y y
или
,
f x x,y y f x,y f x x,y x f y x,y y .
Пример. Вычислить приближенно
ln 3 1,03 4 0,98 1
.

7. Дифференциалы высшего порядка

Дифференциалом второго порядка
функции z=f(x,y) называется
d 2 z d (dz )
n 1
Вообще: d z d (d z )
Если х и у независимые переменные, то
2
2
2
.
d z z dx 2 z dxdy z dy
n
xx
xy
yy

8. Экстремумы функции двух переменных

Определение. Говорят, что в точке P0 ( x0 , y0 )
функция f (x,y) имеет максимум, если
cуществует такая окрестность этой точки, что
для всех точек P(x,y) этой окрестности,
отличных от P0 ( x0 , y0 ) , выполнено
неравенство
f ( P0 ) f ( P).
Аналогично определяется минимум функции.
Минимум и максимум функции называются
ее экстремумами.

9. Экстремумы функции двух переменных

Теорема (необходимое условие
экстремума). В точке экстремума
функции нескольких переменных
каждая ее частная производная либо
равна нулю, либо не существует.
Точки, в которых выполнены эти
условия, называются критическими.

10. Достаточные условия экстремума функции двух переменных

Теорема. Пусть функция z=f(x,y) определена и
имеет непрерывные частные производные до 3-го
порядка в некоторой окрестности точки M 0 ( x0 , y 0 ), в
которой z x z y 0 . Если при этом в этой точке
выполнено условие z xx
z yy ( z xy ) 2 0, то точка M 0
является точкой экстремума функции, причем точкой
0 , и точкой минимума, если
максимума, если z xx
z xx 0 .
2
Если же в этой точке z xx z yy ( z xy ) 0 , то
экстремума в точке M 0 нет.
В том случае, если z xx z yy ( z xy ) 2 0 в точке M
, 0
теорема ответа не дает.

11. Пример

Исследовать на экстремум функцию
50 20
z xy , åñëè x 0 u y 0.
x
y

12. Наибольшее и наименьшее значения функции

Определение. Наименьшее или
наибольшее значение функции в
данной области называется
абсолютным экстремумом функции
(абсолютным минимумом или
абсолютным максимумом
соответственно) в этой области.

13.

Известно, что непрерывная в
замкнутой ограниченной области
функция достигает в ней своих
наибольшего и наименьшего
значений.
Абсолютный экстремум
достигается функцией либо в
критических точках, либо на
границе области.

14.

Пусть функция непрерывна в замкнутой
ограниченной области G, дифференцируема
внутри этой области. Чтобы найти
наибольшее и наименьшее значения функции
в этой области, нужно:
1)найти критические точки, принадлежащие
этой области, и вычислить в них значения
функции;
2)найти наибольшее и наименьшее значения
функции на границе области;
3)из всех найденных значений выбрать
наибольшее и наименьшее.

15. Пример

Найти наибольшее и наименьшее
значения функции
z x 3y x y
2
,
.
2
в треугольнике, ограниченном прямыми
x 0, y 0, x y 1.

16. Скалярное поле

Лекция 3

17. Основные определения

Пусть в области D пространства
Охуz задана функция u=u(х,у,z). В этом
случае говорят, что в области D задано
скалярное поле, а саму функцию
u=u(х,у,z)называют функцией поля.
Например, поле давлений, температур
и т.д.

18. Основные определения

Множество точек М области D, для
которых скалярное поле сохраняет
постоянное значение, т. е. u(М)=С,
называется поверхностью уровня ( или
изоповерхностью) скалярного поля.

19.

Если область D расположена на
плоскости Оху, то поле u=u(х,у)
является плоским.
Поверхности уровня называют в
этом случае линиями уровня.

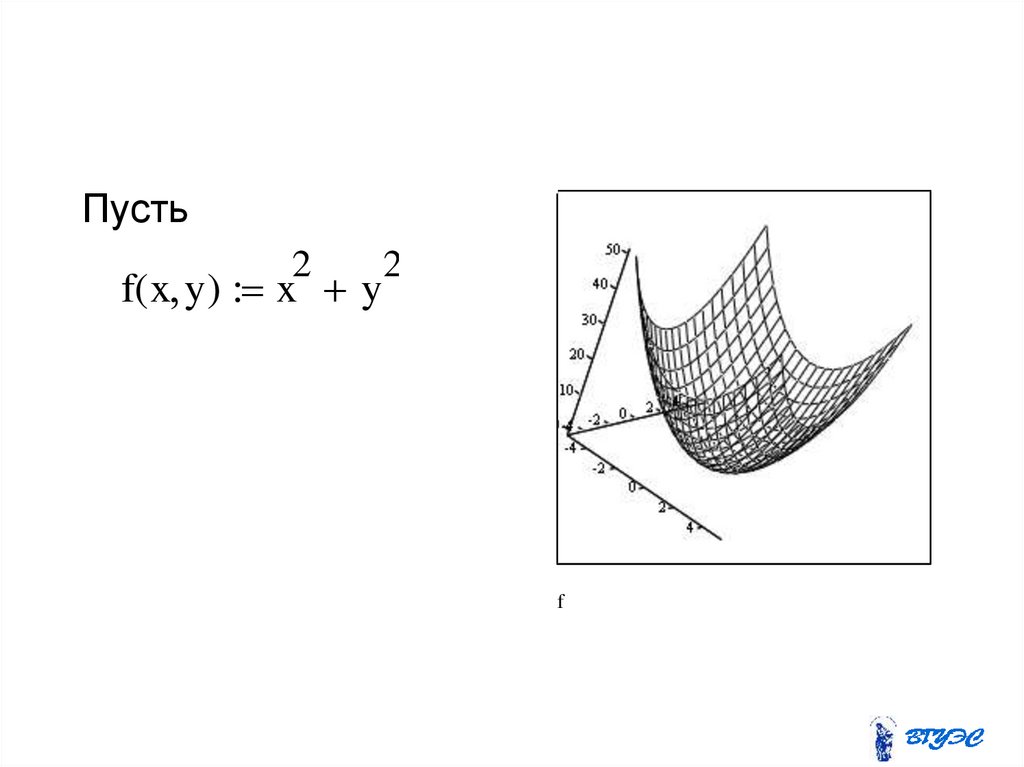
20.

Пусть
2
f( x y) x y
2
f

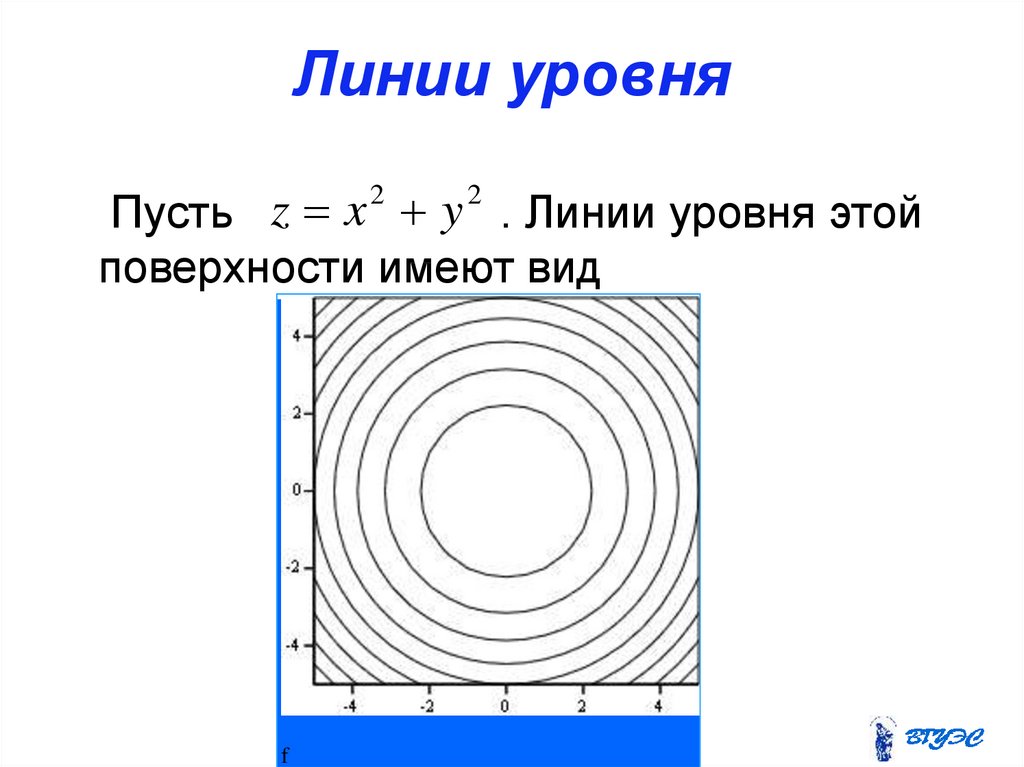
21. Линии уровня

Пусть z x y . Линии уровня этой
поверхности имеют вид
2
f
2

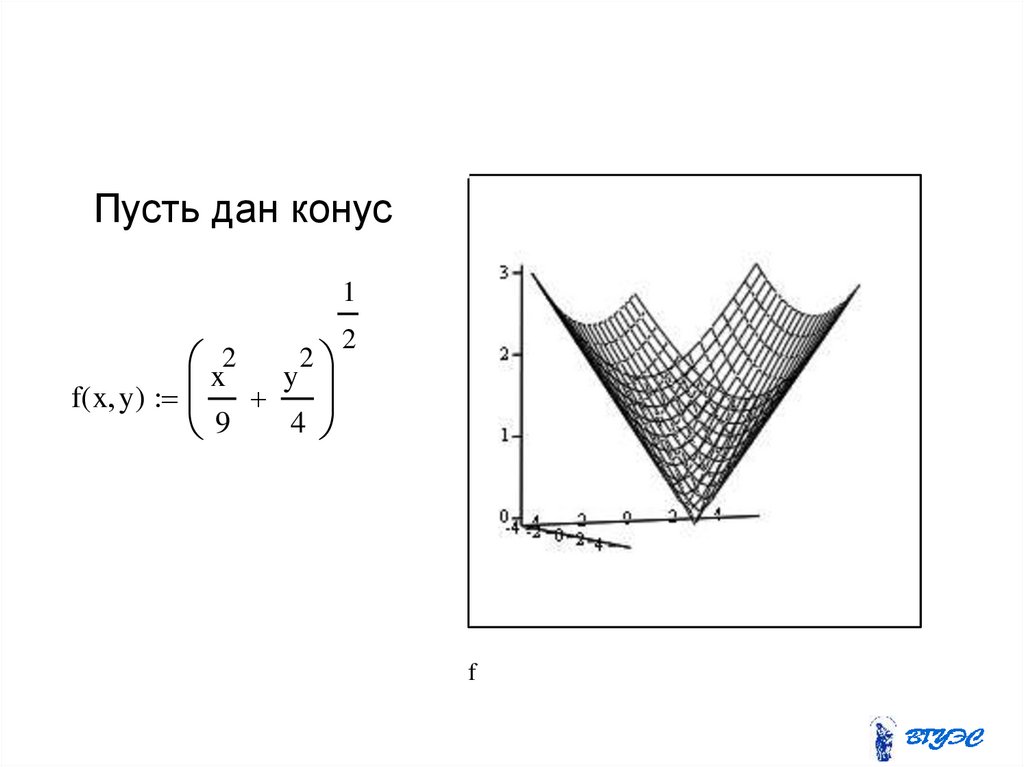
22.

Пусть дан конус
1
x
y
f( x y )
4
9
2
2
2
f

23. Линии уровня конуса

f

24.

Пусть задана дифференцируемая
функция u u x, y, z скалярного поля.
Рассмотрим точку P x, y, z этого поля и
луч , выходящий из точки P в
направлении единичного вектора
cos α; cos β; cos γ ,
0
где α, β,
вектором
γ –углы, образованные
0
с осями координат .

25. Определение

z
P1
γ
ℓ
β
P
PP1 x 2 y 2 z 2
α
0
x
x
y
Рис.
Пусть P1 x x , y y , z z
– какая-нибудь другая
точка этого луча.
Обозначим
– расстояние между
точками P и Ρ1 ;
называют величиной
перемещения.
Приращением функции
в направлении
назовем разность
u u Ρ1 u Ρ

26.

Производной функции u u x, y, z
в точке P по направлению называется
предел отношения приращения
функции в направлении
к величине перемещения
при 0 :
.
u
u
lim
0

27. Вычисление производной по направлению

Формула вычисления производной по
направлению:
u u
u
u
cos cos cos , ãäå
x
y
z
ly
lx
lz
cos , cos , cos ,
l
l
l
l lx2 l y2 lz2 .

28. Градиент скалярного поля

Градиентом скалярного поля
u=u(x,y,z), где u=u(x,y,z)дифференцируемая функция,
называется вектор с координатами
u u u
.
, ,
x y z
u u u
Таким образом, gradu ( , , )
x y z
u
u
u
j
k
или gradu i
x
y
z
.

29. Пример

2
2
Найти градиент функции u= x y z
2
в
точке M(6,2,3).
Решение. Вычислим градиент функции.
y
x
u
u
y
x
2
2
2
x2 y 2 z 2
x y z
z
u
z
Тогда grad u =
А в точке М
x2 y 2 z 2
x
x y z
2
2
2
i+
y
x y z
2
2
2
6 2
3
gradu i j k .
7 7
7
j+
z
x y z
2
2
2
k

30. Направление градиента

Теорема. Производная u l
функции по направлению равна
проекции градиента этой
функции на данное
направление (в
соответствующей точке).

31. Направление градиента

Так как производная по направлению
представляет собой скорость изменения
функции в данном направлении , а проекция
вектора на другой вектор имеет
максимальное значение, если оба вектора
совпадают по направлению, то
градиент функции в данной точке указывает
направление наиболее быстрого возрастания
функции.

32. Величина градиента плоского скалярного поля

Величина градиента плоского
скалярного поля ,т.е.
2
2
u u
grad u = x y
обозначается tg и определяет
крутизну наибольшего ската или
подъема поверхности u = f (x, y).

33.

Градиент скалярного поля в данной
точке по величине и направлению равен
максимальной скорости изменения поля
в этой точке, т. е.
u u
,
max
gradu
l l *
*
где l gradu .
l

34. Направление градиента

Точка Р, в которой gradu(P)=0, называется
особой точкой скалярного поля. В противном
случае эту точку называют неособой или
обыкновенной точкой поля.
Теорема. Во всякой неособой точке
плоского скалярного поля градиент поля
направлен по нормали к линии уровня ,
проходящей через эту точку, в сторону
возрастания поля.