Similar presentations:
Функции нескольких переменных
1. Функции нескольких переменных
2.
• Функцией двух переменных называется правило,по которому каждой паре чисел x; y некоторого
М соответствует единственное
число z другого множества N.
множества
z f x; y
y - независимые переменные (аргументы);
x
и
z
- зависимая переменная;
М - область определения функции;
N - множество значений функции.
3.
z 0 z xy xy0
0
z 0 f x0 ; y 0
4. Способы задания функции двух переменных
• Аналитический• Табличный
• Графический
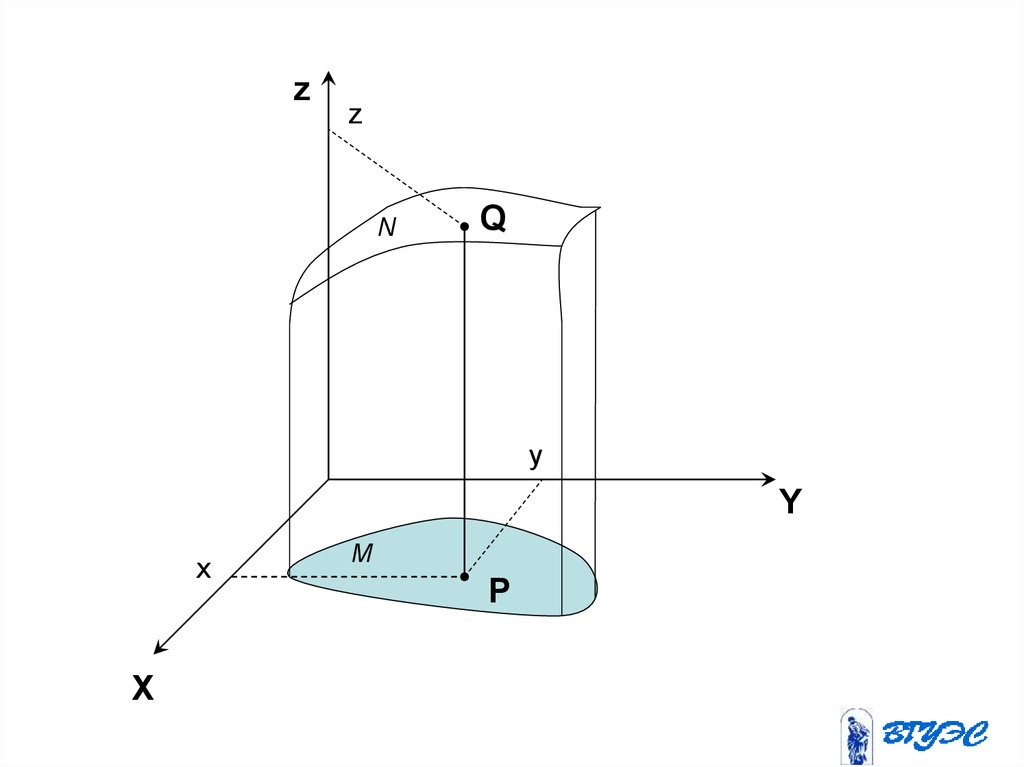
5.
zz
N
Q
y
Y
x
X
M
P
6. Частные производные
7.
Рассмотрим функцию z f x; y .Зафиксируем y y 0 ,тогда функция
примет вид
z f x; y0 .
Пусть аргумент x в точке
приращение x , тогда
x0
получил
x z f ( x0 x; y0 ) f ( x0 ; y0 )
8.
f ( x0 x, y0 ) f ( x0 , y0 )xz
lim
Предел lim
,
x 0
x 0 x
x
если он существует, называется частной
производной (первого порядка) функции
z f x; y по x в точке ( x0 , y0 ) и обозначается:
z
( x0 , y 0 ) ;
x
f
( x0 , y0 ) ; z x x0 ; y0
f x x0 ; y0 ;
x
9.
Рассмотрим функцию z f x; y .Зафиксируем x x0 ,тогда функция
примет вид
z f x0 ; y
Пусть аргумент y в точке
приращение y , тогда
y0
получил
y z f ( x0 ; y0 y) f ( x0 ; y0 )
10.
yzf ( x0 , y0 y) f ( x0 , y0 )
lim
lim
y 0
y 0 y
y
называется частной производной
(первого порядка) функции z f x; y по y
в точке ( x0 , y0 ) и обозначается:
z
( x0 , y0 ) ; f y x0 ; y0 ; f ( x , y ) ; z y x0 ; y0
0
0
y
y
11. Частные производные высших порядков.
z2
x z
2
x
x
z
2
x z
y
x y
12.
Пример.Вычислить частные производные
второго порядка функции
z x y
2
3
13.
z3
2x y
x
z
3x 2 y 2
y
2 z
3
2y
2
x
z
2
6x y
2
y
2
14.
z2
6xy
x y
2
z
2
6xy
y x
2
z
z
x y y x
2
2
15. Полный дифференциал.
zz
dz dx dy
x
y
16.
Пример.Найти полный дифференциал функции
2
z x y в произвольной точке.
z
2
y,
x
z
2 xy
y
dz y dx 2 xydy
2
17. Скалярное поле
18.
• Часть пространства (или всёпространство), каждой точке P x; y; z
которого соответствует численное значение
некоторой скалярной величины
u u x; y; z
называется скалярным полем.
19. Производная по направлению.
yM
0
M1
y
x
P
l0
l
x
z z
z
cos cos
y
l x
20. Градиент
uu
u
grad u i j k
x
y
z
21. Экстремум функции двух переменных
22. Необходимое условие существования экстремума.
Пусть функция z f x; y в точке P0 ( x0 , y 0 )имеет экстремум и пусть существует
f ' x ( x0 , y0 ) и f ' y ( x0 , y0 ) .
Тогда f ' x ( x0 , y0 ) 0 , f ' y ( x0 , y0 ) 0.
23. Достаточное условие существования экстремума
24.
Пусть для функции z f x; y вкритической точке P0 ( x0 , y0 ) существуют
производные f xx " ( P0 ) , f yy " ( P0 ), f xy " ( P0 ) .
Составим определитель
z xx
z xy
z xy
z xx z yy z xy z xy
z yy
25.
A B CA z xx
B z yy
C z xy
2
26.
Возможны три случая:1) ( P0 ) >0 , тогда точка P0 – точка
экстремума:
при A >0 – P0 точка минимума;
при
A <0 – P0
2) ( P0 ) <0, тогда
экстремума.
точка максимума.
P0
не является точкой
27.
3) ( P0 ) =0 , тогда необходимыдополнительные исследования.
28.
z x 3 xy 15 x 12 y3
2
1. z x 3 x 3 y 15
z y 6 xy 12
2
2
3 x 3 y 15 0
6 xy 12 0
2
2
29.
Решая систему ,получим четырестационарные точки
P1 (1,2);
P2 (2,1);
P3 ( 1, 2);
P4 ( 2, 1).
30.
Проверим достаточное условие экстремумав каждой из точек.
"
"
"
;
;
.
z
6
y
z
6
x
z 6x
xx
xy
yy
A В С
2
1) Для точки P1 (1,2) :
A 6;
B 6;
C 12
6 6 12 0
2
Значит, в точке
P1
экстремума нет.
31.
2) Для точки P2 (2,1) : 0 , A 0 .В точке
P2 функция имеет минимум.
f min f ( P2 ) 28
Аналогично, проверяют точки P3 и P4 .


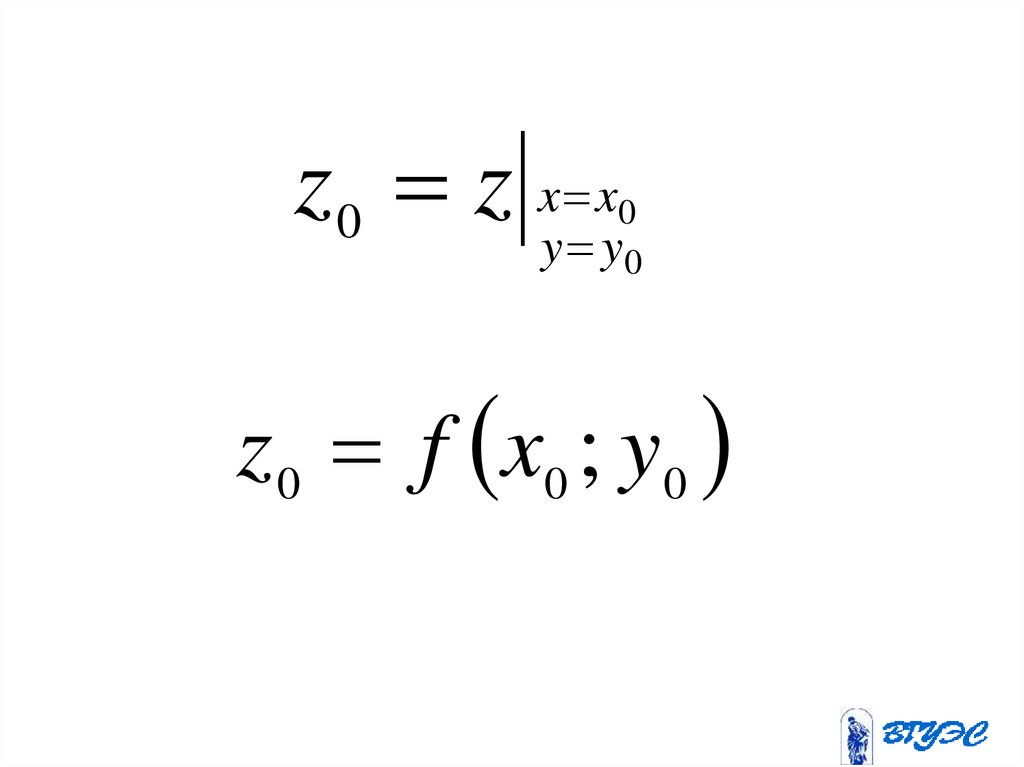








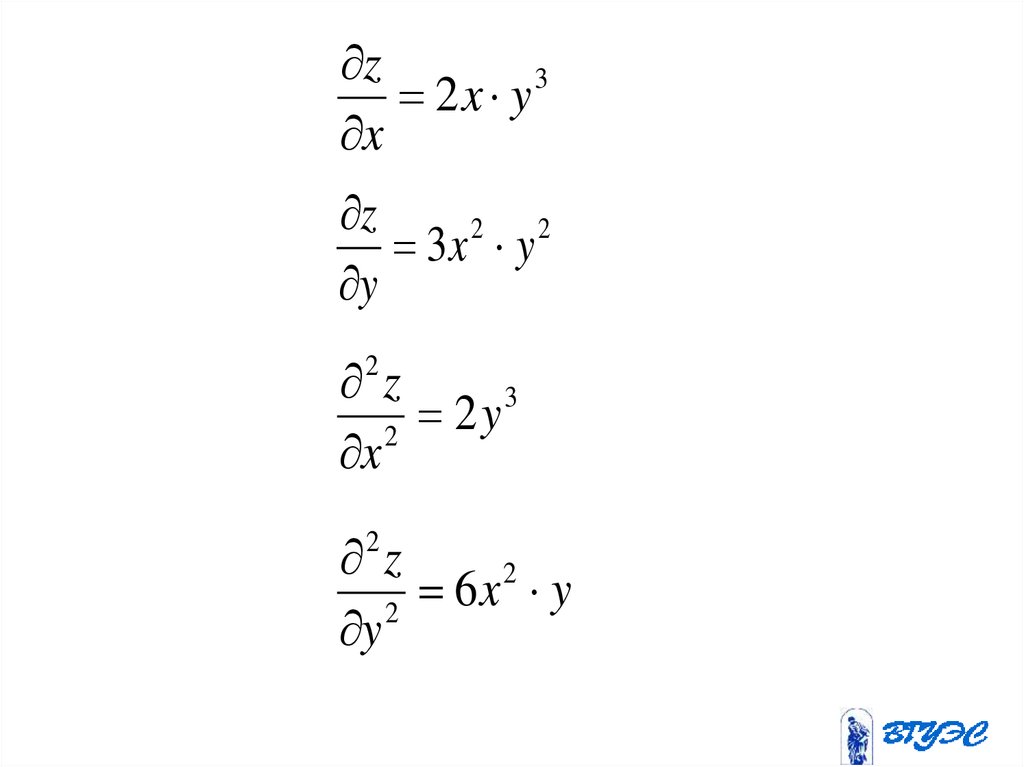
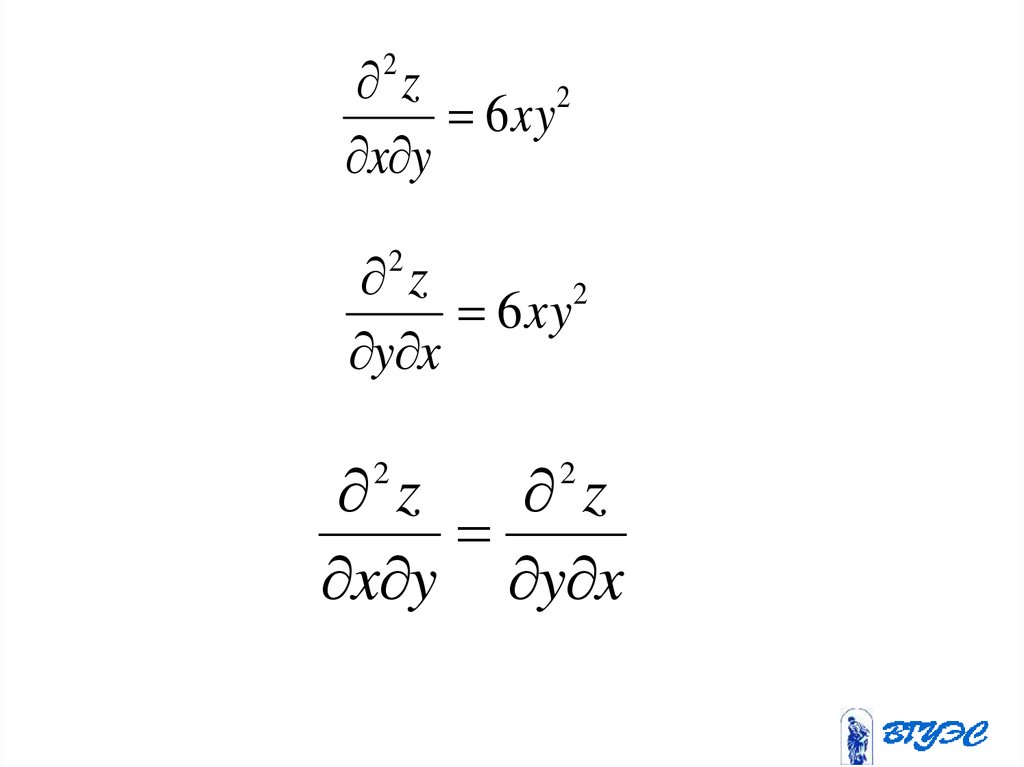













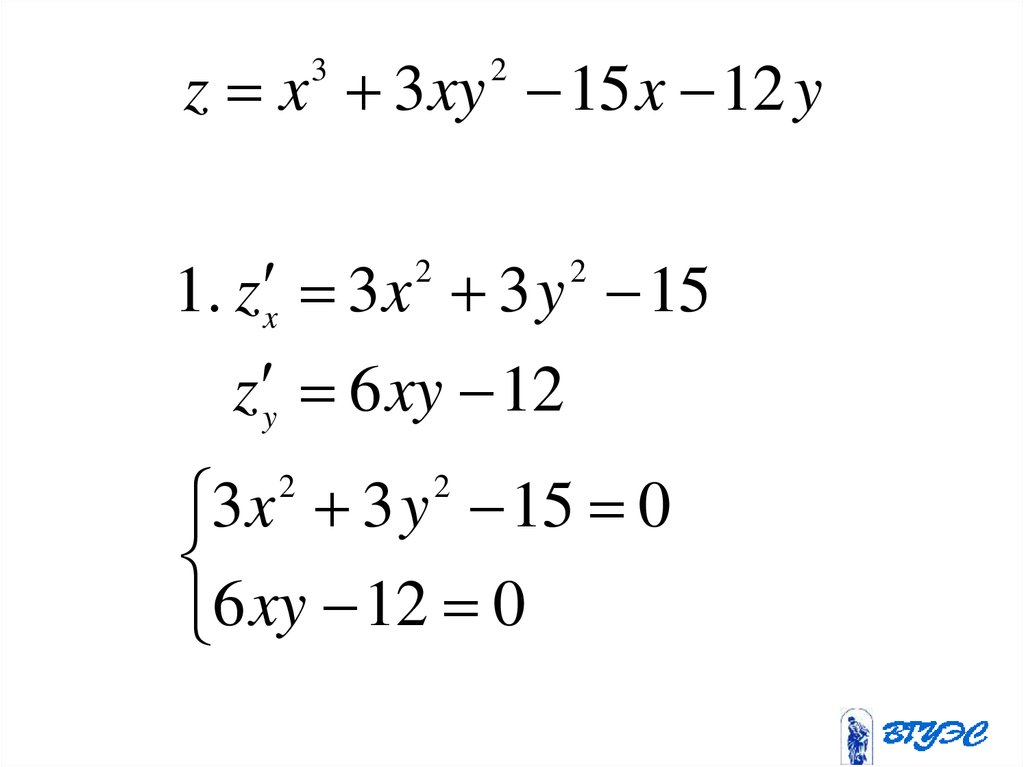



 mathematics
mathematics








