Similar presentations:
Частные производные функции нескольких переменных
1. Частные производные функции нескольких переменных.
z f ( x, y )x z f ( x x, y) f ( x, y)
y z f ( x, y y ) f ( x, y )
z f ( x x, y y ) f ( x, y )
z x ';
z
;
x
f x ';
f
x
2.
xzf ( x x, y ) f ( x, y )
z x ' lim
lim
x 0 x
x 0
x
yz
f ( x, y y) f ( x, y)
z y ' lim
lim
y 0 y
y 0
y
z x
y
z x 2y
2
1 2
z x tg (2 x 3 y )
2
3. Частные производные высших порядков
z f ( x, y )Т.е.
z x
z xx ( z x ) x ;
z xy ( z x ) y
z y
z yy ( z y ) y ;
z yx ( z y ) x
Замечание:
z
z xx 2 ;
x
2
D R
2
z xy z yx
z
z
z
z yy 2 ; z yx z xy
y
x y y x
2
2
2
4. Дифференциал функции нескольких переменных
Определение. Дифференциалом функциинескольких переменных называется сумма
произведений частных производных этой
функции на приращения соответствующих
независимых переменных, т.е.
dz z x x z y y
.
Учитывая, что для функций f ( x, y ) x и
,
g ( x, y ) y
выполнено x dx; y dy
имеем
dz z x dx z y dy
5. Градиент функции нескольких переменных
Определение. Градиентом функции zназываетсяf ( x, y )
вектор с координатами
Обозначается
Пример.
z ( z х ; z y ).
z ( x 2) 2 ( y 3) 2
( z х ; z y ).
6. Экстремум функции нескольких переменных.
Определение. Пусть функция z=f (x; y)определена на множестве D R2. Точка
M(x0;y0) называется точкой максимума
(минимума) функции z=f(x;y) , если
существует окрестность точки М такая, что
для каждой точки (x; y) отличной от (x0; y0) из
этой окрестности выполняется неравенство:
f ( x0 , y0 ) f ( x, y)
f ( x0 , y0 ) f ( x, y)
7.
zМ ( x0 , y0 )
точка минимума,
z ( x0 , y0 ) z ( x, y)
М
y
x
(x,y)
(x0,y0)
Теорема. (необходимое условие экстремума).
f x ( x0 , y0 ) 0
f y ( x0 , y 0 ) 0
8.
Замечание:Точки, в которых выполнены необходимые
условия экстремума функции
z=f (x; y), т.е.
z x 0
z y 0
называются критическими или стационарными.
9.
Пример.z xy
z x y
z y x
y 0
x 0
(0,0) критическая
точка.
z(0,0)=0,
но существует точка (1, 1) такая, что
z( 1, 1)= 1<z(0,0);
или точка (2,3) такая, что z(2,3)=6>z(0,0).
Следовательно,
необходимого
условия
недостаточно, для того чтобы сказать, что
критическая точка является экстремумом.
10.
Пример.z
N
x
y
11. Теорема. (достаточное условие экстремума функции 2-х переменных).
Пусть функцияz f ( x, y )
а) определена в некоторой окрестности
критической точки (x0;y0), в которой частные
производные равны нулю, т.е.
f ( x , y ) 0
x 0 0
f y ( x0 , y 0 ) 0
б) имеет в этой точке непрерывные частные
производные второго порядка такие, что
f xx ( x0 , y0 ) A,
f xy ( x0 , y0 ) f yx ( x0 , y0 ) B,
f yy ( x0 , y0 ) C
12.
Тогда:1) если выражение AC B 0
2
то в точке (x0;y0) существует экстремум, причем
если
AC B 2 0 и А>0, то это min,
если
AC B 0 и А<0, то это max,
2
2) если AC B2 0,
то экстремума в точке (x0;y0) нет;
3) если
AC B2 0,
то вопрос об экстремуме остается открытым
(нужны дополнительные исследования).
13. Схема исследования функции на экстремум
1. Определить область определения функцииz f ( x, y)
z x 0
2. Найти z x и z у и решить систему
z y 0
Найти критические точки.
3. Найти частные производные второго порядка.
Для каждой критической точки вычислить
A, B, C , AC B
2
С помощью достаточного условия сделать вывод
о наличии экстремумов.
4. Найти значение функции в точках экстремума.
14.
23
4
z
3
x
y
x
y
Пример.
2
D
(
z
)
R
1.
2
z
6
xy
3
x
2. x
3x(2 y x) 0
2
3
2
3
3
x
4
y
0
z y 3x 4 y
3x 0
2 y x 0
или
2
2
3
3
3
x
4
y
0
3
x
4
y
0
x 0
y 0
Таким образом
M1 (0;0),
x 2 y
2
3
3
4
y
4
y
0
4 y 2 (3 y ) 0
y 0
y 3
или
x
0
x 6
M 2 (6;3) критические точки.
15.
3. z xx 6 y 6 x;z xy 6 x
z yy 12y 2
Для точки M 1 (0;0) :
A 0, B 0, C 0, AC B 0
Следовательно, нужны дополнительные
исследования.
2
Для точки M 2 (6;3) :
A 18, B 36, C 108, AC B 2 648 0
0,
A 0
Следовательно, точка M 2 (6;3) :
является точкой максимума.
4.
z max (6;3) 27
16.
Условный экстремум функции несколькихпеременных.
min
17.
Определение. Точка (x0; y0) называется точкойусловного максимума (минимума) функции z=f (x;y),
если существует такая окрестность этой точки, что
для всех точек (x; y) из этой окрестности и
удовлетворяющих условию g(x,y)=0 выполняется
неравенство:
f ( x0 , y0 ) f ( x, y)
f ( x0 , y0 ) f ( x, y)
1 способ. (Сведение задачи на условный экстремум к
задаче отыскания экстремума функции одной
переменной).
18.
1 способ.Пример.
z xy
x y 1
2 способ. Метод Лагранжа.
Строим функцию Лагранжа:
L ( x, y , ) f ( x, y ) g ( x, y )
Lx ( x, y, ) f x ( x, y ) g x ( x, y ) 0
L y ( x, y, ) f y ( x, y ) g y ( x, y ) 0
L ( x, y, ) g ( x, y ) 0
19.
Пример 1.z xy
x y 1
Пример 2.
z xy
x2 y2 2

















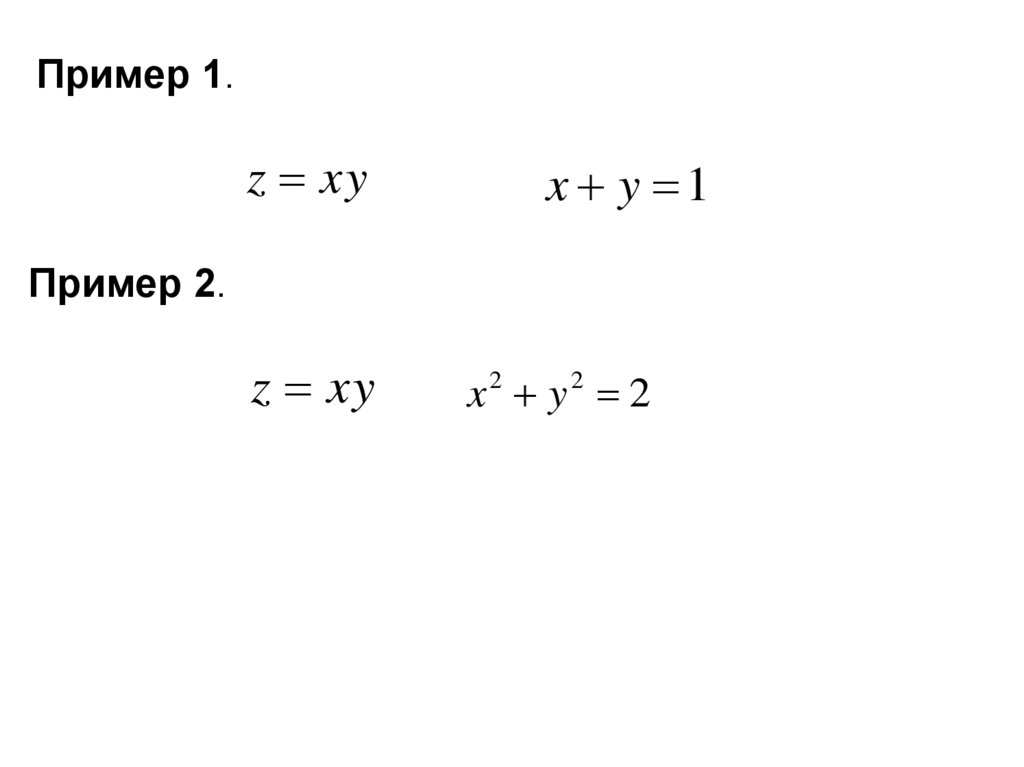
 mathematics
mathematics








