Similar presentations:
10. Дифференциал. Вычисление производных и дифференциалов функции
1.
• Ньютон – флюксия; Лейбниц – дифференциал.• differentia – разность
• Л. Эйлер (1707 – 1783) обозначение ∆
• Ж. Лагранж (1736 – 1813) обозначение у/
• Термин «производная (derivee)» в 1800г. в
книге фр. математика Л. Арбогаста.
• Процесс вычисления производной
называется дифференци́рованием.
• Функцию, имеющую конечную производную в
каждой точке интервала, называют
дифференцируемой в данном интервале.
1
2. Дифференциальное исчисление функций одной действительной переменной
10. Дифференциал.Вычисление производных и
дифференциалов функции.
3. Дифференцируемая функция
• Пусть функция y=f(x) определена и непрерывна внекоторой окрестности точки x0.
• Функция y=f(x) называется дифференцируемой в
точке x0, если её приращение можно записать в
виде ∆f(x0)=А∙∆х+о(∆х), где ∆х – приращение
независимой переменной, А – постоянная, не
зависящая от ∆х, о(∆х) – бесконечно малая
функция высшего порядка, чем ∆х. lim o( x) 0
x 0
x
• Дифференциалом функции y=f(x) в точке x0
(дифференциалом приращения ∆f(x)) называется
главная часть ее приращения в точке x0,
линейная относительно ∆x.
4. Определения дифференциала
• Дифференциалом функции y=f(x) в точке x0называется главная часть ее приращения в
точке x0, линейная относительно ∆x.
dy
df (x) df
y f ( x x) f ( x)
y A x o( x)
Линейная часть
приращения функции
dy A x
dy ( x0 )
y x
y 1 x
dy dx
dy x
dx x
dy A dx
4
5. Связь между непрерывностью и дифференцируемостью
• Еслифункция дифференцируема
в
Непрерывность
Дифференцируемость
некоторой точке, то она непрерывна в ней.
Дифференцируемость
Непрерывность
• Производная
непрерывной функции сама не
Непрерывность
Дифференцируемость
обязательно является непрерывной.
• Если функция имеет непрерывную
производную в некотором интервале, то она
называется гладкой.
5
6.
• Теорема. Для того чтобы функция у=f(x) быладифференцируема в точке x0, необходимо и
достаточно, чтобы в этой точке она имела
конечную производную:
y
f ( x0 ) lim
R
y( x0 ) A x o( x)
x 0 x
y
A x o( x)
f ( x0 ) lim
lim
A
x 0 x
x 0
x
y
y
f ( x0 ) lim
f ( x0 ) ( x)
x 0 x
x
y f ( x0 ) x ( x) x f ( x0 ) x o( x)
dy ( x0 ) f ( x0 )dx
dy f ( x)dx
6
7.
f ( x0 x) f ( x0 )f ( x0 ) lim
x 0
x
у
Функция f(x) имеет в
точке x0 бесконечную
производную.
у=f(x)
Δy
f ( x0 )
0
х0 Δх
х
Функция f(x) не
дифференцируема в
точке x0.
7
8.
f ( x0 x) f ( x0 )f ( x0 ) lim
x 0
x
у
Функция f(x) не имеет в
точке x0 производную.
Δх>0
у=f(x)
Δх<0
f ( x0 ) 0
f ( x0 ) 0
Δy
y0
0
Δх х0 Δх
х
Функция f(x) не
дифференцируема в
точке x0.
8
9. Вычисление производных
Правила дифференцирования9
10. Правила дифференцирования
• u=u(x), v=v(x) – дифференцируемые на (a; b)функции, с – const
u v u v
u v u v u v
u u v u v
2
v
v
c u c u
u u
с
с
10
11.
u v u v u vu ( x x) v( x x) u ( x) v( x)
(u v) lim
x 0
x
u ( x x) v( x x) u ( x) v( x x)
lim
x 0
x
u ( x) v( x x) u ( x) v( x)
lim
x 0
x
u ( x x) u ( x)
lim
v( x x)
x 0
x
v( x x) v( x)
lim
u ( x ) u v u v
x 0
x
11
12. Правила дифференцирования
d (u v) du dvd (u v) v du u dv
u v du u dv
d
2
v
v
d (u v) (u v) dx (u v u v )dx
u vdx u v dx vdu udv
12
13. Таблица производных
c 0 x nxn
a a ln a
e e
x
x
1
log a x
x ln a
sin x cos x
1
tgx 2
cos x
1
arcsin x
1 x2
x 1 x 2 x
n 1
x
x
1
ln x
x
cos x sin x
1
ctgx 2
sin x
1
arctgx
1 x2
1
1
1
2
x
x
sh x ch x
ch x sh x
cth x
1
sh 2 x
arccos x
1
1 x2
1
arcctgx
1 x2
14.
xf ( x) f ( x0 )
f ( x0 x) f ( x0 )
f ( x0 ) lim
lim
x x0
x 0
x x0
x
f ( x x) f ( x)
f ( x) lim
x 0
x
( x ) lim
x 0
x x x
( x x x )( x x x )
lim
x 0
x
x ( x x x )
1
x x x
1
lim
lim
x 0 x ( x x
x ) x 0 x x x 2 x
14
15.
sin xf ( x x) f ( x)
f ( x) lim
x 0
x
sin( x x) sin x
(sin x) lim
x 0
x
x x x
x x x
x
2 x x
2 sin
cos
2 sin
cos
2
2
2
2
lim
lim
x 0
x 0
x
x
x
2
2x
2
lim
cos
cos x
x 0 x
2
15
16. Вычисление дифференциала
y=f(x)df(x)
с, с – const
0 dx=0
x
xn
dx
nxn-1dx
ax
axlna dx
sinx
cosx dx
tg x
dx
cos 2 x
arcsinx
dx
1 x2
d (cos x) (cos x) dx
sin x dx
dx
d (ln x)
x
dx
d (arctgx)
1 x2
d (chx) shx dx
dx
d (cthx) 2
sh x
16
17. Производная сложной функции.
• Если функции y=f(u) и u=g(x) имеютпроизводные в точках u0=g(x0) и x0
соответственно, то сложная функция y=f(g(x))
имеет производную в точке x0, которая
находится по формуле: y x yu u x
y f (u ( x)) f u u x
y
y u
y
u
y ( x) lim
lim
lim
lim
x 0 x
x 0 u x
u 0 u x 0 x
( x 0 )
17
18. Дифференциал сложной функции
• Пусть функции y=f(u) и u=g(x) –дифференцируемые функции, y=f(g(x)) – сложная
функция
y x yu u x
y x dx yu u x dx
dy y x dx
dy yu du
dy y dx
dx x
du u
Первый дифференциал сложной функции обладает
свойством инвариантности (неизменности) формы.
18










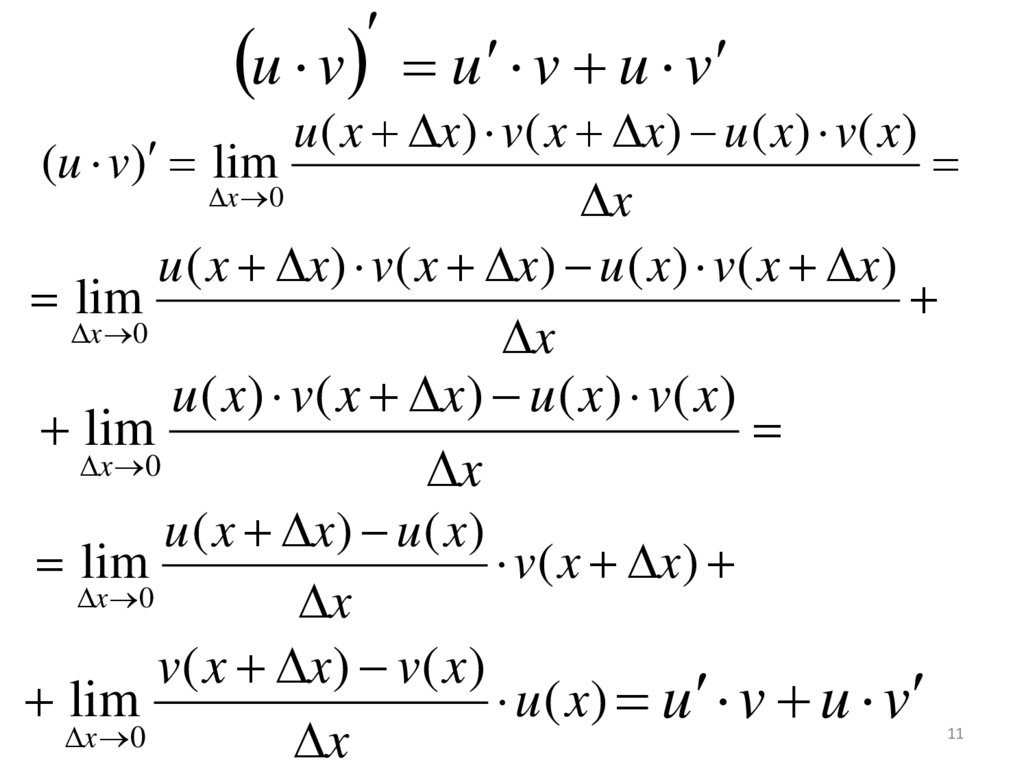
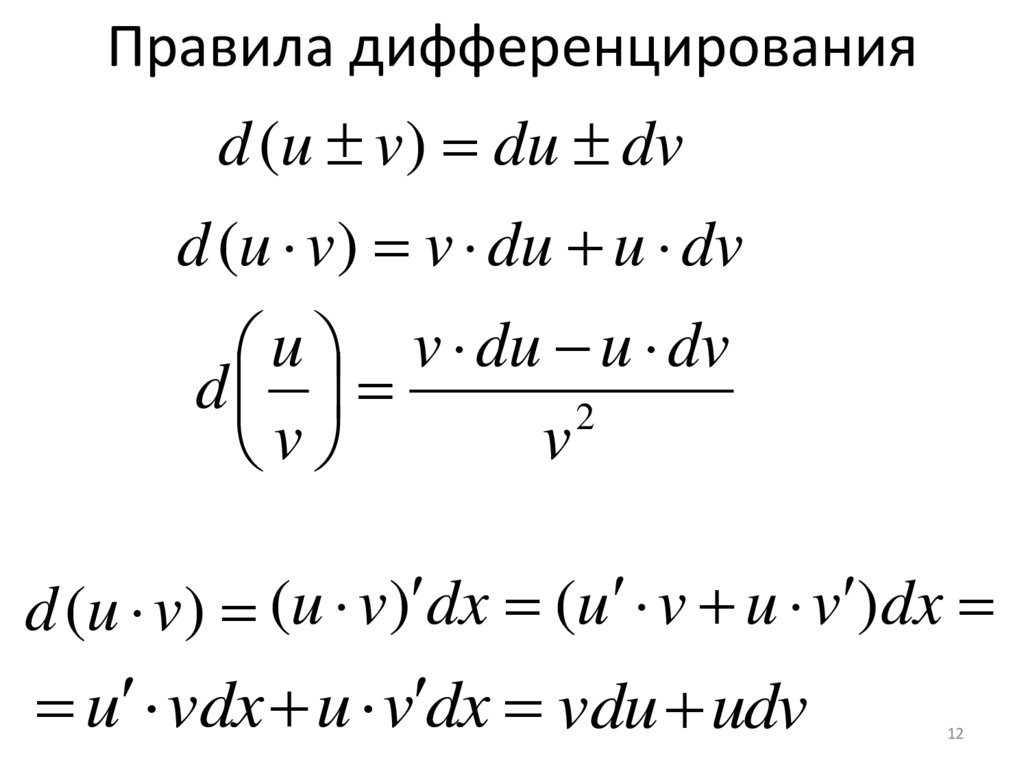






 mathematics
mathematics








