Similar presentations:
Понятие производной. Дифференциал функции. Использование дифференциала в приближенных вычислениях
1. Понятие производной. Дифференциал функции. Использование дифференциала в приближенных вычислениях.
Лекция22. План лекции:
Понятие производнойПравила дифференцирования, производная
сложной функции
Таблица производных от основных функций
Понятие дифференциала. Частные
производные. Полный дифференциал
Использование дифференциала в
приближенных вычислениях
3. Понятие производной
Производной функции f(x) называетсяпредел
отношения
приращения
функции к приращению аргумента при
стремлении последнего к нулю, т.е.
y
y lim
x 0 x
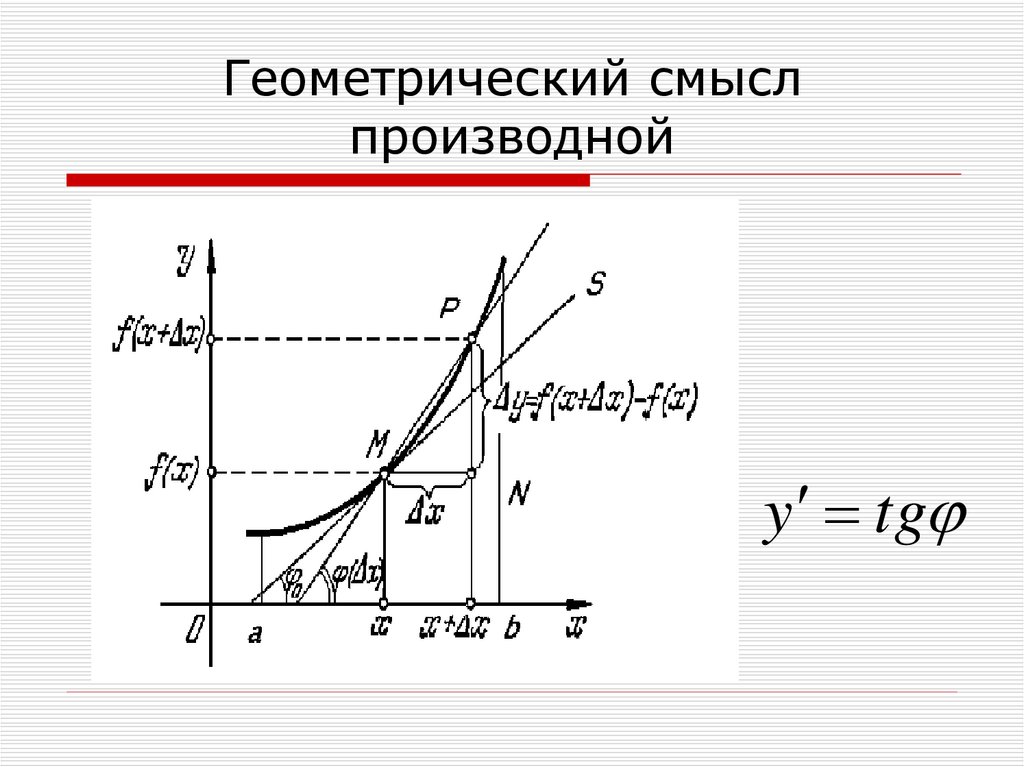
4. Геометрический смысл производной
y tg5. Правила дифференцирования производная сложной функции
(U V ) U V(U V ) U V V U
С 0
(С U ) C U
U U V V U
2
V
V
у f z ( x )
y f z z x
6. Таблица производных от основных функций
Функцияxn
ax
Производная
n∙xn–1
ax∙lna
ex
logax
ex
lnx
sin(x)
cos(x)
1
x ln a
1
x
cos(x)
– sin(x)
7. Исследование функций с помощью производных
Значения аргумента, при котором производнаяравна 0, называются стационарными точками.
Стационарные точки и точки, в которых
производная не существуют – критические
точки.
На интервале положительности производной
функция возрастает, а на интервале
отрицательности – убывает.
8. Исследование функций с помощью производных
В критической точке, отделяющей интервалвозрастания от интервала убывания,
функция имеет максимум (производная
меняет знак с плюса на минус).
В критической точке, отделяющей интервал
убывания от интервала возрастания ,
функция имеет минимум (производная
меняет знак с минуса на плюс ).
9. Задание: Найти интервалы монотонности и экстремумы функции
Дана функцияx2
y
x 2
Функция не определена при х=2
х 2 4 х х( х 4)
у
2
( х 2)
( х 2) 2
/
у / 0, х1 0; х2 4
х
у
у/
(-∞,0)
+
0
умах=0
0
(0,2)
–
2
(2,4)
–
4
Уmin=8
0
(4,+ ∞)
+
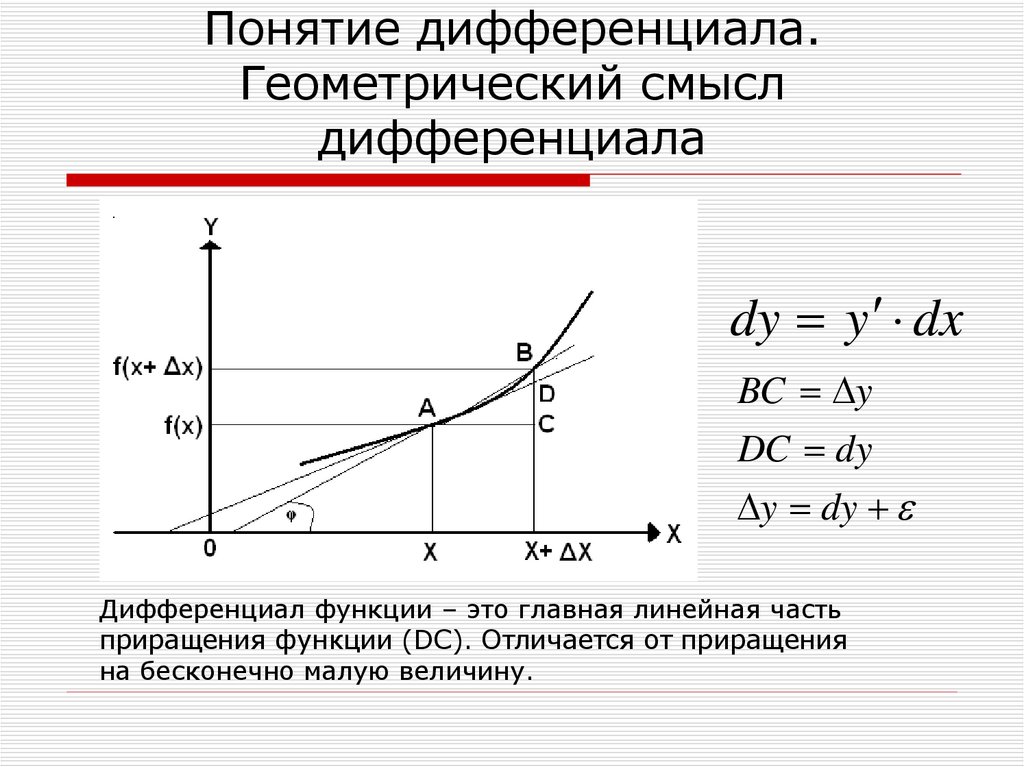
10. Понятие дифференциала. Геометрический смысл дифференциала
dy y dxBC y
DC dy
y dy
Дифференциал функции – это главная линейная часть
приращения функции (DC). Отличается от приращения
на бесконечно малую величину.
11. Использование дифференциала в приближенных вычислениях
Длянахождения
приближенного
значения приращения функции
y dy y dx
Для
нахождения
приближенного
значения функции в заданной точке
f ( x x ) f ( x ) f x dx
Для вычисления погрешностей
N абс dN ; N отн
dN абс
N










 mathematics
mathematics








