Функции нескольких переменных. Лекция 12

1.

Лекция 12
Функции нескольких переменных

2.

Функция n переменных.
Функция двух переменных.
Геометрический смысл функции двух переменных.
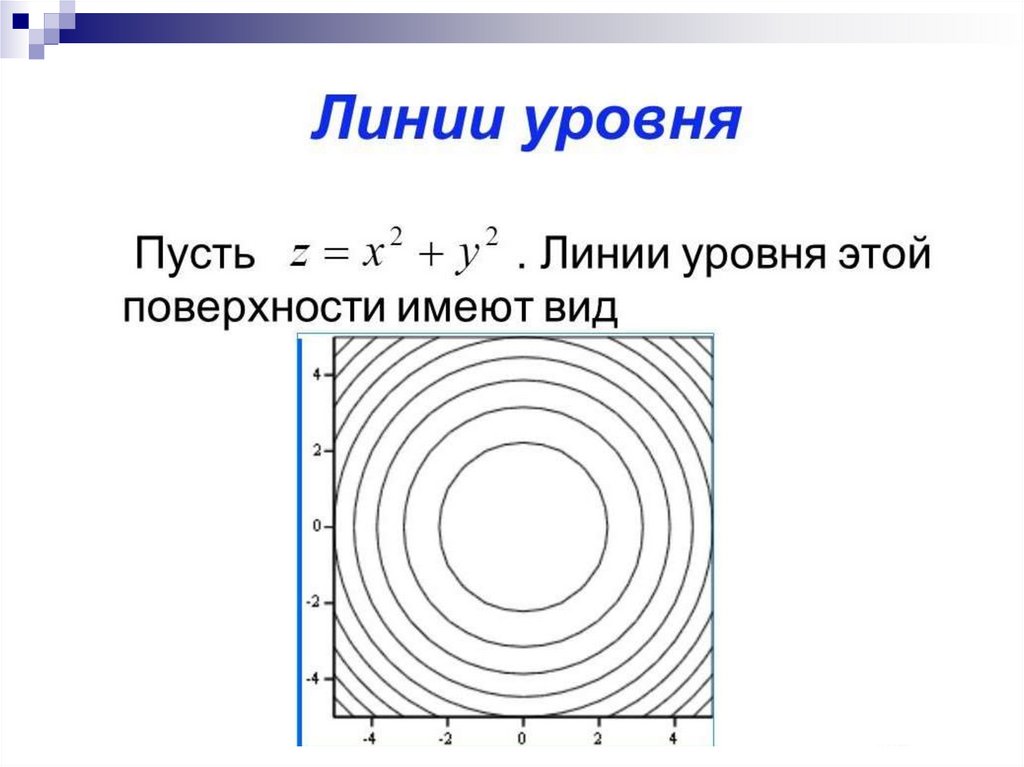
Поверхности и линии уровня.
Частные производные и их геометрический смысл.
Полный дифференциал

3. Функция n переменных

Переменная u называется функцией n переменных
(аргументов) x,y,z,…,t, если каждой системе значений
x,y,z,…,t, из области их изменений (области определения),
соответствует определенное значение u.
Областью определения функции называется
совокупность всех точек, в которых она имеет
определенные действительные значения.
Для функции двух переменных z=f(x,y) область
определения представляет некоторую совокупность точек
плоскости, а для функции трех переменных
u = f (x,y,z) –некоторую совокупность точек пространства.

4. Функция двух переменных

Функцией двух переменных называется закон,
по которому каждой паре значений независимых
переменных x,y (аргументов) из области
определения соответствует значение зависимой
переменной z (функции).
Данную функцию обозначают следующим образом:
z = z(x,y) либо z= f(x,y) ,
или же другой стандартной буквой: u=f(x,y) , u = u (x,y)

5.

Геометрический смысл функции 2-х
переменных
Если функции
одной переменной
соответствует
определённая линия на плоскости
(например,
– всем знакомая школьная
парабола), то график функции двух
переменных
располагается в
трёхмерном пространстве.
На практике чаще всего приходится иметь дело с
поверхностью, но иногда график функции может
представлять собой, например, пространственную прямую
(прямые) либо даже единственную точку.

6.

Областью определения функции двух
переменных
называется множество всех пар
, для которых
существует значение
.
Графически область определения представляет
собой всю плоскость
либо её часть.
Так, областью определения
функции
является вся координатная
плоскость
любой точки
– по той причине, что для
существует значение
.

7. Нахождение области определения функции двух переменных

При нахождении области определения обращаем
особое внимание на те функции, в которых есть
дроби, корни чётной степени, логарифмы и т. д.

8.

9.

10.

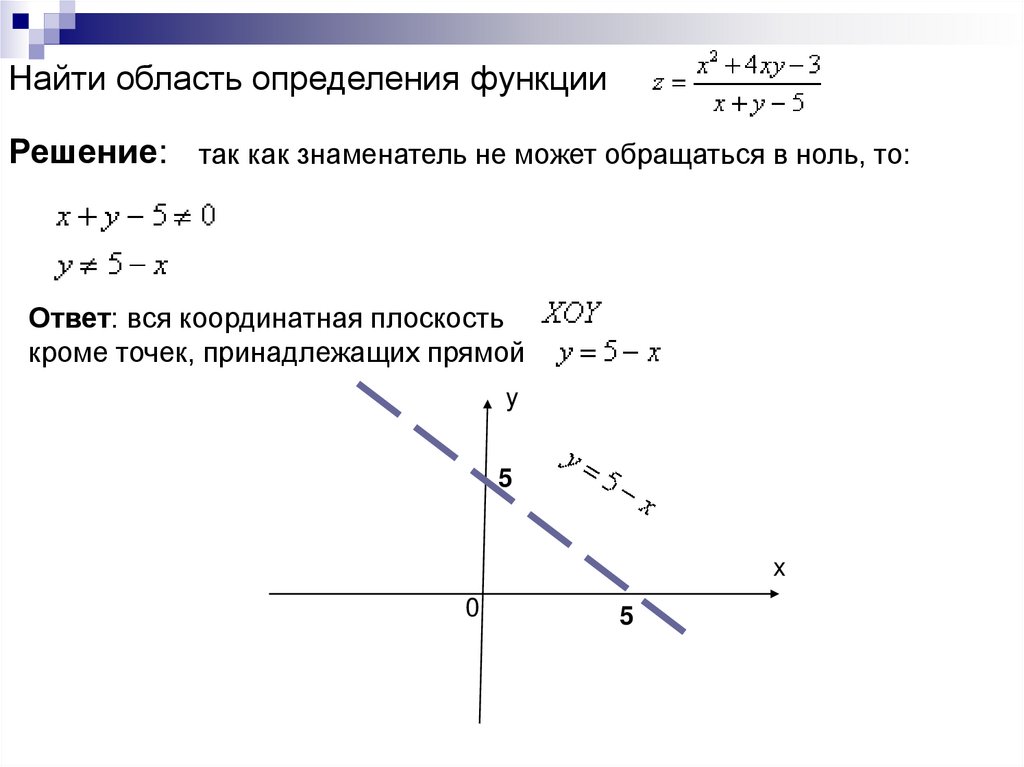
Найти область определения функции
Решение: так как знаменатель не может обращаться в ноль, то:
Ответ: вся координатная плоскость
кроме точек, принадлежащих прямой
y
5
x
0
5

11. Найти область определения функции 

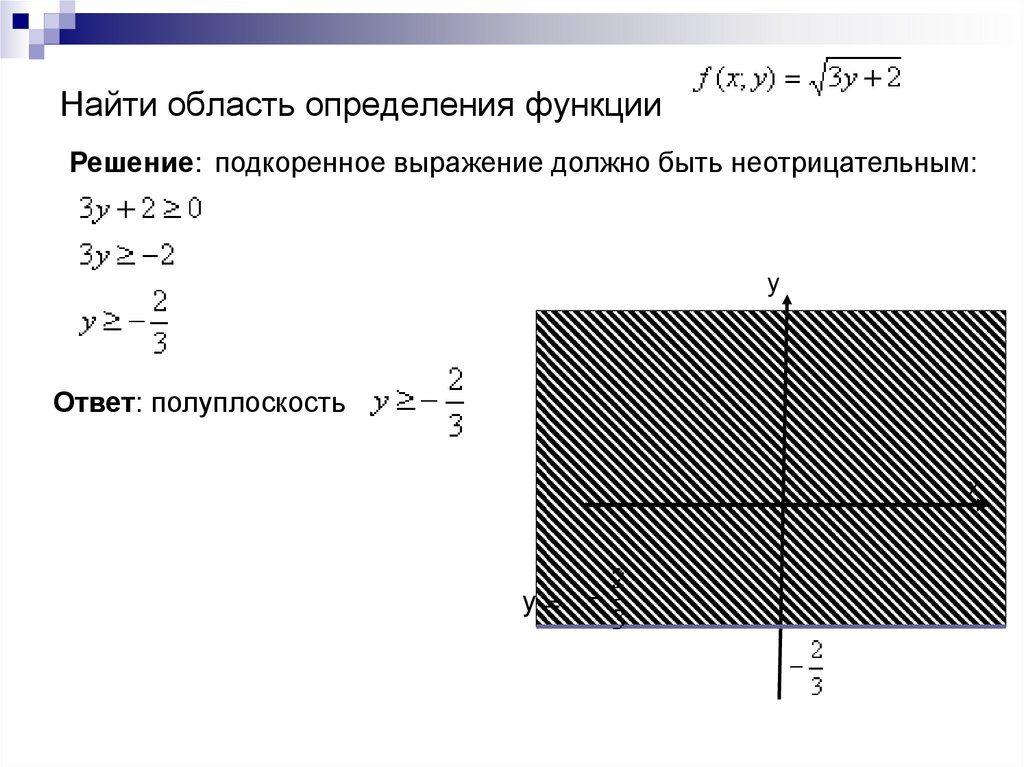
Найти область определения функции
Решение: подкоренное выражение должно быть неотрицательным:
у
Ответ: полуплоскость
x
y=

12. Найти область определения функции и изобразить её на чертеже

Решение: подкоренное выражением должно быть неотрицательным:
и, учитывая, что знаменатель не может обращаться в
ноль, неравенство становится строгим:
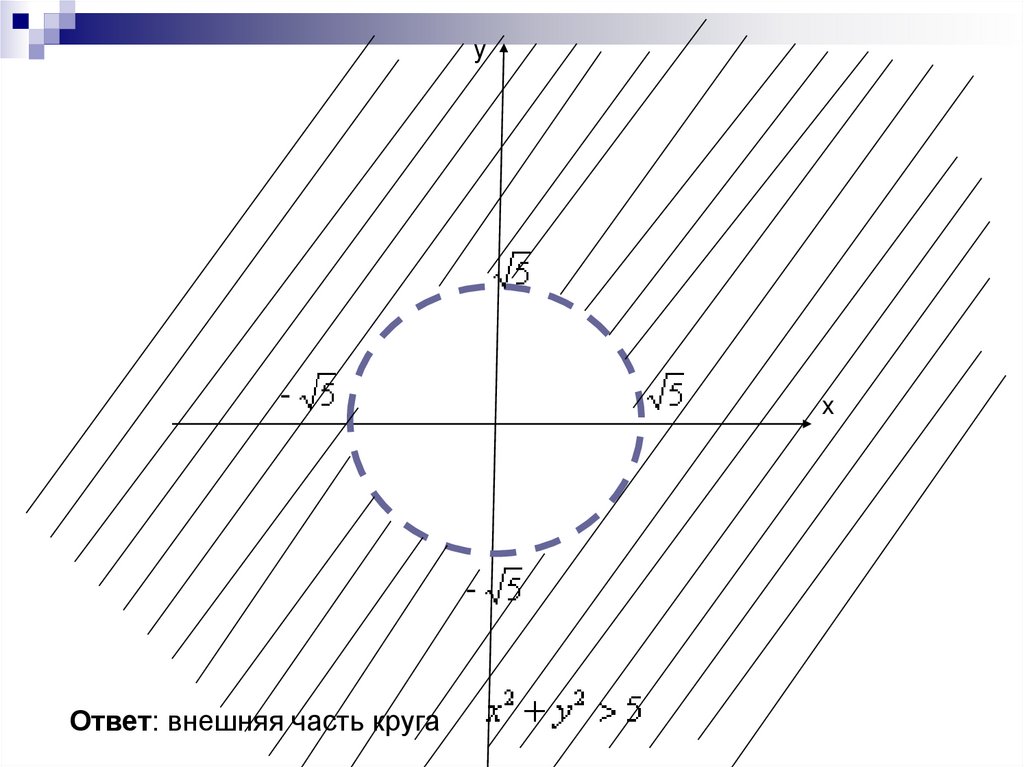
Уравнение
определяет окружность с
центром в начале координат радиуса
,
которая делит координатную плоскость на две части –
«внутренность» и «внешность» круга.
Так как неравенство у нас строгое, то сама окружность
заведомо не войдёт в область определения
и поэтому её нужно провести пунктиром.

13.

y
-
x
-
Ответ: внешняя часть круга

14. Частные производные, геометрический смысл

15. Частное приращение по одному из аргументов

Если одному из аргументов функции z = f(x,y) придать
приращение, а другой аргумент не изменять, то функция
получит частное приращение по одному из
аргументов:
– это частное приращение
функции z по аргументу x;
– это частное приращение
функции z по аргументу у.

16.

Частной производной функции нескольких
переменных по одному из её аргументов называется
предел отношения частного приращения функции по
этому аргументу к соответствующему приращению
аргумента при условии, что приращение аргумента
стремится к нулю:
– это частная производная функции z по
аргументу x;
– это частная производная функции z по
аргументу у.

17.

Чтобы вычислить частную производную ФНП по одному
из её аргументов, нужно все другие её аргументы считать
постоянными и проводить дифференцирование
по правилам дифференцирования
Частные производные функции двух переменных
вычисляются по тем же правилам, что и производные
функции одного переменного.
Пример. Найти частные производные функции z=x 2e x-2y
Решение.
Частные
производные
функции любого
числа переменных
определяются
аналогично

18. Геометрическая интерпретация частных производных функции двух переменных

Частная производная
от функции
в точке
равна тангенсу угла, составленного
осью
и касательной
к линии
в
, проведенной
.

19. Полное приращение функции 2-х переменных

Если обеим переменным дать приращение,
то функция получит полное приращение
z f ( x x, y y ) f ( x, y )

20. Определение дифференцируемой функции

Функция z f ( x, y ) называется
дифференцируемой в точке М(х,у), если ее
полное приращение можно представить в виде
z A x B y o( )
где Δx и Δy -произвольные приращения
аргументов
х и у в некоторой окрестности
точки М(х,у), А и В –постоянные, независящие
от Δx и Δy , o(ρ)-бесконечно малая более
2
2
x
y
высокого порядка, чем
-расстояние между М(х,у) и M 1 ( x x, y y )

21. Определение дифференциала

Главная линейная относительно Δx и
Δy часть полного приращения функции
z f ( x, y ) называется полным
дифференциалом этой функции и
обозначается dz или df(x,y) .
Таким образом, dz A x B .y

22. Формула для вычисления дифференциала

Если функция z f ( x, y ) дифференцируема
в точке М(х,у),то она имеет в этой точке частные
производные f x ( x, y ) и f y ( x, y ), причем
f y ( x, y ) =В .
f x ( x, y )
=А,
а
Таким образом,
dz f x ( x, y ) x f y ( x, y ) y
.
Если положить
x dx, y dy ,
dz f x ( x, y )dx f y ( x, y )dy
то