Similar presentations:
Дифференциал функции. Исследование функции с помощью производной
1.
Лекция N12Лектор: доц. Лаптева Надежда Александровна
Тема: Дифференциал функции.
Исследование функции
с помощью производной
2.
Дифференциал функцииРассмотрим функцию
Найдем y.
y x .
3
y x x x
3
3
x 3x x 3 x x x x
3
2
2
3
3
3x x 3x x x .
2
2
3.
Приращение функции можнорассматривать как сумму двух слагаемых:
3x x
2
- линейное относительно
3x x x
2
- нелинейное
относительно
x;
x.
4.
При x 0 оба слагаемых стремятся кнулю, но второе слагаемое быстрее
стремится к нулю. Поэтому при малых x
2
считают, что y 3x x (т.е. считают,
что y приближенно равно линейной
части). Эту часть называют главной
частью приращения функции или
дифференциалом.
Дифференциал функции y
обозначают dy.
f ( x)
5.
Теорема. Если функция y f ( x) имеетв точке x дифференциал, то она имеет в
этой точке производную и наоборот, если
функция y f ( x) имеет в точке x
производную, то она имеет в этой точке
дифференциал.
Выражение для дифференциала
записывается в форме
dy f ( x) dx.
6.
Примеры.Найти дифференциалы функций
1)
2)
y sin x. dy cos x dx.
y e .
3x
dy e
3x
dx
dy 3e dx.
3x
7.
Связь между дифференцируемостьюи непрерывностью функции
Теорема. Если функция y f ( x)
дифференцируема в точке x0 , то она
в этой точке непрерывна.
Обратная теорема неверна: существуют
непрерывные функции, которые в
некоторых точках не являются
дифференцируемыми.
8.
Пример.y
y x.
0
x
В точке x 0 функция
непрерывна, так как
f ( x) x
lim f ( x) lim x .
x 0
x 0
9.
x x, поэтомуy
lim
1.
x 0 x
Справа от нуля
Слева от нуля
x x, поэтому
y
lim
1.
x 0 x
10.
Таким образом, отношениеx 0
y
x
при
справа и слева имеет различные
пределы, а это значит, что при x 0
это отношение предела не имеет, т.е.
производная f ( x ) в точке x 0
не существует.
11.
Схема исследования функции1) Найти область определения функции
2) Исследовать функцию на четность и
нечетность
3) Найти точки пересечения с осями
координат
12.
4) Найти асимптоты кривой5) Исследовать функцию по знаку
первой производной y , т.е. найти
интервалы возрастания, убывания,
точки экстремума
13.
6) Исследовать функцию по знакувторой производной y , т.е. найти
интервалы выпуклости, вогнутости,
точки перегиба
7) Построить график. Для построения
графика можно все результаты
исследования свести в таблицу.
14.
Пример. Исследовать функцию ипостроить график:
3
2x
y 2 .
x 1
1) Область определения:
x 1 0; x 1.
2
15.
2) Чётность, нечётность.y ( x) четная, если y( x)
y ( x)
нечетная, если
y( x);
y( x) y( x).
2( x)
2 x
y ( x)
y
(
x
)
2
2
( x) 1 x 1
3
3
функция нечетная, следовательно
график функции симметричен
относительно начала координат.
16.
3) Точки пересечения с осями координатx 0 y 0. O(0,0).
4) Асимптоты – это прямые, к которым
стремится график функции при
неограниченном удалении от начала
координат.
17.
Асимптоты бывают:a) вертикальные. Они параллельны оси Oy.
Уравнение вертикальной асимптоты x a.
b) наклонные. Уравнение
где
y kx b,
y ( x)
y ( x) kx .
k lim
, b lim
x
x
x
18.
c) если k 0, то y b и наклоннаяасимптота становится горизонтальной,
т.е. параллельной оси Ox.
3
Найдем асимптоты кривой
3
2x
y 2 .
x 1
2
x
Т.к. lim
,
x 1 x 2 1
то x 1 - вертикальная асимптота.
19.
Аналогично,x 1 - вертикальная асимптота.
Заметим, что кривая может иметь сколько
угодно вертикальных асимптот.
Пример. y
ctg x.
Вертикальные асимптоты
x k,
где
k Z.
20.
Найдем наклонную асимптоту3
y kx b.
2
2x
2x
k lim 2
lim 2
x x 1 x
x x 1
2
lim
2.
x
1
1 2
x
k 2.
21.
2xb lim 2
2x
x x 1
3
2
2 x 2 x x 1
lim
2
x
x 1
3
3
2x 2x 2x
lim
2
x
x 1
3
22.
2x
0
2x
0.
lim 2
lim
x
x x 1
1
1 2
x
0
b 0.
y 2 x - наклонная асимптота.
23.
y .3
x
y 2 2
x 1
Найдем
3x ( x 1) 2 x x
2
2
2
( x 1)
4
2
2
2
x 3x
x ( x 3)
2 2
2 2
.
2
2
( x 1)
( x 1)
2
2
3
24.
y 0 x1 0; x2,3 3.-
+
3
0
+
3
x
M 1 ( 3; 3 3)
- точка максимума.
M 2 ( 3;3 3)
- точка минимума.
25.
Можно было не рассматривать x 0,т.е. функция нечетная и
достаточно построить график
только для x 0, а затем
отобразить график симметрично
относительно начала координат.
26.
Найдемy .
x 3x
y 2 2
2
( x 1)
4
2
(4 x 6 x)( x 1) 2( x 1)2 x( x 3 x )
2
2
4
( x 1)
3
2
2
2
4
2
27.
4 x 4 x 6 x 6 x 4 x 12 x2
2
3
( x 1)
5
3
3
5
2x 6x
x 3x
2 2
4
3
2
3
( x 1)
( x 1)
2
x( x 3)
4 2
.
3
( x 1)
3
3
3
28.
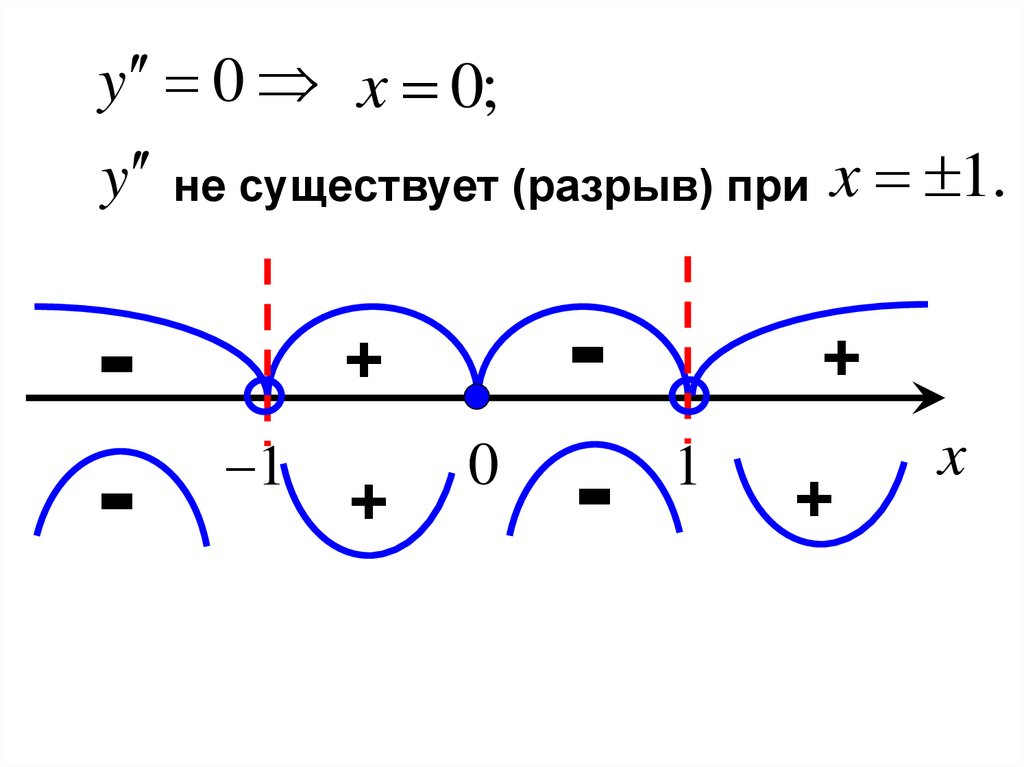
y 0 x 0;y не существует (разрыв) при x 1.
-
+
1
+
0
-
+
1
+
x
29.
Еслиy 0,
то функция вогнута.
+
Если
y 0,
-
то функция выпукла.
P
+
30.
Точки, в которых выпуклость меняетсяна вогнутость или наоборот,
называются точками перегиба.
P(0;0)
- точка перегиба.
7) Для построения графика сделаем
сводную таблицу. Т.к. функция
нечетная, то будем рассматривать
только x 0.
31.
xy
y
y
0 (0;1) 1 (1; 3) 3 ( 3; )
0
0
+
0
+
+
0
3 3
-
-
32.
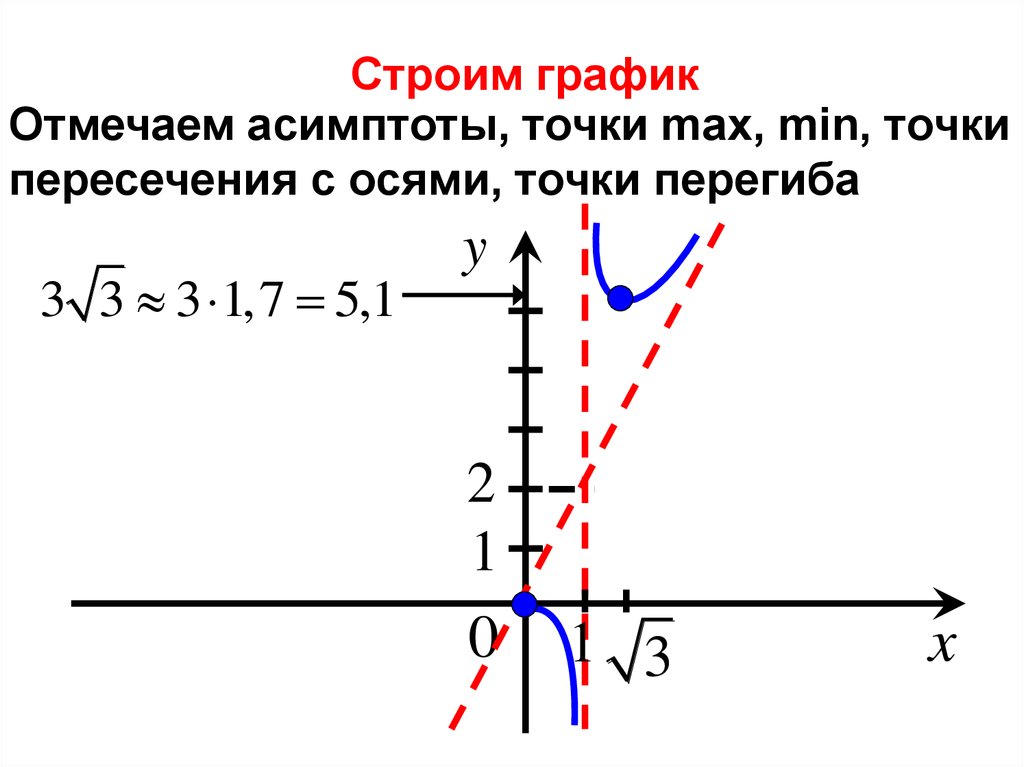
Строим графикОтмечаем асимптоты, точки max, min, точки
пересечения с осями, точки перегиба
3 3 3 1,7 5,1
y
2
1
0
1 3
x
33.
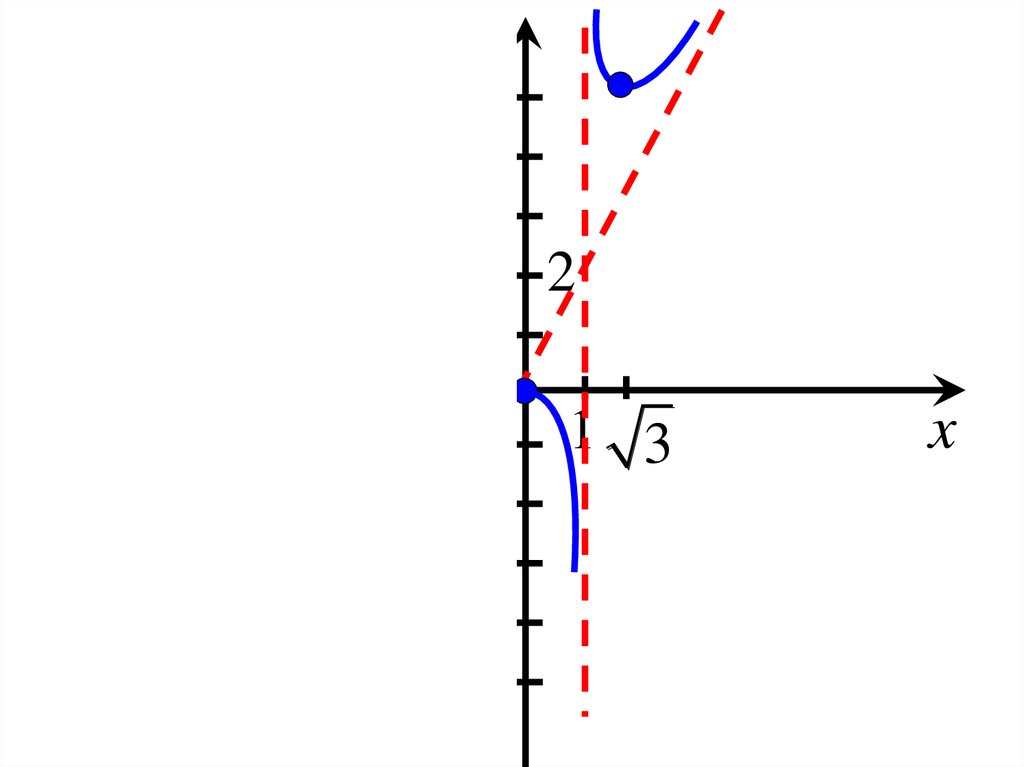
Для x 0 строим график, используянечетность функции.
34.
y2
0
1 3
x








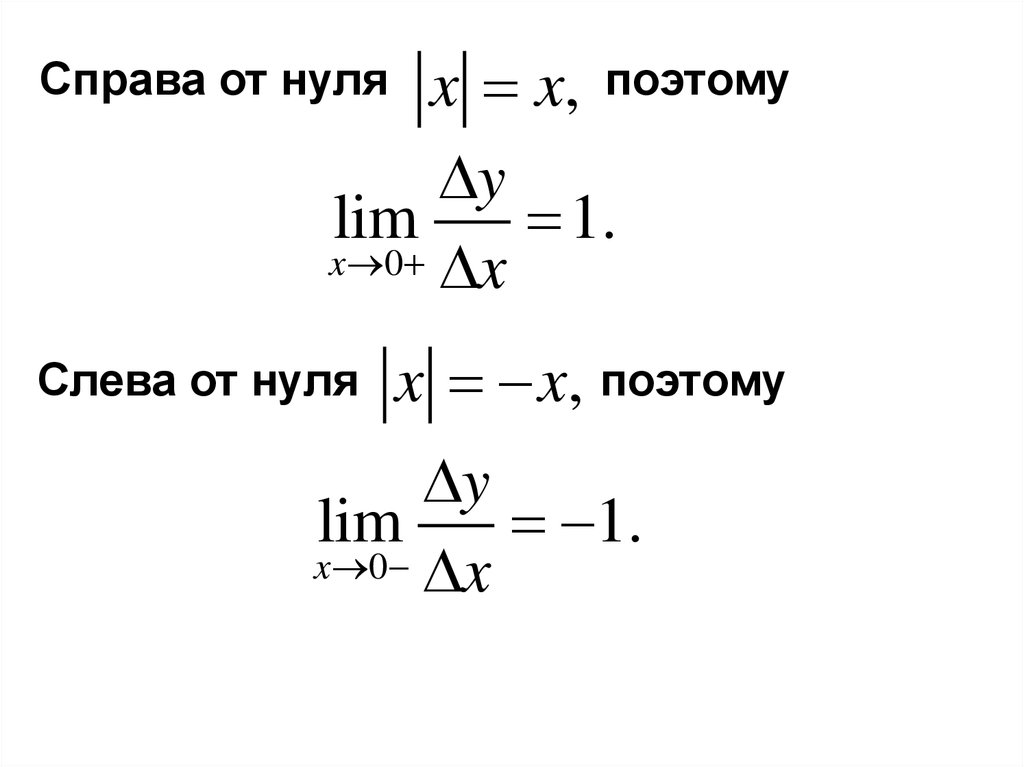






















 mathematics
mathematics








