Практика. Примеры решения задач по темам: предел функции, вычисление производных, исследование функции

1. Практика. Примеры решения задач по темам

1.
Вычисление предела функции
2. Вычисление производных
3. Исследование функции
1

2.

1. Предел функции
Приведены примеры решения следующих классов
задач
1.1. Предел дробно-рациональной функции
1.2. Предел сложной функции
1.3. Второй замечательный предел
1.4. Первый замечательный предел
2

3. 1. Предел функции. Теоретические сведения

Предел – величина А, к которой сколь угодно близко стремится
некоторый процесс. В математическом анализе это – предел
функции в бесконечности, предел функции в точке.
Основные обозначения:
- Предел функции в бесконечности
или
lim f ( x) A
lim f ( x ) A
x
x
-
Предел функции в точке х0 :
- слева, левосторонний
lim f ( x ) A
x x0 0
lim f ( x ) A
- справа, правосторонний
x x0 0
Условие непрерывности функции в точке
lim f ( x) lim f ( x) f ( x0 )
x x0 0
x x0 0
3

4. 1. Предел функции. Теоретические сведения.

В любом процессе значение предела, величина А, может равняться :
а)±∞ . А - бесконечно большая величина (ББВ). Процесс не ограничен
б)±0 . А - бесконечно малая величина (БМВ). Процесс ограничен
с)константе С. Процесс ограничен
Основные теоремы о пределах:
1).Функция не может иметь более одного предела
2).Предел алгебраической суммы функций равен алгебраической
сумме пределов этих функций
3). Предел произведения функций равен произведению их пределов
4). Предел частного от деления двух функций равен частному их
пределов, при условии, что предел делителя не равен нулю
5). Предел сложной функция f(U(x)), равен пределу f от предела U
lim
x x0 ( )
f (U ( x)) lim(lim f (U ( x ))
x
x
4

5.

1.1. Предел дробно-рациональной функции
an
,n m
bm
n
n 1
an x an 1 x a1 x a0
lim
0, n m
m
m
1
x b x b
b1 x b0
m
m 1 x
, n m
2
Примеры решения:
3x x 1 3
lim
3
2
x
1
x 1
3x x 1 3
lim
3
2
x
x 1
1
2
5

6.

1.1. Предел дробно-рациональной функции
an
,n m
bm
n
n 1
an x an 1 x a1 x a0
lim
0, n m
m
m
1
x b x b
b1 x b0
m
m 1 x
, n m
Примеры решения:
3x 3 x 1
3x 3 x 1
lim 2
lim 3x lim
lim 3x
2
x
x
x
x
x 1
x 1
3x 4 x 1
2
lim
lim
3
x
2
x
x
x 1
3x 2 x 1
3
lim
lim
0
x 2 x 3 x 2
x 2 x
6

7.

1.2. Предел сложной функции
правилу
f (u ( x )) вычисляется по
lim f (u ( x)) lim f (lim u ( x))
x
Примеры решения
а)
x
.
x
x
x
2x 1
2x 1
lim
lim lim
lim 2 x
x
x x
x
x 2
x 2
б)
x
x
2x 1
2x 1
x
lim
lim
lim
lim
2
0
x
x x
x
x 2
x 2
Решение данного класса задач основано на свойствах и графиках
функции ax при ограничениях (a 0); (a 0) (a 1) Рассматриваются
два диапазона значений а:
0 a 1; a 1
7

8.

1.2. Предел сложной функции
правилу
lim f (u ( x)) lim f (lim u ( x))
x
x
x
в)
x
x
вычисляется по
.
x
x 1
x 1
1
lim
lim
lim
lim
0
x 2 x 2
x x 2 x 2
x 2
x
г)
f (u ( x ))
x
x
x 1
x 1
1
lim
lim lim
lim
x 2 x 2
x x 2 x 2
x 2
Решение данного класса задач основано на свойствах и
графиках функции ax при ограничениях 0 a 1; a 1
Рассматриваются два диапазона значений а:
(a 0); (a 0) (a 1)
8

9.

1.3. Второй замечательный предел и его следствие
1 n
lim (1 ) e
n
n
а)
lim
x
lim (1
n
x
x 1
3
lim 1
x
x 2
x 2
a n
) e a
n
x
Вводим новую переменную t=x-2;x=t+2
x
x
3
x 1
3
lim
lim 1
lim 1
x x 2
x x 2 t t
t
t 2
2
3
3
3 3
3
lim 1 . lim 1 e .1 e
t
t t t
9

10.

1.3. Второй замечательный предел и его следствие
1 n
lim (1 ) e
n
n
б)
5
lim 1
x
x
1 3y
в) lim
y 0
2
y
3x
a n
lim(1 ) e a
n
n
3
5
lim lim 1 (e 5 ) 3 e15
x x
x
x
2
lim lim 1 3 y e 3
y 0 y 0
1
y
2
e 6
10

11.

1.4. Первый замечательный предел и его следствие
sin x
lim
1
x 0
x
tgx
lim
1
x 0
x
а)
sin 6 x
sin 6 x 6 x
sin 6 x 6 x
sin 6 x
6
lim 2 lim 2 lim
2 lim
lim 1
x 0 x
x 0 x
6 x x 0 6 x x x 0 6 x x 0 x
б)
1 cos x
x 0
x2
lim
x
2 x
2
1
cos
x
2
sin
Преобразуем числитель и знаменатель
; x 4
2
2
Тогда
2
2
x
x
2 sin 2
sin
1 cos x
2 lim 1
2 11 1
lim
lim
2
x 0
x 0
x 0 2
x
2
2
x2
x
4
2
2
11

12. 2. Вычисление производных

Производная функции в точке х=х0 -предел отношения приращения
функции у = f(х0+ х)-f(х0) к приращению аргумента х при х ->0
Обозначается производная функции f(х) в точке х0 символом f'(х0).
f ( x0 x ) f ( x0 )
f ( x0 ) lim
x 0
x
или
y ( x0 ),
dy
df
( x0 ), ( x0 ), y |x x0
dx
dx
Дифференциал функции dy=df= f'(x0) х =f'(x)dx
Геометрический смысл производной: тангенс угла касательной к
функции в точке х0 , тангенс угла , tg
Геометрический смысл дифференциала: первое линейное
приращение функции в точке х0 + х, отрезок KN
12

13. 2. Таблица производных.

1.
y c , y 0, c
3.
y a x , y a x ln a; y e x , y e x
4.
5.
постоянная;
2.
y x , y x 1
1
x ln a
y log a x, y
y sin x, y cos x
6.
y cos x, y sin x
Правила дифференцирования
1.
3.
5.
( cu ) c u
2.
(u v ) u v v u
y (u ( x ))
(u v ) u v
u v v u
4. u
v2
v
dy
dy du
y (u ) u ( x )
dx
du dx
13

14. 2.1. Вычислить первую и вторую производную, дифференциал функции

а)
y
Решение.
x
x2 1
y
1( x 2 1) x( 2 x)
x
2
1
2
dy y dx
x2 1
x
2
1
x2 1
x
2
1
2
2
dx
x 1
y y 2
2
x 1
2 x ( x 2 1)2 ( x 2 1)2( x 2 1) 2 x 3 4 x 2 2 x 4
4
3
2
2
x 1
x 1
2
14

15. 2.1. Вычислить первую и вторую производную, дифференциал функции

б)
1 ex
y
x
Решение.
(1 e x ) x (1 e x )( x) e x x (1 e x ) 1 e x ( x 1) 1
y
2
2
x
x
x2
e x ( x 1) 1
dy y dx
dx
2
x
x
x
e ( x 1) 1 e ( x 1) e x (e x ( x 1) 1)2 x e x 2 xe x 2 e x (2 x 1) 2
y y
2
4
3
3
x
x
x
x
15

16. 2.1. Вычислить первую и вторую производную, дифференциал функции

в)
y 3 x cos(1 x 2 )
Решение. Обозначим: f1(x)=3x; f2(x)= cos(1-x2)
Функция
f 2( x) cos(1 x 2 ) - сложная функция. Тогда
y (3x cos(1 x 2 )) 3 cos(1 x 2 ) 3x( sin(1 x 2 )( 2 x)
3(cos(1 x 2 ) 2 x 2 sin(1 x 2 ))
dy y dx 3 (cos(1 x 2 ) 2 x 2 sin(1 x 2 ))dx
y 3 (( sin(1 x 2 )( 2 x) 4 x(sin(1 x 2 ) 2 x 2 ( cos(1 x 2 )( 2 x))
16

17. 2.1. Вычислить первую и вторую производную, дифференциал функции

г)
y e x ln sin x
f 1( x) e x ; f 2( x) ln sin x
Решение. Обозначим
Тогда
1
y (e ) ln sin x e (ln sin x) e ln sin x e
( cos( x))
sin x
1
x
dy y dx e (ln sin x
cos( x ))dx
sin x
x
y (e x (ln sin x
x
x
x
1
cos x
1
cos( x))) e x (ln sin x ctgx) e x (
2 )
sin x
sin x sin x
17

18.

3. Исследование функции
Решение задачи исследования функции сводится к
выполнению следующих действий:
1. Определение точек разрыва, интервалов непрерывности,
области определения функции (ООФ)
2. Анализ на четность, нечетность, периодичность
3. Определение (если возможно) точек пересечения функции с
осями координат Х, У
4. Вычисление пределов – на границах ООФ, в точках разрыва
5. Определение точек экстремума и перегиба. Решение этой
задачи связано с вычислением и последующим анализом
поведения первой и второй производных функции
6. Построение графика функции
7. Определение области значений функции, ОЗФ
18

19.

3. 1. Исследование функции – примеры
а) Исследуемая функция
y x 2 (2 x 2 1)
- точек разрыва нет; вертикальных асимптот нет; ООФ=(-∞;∞)
- Четность: y(-1)=y(1) –функция четная
- Пределы функции:
lim( x 2 (2 x 2 1) . Функция четная
– На границах ООФ
x
– Левый и правый пределы в точках разрыва – нет
– Уравнение наклонной асимптоты
y
k lim( ) lim( x(2 x 2 1) Наклонной асимптоты нет
x x
x
–
– Точки пересечения графика с осями координат
y x 2 (2 x 2 1) 0
x01
1
0.707; x02 0; x03 0.707
2
19

20.

а) Исследуемая функция
y x 2 (2 x 2 1)
- Точки экстремумов и интервалы монотонности
y ( x 2 (2 x 2 1)) (2 x 4 x 2 ) 8 x 3 2 x 2 x(4 x 2 1) 0;
1
x 2 0; x1,3 0.5
2
- Точки перегиба, выпуклость, вогнутость
y 8 x 3 2 x; y y 24 x 2 2 2(12 x 2 1) 0
x 21 0.3; x 22 0.3
y 0.3 0 0; y 0.3 0 0; x 21 0.3 òî÷êà ïåðåãèáà
y 0 .3 0 0; y 0 .3 0 0; x 22 0.3 òî÷êà ïåðåãèáà
y ( 0.3) y (0.3) 0.074
Результат исследования представлен в таблице 3.1.а
20

21.

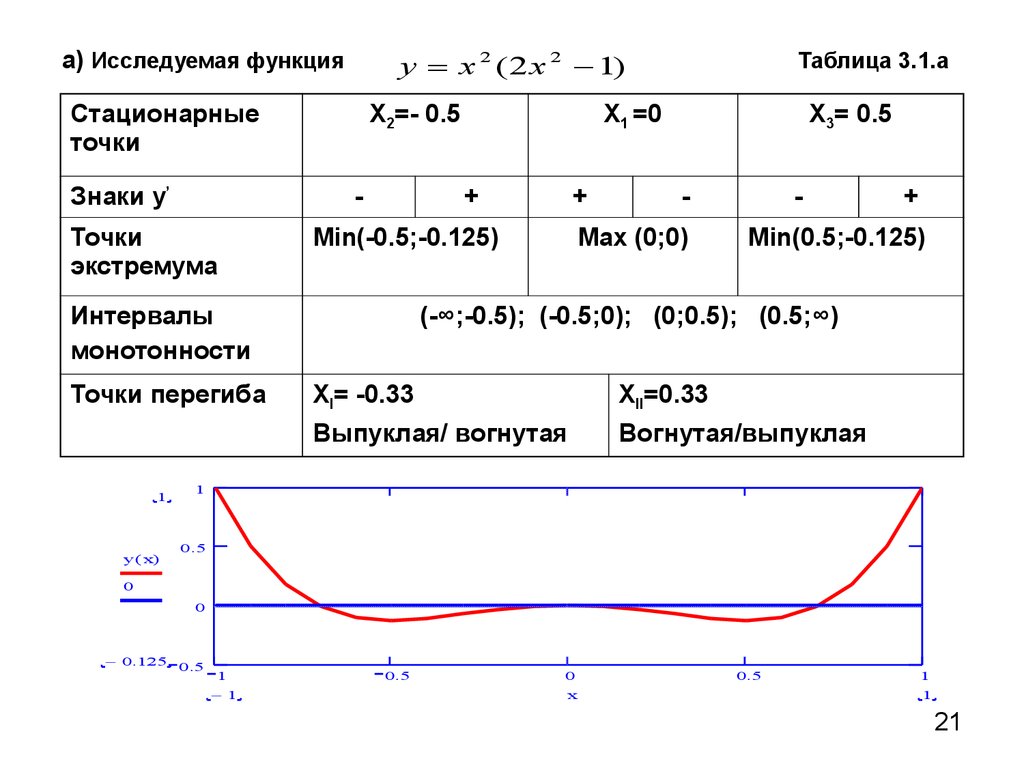
а) Исследуемая функция
y x 2 ( 2 x 2 1)
Стационарные
точки
Знаки y’
Х2=- 0.5
-
Точки
экстремума
Точки перегиба
1
y ( x)
Х1 =0
+
+
Min(-0.5;-0.125)
Интервалы
монотонности
Таблица 3.1.а
Х3= 0.5
-
Max (0;0)
-
+
Min(0.5;-0.125)
(-∞;-0.5); (-0.5;0); (0;0.5); (0.5;∞)
XI= -0.33
XII=0.33
Выпуклая/ вогнутая
Вогнутая/выпуклая
1
0.5
0
0
0.125 0.5
1
1
0.5
0
x
0.5
1
1
21