Similar presentations:
Исследование функции с помощью производной и построение графиков функций
1.
Тема. Исследование функции с помощьюпроизводной и построение графиков
функций.
2.
1.Возрастание и убывание функции.2. Максимум и минимум функции.
3.Наибольшее и наименьшее значения функции на отрезке.
4. Выпуклость графика функции. Точки перегиба.
5. Асимптоты графика функции и построение графика.
3.
1.Возрастание и убывание функции.Теорема 1. (достаточное условие возрастания функции)
Если производная дифференцируемой
функции положительна внутри
некоторого промежутка Х, то функция
возрастает на этом промежутке.
4.
Теорема 2. (достаточное условие убывания функции)Если производная дифференцируемой
функции отрицательна внутри
некоторого промежутка Х, то она
убывает на этом промежутке.
5.
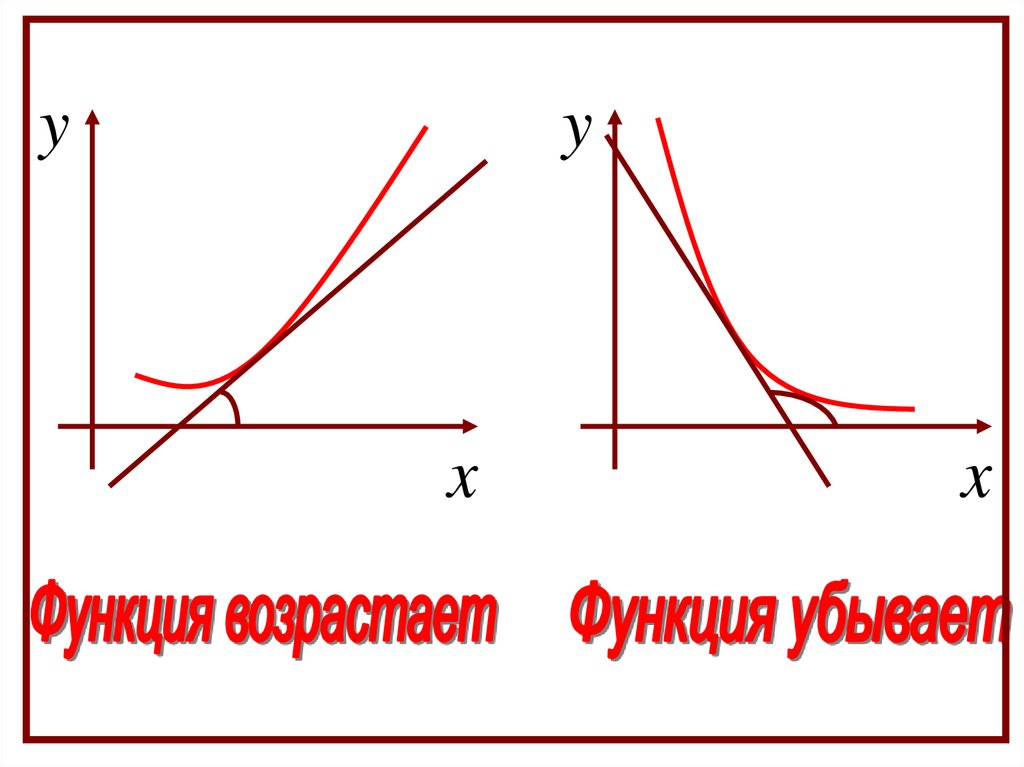
Если касательные к кривой на некоторомпромежутке направлены под острыми
углами к оси х, то функция возрастает.
если они направлены под тупыми углами,
то функция убывает.
6.
yy
x
x
7.
Найти интервалы монотонностифункции
y x 4x 3
2
8.
Найдем производную этой функции:y ( x 4x 3) 2x 4
2
Исследуем знак этой производной:
y 2 x 4 0 при
x 2
y 2 x 4 0
x 2
при
Следовательно, функция будет возрастать на
промежутке ( 2 ; )
Функция будет убывать на промежутке
( ; 2)
9.
2. Максимум и минимум функции.Точка х0 называется точкой максимума функции
f(x), если в некоторой окрестности точки х0
выполняется неравенство
f ( x) f ( x0 )
10.
Точка х1 называется точкой минимума функцииf(x), если в некоторой окрестности точки х1
выполняется неравенство
f ( x) f ( x1 )
Значения функции в точках х0 и х1
называются соответственно
максимумом и минимумом функции.
Максимум и минимум функции называется
экстремумом функции.
11.
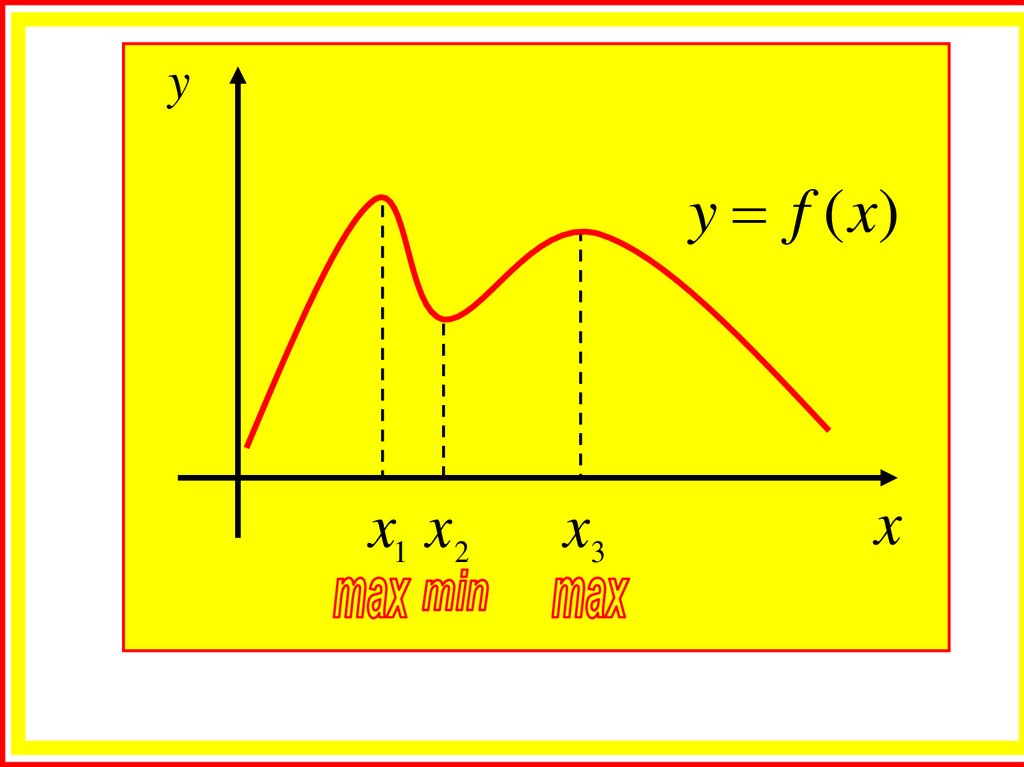
yy f (x)
x1 x2
x3
x
12.
На одном промежутке функция может иметь несколькоэкстремумов, причем может быть, что минимум в одной
точке больше максимума в другой.
Максимум или минимум функции на некотором
промежутке не являются в общем случае наибольшим и
наименьшим значением функции.
Если в некоторой точке х0 дифференцируемая функция f(x)
имеет экстремум, то в некоторой окрестности этой точки
выполняется теорема Ферма и производная функции в
этой точке равна нулю:
f ( x0 ) 0
13.
Однако, функция может иметь экстремум в точке, вкоторой она не дифференцируема.
Например, функция
y x
имеет минимум в точке
x 0
но она в этой точке не дифференцируема.
14.
Для того, чтобы функция y=f(x) имелаэкстремум в точке х0 , необходимо, чтобы
ее производная в этой точке равнялась
нулю или не существовала.
15.
Точки, в которых выполняется необходимоеусловие экстремума, называются
критическими или стационарными.
Т.об., если в какой-либо точке имеется экстремум, то эта
точка является критической.
Но критическая точка не обязательно является точкой
экстремума.
16.
Найти критические точки и экстремумыфункций:
1
y x
2
17.
Применим необходимое условие экстремума:y ( x ) 2 x
y 2 x 0 при x 0
2
x 0
y 0
- критическая точка
18.
yx 0
y x
2
x
19.
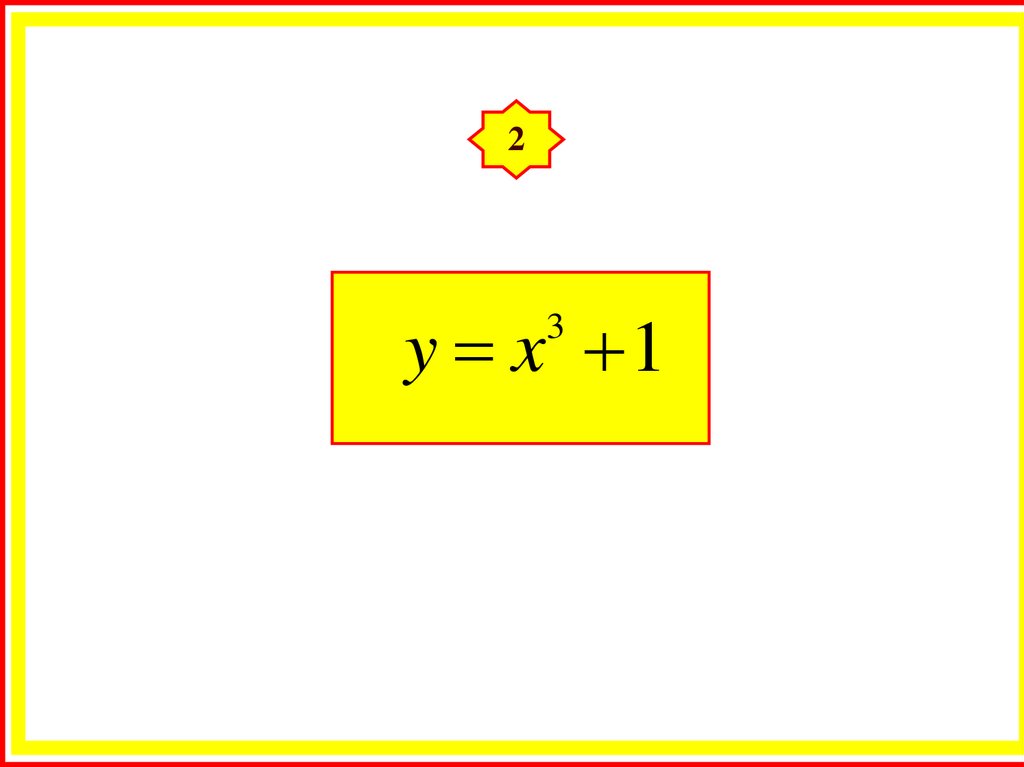
2y x 1
3
20.
Применим необходимое условие экстремума:y ( x 1) 3x
2
y 3x 0 при x 0
3
x 0
y 1
2
- критическая точка
21.
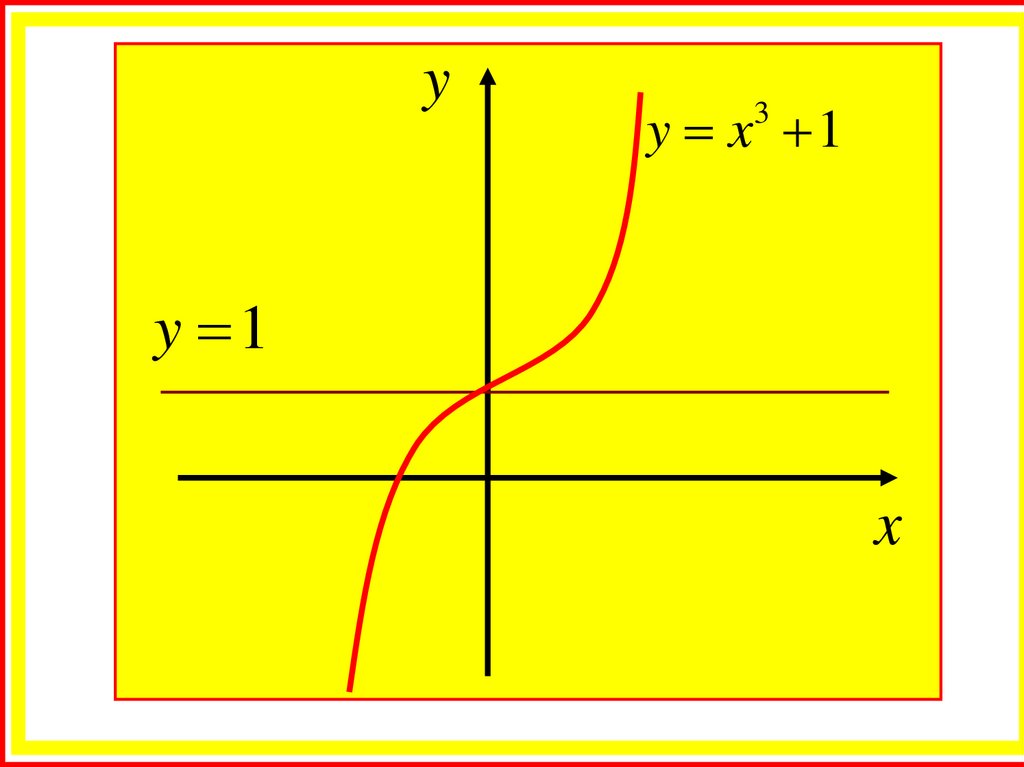
yy x 1
3
y 1
x
22.
Если при переходе через точку х0 производнаядифференцируемой функции y=f(x)меняет
знак с плюса на минус, то х0 есть точка
максимума, а если с минуса на плюс, то х0
есть точка минимума.
23.
1Найти производную функции
y f (x)
2
Найти критические точки функции, в
которых производная равна нулю или не
существует.
24.
3Исследовать знак производной слева и справа
от каждой критической точки.
4
Найти экстремум функции.
25.
Исследовать функцию на экстремум:y x( x 1)
3
26.
Применим схему исследования функции на экстремум:1
Находим производную функции:
y ( x( x 1) ) ( x 1) 3x ( x 1)
3
3
2
( x 1) ( x 1 3x) ( x 1) (4 x 1)
2
2
27.
2Находим критические точки:
( x 1) (4 x 1) 0
2
x1 1
1
x2
4
28.
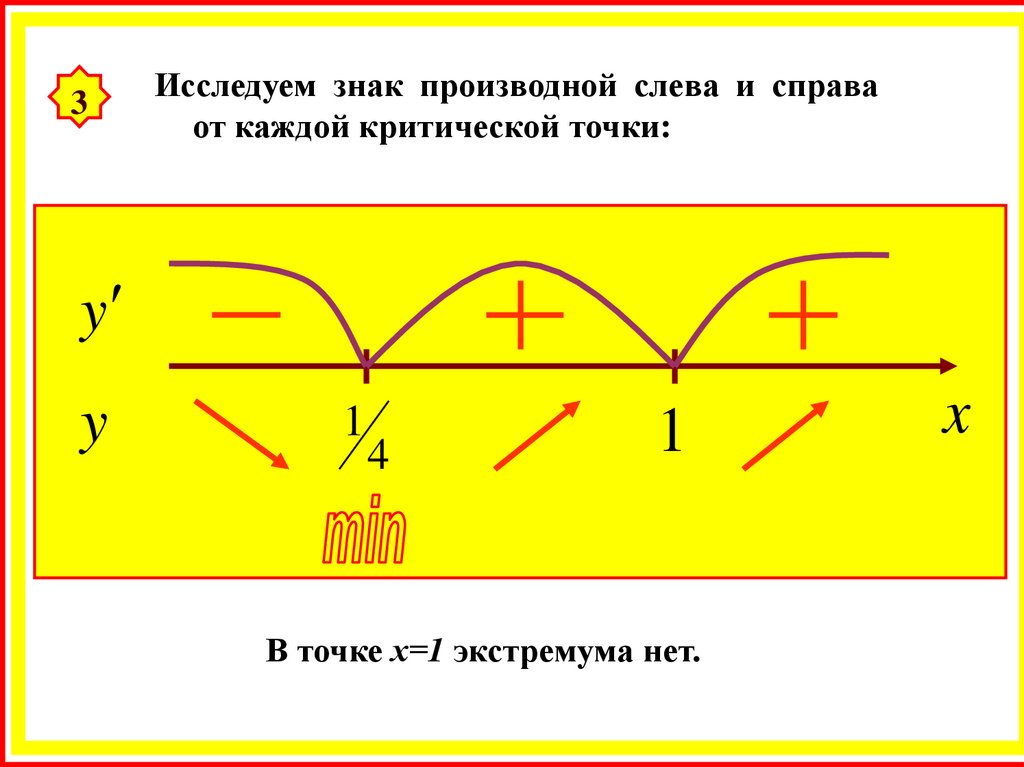
3Исследуем знак производной слева и справа
от каждой критической точки:
y
y
1
4
1
В точке х=1 экстремума нет.
x
29.
4Находим экстремум функции:
27
1
f min
256
4
30.
3.Наибольшее и наименьшее значения функции наотрезке.
Согласно теореме Вейерштрасса, если функция
непрерывна на отрезке [a;b], то она достигает
на нем наибольшего и наименьшего значений.
Эти значения могут быть достигнуты на концах
отрезка или в точках экстремума.
31.
1Найти производную функции.
32.
2Найти критические точки, в которых
производная равна нулю или не существует.
3
Найти значения функции в критических
точках и на концах отрезка, и выбрать из
них наибольшее и наименьшее значения.
33.
Найти наибольшее и наименьшеезначения функции
y ( x 2) e
2
на отрезке
0 ; 5
x
34.
1Находим производную функции:
y ( x 2) e
2
x
2( x 2) e
x
x
e ( x 2) ( x 4)
2
Находим критические точки:
x
y e ( x 2) ( x 4) 0
x1 2
x2 4
x
( x 2) e
2
35.
3Находим
значения
функций
в
критических точках и на концах
отрезка:
f (2) 0
4
f (4) 4
e
f наиб (0) 4
f (0) 4
9
f (5) 5
e
f наим (2) 0
36.
Если функция непрерывна на интервале (а;в),то она может не принимать на нем наибольшее
и наименьшее значения. В частности, если
дифференцируемая функция y=f(x) на интервале
(а;в) имеет лишь одну точку максимума (или
минимума), то наибольшее (или наименьшее)
значение функции совпадает с максимумом
(минимумом) этой функции.
37.
4. Выпуклостьперегиба.
графика
функции.
Точки
Функция y=f(x) называется выпуклой вниз
(вогнутой) на промежутке Х, если для любых
х1, х2 из этого промежутка выполняется
неравенство:
x1 x2 f ( x1 ) f ( x2 )
f
2
2
38.
yy f (x)
f ( x1 ) f ( x2 )
2
x1 x2
f
2
x1
x1 x2
2
x2
x
39.
Функция y=f(x) называется выпуклой вверх напромежутке Х, если для любых х1, х2 из этого
промежутка выполняется неравенство:
x1 x2 f ( x1 ) f ( x2 )
f
2
2
40.
yx1 x2
f
2
y f (x)
f ( x1 ) f ( x2 )
2
x1
x1 x2
2
x2
x
41.
Функция выпукла вверх (вниз) напромежутке Х тогда и только тогда,
когда ее первая производная на этом
промежутке монотонно возрастает
(убывает).
42.
Если вторая производная дифференцируемойфункции положительна (отрицательна)
на некотором промежутке Х, то функция
выпукла вниз (вверх) на этом промежутке.
43.
Точкой перегиба графика непрерывной функцииназывается точка, разделяющая интервалы,
на которых функция выпукла вверх и вниз.
Точка перегиба – это точка экстремума первой
производной.
44.
Вторая производная дифференцируемойфункции в точке перегиба х0 равна нулю:
f ( x0 ) 0
45.
Если вторая производнаядифференцируемой функции в точке х0
меняет свой знак, то х0 - точка перегиба
ее графика.
46.
1Найти вторую производную функции.
2
Найти точки, в которых вторая
производная функции равна нулю или
не существует.
47.
3Исследовать знак второй производной
слева и справа от найденных точек
и сделать вывод об интервалах
выпуклости и точках перегиба.
4
Найти значения функции в точках
перегиба.
48.
Найти интервалы выпуклости иточки перегиба функции
y x ( x 1)
3
49.
1Находим вторую производную:
y x ( x 1)
3
( x 1)
3
3x ( x 1)
2
( x 1) ( x 1 3x) ( x 1) (4 x 1)
2
2
y ( x 1) (4x 1) 2( x 1) (4x 1) 4( x 1)
2
2
( x 1) 8x 2 4x 4 ( x 1) 12x 6
2
Находим точки, в которых вторая производная
обращается в нуль: y ( x 1) 12 x 6 0
50.
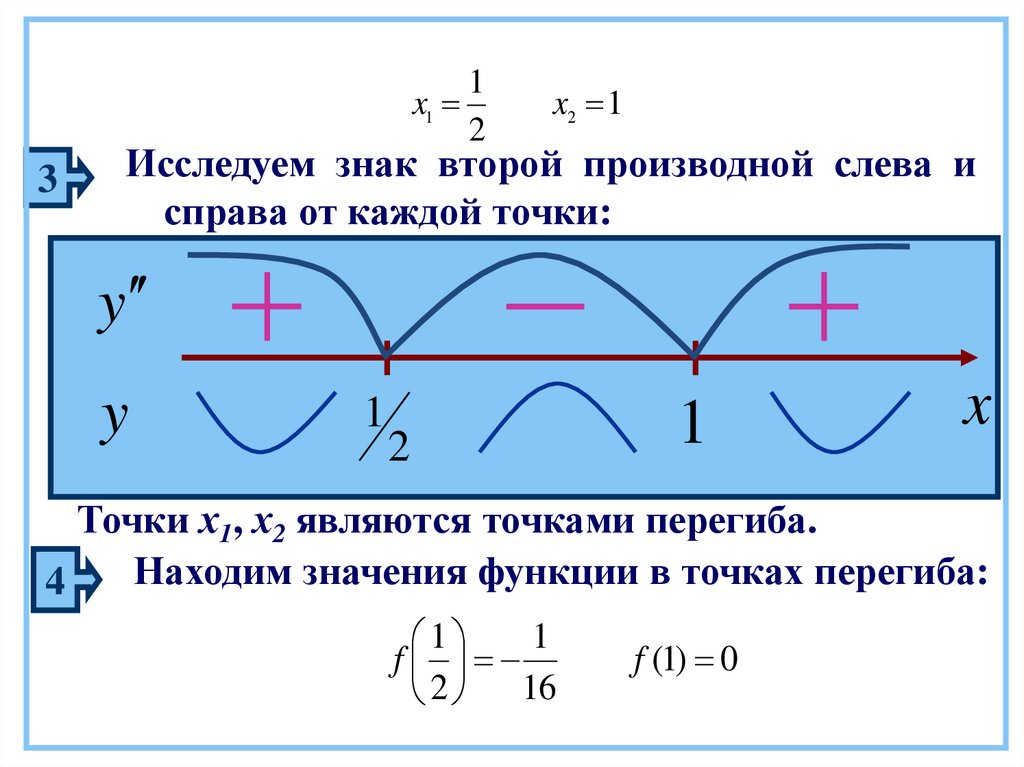
1x1
2
3
x2 1
Исследуем знак второй производной слева и
справа от каждой точки:
y
y
1
2
1
x
Точки х1, х2 являются точками перегиба.
Находим значения функции в точках перегиба:
4
1
1
f
16
2
f (1) 0
51.
5. Асимптоты графика функции и построение графикаАсимптотой графика функции y=f(x)
называется прямая, такая что
расстояние от точки (x,f(x)) до этой
прямой стремиться к нулю при
неограниченном удалении точек графика
от начала координат.
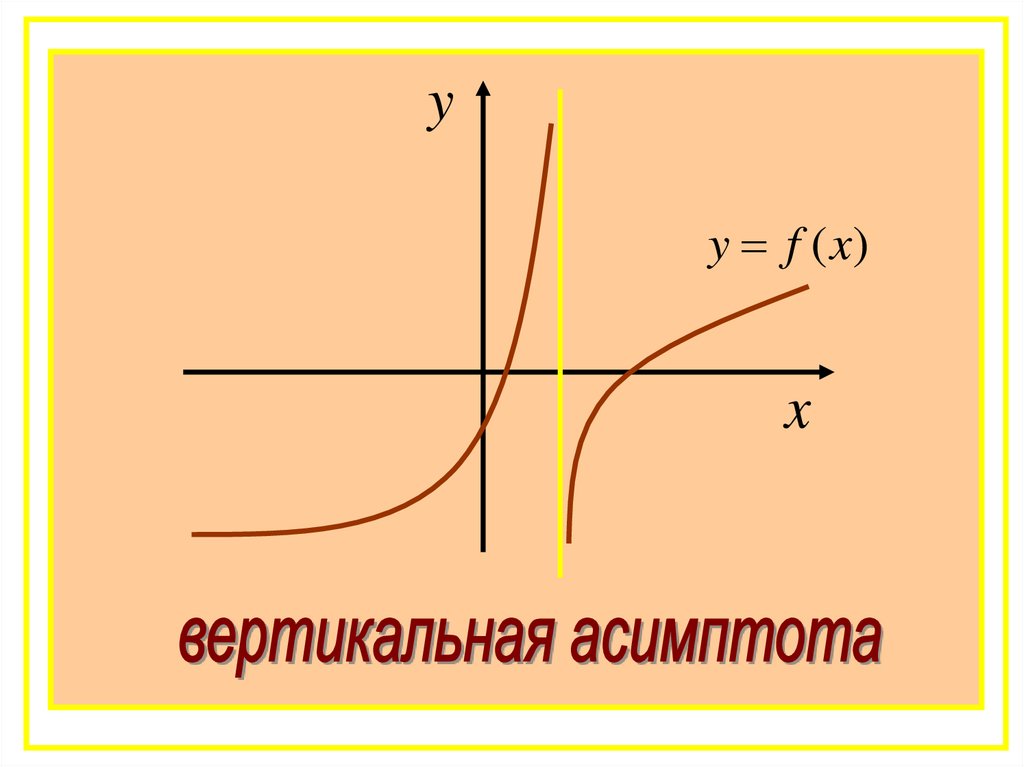
52.
yy f (x)
x
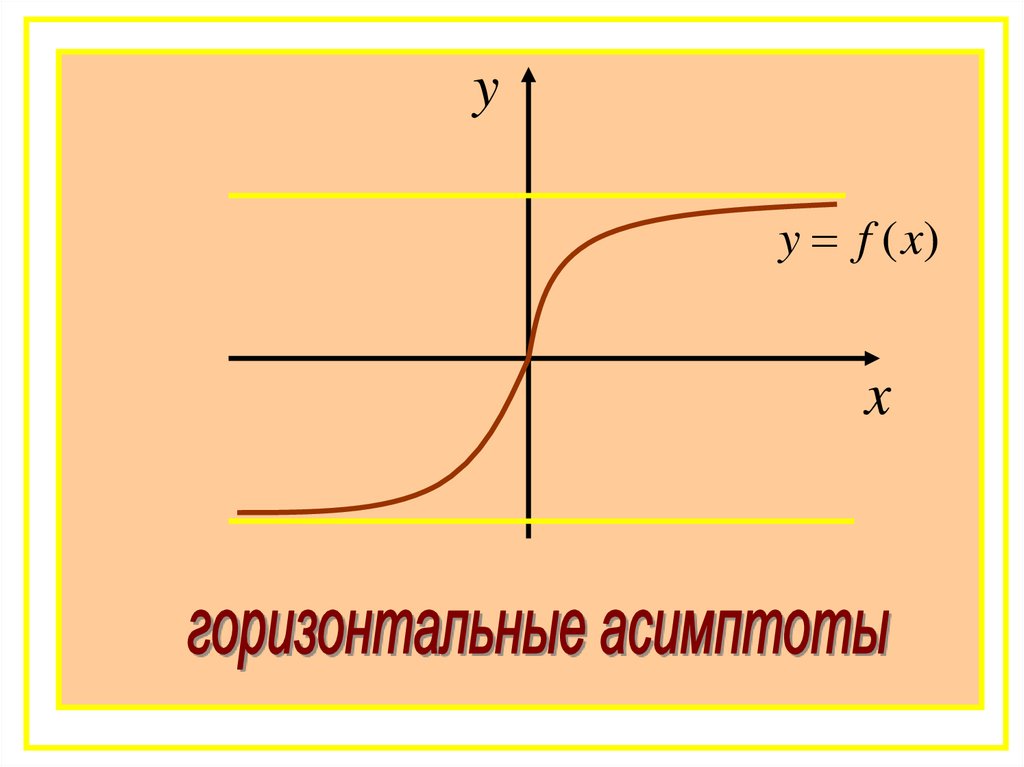
53.
yy f (x)
x
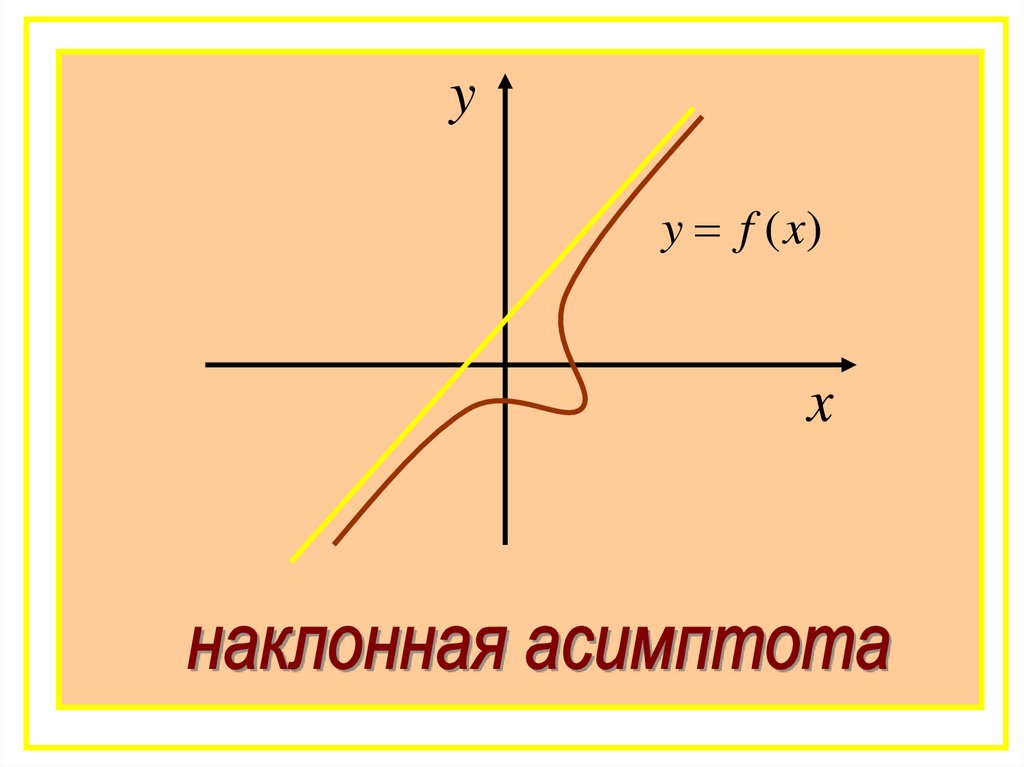
54.
yy f (x)
x
55.
Пусть функция y=f(x) определена внекоторой окрестности точки х0
(исключая, может быть, саму эту
точку) и хотя бы один из пределов
функции при
x x0 0
или
x x0 0
(слева )
(справа )
равен бесконечности, т.е.
56.
lim f ( x)x x0 0
или
lim f ( x)
x x0 0
Тогда прямая х=х0 является
вертикальной асимптотой графика
функции y=f(x).
57.
Очевидно, что прямая х=х0 не может бытьвертикальной асимптотой, если функция
непрерывна в точке х0, т.к. в этом случае
lim f ( x) f ( x0 )
x x0
Следовательно, вертикальные асимптоты х=х0
следует искать в точках разрыва функции
y=f(x) или на концах ее области определения
(a,b), если a и b – конечные числа.
58.
Пусть функция y=f(x) определена придостаточно больших х и существует
конечный предел функции
lim f ( x) b
x
Тогда прямая y=b является
горизонтальной асимптотой
графика функции y=f(x).
59.
Пусть функция y=f(x) определена придостаточно больших х и
существуют конечные пределы
f ( x)
lim
k
x
x
lim f ( x) k x b
x
Тогда прямая y=kx+b является
наклонной асимптотой графика
функции y=f(x).
60.
Найти асимптоты графика функции3
x
y 2
x 1
61.
12
Функция
не
имеет
точек
разрыва,
следовательно вертикальных асимптот у нее
нет.
Найдем горизонтальные асимптоты:
3
x
lim 2
x
x 1
Предел равен бесконечности, следовательно
горизонтальных асимптот нет.
3
Найдем наклонные асимптоты:
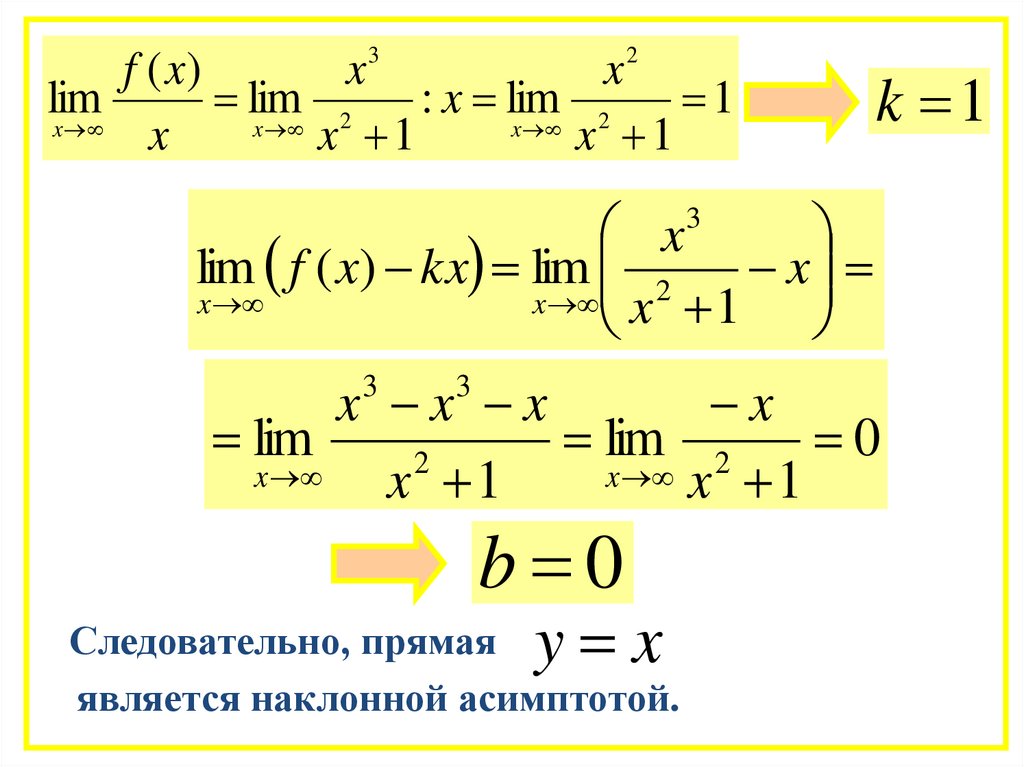
62.
f ( x)x3
x2
lim
lim 2 : x lim 2
1
x
x
x
x
x 1
x 1
k 1
x3
lim f ( x) kx lim 2
x
x
x x 1
x x x
x
lim
lim
0
2
2
x
x
x 1
x 1
3
3
b 0
y x
Следовательно, прямая
является наклонной асимптотой.
63.
Схема исследования функции и построение графика1
Найти область определения функции.
2
Исследовать функцию на четность и
периодичность.
64.
3Найти вертикальные асимптоты.
4
Исследовать поведение функции на
бесконечности и найти горизонтальные
или наклонные асимптоты.
5
Найти экстремумы и интервалы
монотонности функции.
65.
6Найти интервалы выпуклости функции
и точки перегиба.
7
Найти точки пересечения графика с осями
координат и некоторые дополнительные
точки, уточняющие график.
66.
Исследовать функцию и построитьее график
1 x
y
2
1 x
2
67.
Находим область определения функции.Функция определена при всех значениях х,
кроме x 1
Следовательно, область определения функции
будет объединение интервалов:
1
( ; 1) ( 1;1) (1; )
2
Исследуем
функцию
периодичность:
на
четность
1 ( x) 1 x
f ( x)
f ( x)
2
2
1 ( x) 1 x
2
2
и
68.
Функция является четной, следовательно ееграфик будет симметричен относительно оси
ординат.
Функция не периодична.
3
Находим вертикальные асимптоты.
Вертикальные асимптоты могут быть в точках
разрыва функции х =1 и х = -1.
Сначала рассмотрим точку х =1.
Если хотя бы один из пределов при
x 1
слева и справа равен бесконечности, то прямая
х =1 является вертикальной асимптотой.
69.
ПриПри
1 x2
lim
2
x 1 0 1 x
x 1
слева
x 1
1 x2
справа lim
2
x 1 0 1 x
Следовательно,
прямая
х=1
является
вертикальной асимптотой.
Аналогично можно проанализировать х=-1, но так
как
график
функции
симметричен
относительно оси ординат, то прямая х=-1
также будет вертикальной асимптотой.
4
Исследуем
поведение
функции
на
бесконечности и найдем горизонтальные и
наклонные асимптоты.
70.
1 x21
lim
2
x 1 x
1 x2
1
lim
2
x 1 x
Следовательно, y=-1 - горизонтальная асимптота.
Т.к.
lim
x
f ( x)
1 x2
lim
2
x x (1 x )
x
то наклонных асимптот нет.
5
Найдем
интервалы
монотонности
и
экстремумы функции.
Для этого вычислим первую производную:
1 x 2 x(1 x 2 ) ( 2 x)(1 x 2 )
y
2
2 2
(1 x )
1 x
2
71.
2 x 2 x3 2 x 2 x34x
2 2
(1 x )
(1 x 2 ) 2
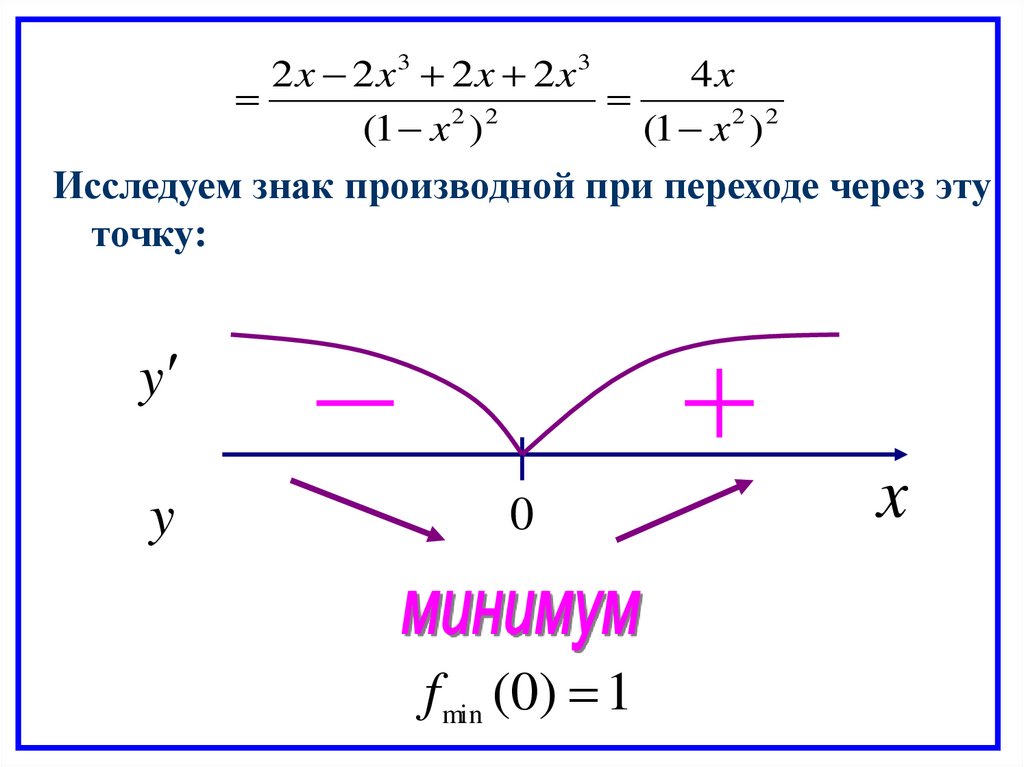
Исследуем знак производной при переходе через эту
точку:
y
y
0
f min (0) 1
x
72.
Интервалы монотонности функции:( ; 1) ( 1;0)
Функция возрастает на: (0;1) (1; )
Функция убывает на:
6
Найдем интервалы выпуклости и точки
перегиба.
Для этого вычислим вторую производную:
2 2
2 2
4 x (4 x) (1 x ) 4 x (1 x )
y
2 2
2 4
(1 x )
(1 x )
4 (1 x 2 ) 2 4 x 2(1 x 2 ) ( 2 x) 4 4 x 2 16 x 2
2 4
2 3
(1 x )
(1 x )
73.
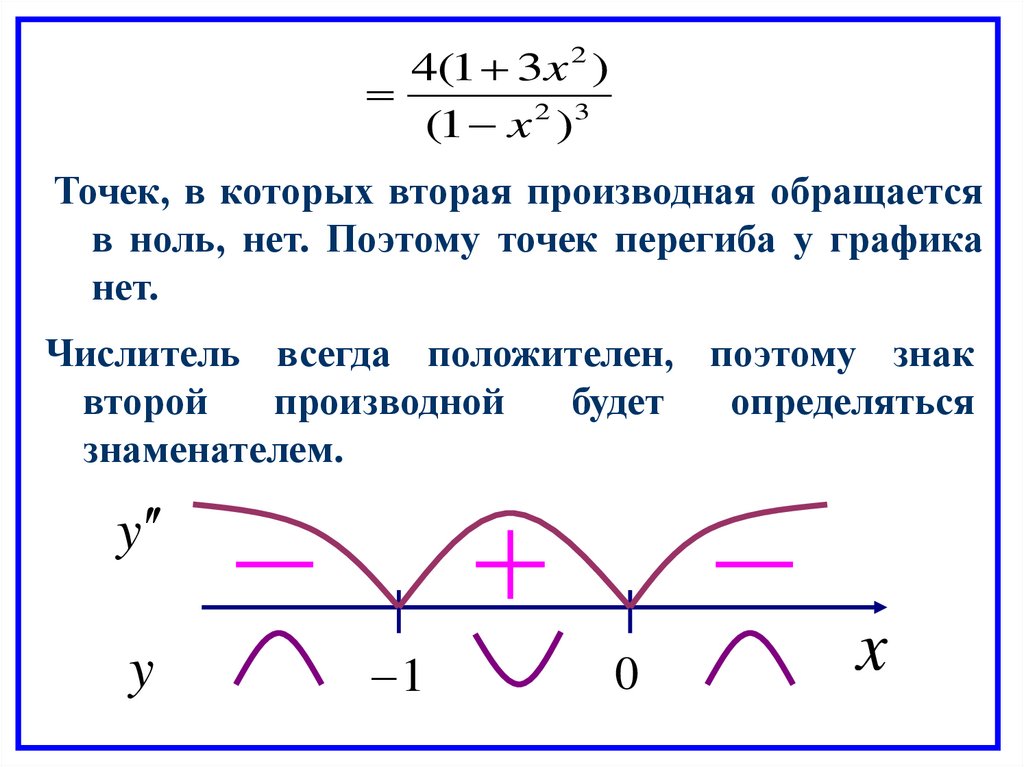
4(1 3x 2 )(1 x 2 )3
Точек, в которых вторая производная обращается
в ноль, нет. Поэтому точек перегиба у графика
нет.
Числитель всегда положителен, поэтому знак
второй
производной
будет
определяться
знаменателем.
y
y
1
0
x
74.
Интервалы выпуклости функции:Функция выпукла вниз на:
( 1 ; 1)
Функция выпукла вверх на: ( ; 1) (1; )
Найдем точки пересечения графика функции с
осями координат:
При x 0
1 0
y
1
1 0
(0,1) - точка пересечения с осью ординат.
7
Точек пересечения с осью абсцисс нет.
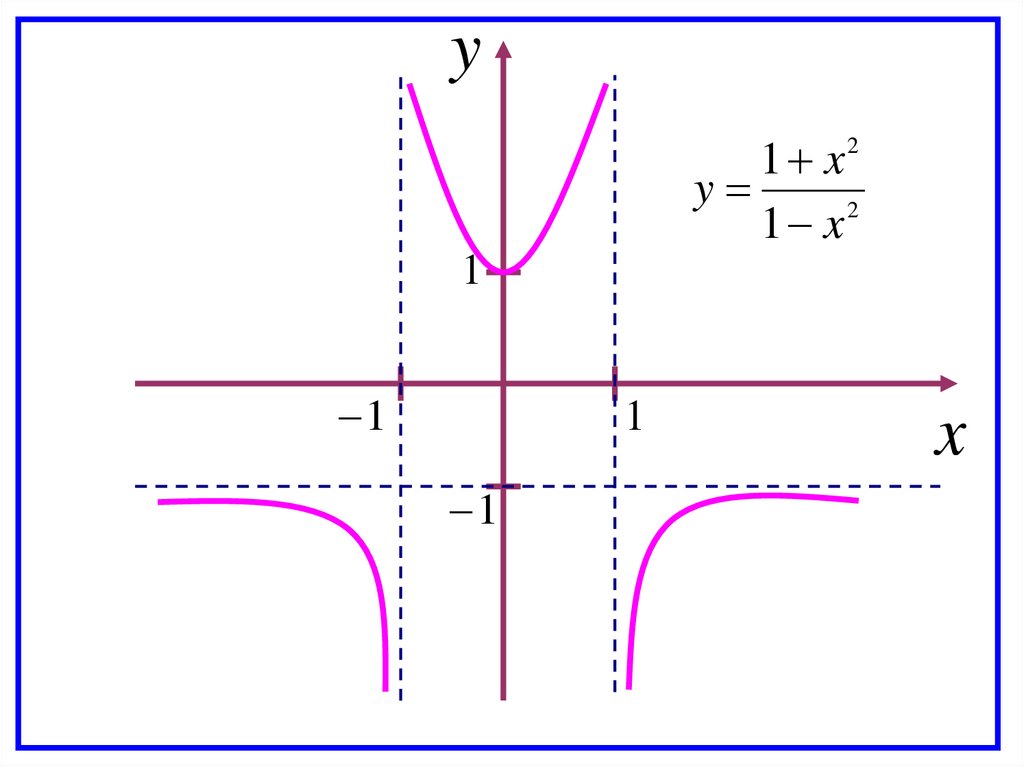
8 Строим график функции:
75.
y1 x2
y
2
1 x
1
1
1
1
x




























































 mathematics
mathematics








