Дифференциальное исчисление. Определение производной

1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

2.

1. Определение производной
Рассмотрим функцию y = f (x), определенную на множестве X.
Возьмем некоторое фиксированное значение x0 X и столь малое приращение
независимой переменной x, что точка (x0 + x) X, причем приращение x –
положительное или отрицательное число.
Выражение y = f (x0 + x) - f (x0) является приращением функции,
соответствующим указанному приращению x.
y f ( x0 x) f ( x0 )
- разностное отношение.
x
x
Определение 1. Производной функции y=f(x) в точке х0 называется предел
(если он существует) отношения приращения функции к вызвавшему его
приращению аргумента при условии, что последнее стремится к нулю.
Обозначение f ( x0 )
или
y x' ( x0 ).
y ( x0 x) y ( x0 )
y
lim
x 0 x
x 0
x
y x' ( x0 ) lim
Если функция y = f (x) определена и имеет производную для всех x из
интервала (a;b), то эта производная будет представлять собой некоторую
функции переменной x, также определенную на интервале (a;b).

3.

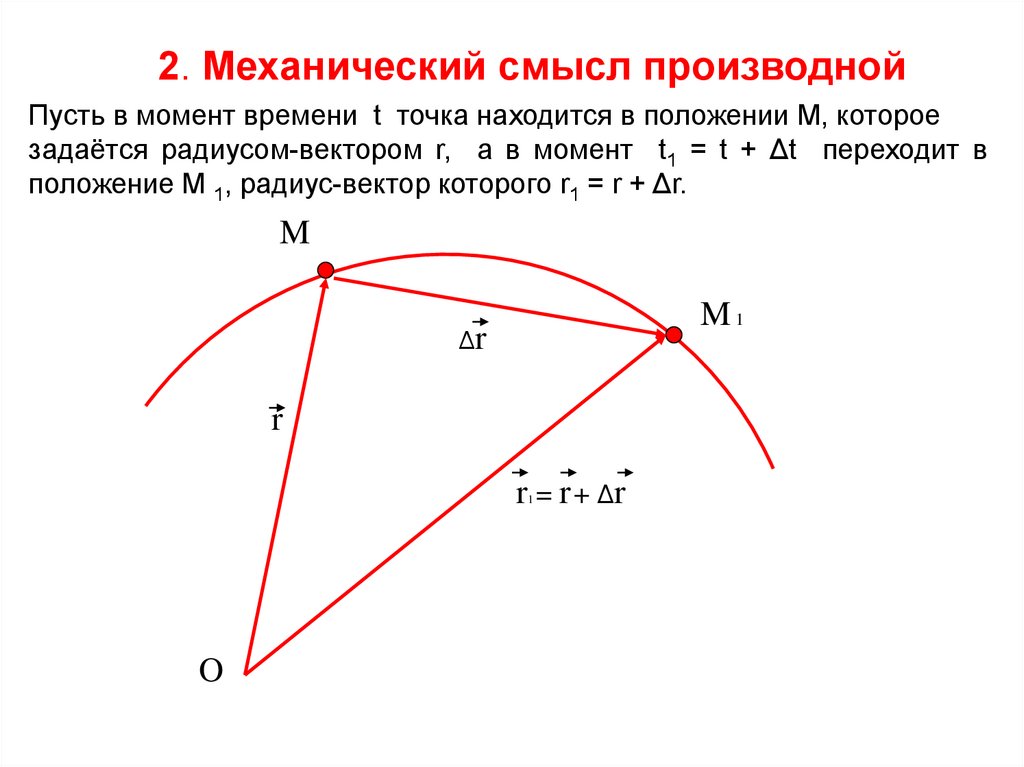
2. Механический смысл производной
Пусть в момент времени t точка находится в положении М, которое
задаётся радиусом-вектором r, а в момент t1 = t + Δt переходит в
положение М 1, радиус-вектор которого r1 = r + Δr.
M
M1
Δr
r
r = r + Δr
1
O

4.

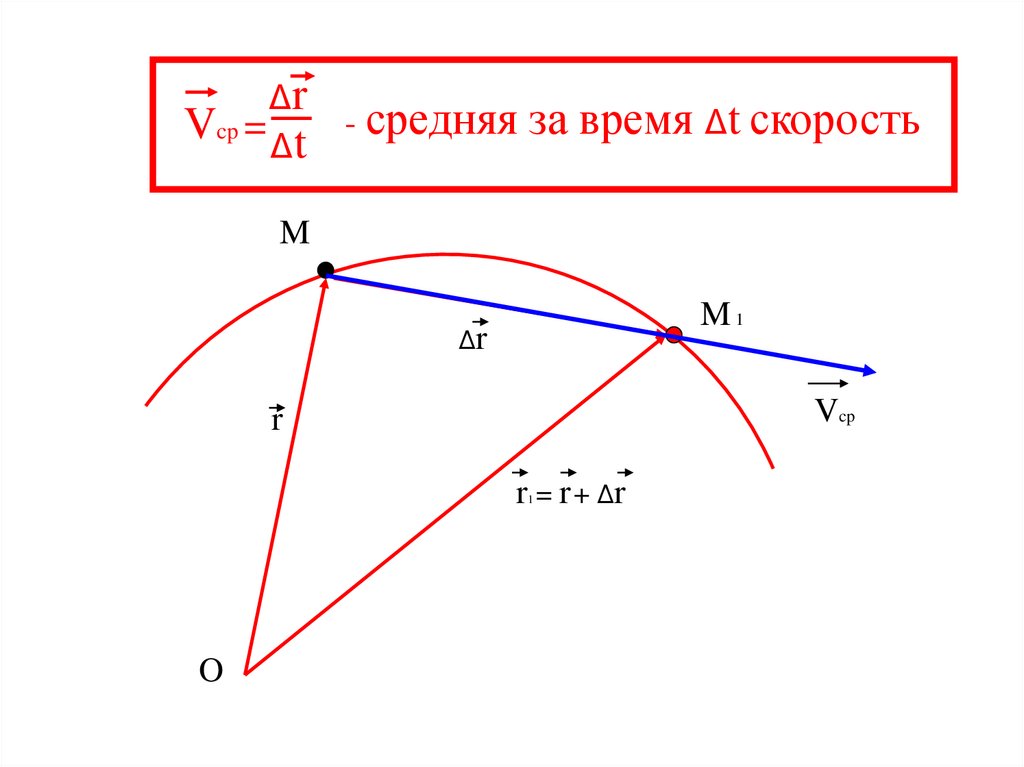
Δr
Vcp = Δt
- средняя за время Δt скорость
M
M1
Δr
Vcp
r
r = r + Δr
1
O

5.

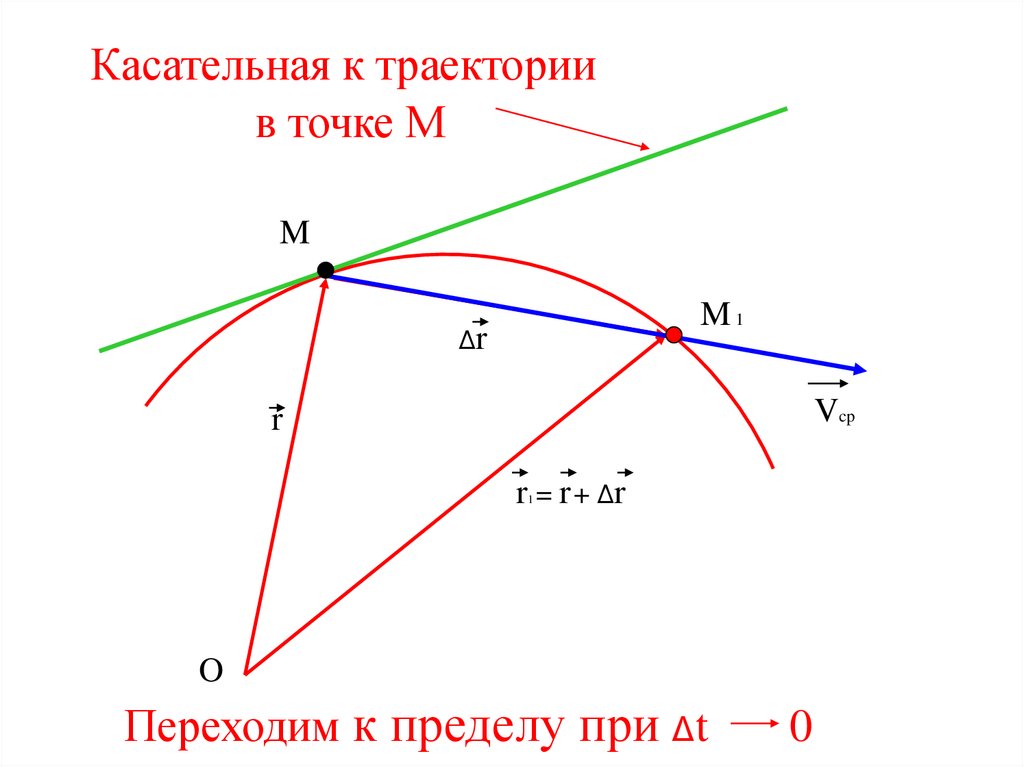
Касательная к траектории
в точке М
M
M1
Δr
Vcp
r
r = r + Δr
1
O
Переходим к пределу при Δt
0

6.

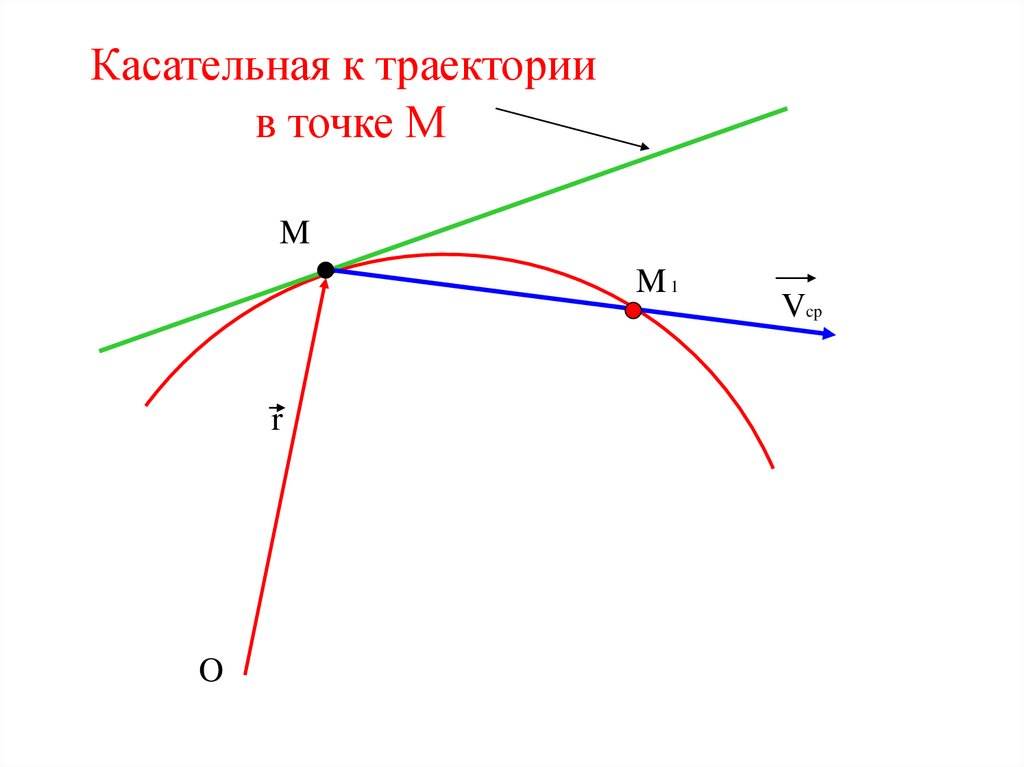
Касательная к траектории
в точке М
M
M1
r
O
Vcp

7.

Касательная к траектории
в точке М
M
r
O
M1
Vcp

8.

Касательная к траектории
в точке М
M
r
O
M1
Vcp

9.

Касательная к траектории
в точке М
Vcp
M
M1
r
O

10.

Касательная к траектории
в точке М
Vcp
M
M1
r
O

11.

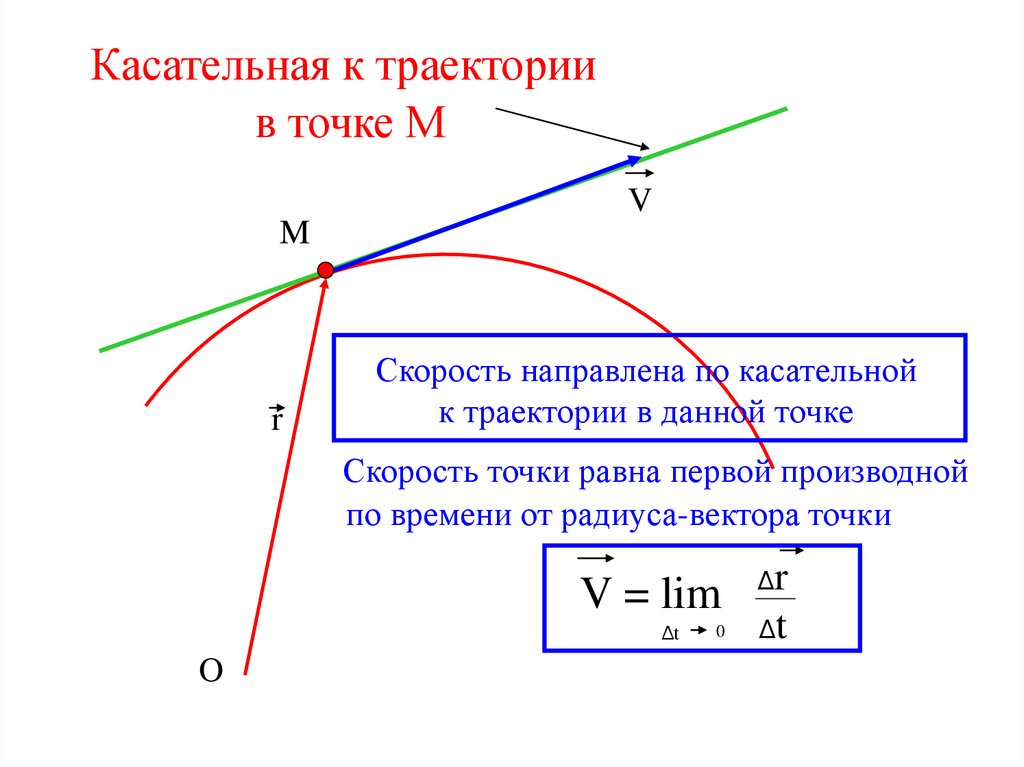
Касательная к траектории
в точке М
V
M
r
Скорость направлена по касательной
к траектории в данной точке
Скорость точки равна первой производной
по времени от радиуса-вектора точки
V = lim
Δt
O
0
Δr
Δt

12.

2. Механический смысл производной
В случае прямолинейного движения получаем:
S1
S2
t1
t2
Δt =t2–t1
ΔS
S
Vcp
t
S
При Δt 0 V lim
мгновенная скорость
t 0 t

13.

2. Механический смысл производной
Таким образом, производная функции с физической точки зрения равна
скорости движения точки в данный момент времени.
Более того, заметим, что производная любой функции при данном значении
аргумента равна скорости изменения этой функции при рассматриваемом
х.
Так, например:
а) если функция N=N(t) определяет количество вещества, уже вступившего в
химическую реакцию к моменту t, то тогда производная определяет скорость
химической реакции в данный момент времени t:
N
N (t t ) N (t )
V (t ) lim
lim
.
t 0 t
t 0
t
б) если функция Q=Q(t) определяет количество электричества, проходящее
через поперечное сечение проводника за время t, то тогда производная
определяет силу тока в проводнике в данный момент времени t:
Q
Q(t t ) Q(t )
lim
.
t 0 t
t 0
t
I (t ) lim

14.

§ 2. Механический смысл производной
в) если функция N=N(t) определяет численности популяции в момент t, то тогда
производная определяет относительный прирост в данный момент времени t:
N
N (t t ) N (t )
Р(t ) lim
lim
.
t 0 t
t 0
t

15.

3. Основные правила дифференцирования
Теорема. Если функции u(x) и v(x) дифференцируемы в
точке x, то их сумма, произведение и частное (последнее
при условии, что v(x) 0) также дифференцируемы в этой
точке, и имеют место равенства
u u v uv
(u v) u v , (uv) u v uv ,
.
2
v
v

16.

3. Основные правила дифференцирования
Пример. Найти производные следующих функций:
1) y=ex + x2 sinx
у =(ex) + (x2 sinx) = ex + 2x sinx + x2 cosx.
x3 1
2) y
.
x
3
2
3
x 1
x 1 x x 3 1 x 3 x x x 1 2 x 1 .
2
2
2
x
x
x
x
3
3

17.

4. Производная сложной функции
Теорема. Пусть функция u= (x) имеет в точке x производную u x= (x),
функция y=f(u) имеет в точке u производную y u=f
(u). Тогда сложная
функция y=f( (x)) имеет в точке
равную произведению
x производную,
производных функций f(u) и (x):
y x yu u x
(правило цепочки).

18.

4. Производная сложной функции
Пример 1. Найти производную функции y ln sin x.
Решение.
y ln u; u sin x
y yu u x
1
1
cos x
cos x ctg x.
u
sin x
1
x
Пример 2. Найти производную функции y arctg .
Решение.
1
x
1
1
1 1
1 x2 1 .
y yu u x
2 2 1 (1 / x) 2 2
2
2
2
1
x
x
x
1 u x
1 x
y arctg u; u
Пример 3. Найти производную функции y 3sin 3 x .
Решение.
u
y 3 ; u sin v; v 3x .
y yu uv v x 3sin 3 x ln 3 cos 3x 3.

19.

Таблица производных

20.

Таблица производных сложных функций
№
Функция
1.
y C
2.
y иn
3.
y u
4.
1
y
u
Производная
№
Функция
Производная
0
9.
y sin u
cos u u x'
nu n 1 u x'
10.
y cosu
sin u u x'
11.
y tg x
1
u x
2
cos u
12.
y ctg u
13.
y arcsin u
14.
y arccosu
15.
y arctg u
16.
y arcctgu
1
2 u
u x
1
2 u x
u
a u ln a u x'
5.
y a
6.
y eu
eu u x'
y log a u
1
u x
u ln a
1
u x
u
7.
8.
u
y ln u
1
u x
2
sin x
1
1 u
1
2
1 u
u x
2
u x
1
u x
2
1 u
1
u x
2
1 u