Similar presentations:
Дифференциальное исчисление
1.
Российская академия народного хозяйства игосударственной службы при Президенте РФ
Факультет национальной безопасности
Раздел 2 тема № 2
«ДИФФЕРЕНЦИАЛЬНОЕ
ИСЧИСЛЕНИЕ »
Лекция №1
профессор Резниченко Александр Васильевич
Москва – 2013
2.
УЧЕБНЫЕ ВОПРОСЫ:1. Понятие производной функции
2. Основные правила
дифференцирования
3. Дифференциал функции
4. Основные теоремы
дифференциального исчисления
3. Литература
1. «Высшая математика для экономических специальностей». Учебник и Практикум (части I и II) / Под ред.Н.Ш. Кремера. М.: Высшее образование, 2008.
2. «Математика: Математический анализ. Дифференциальные уравнения. Теория вероятностей. Математическая статистика». Учебно-методическое пособие /
Под ред. А.Н. Данчула. М.: Изд-во РАГС, 2004.
3. Гельман В.Я. «Решение математических задач средствами Excel: Практикум». Учебник для вузов. СПб.:
ПИТЕР, 2003.
4. «Сборник задач по математике». М.: Изд. РАГС, 2005.
4.
ПЕРВЫЙ ВОПРОСПонятие производной функции
5.
Определение.Пусть функция у = f (x) определена на промежутке Х (х Х) или
О(х,ε). Производной функции у = f (x) в точке x называется предел отношения приращения функции к приращению независимой
переменной при стремлении последнего к нулю (при условии, что
этот предел существует):
Пример.
Замечание.
dy f(df
(=xx) 2 в точке
Найти производную
функции
x
)
( x) x. = x0.
y
,
f
(
x
),
,
,
y
,
f
Обозначение:
Можно доказать, что и для любого (не только натурального n):
Решение.
dx
dx
n x1) 2 x 2 2 x x x 2 .
y f ( x0 x) f ((xx0 n) ) ( x0nx
. 0 2 0
2 x0 x x
y
f ( x0 ) lim
lim
2 x0 .
x 0 x
x 0
x Г.В. Лейбниц
Исаак Ньютон
6.
Геометрический смысл производнойНа графике
функции
f выбираетсяк графику в точке (х , у ):
Уравнение
касательной
0 0
абсцисса x0 и вычисляется соответf
ствующая ордината f (x0tg
). y y0 f ( x )
0
x
x
В окрестности точки x0 выбира0
ется произвольная точка x. Через
y y0 f ( x0 ) ( x x0 ).
указанные точки на графике функции
f проводится секущая (светло-серая
Уравнение нормали к графику в точке (х0, у0):
линия C5).
α (Δ х )
Расстояние Δ x = x - x0 устремляy y0
1
tg н секущая
1, tg н
ется к нулю, вtgрезультате
x x0
f ( x0 )
переходит в касательную (постепенно темнеющие линии C5 – C1),x x0
y y
.
если существует lim ( х) 0.
f ( x )
x 0
0
Тангенс угла α наклона этой касательной – и есть
производная функции f в точке x0.
7.
Определение.Правой (левой) производной функции y = f (x) в точке x0,
называется правый (левый) предел отношения Δy /Δx при Δx → 0
(при условии, что этот предел существует):
y
y
f ( x0 ) lim
f
(
x
)
lim
.
0
x 0 x
x 0 x
Если функция f (x) имеет в точке x0, производную, то она
имеет в этой точке правую и левую производные, которые
совпадают.
Замечание.
Обратное утверждение неверно.
Пример.
Функция y =│x│ имеет в точке x = 0 правую и левую производные:
y
y
f (0) lim
1 (при x 0 y х), f (0) lim
1 (при x 0 y х),
x 0 x
x 0 x
но не имеет в этой точке производной, т.к. не имеет предела.
8.
Определение.Функция y = f (x) называется дифференцируемой в точке x0 –
f D(x0), если ее приращение Δy в этой точке можно представит в
виде:
Δy = А∙Δx + α(Δx)∙Δx,
где А - некоторое число, не зависящее от Δx;
α(Δx) - функция аргумента Δx, являющаяся бесконечно малой
при Δx → 0,т.е. lim ( х) 0.
x 0
Установим связь между дифференцируемостью функции в
точке и существованием производной в той же точке.
Замечание.
Теорема.
Определение.
Для функции одной переменной дифференцируемость и
Для того
чтобыy=f(x)
функция
y = f (xx)0 была
дифференцируема
в
Если
функция
в
точке
имеет
конечную
производсуществование производной – понятия равносильные.
точке
, необходимо
и достаточно,
чтобы она часто
имеланазывают
этой
ную,
тоx0функция
называется
дифференцируемой
вв этой
Поэтому
операцию
нахождения
производной
точке
дифференцированием.
точке.конечную производную.
9.
Зависимость между непрерывностью идифференцируемостью функции
Теорема.
Если функция y = f (x) дифференцируема в точке x0, то она и
непрерывна в этой точке.
Замечание.
Обратное утверждение неверно.
Пример.
Определение.
Функция y =│x │ непрерывна в точке x = 0, но не имеет в этой
Определение.
точке
производной,
является
дифференцируемой.
Если
функция y =т.е.
f
(xне
) имеет
производную
в каждой точке неЕсли функция имеет непрерывную производную на некотором
которого промежутка Х (дифференцируема в каждой точке пропромежутке Х, то функцию называют гладкой (непрерывно дифмежутка Х, т.е. f (x) D(x) x Х или f D(X)), то говорят, что эта
ференцируемой) на этом промежутке и пишут: f C (1) (Х).
функция дифференцируема на данном промежутке.
10.
ВТОРОЙ ВОПРОСОсновные правила
дифференцирования
11.
Правила дифференцированияПусть с – постоянная, и = и(х), v = v(x) – дифференцируемые
функции:
1. Производная постоянной равна нулю: с 0.
2. Производная аргумента равна единице: х 1.
3. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме из производных:
(u v ) u v .
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на
второй плюс произведение первого сомножителя на производную
второго:
(u v) u v u v .
12.
Правила дифференцированияСледствие 1. Постоянный множитель можно выносить за
знак производной:
( u ) u u u .
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные:
(u v w) u v w u v w u v w .
5. Производная частного двух дифференцируемых функций
может быть найдена по формуле:
u u v u v
2
v
v
(при условии, что v 0).
13.
Правила дифференцированияПример.
Найти производную функции f (х) и вычислить ее значение в
точке х = 1:
3 4
а) y x ( x 1)
1
4
1
4
1
4
3
1
3
3
2
3
2 13 4
4
y ( x ) ( х 1) x ( х 1) 3х ( х 1) x ( х 0) х (
х 1).
4
4
13
y
(
1
)
1
(
1 1) 4,25.
Значение производной в точке х = 1 есть:
4
x3 1
б) y
х
( x 1) х ( x 3 1)( х )
y
2
( х)
3
y (1) 3.
3х
2
х ( x 1)
3
х
1
3
5
х
1
2 х
.
2х х
14.
Правила дифференцирования6. Если у = f(u) и u = g(x) – дифференцируемые функции от своих
аргументов, то производная сложной функции существует и
равна производной данной функции по промежуточному
аргументу u, умноженной на производную самого промежуточного
аргумента u по независимой переменной х, т.е.
Пример. Найти производную y ( x 5)3 .
Решение.
3( x 5) 2
3
2
2
y u (u x 5) y 3u u 3( x 5) ( x 5)
.
2 x
7. Если у = f(x) – дифференцируемая и строго монотонная
функция на промежутке X, то тогда функция, обратная к данной
x = g(у), также дифференцируема и ее производная определяется соотношением:
15.
Таблица производных некоторых функцийФункция f(x)
Производная f’(x)
Функция f(x)
Производная f’(x)
Функция f(x)
c
0
sin x
cos x
arcsin x
xa
a x a 1
cos x
sin x
arccos x
x
a ln a
tg x
1
cos 2 x
arctg x
1
sin 2 x
arcctg x
a
log a x
x
1
x ln a
ctg x
Производная f’(x)
Пример. Найти производную функции y e arctg x .
Решение.
u
Представим функцию в виде y e , где u arctg x.
1
1
u
arctg x
y ( x) y (u ) u ( x) e
y ( x) e
.
2
2
1 x
1 x
16.
Правила дифференцирования8. Производная неявной функции.
Если зависимость между х и у задана в неявной форме уравнением F(x, у) = 0, то для нахождения производной функции у необходимо продифференцировать по х обе части данного уравнения, рассматривая у как функцию от х.
Из полученного уравнения находится у'.
Пример.
Найти производную функции x2 - xy + lny - 2 = 0, заданной неявно,
и вычислить ее значение в точке (2;1).
Решение.
Дифференцируя обе части равенства и учитывая, что y есть
функция от х, получаем:
2
y
2 xy y
2 x y xy 0, откуда y
.
y
xy 1
Значение производной при x = 2, y = 1 – y'(2) = 3.
17.
Правила дифференцирования9. Дифференцирование параметрически заданной функции.
Если функция y = f (х) аргумента х задана параметрически уравнениями х = х (t) и у = у(t), где х(t) и у(t) определенны и дифференцируемы на некотором
промежутке Т, причем х'(t) ≠ 0 t Т, а для
х = х (t) существует обратная t = t(х), определенная и дифференцируемая на Х = х(Т), то:
Пример.
Найти производную от функции,
заданной параметрически:
Решение.
Последовательно дифференцируя функцию, получаем:
18.
Правила дифференцирования10. Производные высших порядков.
Понятие производной произвольного порядка задается
рекуррентно.
а) Полагаем
б) Если функция f (х) дифференцируема в x0, то производная
первого порядка определяется соотношением
в) Пусть теперь производная (n-1)-го порядка определена в некоторой окрестности точки x0 и дифференцируема.
Тогда производной п-го порядка называется производная
от производной (п - 1)-го порядка:
Пример.
Найти производную 4-го порядка от функции у = sin2х.
Решение.
Последовательно дифференцируя функцию, получим:
19.
ТРЕТИЙ ВОПРОСДифференциал функции
20.
Определение.Функция y = f (x) называется дифференцируемой в точке x –
f D(x), если ее приращение Δy в этой точке можно представить в
виде:
Δy = А∙Δx + α(Δx)∙Δx,
Определение.
где
А - некоторое число, не зависящее от Δ x;
Дифференциалом
функции
= f (x) в точке
x называется
α(Δx) - функция аргумента
Δ x,yявляющаяся
бесконечно
малой
главная
Δ x часть приращения Δy, равная
( х) 0.
при
Δ x →линейная
0,т.е. lim относительно
x 0
произведению производной
на приращение Δ x независимой переменной:
dy = А∙Δx = f '(x)Δ x.
Замечание.
dy
Если
f'(x)
=
0,
то
f'(x)
∙Δ
x
не
является
главной
Для
функции
y
=
x
dy
=
dx
=
x'·∆x
,
откуда
dx. = ∆x,приращет.е.
Кроме того, dy = f '(x)Δ x = f '(x)dx f ( x) частью
ния Δy, посколькунезависимой
α(Δx)∙Δ x, вообще
говоря, отлична
от нуля.
дифференциал
переменной
равен
dx приращению
В этом
случае полагают dy = 0.
этой
переменной.
21.
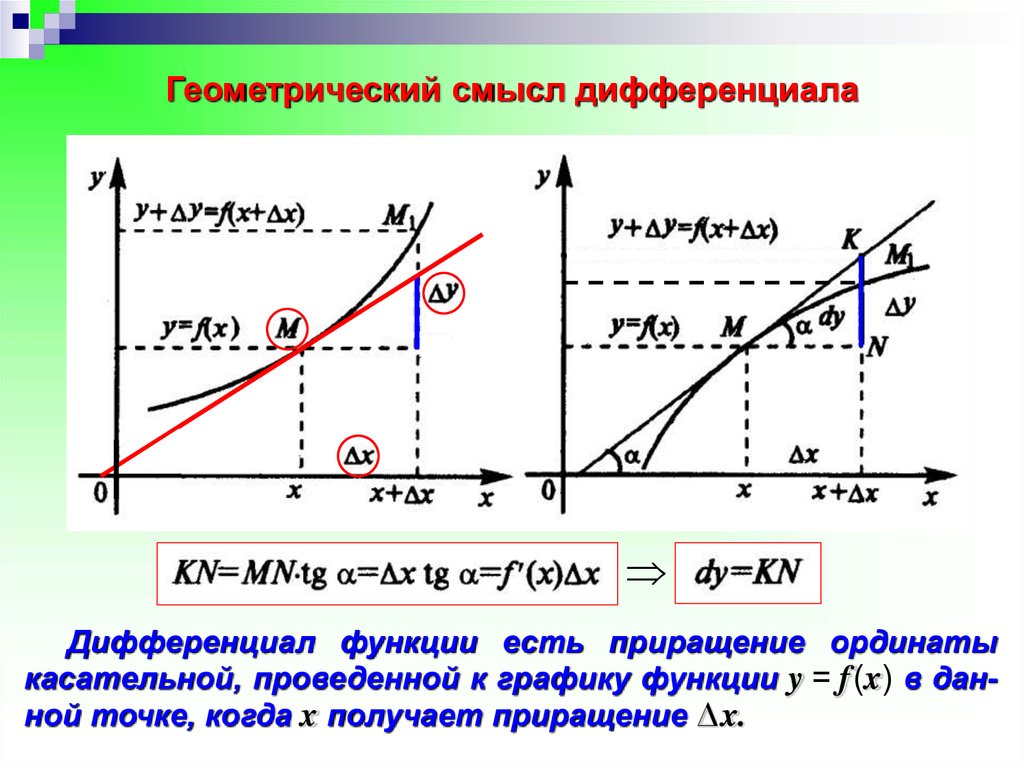
Геометрический смысл дифференциалаДифференциал функции есть приращение ординаты
касательной, проведенной к графику функции y = f(x) в данной точке, когда x получает приращение ∆x.
22.
Свойства дифференциала1. Дифференциал постоянной равен нулю:
2. Постоянный множитель можно
выносить за знак дифференциала:
dс 0.
d ( u ) du.
3. Дифференциал алгебраической суммы конечного числа
дифференцируемых функций равен такой же сумме дифференциалов:
d (u v ) du dv.
4. Дифференциал произведения двух дифференцируемых
функций равен произведению дифференциалу первого сомножителя на второй плюс произведение первого сомножителя на
дифференциал второго:
d (u v) d u v u dv.
5. Дифференциал частного
двух дифференцируемых функций
может быть найден по формуле:
u v du u dv
d
(v 0).
2
v
v
23.
Инвариантность формы дифференциалаРассмотрим у = f(u) и u = g(x) – дифференцируемые функции
от своих аргументов, тогда для f ( g ( x)) – сложной функции
дифференциал равен
dy f ( x)dx f (u ) g ( x)dx f (u )du.
Формула дифференциала не изменяется, если вместо
функции от независимой переменной х рассматривать функцию от зависимой переменной u.
Дифференциалы высших порядков
Дифференциалом n-го порядка d ny функции у = f(x) называется
дифференциал от дифференциала (n-1)-го порядка этой функции:
d 2 y d (dy) d[ f ( x) dx ] d[ f ( x)] dx [ f ( x) dx]dx f ( x)(dx) 2 ;
...
d n y d (d ( n 1) y ) f ( n ) ( x)( dx) n f ( n ) ( x)dx n .
24.
Использование дифференциала в приближенных вычисленияхИз определения дифференциала следует, что
с погрешностью α(Δx)∙Δx.
Если положить х = а + ∆х, то ∆х = х - а и
Таким образом, для значений x, близких к а, функция f (x) заменена линейной функцией (или линеаризована в окрестности
точки а).
Геометрически это соответствует замене участка кривой графика у = f (x) около точки (а, f (а)) отрезком касательной к кривой
в этой точке.
Погрешность подобной замены приближенно равна половине
второго дифференциала функции – 1/2 d 2f = 1/2 f " (a)(x – a)2.
Пример.
При а = 0
25.
ЧЕТВЕРТЫЙ ВОПРОСОсновные теоремы
дифференциального
исчисления
26.
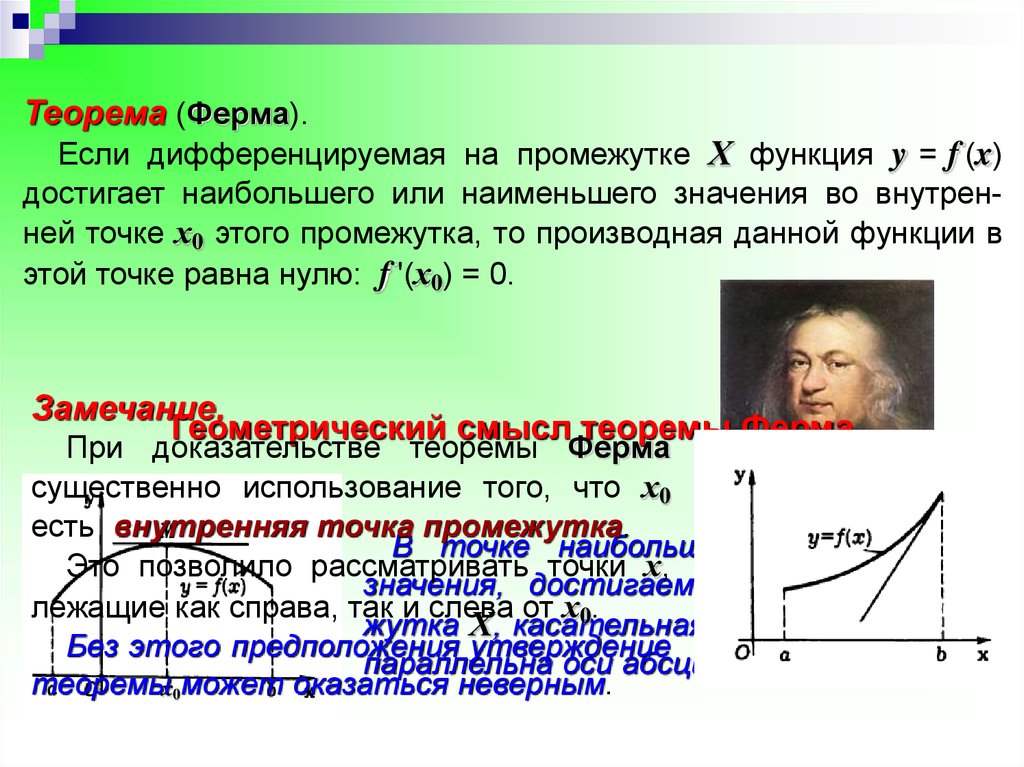
Теорема (Ферма).Если дифференцируемая на промежутке Х функция y = f (x)
достигает наибольшего или наименьшего значения во внутренней точке х0 этого промежутка, то производная данной функции в
этой точке равна нулю: f '(х0) = 0.
Замечание.
Геометрический смысл теоремы Ферма
При доказательстве теоремы Ферма
существенно использование того, что х0
есть внутренняя точка промежутка.
В точке наибольшего (наименьшего)
Это позволило рассматривать точки х,
значения, достигаемогоПьер
внутри
де Фермапромележащие как справа, так и слева от х0.
жутка Х, касательная к графику функции
Без этого предположения утверждение
параллельна оси абсцисс.
теоремых0может оказаться неверным.
27.
Теорема (Ролля).Пусть функция y = f (x) удовлетворяет следующим условиям:
1) непрерывна на отрезке [а, b];
2) дифференцируема на интервале (а, b);
3) на концах отрезка принимает равные значения: f (а) = f (b).
Тогда внутри отрезка существует по крайней мере одна такая
точка ξ (а, b), в которой производная функции равна нулю:
f '(ξ ) = 0.
Геометрический смысл
теорема Ролля
Следствие.
Если
ординаты
непрерывной
криМежду
двумя нулями
дифференцируемой
вой
на концах
отрезка [а, b] равны
функции
–
между собой и f(кривая
a) = f(b) =в 0,каждой
внутренней точке этого отрезка имеет
невертикальную
касательную,
то нуль ее
всегда
лежит хотя
бы один
на
кривой найдется
хотя бы одна
производной
.
точка, в которой касательная
параллельна оси Ох.
Мишель Ролль
28.
Замечание.Замечание.
Все
условия
теоремы
существенны для
справедлиТеорема
Ролля
носит Ролля
лишь достаточный
характер,
т.е.
вости ее утверждения.
если все условия теоремы выполнены, то ее утверждение верно,
но если нарушено хотя бы одно ее условие, то нельзя сказать
Пример.
что-либо определенное о существовании точки, в которой
производная рассматриваемой функции обращалась бы в нуль.
Пример.
Функция f (x) непрерывна на отрезке [а, b], на концах отрезка
имеет равные значения, но не является дифференцируемой во
внутренней точке хо этого отрезка.
Тем не менее существует точка
Нарушены условия:
х = с, в которой f '(с) = 0, т.к.
а) непрерывности на отрезке [a, b];
касательная в соответствующей
б) дифференцируемости на интервале (a, b);
точке кривой графика этой функв) равенства значений f (а) = f (b),
ции параллельна оси Ох.
Поэтому не существует ξ (а, b), в которой f '(ξ ) = 0.
29.
Теорема (Лагранжа).Пусть функция y = f (x) удовлетворяет следующим условиям:
1) непрерывна на отрезке [а,b];
2) дифференцируема на интервале (а,b).
Тогда внутри отрезка существует по крайней мере одна такая
точка ξ (а,b), в которой выполняется равенство:
f (b) f (a)
f ( )
или f (b) f (a) f ( ) (b a).
b a
Геометрический смысл теоремы
Лагранжа
Следствие.
На
непрерывном
графика
Если
функция участке
y = f (x)АВнепрерывна
на
функции
имеющей
в каждой
отрезке y[а=, bf ](x),
и во
всех его
внутренних
точке
касательную,
точках невертикальную
имеет равную нулю
производную,
всегда
крайней мере
то этанайдется
функцияпопостоянна
на одна
указанном
точка
М, в которой касательная паотрезке.
раллельна хорде АВ.
Жозеф Луи Лагранж
Теорема Ролля – частный случай теоремы Лагранжа, так как при f(а) = f(b) хорда
АВ параллельна оси Ох.
30.
Замечание.Теорема(Коши).
Лагранжа носит лишь достаточный характер, т.е.
Теорема
если
всефункции
условияf (теоремы
Пусть
x) и g(х): выполнены, то ее утверждение верно,
но если нарушено хотя бы одно ее условие, то нельзя сказать
1) непрерывны
на отрезкео [а,b
];
что-либо
определенное
существовании
точки, в которой
2) дифференцируемы
в интервале
(а,b);
выполнялось
бы указанное
равенство.
3) производная g'(х) не обращается в нуль
Пример.
Огюстен Луи Коши
в интервале (а,b).
На рисунке изображены графики функций, непрерывных на
Тогда [а,b]
существует
точка ξ (а, b), во
в внутренней
которой выполняется
отрезке
, но не дифференцируемых
точке х .
o
равенство:
График а) не имеет точки, в которой касательная параллельна
) f (aточка
) f (М
)существует.
хорде АБ, а у графика fб)(bтакая
.
g (b) g (a) g ( )
Замечание.
Теорема Лагранжа является частным случаем теоремы
Коши при g(х) = х.
31.
Замечание.Теорема
(правило
(правило Лопиталя).
Бернулли – Лопиталя).
Правило
Лопиталя можно
применять
также
и для раскрытия
При использовании
правила
Бернулли
– Лопиталя
для расПредел отношения двух бесконечно малых или бесконечно
крытия неопределенности
или [∞произведение
/ ∞] производные
неопределенностей
вида [0вида
∙∞]. [0/0]
Для этого
f (x)∙fg'((x)
больших функций равен пределу отношения их производных
и g'(х) исходных
следует
записать функций
в виде: f(x) и g(х) сами могут быть бесконечно
(конечному или бесконечному), если последний существует в
малыми или бесконечно большими функциями при x → А, где А –
указанном
смысле:
конечная или
бесконечно удаленная
точка числовой
чем получить
0 прямой.
Если для функций f '(x) и gнеопределенность
'(х) выполнены условия
одной
0 или
.из
указанных теорем, то правило Бернулли – Лопиталя можно
применить повторно, в виде
Если имеется неопределенность вида [0 0] или [∞0] при вычисПравилофункции f(х) g(x), то логарифм этой функции предлении предела
Бернулли
– Лопиталя
Лопиталя
Правило
ставляет
собой
неопределенность вида [0 ∙ ∞].
используется
раскрытиясоотношение (полученное на основе
При этом для
используется
неопределенностей
свойств
и непрерывности
функции):
В томлогарифмов
случае, вида
когда
вторые и показательной
более высокого
порядка
производные исходных функций удовлетворяют указанным вы 0 правило
Бернулли – Лопиталя можно применять
ше условиям,
или .
последовательно
Гийом Франсуа
0
и далее.
Иоганн I Бернулли
маркиз де Лопиталь
32.
Пример.Пример.
Найти
x 1
.
Найти lim
Решение. x x 1
Имеется неопределенность вида [0 / 0], следовательно можно
Решение.
применить правило Лопиталя
Имеется неопределенность вида [∞/∞], и поэтому применим
правило Лопиталя:
lim
Пример.x
Найти
1
x 1
x 1
2
x
1
lim
lim
.
x
x
1
x 1
x 1
2 x 1
Решение.
1
Имеется неопределенность вида [∞ /∞], 1следовательно
можно
x 1
x 1.
применить правило Лопиталя
lim
lim
Однако легко видеть
x
x 1
x
1
1
x
33.
Благодарю за внимание,лекция окончена!































 mathematics
mathematics








