Similar presentations:
Дифференциальное исчисление
1.
ДИФФЕРЕНЦИАЛЬНОЕИСЧИСЛЕНИЕ
©И.В.Гутарова
2.
§1. Производная функциип 1. Задачи, приводящие к понятию
производной
©И.В.Гутарова
3.
п 1. Задачи, приводящие к понятию производнойЗадача №1
О
скорости
движения
(задача,
которая
привела И. Ньютона к понятию производной)
©И.В.Гутарова
4.
п 1. Задачи, приводящие к понятию производнойПусть материальная точка (некоторое тело) М
движется
неравномерно
Каждому
значению
по
некоторой
времени
t
прямой.
соответствует
определенное расстояние ОМ = S до некоторой
фиксированной точки О.
Это расстояние зависит от времени t, т.е. S = S(t). Это
равенство называют законом движения точки.
Требуется найти скорость движения точки.
©И.В.Гутарова
5.
п 1. Задачи, приводящие к понятию производнойЕсли в некоторый момент времени t точка занимает
положение М, то в момент времени t + Δt (Δt приращение времени) точка займет положение М1,
где ОМ1 = S + ΔS (ΔS – приращение расстояния).
©И.В.Гутарова
6.
п 1. Задачи, приводящие к понятию производнойТаким образом, перемещение точки М за
время Δt будет равно ΔS = S(t + Δt) - S(t).
©И.В.Гутарова
7.
п 1. Задачи, приводящие к понятию производнойТаким образом, перемещение точки М за
время Δt будет равно ΔS = S(t + Δt) - S(t).
S
Отношение
выражает
среднюю
t
скорость движения точки за время Δt :
S
vср
t
©И.В.Гутарова
8.
п 1. Задачи, приводящие к понятию производнойПредел средней скорости движения при
стремлении к нулю промежутка времени Δt
называется скоростью движения точки в
данный момент времени. Обозначив эту
скорость через v, получим:
S
S t t S t
v lim
lim
t 0 t
t 0
t
1
©И.В.Гутарова
9.
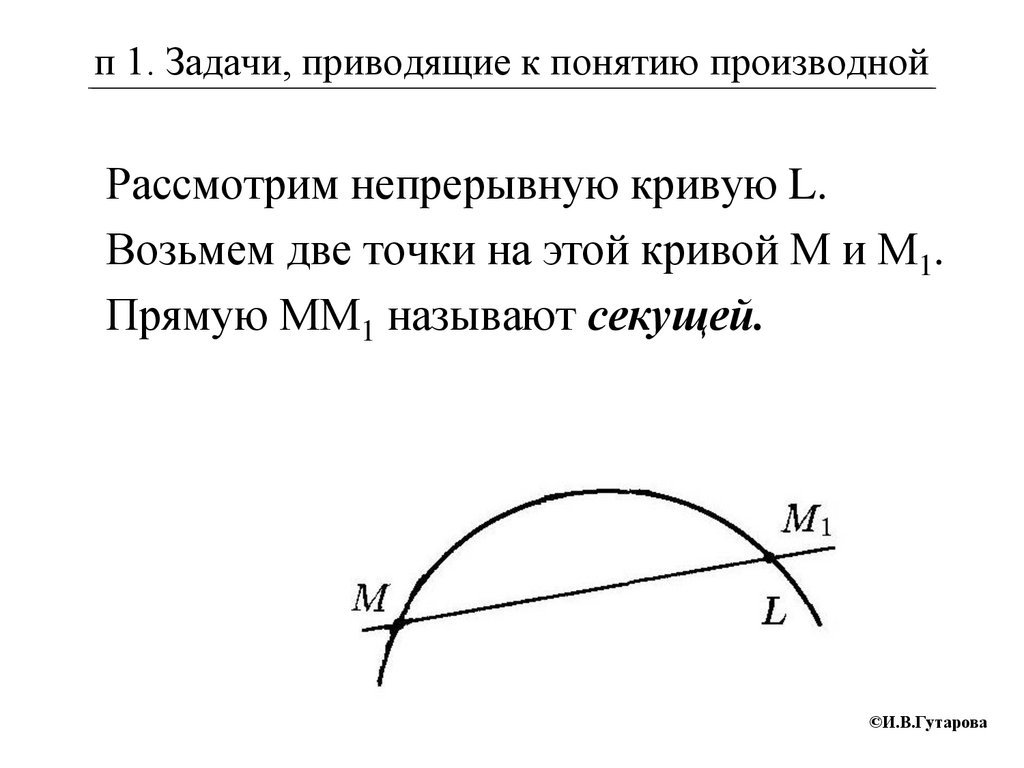
п 1. Задачи, приводящие к понятию производнойРассмотрим непрерывную кривую L.
Возьмем две точки на этой кривой М и М1.
Прямую ММ1 называют секущей.
©И.В.Гутарова
10.
п 1. Задачи, приводящие к понятию производной©И.В.Гутарова
11.
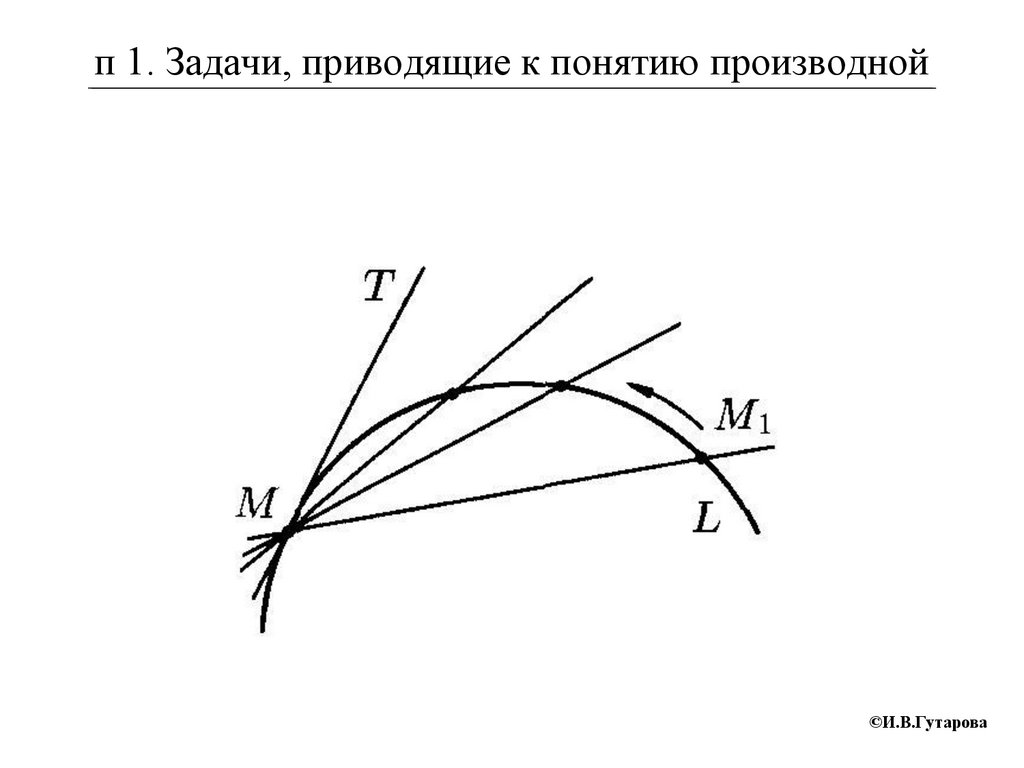
п 1. Задачи, приводящие к понятию производнойПусть точка М1, двигаясь вдоль кривой L,
неограниченно приближается к точке М.
Тогда секущая, поворачиваясь около точки
М, стремится к
некоторому
предельному
положению МТ.
©И.В.Гутарова
12.
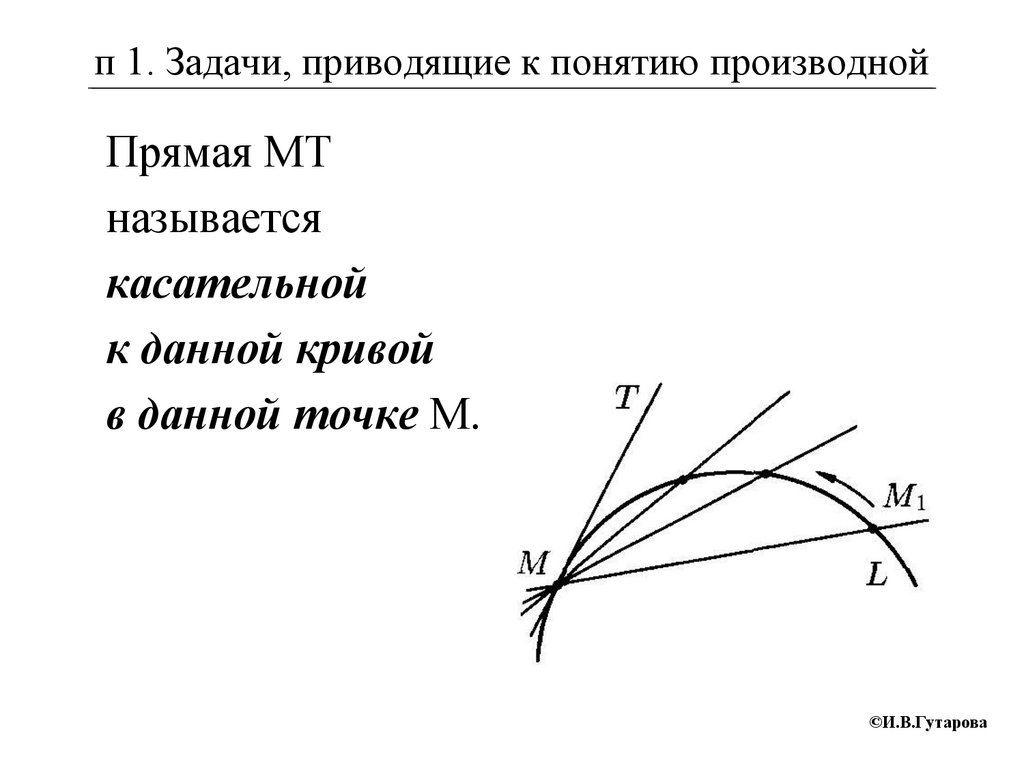
п 1. Задачи, приводящие к понятию производнойПрямая МТ
называется
касательной
к данной кривой
в данной точке М.
©И.В.Гутарова
13.
п 1. Задачи, приводящие к понятию производнойЗадача №2
Об угловом коэффициенте (задача, которая
привела Лейбница к понятию производной)
©И.В.Гутарова
14.
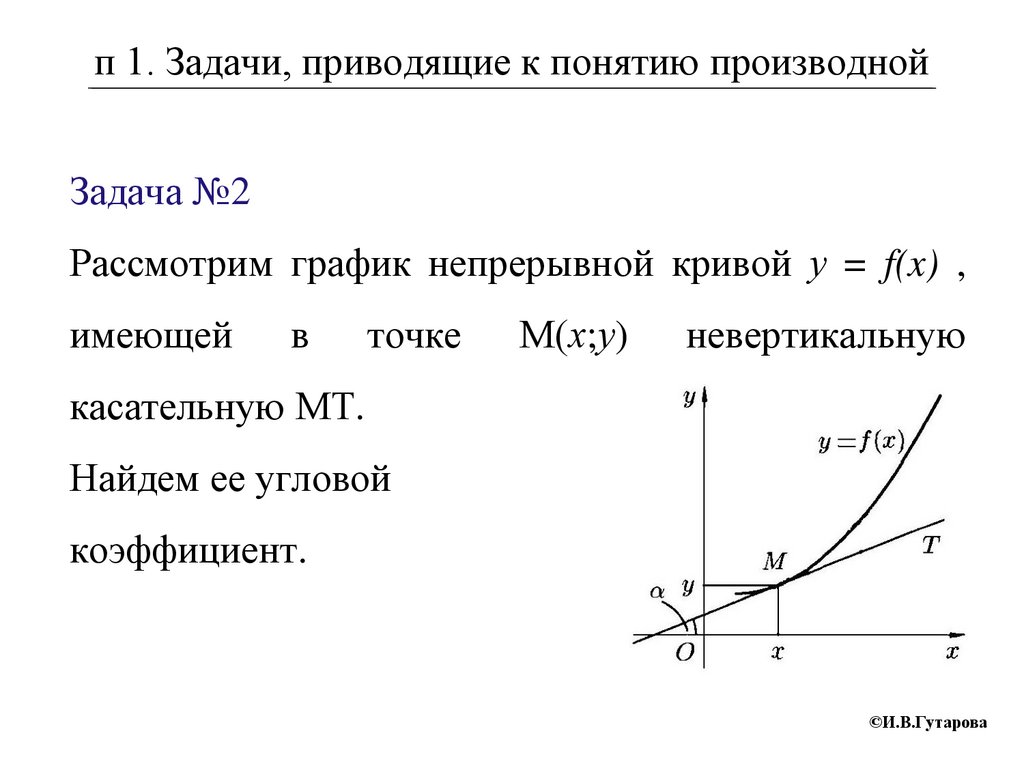
п 1. Задачи, приводящие к понятию производнойЗадача №2
Рассмотрим график непрерывной кривой у = f(x) ,
имеющей
в
точке
М(х;у)
невертикальную
касательную МТ.
Найдем ее угловой
коэффициент.
©И.В.Гутарова
15.
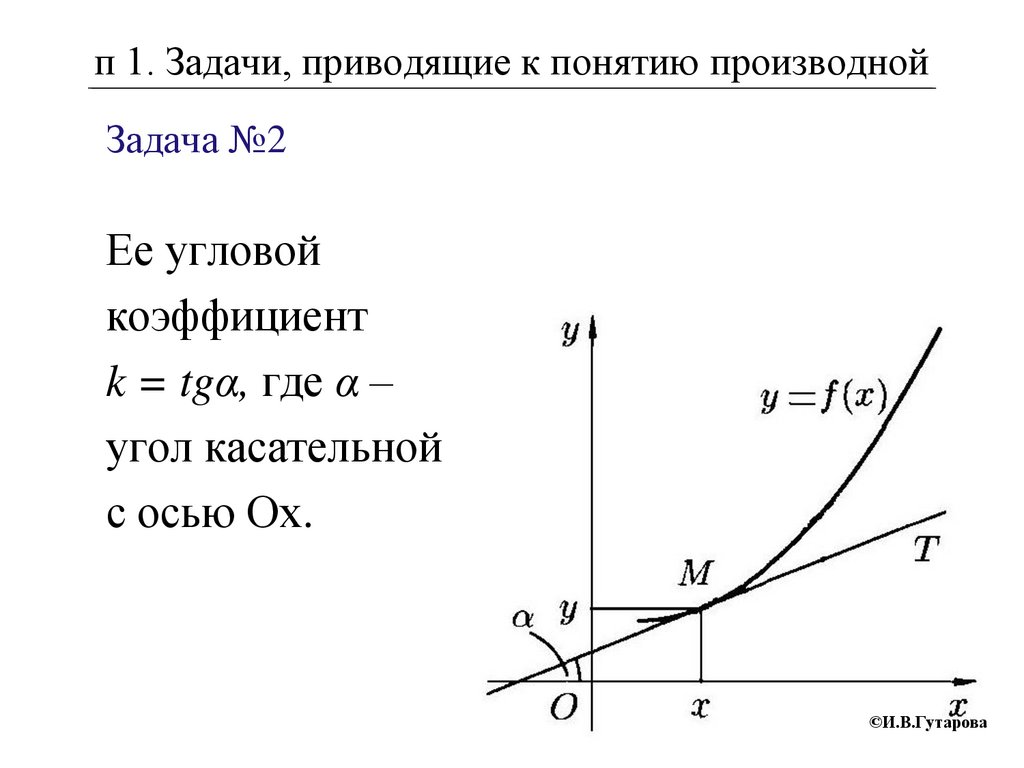
п 1. Задачи, приводящие к понятию производнойЗадача №2
Ее угловой
коэффициент
k = tgα, где α –
угол касательной
с осью Ох.
©И.В.Гутарова
16.
п 1. Задачи, приводящие к понятию производнойВозьмем точку М1(х + Δх; у + Δу) и
проведем секущую ММ1. Обозначим через
- угол
между
секущей и
осью Ох.
©И.В.Гутарова
17.
п 1. Задачи, приводящие к понятию производнойИз треугольника ММ1А
y
k cek tg
x
f x x f x
x
При Δх→0 в силу непрерывности функции Δу→0,
М1→М, ММ1→МТ, →α.
©И.В.Гутарова
18.
п 1. Задачи, приводящие к понятию производнойlim
x 0
lim tg tg
x 0
y
k tg lim tg lim
x 0
x 0 x
f x x f x
lim
x 0
x
2
©И.В.Гутарова
19.
п 1. Задачи, приводящие к понятию производнойПределы (1) и (2) имеют одинаковый вид.
Этот предел называют производной.
©И.В.Гутарова
20.
п 2. Определение производной.Уравнение касательной и нормали к
кривой
©И.В.Гутарова
21.
п 2. Определение производной. Уравнение касательнойи нормали к кривой
Определение.
Производной функции у = f(x) в
точке х0 называется предел отношения
приращения функции к приращению аргумента,
когда последний стремится к нулю.
Обозначаем:
y ,
f x ,
y x ,
f x ,
dy
dx
Итак, по определению
f x0 x f x0
у lim
x 0
x
©И.В.Гутарова
22.
п 2. Определение производной. Уравнение касательной инормали к кривой
Производная функции f(x) есть некоторая
функция f′(x) , произведенная из данной
функции.
©И.В.Гутарова
23.
п 2. Определение производной. Уравнение касательной и нормали к кривойОпределение.
Функция
у
=
f(x)
называется
дифференцируемой на интервале
(а; b) …
©И.В.Гутарова
24.
п 2. Определение производной. Уравнение касательной инормали к кривой
Определение.
Функция у = f(x), имеющая производную в каждой
точке
интервала
(а;b),
называется
дифференцируемой в этом интервале.
Операция
нахождения
производной
функции
называется ее дифференцированием.
©И.В.Гутарова
25.
п 2. Определение производной. Уравнение касательной и нормали к кривойПример 1.
Найти производную функции у = С,
где С = const.
©И.В.Гутарова
26.
п 2. Определение производной. Уравнение касательной инормали к кривой
Пример 1.
Найти производную функции у = С, где С=const.
Решение:
Значению х дадим приращение Δх.
Найдем приращение функции:
Δу = f(x+Δx) – f(x) = C – C = 0.
Cледовательно,
y
у lim
lim 0 0
x 0 x
x 0
Т.е. (С)′ = 0
©И.В.Гутарова
27.
п 2. Определение производной. Уравнение касательной и нормали к кривойПример 2.
Найти производную функции
у = х2 + 7.
©И.В.Гутарова
28.
п 2. Определение производной. Уравнение касательной инормали к кривой
Пример 2.
Найти производную функции у = х2 + 7.
Решение:
Значению х дадим приращение Δх.
Найдем приращение функции:
Δу = f(x+Δx) – f(x) =
=((х + Δх)2 + 7) – (х2 + 7) = 2хΔх + Δх2.
©И.В.Гутарова
29.
п 2. Определение производной. Уравнение касательной инормали к кривой
Найдем приращение функции:
Δу = f(x+Δx) – f(x) =
=((х+ Δх)2+7) – (х2 + 7)=2хΔх + Δх2.
Cледовательно,
y
у lim
lim 2 х х 2 х
x 0 x
x 0
Т.е. (х2 + 7)′ = 2х
©И.В.Гутарова
30.
п 2. Определение производной. Уравнение касательной и нормали к кривойМеханический смысл
производной…
©И.В.Гутарова
31.
п 2. Определение производной. Уравнение касательной и нормали к кривойВ задаче про скорость прямолинейного
движения получили формулу (1) или v = S′(t),
т.е.
скорость
прямолинейного
движения
материальной точки в момент времени t есть
производная от пути S по времени t.
В этом заключается механический смысл
производной.
©И.В.Гутарова
32.
п 2. Определение производной. Уравнение касательной и нормали к кривойГеометрический
смысл
производной…
©И.В.Гутарова
33.
п 2. Определение производной. Уравнение касательной инормали к кривой
В задаче про касательную к кривой была
получена формула (2) или k = f′(x), т.е.
производная
в
точке
х0
равна
угловому
коэффициенту касательной к графику функции
у = f(x), в точке, абсцисса которой равна х0.
В этом заключается геометрический смысл
производной.
©И.В.Гутарова
34.
п 2. Определение производной. Уравнение касательной инормали к кривой
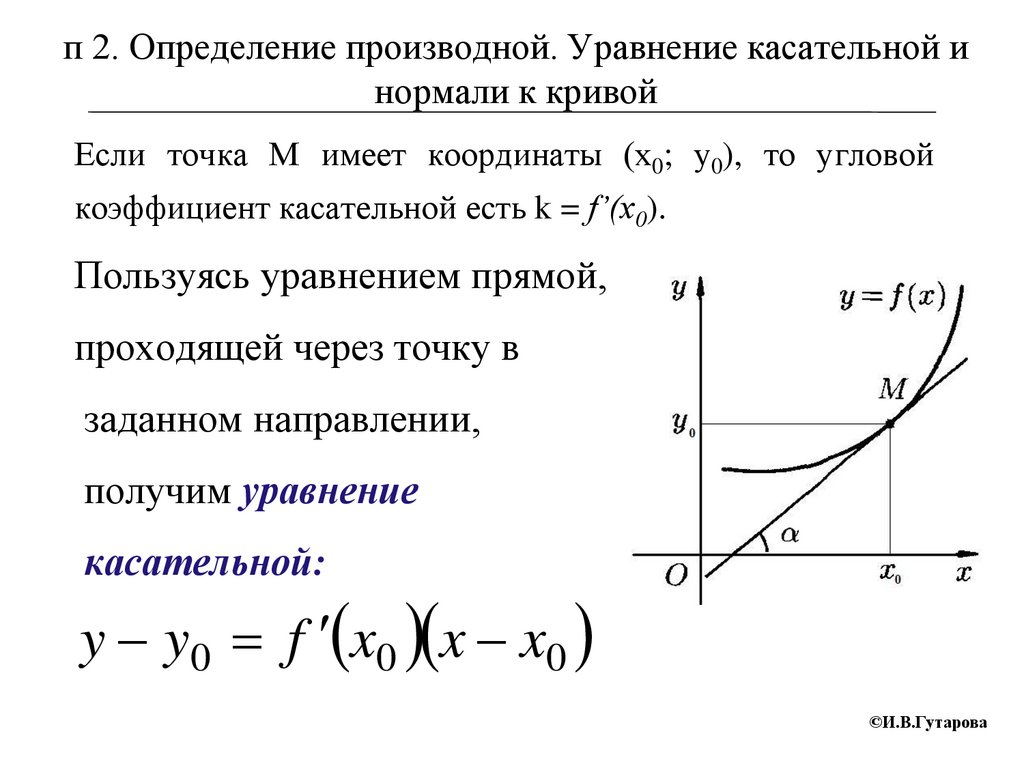
Если точка М имеет координаты (х0; у0), то угловой
коэффициент касательной есть k = f’(x0).
Пользуясь уравнением прямой,
проходящей через точку в
заданном направлении,
получим уравнение
касательной:
y y0 f x0 x x0
©И.В.Гутарова
35.
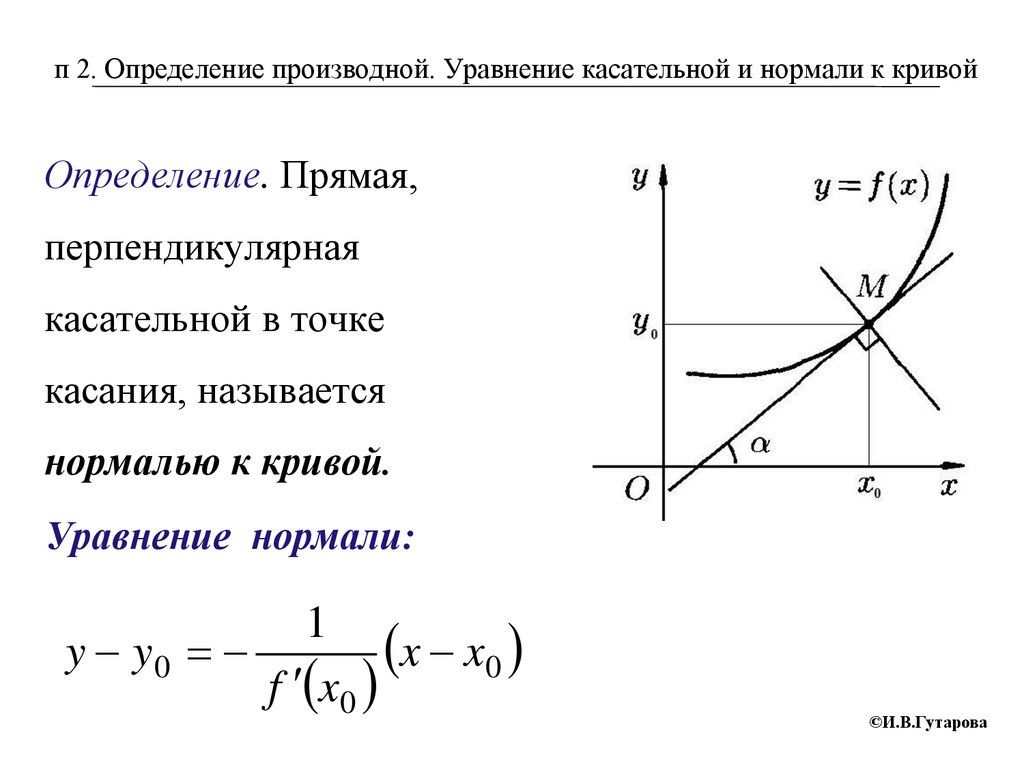
п 2. Определение производной. Уравнение касательной и нормали к кривойОпределение. Прямая,
перпендикулярная
касательной в точке
касания, называется
нормалью к кривой.
Уравнение нормали:
1
x x0
y y0
f x0
©И.В.Гутарова
36.
п 3. Связь между непрерывностью идифференцируемостью функции
©И.В.Гутарова
37.
п 3. Связь между непрерывностью и дифференцируемостьюфункции
Теорема.
Если функция дифференцируема в
некоторой точке, то она непрерывна в
ней.
©И.В.Гутарова
38.
п 3. Связь между непрерывностью и дифференцируемостьюфункции
Доказательство.
Пусть функция у = f(x) дифференцируема в
некоторой точке х. Следовательно, существует
предел
y
lim
f x
x 0 x
©И.В.Гутарова
39.
п 3. Связь между непрерывностью и дифференцируемостьюфункции
y
lim
f x
x 0 x
По теореме о связи функции ее предела и б.м.ф.,
имеем
y
f x х ,
x
где α(х) – б.м.ф. при Δх→0.
©И.В.Гутарова
40.
п 3. Связь между непрерывностью и дифференцируемостьюфункции
Или
y f x x х x
Переходя к пределу при Δх→0, получим
lim y 0
x 0
А это означает (определение №3), что функция
непрерывна в точке х.
Теорема доказана.
©И.В.Гутарова
41.
Если вы хотите научиться плавать,то смело входите в воду,
а если хотите научиться решать задачи,
то решайте их. (и решайте их много)
Дьёрдь По́йа
(1887 — 1985) — венгерский, швейцарский и
американский математик, популяризатор науки.
©И.В.Гутарова
42.
п 4. Правила дифференцированияфункций
©И.В.Гутарова
43.
п 4. Правила дифференцированияПусть функции u = u(x) и v = v(x) две
дифференцируемые в некотором интервале (a ; b)
функции.
Это означает, что функции имеют производные
©И.В.Гутарова
44.
п 4. Правила дифференцированияТеорема
Производная суммы (разности) двух функций
равна сумме (разности) производных этих
функций.
u v u v
©И.В.Гутарова
45.
п 4. Правила дифференцированияДоказательство.
Пусть у = u + v. По определению производной
получаем:
f x x f x
у lim
x 0
x
u x x v x x u x v x
lim
x 0
x
©И.В.Гутарова
46.
п 4. Правила дифференцированияu x x v x x u x v x
lim
x 0
x
u x x u x v x x v x
lim
x 0
x
x
©И.В.Гутарова
47.
п 4. Правила дифференцированияu x x u x v x x v x
lim
x 0
x
x
По теореме о сумме пределов получаем:
u
v
v
lim
lim
u
x 0
x x 0 x
©И.В.Гутарова
48.
п 4. Правила дифференцированияВ результате получили:
u v u v
Теорема справедлива для любого конечного
числа слагаемых.
Для разности теорема доказывается аналогично.
©И.В.Гутарова
49.
п 4. Правила дифференцированияТеорема
Производная произведения двух функций равна
произведению производной первого множителя
на второй плюс произведение первого множителя
на производную второго.
u v u v u v
©И.В.Гутарова
50.
п 4. Правила дифференцированияДоказательство.
Пусть у = u · v. По определению производной
получаем:
u x x v x x u x v x
у lim
x 0
x
©И.В.Гутарова
51.
п 4. Правила дифференцированияВспомним , что приращение Δу функции f(х) в
точке х0 равно Δу = f(x) – f(x0).
Или Δу = f(x0+Δх) – f(x0), тогда f(x0+Δх) =f(x0) + Δу,
следовательно u(x0+Δх) = u(x0) +Δu и
v(x0+Δх) = v(x0) +Δv .
u x x v x x u x v x
у lim
x 0
x
Заменяем
u x u v x v u x v x
lim
x 0
x
©И.В.Гутарова
52.
п 4. Правила дифференцированияu x u v x v u x v x
lim
x 0
Раскрываем
скобки
x
u х v х u х v v х u u v u х v х
lim
x 0
x
©И.В.Гутарова
53.
п 4. Правила дифференцированияu х v х u х v v х u u v u х v х
lim
x 0
x
v
u
u
lim
u
x
v
x
v
x 0
x
x
x
©И.В.Гутарова
54.
п 4. Правила дифференцированияv
u
u
lim
u
x
v
x
v
x 0
x
x
x
Используем свойства пределов
u
v
u
v x lim
u
x
lim
lim
v
lim
x 0
x 0
x 0
x
x x 0
x
©И.В.Гутарова
55.
п 4. Правила дифференцированияu
v
u
lim
v
lim
lim
x
u
v x lim
x 0
x 0
x 0
x
x x 0
x
v x u u x v 0 u
u v u v
©И.В.Гутарова
56.
п 4. Правила дифференцированияВ результате получили:
u v u v u v
©И.В.Гутарова
57.
п 4. Правила дифференцированияСледствие 1. Если С = const, то
С u C u
©И.В.Гутарова
58.
п 4. Правила дифференцированияСледствие 2.
u v w u v w u v w u v w
©И.В.Гутарова
59.
п 4. Правила дифференцированияТеорема
Производная частного двух функций, если знаменатель
≠0, равна дроби, числитель которой есть разность
произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель
есть квадрат прежнего знаменателя.
u u v u v
2
v
v
©И.В.Гутарова
60.
п 4. Правила дифференцированияДоказательство.
Пусть у = u / v. По определению производной получаем:
u x x u x
v x x v x
у lim
x 0
x
u x u u x
v x v v x
lim
x 0
x
©И.В.Гутарова
61.
п 4. Правила дифференцированияu x u u x
v x v v x
lim
x 0
x
u x v x v x u u x v x u x v
lim
x 0
x v x v x v
©И.В.Гутарова
62.
п 4. Правила дифференцированияu x v x v x u u x v x u x v
lim
x 0
x v x v x v
v u u v
lim
2
x 0
x v x v x v
©И.В.Гутарова
63.
п 4. Правила дифференцированияu
v
v
u
x
x
lim
x 0
v 2 x v x v
u
v
u u lim v
v lim
x 0
x 0
v lim
u
lim
x
x
x 0
2x 0 x
x
v2 x v x lim v
v x v x lim
x
0v
x 0
u v u v
v2
©И.В.Гутарова
64.
п 4. Правила дифференцированияВ результате получили:
u u v u v
2
v
v
©И.В.Гутарова
65.
п 4. Правила дифференцированияСледствие 1. Если С = const, то
u 1
u
С C
©И.В.Гутарова
66.
п 4. Правила дифференцированияСледствие 2. Если С = const, то
C v
С
2
v
v
©И.В.Гутарова
67.
п 5. Производная сложной и обратнойфункций
©И.В.Гутарова
68.
п 5. Производная сложной и обратной функцийПусть у = f(u) и u = φ(x), тогда у = f(φ(х)) –сложная
функция с промежуточным аргументом u и независимым
аргументом х.
©И.В.Гутарова
69.
п 5. Производная сложной и обратной функцийТеорема
Если функция u = φ(x) имеет производную u x в точке х0,
y u
а функция у = f(u) имеет производную
в
соответствующей точке u0 = φ(x0), то сложная функция
у = f(φ(х)) имеет производную y x
в точке х0, которая
находится по формуле:
y x y u u x
©И.В.Гутарова
70.
п 5. Производная сложной и обратной функцийДоказательство.
у
По условию lim
u .
y
u 0
u
Отсюда, по теореме о связи функции, ее предела
и б.м.ф. имеем
или
у
y u
u
у y u u u
где α → 0 при Δu → 0.
©И.В.Гутарова
71.
п 5. Производная сложной и обратной функцийПо условию
Поэтому
u
x .
lim
u
х 0
x
u u x x x
где β → 0 при Δх → 0.
©И.В.Гутарова
72.
п 5. Производная сложной и обратной функцийПодставим значение Δu в равенство для Δу,
получим
у у u u x x x u x x x
у у u u x x у u x
u x x x
©И.В.Гутарова
73.
п 5. Производная сложной и обратной функцийу
уu u x уu u x
х
у
у х lim
lim
у
u u x lim уu
x 0
x 0
ху x 0
u x lim уu
у х lim
lim
у
u
x 0
x 0
х x 0
x lim
lim
u
x 0
x 0
x lim
lim
u
x 0
x 0
уu u x 0 0 0 уu u x
©И.В.Гутарова
74.
п 5. Производная сложной и обратной функцийВ результате получили
y x y u u x
©И.В.Гутарова
75.
п 5. Производная сложной и обратной функцийИтак, для нахождения производной сложной функции
надо производную данной функции по промежуточному
аргументу
умножить
промежуточного
аргумента
на
производную
по
независимому
аргументу.
Это правило остается в силе, если промежуточных
аргументов несколько.
©И.В.Гутарова
76.
п 5. Производная сложной и обратной функцийПусть у = f(х) и х = φ(у) - взаимно обратные
функции.
©И.В.Гутарова
77.
п 5. Производная сложной и обратной функцийТеорема
Если функция у = f(х) строго монотонна на интервале (a;b) и
имеет неравную нулю производную f x в произвольной точке
этого интервала, то обратная ей функция х = φ(у) также имеет
производную у в соответствующей точке, определяемую
1
у
равенством
или
f x
1
х у
у х
©И.В.Гутарова
78.
п 5. Производная сложной и обратной функцийДоказательство :
Рассмотрим обратную функцию х = φ(у). Дадим
аргументу у приращение Δу ≠ 0.
Функция получит приращение Δх, причем Δх≠0 в силу
строгой монотонности функции у = f(х).
Тогда
х 1
у у
х
©И.В.Гутарова
79.
п 5. Производная сложной и обратной функцийЕсли Δу →0, то в силу непрерывности обратной функции
Δх →0.
y
x 0,
f
Так как lim
x 0
x
то
lim
y 0
х
1
1
у lim у f x
y 0
х
Т.е.
1
у
f x
Таким образом, производная обратной функции равна
обратной величине производной данной функции.
©И.В.Гутарова
80.
п 6. Производные основныхэлементарных функций
©И.В.Гутарова
81.
п 6. Производные основных элементарных функцийЭлементарные функции:
Степенная функция у = xn.
Показательная функция у = ах.
Логарифмическая функция у = logах.
Тригонометрические функции.
Обратные тригонометрические функции.
Найдем их производные.
©И.В.Гутарова
82.
Степенная функция у = xn.Бином Ньютона
©И.В.Гутарова
83.
Показательная функция у = ах.©И.В.Гутарова
84.
Обратные тригонометрические функции.Найти производную функции
у arcsin x и
y arctgx
Так как у = arcsinx имеет обратную функцию x = sinу, то по
правилу их дифференцирования имеем
1
1
1
1
arcsin x
2
2
cos y
1
sin
y
1
x
sin y
©И.В.Гутарова
85.
Найти производную функцииу arcsin x и
y arctgx
Так как у = arctgx имеет обратную функцию x = tgу, то по
правилу их дифференцирования имеем
1
1
1
1
2
arctgx
cos y
2
2
1
1
tg
y
1
x
tgy
cos2 y
©И.В.Гутарова
86.
Производные остальных функций находятсяаналогично.
©И.В.Гутарова
87.
п 7. Таблица производных©И.В.Гутарова
88.
Таблица производных1) (x ) x
'
1
2) (a )' a ln a
x
x
( e x )' e x
1
3) (loga x )'
x ln a
(ln x )'
1
x
4) (sin x)' cos x
5) (cos x)' sin x
1
6) ( tg x )'
cos 2 x
1
7) (ctg x )' 2
sin x
8) (arcsin x )'
1
1 x
1
9) (arccos x )'
1 x2
1
10) (arctg x )'
1 x2
2
©И.В.Гутарова
89.
Таблица производных (сложная функция)1) ( u ) k u
k
'
k 1
u
2 ) ( a )' a ln a u
u
u
( eu )' eu u
1
3 ) (log a u )'
u
u ln a
1
(ln u ) u
u
'
4 ) (sin u )' cos u u
5 ) (cos u )' sin u u
1
6 ) ( tg u )'
u
2
cos u
1
7 ) ( ctg u )' 2 u
sin u
8 ) (arcsin u )'
9 ) (arccos u )'
1
1 u
u
2
1
1 u
2
u
1
10 ) ( arctg u )'
u
2
1 u
1
11 ) ( arcctg u )'
u
2
1 u
©И.В.Гутарова
90.
Пример 1Найти производную сложной функции
у log tgx
3
2
4
©И.В.Гутарова
91.
у log tgx3
2
Пример 1
4
y 3 log tgx log2 tgx
2
2
4
4
1
4
3 log tgx 4
tgx
tgx ln 2
2
2
4
1
1
4
3 log tgx 4
x
2 4
tgx ln 2 cos x
1
1
1
1
22
44
3 3
log22tgx
tgx 4 4
y 33 log
2 2 4 4 4 x4 x
tgx ln
ln22 cos
cosx x
tgx
3
2
4
24x log2 tgx
sin 2 x 4 ln 2
2
2
4
©И.В.Гутарова
92.
§2 Дифференцирование функцийп1. Неявно заданная функция
©И.В.Гутарова
93.
Если неявная функция задана уравнением F(x,y) = 0, тодля нахождения производной от у по х нет необходимости
разрешать уравнение относительно у.
Достаточно продифференцировать это уравнение по х,
рассматривая при этом у как функцию от х.
Полученное уравнение затем разрешить относительно y .
Производная
неявной
функции
выражается
через
аргумент х и функцию у.
©И.В.Гутарова
94.
Пример 1Найти производную функции
х у 3ху 0
3
3
©И.В.Гутарова
95.
Пример 1Найти производную функции
х 3 у 3 3ху 0
Продифференцируем уравнение:
3х 3 у у 3 у ху 0
2
2
3х 3 у у 3 у 3ху 0
2
Выразим y :
2
3 у 3х 2
у 2
3 у 3х
у х
у 2
у х
2
©И.В.Гутарова
96.
Пример 2Найти производную функции
е х у
ху
3
©И.В.Гутарова
97.
Продифференцируем уравнение:2
е у ху 1 3 у у
ху
Выразим у
е у е ху 1 3 у у
ху
ху
2
ху
2
ху
у хе 3 у 1 уе
1 уе
у ху
2
хе 3 у
ху
©И.В.Гутарова
98.
п 2. Функция, заданная параметрически©И.В.Гутарова
99.
Пусть зависимость между аргументом х и функцией у заданапараметрически ( в виде двух уравнений),
х х( t )
y y( t )
где t – вспомогательная переменная, называемая параметром.
Найдем производную у по х , считая, что функции х(t) и у(t)
имеют производные, и х(t) имеет обратную функцию t = t(x).
Тогда у = у(t) = у(t(х)).
По правилу дифференцирования сложной функции имеем:
у х уt t x
©И.В.Гутарова
100.
1Но производная обратной функции: t x
хt
1
Тогда у у
х
t
хt
Т.е.
уt
у х
хt
- формула, позволяющая
находить производную от функции заданной
параметрически, не находя непосредственной зависимости
у от х.
©И.В.Гутарова
101.
Пример 1.Найти производную функции, заданной параметрически
х 3 cos t
y 2 sin t
Находим производную по формуле
уt
у х
хt
2 cos t
2
у х
ctgt
3 sin t
3
©И.В.Гутарова
102.
п3. Логарифмическое дифференцирование©И.В.Гутарова
103.
Вряде
целесообразно
случаев
для
нахождения
производной
заданную
функцию
сначала
прологарифмировать,
а
затем
результат
продифференцировать.
Такую
операцию
называют
логарифмическим дифференцированием.
©И.В.Гутарова
104.
п3. Логарифмическое дифференцированиеФункция называется показательной, если независимая
переменная входит в показатель степени, и степенной, если
переменная является основанием. Если же и основание и
показатель степени зависят от переменной, то такая функция
будет показательно – степенной.
Производные
таких
функций
находят
с
помощью
логарифмического дифференцирования.
©И.В.Гутарова
105.
Пример.Найти производную функции
y ( x 3x )
2
x cos x
Решение:
Логарифмируя, получим: ln y x cos x ln x 2 3x
Продифференцируем это выражение:
y
сosx x sin x ln x 2 3x
y
2x 3
x cos x 2
x 3x
©И.В.Гутарова
106.
§3. Производные высших порядков.©И.В.Гутарова
107.
§3. Производные высших порядков.Пусть функция у = f(x) - дифференцируема на некотором
интервале.
Тогда, дифференцируя ее, получаем производную первого
порядка
df ( x)
y f ( x)
,
dx
которая также является функцией от х.
©И.В.Гутарова
108.
§3. Производные высших порядков.Если функция y = f (x) - дифференцируема, то ее
производная
называется производной второго порядка
функции у = f(x) и обозначается
2
d f ( x)
y f ( x)
2
dx
y = (y ) или
d 2 y d dy
2
dx dx
dx
©И.В.Гутарова
109.
§3. Производные высших порядков.Этот процесс можно продолжить и далее, находя
производные порядка n.
d n y d d n 1 y
n 1
n
dx dx
dx
Производные
порядка
выше
первого
называются
производными высших порядков.
Начиная с производной четвертого порядка, производные
обозначают римскими цифрами или числами в скобках.
©И.В.Гутарова
110.
ПримерНайти производную n-порядка функции у = sinx.
Решение:
y sin x cos x sin x
2
y y cos x sin x sin x
y sin x sin x 2
y
sin x 2
2
2
y y sin x cos x
sin x 3
2
©И.В.Гутарова
111.
Следовательно, производная n-порядка функции у = sinx.y sin x n
2
n
©И.В.Гутарова
112.
§3. Производные высших порядков.Пусть неявная функция задана уравнением F(x,y)=0.
Найдем
производную
Продифференцировав
ее
по
первого
порядка.
х,
вторую
получим
производную от неявной функции.
В нее войдут х, у и у’. Подставив уже найденное значение
у’, выразим у’’ через х и у.
©И.В.Гутарова
113.
ПримерНайти у′′′, если х2 + у2=1
Дифференцируем по х:
2х + 2у·у’=0 ⟹
Дифференцируем еще раз по х:
х
у
у
1 у х у
у
у2
х
у х
2
2
у
у
х
1
у
3
2
3
у
у
у
©И.В.Гутарова
114.
ПримерИтак,
у
х
у
1
у 3
у
Дифференцируем еще раз по х:
3 у у 3
3х
у
4 у 5
6
у
у
у
2
©И.В.Гутарова
115.
§3. Производные высших порядков.Пусть функция задана параметрически
х х( t )
y y( t )
уt
Ее первая производная находится по формуле у х
хt
Найдем производную второго порядка
у х t
у хх у х х у х t t x
xt
©И.В.Гутарова
116.
§3. Производные высших порядков.Итак, если функция задана параметрически
х х( t )
y y( t )
То ее производные находятся по формулам
уt
у х ,
хt
ух t
у хх
,
xt
ухх t
у
, ...
xt
©И.В.Гутарова
117.
§4. Основные теоремыдифференциального исчисления
©И.В.Гутарова
118.
§4. Основные теоремы дифференциального исчисленияТеорема Ролля.
Если функция y = f(x) непрерывна на отрезке [a, b],
дифференцируема на интервале (а, b) и значения функции на
концах отрезка равны f(a) = f(b), то на интервале (а, b)
существует точка с, a < с < b, в которой производная
функция f(x) равная нулю, т.е. f (с) = 0.
©И.В.Гутарова
119.
Доказательство.Так как функция непрерывна на отрезке, то она
достигает на этом отрезке своего наибольшего
и наименьшего значений.
Обозначим:
М - наибольшее значение,
m - наименьшее значение.
©И.В.Гутарова
120.
Доказательство.Возможны два случая:
1) М = m,
2) M m.
©И.В.Гутарова
121.
Доказательство.Рассмотрим первый случай: M = m.
Тогда функция есть постоянное число,
производная которой нулю в любой точке
заданного
отрезка.
Значит,
точка
с
существует.
©И.В.Гутарова
122.
Доказательство.Рассмотрим второй случай: M m.
Тогда функция достигает хотя бы одно из
значений М или m во внутренней точке
интервала (а, b) , так как f(a) = f(b).
©И.В.Гутарова
123.
Доказательство.Обозначим за с (a < с < b) точку, в которой
f(с) = M, тогда для любого х из интервала
(а, b) верно f(с) ≥ f(х).
Тогда
f(с) = f(с+ x) – f(с) 0
©И.В.Гутарова
124.
Значит,f ( с ) 0, если x 0
x
0, если x 0
f ( с )
Найдем производную функции в точке с: lim
x 0
x
Получим:
f (с)
1) lim
0
x 0 x
x 0
f (с)
2) lim
0
x 0 x
x 0
©И.В.Гутарова
125.
Таким образом:f ( с )
lim
0, т.е.
x 0
x
f ( с ) 0.
Если f(с) = m, то доказательство аналогично.
Теорема доказана.
©И.В.Гутарова
126.
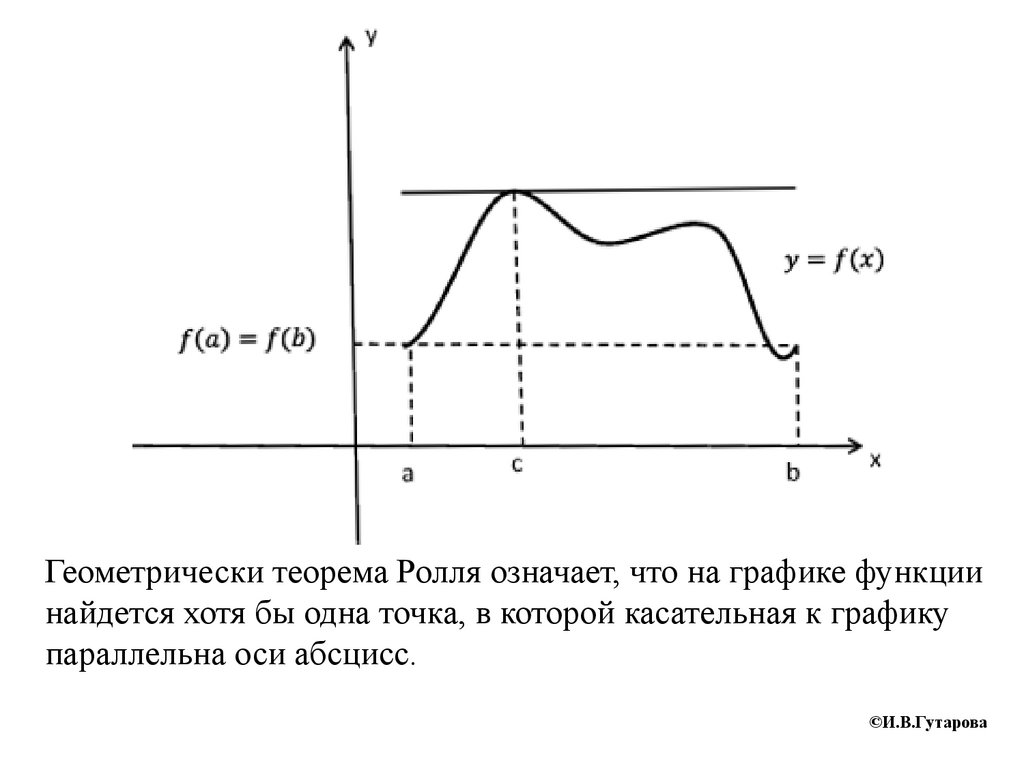
Геометрически теорема Ролля означает, что на графике функциинайдется хотя бы одна точка, в которой касательная к графику
параллельна оси абсцисс.
©И.В.Гутарова
127.
Теорема Коши.Если функции f(x) и g(x) непрерывны на отрезке [a, b] и
дифференцируемы на интервале (a, b) и g (x) 0 на
интервале (a, b), то существует по крайней мере одна
точка с, a < с < b, такая, что
f ( b ) f ( a ) f ( с )
g( b ) g( a ) g ( с )
©И.В.Гутарова
128.
Доказательство.g (b) g (a) 0
Так как по теореме Ролля нашлась бы такая точка с, что g (с)
= 0 , чего не может быть по условию теоремы.
©И.В.Гутарова
129.
Доказательство.Рассмотрим вспомогательную функцию
f (b) f (a)
F ( x) f ( x) f ( a )
( g ( x) g (a))
g (b) g (a)
Она удовлетворяет условиям теоремы Ролля: непрерывна,
дифференцируема, так как является линейной комбинацией
функций f(x) и g(x) и на концах отрезка принимает
одинаковые значения:
f (b) f (a)
F (а) f (а) f (a)
( g (а) g (a)) 0
g (b) g (a)
f (b) f (a)
F (b) f (b) f (a)
( g (b) g (a)) 0
g (b) g (a)
©И.В.Гутарова
130.
Доказательство.На основании теоремы Ролля найдется такая
точка с, что
F (c) = 0.
©И.В.Гутарова
131.
Доказательство.На основании теоремы Ролля найдется такая точка с, что
F (c) = 0.
Найдем производную функции:
f (b) f (a)
F ( x) f ( x) f ( a )
( g ( x) g (a))
g (b) g (a)
f (b) f (a)
F ( x) f ( x)
g ( x)
g (b) g (a)
©И.В.Гутарова
132.
Доказательство.f (b) f (a)
F ( x) f ( x)
g ( x)
g (b) g (a)
тогда
f (b) f (a )
F ( с ) 0 f ( с )
g ( с )
g( b ) g( a )
т.е.
f ( b ) f ( a ) f ( с )
g( b ) g( a ) g ( с )
Теорема доказана.
©И.В.Гутарова
133.
Теорема Лагранжа (о среднем значении).Если функция y = f(x) непрерывна на отрезке [a, b] и
дифференцируема на интервале (а, b), то на этом интервале
найдется по крайней мере одна точка с (a < с < b), такая,
что
f (b) f (a )
f ( с )
b a
©И.В.Гутарова
134.
Доказательство:Можем рассмотреть как частный случай теоремы
Коши.
Пусть g(х) = х, найдем:
g(b) - g(a) = b - a,
g′(x)=1.
©И.В.Гутарова
135.
Доказательство:Подставим в формулу теоремы Коши, получим:
f (b) f (a )
f ( с )
b a
или
f b f a f c b a .
Теорема доказана.
©И.В.Гутарова
136.
f b f a f c b a- формула Лагранжа или формула о конечном приращении,
т.е. приращение дифференцируемой функции на отрезке
равно приращению аргумента, умноженному на значение
производной функции в некоторой внутренней точке этого
отрезка.
©И.В.Гутарова
137.
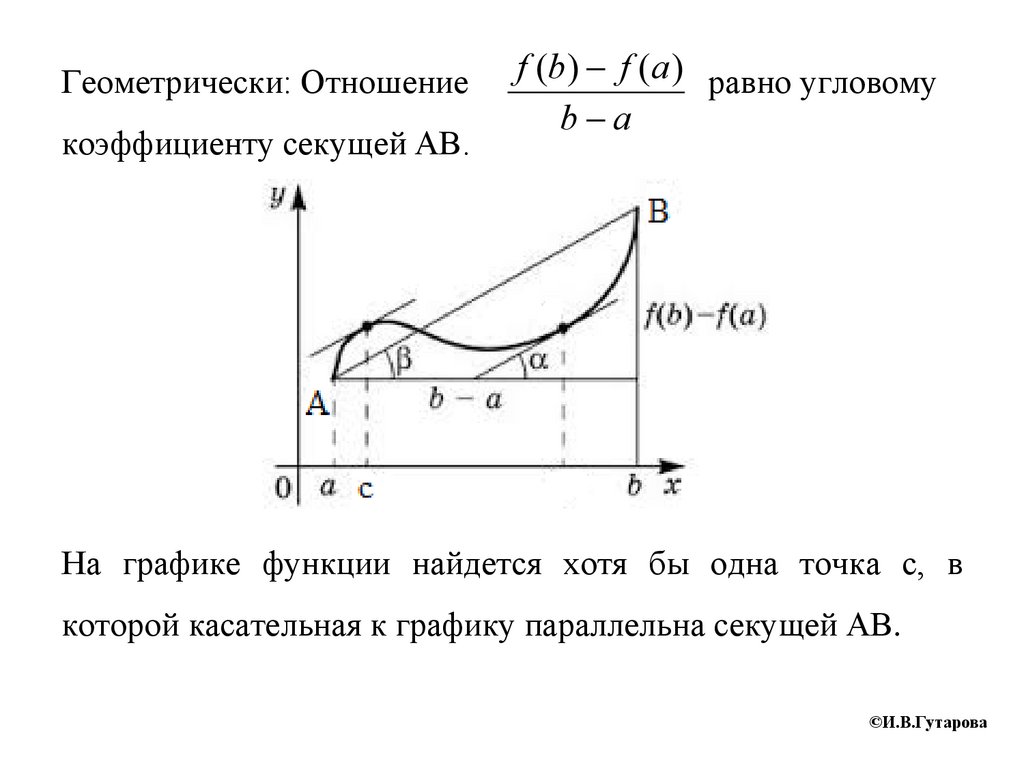
Геометрически: Отношениекоэффициенту секущей АВ.
f (b) f (a) равно угловому
b a
На графике функции найдется хотя бы одна точка с, в
которой касательная к графику параллельна секущей АВ.
©И.В.Гутарова



















































































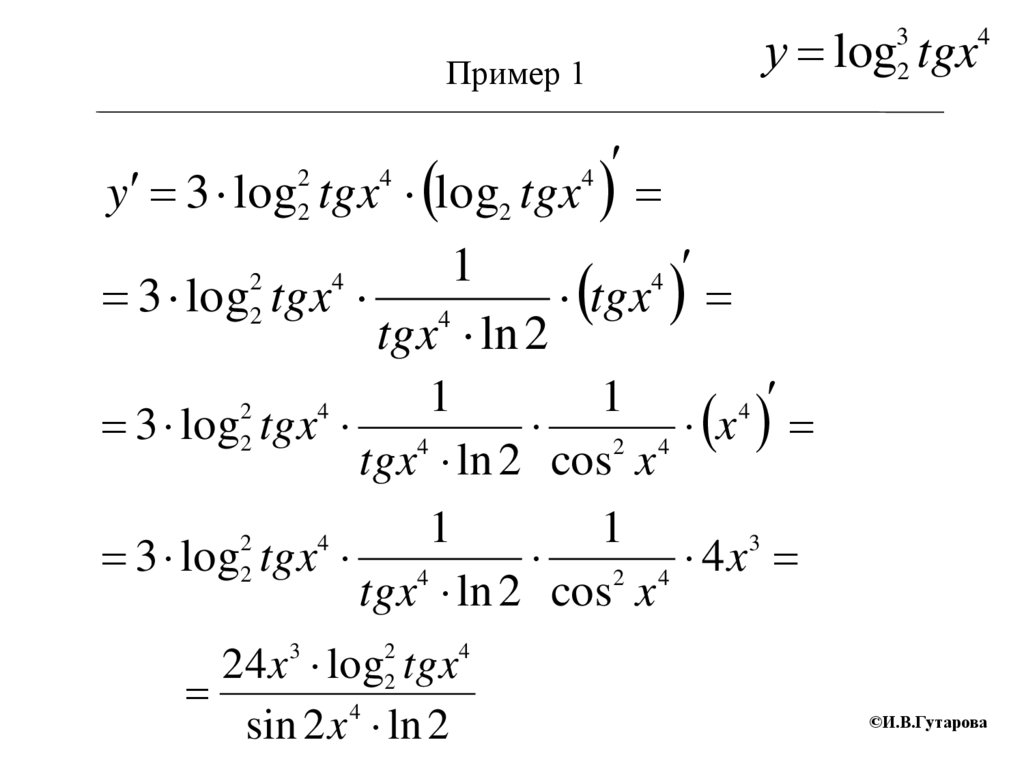












































 mathematics
mathematics








