Similar presentations:
Численное интегрирование. (Лекция 2)
1.
bI f ( x)dx
a
2.
bf
x
dx
F
b
F
a
a
3. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
4.
1.Отрезок [a,b] разбивают на k равных частей:a=d0<d1<…<dk=b,
di=a+i*h, где h=(b-a)/k.
2.Интеграл по всему отрезку [a,b] разбивается на
сумму интегралов по получившимся отрезкам
[di,di+1] при i=0,1,2,…,k-1.
3.На каждом из маленьких отрезков интеграл
приближенно вычисляют по формулам
b
n
a
i 0
I f ( x)dx ci f ( xi )
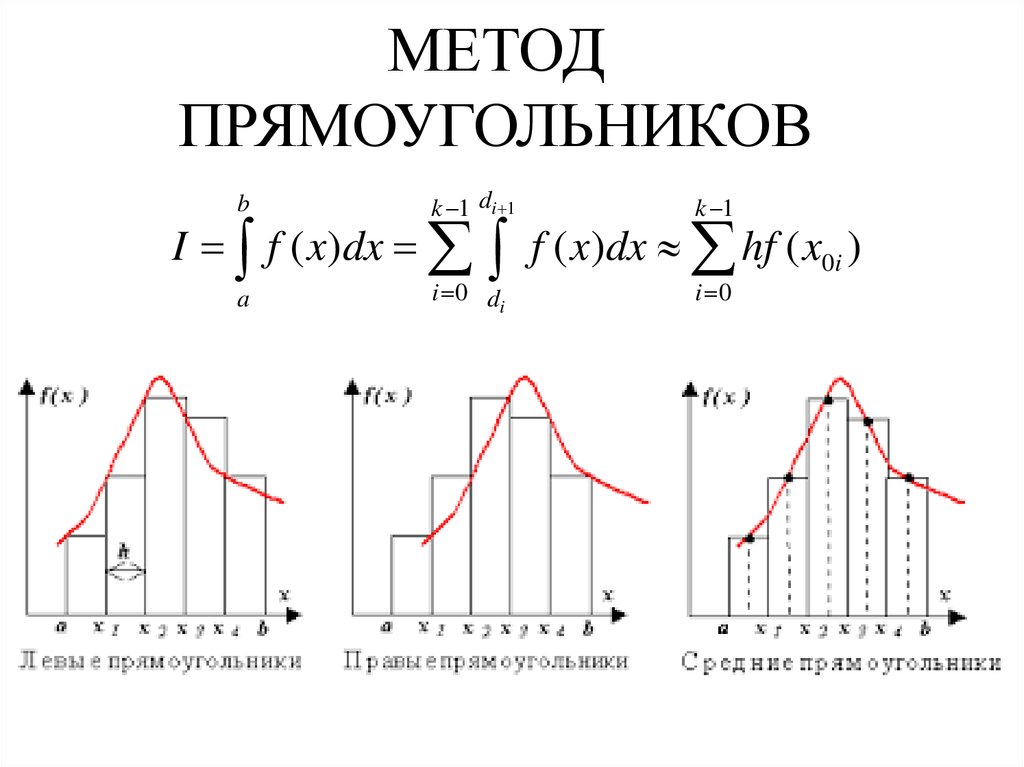
5. МЕТОД ПРЯМОУГОЛЬНИКОВ
bk 1 di 1
a
i 0 di
I f ( x)dx
k 1
f ( x)dx hf ( x0i )
i 0
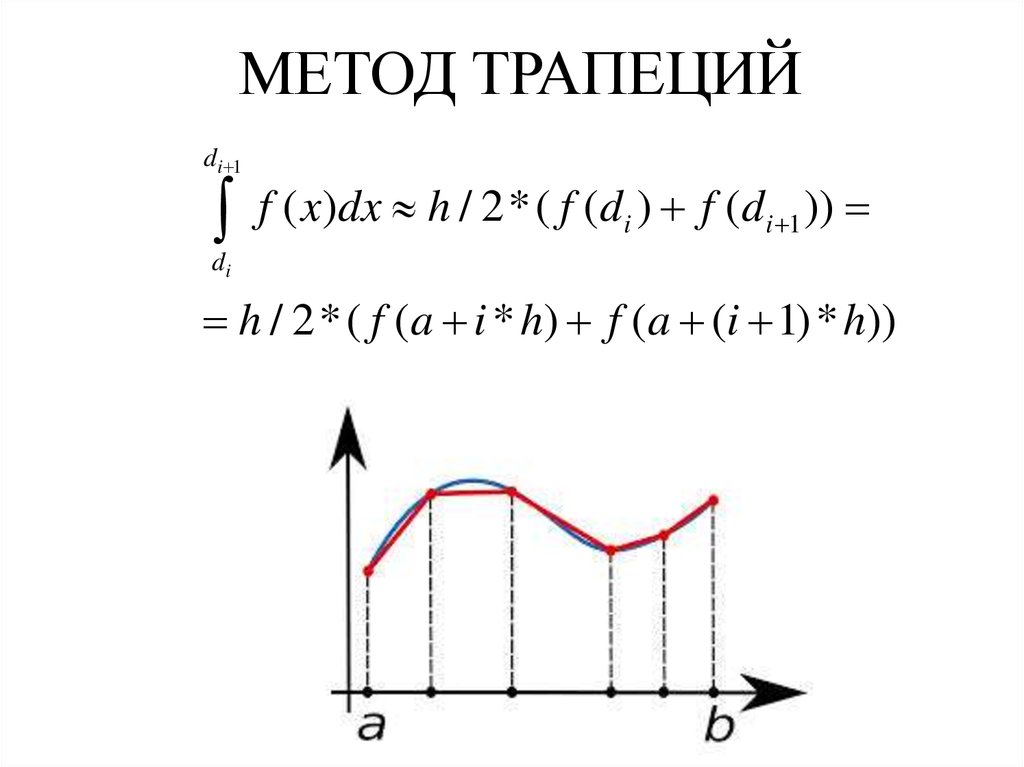
6. МЕТОД ТРАПЕЦИЙ
di 1f ( x)dx h / 2*( f (di ) f (di 1 ))
di
h / 2*( f (a i * h) f (a (i 1) * h))
7. МЕТОД СИМПСОНА
Шаблон содержит 3 узла, которые расположеныпо краям и в середине отрезка [di,di+1];
интерполяционный многочлен имеет вторую
степень.
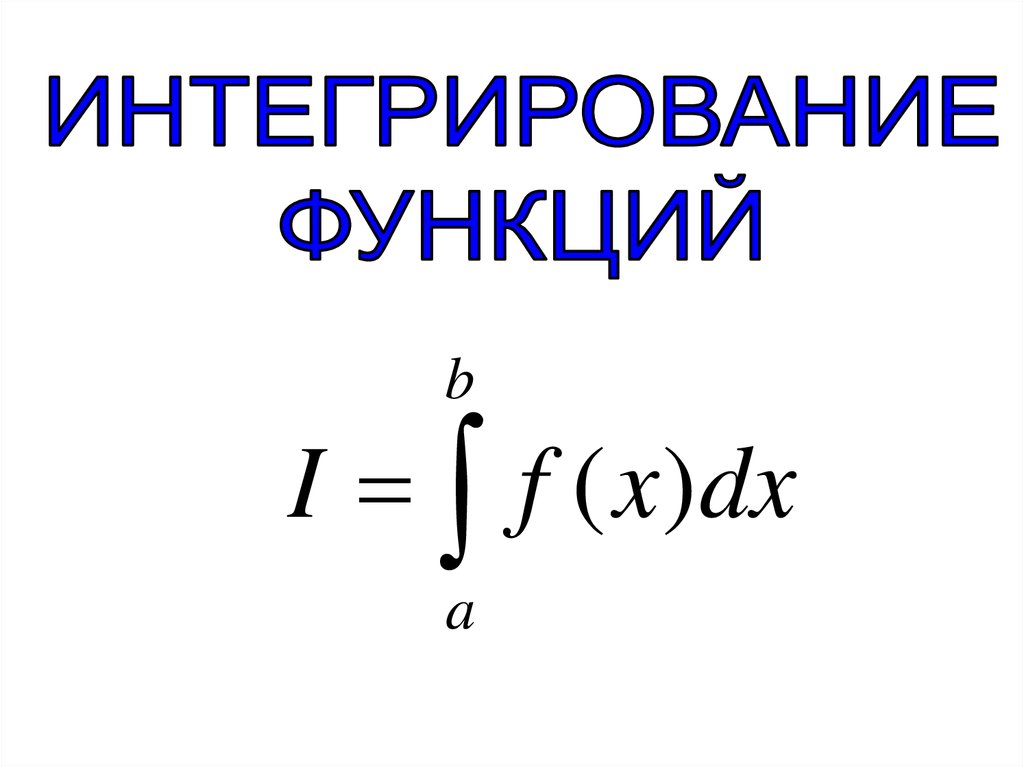
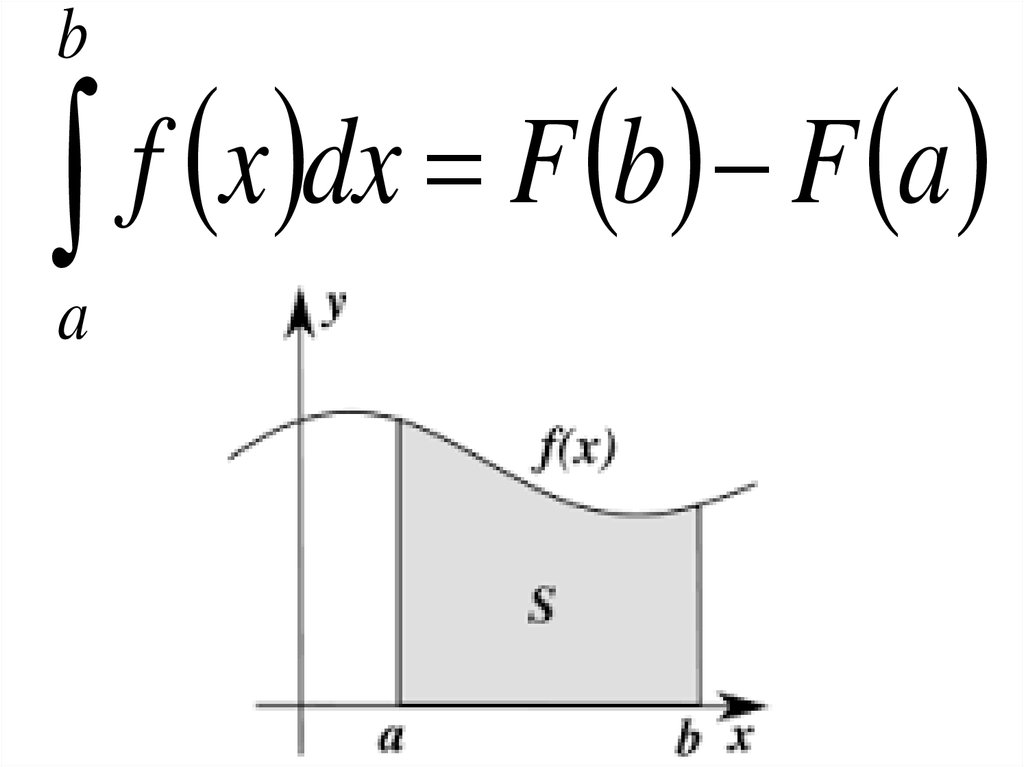


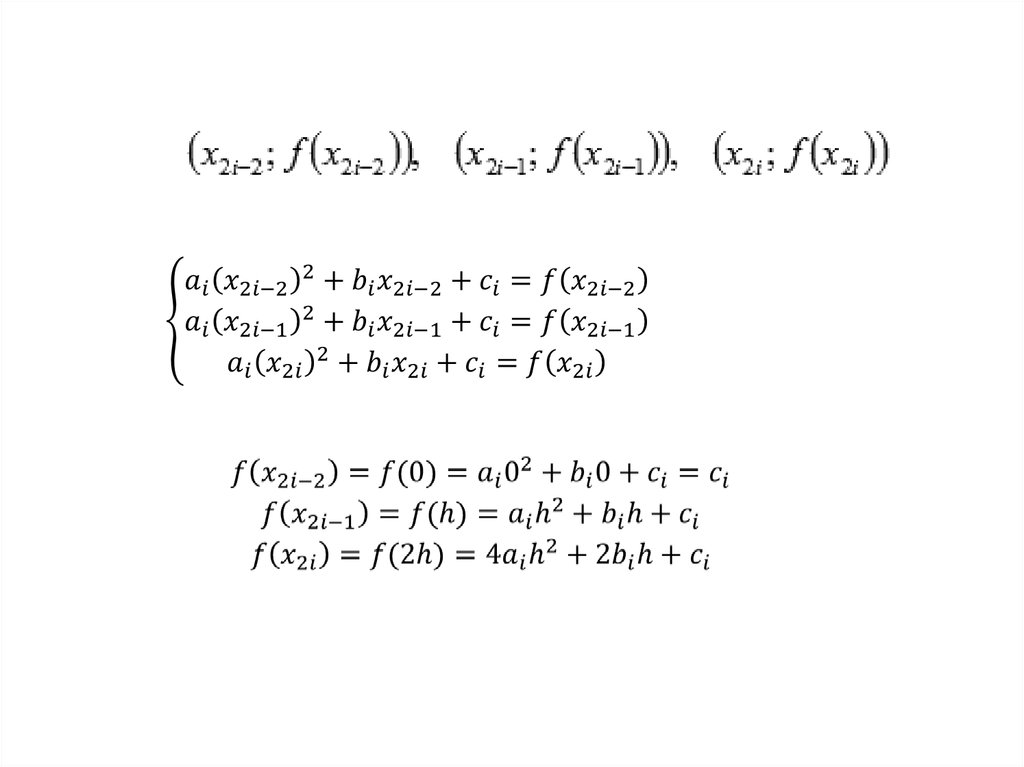

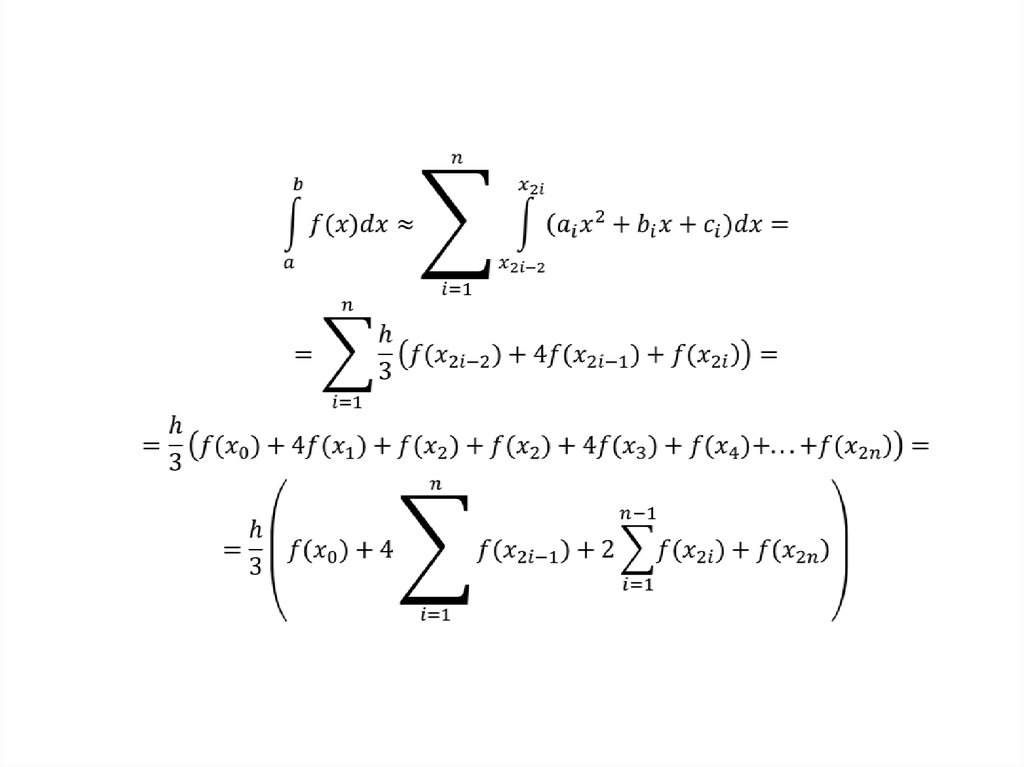
 mathematics
mathematics








