Нелинейные вычислительные процессы. Лекция № 9

1.

Нелинейные вычислительные процессы
Лекция № 9
Характеристический анализ уравнений
Эйлера. Автомодельные решения
уравнений Эйлера. Волны Римана.
1

2.

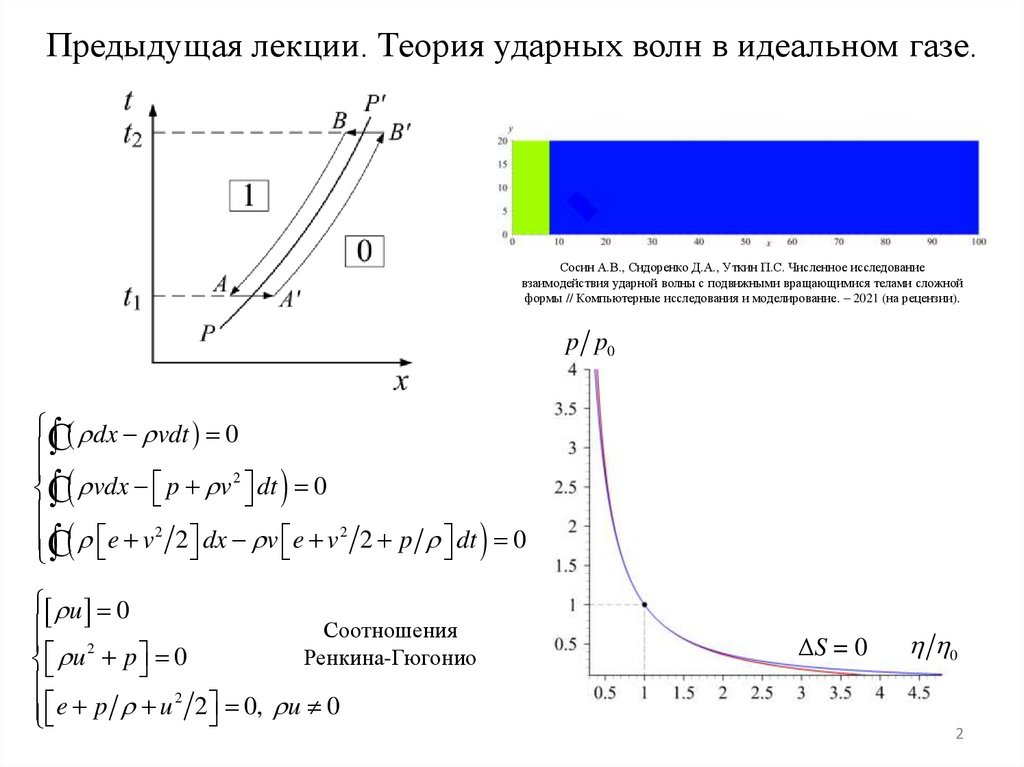
Предыдущая лекции. Теория ударных волн в идеальном газе.
Сосин А.В., Сидоренко Д.А., Уткин П.С. Численное исследование
взаимодействия ударной волны с подвижными вращающимися телами сложной
формы // Компьютерные исследования и моделирование. – 2021 (на рецензии).
p p0
dx vdt 0
С
2
dt 0
vdx
p
v
С
e v 2 2 dx v e v 2 2 p dt 0
С
u 0
Соотношения
2
Ренкина-Гюгонио
u p 0
e p u 2 2 0, u 0
ΔS = 0
0
2

3.

Характеристический анализ системы уравнений Эйлера
Дивергентная векторная форма
записи
Дивергентная покомпонентная
форма записи
q f
0
t x
v
2
q v f v p
E p v
E
v2
p
E e e
2
1
t x v 0
v
2
v
p 0
x
t
E
E p v 0
x
t
3

4.

Система уравнения в частных производных
первого порядка гиперболического типа
U
U
A t , x, U
f t , x, U
t
x
U I , f I , A I I
A E 0 i , i 1,I
A i E ωi 0 ωi
Ω R ω1 , ω 2 ,..., ω I Ω R 0
I
Вектор
консервативных
переменных
w v
p
Вектор
примитивных
переменных
• Наличие конечной скорости распространения бесконечно слабых
возмущений
• Возможность существования разрывных решений даже для гладких
начальных данных
4

5.

Характеристический анализ системы уравнений Эйлера
в примитивных переменных ρ, v, p (1)
Закон сохранения массы
v 0
t x
v
v
0
t
x
x
Закон сохранения импульса
v
v2 p 0
t
x
Закон сохранения массы
v p
v
v
t v t v x v x x 0
v
v 1 p
v
0
t
x x
5

6.

Характеристический анализ системы уравнений Эйлера
в примитивных переменных ρ, v, p (2)
Закон сохранения энергии
E
E p v 0
t
x
E
v
p
E
t E t E x v v x p x v x 0
Закон сохранения массы
v2
E e
2
e v e
v
p
v
v t t v v x x p x v x 0
Закон сохранения импульса
6

7.

Характеристический анализ системы уравнений Эйлера
в примитивных переменных ρ, v, p (3)
e
e
v
v p 0
t
x
x
p
e
1
p 1 p v p 1 p
v
2
2
p 0
1 t t 1 x x
x
p p
p p
v
t t v x x p 1 x 0
p
p
v p
v
v p
v
0
t
x
x t
x
x
Закон сохранения массы
p
p
v
v p 0
t
x
x
7

8.

Характеристический анализ системы уравнений Эйлера
в примитивных переменных ρ, v, p (4)
Характеристическая
покомпонентная форма записи
Характеристическая векторная
форма записи
v
t v x x 0
v 1 p
v
0
v
x x
t
p
v
p
0
p v
x
x
t
w
w
A
0
t
x
0
v
A
0
v
1
w v
0 p v
p
8

9.

Исследование на гиперболичность. Собственные числа.
v
A E 0
0
0
p
v 1 v
v 0
p v
1 v
v c
2
3 v c
3
p
c
скорость звука
Годунов С.К. и др. Численное решение многомерных задач газовой динамики. – М.: Наука, 1976.
9

10.

Исследование на гиперболичность.
Матрицы собственных векторов.
A 1E ω1 0
A 2E ω 2 0
A E ω 0
3
3
1
Ω R ω1 , ω 2 , ω3 0 c c
Матрица правых
0 p p
собственных векторов
0
2 c
2 pc
1
1
Ω
Ω
0
p
c
Ω R 2 pc 0
L
R
ΩR
Матрица левых
p c
0
собственных векторов
Λ diag v, v c, v c
A Ω R ΛΩ L
10

11.

Условия совместности вдоль характеристик
w
w
A
0
t
x
A Ω R ΛΩ L
w
w
Ω R ΛΩ L
0
t
x
Ω L Ω R 1 Ω L pk
w
w
ΩL
ΛΩ L
0
t
x
Развернутый вид:
3
w k
w k
Ω L pk t p Ω L pk x 0, p 1,2,3
k 1
k 1
3
11

12.

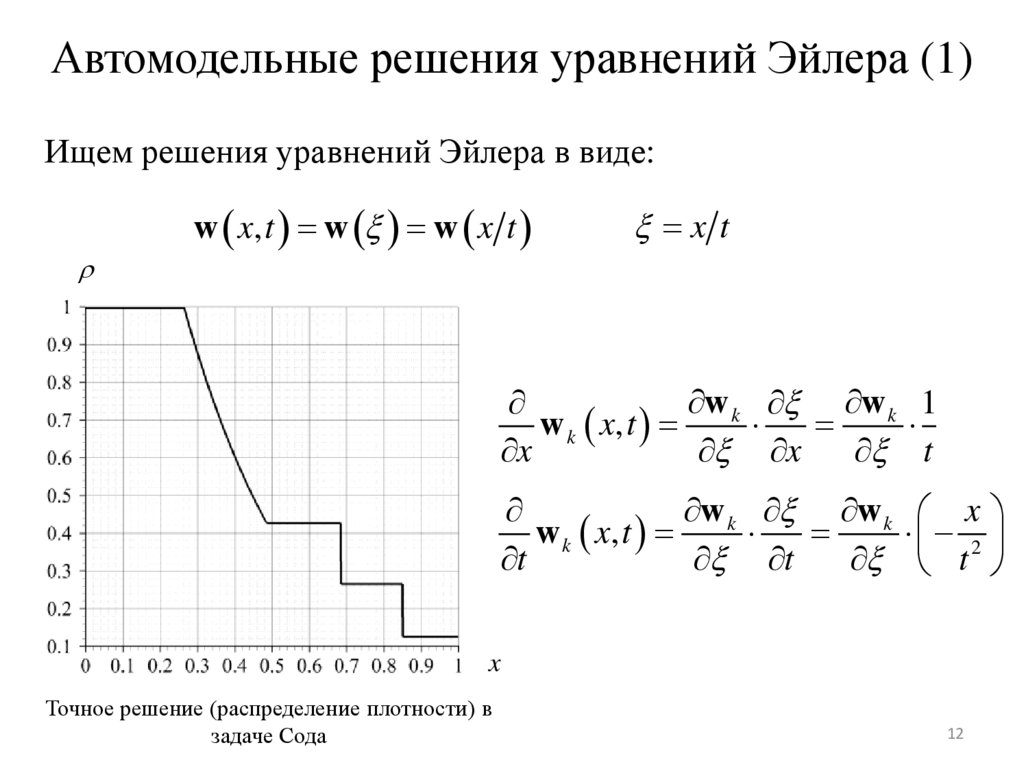
Автомодельные решения уравнений Эйлера (1)
Ищем решения уравнений Эйлера в виде:
w x, t w w x t
x t
w k w k 1
w k x, t
x
x
t
w k w k x
w k x, t
2
t
t
t
x
Точное решение (распределение плотности) в
задаче Сода
12

13.

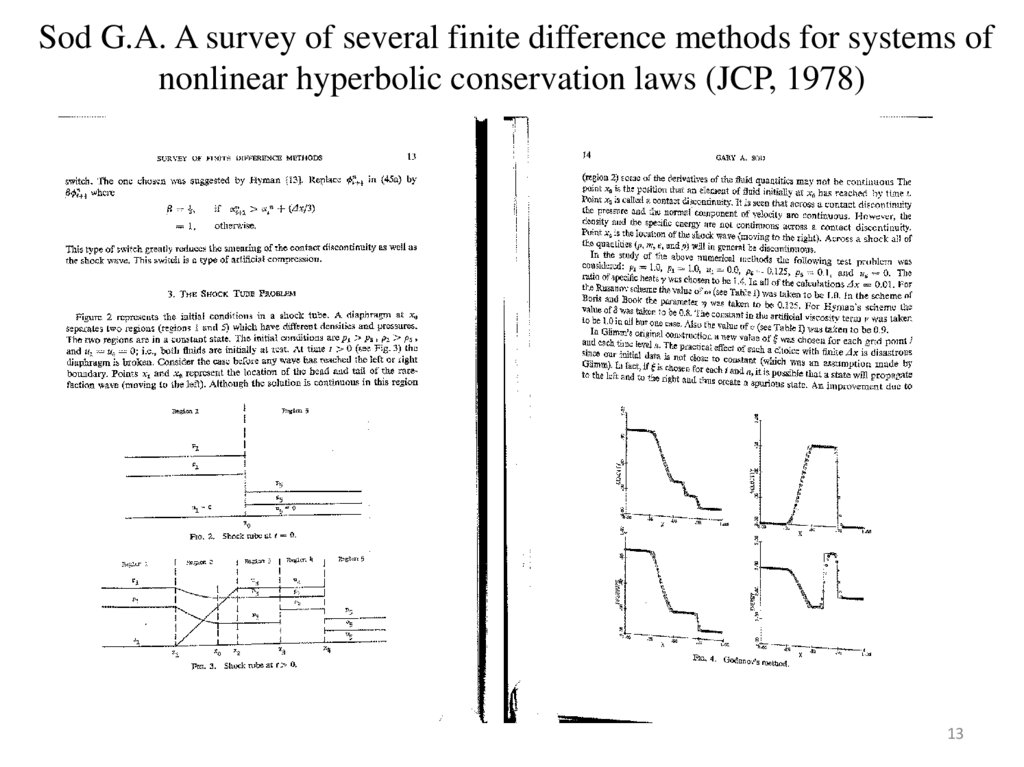
Sod G.A. A survey of several finite difference methods for systems of
nonlinear hyperbolic conservation laws (JCP, 1978)
13

14.

Автомодельные решения уравнений Эйлера (2)
3
w k x
w k 1
Ω L pk t 2 p Ω L pk t 0, p 1, 2,3
k 1
k 1
3
w k
p ΩL pk 0, p 1, 2,3
k 1
3
w v
p
0
2 c
2 pc
1
ΩL
0
p c
2 pc
p c
0
p
0
1 1
p
1 v
1 p
0
2
2c 2 p
1 v
1 p
3
0
2c 2 p
14

15.

Автомодельные решения уравнений Эйлера (3)
Рассмотрим решение, соответствующее ξ = λ2:
v c
2
S
0
p
0
p
1 v
1 p
0
2c 2 p
Изоэнтропический
процесс:
p
const
p
1
p 1
0
1
p p
0
15

16.

Левый инвариант Римана
1 v
1 p
0
2c 2 p
v
с p
0
p
p
с
2
с p p p p 1 p
2с
2
2
2
1 c 2
v с 2 с
0
1 c
с 1 c
2
2
v 1 с wL 0
16

17.

Левая волна разрежения (волна Римана)
x
v c
t
p
S const
2с
w
v
const
L
1
wL const
Волна – «левая», если поток массы
через нее направлен слева направо:
v 0
17

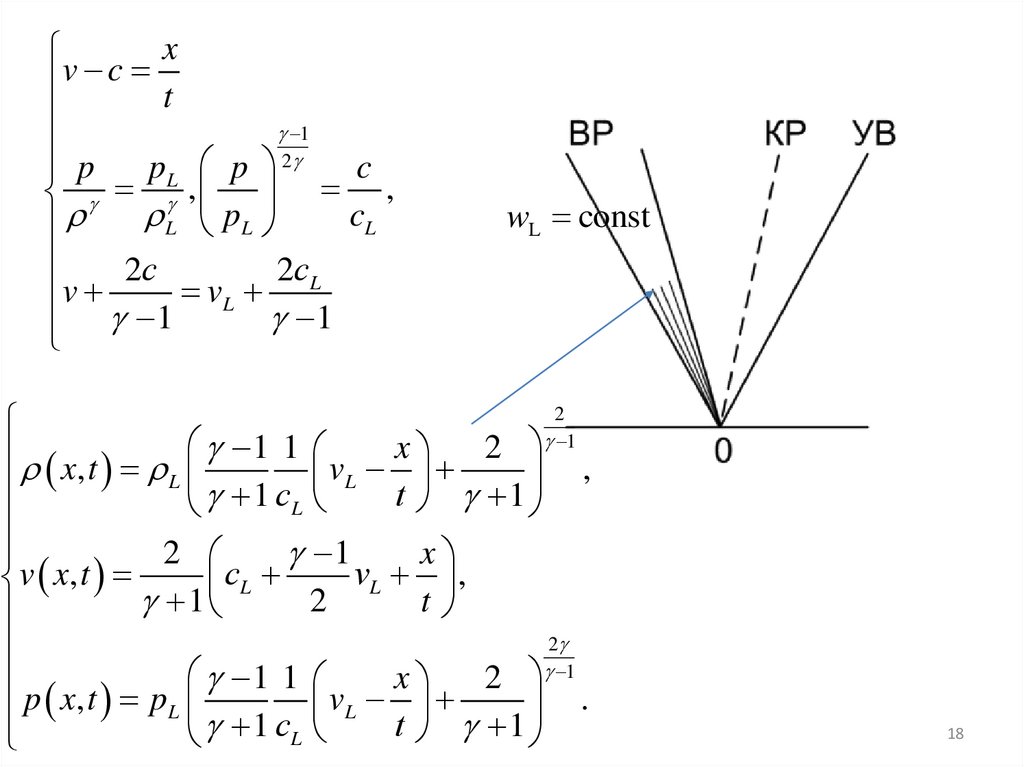
18.

x
v c t
1
p
pL p 2
c
, ,
L pL
cL
2с L
2с
vL
v
1
1
wL const
2
1
1
1
x
2
x, t
L
,
vL
t 1
1 сL
2
1
x
vL ,
v x, t
сL
1
2
t
2
1 1
x
2 1
p x, t pL 1 с vL t 1 .
L
18

19.

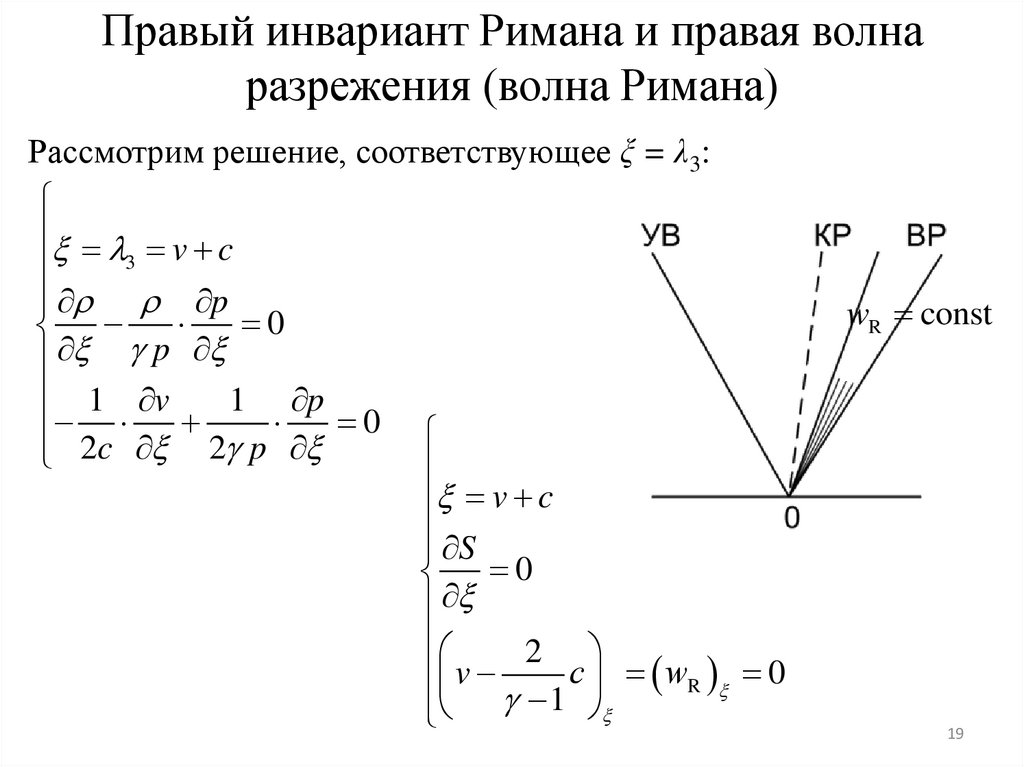
Правый инвариант Римана и правая волна
разрежения (волна Римана)
Рассмотрим решение, соответствующее ξ = λ3:
v c
3
p
0
p
1 v
1 p
0
2c 2 p
v c
S
0
2
с wR 0
v
1
wR const
19