Similar presentations:
Нелинейные волны в жидкости. Солитоны. Лекция 6
1. Лекция 6 Нелинейные волны в жидкости. Солитоны
Содержание1.
2.
3.
4.
5.
Нелинейные акустические волны
Общие сведения
Уравнение Кортевега-де Вриза
Солитонное решение ур-ия КдВ
Другие виды солитонов
2.
1) Решение Римана (1860 г. первое точное решение нелинейной проблемы)Ранее акустические волны рассматривались как малые
возмущения p, , v. Уравнения Эйлера и непрерывности
линеаризовывались
классическое волновое уравнение.
Откажемся от этого подхода, но ограничимся одномерным
случаем: p p(x,t), (x,t), v v (x,t).
Жидкость не вязкая, процесс адиабатический
3.
Уравнение Эйлераv
v
1 p
v
t
x
x
исключаем p !
Уравнение непрерывности
v 0
t x
Адиабатичность процесса
p
c 2 ( )
p c2
с( ) - скорость звука, являющаяся функцией плотности
v
v
c 2
v
t
x
x
Введем функцию ( ) (c / )d
Работаем далее в переменных v и
c 1 p
x x c x
c
t t
4.
Уравнение непрерывностиУравнение Эйлера
v
v c 0
t
x
x
( v) (c v) ( v) 0
t
x
решение
v 0
v
v
v c 0
t
x
x
( v) (c v) ( v) 0
t
x
решение
v 0
Вспомогательную величину теперь можно исключить: v
Уравнение Римана
v
v
(c v) 0
t
x
В линейной акустике факторизацией 1-мерного волнового
уравнения имеем
v
v
c 0
t
x
v F ( x ct ) G( x ct )
5.
По аналогии уравнение Римана также описывает 2 волны,бегущие со «скоростью» с v. Ее называют местной или локальной
скоростью, зависящей от координаты x ( v v(x), c const ) .
Если уравнением состояния жидкости является адиабата, то
c v c0 v , (1 )/2 , - показатель адиабаты
и решение Римана для волны бегущей в положительном
направлении оси x
x
v v0 sin t
c0 v
• решение содержит искомую величину v под знаком синуса
• там, где v>0 точки профиля волны ускоряются, где v<0 –
тормозятся искажению волны в процессе распространения
6.
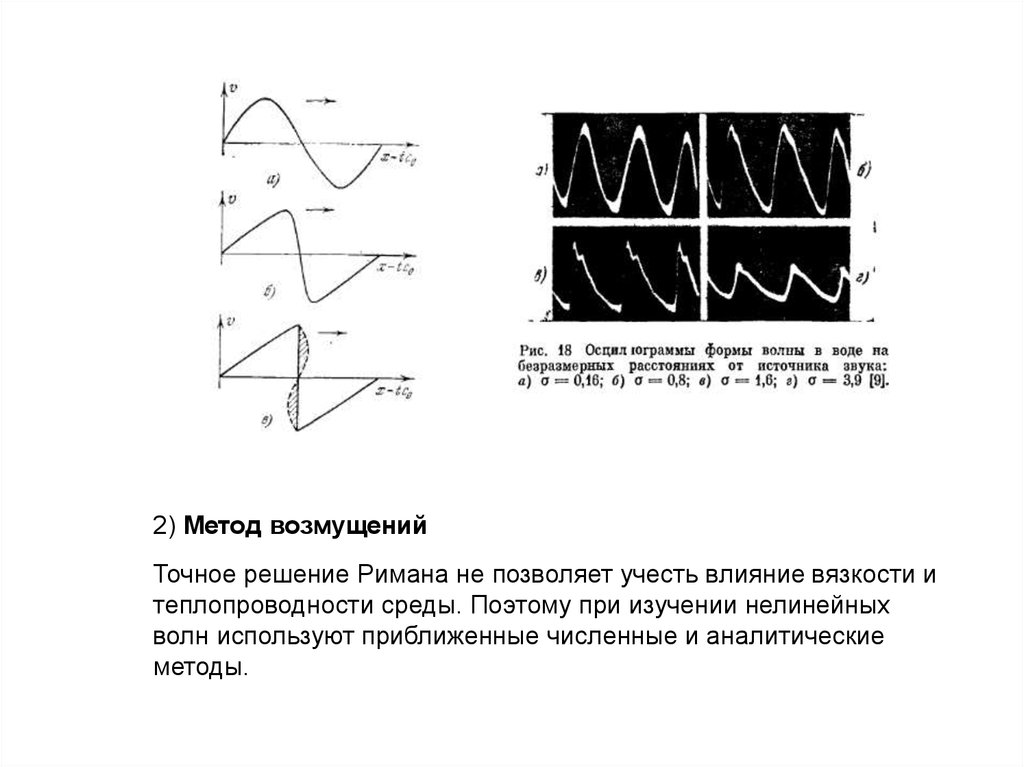
2) Метод возмущенийТочное решение Римана не позволяет учесть влияние вязкости и
теплопроводности среды. Поэтому при изучении нелинейных
волн используют приближенные численные и аналитические
методы.
7.
Широкое распространение при изучении нелинейных волнполучил метод возмущений (часто в комбинации со спектральным
подходом).
Идея метода: в исходные уравнения гидродинамики полевые
характеристики (давление, плотность, скорость и.т.д.) подставляют
в виде ряда по малым поправкам
p p0 p p p
v v v v
0
Задаваясь параметром малости задачи (число Рейнольдса, Маха
и пр.) уравнения гидродинамики представляют для каждого уровня
приближения в виде неоднородного волнового уравнения с
известной из решения на предыдущем шаге правой частью. Так
Образуется система зацепляющихся волновых уравнений, которые
обрывают по достижении необходимой точности решения.
8.
Например, если начать со второго приближения (1-ое приближенийсоответствует известным результатам линейной акустики), то имеем
2 p
t 2
2 p
c22 2 p 2 f 2 ( p , r, t )
c32 2 p 3 f3 ( p , r, t )
t 2
2 p( N )
t 2
где
i
2 2 (N )
cN
p
N f N ( p ( N 1) , r, t )
- показатели, порядок малости которых соответствует
малости определяемой из уравнения поправки
к решению
9.
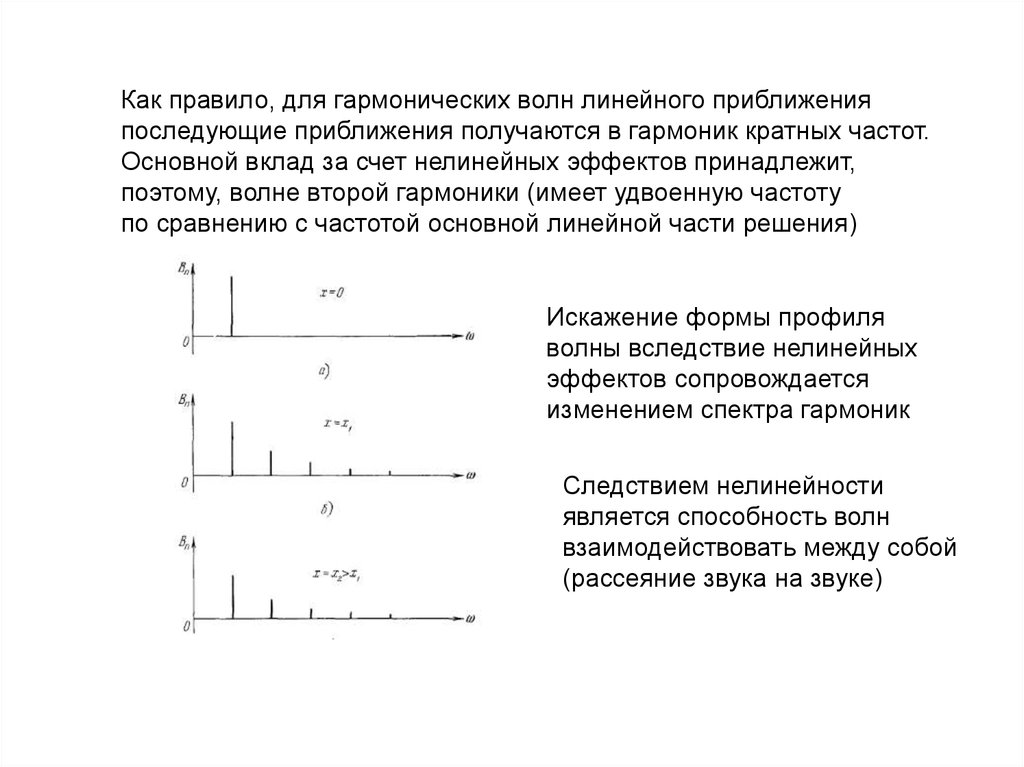
Как правило, для гармонических волн линейного приближенияпоследующие приближения получаются в гармоник кратных частот.
Основной вклад за счет нелинейных эффектов принадлежит,
поэтому, волне второй гармоники (имеет удвоенную частоту
по сравнению с частотой основной линейной части решения)
Искажение формы профиля
волны вследствие нелинейных
эффектов сопровождается
изменением спектра гармоник
Следствием нелинейности
является способность волн
взаимодействовать между собой
(рассеяние звука на звуке)
10.
1) Солитон как особый класс нелинейных волнРешение Римана – точное решение нелинейного
уравнения (действует только нелинейность)
выводу:
нелинейная волна этого типа распространяется с изменением
волнового профиля т.е.не обладает структурной устойчивостью.
В реальных условиях действует не только нелинейность.
Включаются дополнительно такие факторы, как диссипация энергии
и дисперсия.
Сильная диссипация всегда
к разрушению волны через
ослабление. Можно ожидать, что при слабой диссипации сочетание
дисперсии с нелинейностью позволит обеспечить высокую
структурную устойчивость нелинейной волны.
Именно этот класс нелинейных волн, способных распространяться
без изменения волнового профиля, форма которого отлична от
гармонической, получил название солитонов – уединенных волн.
11.
2) Классические признаки солитона• распространение без изменения профиля
• постоянство скорости распространения
• отсутствие изменений при встрече (взаимодействии)
с другим солитоном
Условность признаков: считать ли волну солитоном, если
она периодически меняет свою форму (в целом оставаясь
структурно устойчивой не в статическом, а динамическом
cмысле)?
12.
3) Первые наблюдения солитонаприписываются англичанину С. Расселу (1834 г.), описавшему
возникновение в узком канале из-за резкого торможения баржи
возмущения поверхности воды выпуклой формы, распространяющегося с постоянной скоростью на большое расстояние.
В природе также известны волны явно солитонного типа
или близкие к ним – ударные волны в атмосфере при взрывах
и грозовых разрядах, приливные волны в устьях рек,
впадающих в море и пр.
13.
По размерности пространства, в котором существуютсолитоны, различают: одно-, двух- и трехмерные солитоны.
К одномерным солитонам относятся волны в каналах
(солитоны Рассела), цунами, доменные границы в
в магнетиках, оптические солитоны в световодах.
Цунами: слева – вид со спутника
14.
15.
Двухмерными солитонами являются дислокации кристаллическойрешетки, вихри Абрикосова в сверхпроводиках 2-го рода,
антициклоны, в частности красное пятно Юпитера.
Трех- и многомерными солитонами являются модели в
астрофизике и физике элементарных частиц.
1) Исходные посылки
Линейная среда
Обычное волновое ур-е
2
t 2
c 2 2 0
2 k 2c2
Слабая нелинейная среда
с дисперсией
В какой форме взять
добавок на дисперсию?
2 k 2c2
16.
2) Соображения по поводу выбора добавка:• для механических волн обычно скорость сигнала меньше
фазовой скорости добавок нужно брать со знаком « »
• чтобы сохранить «отрицательность» добавляемого члена
его нужно брать с четной степенью по k т.к. иначе с
обращением волны (k k) менялся бы характер дисперсии
2 k 2c 2 2k 4
или, полагая поправку малой получим
2
2 3
kc 1 2 k kc k
2c
c
2
При таком приближенном способе учета дисперсии добавок
оказывается с нечетной степенью по k. Имеем право
рассматривать только прямые волны!
17.
Для наблюдения за волной выберем движущуюся соскоростью с систему координат и перенормируем длину
так, чтобы избавиться от коэффициента 2 /( 2c)
3) Реконструкция дифференциального уравнения
Новый закон дисперсии
kc k 3
Такую связь с k дает уравнение вида
u 3u
3 0
t x
Недостатки: 1) ур-е не инвариантно к преобразованию
Галилея; 2) не подходит на роль уравнения, имеющего
решением солитон – дает решение с расплывающимися
(из-за дисперсии) начальными импульсами u(x,0)
18.
Первый член уравнения требует заменуu
u
u
t
t
x
du / dt
по той причине, что уславливаясь рассматривать волну в
системе, движущейся со скоростью c мы фактически
перешли на язык Лагранжа (роль частицы играет волна)
Итог
u
u 3u
u 3 0
t
x x
- имеем простейшую
форму уравнения
Кортевега – де Вриза(1895)
Основание считать, что решение его будет солитонным в
следующем: заменяя частную производную u/ t на полную
конвективную производную мы, по сути, добавили к
дисперсионному члену член, выражающий геометрическую
нелинейность. Этим самым, открылась возможность для
компенсации дисперсионного расплывания импульса
противоположным действием нелинейности.
19.
3u
u
u
Решение ур-ия
u 3 0 ищем в виде
t
x x
u u( ) , x Vt , V const
u
Vu ,
t
2
u
u
u u
Vu 0
2
x
u2
u Vu C Полагая С=0 получаем ОДУ со структурой
2
нелинейного, консервативного осциллятора
u2
u
Vu 0
2
20.
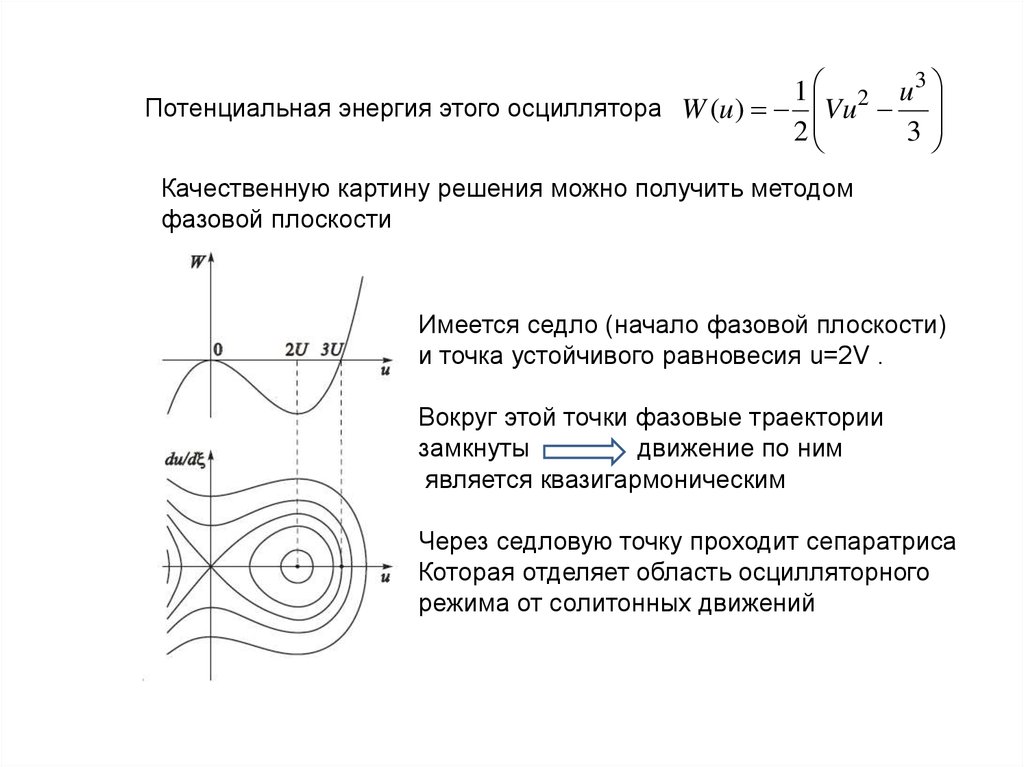
1 2 u 3Потенциальная энергия этого осциллятора W (u ) Vu
2
3
Качественную картину решения можно получить методом
фазовой плоскости
Имеется седло (начало фазовой плоскости)
и точка устойчивого равновесия u=2V .
Вокруг этой точки фазовые траектории
замкнуты
движение по ним
является квазигармоническим
Через седловую точку проходит сепаратриса
Которая отделяет область осцилляторного
режима от солитонных движений
21.
Квазилинейные осцилляцииКноидальные колебания
Солитон (движение по
сепаратрисе
22.
Аналитическое решение для солитона (можно убедитьсяпрямой подстановкой)
V
u 3V sech2
( x Vt )
2
3
u
u
u
6u 2
3 0
t
x x
модифицированное
уравнение КдВ имеет
многосолитонное
бризерное решение
23.
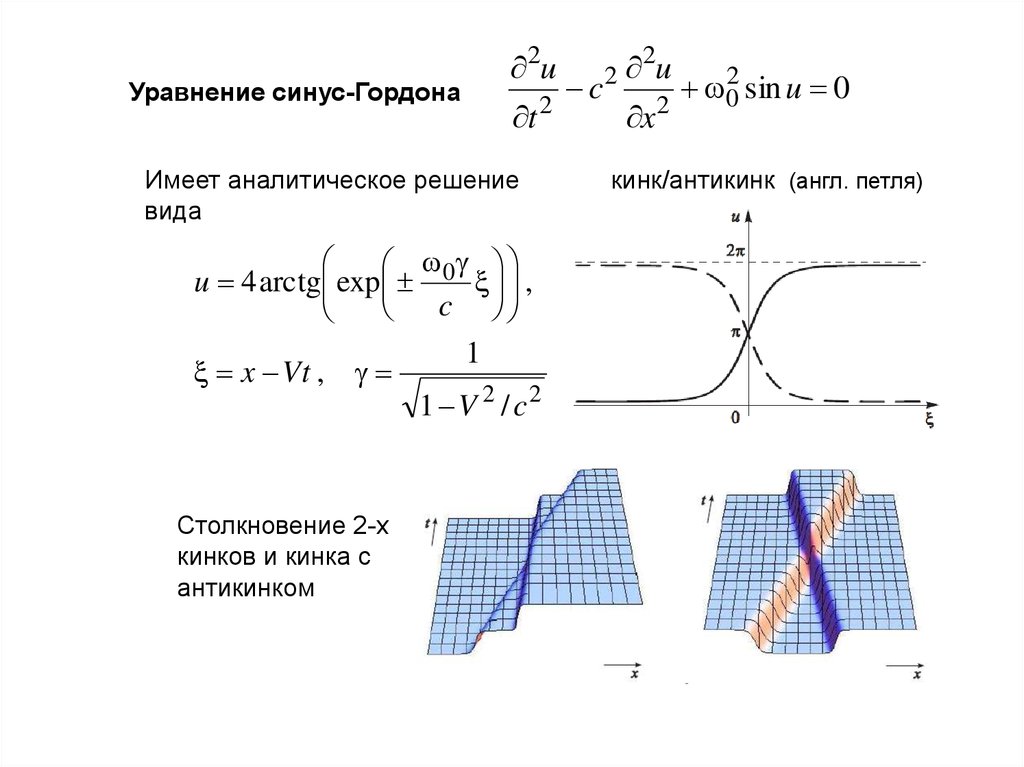
Уравнение синус-Гордона2u
t 2
Имеет аналитическое решение
вида
0
u 4 arctg exp
,
c
1
x Vt ,
1 V 2 / c2
Столкновение 2-х
кинков и кинка с
антикинком
c
2
2
u
x 2
02 sin u 0
кинк/антикинк (англ. петля)
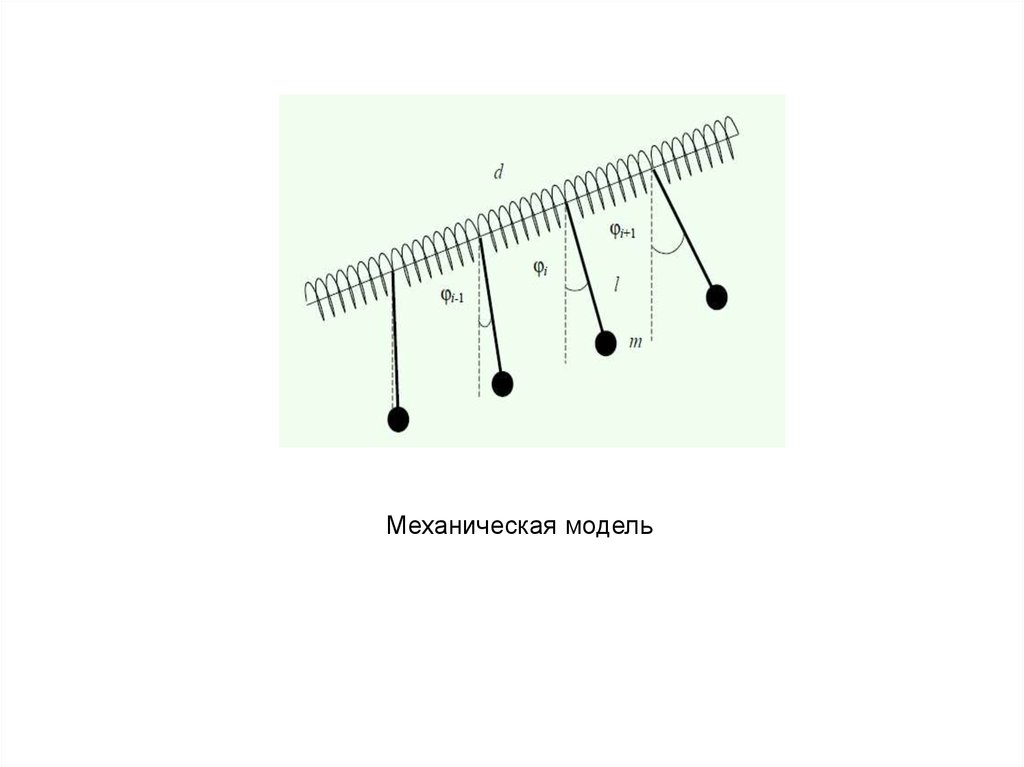
24.
Механическая модель25.
Нелинейное уравнение Шредингера2
2
i
k
|
|
0
2
t
x
Приложения:
• стационарная самофокусировка плоских волн
• одномерная автомодуляция монохроматических волн
• распространение термоимпульсов в твердом теле
• волоконная оптика, сверхпроводимость
Аналитическое решение
0 sch[ 0 k / 2 ( x Ut)] exp[ i(U / 2)( x ut )]
U 2u
U скорость огибающей импульса
u скорость несущей
26.
Uu
x





















 physics
physics








