Поверхностные волны глубокой жидкости со сдвигом скорости

1. ПОВЕРХНОСТНЫЕ ВОЛНЫ ГЛУБОКОЙ ЖИДКОСТИ СО СДВИГОМ СКОРОСТИ

Филиал МГУ им. М.В. Ломоносова в г. Севастополе
кафедра прикладной математики
кафедра программирования
ПОВЕРХНОСТНЫЕ ВОЛНЫ ГЛУБОКОЙ
ЖИДКОСТИ СО СДВИГОМ СКОРОСТИ
Дипломная работа
Величанского И.А.
студента 401 группы
Научный руководитель
Рецензент
Санников В. Ф.

2.

1
Введение
2
Постановка задачи
3
Построение решения
4
Результаты

3. Введение

Большой интерес в гидродинамике представляет собой задача
движения тела под поверхностью жидкости.
Решение такого рода задач сводится к решению систем
дифференциальных уравнений в частных производных для волновых
возмущений.
Решение может быть весьма трудоёмким и ресурсозатратным.
Выход: влияние всех этих факторов можно понизить посредством
сведения самой математической модели к более простой форме
посредством аналитического аппарата
В данной работе исследуется задача о поверхностных волнах,
создаваемых в большом объеме невязкой жидкости, движущейся
неравномерно со сдвигом скорости. Целью работы является получение и
упрощение решения задачи аналитическим путём.

4.

Введение
Зачем это нужно?
- Обнаружение подводных плавающих средств вероятного
противника.
- Скрытие подводных плавающих средств союзника.

5.

Введение
Что нового?
- Пространственная (трёхмерная) задача.
- Наличие сдвига скорости.
- Двухслойное течение.
- Метод источников - стоков

6.

Введение
Таким образом,
Цель :
определение физических закономерностей генерации и
распространения поверхностных волн
Объект :
волновые движения жидкости в течениях
Предмет :
Метод :
поверхностные волны
нахождение аналитического и численного решений

7.

Постановка задачи:
Система уравнений гидродинамики в
напряжениях.
Уравнение неразрывности.
Граничные условия.
Условия излучения.
Требуетсясоставить физическую модель поверхности водногообъёма,
(тоесть получить выражение для функции сдвига поверхностных волн)
ипреобразовать её аналитическим путём в простуюформу.

8.

Постановка задачи
Система уравнений гидродинамики:
U
µqxy µqxz 1 P
1 µq xx
U
V
W U
gx
y
z
y
z ρ x
x
t x
V
µq yx µq yy µq yz 1 P
1
U
V
W
V
gy
y
z
y
z ρ y
x
t x
W
µqzy µqzz 1 P
1 µq zx
U
V
W W
gz
t
x
y
z
x
y
z
ρ
z
V U,V,W скорость сплошной среды набегающей жидкости ;
U x,y,z,t ,V x,y,z,t ,W x,y,z,t проекции на координатные плоскости;
gx ,gy ,gz – проекции массовых сил;
 P x,y,z,t – давление;
qij компоненты тензора скоростей деформации;
µ – коэффициент динамической вязкости жидкости

9.

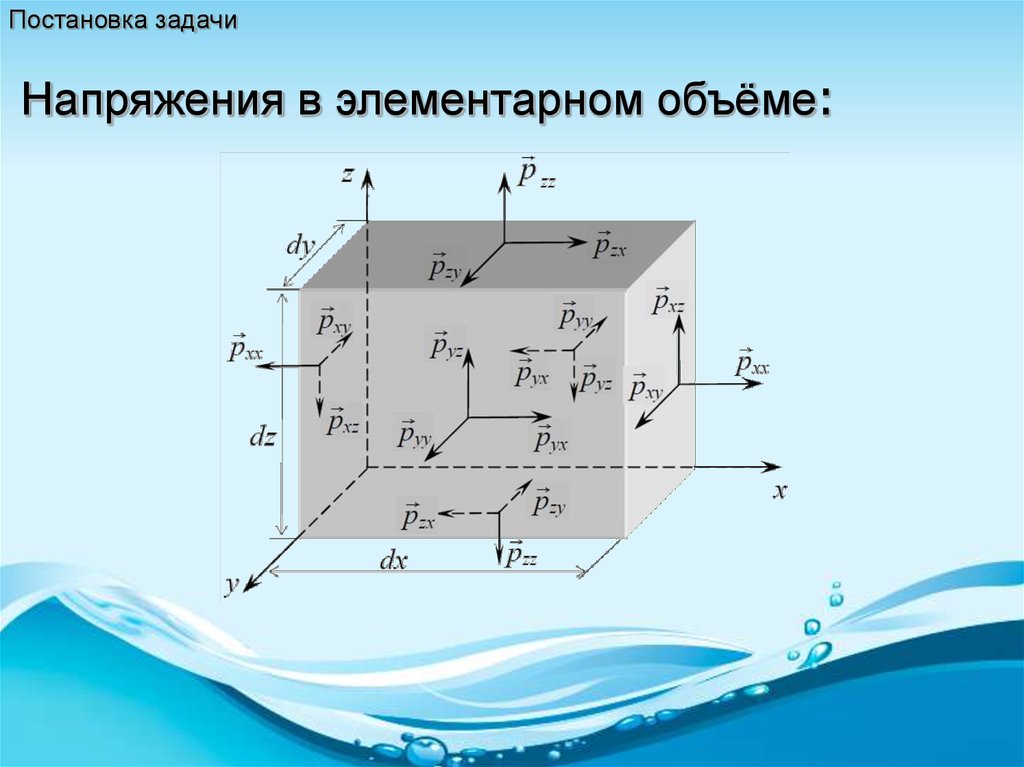
Постановка задачи
Напряжения в элементарном объёме:

10.

Постановка задачи
Уравнение
неразрывности :
U V W
q 4
x y
z
x a
2
y z h
2
1
;
U x, y, z , t ,V x, y, z , t ,W x, y, z , t проекции на координатные плоскости;
q интенсивность стока и сточника;
x, y, z– пространственные координаты;
h глубина погружённого тела;

11.

Постановка задачи
Источник и сток :
q+
q-

12.

Постановка задачи
Граничные условия :
V
0;
n
1.
Граница тела и жидкости ( условие непротекания ) : Vn
2.
U 0 x V0 y W
На поверхности (z 0) :
P P g
0
3.
На дне (z ) : W 0;
4.
V V
условие неразрывности скорости ;
Vz Vz в силу кусочнолинейного сдвига скорости ;
W
W
На границе раздела (z h0 ) :
кинематическое условие ;
(U V )
(U 0 V0 )
0 x 0 y
x
y
динамическе условие ;
P P
кинематическое условие ;
динамическе условие ;

13.

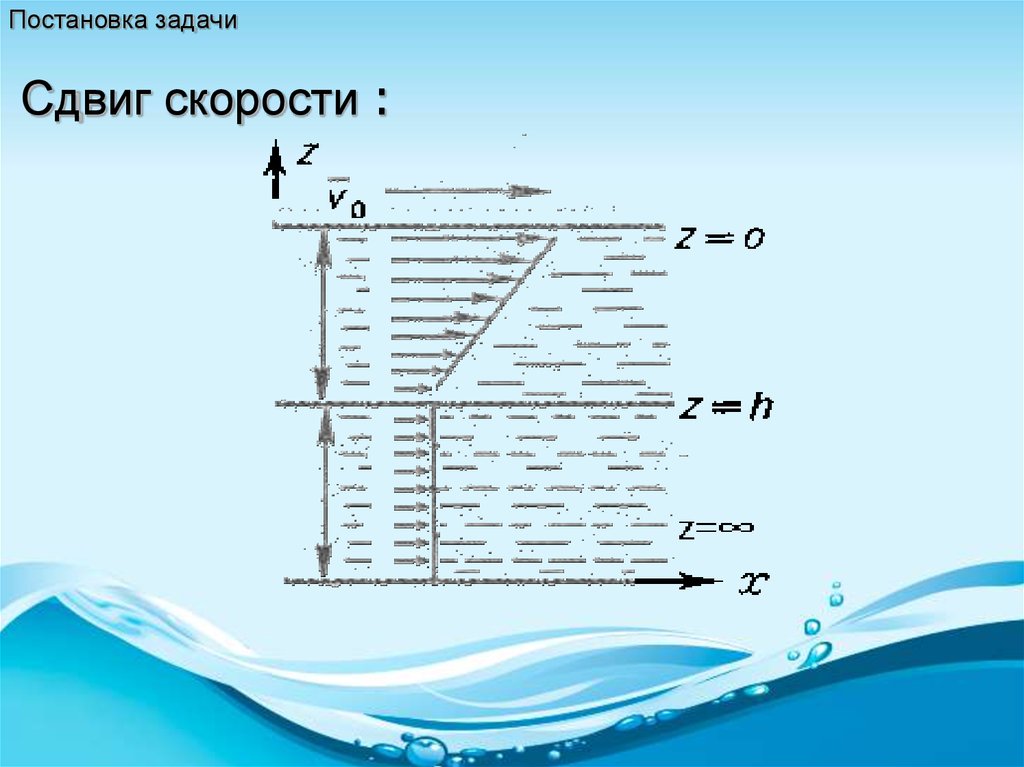
Постановка задачи
Сдвиг скорости :

14.

Решение:
->ЛИНЕАРИЗАЦИЯ
->ПРЕОБРАЗОВАНИЕФУРЬЕ
->РЕШЕНИЕОДНОРОДНОГОУРАВНЕНИЯ
->РЕШЕНИЕНЕОДНОРОДНОГОУРАВНЕНИЯ
->РЕШЕНИЕНАГРАНИЦАХ
->ОБРАТНОЕПРЕОБРАЗОВАНИЕФУРЬЕ
->ЧИСЛЕННОЕРЕШЕНИЕ

15.

Решение:
ЛИНЕАРИЗАЦИЯ
Переход в систему координат, связанную с телом;
Используется эйлерово приближение;
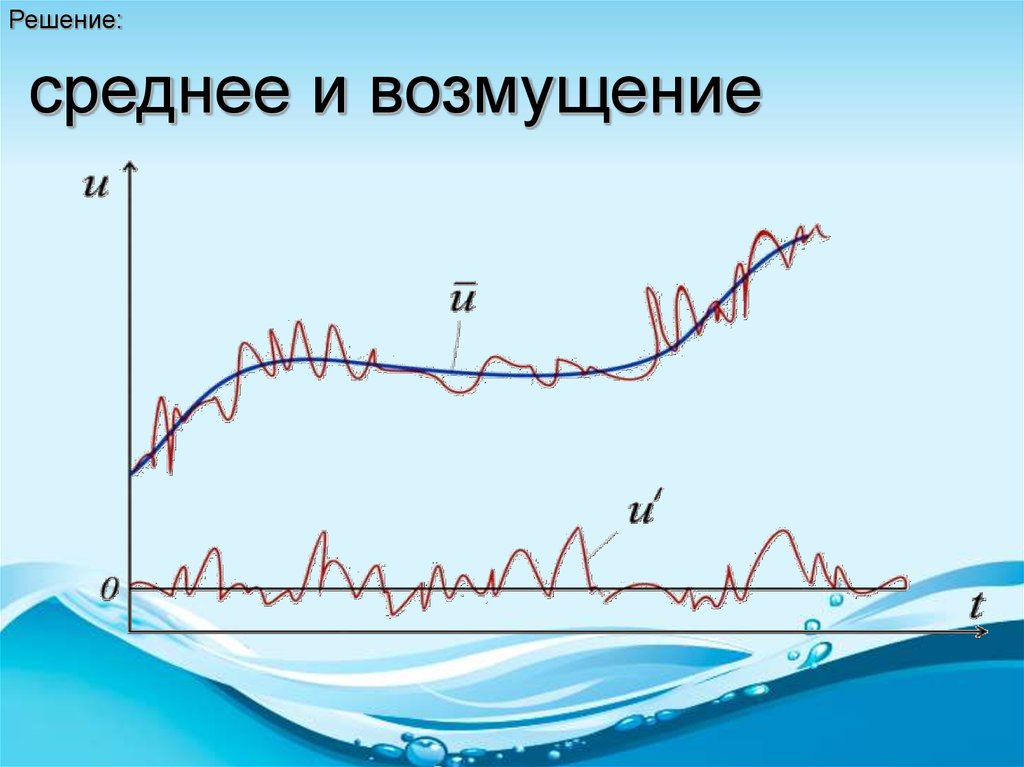
Представление функцй в виде суммы среднего и возмущения :
U U 0 U
(U 0 U )
V V0 V
(V0 V )
W W0 W
P P0 P
(W
W0 )

16.

Решение:
среднее и возмущение

17.

Решение:
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Замена дифференцирования алгебраическим умножением :
f x, y F m, n
F m, n f x, y
1
f x, y
imF m, n
x
f x, y
inF m, n
y

18.

Решение:
РЕШЕНИЕ НА ГРАНИЦАХ:
Wобщее нижнего слоя С1 e kz С2 e kz
Wобщее верхнего слоя С3 e С4 e
kz
kz
q z h e k z h
2
z h
q z h k z h
e
2
z h
1.
На дне (z ) : С2 0 из условия ограниченности решения;
2.
На границе раздела (z h0 ) : константы С3 С4 выражаются через С1;
3.
На поверхности (z 0) : остаётся выразить функцию возмущения;

19. Идея – свести к однократному интегралу от действительной функции. Проблема – интегральная экспонента.

Решение:
ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
x, y, z, t
1
4
2
e
∬
i mx ny
Z m, n, z, t dmdn
Идея – свести к однократному интегралу от
действительной функции.
Проблема – интегральная экспонента.
Ei
0
Z
e
dt
Z λk0

20. ЧИСЛЕННОЕ РЕШЕНИЕ

• Метод Гаусса позволяет достичь хорошую алгебраическую
точность.

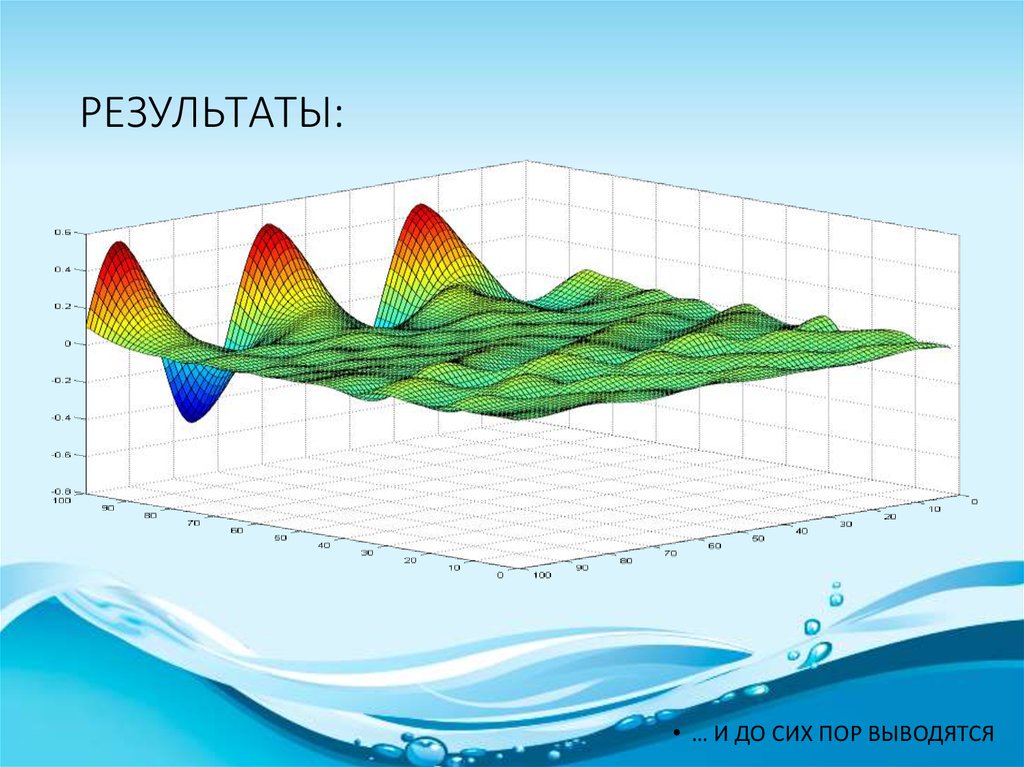
21. РЕЗУЛЬТАТЫ:

• … И ДО СИХ ПОР ВЫВОДЯТСЯ

22. Список использованной литературы:

• С.Д. Чижиумов, «Основы гидродинамики»
• А.Б.Мазо, К.А. Поташев, «Гидродинамика»
• Н.Е. Кочин, И.А. Кибель, Н.В. Розе, «Теоретическая
гидромеханика»
• О.В.Бесов, «Тригонометрические ряды Фурье»
• В.М.Ларионов, С.Е. Филипов «Введение в гидродинамику»
• «Математические модели гидродинамики»
• В.Ф.Санников, «Простое выражение для функции Грина.
Задачи о корабельных волнах в глубокой однородной
жидкости»
• Simen A. Ellinsgen «Ship waves in the presence of uniform
vorticity»

23. Спасибо за внимание!