Конус. Определение конуса

1.

2.

ОПРЕДЕЛЕНИЕ КОНУСА
КОНУС (от лат. conus, от греч. konos) (в элементарной
геометрии), геометрическое тело, образованное
вращением прямоугольного треугольника около одного
из его катетов.

3.

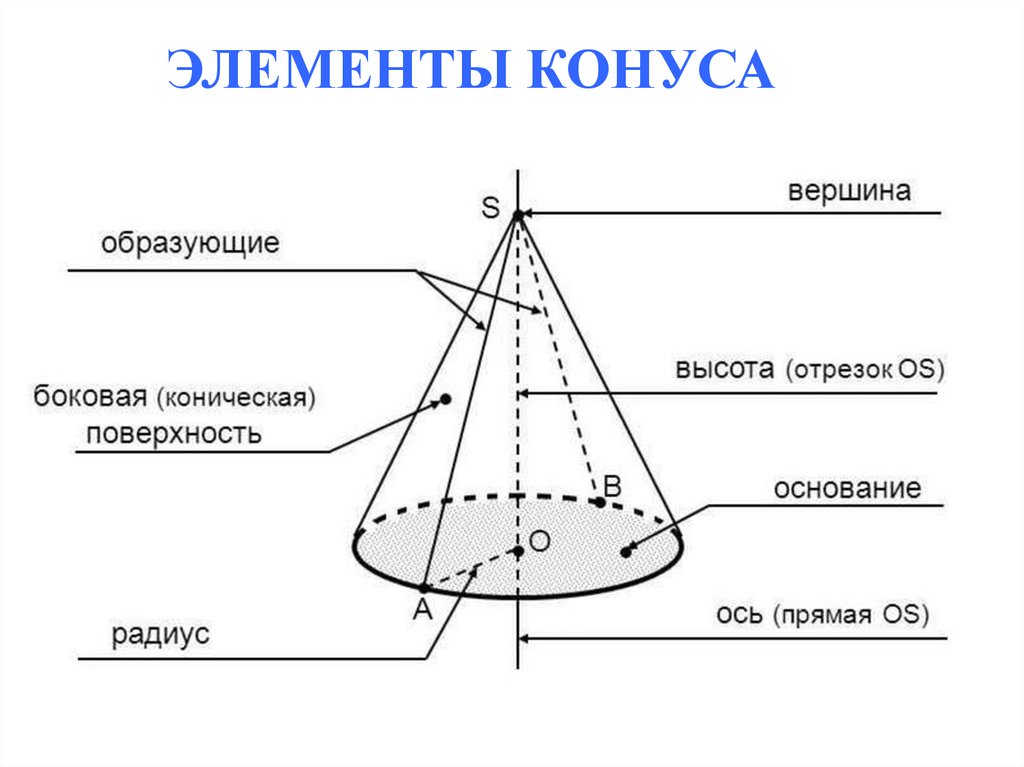
ЭЛЕМЕНТЫ КОНУСА

4.

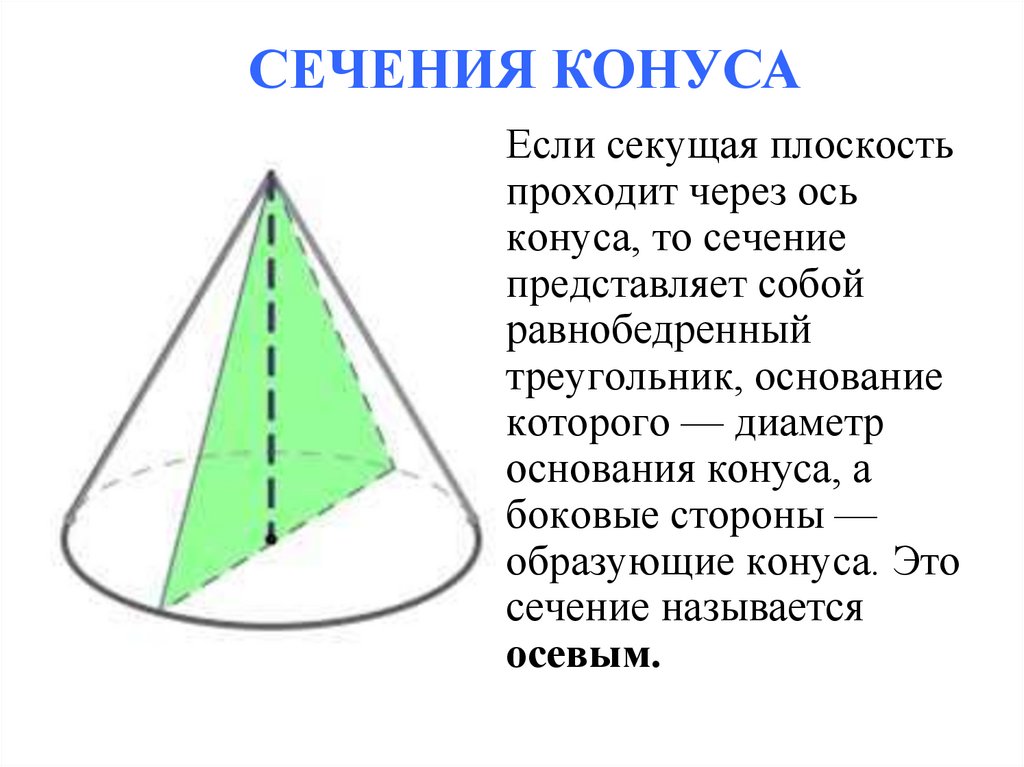
СЕЧЕНИЯ КОНУСА
Если секущая плоскость
проходит через ось
конуса, то сечение
представляет собой
равнобедренный
треугольник, основание
которого — диаметр
основания конуса, а
боковые стороны —
образующие конуса. Это
сечение называется
осевым.

5.

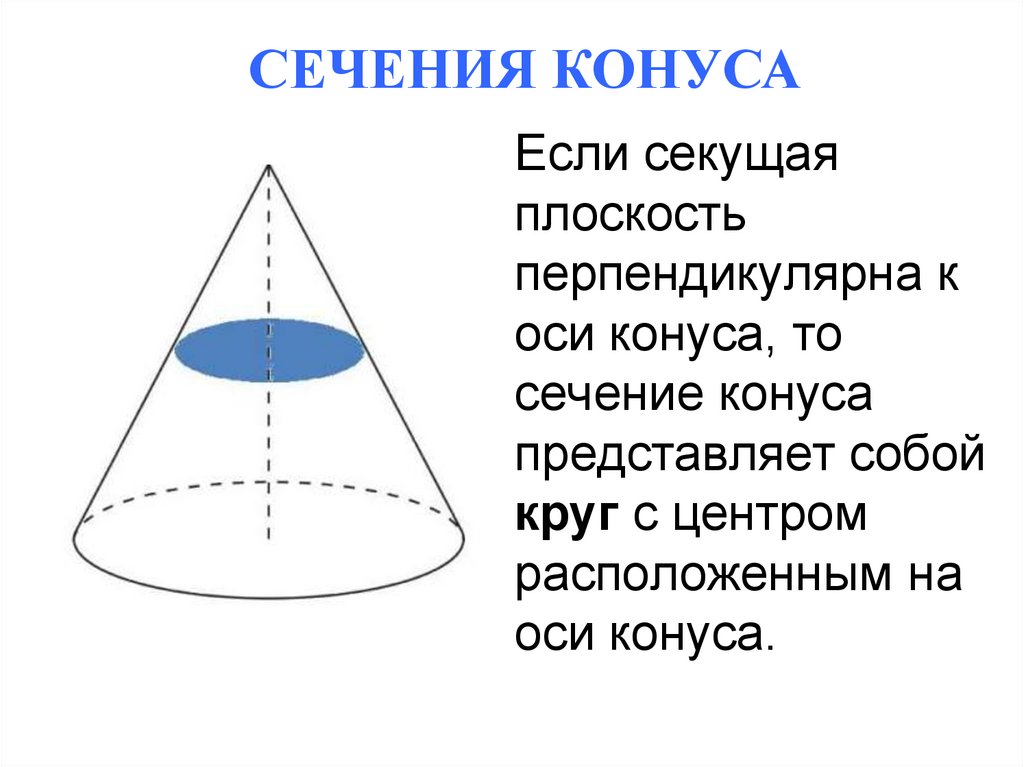
СЕЧЕНИЯ КОНУСА
Если секущая
плоскость
перпендикулярна к
оси конуса, то
сечение конуса
представляет собой
круг с центром
расположенным на
оси конуса.

6.

S
СЕЧЕНИЯ КОНУСА
∆SMN-равнобедренный
SM=SN - образующие
O
α
φ
M
K
N
φ

7.

РАЗВЕРТКА КОНУСА

8.

ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ КОНУСА

9.

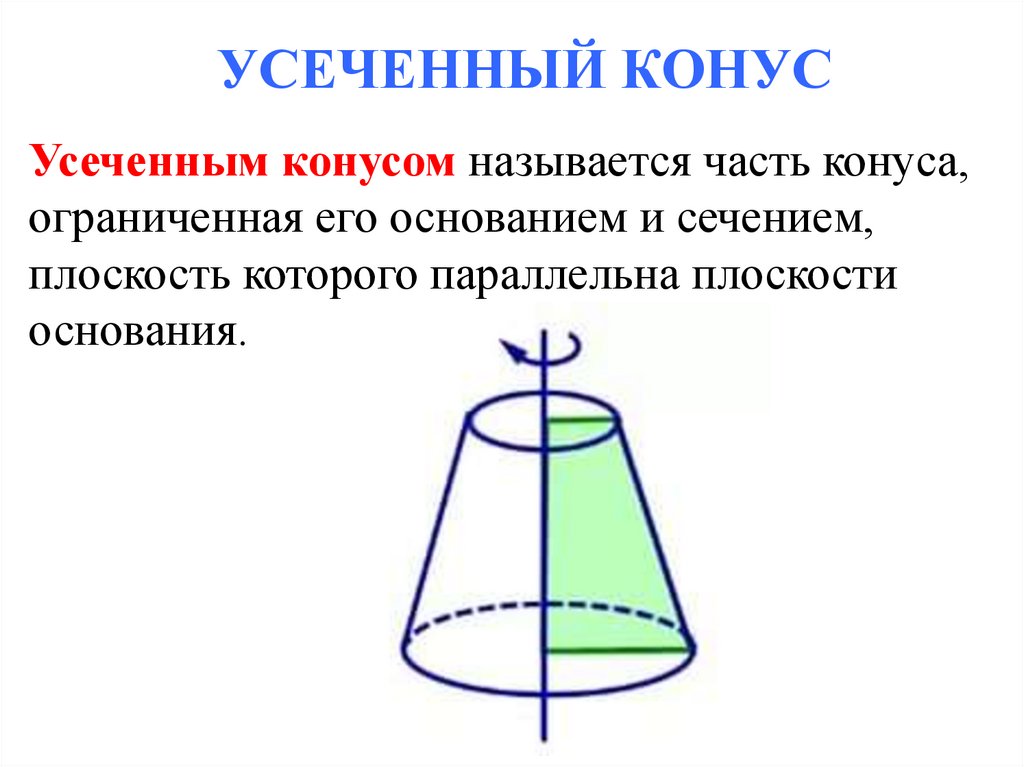
УСЕЧЕННЫЙ КОНУС
Усеченным конусом называется часть конуса,
ограниченная его основанием и сечением,
плоскость которого параллельна плоскости
основания.

10.

ЭЛЕМЕНТЫ УСЕЧЕННОГО КОНУСА

11.

ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ
УСЕЧЕННОГО КОНУСА
Sбок = π(r+r1)l

12. Задача 1

Найти площадь боковой и полной поверхности
конуса, если радиус основания равен 2 см, а
образующая равна 6 см.
Дано:
Конус,
r = 2 см
L = 6 см
Найти:
Sбок
Sполн. пов.
Решение:
Sбок. = πrL = π·2·6 = 12π см2
Sполн. пов = πr (L+r) = π·2·(6+2) =
=16π см2
Ответ: 12π см2; 16π см2

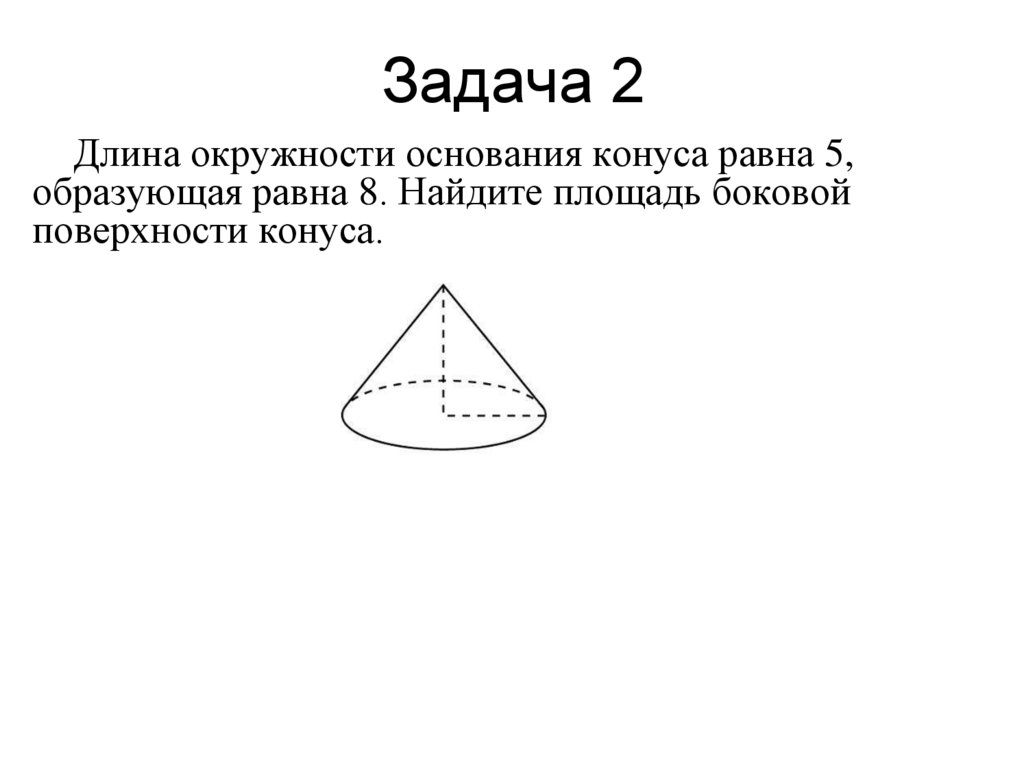
13. Задача 2

Длина окружности основания конуса равна 5,
образующая равна 8. Найдите площадь боковой
поверхности конуса.

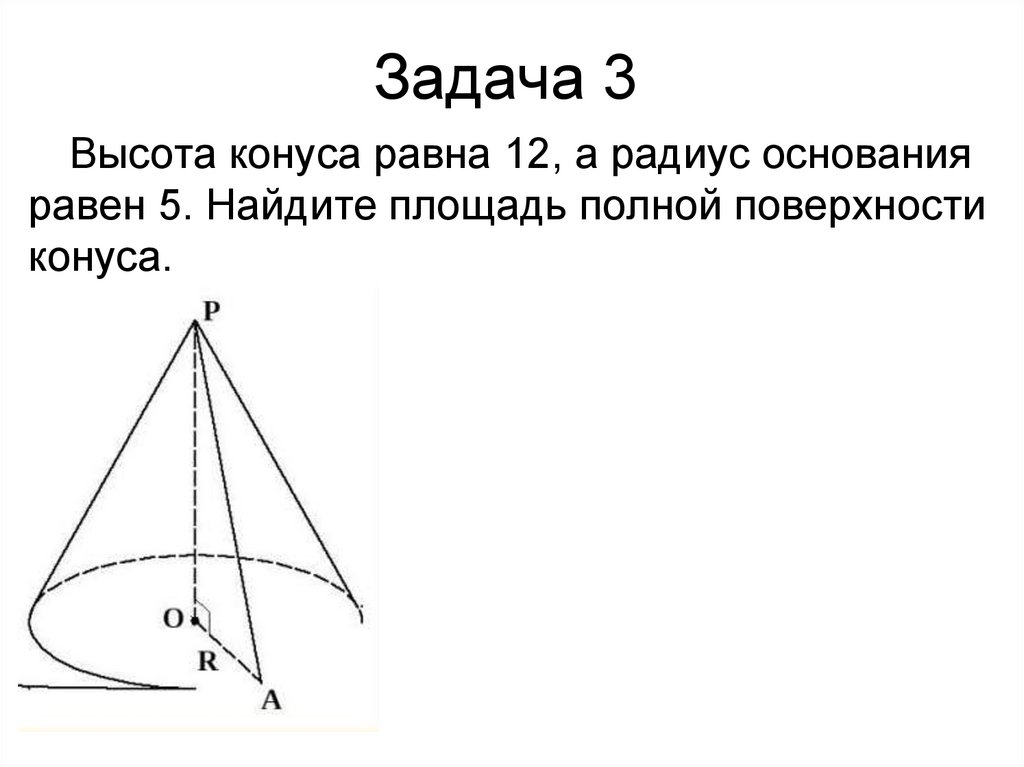
14. Задача 3

Высота конуса равна 12, а радиус основания
равен 5. Найдите площадь полной поверхности
конуса.

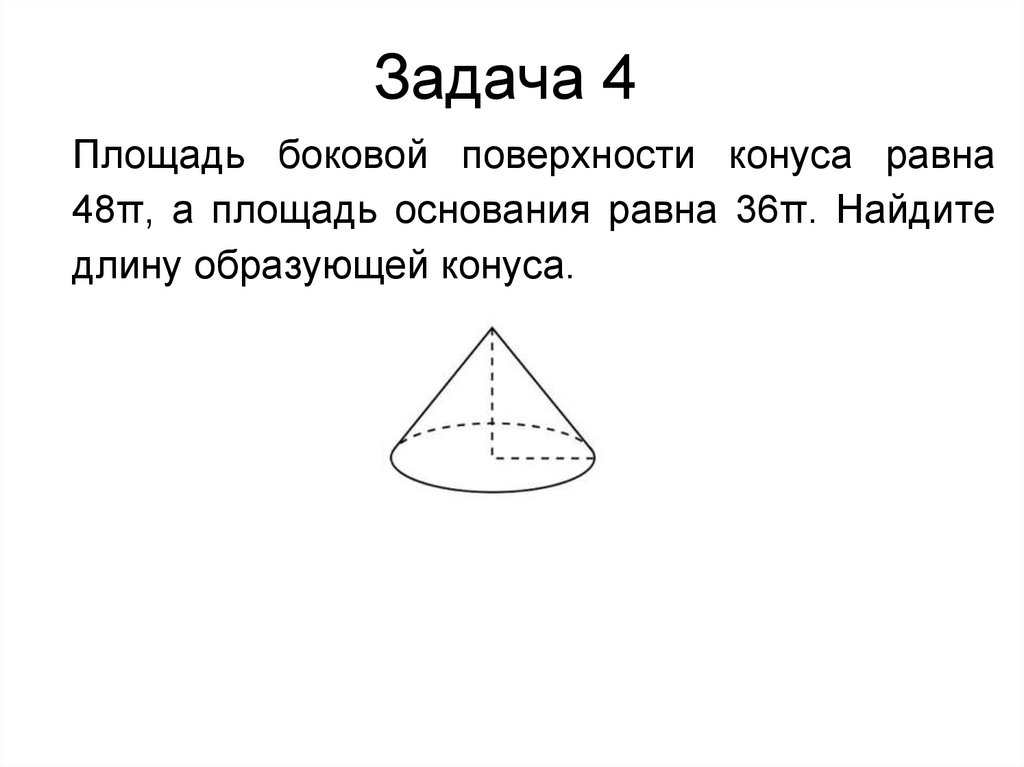
15. Задача 4

Площадь боковой поверхности конуса равна
48π, а площадь основания равна 36π. Найдите
длину образующей конуса.

16. Домашнее задание

Ответьте на вопросы:
1. Какая фигура лежит в основании конуса?
2. Что представляет собой развертка боковой поверхности конуса?
3. Как найти площадь боковой поверхности конуса?
4. Что представляет собой осевое сечение усеченного конуса?
5. Как найти площадь полной поверхности конуса?
6. Какой фигурой является сечение конуса плоскостью перпендикулярной оси конуса?
7. Что представляет собой сечение конуса плоскостью, параллельной двум образующим
конуса?
8. Что представляет собой сечение конуса плоскостью, проходящей через вершину конуса?
9. Равны ли друг другу углы между образующими конуса и:
а) плоскостью основания
б) его осью
10. Что представляет собой сечение конуса плоскостью, проходящей через его вершину?
Решите задачу:
Радиус основания конуса равен 4. Осевым сечением является прямоугольный
треугольник. Найти его площадь.