Определение конуса

1.

г. Елец
ГАПОУ «Елецкий медицинский колледж имени Героя Советского
Союза Ксении Семеновны Константиновой»
Преподаватель дисциплины "Математика" Абреимова Анна
Александровна
2017 г.

2.

ОПРЕДЕЛЕНИЕ КОНУСА
КОНУС (от лат. conus, от греч. konos) (в элементарной
геометрии), геометрическое тело, образованное
вращением прямоугольного треугольника около одного
из его катетов.

3.

Конус в переводе с греческого «konos» означает
«сосновая шишка».

4.

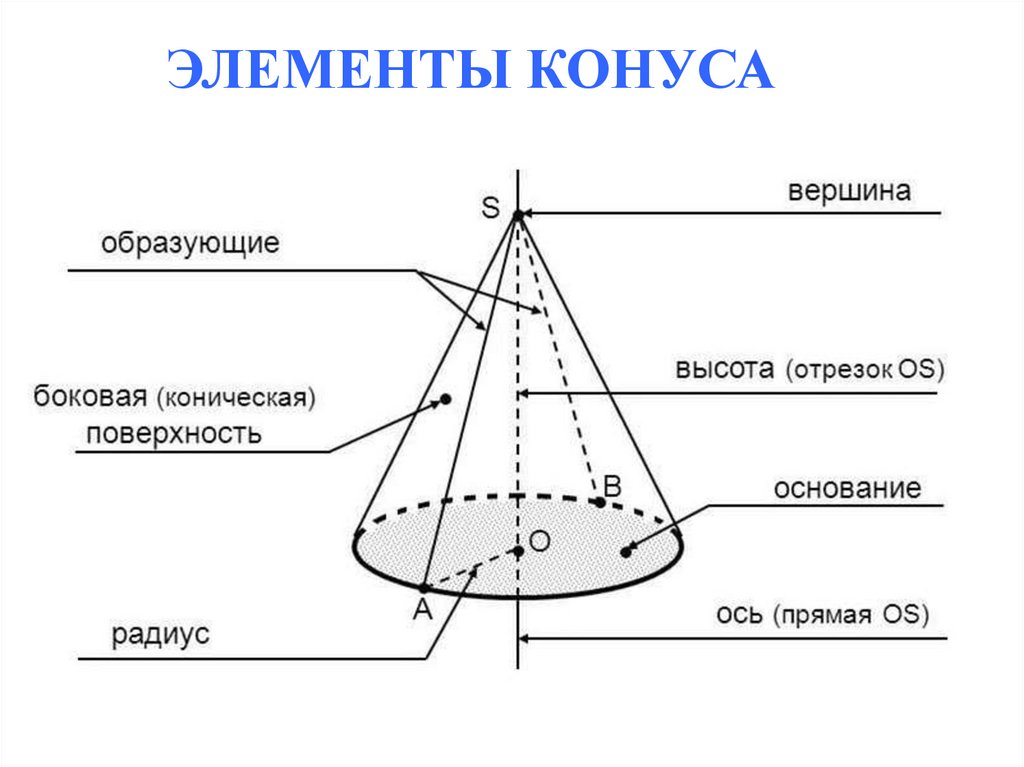
ЭЛЕМЕНТЫ КОНУСА

5.

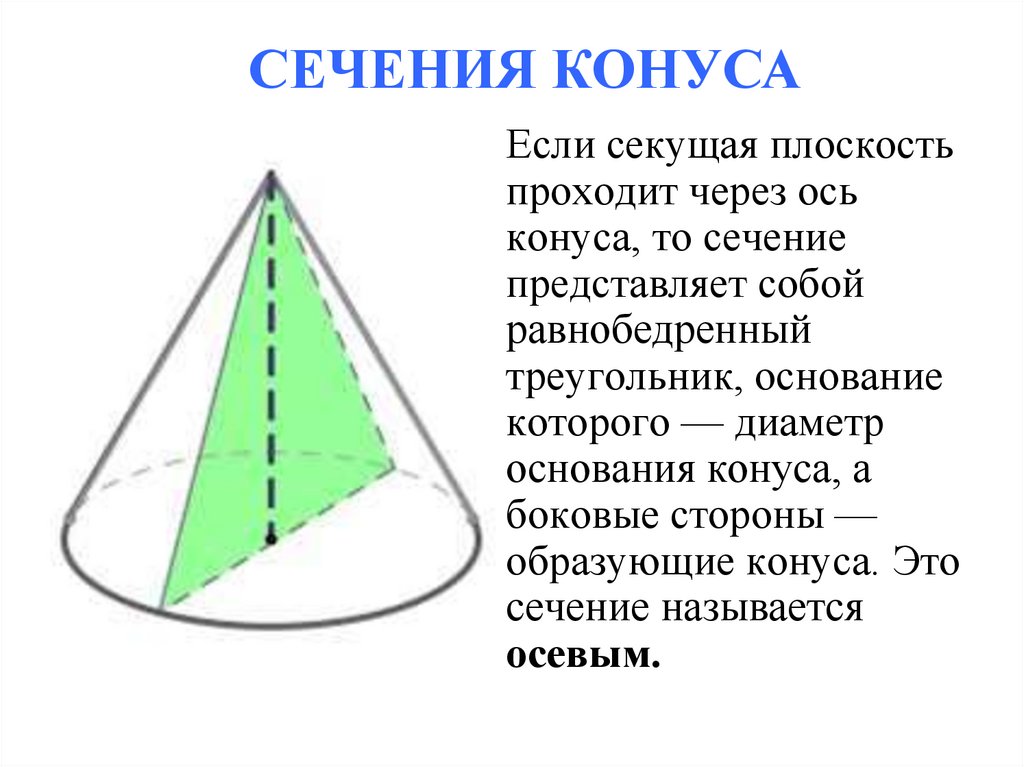
СЕЧЕНИЯ КОНУСА
Если секущая плоскость
проходит через ось
конуса, то сечение
представляет собой
равнобедренный
треугольник, основание
которого — диаметр
основания конуса, а
боковые стороны —
образующие конуса. Это
сечение называется
осевым.

6.

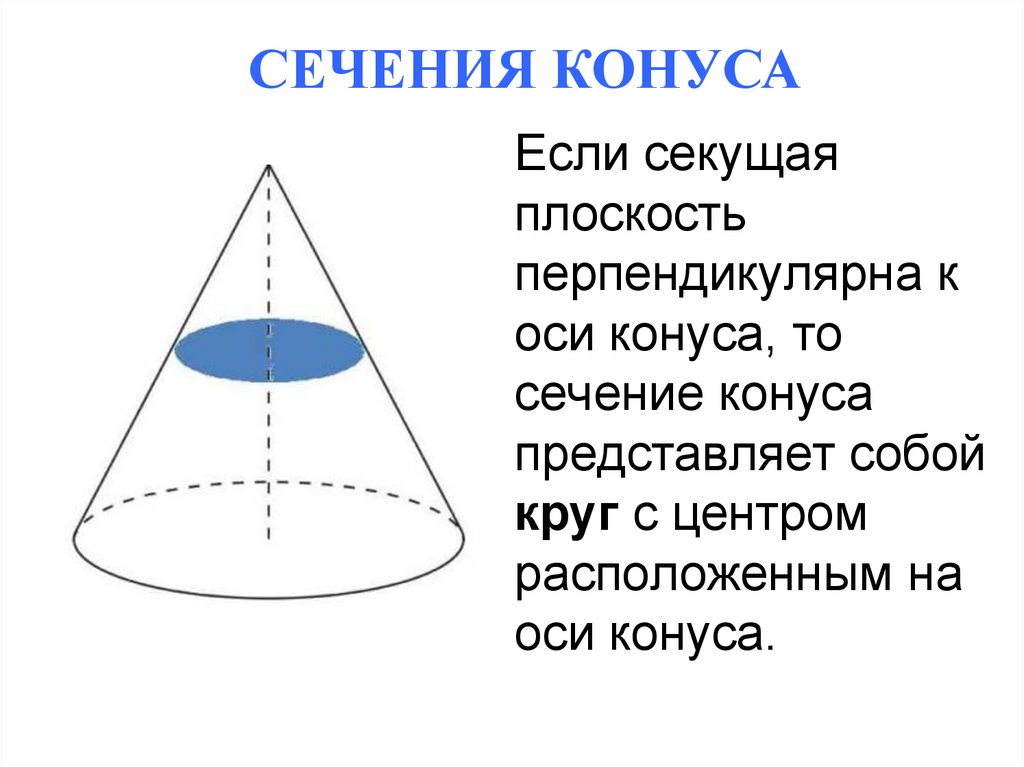
СЕЧЕНИЯ КОНУСА
Если секущая
плоскость
перпендикулярна к
оси конуса, то
сечение конуса
представляет собой
круг с центром
расположенным на
оси конуса.

7.

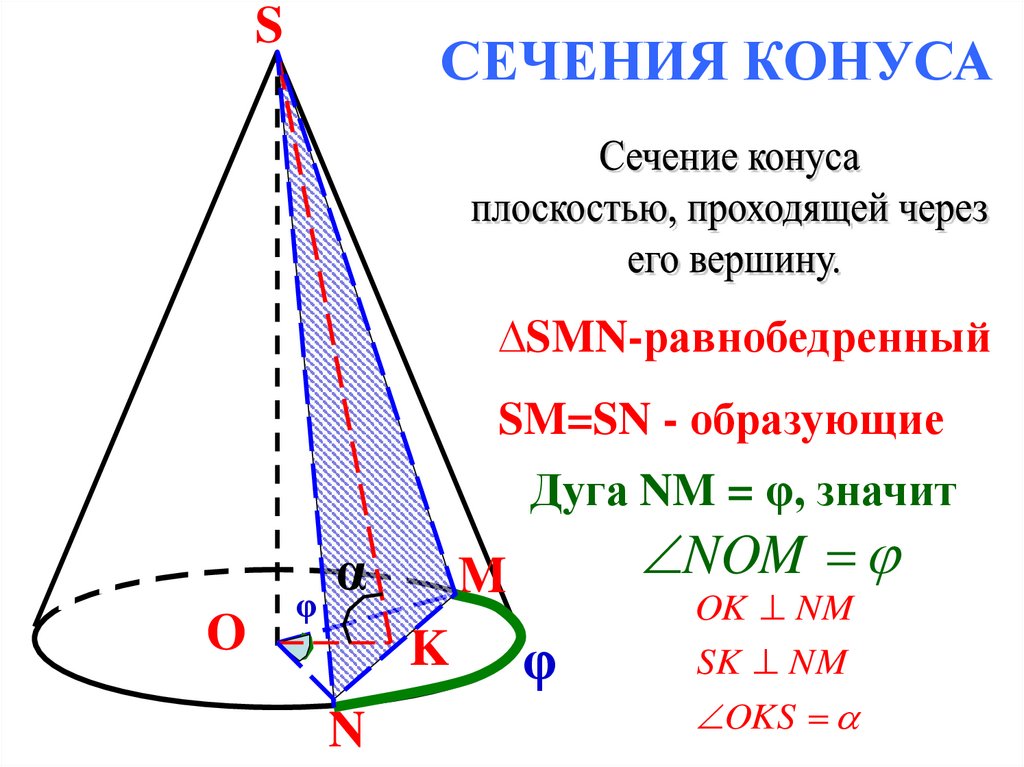
S
СЕЧЕНИЯ КОНУСА
∆SMN-равнобедренный
SM=SN - образующие
Дуга NM = φ, значит
O
α
φ
M
K
N
NOM
φ
OK NM
SK NM
OKS

8.

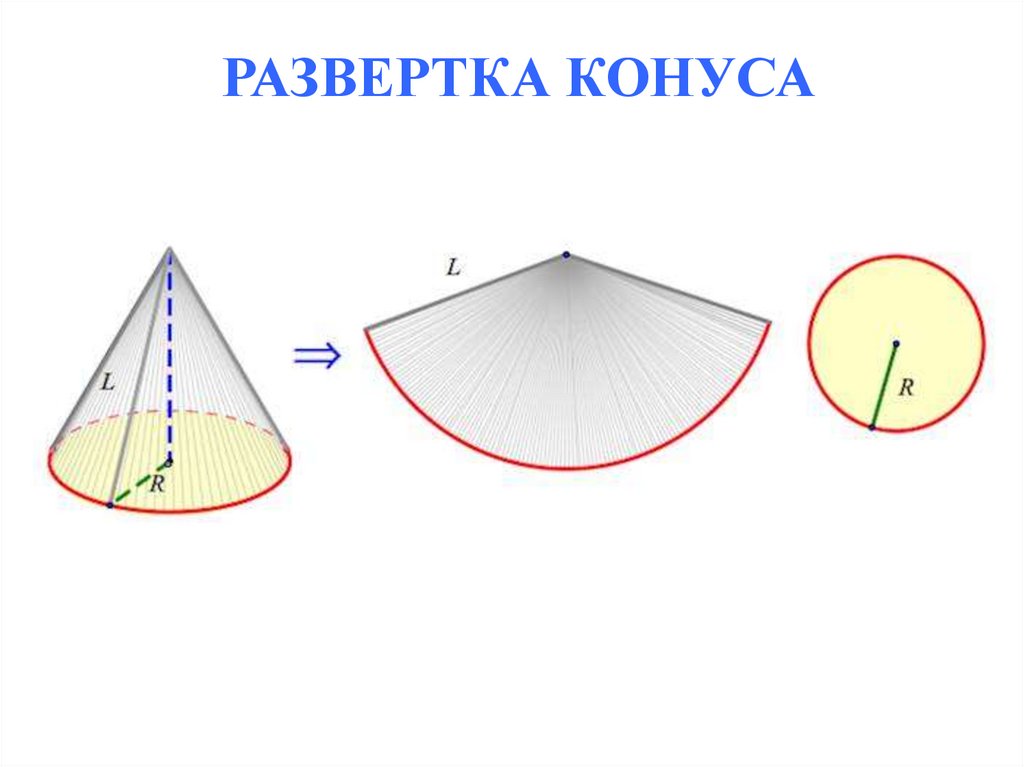
РАЗВЕРТКА КОНУСА

9.

ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ КОНУСА

10.

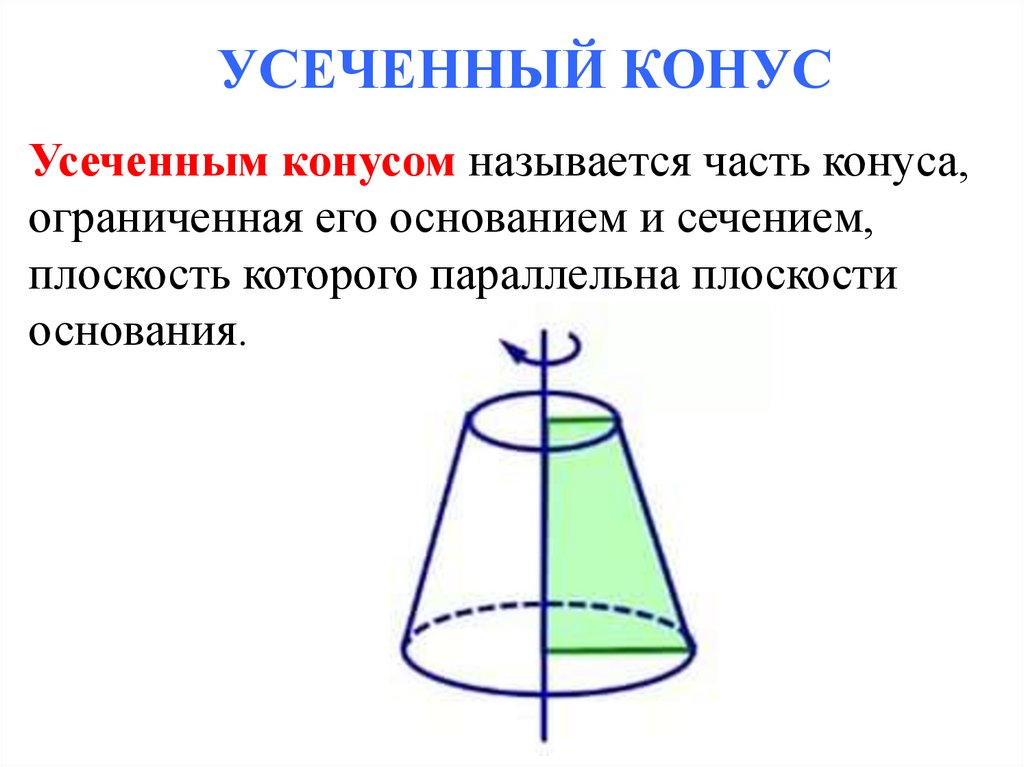
УСЕЧЕННЫЙ КОНУС
Усеченным конусом называется часть конуса,
ограниченная его основанием и сечением,
плоскость которого параллельна плоскости
основания.

11.

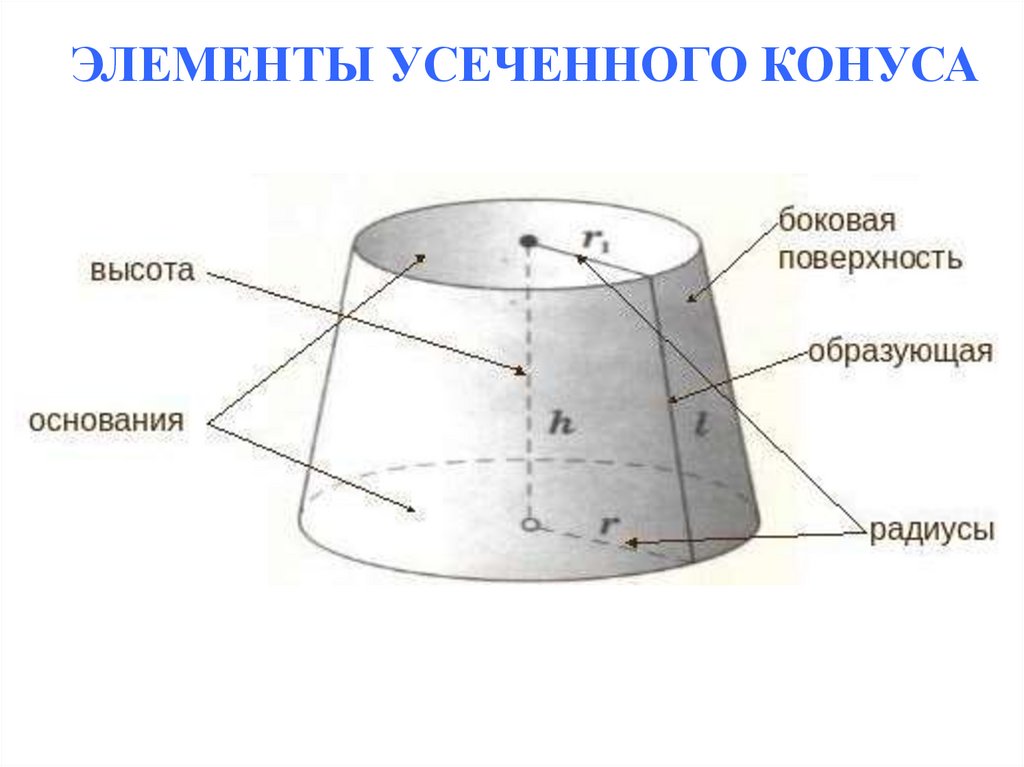
ЭЛЕМЕНТЫ УСЕЧЕННОГО КОНУСА

12.

ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ
УСЕЧЕННОГО КОНУСА
Sбок = π(r+r1)l

13.

14. Задача 1

Найти площадь боковой и полной поверхности
конуса, если радиус основания равен 2 см, а
образующая равна 6 см.
Дано:
Конус,
r = 2 см
L = 6 см
Найти:
Sбок
Sполн. пов.
Решение:
Sбок. = πrL = π·2·6 = 12π см2
Sполн. пов = πr (L+r) =
π·2·(6+2) = 16π см2
Ответ: 12π см2; 16π см2

15. Задача 2

Длина окружности основания конуса равна 5,
образующая равна 8. Найдите площадь боковой
поверхности конуса.
Решение: Площадь боковой поверхности конуса есть
Sбок. = πrL, где r – радиус основания конуса и L образующая конуса.
А поскольку длина окружности основания конуса
равна 2πR и равна 5 по условию, то 5 = 2, πR = 2, 5.
Sбок. = πrL = 2, 5 ·8 = 20.
Ответ: 20.

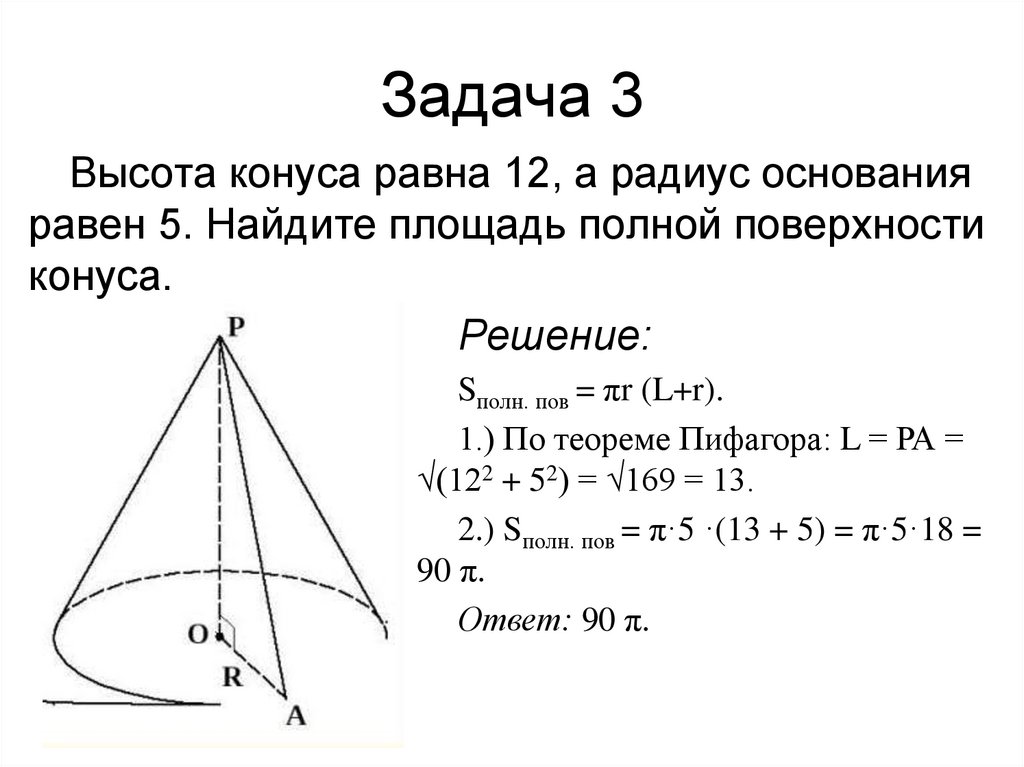
16. Задача 3

Высота конуса равна 12, а радиус основания
равен 5. Найдите площадь полной поверхности
конуса.
Решение:
Sполн. пов = πr (L+r).
1.) По теореме Пифагора: L = РА =
√(122 + 52) = √169 = 13.
2.) Sполн. пов = π·5 ·(13 + 5) = π·5·18 =
90 π.
Ответ: 90 π.

17.

18.

19.

20.

21.

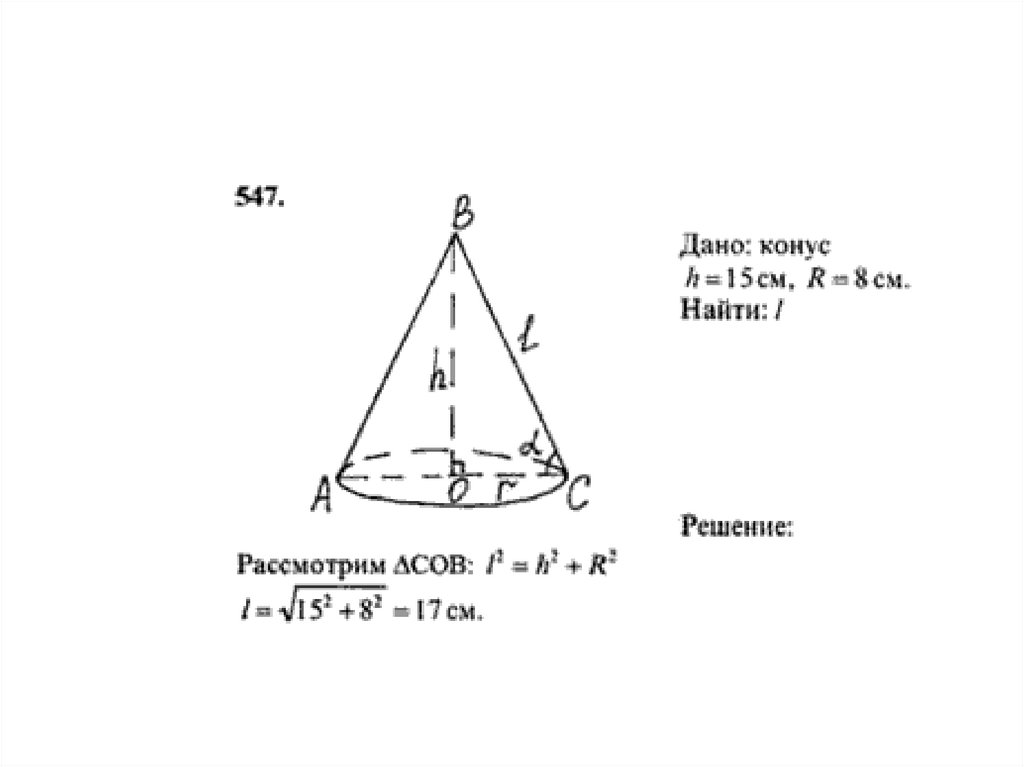
• Задача 1 Высота конуса равна 4, а диаметр
основания - 6. Найдите образующую конуса.
• Дано: SO = h = 4, AC = 2 r =
6. Найти: SA = l = ?
• Решение:
• l 2 = r 2 + h 2;
• r = 6/2 = 3; l 2 = 3 2 + 4 2 = 9 + 16 = 25;
• l 2 = 25;
• l = 5.
• Ответ: 5

22.

• Задача 2.
• Высота конуса равна 4, а длина образующей
- 5. Найдите диаметр основания конуса.
• Дано:SO = h = 4, SA = l = 5,
• Найти: AC = 2 r = ? Решение:
• l 2 = r 2 + h 2; 52 = r 2 +42;52 −4
2 = r 2 или
• r 2 = 5 2 − 4 2 = 25 − 16 = 9; r 2 = 9;
• r = 3;
• AC = 2 r = 2×3 = 6.

23.

• Задача 3
• Диаметр основания конуса равен 6, а длина
образующей - 5. Найдите высоту конуса.
• Дано:AC = 2 r = 6, SA = l = 5,
• Найти: SO = h = ?
• Решение: l 2 = r 2 + h 2 ; r = 6/2 = 3; 5
2 = 3 2 + h 2 ; 5 2 − 3 2 = h 2 или
• h 2 = 5 2 − 3 2 = 25 − 9 = 16; h 2 = 16;
• h = 4.