Similar presentations:
Конус. Урок 8
1.
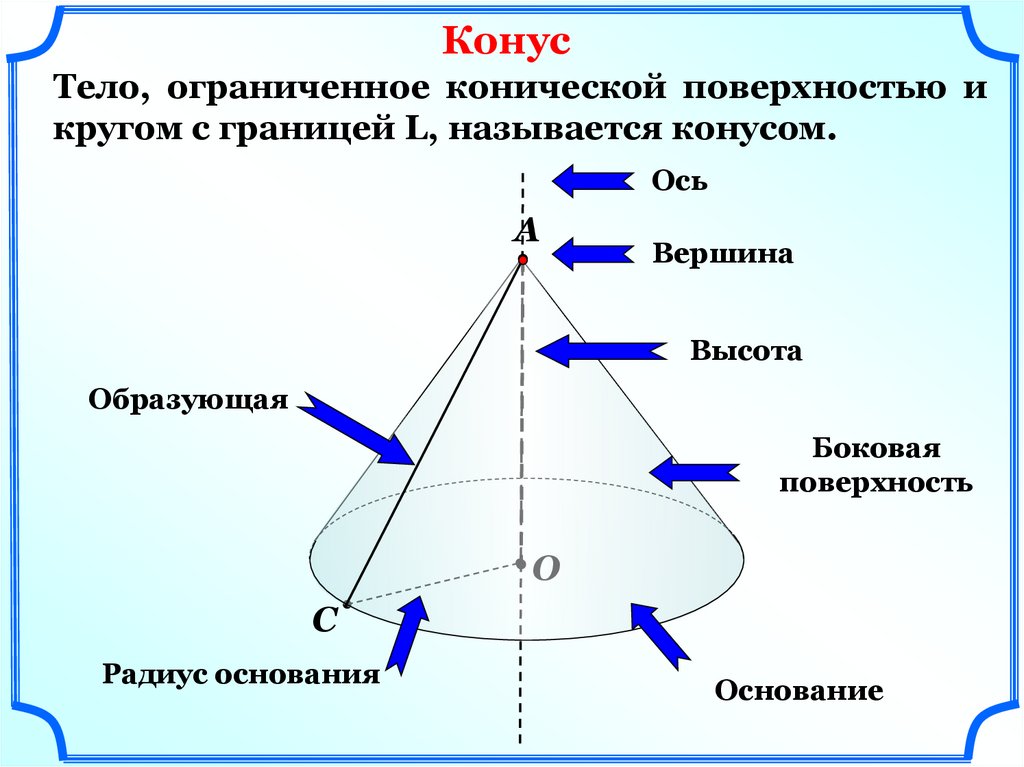
КонусТело, ограниченное конической поверхностью и
кругом с границей L, называется конусом.
Ось
A
Вершина
Высота
Образующая
Боковая
поверхность
O
C
Радиус основания
Основание
2.
3.
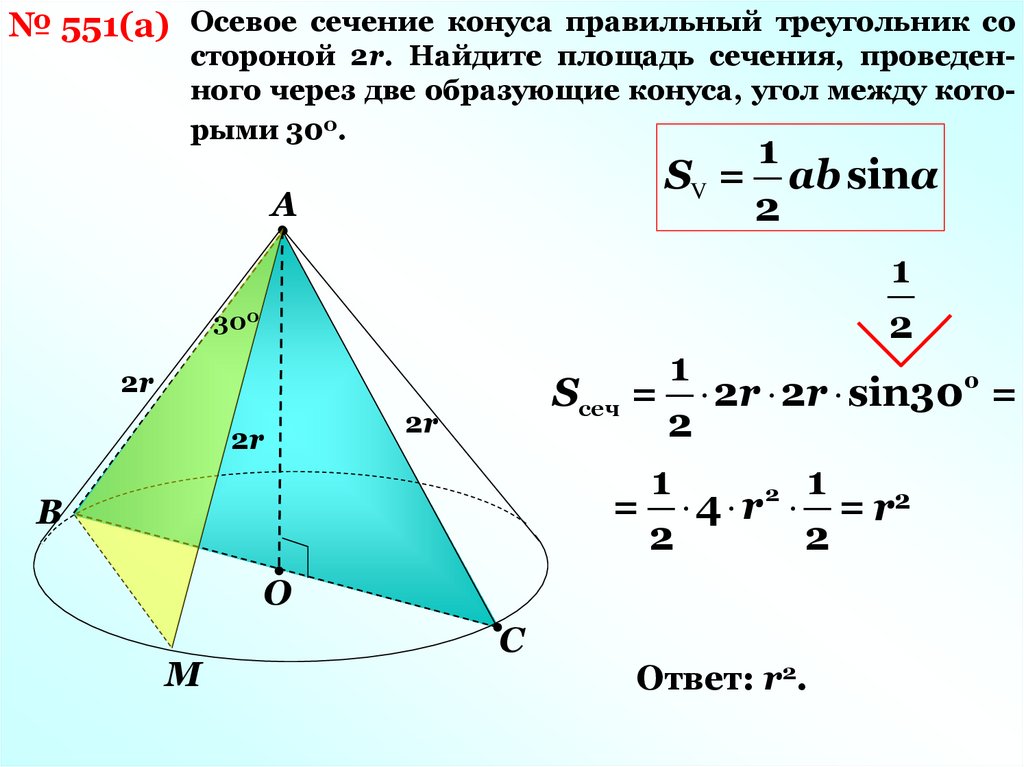
№ 551(а) Осевое сечение конуса правильный треугольник состороной 2r. Найдите площадь сечения, проведенного через две образующие конуса, угол между которыми 300.
1
SV = аb sinα
2
A
1
2
300
1
Sсеч = 2r 2r sin300 =
2
1
2 1
= 4 r = r2
2
2
2r
2r
2r
B
O
M
C
Ответ: r2.
4.
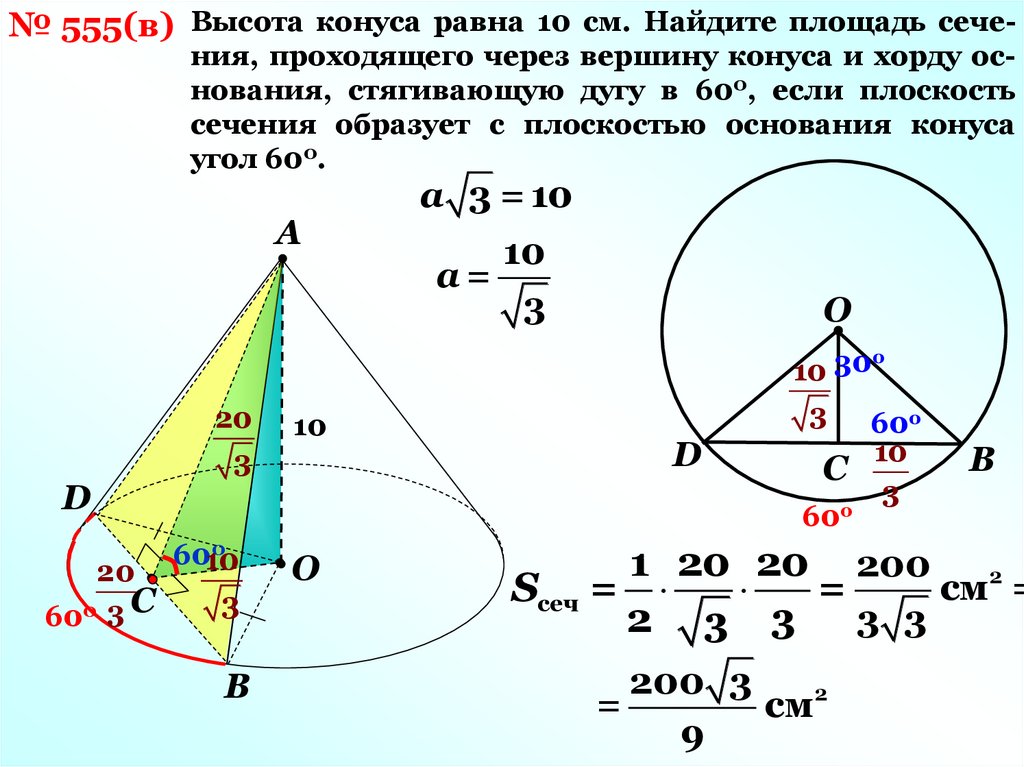
№ 555(в) Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 600, если плоскостьсечения образует с плоскостью основания конуса
угол 600.
A
а 3 = 10
10
а=
3
О
10 30
3 60о
10
C
3
о
60
о
20
3
10
D
20
600 3 C
0
6010
3
B
O
D
В
1 20 20 200 2
см =
Sсеч =
=
3 3
2 3 3
200 3
=
см2
9
5.
17.10.2024К л а с с н а я р а б о т а.
Площадь поверхности
конуса.
6.
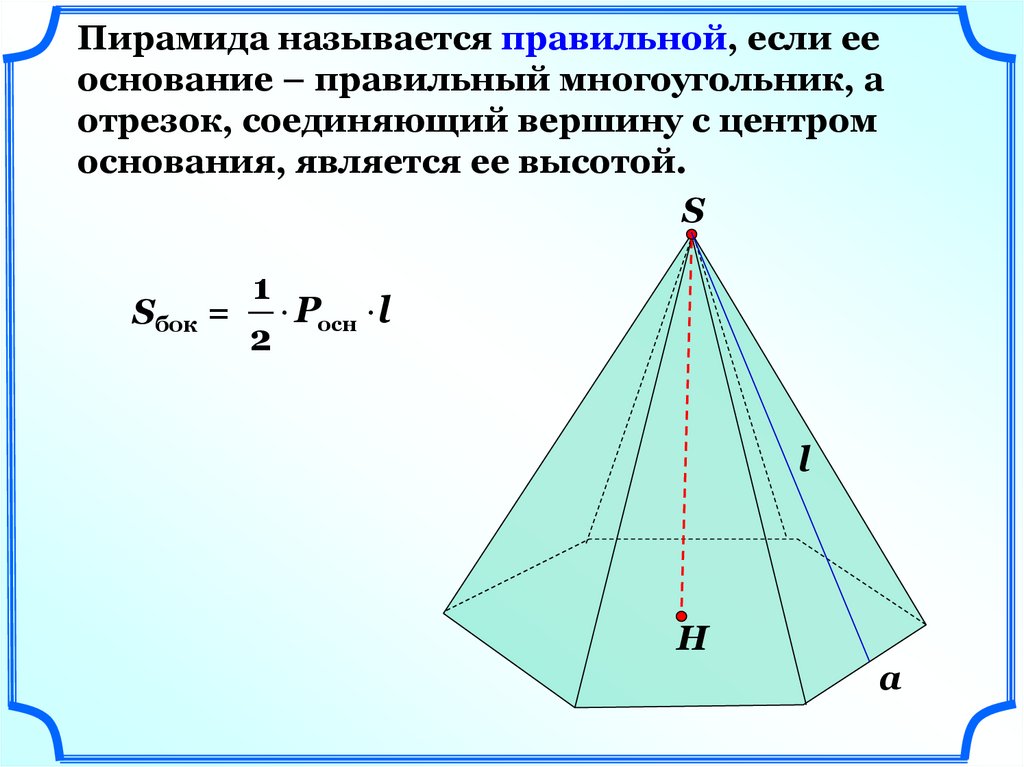
Пирамида называется правильной, если ееоснование – правильный многоугольник, а
отрезок, соединяющий вершину с центром
основания, является ее высотой.
S
1
Sбок = Pосн l
2
l
H
a
7.
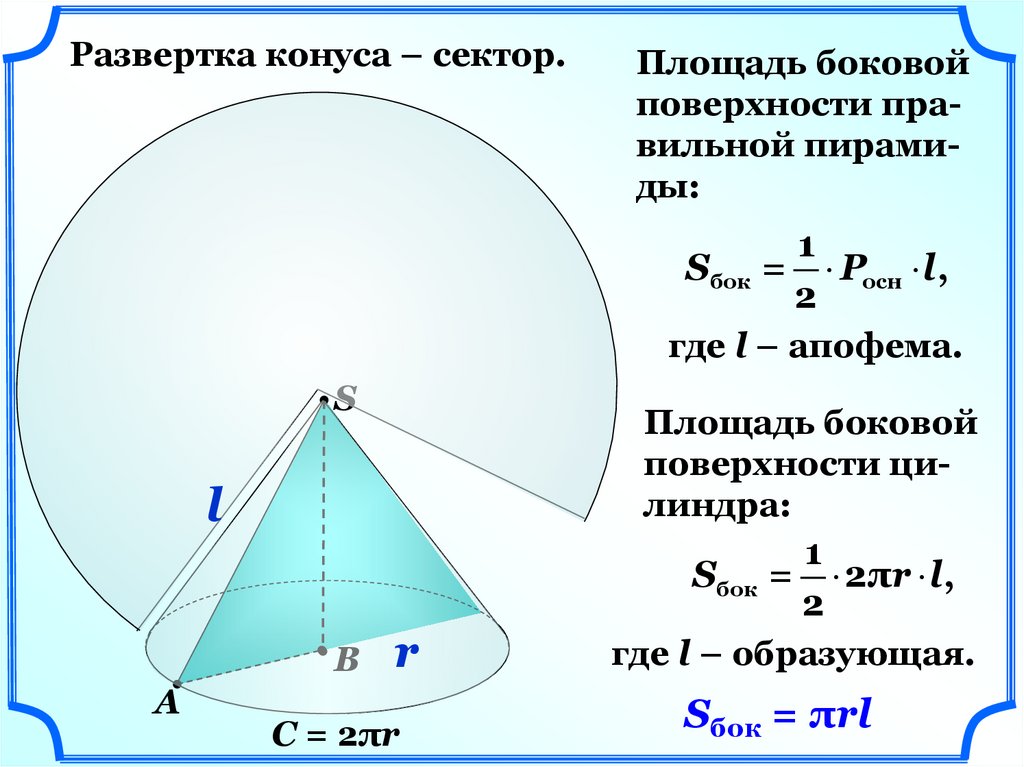
Развертка конуса – сектор.Площадь боковой
поверхности правильной пирамиды:
1
Sбок = Pосн l,
2
где l – апофема.
S
Площадь боковой
поверхности цилиндра:
l
1
Sбок = 2πr l,
2
B
A
r
C = 2πr
где l – образующая.
Sбок = πrl
8.
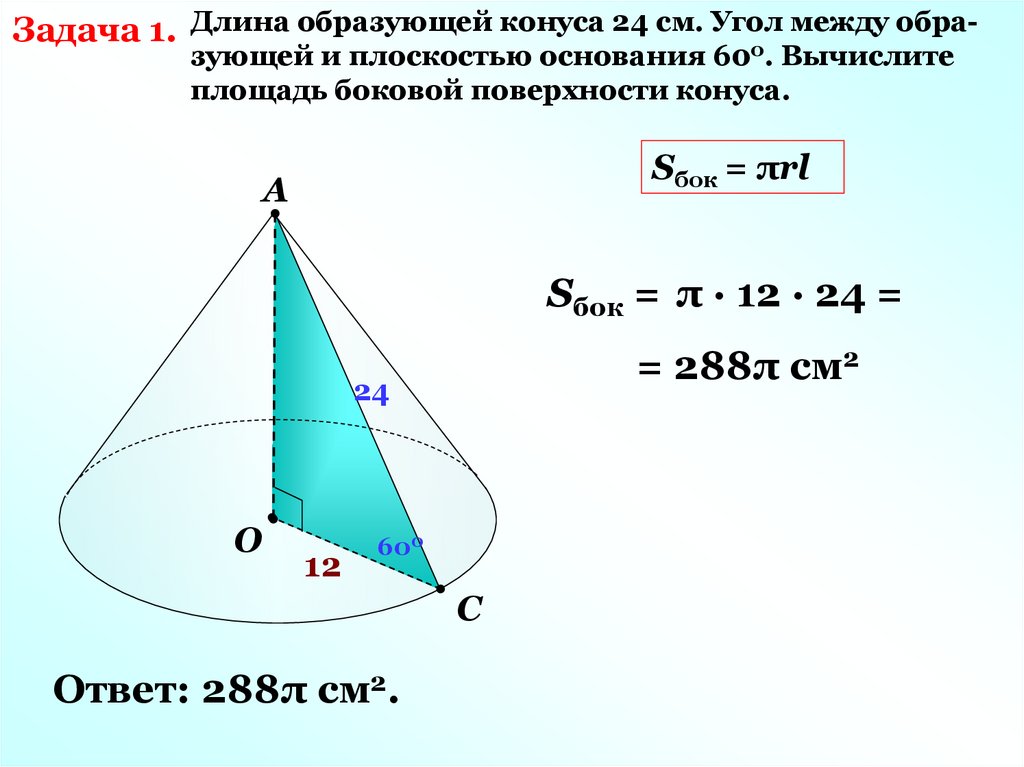
между обраЗадача 1. Длина образующей конуса 24 см. Угол0
зующей и плоскостью основания 60 . Вычислите
площадь боковой поверхности конуса.
Sбок = πrl
A
Sбок = π · 12 · 24 =
= 288π см2
24
O
12
600
C
Ответ: 288π см2.
9.
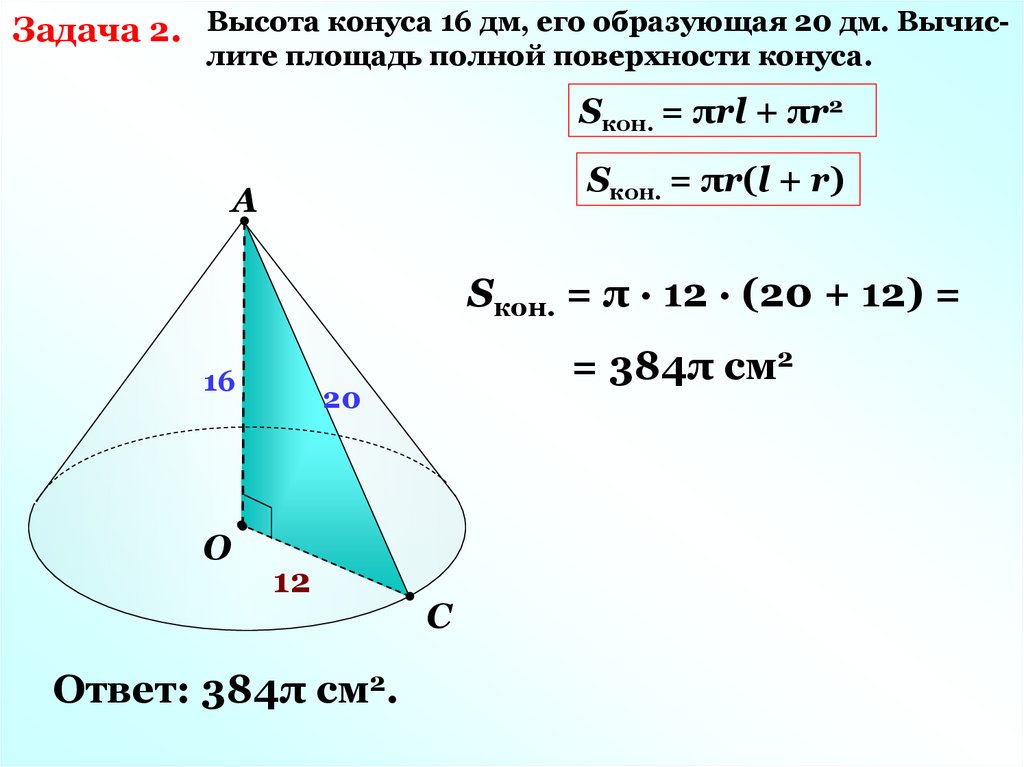
Задача 2. Высота конуса 16 дм, его образующая 20 дм. Вычислите площадь полной поверхности конуса.Sкон. = πrl + πr2
Sкон. = πr(l + r)
A
Sкон. = π · 12 · (20 + 12) =
16
O
= 384π см2
20
12
Ответ: 384π см2.
C
10.
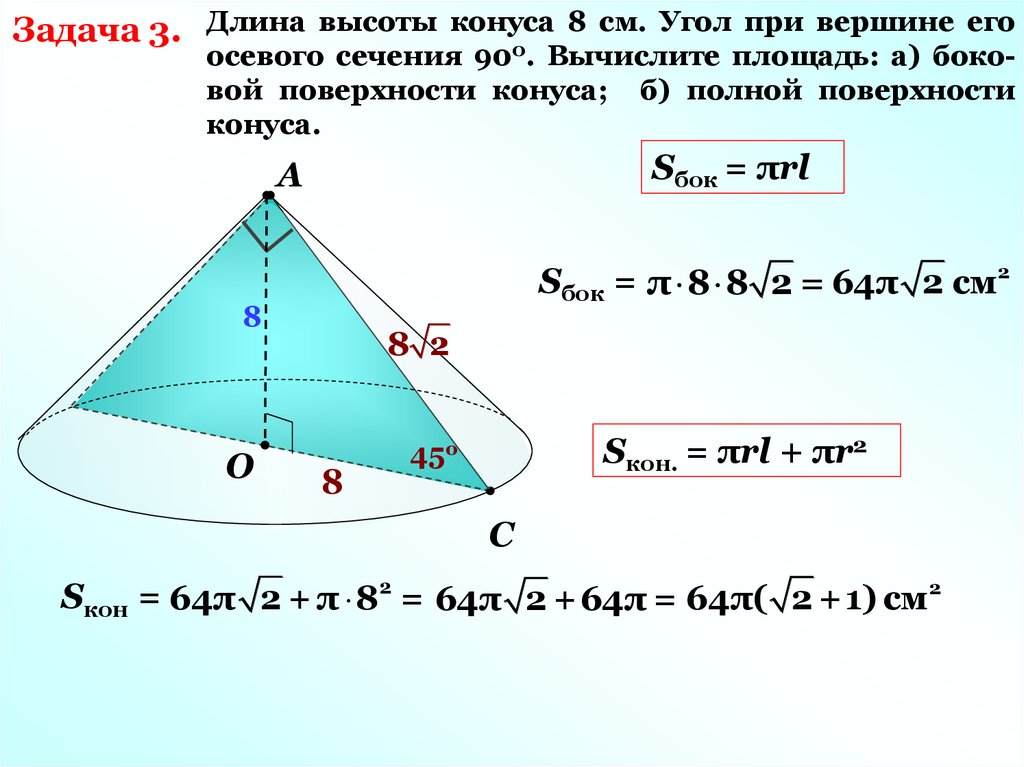
8 см. Угол при вершине егоЗадача 3. Длина высоты конуса
0
осевого сечения 90 . Вычислите площадь: а) боковой поверхности конуса; б) полной поверхности
конуса.
Sбок = πrl
A
Sбок = π 8 8 2 = 64π 2 см2
8
O
8 2
8
Sкон. = πrl + πr2
45о
C
Sкон = 64π 2 + π 82 = 64π 2 +64π = 64π( 2 +1) см2
11.
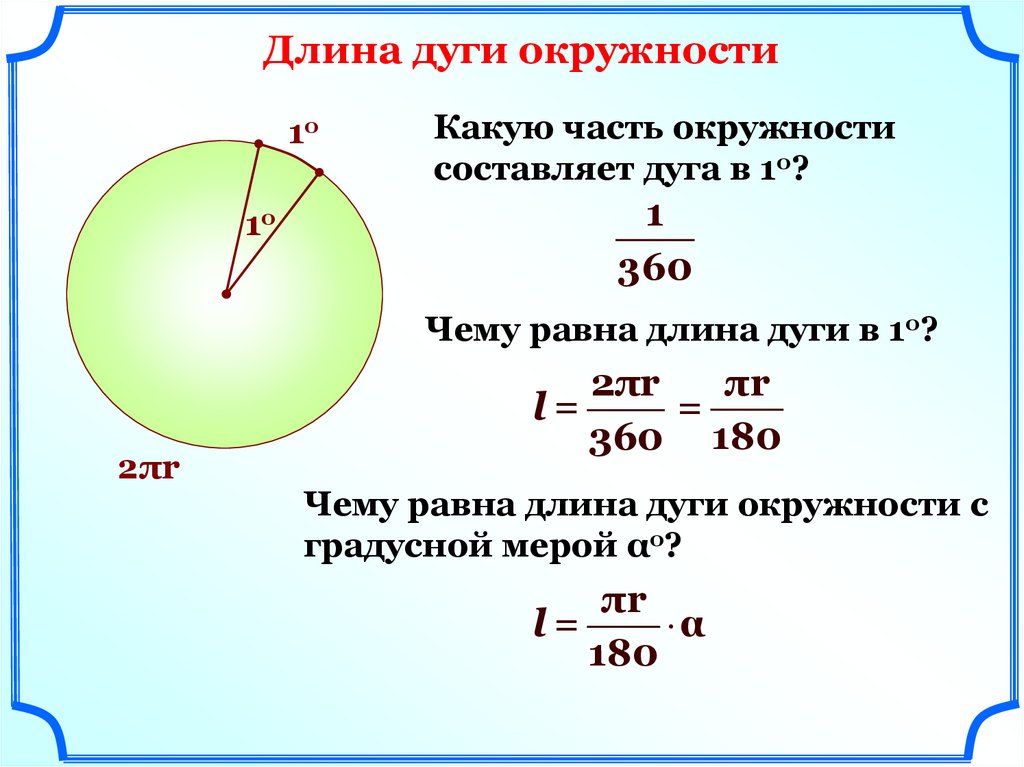
Длина дуги окружности1о
1о
Какую часть окружности
составляет дуга в 1о?
1
360
Чему равна длина дуги в 1о?
2πr
πr
2πr
=
l=
360 180
Чему равна длина дуги окружности с
градусной мерой αо?
πr
l=
α
180
12.
C1S
C
=l
O
r
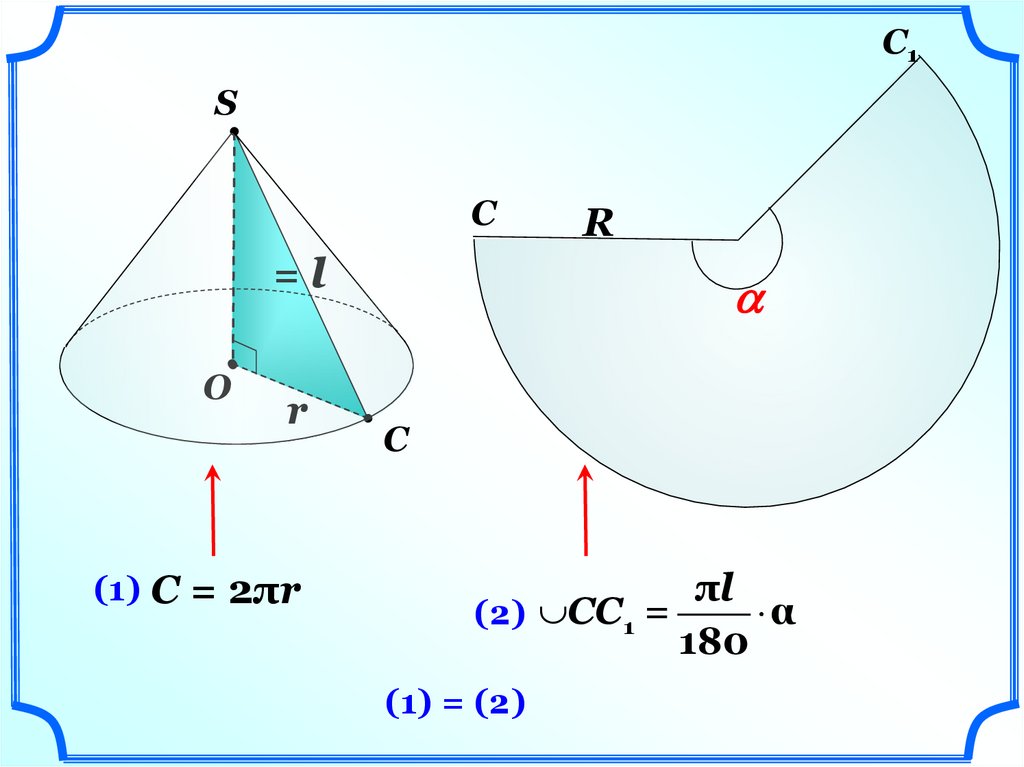
(1) C = 2πr
R
a
C
πl
α
(2) СС1 =
180
(1) = (2)
13.
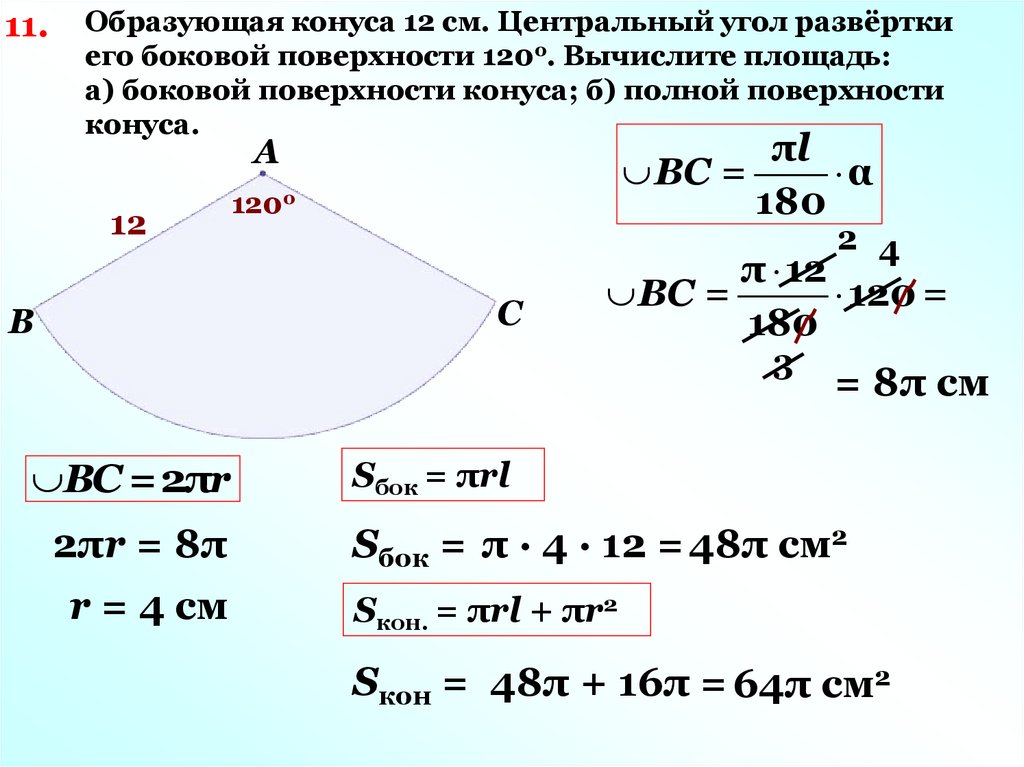
11.Образующая конуса 12 см. Центральный угол развёртки
его боковой поверхности 120о. Вычислите площадь:
а) боковой поверхности конуса; б) полной поверхности
конуса.
πl
ВС =
α
180
А
12
120о
2 4
С
В
π 12
ВС =
120 =
180
3
= 8π см
ВС =2πr
Sбок = πrl
2πr = 8π
Sбок = π · 4 · 12 =48π см2
r = 4 см
Sкон. = πrl + πr2
Sкон = 48π + 16π = 64π см2
14.
14. Образующая конуса 40 см, диаметр его основания 12 см.Вычислите: а) Sбок; б) градусную меру центрального угла
развёртки боковой поверхности конуса.
A
Sбок = πrl
Sбок = π · 6 · 40 =240π см2
πl
ВС =
α
180
40
ВС =2πr
ВС = 2π · 6 = 12π см
O
π 40
12π =
α
180
α 9
6=
α = 54о
9
6
6
C
2
15.
№ 562;563.




 mathematics
mathematics