Цилиндр, конус, шар

1.

2.

МБОУ «Криушинская СОШ»
учитель Погодина Г.Б.
на тему:

3.

Рассмотреть геометрические тела – цилиндр,
конус, шар;
какими элементами они образованы;
виды сечений;
каким образом вычисляются площади
поверхностей данных фигур.
Научить строить данные геометрические тела.
Научить применять полученные знания и умения
при решении задач

4.

L1
β
L
Тело, ограниченное цилиндрической
поверхностью и двумя кругами с
границами L и L1, называется
цилиндром
ά
Осевое сечение
Сечение цилиндра
плоскостью,
перпендикулярной к оси

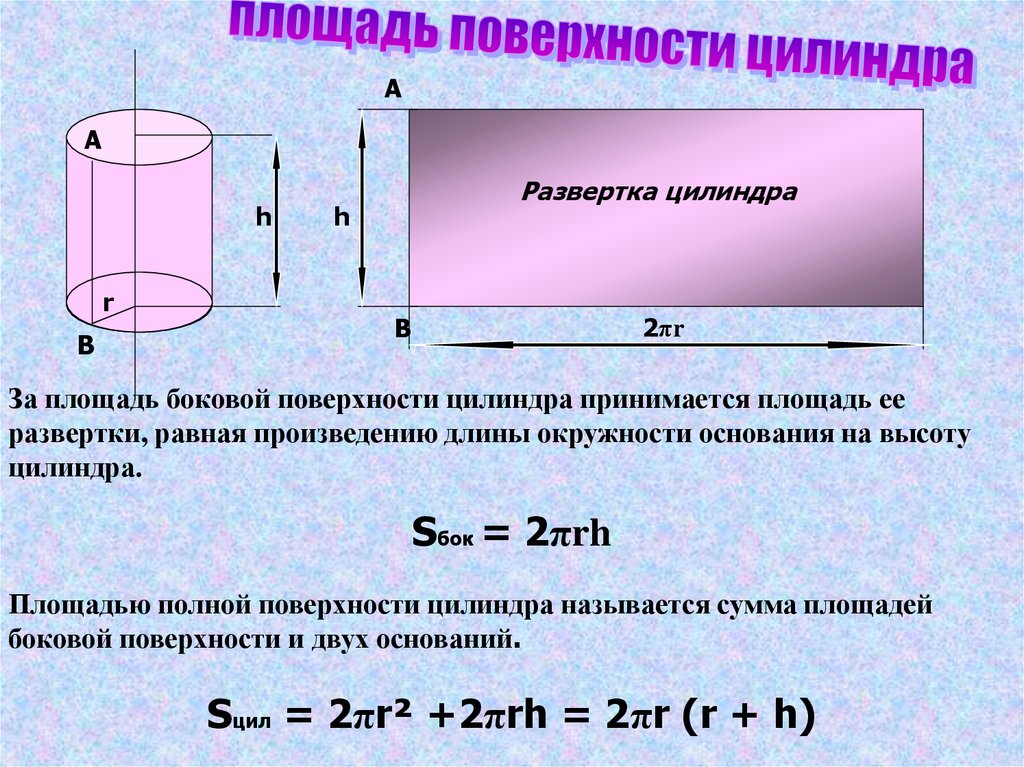
5.

A
A
h
r
B
Развертка цилиндра
h
2πr
B
За площадь боковой поверхности цилиндра принимается площадь ее
развертки, равная произведению длины окружности основания на высоту
цилиндра.
Sбок = 2πrh
Площадью полной поверхности цилиндра называется сумма площадей
боковой поверхности и двух оснований.
Sцил = 2πr² +2πrh = 2πr (r + h)

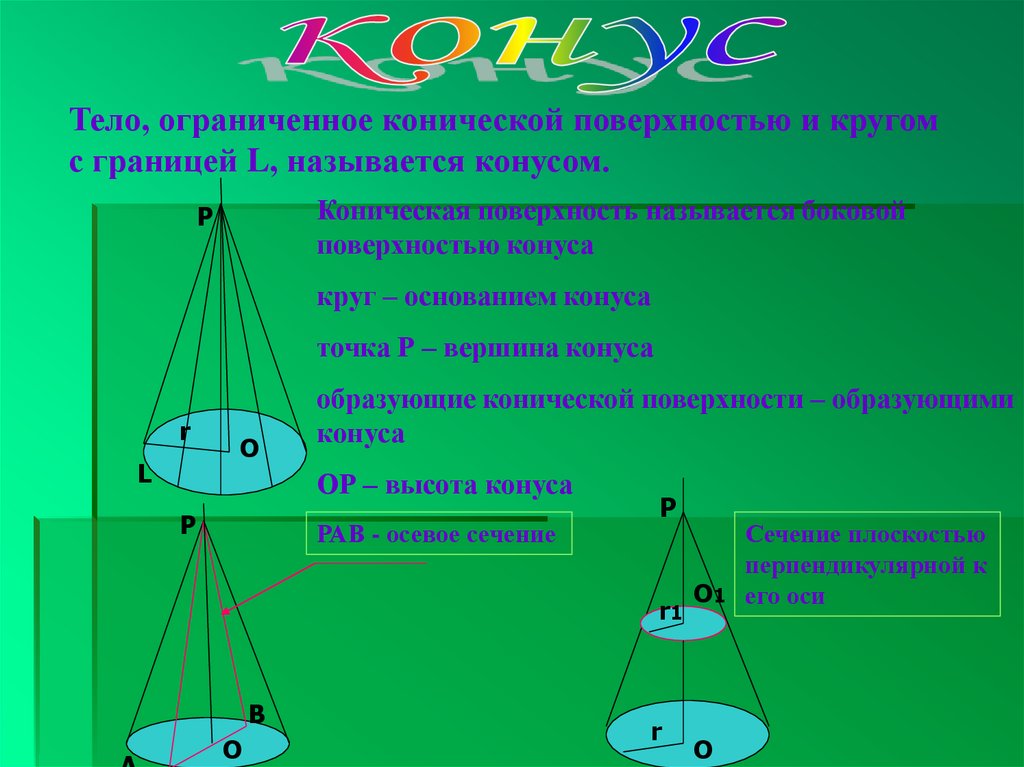
6.

Тело, ограниченное конической поверхностью и кругом
с границей L, называется конусом.
Коническая поверхность называется боковой
поверхностью конуса
Р
круг – основанием конуса
точка Р – вершина конуса
r
L
О
образующие конической поверхности – образующими
конуса
ОР – высота конуса
Р
РАВ - осевое сечение
Р
r1
В
О
r
О1
О
Сечение плоскостью
перпендикулярной к
его оси

7.

Р
За площадь боковой поверхности конуса
принимается произведение половины длины
окружности основания на образующую
Sбок = πrl
О
Площадью полной поверхности конуса
называется сумма площадей боковой
поверхности и основания.
Sкон = πr (l+r)
r1
r
О1
Площадь боковой поверхности усеченного
конуса равна произведению полусуммы длин
окружностей оснований на образующую
О
Sбок = π(r +r1)l

8.

z А
В
α
y
x
Сферой называется поверхность, состоящая из всех точек
пространства, расположенных на данном расстоянии от
данной точки
В прямоугольной системе координат уравнение сферы
радиуса R с центром С(x0;y0;z0) имеет вид
(x-x0)²+(y-y0)²+(z+z0)²=R

9.

α - касательная плоскость к сфере
А
α
О
А – точка касания
Теорема:
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен
к касательной плоскости.
R
За площадь сферы примем предел
последовательности площадей поверхностей
описанных около сферы многогранников при
стремлении к нулю наибольшего размера
каждой грани
S=4πR²

10.

1. Осевое сечение цилиндра - квадрат, диагональ
которого равна 20 см. Найдите: а)высоту цилиндра;
в) площадь основания цилиндра.
2. Найдите высоту конуса, если площадь его
осевого сечения равна 6 дм², а площадь основания равна
8 дм².
3. Найдите уравнение сферы радиуса R с
центром А, если а) А(2;-4;7), R=3; А(0;0;0),
R=√2; в) А(2;0;0), R=4

11.

§1,2,3
Решить упражнения №
525, 547, 574