Similar presentations:
Цилиндр, конус, шар, тор
1. Новоазовский индустриальный техникум
Презентацияна тему «ТЕЛА ВРАЩЕНИЯ»
2. Цилиндр
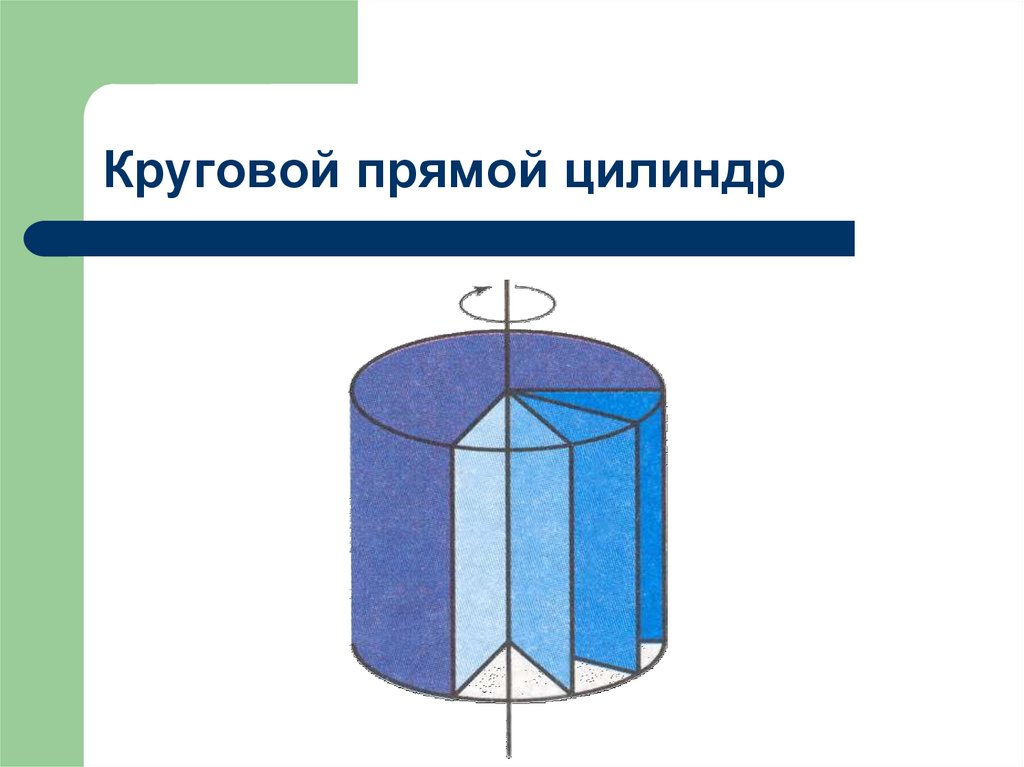
Определение.Тело, которое образуется при
вращении прямоугольника вокруг
прямой, содержащей его сторону,
называется цилиндром.
3. Круговой прямой цилиндр
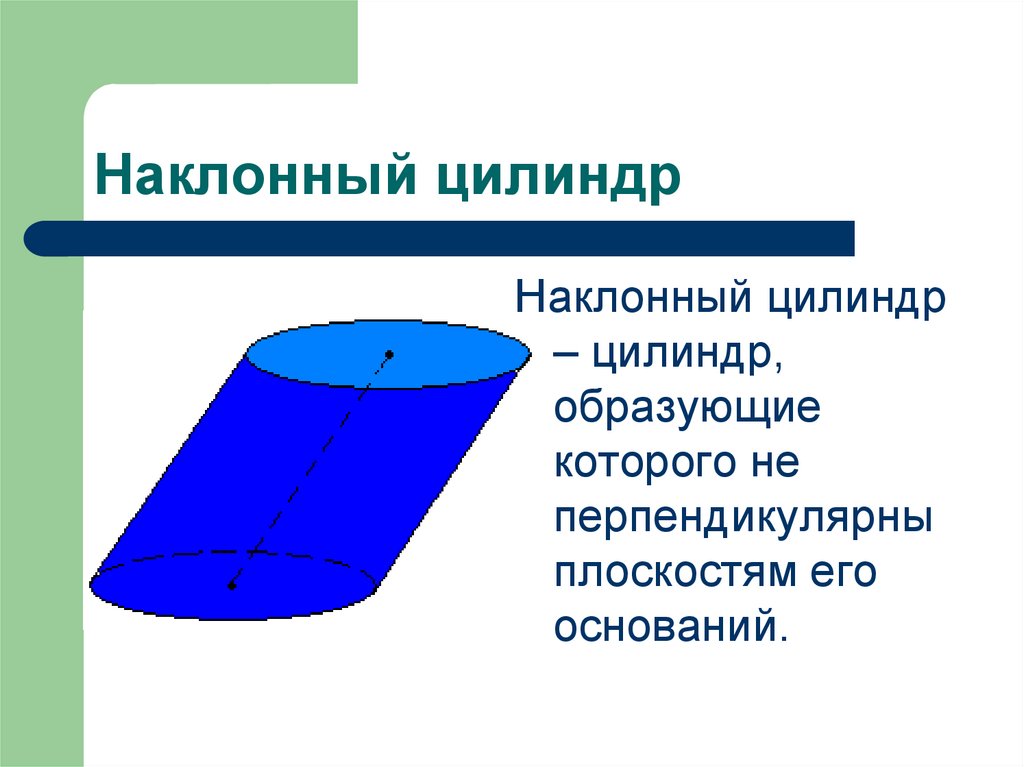
4. Наклонный цилиндр
Наклонный цилиндр– цилиндр,
образующие
которого не
перпендикулярны
плоскостям его
оснований.
5.
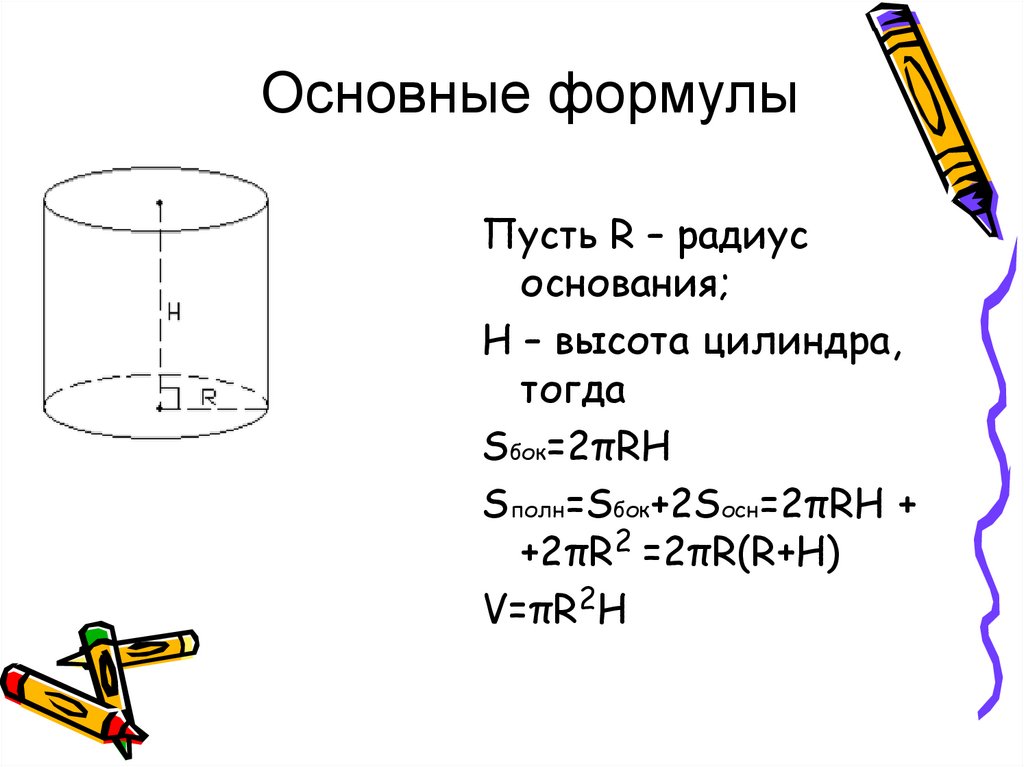
Основные формулыПусть R – радиус
основания;
H – высота цилиндра,
тогда
Sбок=2πRH
Sполн=Sбок+2Sосн=2πRH +
+2πR2 =2πR(R+H)
V=πR2H
6. Конус
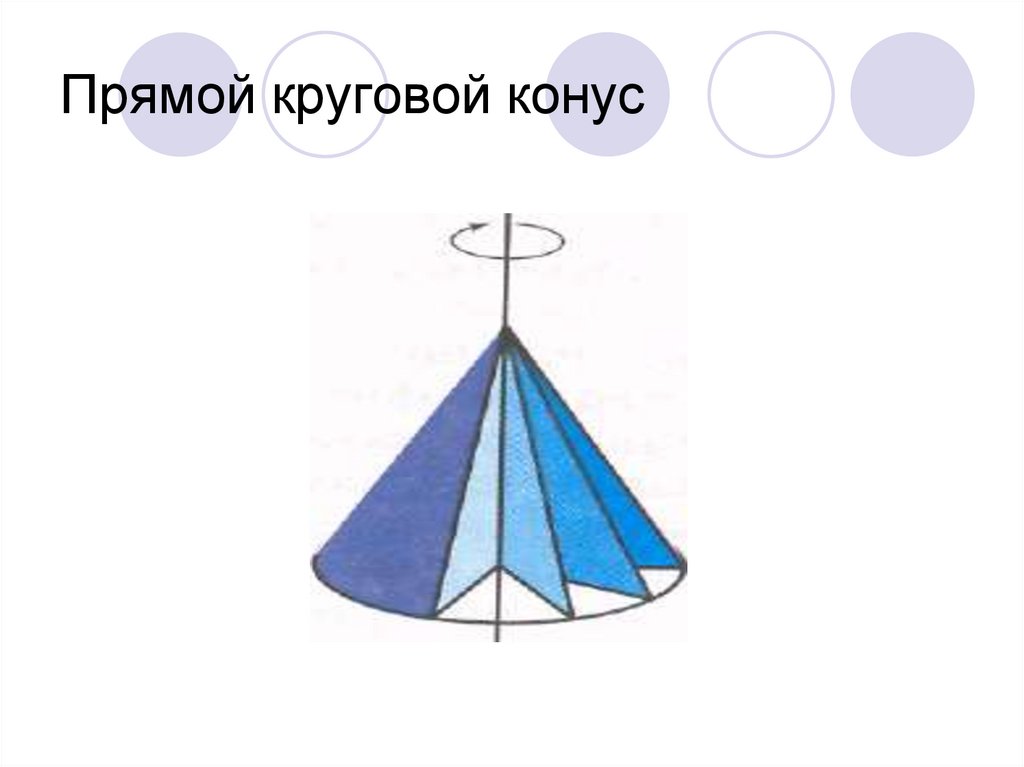
Определение.Тело, которое образуется при
вращении прямоугольного
треугольника вокруг прямой,
содержащий его катет, называется
прямым круговым конусом.
7. Прямой круговой конус
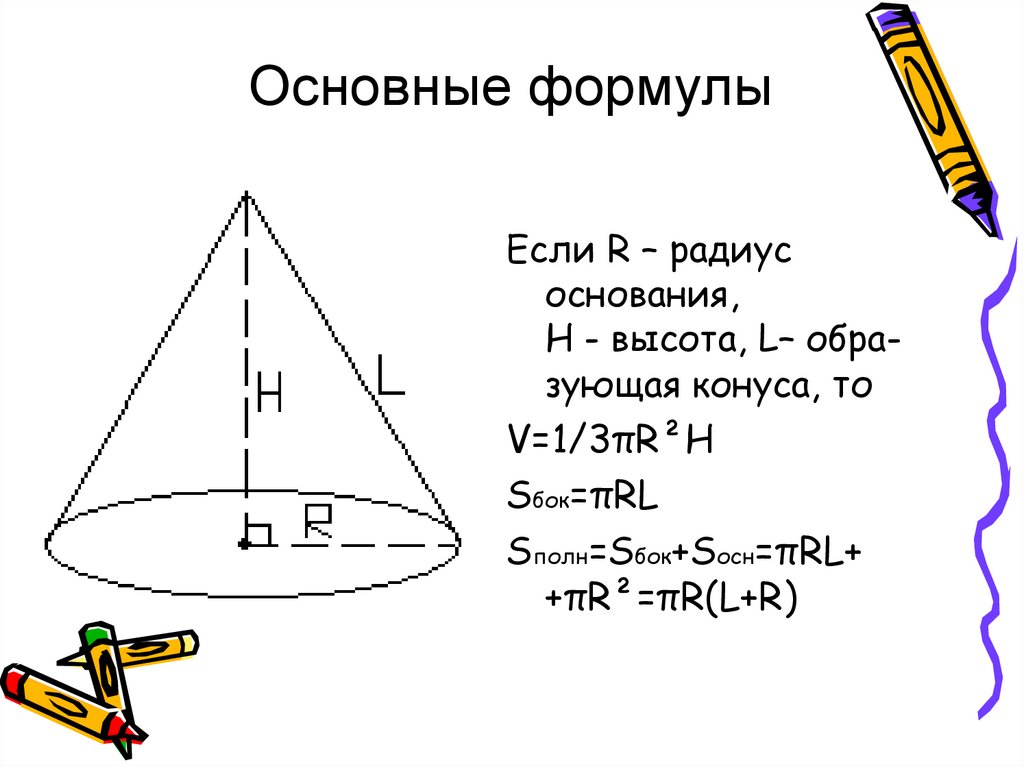
8.
Основные формулыЕсли R – радиус
основания,
H - высота, L– образующая конуса, то
V=1/3πR²H
Sбок=πRL
Sполн=Sбок+Sосн=πRL+
+πR²=πR(L+R)
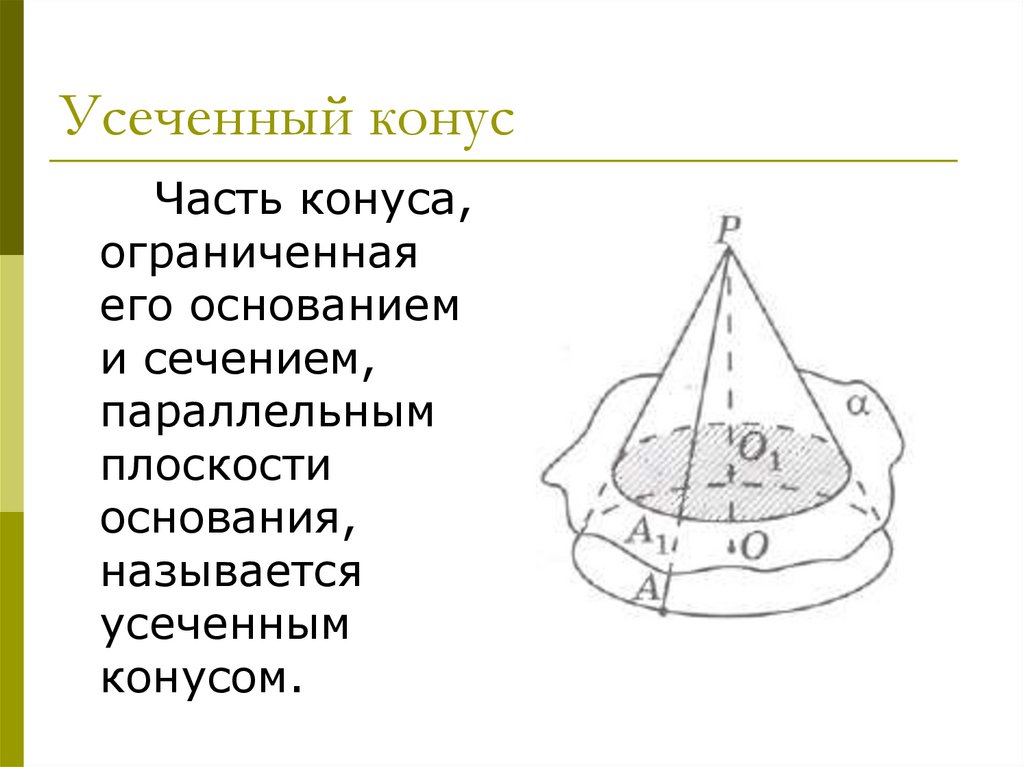
9. Усеченный конус
Часть конуса,ограниченная
его основанием
и сечением,
параллельным
плоскости
основания,
называется
усеченным
конусом.
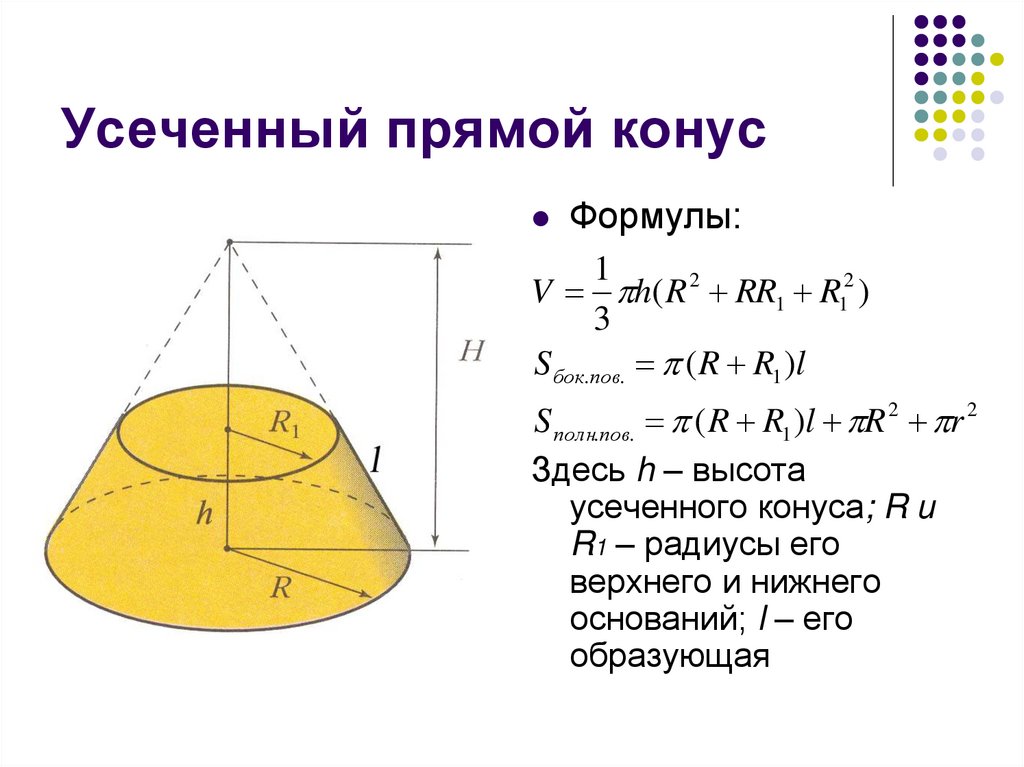
10. Усеченный прямой конус
Формулы:1
V h( R 2 RR1 R12 )
3
S бок.пов. ( R R1 )l
S полн.пов. ( R R1 )l R 2 r 2
Здесь h – высота
усеченного конуса; R и
R1 – радиусы его
верхнего и нижнего
оснований; l – его
образующая
11. Шар и сфера
Определение.Фигура, полученная в результате
вращения полукруга вокруг диаметра,
называется шаром. Поверхность,
образуемая при этом
полуокружностью, называется
сферой.
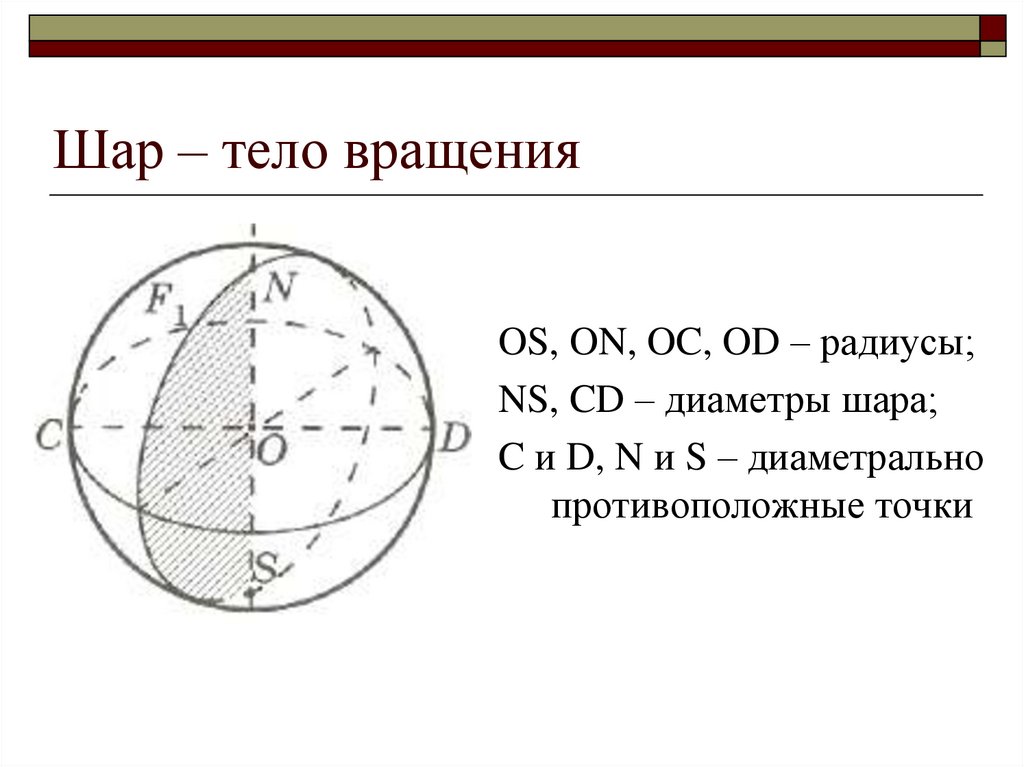
12. Шар – тело вращения
OS, ON, OC, OD – радиусы;NS, CD – диаметры шара;
C и D, N и S – диаметрально
противоположные точки
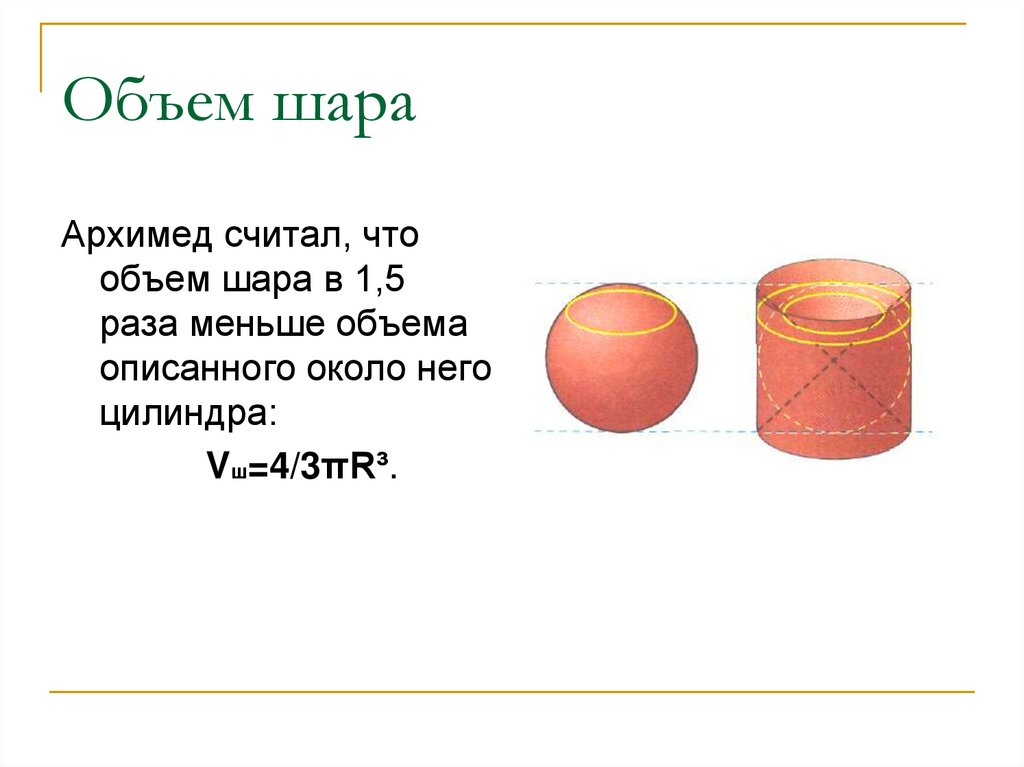
13. Объем шара
Архимед считал, чтообъем шара в 1,5
раза меньше объема
описанного около него
цилиндра:
Vш=4/3πR³.
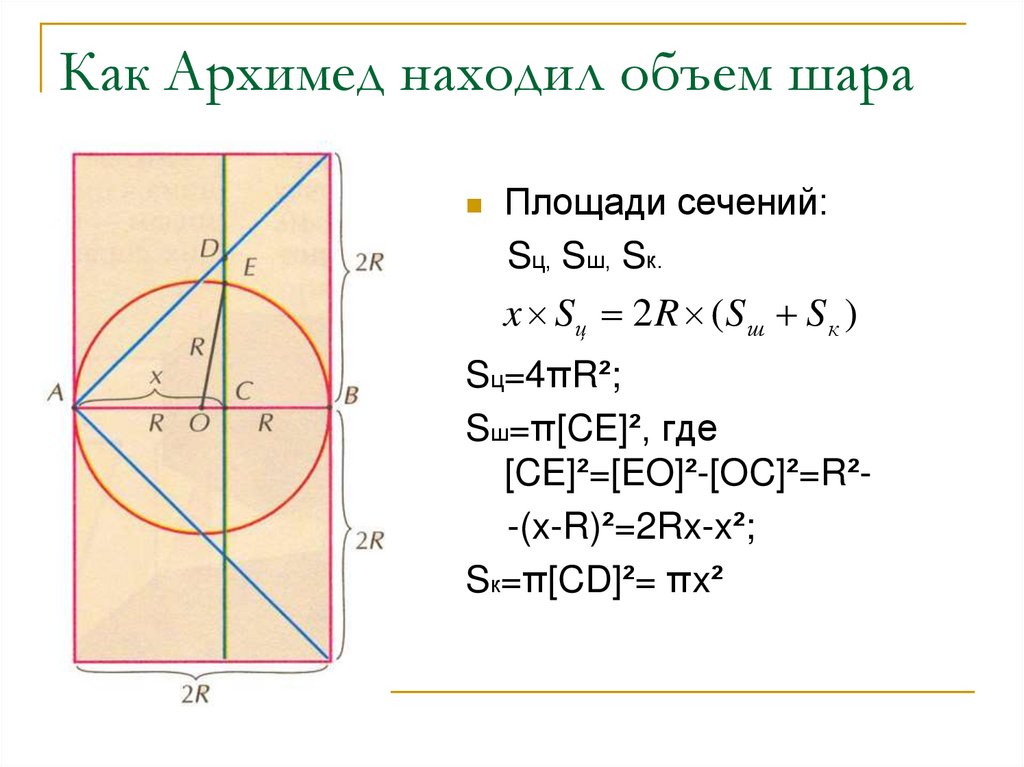
14. Как Архимед находил объем шара
Площади сечений:Sц, Sш, Sк.
x Sц 2 R ( S ш S к )
Sц=4πR²;
Sш=π[CE]², где
[CE]²=[EO]²-[OC]²=R²-(x-R)²=2Rx-x²;
Sк=π[CD]²= πx²
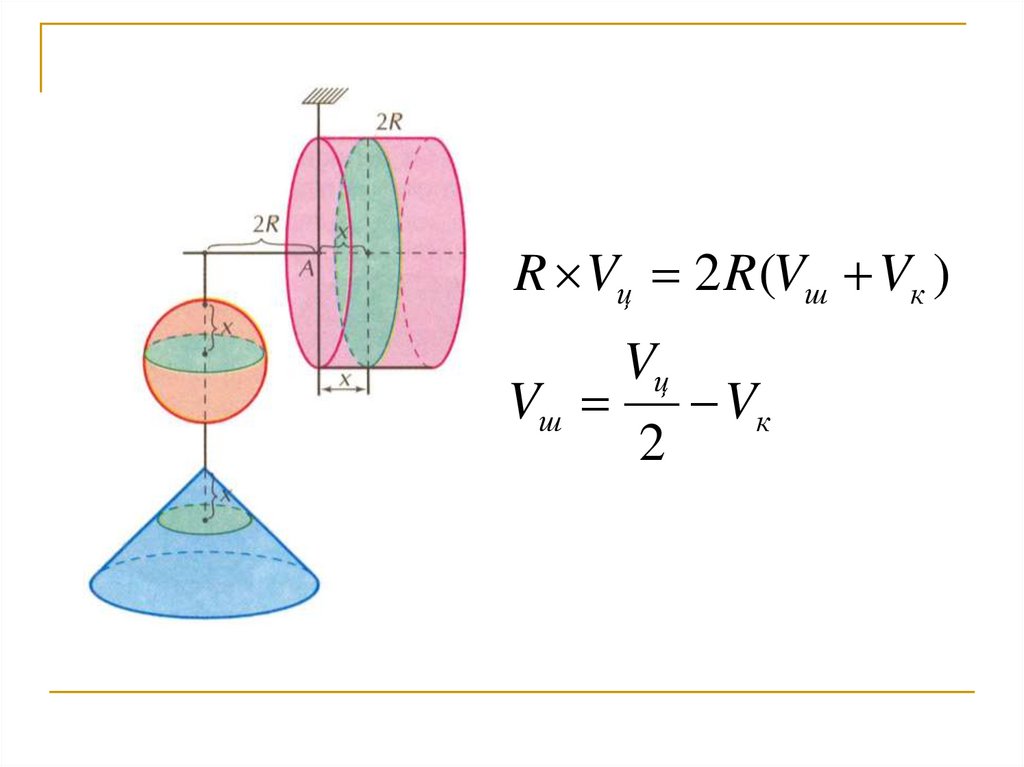
15.
R Vц 2 R (Vш Vк )Vш
Vц
2
Vк
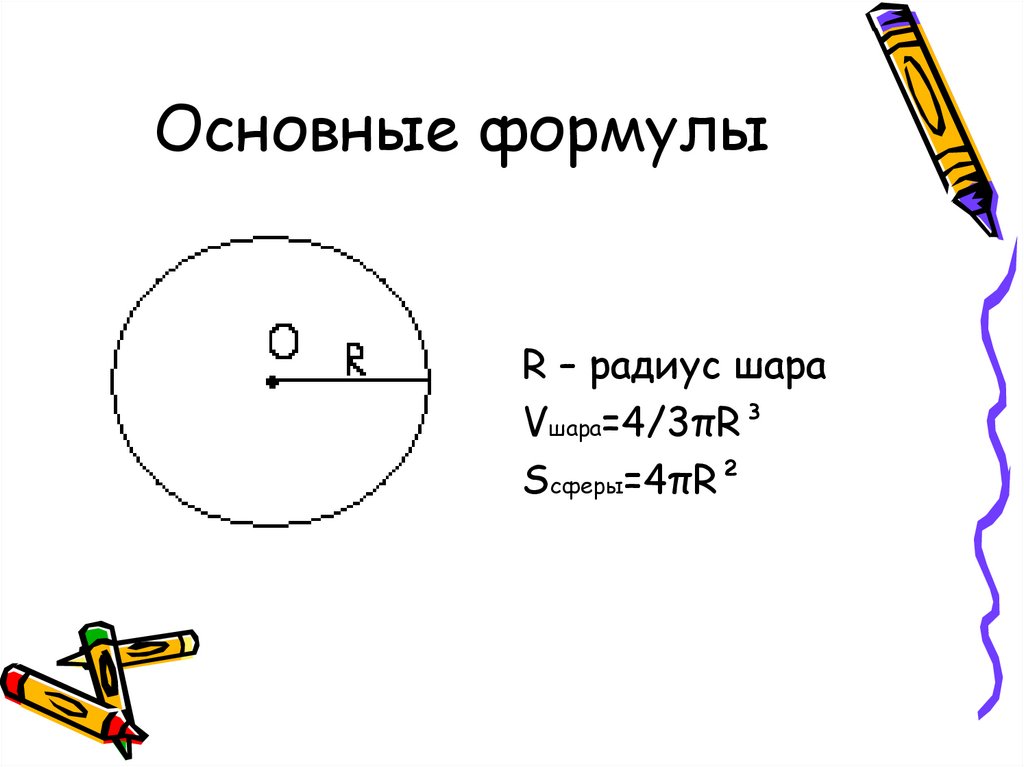
16. Основные формулы
R – радиус шараVшара=4/3πR³
Sсферы=4πR²
17. Уравнение сферы
Пусть A – центр(a; b; c)MA – радиус, тогда
MA²=(x-a)²+(y-b)²+(z-c)²;
(x-a)²+(y-b)²+(z-c)²=R²
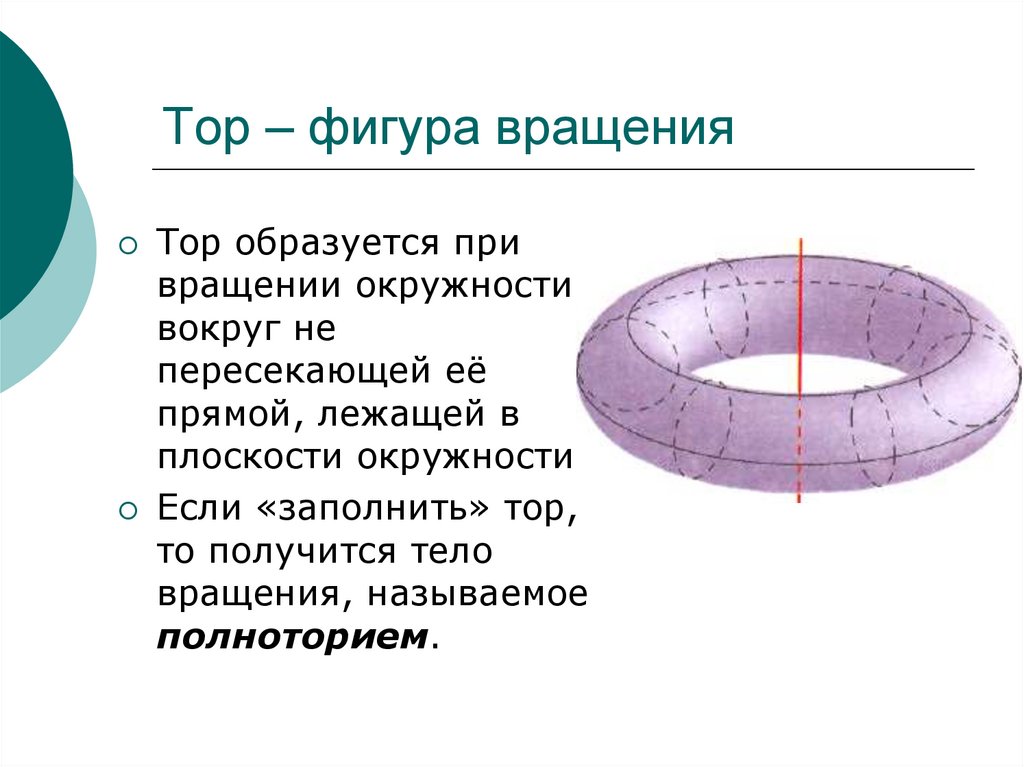
18. Тор – фигура вращения
Тор образуется привращении окружности
вокруг не
пересекающей её
прямой, лежащей в
плоскости окружности.
Если «заполнить» тор,
то получится тело
вращения, называемое
полноторием.
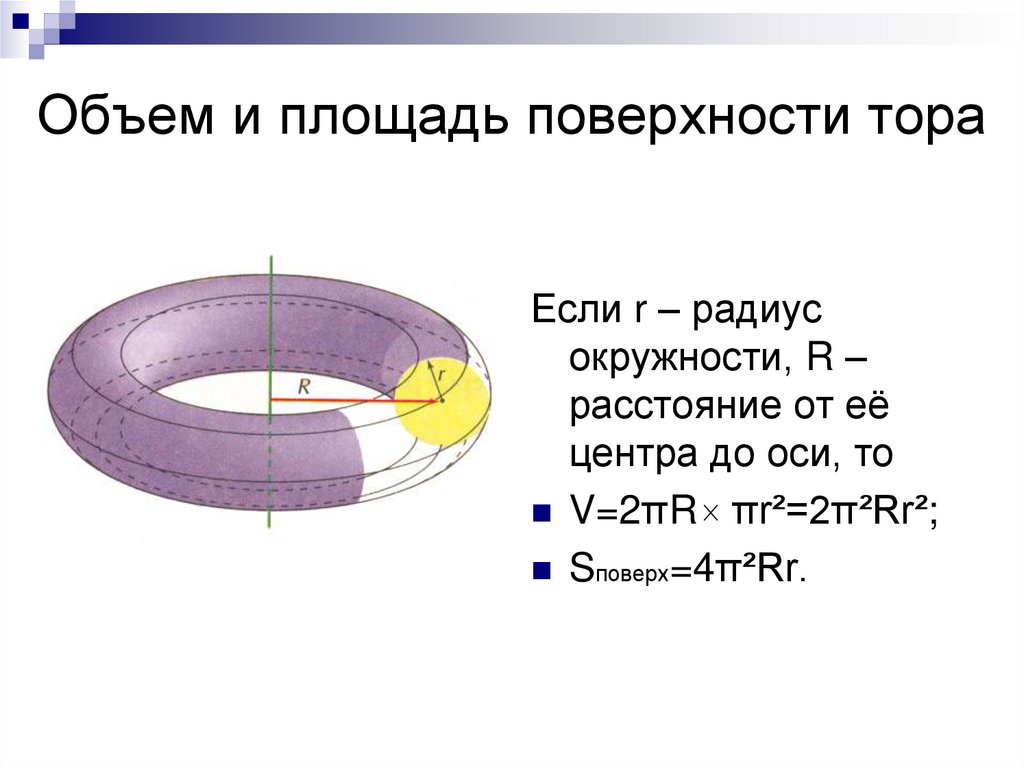
19. Объем и площадь поверхности тора
Если r – радиусокружности, R –
расстояние от её
центра до оси, то
V=2πR πr²=2π²Rr²;
Sповерх=4π²Rr.
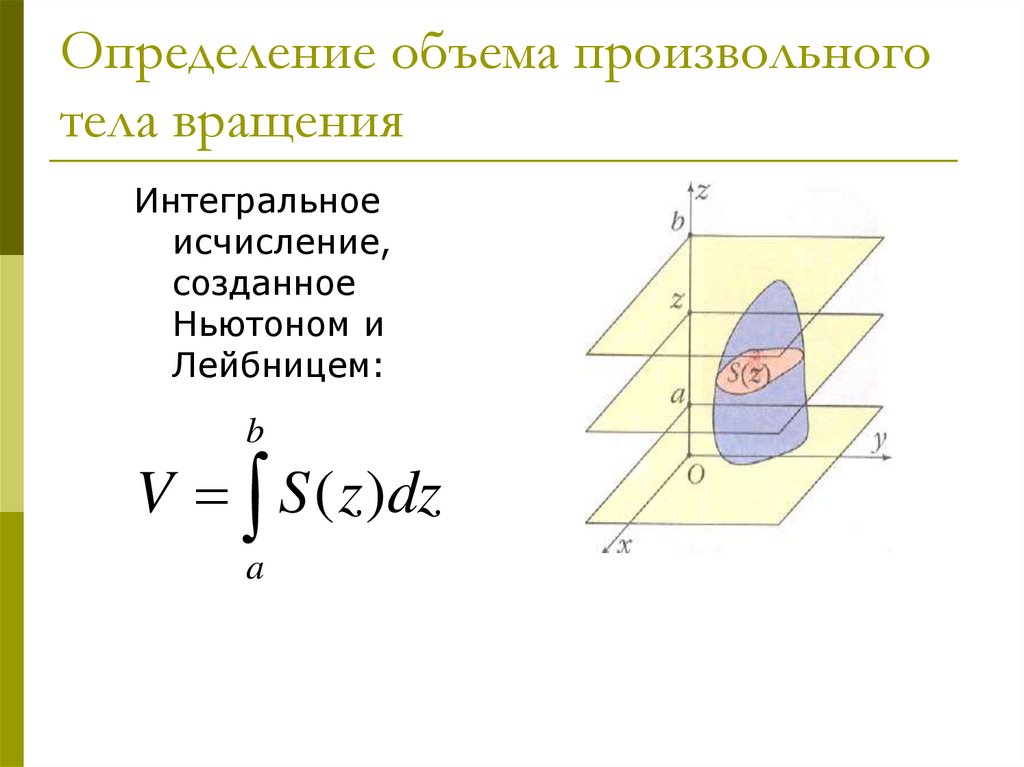
20. Определение объема произвольного тела вращения
Интегральноеисчисление,
созданное
Ньютоном и
Лейбницем:
b
V S ( z )dz
a





 mathematics
mathematics








