Similar presentations:
Цилиндр, конус, шар
1. ЦИЛИНДР. КОНУС. ШАР
Учитель: Назипов Р.Г.,МБОУ «Вечерняя (сменная) общеобразовательная школа
2. ЦИЛИНДР
3. ОПРЕДЕЛЕНИЕ ЦИЛИНДРА
Цили́ндр (др.-греч. κύλινδρος —валик, каток)
Цилиндр - тело, ограниченное
цилиндрической поверхностью и двумя
кругами с границами L и L1.
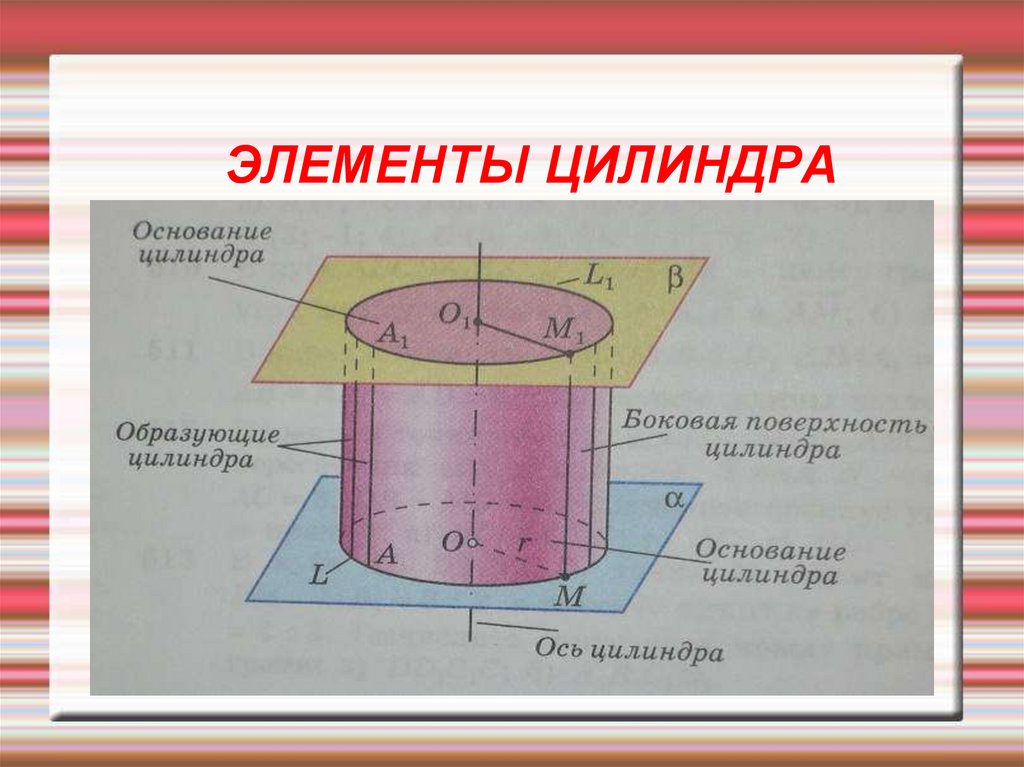
4. ЭЛЕМЕНТЫ ЦИЛИНДРА
Цилиндрическая поверхность — поверхность, получаемаядвижением прямой (образующей) в пространстве, так выделенная
точка образующей движется вдоль плоской кривой (направляющей).
Цилиндрическая поверхность называется боковой поверхностью
цилиндра.
Часть цилиндра, ограниченная параллельными плоскостями, это
основания цилиндра.
В большинстве случаев под цилиндром подразумевается прямой
круговой цилиндр,
У такого цилиндра имеется ось симметрии.
5. ЭЛЕМЕНТЫ ЦИЛИНДРА
6. ПОЛУЧЕНИЕ ЦИЛИНДРА
Цилиндр можетбыть получен
вращением
прямоугольника
вокруг одной из
его сторон.
7. ПРИМЕРЫ ЦИЛИНДРА
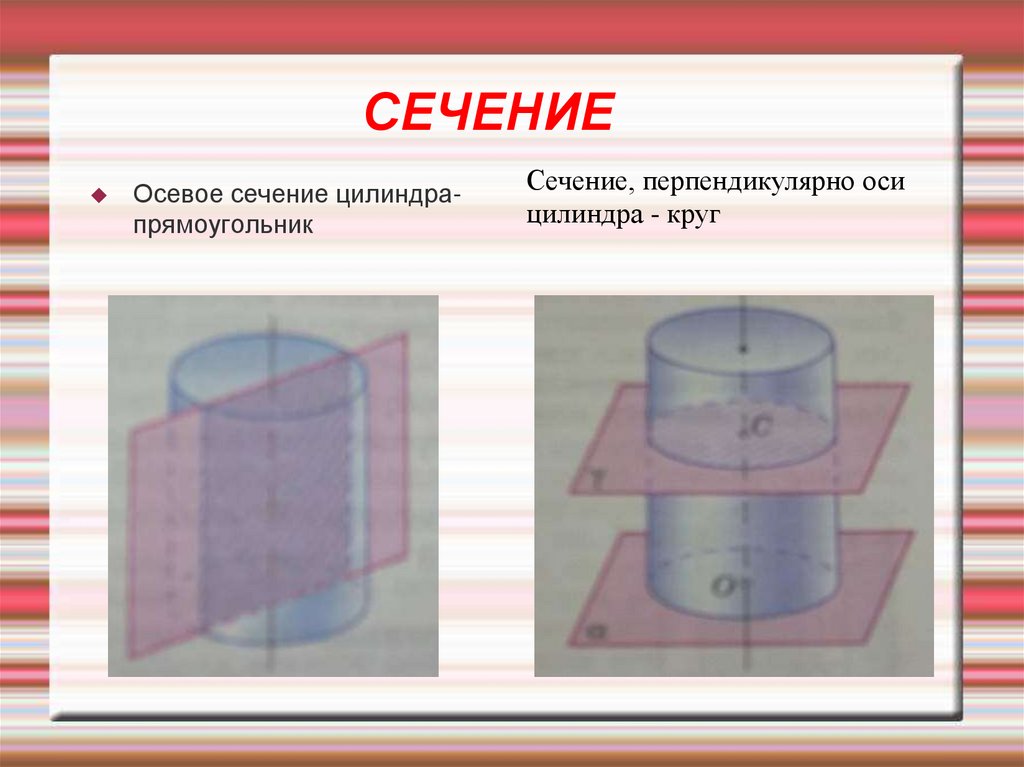
8. СЕЧЕНИЕ
Осевое сечение цилиндрапрямоугольникСечение, перпендикулярно оси
цилиндра - круг
9. ПЛОЩАДЬ ПОВЕРХНОСТИ
Sбок = 2ПrhSцил =2Пr(r+h)
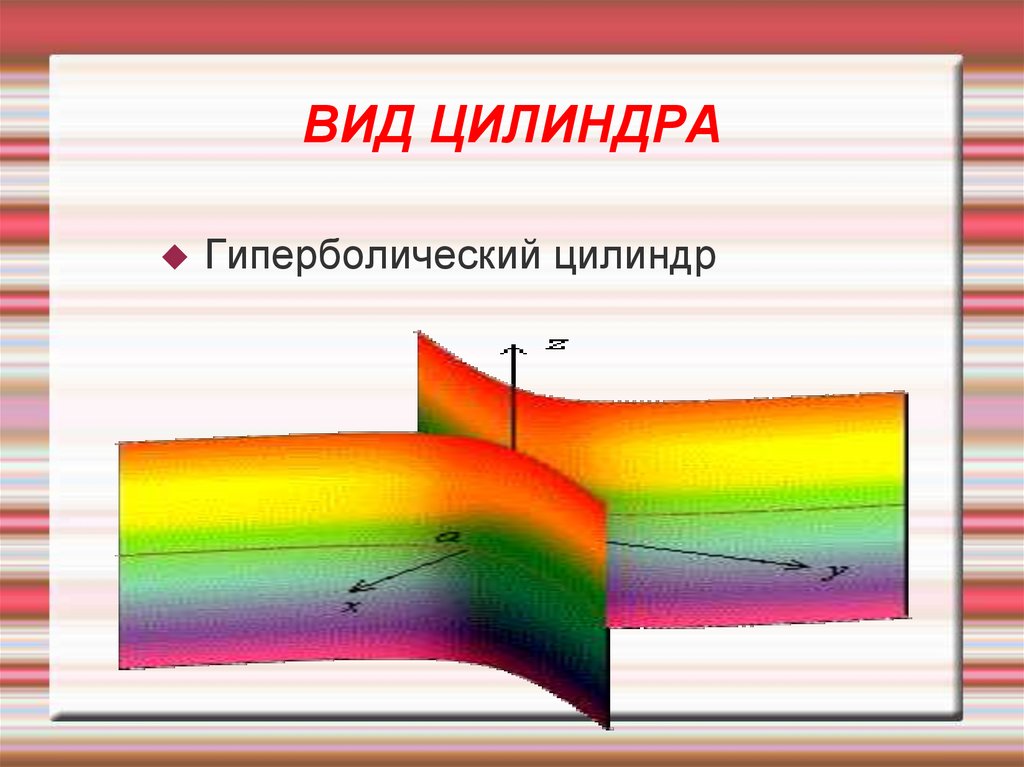
10. ВИД ЦИЛИНДРА
Эллиптический цилиндр11. ВИД ЦИЛИНДРА
Гиперболический цилиндр12. ВИД ЦИЛИНДРА
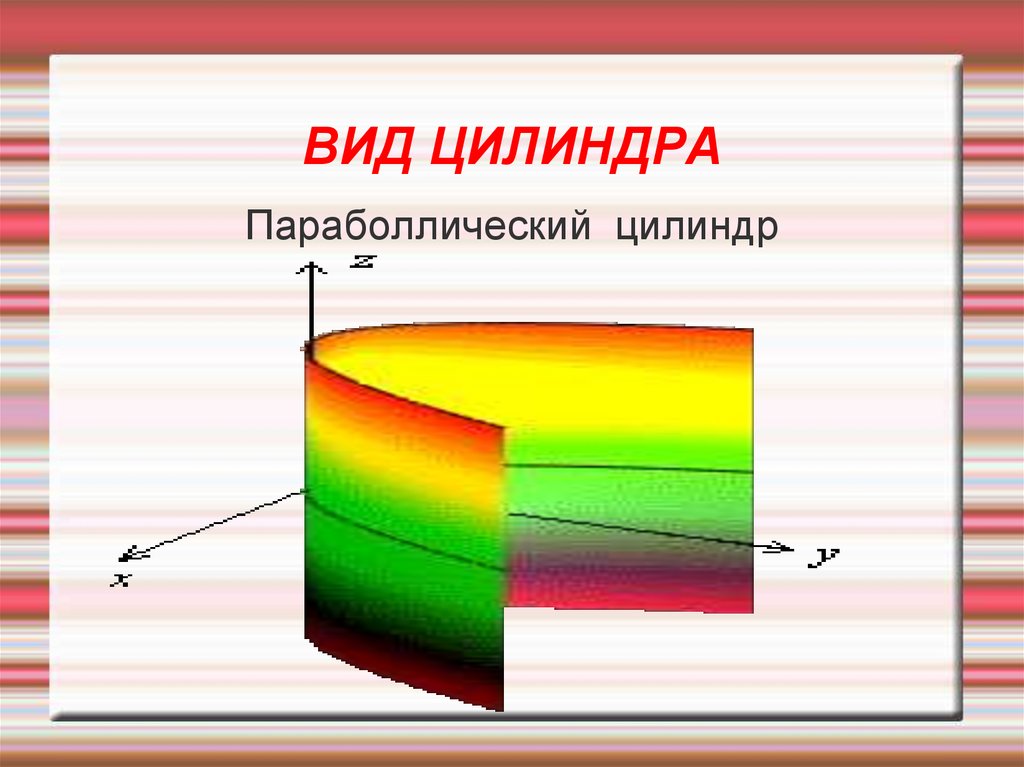
Параболлический цилиндр13. КОНУС
14. Определение конуса
Латинское слово CONUS позаимствовано изгреческого языка
( «конос» - затычка, втулка, сосновая шишка).
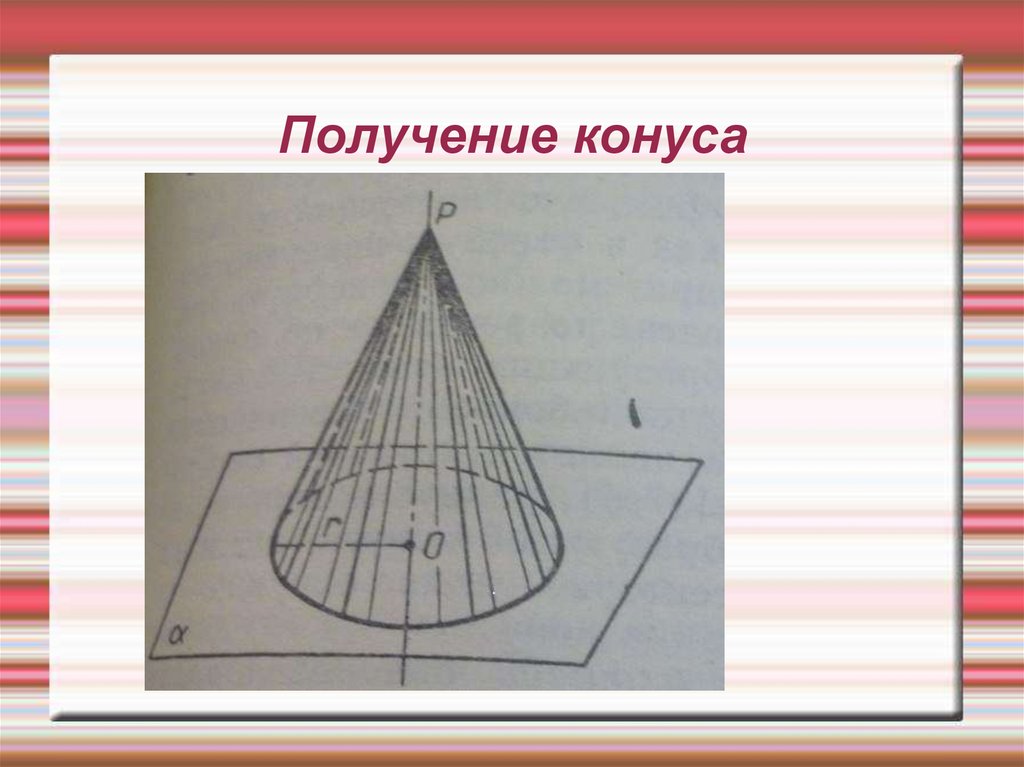
Конус - тело, ограниченное
конической
поверхностью
и
кругом с границами L .
.
15. Получение конуса
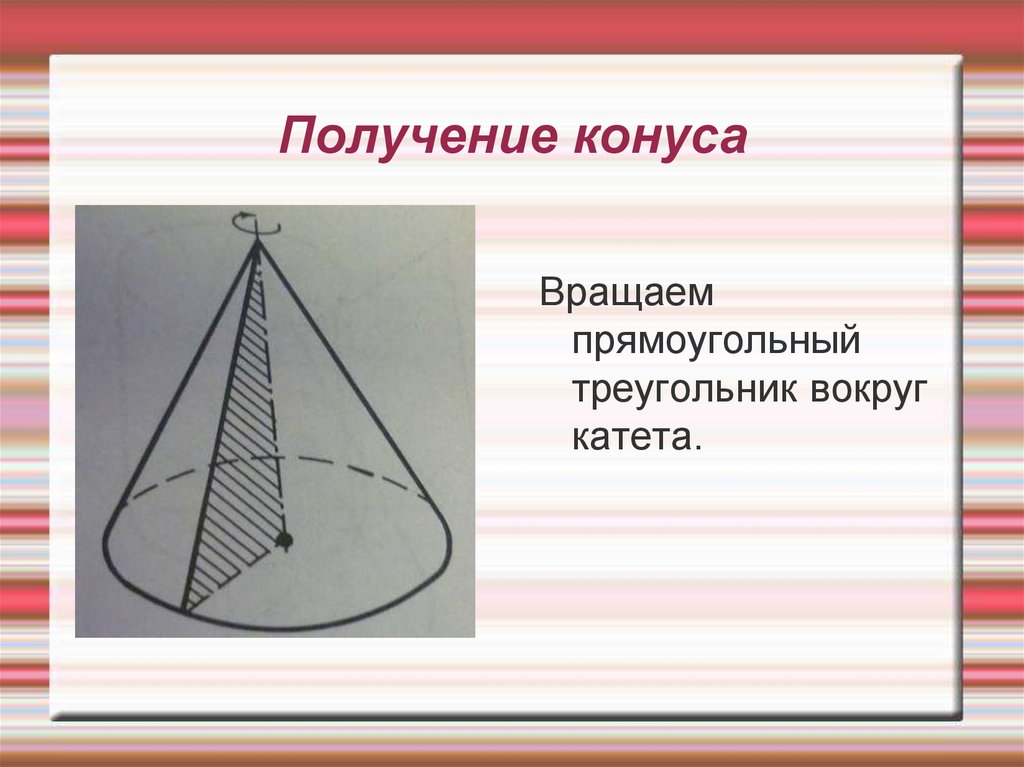
16. Получение конуса
Вращаемпрямоугольный
треугольник вокруг
катета.
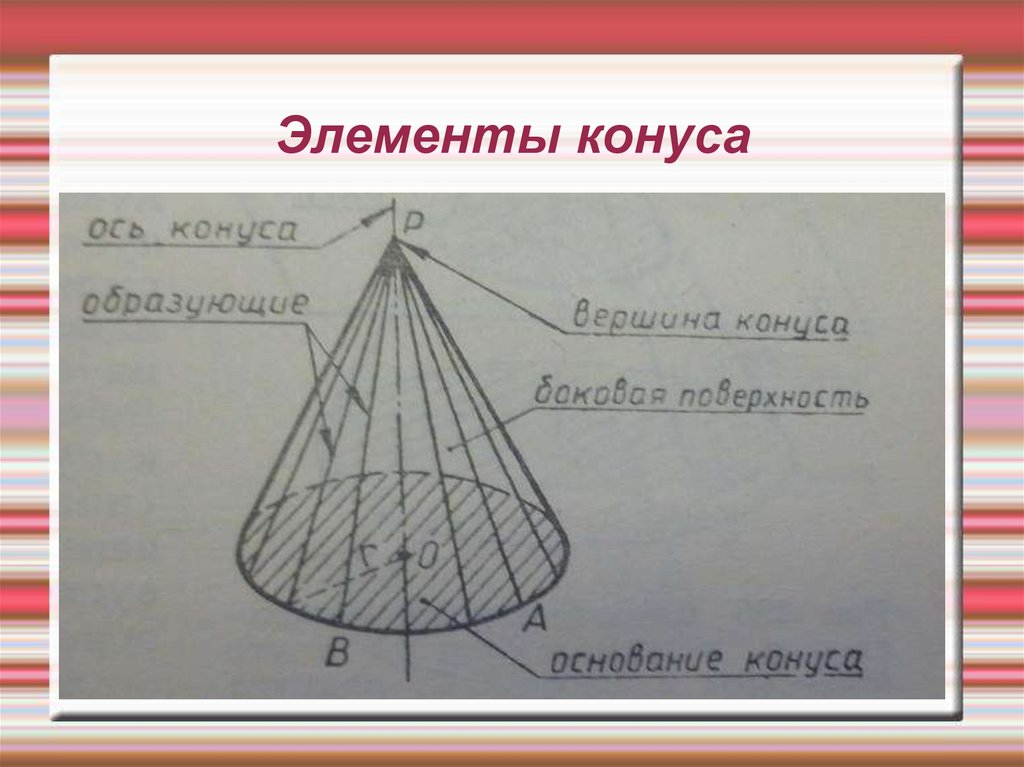
17. Элементы конуса
18. Примеры конуса
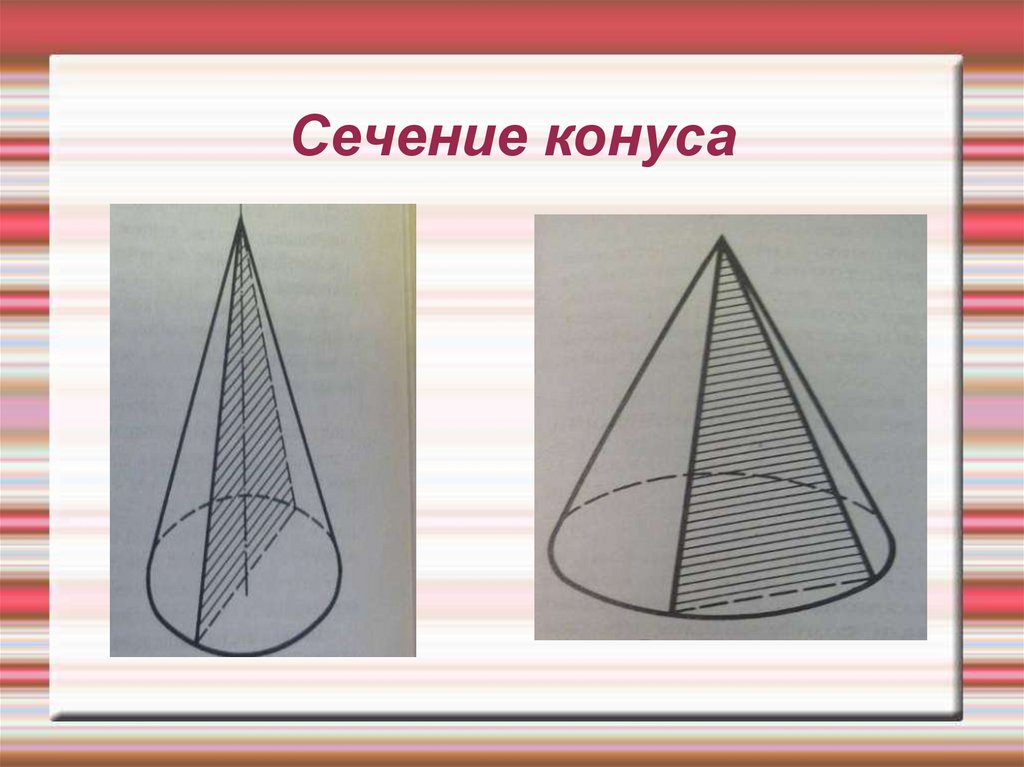
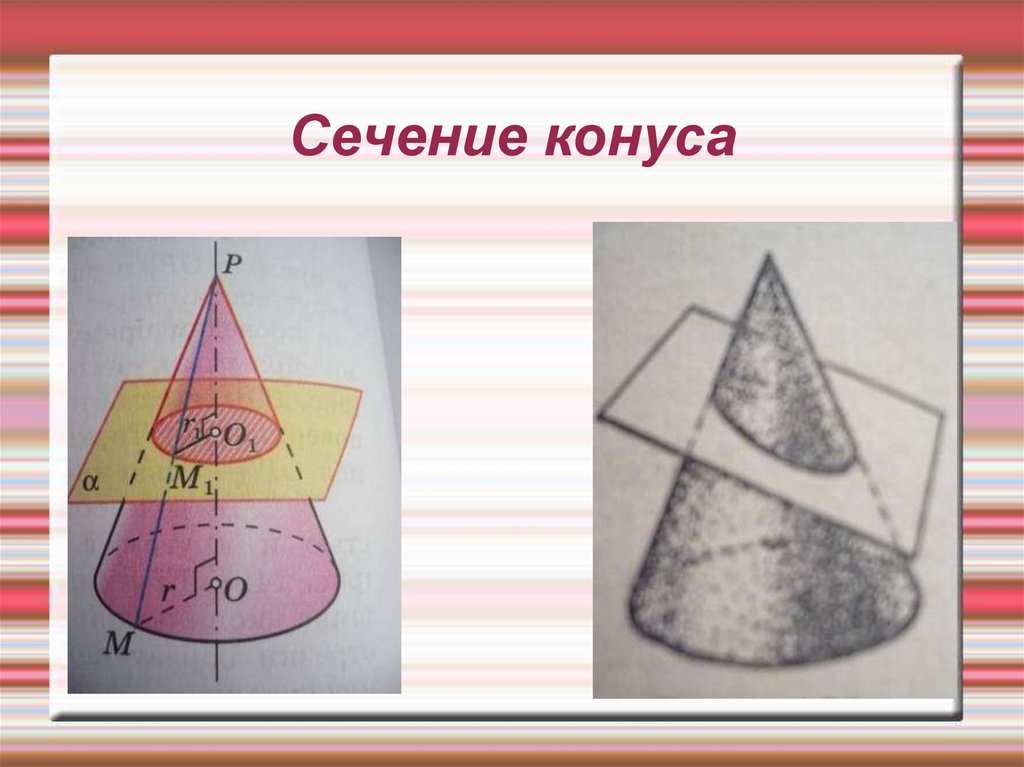
19. Сечение конуса
20. Сечение конуса
21. Формулы площадей
КонусSполн. = πR(R + L)
Sбок. = πRL
Sосн. = πR2
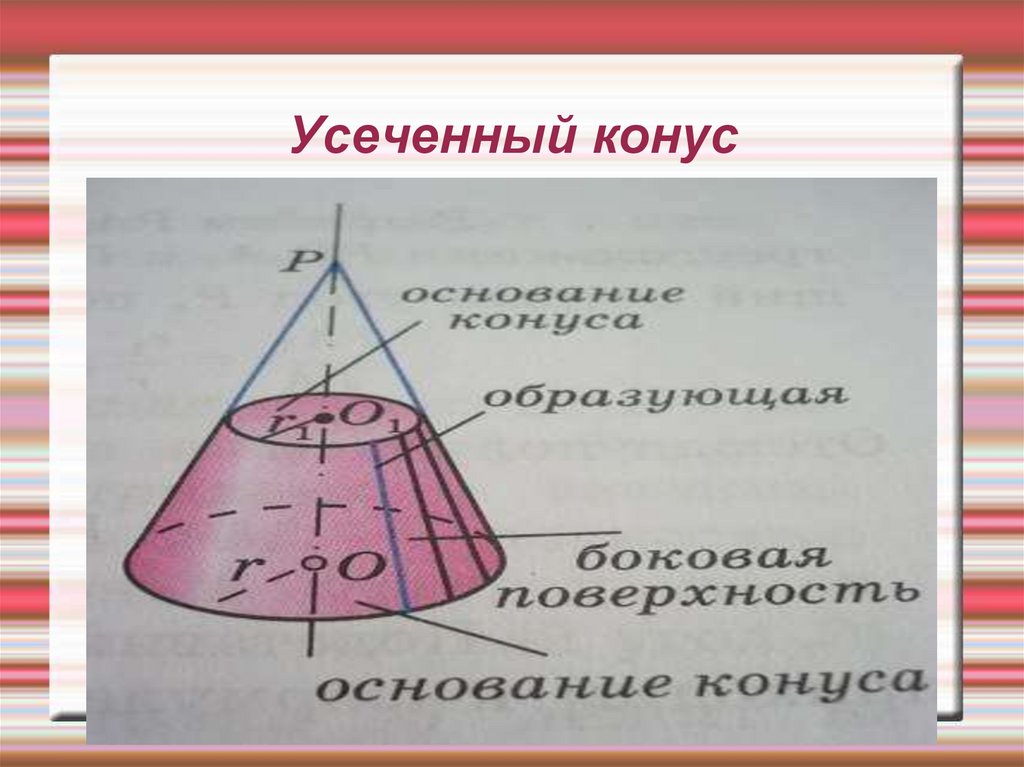
Усеченный конус
Sполн. = π(R + r) L + π (R2 + r2)
Sбок. = π(R + r)L
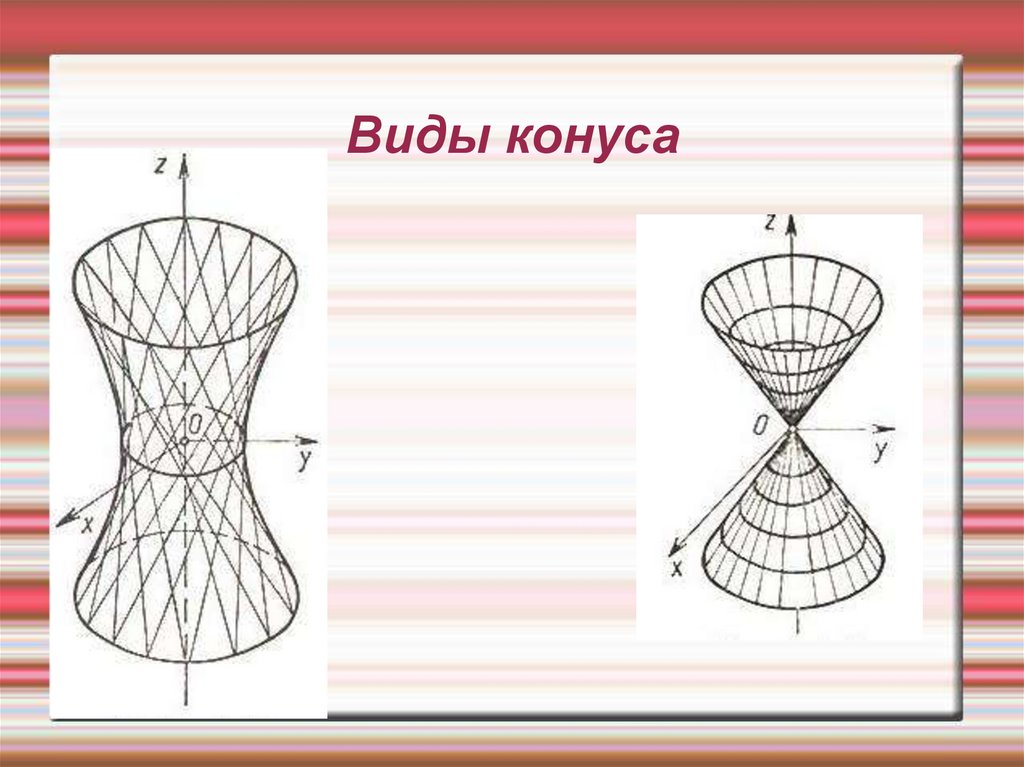
22. Виды конуса
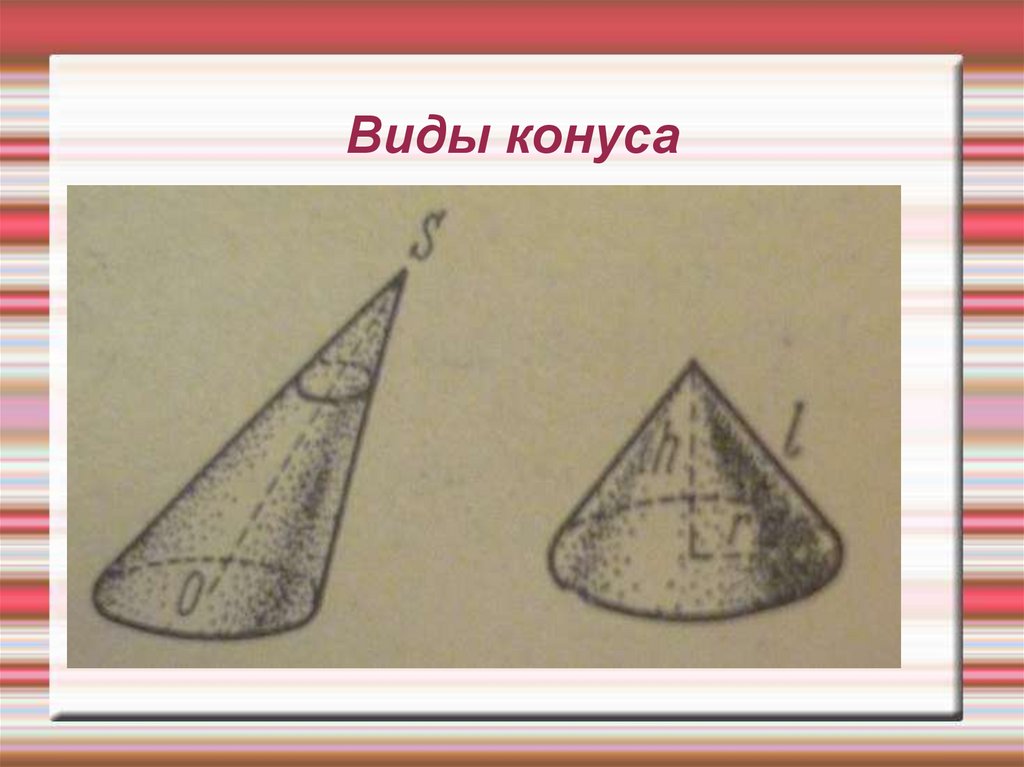
23. Виды конуса
24. Усеченный конус
25. ШАР. СФЕРА
26. ОПРЕДЕЛЕНИЕ
ООООоСферой называется поверхность, которая
состоит из всех точек пространства,
находящихся на заданном расстоянии от
данной точки.
Эта точка называется центром, а заданное
расстояние – радиусом
Шар состоит из всех точек пространства,
находящихся на расстоянии не более
заданного от данной точки.
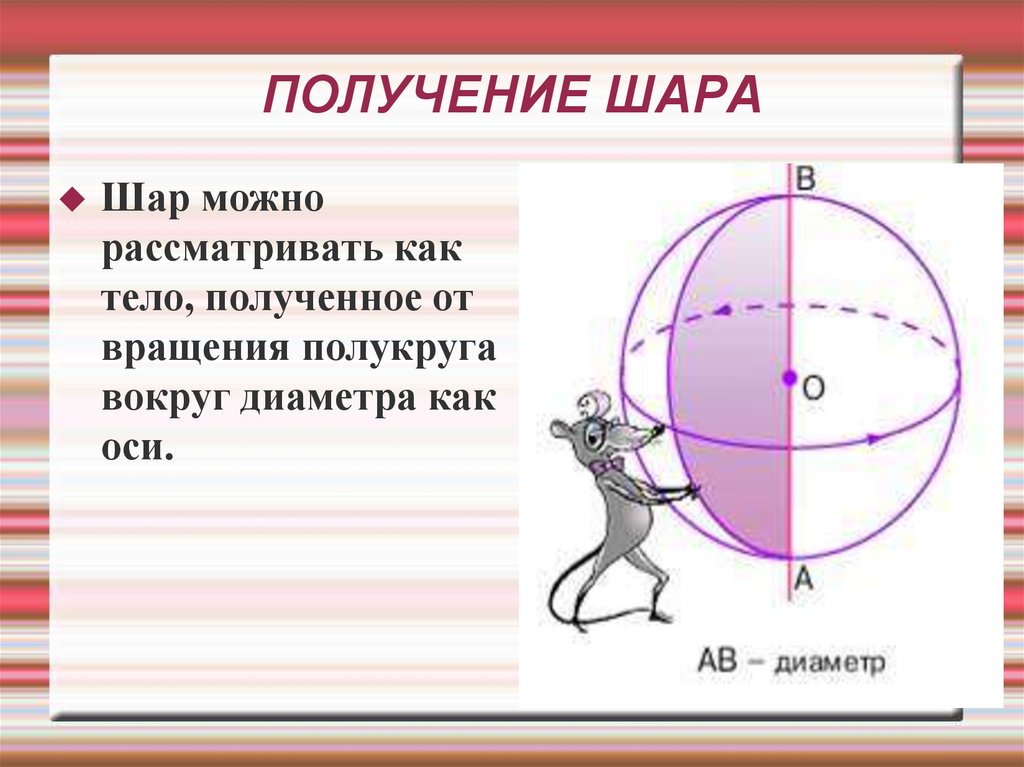
27. ПОЛУЧЕНИЕ ШАРА
Шар можнорассматривать как
тело, полученное от
вращения полукруга
вокруг диаметра как
оси.
28. ПРИМЕРЫ
ГлобусЯблоко
29. ПРИМЕРЫ
ШарикИгрушка
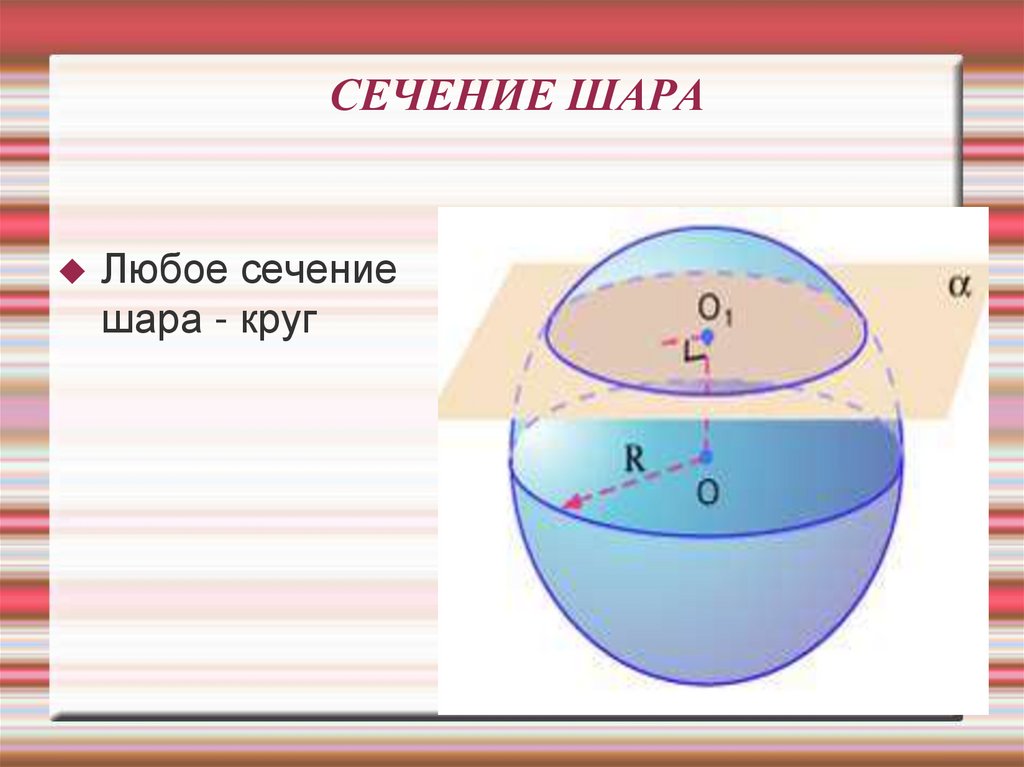
30. СЕЧЕНИЕ ШАРА
Любое сечениешара - круг


















 mathematics
mathematics








