Similar presentations:
Инженерный компьютерный центр Vector
1.
Инженерный компьютерный центр Vector2014 г.
1
2.
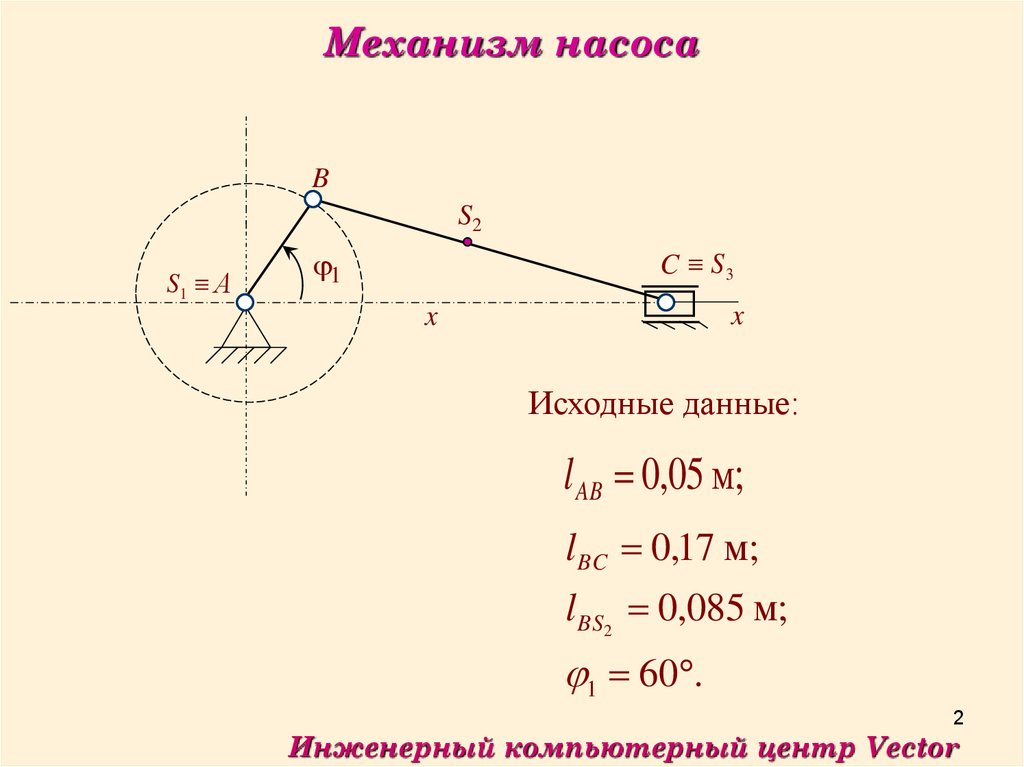
Механизм насосаB
S2
S1 А
1
C S3
x
x
Исходные данные:
l AB 0,05 м;
l BC 0,17 м;
l BS2 0,085 м;
1 60 .
2
Инженерный компьютерный центр Vector
3.
Построение плана механизма насосаВыбрать
масштаб
построения.
Изобразим
на
кинематической схеме звено AB отрезком 25 мм: [AB] = 25 мм.
Масштабный коэффициент длины:
l AB
0,05
м
l
0,002
.
AB 25
мм
Отрезки, изображающие длины звеньев
геометрические параметры на плане механизма:
и
другие
l BC 0 ,17
BC
85 мм;
l 0 ,002
lBS2
0,085
BS 2
42,5 мм.
l 0,002
3
Инженерный компьютерный центр Vector
4.
Построение плана механизма насосаВыбрать систему координат. Начало координат совместить с
шарниром А.
А
x
4
Инженерный компьютерный центр Vector
5.
Построение плана механизма насоса3
4
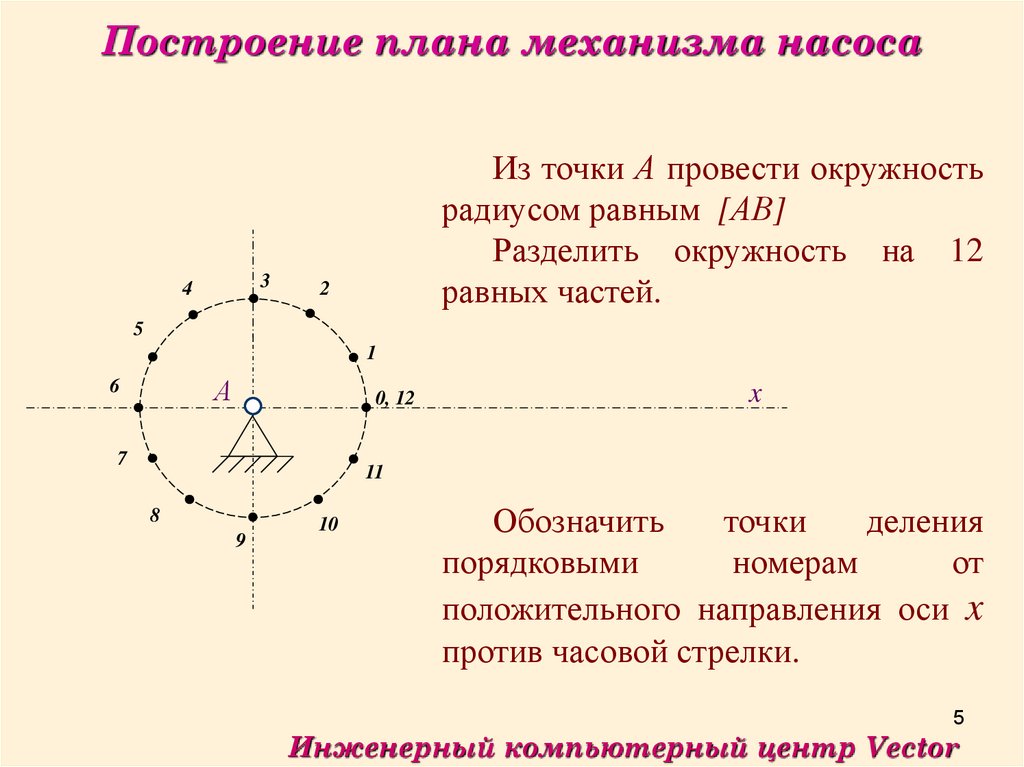
Из точки А провести окружность
радиусом равным [АВ]
Разделить окружность на 12
равных частей.
2
5
1
А
6
0, 12
7
x
11
8
9
10
Обозначить
точки
деления
порядковыми
номерам
от
положительного направления оси x
против часовой стрелки.
5
Инженерный компьютерный центр Vector
6.
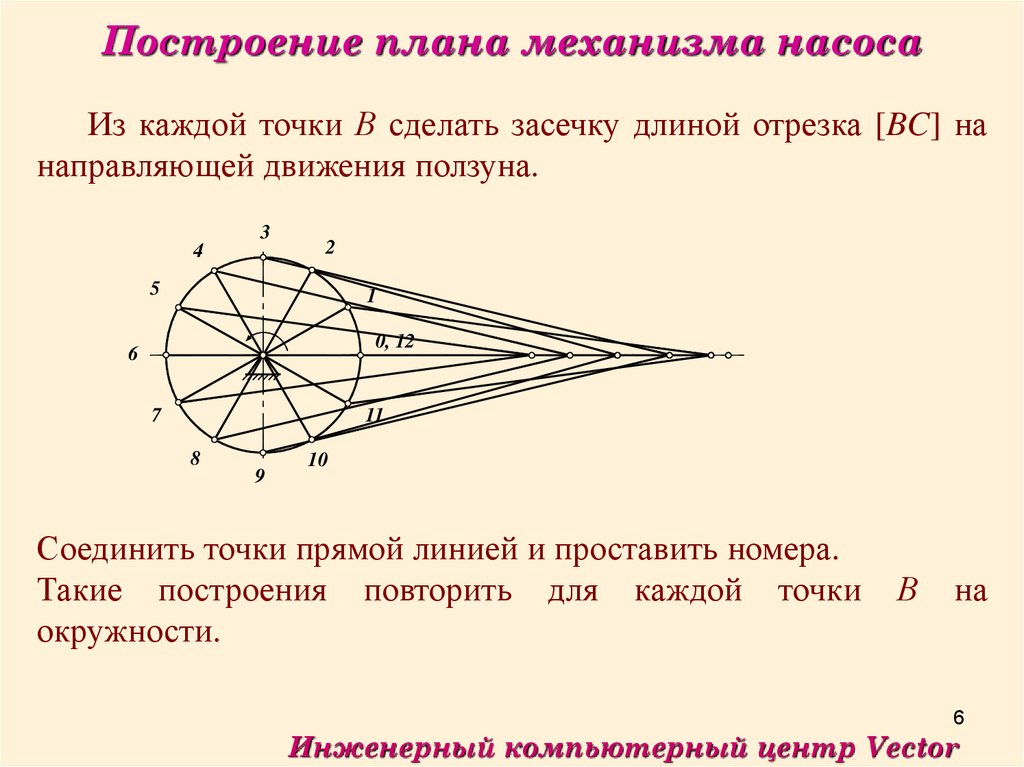
Построение плана механизма насосаИз каждой точки В сделать засечку длиной отрезка [BC] на
направляющей движения ползуна.
4
3
2
5
1
0, 12
6
11
7
8
9
10
Соединить точки прямой линией и проставить номера.
Такие построения повторить для каждой точки
окружности.
В
на
6
Инженерный компьютерный центр Vector
7.
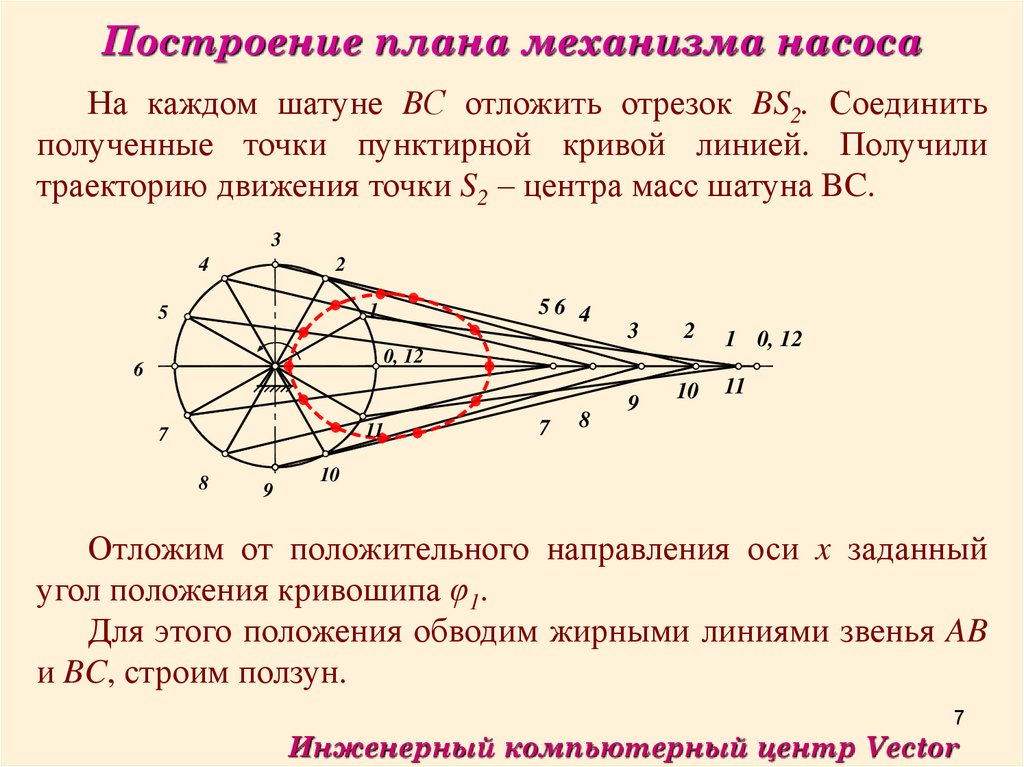
Построение плана механизма насосаНа каждом шатуне BС отложить отрезок BS2. Соединить
полученные точки пунктирной кривой линией. Получили
траекторию движения точки S2 – центра масс шатуна BC.
3
4
2
56 4
1
5
3
2
1 0, 12
10
11
0, 12
6
11
7
8
9
7
8
9
10
Отложим от положительного направления оси x заданный
угол положения кривошипа φ1.
Для этого положения обводим жирными линиями звенья AB
и BC, строим ползун.
7
Инженерный компьютерный центр Vector
8.
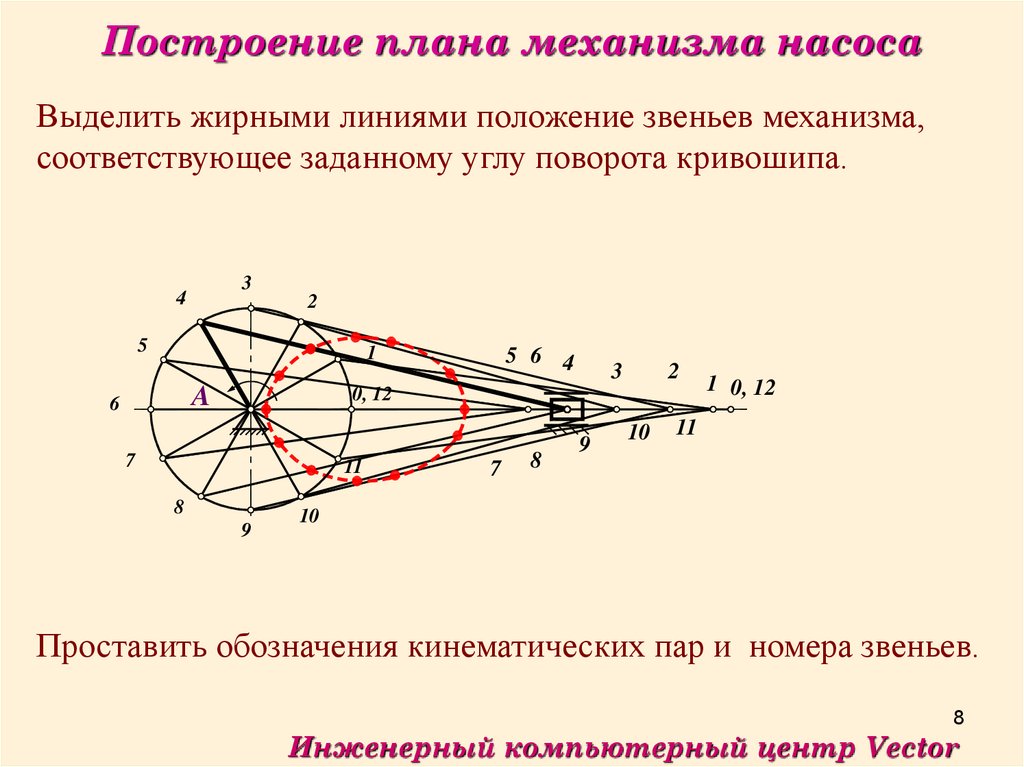
Построение плана механизма насосаВыделить жирными линиями положение звеньев механизма,
соответствующее заданному углу поворота кривошипа.
3
4
2
5
1
A
6
5 6 4
3
2
0, 12
7
11
8
9
7
8
9
10
1 0, 12
11
10
Проставить обозначения кинематических пар и номера звеньев.
8
Инженерный компьютерный центр Vector
9.
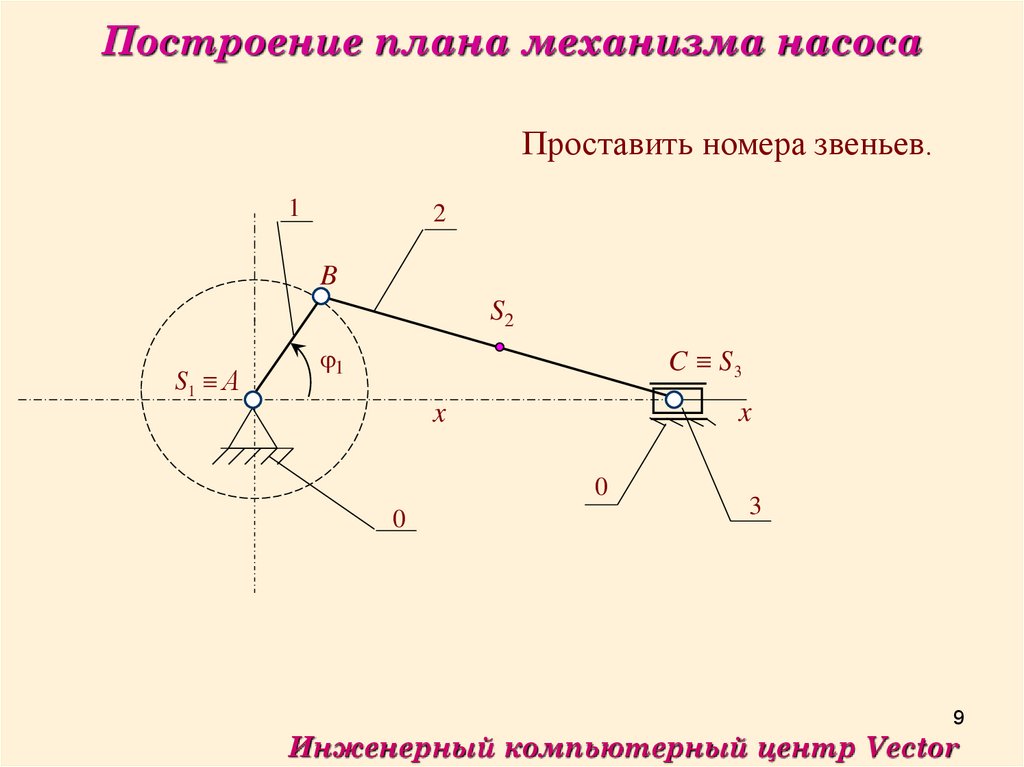
Построение плана механизма насосаПроставить номера звеньев.
1
2
B
S2
S1 А
C S3
1
x
x
0
0
3
9
Инженерный компьютерный центр Vector
10.
План аналогов скоростейПринять, что угловая скорость звена АВ постоянна:
1 const.
Аналогом угловой скорости звена, вращающегося вокруг
неподвижной оси, называется первая производная от угла
поворота звена по обобщенной координате механизма.
Построить план аналогов скоростей, приняв:
d 1 d 1 / dt 1
1
1.
d 1 d 1 / dt 1
(1)
10
Инженерный компьютерный центр Vector
11.
План аналогов скоростейПостроение плана аналогов скоростей начать с входного
звена 1.
Для построения плана скоростей звена BC выбрать
произвольную точку в качестве полюса p1 плана аналогов
скоростей.
В полюсе р1 находится точка а, соответствующая
неподвижной точке механизма А, и направляющая х-х.
p1 a
11
Инженерный компьютерный центр Vector
12.
План аналогов скоростей(2)
Точка B принадлежит кривошипу AB, который совершает
вращательное движение:
V B V A V BA .
Так как точка А неподвижна, то абсолютная и относительная
скорость точки В одинакова, т.е. аналог скорости точки В
известен по величине и направлению:
VB 1 l AB 0,05 м.
Так как точка В совершает движение по окружности, то
вектор её аналога скорости направлен перпендикулярно звену
АВ в сторону его вращения
(V B AB ).
12
Инженерный компьютерный центр Vector
13.
План аналогов скоростейИзобразить аналог скорости точки В вектор VB в виде
отрезка[р1b] произвольной длины, например 50 мм, отложенным
из полюса р1.
Определить масштабный коэффициент плана аналогов
скоростей:
0, 05
м
V
0, 001
.
мм
p1b 50
VB
13
Инженерный компьютерный центр Vector
14.
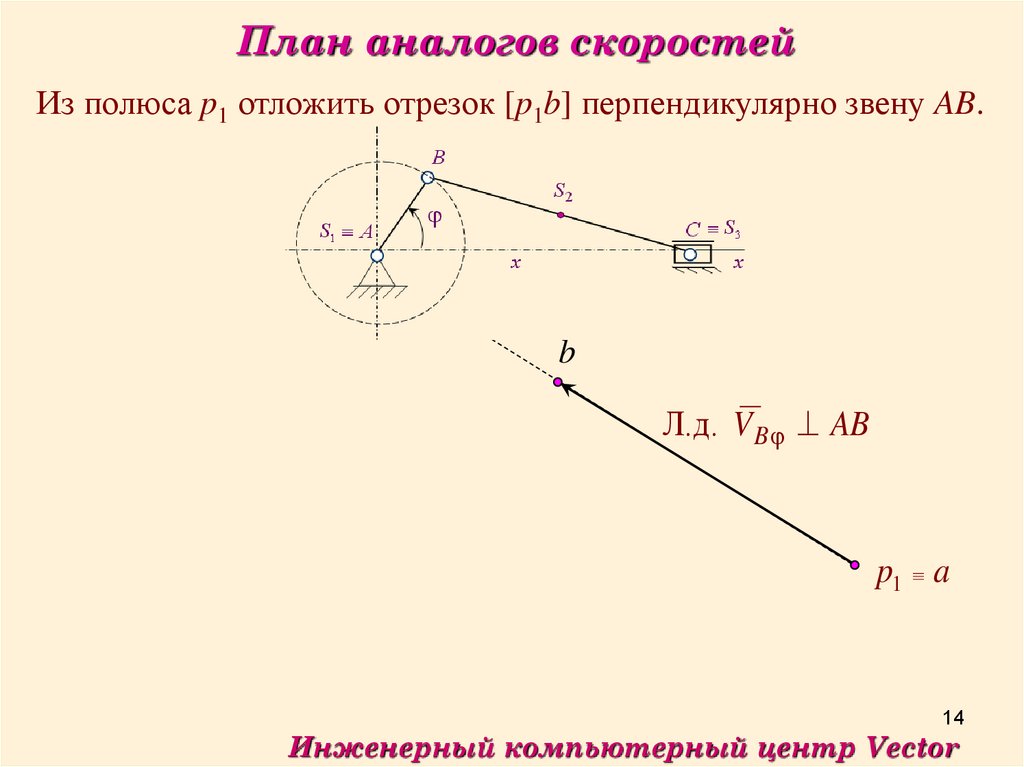
План аналогов скоростейИз полюса p1 отложить отрезок [p1b] перпендикулярно звену AB.
b
Л.д. V B AB
p1 a
14
Инженерный компьютерный центр Vector
15.
План аналогов скоростейТочка С принадлежит
поступательно вдоль оси х-х.
ползуну,
который
движется
Абсолютная скорость точки С равна скорости ползуна. Это
определяет направление вектора аналога абсолютной скорости
точки С:
VС // x x.
15
Инженерный компьютерный центр Vector
16.
План аналогов скоростейСогласно теореме сложения скоростей в переносном и
относительном движениях можно записать векторное
уравнение для определения аналога скорости точки С:
VС VB VСB ,
(3) где
VC вектор аналога абсолютной скорости точки С
V B
VСB
вектор аналога абсолютной скорости точки В
(одновременно это вектор переносной скорости точки С)
вектор аналога мгновенной относительной скорости
точки С во вращательном движении вокруг точки В,
следовательно, VCB BC.
16
Инженерный компьютерный центр Vector
17.
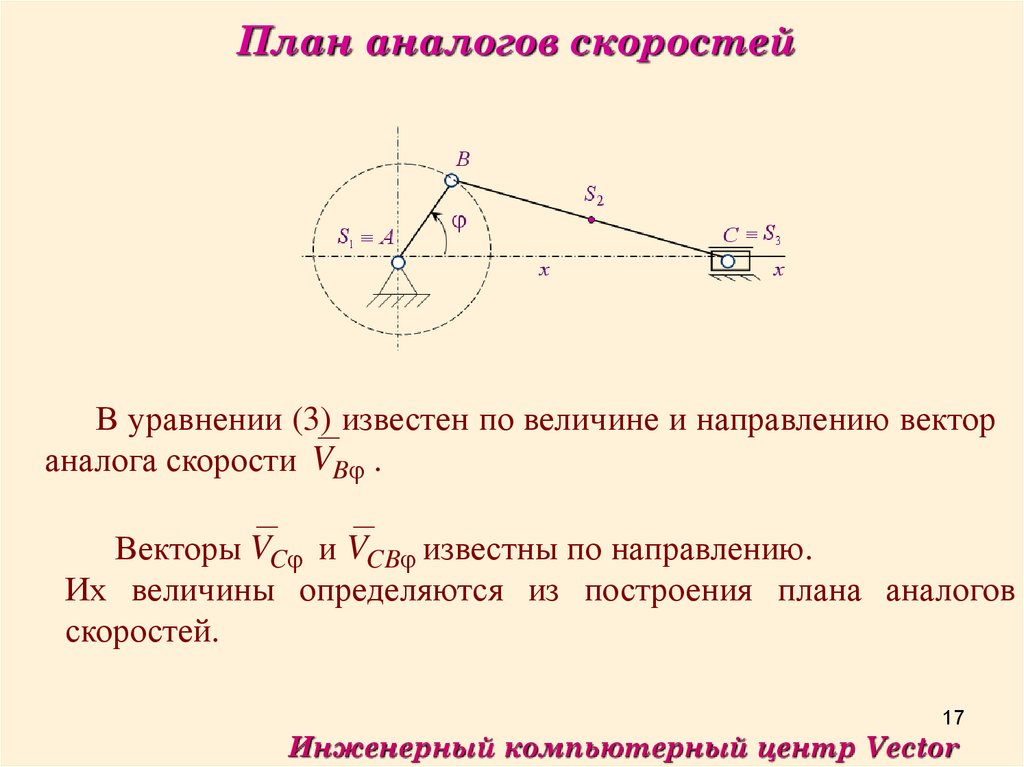
План аналогов скоростейВ уравнении (3) известен по величине и направлению вектор
аналога скорости VB .
Векторы VC и VCB известны по направлению.
Их величины определяются из построения плана аналогов
скоростей.
17
Инженерный компьютерный центр Vector
18.
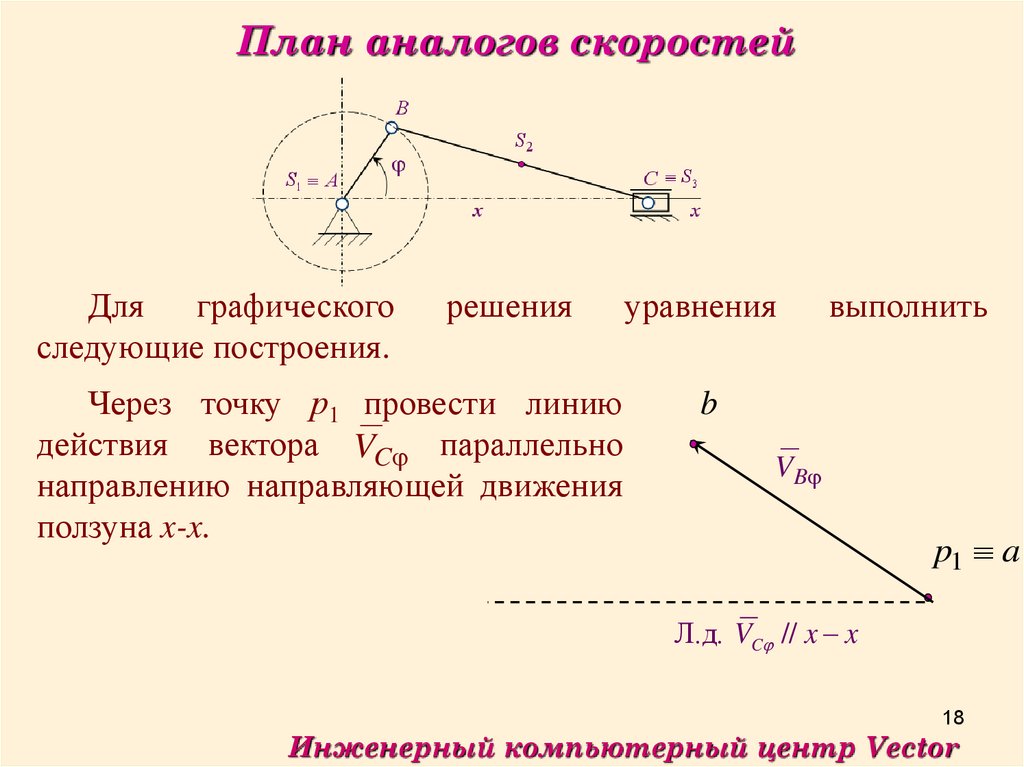
План аналогов скоростейДля
графического
следующие построения.
решения
Через точку р1 провести линию
действия вектора VC параллельно
направлению направляющей движения
ползуна x-x.
уравнения
выполнить
b
VB
p1 a
Л.д. VC // x x
18
Инженерный компьютерный центр Vector
19.
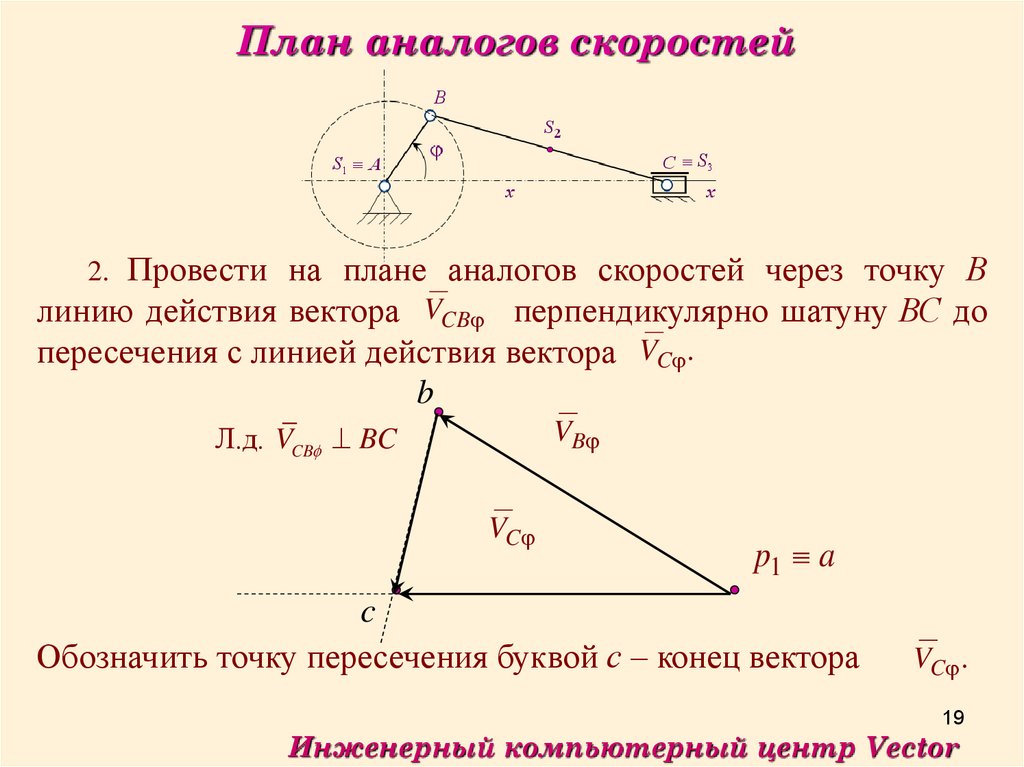
План аналогов скоростей2. Провести на плане аналогов скоростей через точку В
линию действия вектора VCB перпендикулярно шатуну ВС до
пересечения с линией действия вектора VC .
b
Л.д. VCB BC
VB
VC
p1 a
c
Обозначить точку пересечения буквой с – конец вектора
VC .
19
Инженерный компьютерный центр Vector
20.
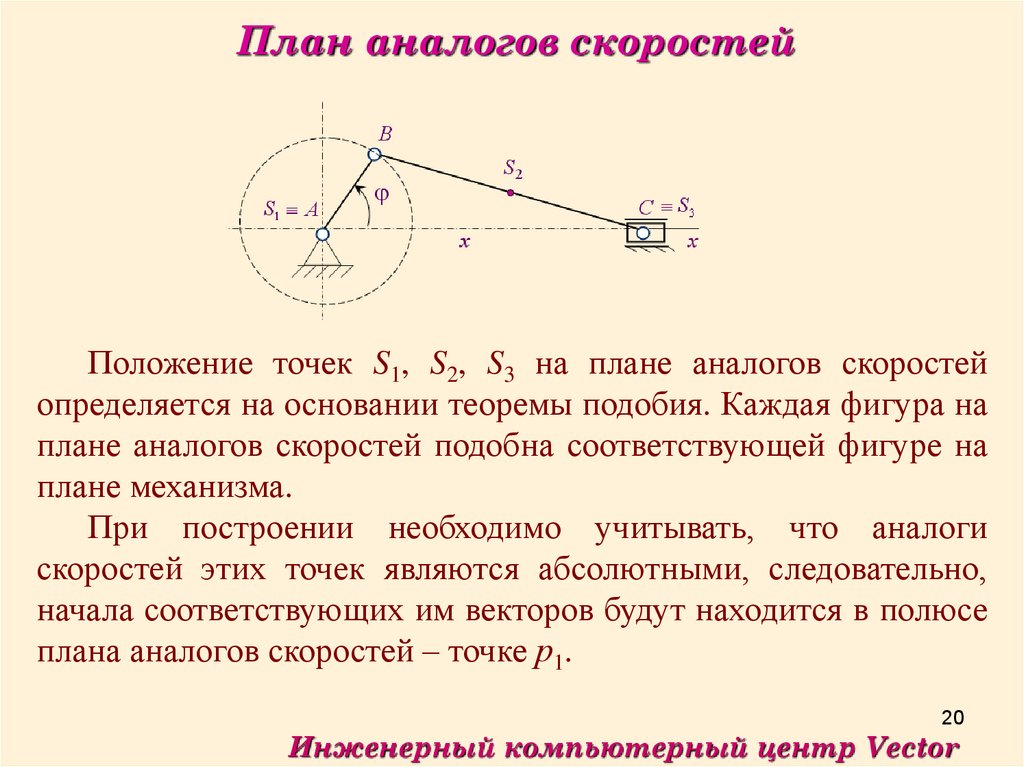
План аналогов скоростейПоложение точек S1, S2, S3 на плане аналогов скоростей
определяется на основании теоремы подобия. Каждая фигура на
плане аналогов скоростей подобна соответствующей фигуре на
плане механизма.
При построении необходимо учитывать, что аналоги
скоростей этих точек являются абсолютными, следовательно,
начала соответствующих им векторов будут находится в полюсе
плана аналогов скоростей – точке р1.
20
Инженерный компьютерный центр Vector
21.
План аналогов скоростейТак как точка S1 находится в точке А, следовательно, и на
плане аналогов скоростей конец вектора VS1 , точка s1 находится
в точке a, т.е. в полюсе p1 .
b
VB
VCB
c
VC
p1 a s1
21
Инженерный компьютерный центр Vector
22.
План аналогов скоростейbs2 BS 2 ;
BS 2
.
По условию подобия фигур: bc BC bs2 bc
BC
Так как [в этом примере] точка S2 находится на середине
звена BC, то точка S2 находится на середине отрезка bc .
Отрезок p1s2 изображает в масштабе аналог абсолютной
b
скорости VS 2 :
p s V .
1 2
VCB
s2
VB
VS2
VC
c
S 2
p1 a s1
22
Инженерный компьютерный центр Vector
23.
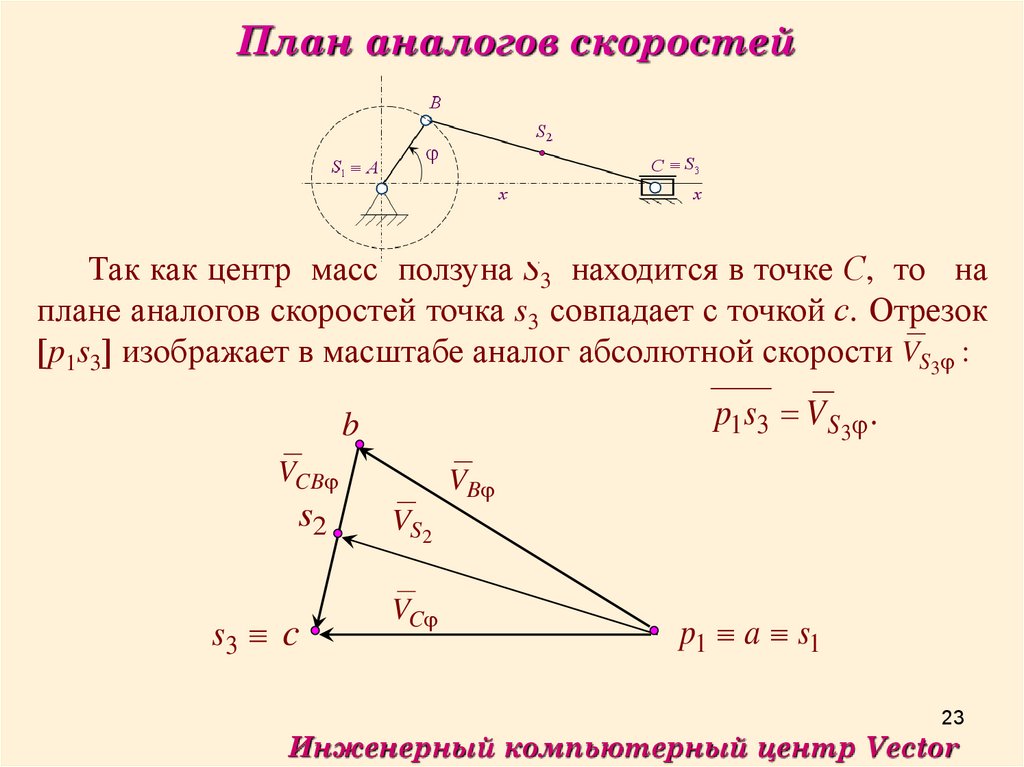
План аналогов скоростейТак как центр масс ползуна S3 находится в точке С, то на
плане аналогов скоростей точка s3 совпадает с точкой с. Отрезок
p1s3 изображает в масштабе аналог абсолютной скорости VS3 :
p1s3 VS 3 .
b
VCB
s2
s3 c
VB
VS2
VC
p1 a s1
23
Инженерный компьютерный центр Vector
24.
План аналогов скоростейОпределение значений аналогов линейных скоростей точек:
VC V [ p1c] 0,001 30 0,03 м.
VCB V bc 0,001 42 0,042 м.
VS2 V [ p1s2 ] 0,001 37 0,037 м.
VS3 V [ p1s3 ] 0,001 30 0,03 м.
Определение значения аналога угловой скорости звена BC:
VCB 0,042
2
0,247
l BC
0,17
24
Инженерный компьютерный центр Vector
25.
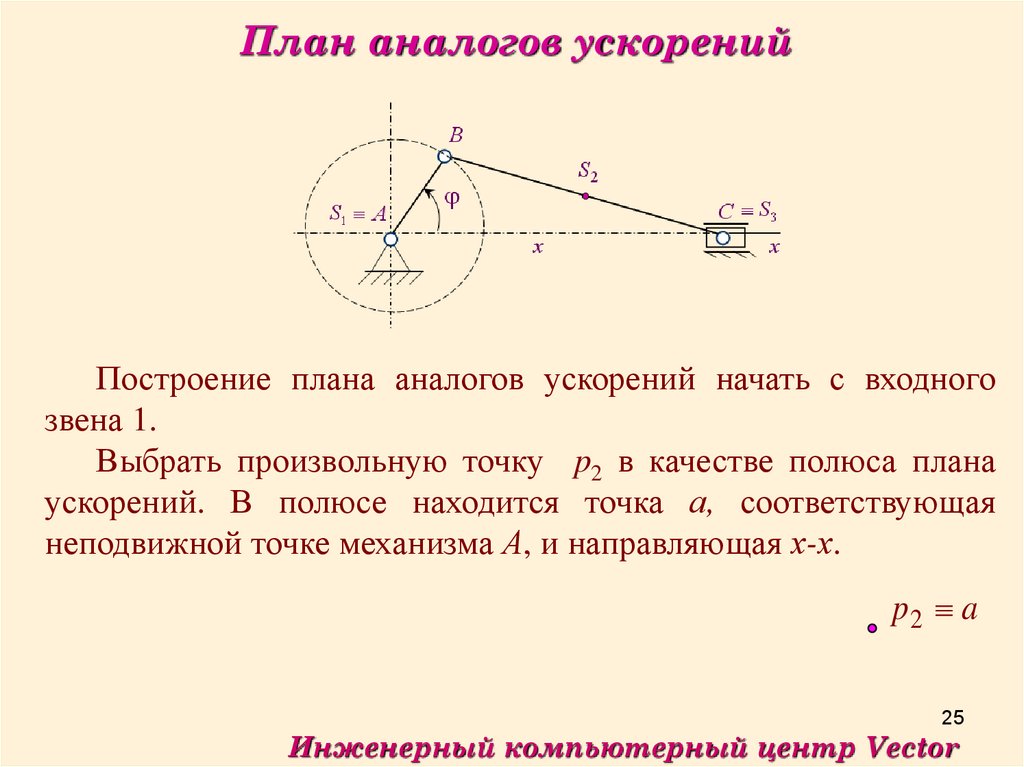
План аналогов ускоренийПостроение плана аналогов ускорений начать с входного
звена 1.
Выбрать произвольную точку p2 в качестве полюса плана
ускорений. В полюсе находится точка а, соответствующая
неподвижной точке механизма А, и направляющая х-х.
p2 a
25
Инженерный компьютерный центр Vector
26.
План аналогов ускоренийТочка В звена АВ движется по криволинейной траектории
(по окружности с центром в точке A), следовательно, вектор
аналога ускорения точки В равен геометрической сумме
аналогов нормального и касательного ускорений:
a B a Bn a B .
(4)
Принято, что звено 1 вращается с постоянной угловой
скоростью. Его угловое ускорение 1 0. Аналог касательного
ускорения точки B равен нулю ( a B 1 l AB 0 ).
Следовательно, аналог абсолютного ускорения точки B равен
только аналогу нормальной составляющей ускорения:
a B a Bn .
26
Инженерный компьютерный центр Vector
27.
План аналогов ускоренийПоэтому направление вектора аналога ускорения a B
точки В совпадает с направлением вектора аналога нормального
ускорения a Bn . Вектор a B направлен вдоль звена АВ от точки
В к точке А ( a B // AB ).
Величина аналога нормального ускорения точки В
aB a l AB 1 0,05 0,05 м.
n
B
2
1
2
27
Инженерный компьютерный центр Vector
28.
План аналогов ускоренийИзобразить аналог ускорения точки В вектор a B в виде
отрезка [р2b] произвольной длины, например 100 мм,
отложенным из полюса р2.
Тогда масштабный коэффициент плана аналогов ускорений:
0,05
м
μ а
0,0005
.
p2b 100
мм
aB
28
Инженерный компьютерный центр Vector
29.
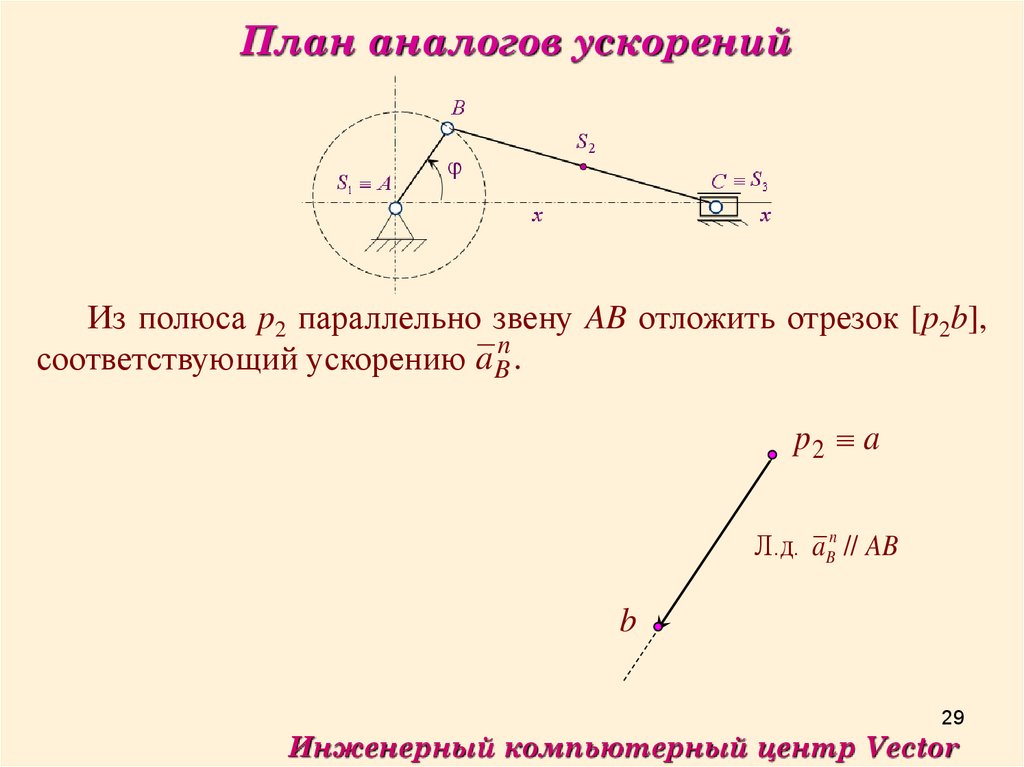
План аналогов ускоренийИз полюса p2 параллельно звену AB отложить отрезок [p2b],
соответствующий ускорению a Bn .
p2 a
Л.д. aBn // AB
b
29
Инженерный компьютерный центр Vector
30.
План аналогов ускоренийСогласно теореме сложения ускорений в переносном и
относительном движениях можно записать векторное уравнение
для определения аналога ускорения точки С:
n
aC a B aCB a B aCB
a
CB ,
aC
(5), где
вектор аналога абсолютного ускорения точки С,
aC // x x;
a B вектор аналога абсолютного ускорения точки В
(одновременно это вектор переносного ускорения точки С);
30
Инженерный компьютерный центр Vector
31.
План аналогов ускоренийaСB вектор аналога абсолютного ускорения точки С во
вращательном движении вокруг точки В, следовательно
n
aCB aCB
a
CB ;
n
aCB
вектор аналога нормального ускорения относительного
вращения точки С вокруг точки В, направленного по
звену ВС от точки С к шарниру В, как центру вращения
n
( aCB
// BC ) ;
aCB
вектор аналога касательного ускорения относительного
вращения точки С вокруг точки В, направленного
перпендикулярно звену ВС ( aCB BC ) .
31
Инженерный компьютерный центр Vector
32.
План аналогов ускоренийaB .
a n C B .
В уравнении (5) известен по величине и направлению вектор
аналога ускорения a B .
n
Вектор aCB
известен по направлению.
Его значение определится:
n
2
2
aCB
l
0
,
247
0,17 0,0104 м.
2
BC
Вектор aCB
известен по направлению.
Его величина определяется из построения плана аналогов
ускорений.
32
Инженерный компьютерный центр Vector
33.
План аналогов ускоренийВычислить отрезок [bnCB], длина которого на плане аналогов
n
ускорений соответствует вектору aCB
:
n
aCB
0,0104
[bnCB ]
20,8 мм.
μ a
0,0005
33
Инженерный компьютерный центр Vector
34.
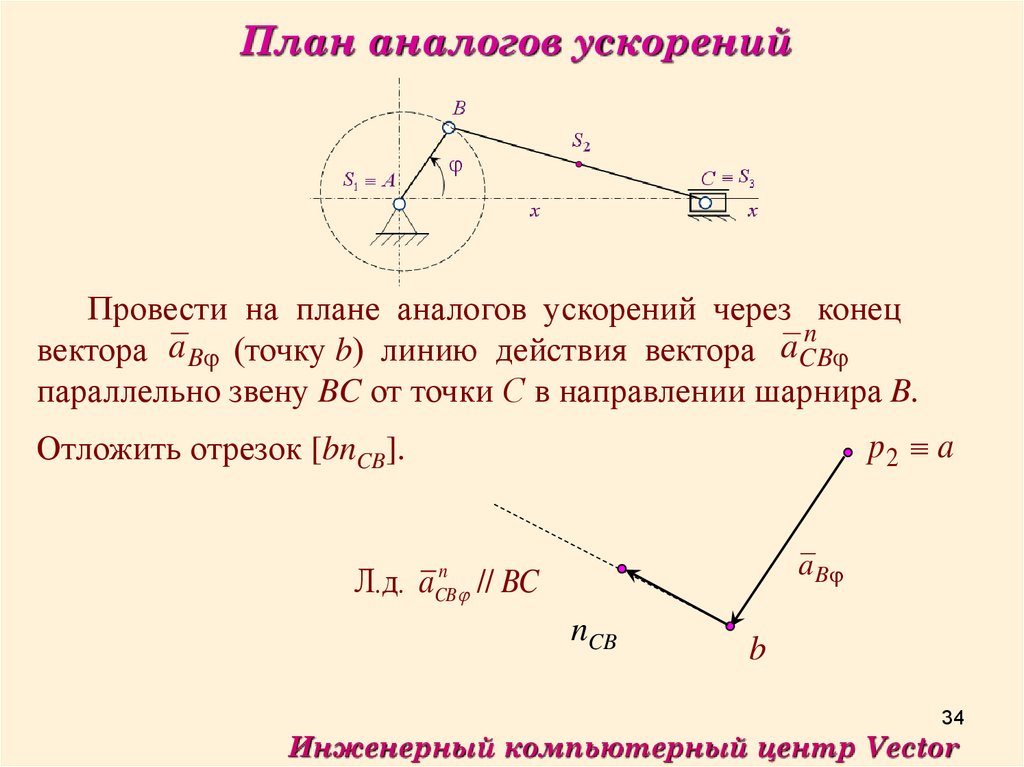
План аналогов ускоренийПровести на плане аналогов ускорений через конец
n
вектора a B (точку b) линию действия вектора aCB
параллельно звену BC от точки С в направлении шарнира B.
p2 a
Отложить отрезок [bnCB].
Л.д. a
n
CB
a B
// BC
nCB
b
34
Инженерный компьютерный центр Vector
35.
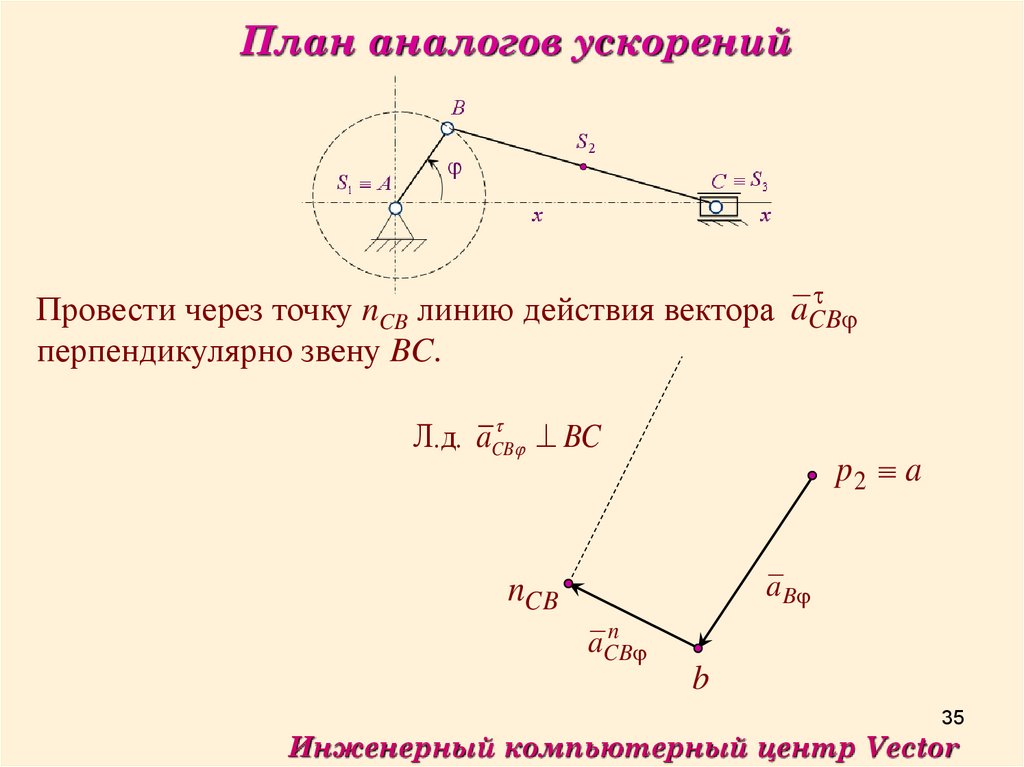
План аналогов ускоренийПровести через точку nCB линию действия вектора aCB
перпендикулярно звену BC.
Л.д. aCB
BC
p2 a
a B
nCB
n
aCB
b
35
Инженерный компьютерный центр Vector
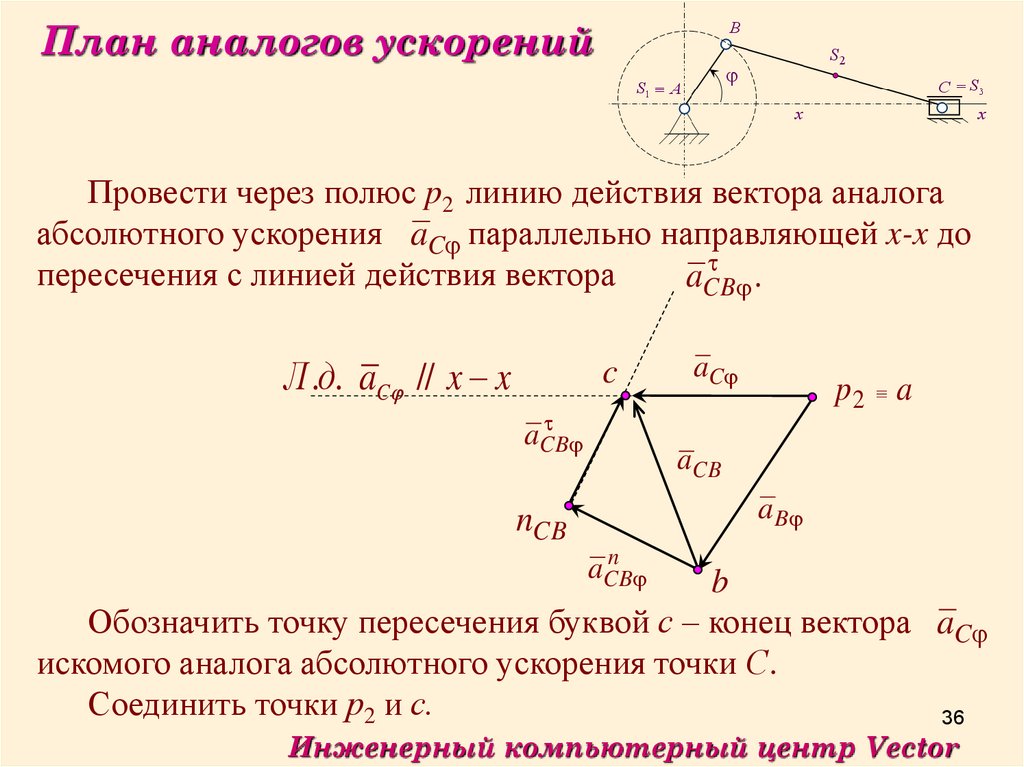
36.
План аналогов ускоренийПровести через полюс p2 линию действия вектора аналога
абсолютного ускорения aC параллельно направляющей x-x до
пересечения с линией действия вектора
aCB
.
Л .д. aC // x x
c
aCB
aC
p2 a
aCB
a B
nCB
n
aCB
b
Обозначить точку пересечения буквой с – конец вектора aC
искомого аналога абсолютного ускорения точки С.
Соединить точки р2 и с.
36
Инженерный компьютерный центр Vector
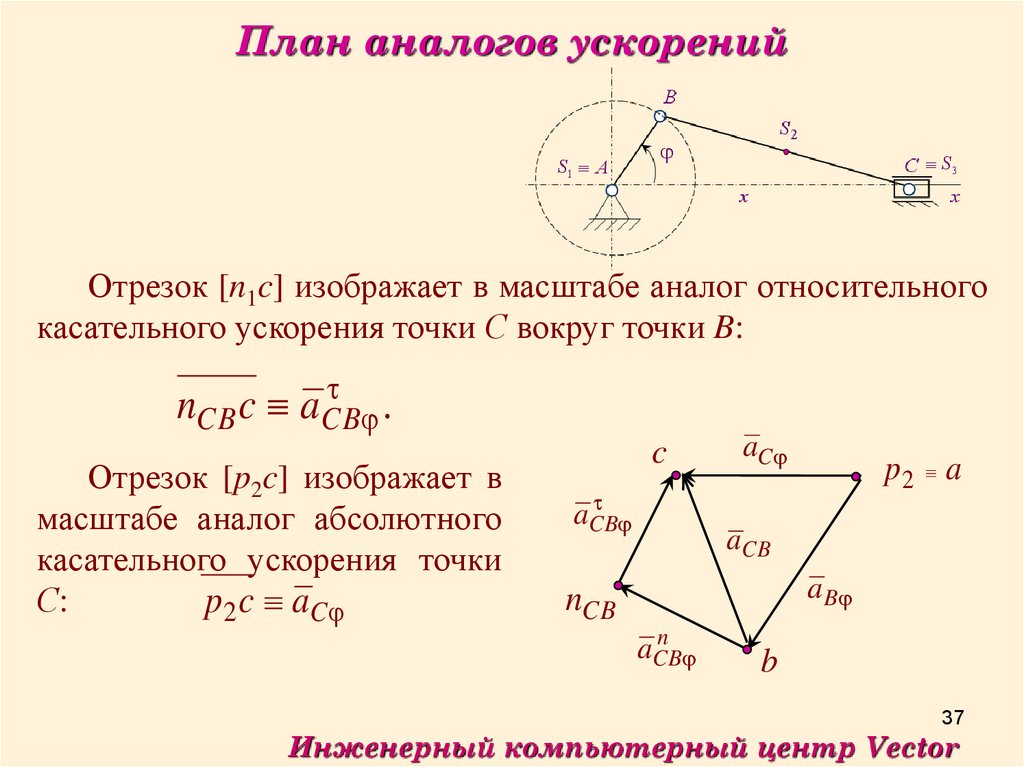
37.
План аналогов ускоренийОтрезок [n1c] изображает в масштабе аналог относительного
касательного ускорения точки С вокруг точки B:
nCB c aCB
.
Отрезок [p2c] изображает в
масштабе аналог абсолютного
касательного ускорения точки
С:
p 2 c aC
c
aCB
aC
p2 a
aCB
a B
nCB
n
aCB
b
37
Инженерный компьютерный центр Vector
38.
План аналогов ускоренийПоложение точек S1, S2, S3 на плане аналогов ускорений
определяется на основании теоремы подобия. Каждая фигура на
плане аналогов ускорений подобна соответствующей фигуре на
плане механизма.
При построении необходимо учитывать, что аналоги
ускорений этих точек являются абсолютными, следовательно,
начала соответствующих им векторов будут находится в полюсе
плана аналогов ускорений – точке р2.
38
Инженерный компьютерный центр Vector
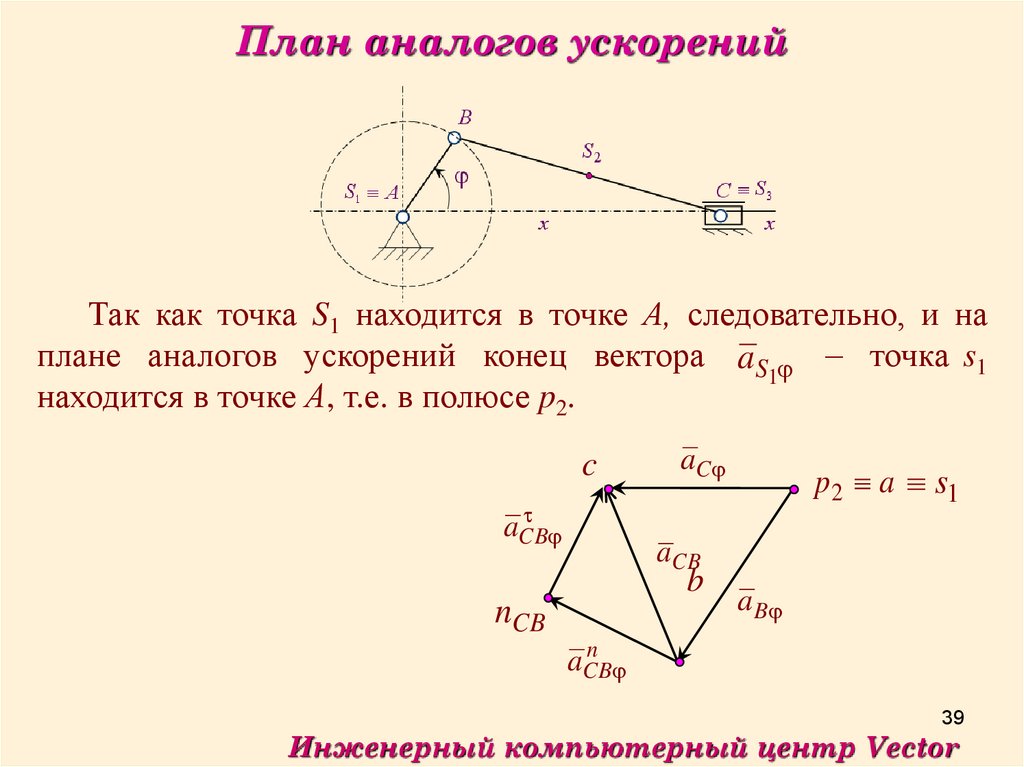
39.
План аналогов ускоренийТак как точка S1 находится в точке А, следовательно, и на
плане аналогов ускорений конец вектора a S точка s1
1
находится в точке А, т.е. в полюсе p2.
c
aCB
aC
p 2 a s1
aCB
b
nCB
a B
n
aCB
39
Инженерный компьютерный центр Vector
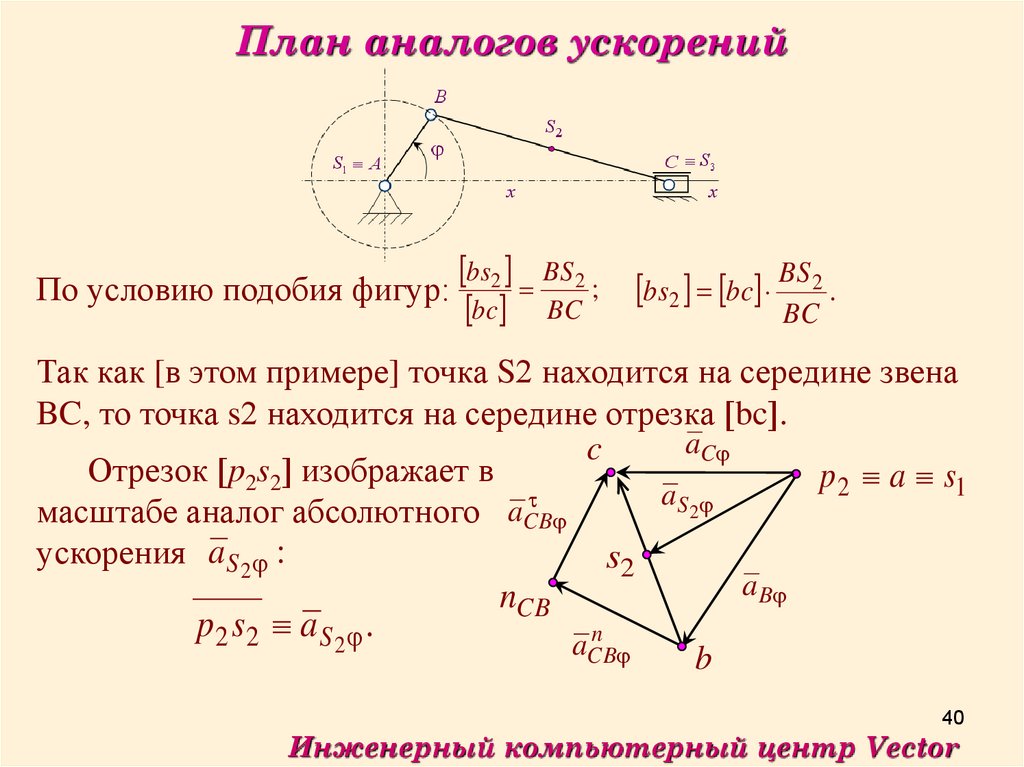
40.
План аналогов ускоренийПо условию подобия фигур:
bs2 BS 2 ;
BS
bs2 bc 2 .
bc BC
BC
Так как [в этом примере] точка S2 находится на середине звена
BC, то точка s2 находится на середине отрезка bc .
aC
c
Отрезок p2s2 изображает в
p 2 a s1
a
S 2
масштабе аналог абсолютного aCB
ускорения a S 2 :
s2
a B
nCB
p2 s2 a S 2 .
n
aCB
b
40
Инженерный компьютерный центр Vector
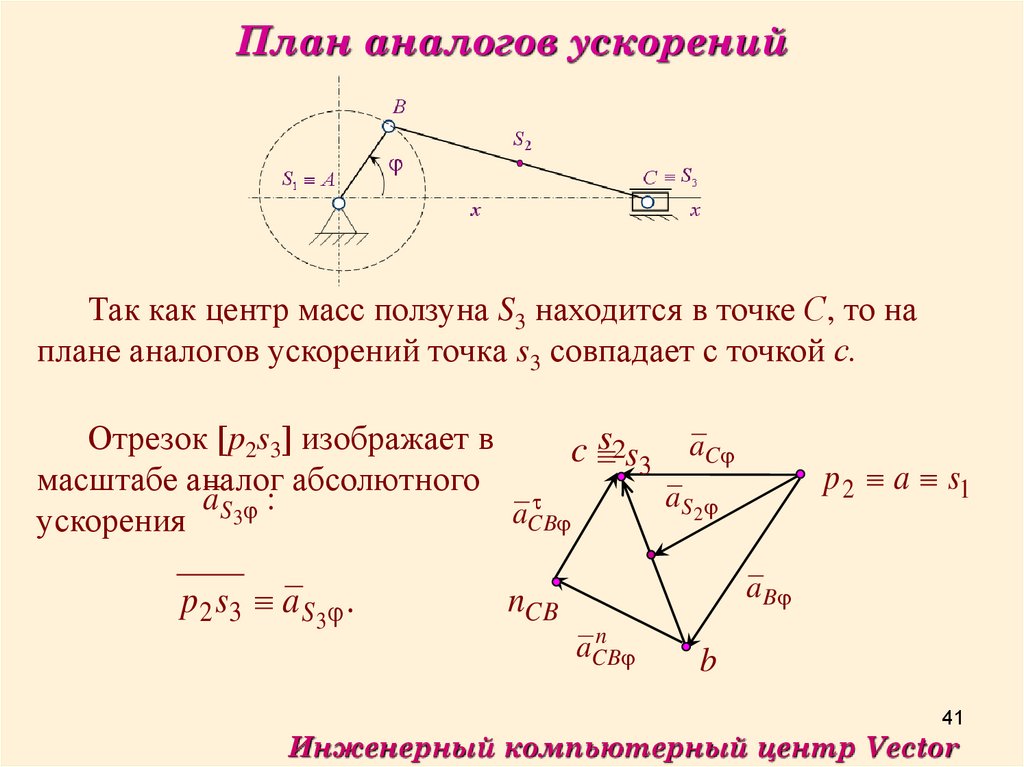
41.
План аналогов ускоренийТак как центр масс ползуна S3 находится в точке С, то на
плане аналогов ускорений точка s3 совпадает с точкой с.
Отрезок p2s3 изображает в
c s2s3 aC
масштабе аналог абсолютного
a S 2
a S 3 :
a
CB
ускорения
p 2 s3 a S 3 .
p 2 a s1
a B
nCB
n
aCB
b
41
Инженерный компьютерный центр Vector
42.
План аналогов ускоренийОпределение значений аналогов линейных ускорений точек:
aC a p2c 0,0005 104 0,052 м;
aCB
a n1c 0,0005 46 0,023 м;
aS2 a p2 s2 0,0005 102 0,051 м;
aS3 a p2 s3 0,0005 104 0,052 м.
Определение значения аналога углового ускорения звена BC:
aCB
0,023
2
0,135.
l BC
0,17
42
Инженерный компьютерный центр Vector
43.
Инженерный компьютерный центр VectorПрофессор, д.т.н., Кузлякина В.В.,
доцент, Нагаева М.В.
43






















 mechanics
mechanics








