Кинематическое исследование механизмов и машин

1.

ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
1

2.

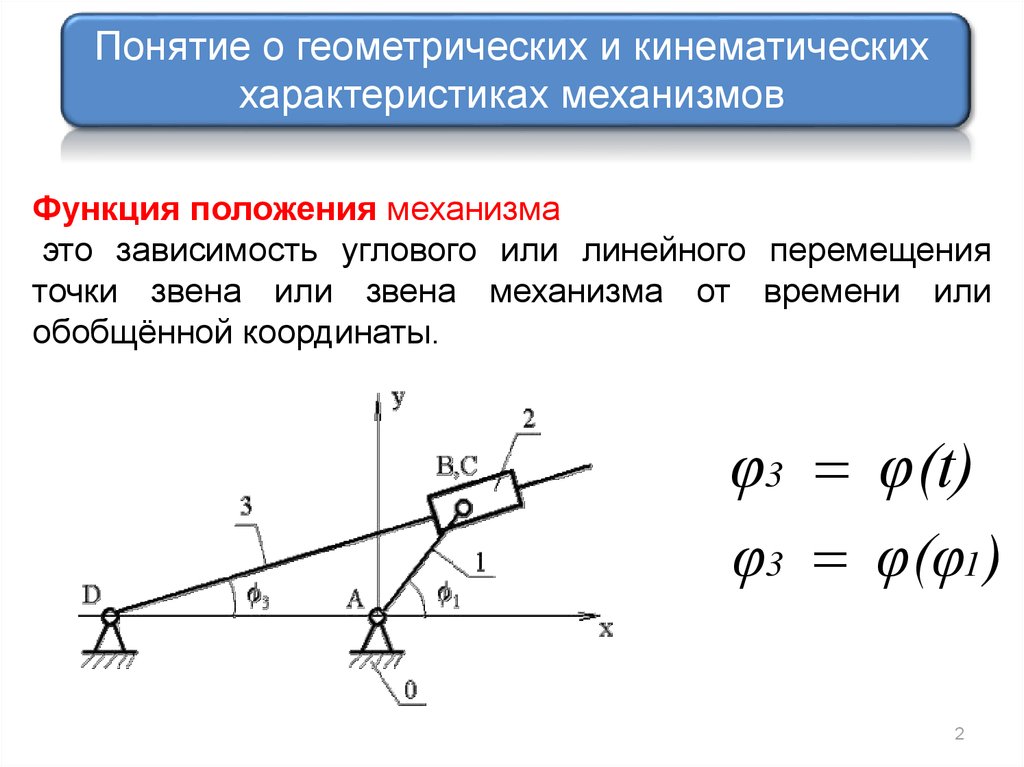
Понятие о геометрических и кинематических
характеристиках механизмов
Функция положения механизма
это зависимость углового или линейного перемещения
точки звена или звена механизма от времени или
обобщённой координаты.
φ3 φ(t)
φ3 φ(φ1)
2

3.

Кинематические передаточные функции механизма –
производные от функции положения по обобщенной координате.
Первая производная называется первой передаточной функцией
или аналогом скорости (обозначается ν q , q ),
Вторая - второй передаточной функцией или аналогом ускорения
(обозначается аq, q ).
Кинематические характеристики механизма –
производные от функции положения по времени.
Первая производная называется скоростью (обозначается v, ),
вторая - ускорением
(обозначается α , ).
3

4.

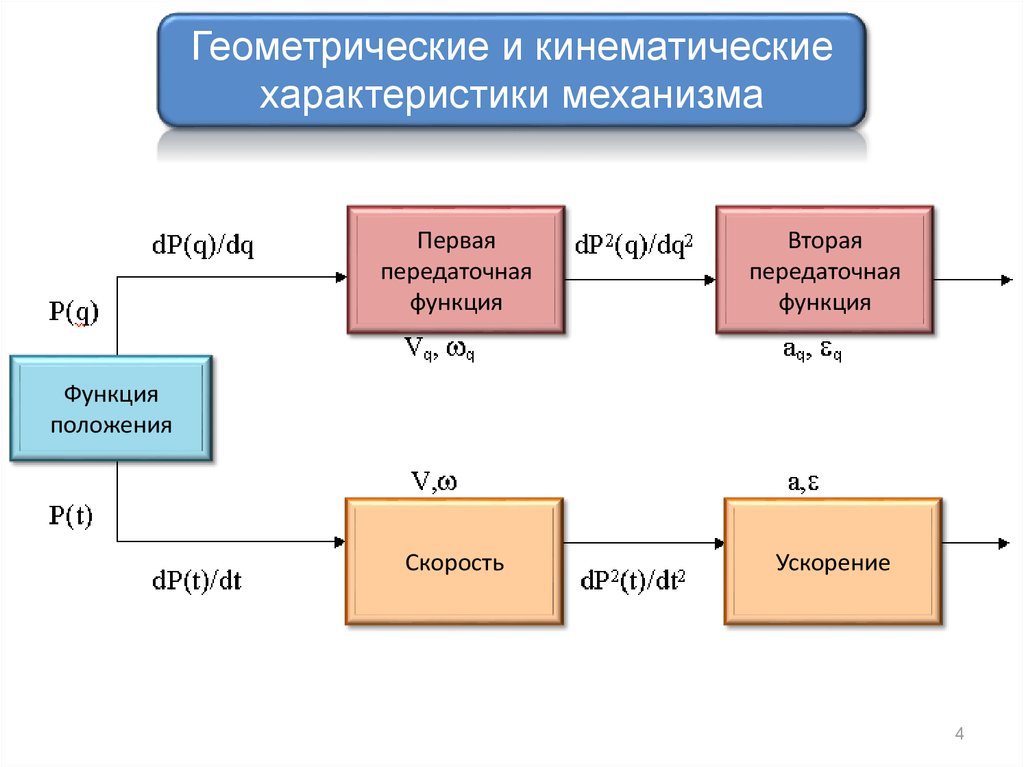
Геометрические и кинематические
характеристики механизма
Первая
передаточная
функция
Вторая
передаточная
функция
Функция
положения
Скорость
Ускорение
4

5.

Механизм с одной подвижностью имеет одно заданное
входное движение и некоторое множество выходных (движение
любого звена или точки звена механизма).
Передаточные функции тех движений, которые в данном
случае используются как выходные, называются главными,
остальные - вспомогательными.
Рассмотрим схему механической системы образованной
последовательно-параллельным
соединением
типовых
механизмов.
5

6.

Схема механической системы
Схема включает входное звено (1), зубчатую передачу (звенья 1-2) ,
кулачковый (звенья 2-3-4) и рычажный (звенья 2-5-6) механизмы и имеет два
6
выходных звена (3 и 6).

7.

Блок-схема рассмотренной механической
системы
Кулачковый механизм
P3(φ2)
Зубчатый
механизм P2(φ1)
Четырехшарнирный
механизм P6(φ2)
7

8.

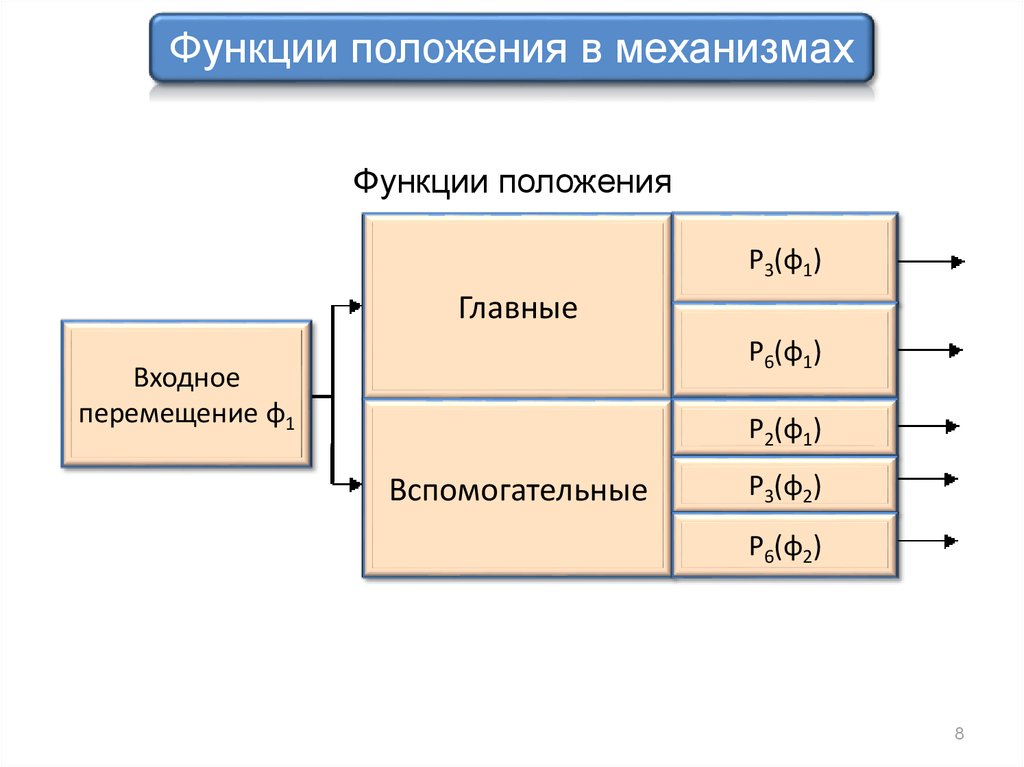
Функции положения в механизмах
Функции положения
P3(φ1)
Главные
P6(φ1)
Входное
перемещение φ1
P2(φ1)
Вспомогательные
P3(φ2)
P6(φ2)
8

9.

Связь кинематических и передаточных функций
Линейные скорости и ускорения
VL dSL / dt (dSL / dφ1 ) (dφ1 / dt) VqL 1 ,
d(V ) / dt (dV / dφ ) (dφ / dt)
qL
L
1
qL
1
1
1
VqL 1 qL VqL 1 ,
2
1
Угловые скорости и ускорения
dφ / dt (dφ / dφ ) (dφ / dt) ,
i
i
i
1
1
qi
1
d( ) / dt (d / dφ ) (dφ / dt)
i
qi
i
1
1
1
1
qi 1 qi 1 qi 1 .
2
9

10.

Методы кинематического
исследования механизмов
- кинематических диаграмм (графический),
- планов положений, скоростей и ускорений
(графо-аналитический),
- проекций векторного контура (аналитический),
- преобразования координат (аналитический),
- экспериментальный.
10

11.

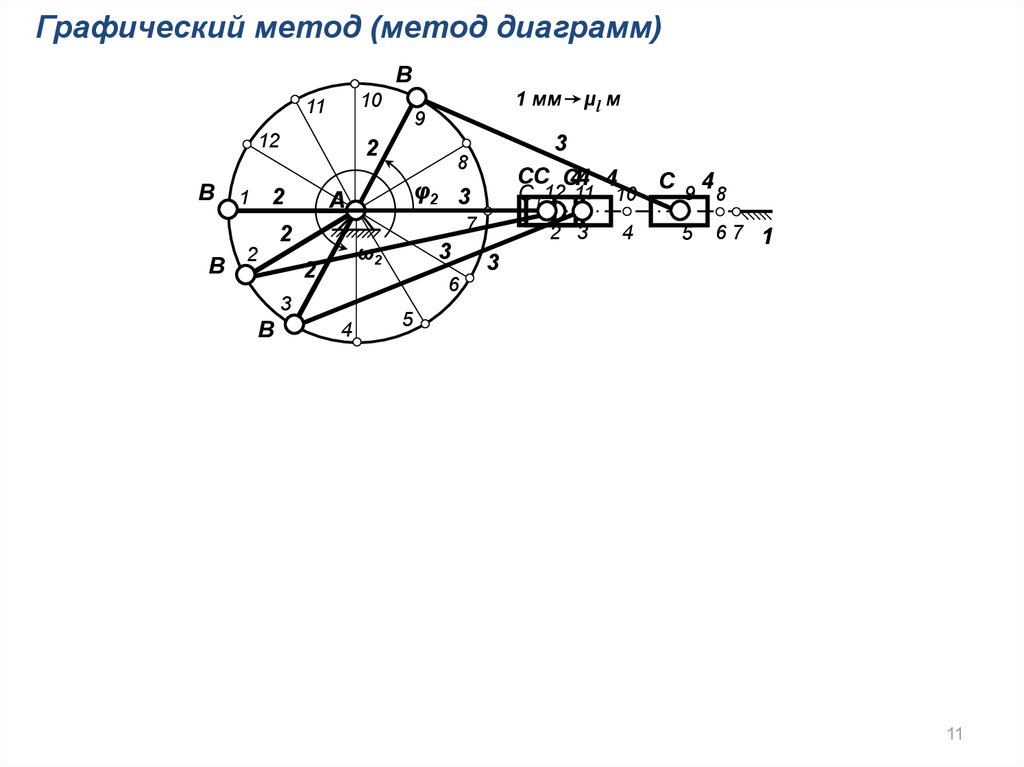
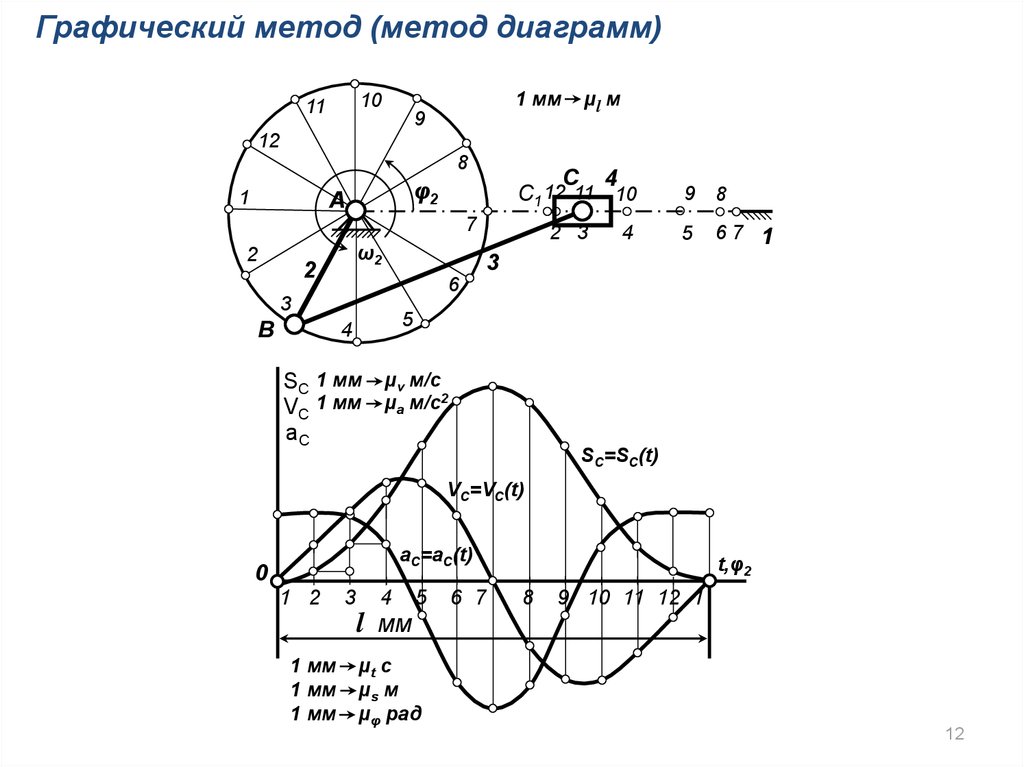
Графический метод (метод диаграмм)
B
12
B
2
7
2
3
2 3
4
5
67 1
3
6
3
B
φ2 3
ω2
μl м
3
CC C44 4
C 94
C1 12 11 10
8
8
A
2
B
9
2
2
1
1 мм
10
11
4
5
11

12.

Графический метод (метод диаграмм)
1 мм
10
11
9
μl м
12
8
1
C 4
C1 12 11 10
φ2
A
7
2
ω2
2
4
8
5
67 1
3
6
3
B
2 3
9
5
4
SC 1 мм μv м/с
VC 1 мм μa м/с2
aC
SC=SC(t)
VC=VC(t)
aC=aC(t)
0
1 2
1 мм
1 мм
1 мм
3
4
l мм
5
μt с
μs м
μφ рад
6 7
t,φ2
8
9 10 11 12 1
12

13.

Графо-аналитический метод (метод планов скоростей)
Метод планов скоростей основан на теореме о распределении скоростей
точек тела совершающего плоскопараллельное движение.
Для звена АВ (шатун) в векторном виде теорема записывается в следующем виде:
VBA
VB = VA + VBA
B
S2
2
A
3
1
VA
O1
v A
м/с
мм.черт.
VB
O3
PV VB b
s2 VBA
VA
s2
a
AS2
S2B
=
as2
s2b
v B Pv b v
v BA ab v
s2 Pv s2 v

14.

Графо-аналитический метод (метод планов ускорений)
Метод планов ускорений основан на теореме о распределении ускорений
точек тела совершающего плоскопараллельное движение
Для шатуна АВ теорема в векторном виде запишется:
aВ а А аВА .
Точка А в абсолютном движении, и т. В в относительном, движутся по криволинейным траекториям значит:
n
t
аA аA аA ;
ц
вр
а BA аBA аBA ,
т.е. вектор абсолютного ускорения т. В есть сумма четырёх векторов:
n
t
ц
вр
а B а A а A аBA аBA .
План ускорений строится также как и план скоростей.
14

15.

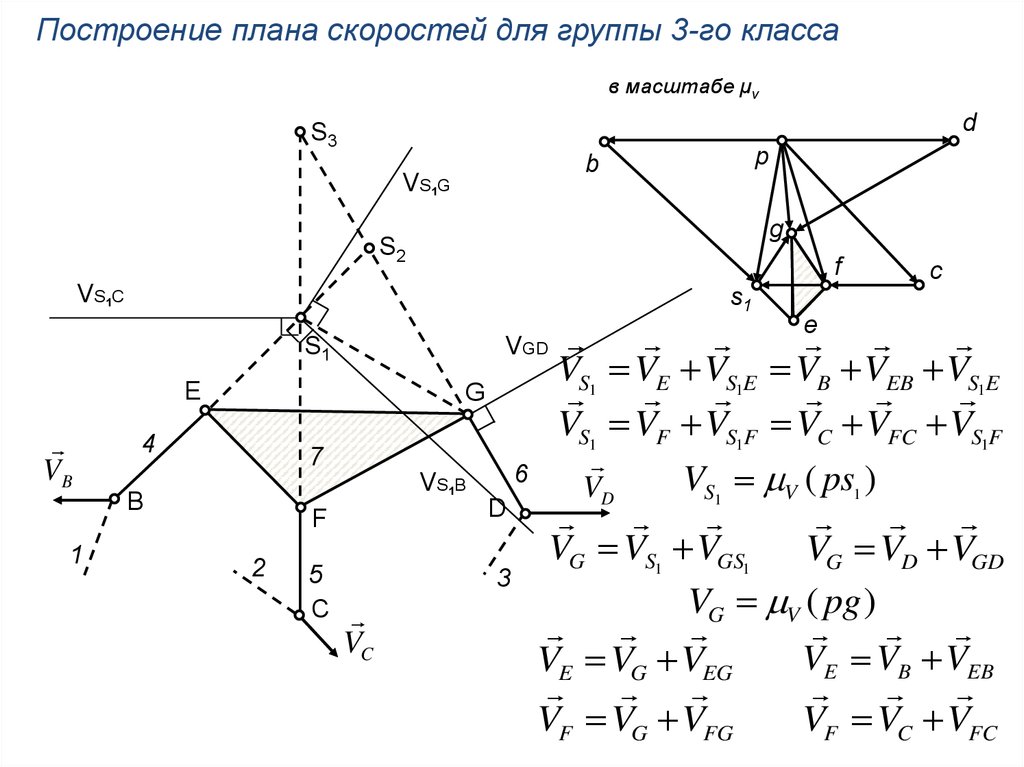
Построение плана скоростей для группы 3-го класса
в масштабе μv
d
S3
VS1G
p
b
g
S2
f
VS1C
s1
S1
E
VB
4
7
e
VGD
VS1 VE VS1E VB VEB VS1E
G
VS1 VF VS1F VC VFC VS1F
6
VS1 V ( ps1 )
VS B
VD
D
VG VS1 VGS1 VG VD VGD
3
VG V ( pg )
VE VB VEB
VE VG VEG
VF VG VFG
VF VC VFC
1
B
1
c
F
2
5
C
VC

16.

n
aEB
2 n n 2 t
t a 2 a n a n t a 2t
(2.1)
V
V
V
aSV
a
a
a
a
a
a
a
a
E
G
EG
EG
n
S1E
n
B
EB
S1E
EB a S1
E FC B
S1Bn
S1B S1F
(2.2)
(5)
(
g
)
a
a
(1)
1aFC
(6)
FC
G
a nS 1E n
S
F
t
t l n 1 n t l t
(2.3)
l
l
aS1 BE
aC aFC aS1ES
CF
aCa B a S1CaEB
a S1Ca
FSEB
(2.4)
1
F 1 aFC aS1FaE
aaES1 aa(( es1 )
S3
t
aS1B
t a t
aS1C EG
t
aEB
4
S2
aS1
E
7
B
1
aB
S1
2
aC
t
aGS1
t
aGD
aG
(3)(7)
a ( nf ) t (8)
aG F aS1 a aGS1 aGS1
n
t (4)
aG aD aGD aGD
в масштабе μa
π
d
G
6
F
D
5
C
3
aD
n4
c
g
n3
n1
s1 e
n5
f
b
n6
n2

17.

Аналитический метод кинематического анализа.
Метод проекций векторного замкнутого контура.
Рассмотрим простейший кулисный механизм.
Заменим кинематическую схему механизма эквивалентным векторным контуром.
Тогда уравнение замкнутости векторного контура запишется:
l АВ l АД l ДВ .
17

18.

Задача о положениях звеньев механизма
Проецируем векторный контур на оси координат и получаем координаты точки В механизма:
xB l AB cos ( φ1 ) l AD cos ( ) lDB cos ( φ3 ),
(1)
yB l AB sin ( φ1 ) l AD sin ( ) lDB sin ( φ3 ),
(2)
18

19.

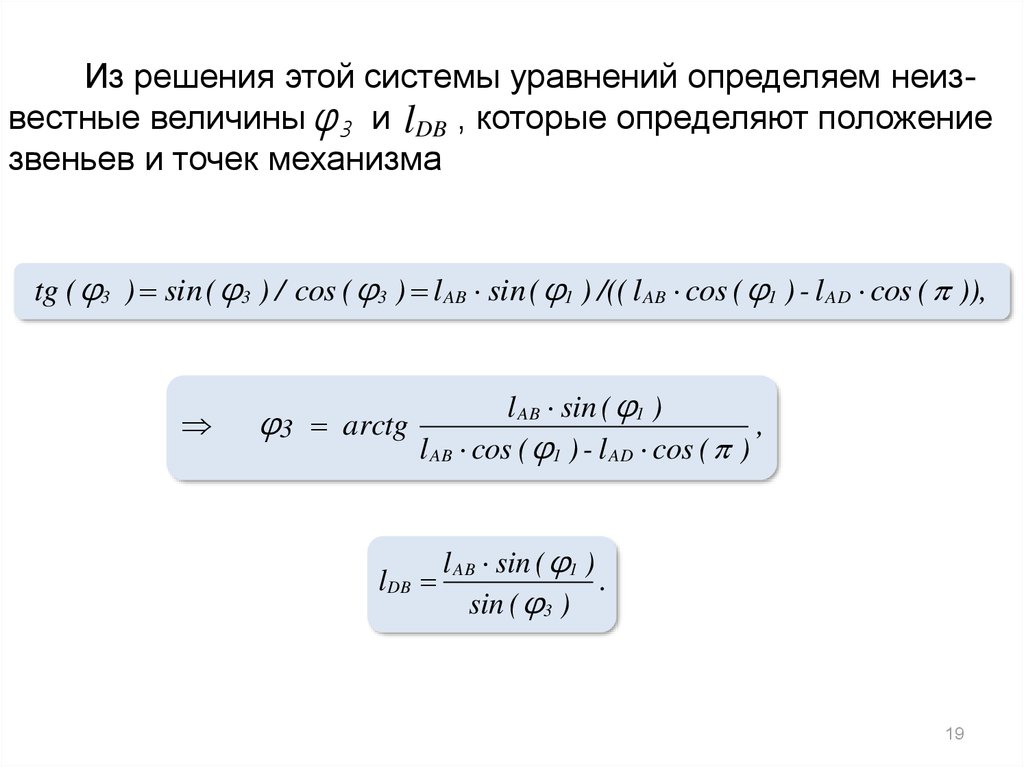
Из решения этой системы уравнений определяем неизвестные величины φ 3 и lDB , которые определяют положение
звеньев и точек механизма
tg ( φ3 ) sin ( φ3 ) / cos ( φ3 ) l AB sin ( φ1 ) /(( l AB cos ( φ1 ) - l AD cos ( )),
φ3 arctg
l AB sin ( φ1 )
,
l AB cos ( φ1 ) - l AD cos ( )
lDB
l AB sin ( φ1 )
.
sin ( φ3 )
19

20.

Задача о первых кинематических передаточных
функциях механизма
Продифференцируем уравнения проекций векторного контура по обобщенной координате и получим
VqBx - lAB sin (φ1 ) V qDB cos (φ3 ) - lDB q3 sin (φ3 ),
VqBy lAB cos (φ1 ) VqDB sin (φ3 ) lDB q3 cos(φ3 ).
Из этой системы уравнений определяем первые передаточные функции VqB и q 3 .
20

21.

Задача о вторых передаточных функциях
механизма
Вторично продифференцируем уравнения проекций векторного контура по обобщенной координате и получим
qBx
- lAB cos (φ1 ) qDB cos (φ3 ) - 2 VqDB 3
sin (φ3 ) - lDB q3 sin (φ3 ) - lDB 32 cos (φ3 ),
qBy
- lAB sin (φ1 ) qDB sin (φ3 ) 2 VqDB 3
cos (φ3 ) lDB q3 cos (φ3 ) – lDB sin (φ3 ).
2
3
Из этой системы уравнений определяем вторые передаточные функции qB и q3 .
21

22.

Выполнив вычисления по приведённым выше зависимостям, построим соответствующие диаграммы.
22

23.

Диаграммы функции положения и
передаточных функций для зубчатой передачи
23

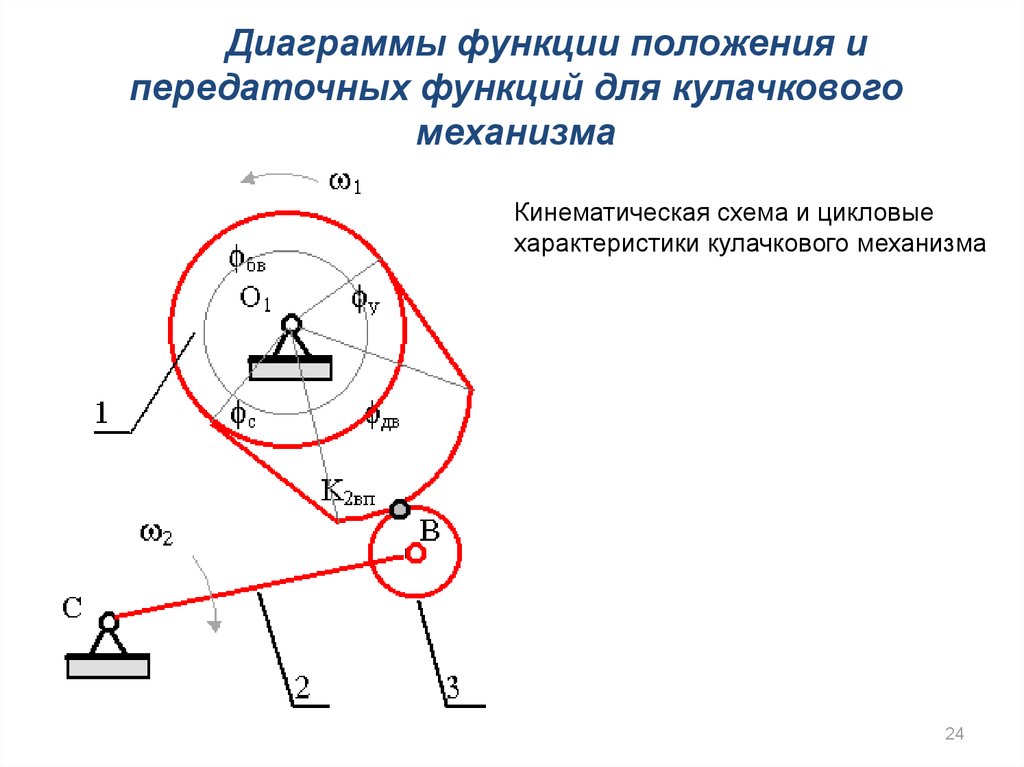
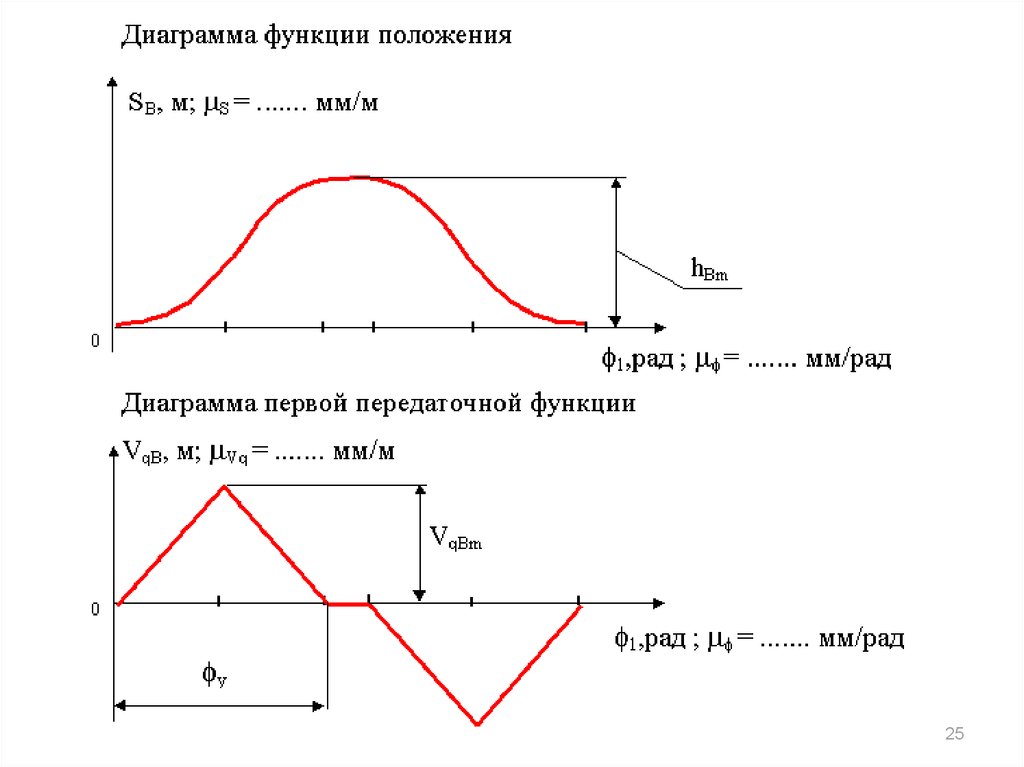
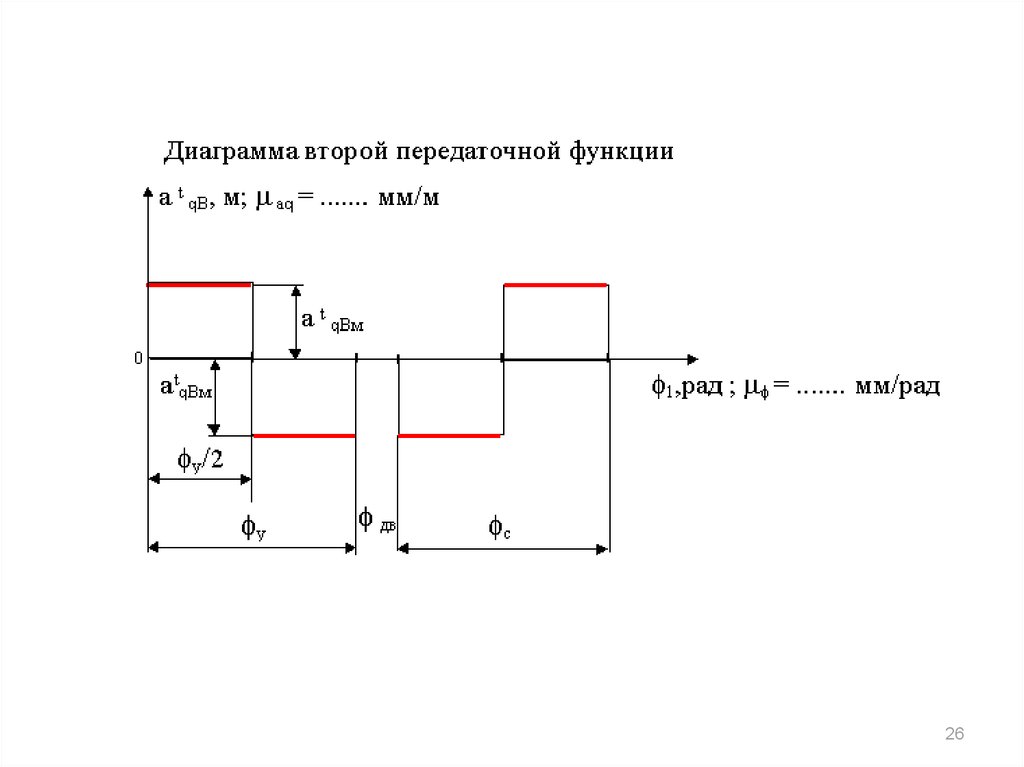
24.

Диаграммы функции положения и
передаточных функций для кулачкового
механизма
Кинематическая схема и цикловые
характеристики кулачкового механизма
24

25.

25

26.

26

27.

Экспериментальный метод кинематического
исследования
При экспериментальном исследовании кинематики механизмов кинематические характеристики звеньев и точек механизма определяются и регистрируются с помощью чувствительных элементов - датчиков, которые используя различные физические эффекты преобразуют кинематические параметры в пропорциональные электрические сигналы. Эти
сигналы регистрируются измерительными самопишущими
приборами (самописцами, осциллографами и др.)
27

28.

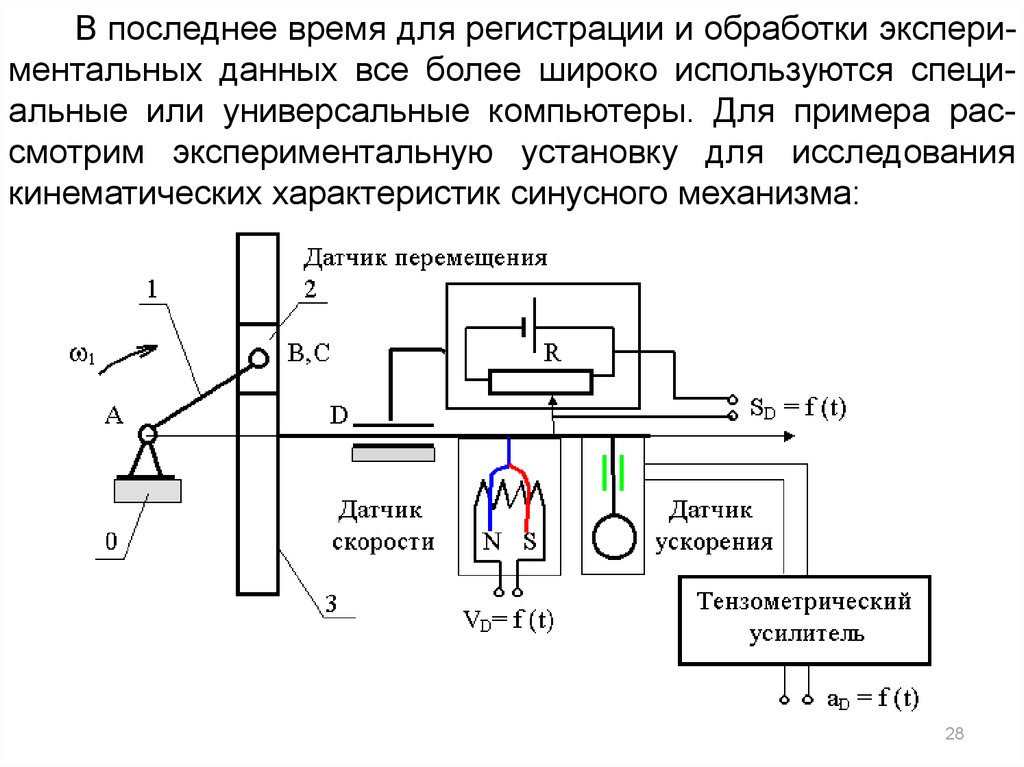
В последнее время для регистрации и обработки экспериментальных данных все более широко используются специальные или универсальные компьютеры. Для примера рассмотрим экспериментальную установку для исследования
кинематических характеристик синусного механизма:
28

29.

В этой экспериментальной установке:
для измерения перемещения выходного звена используется потенциометрический датчик перемещения, в котором
пропорционально положению движка потенциометра изменяется его сопротивление;
для измерения скорости выходного звена используется
идукционный датчик скорости, в котором напряжение на концах катушки движущейся в поле постоянного магнита пропорционально скорости катушки;
29

30.

для измерения ускорения выходного звена используется тензометрический акселерометр. Он состоит из пластинчатой пружины один конец которой закреплен на выходном звене механизма, а на втором закреплена масса. На
пластину наклеены проволочные тензопреобразователи.
При движении выходного звена с ускорением инерционность массы вызывает изгиб пластины , деформацию тензопреобразователей и изменение их сопротивления пропорциональное ускорению выходного звена.
30

31.

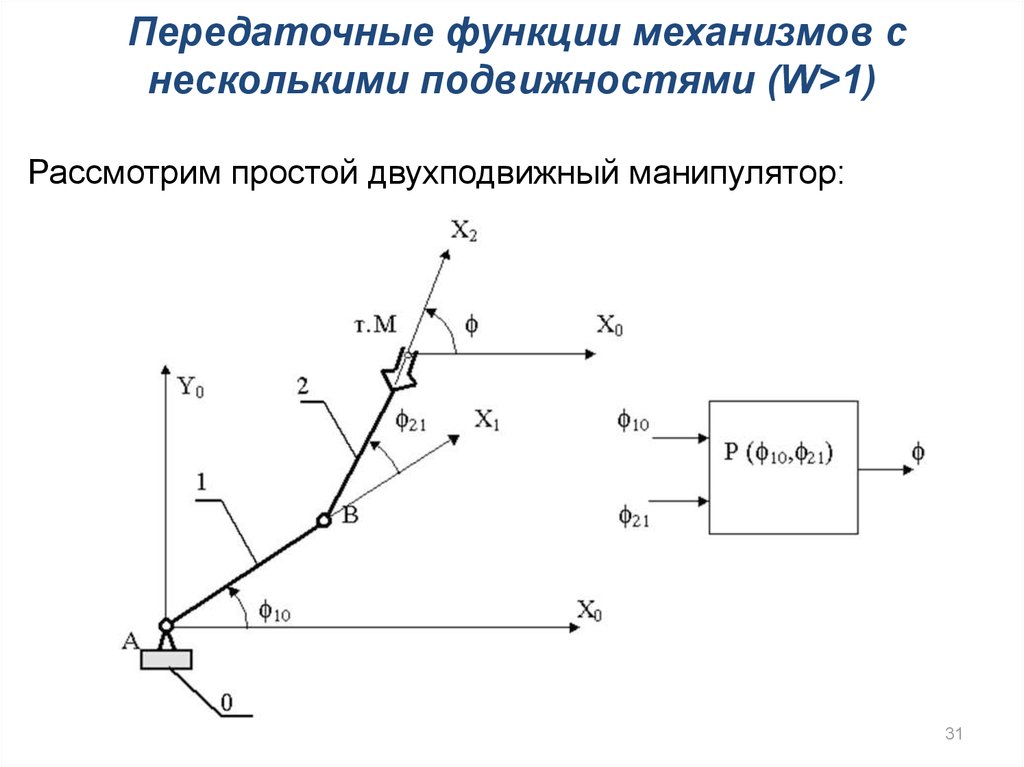
Передаточные функции механизмов с
несколькими подвижностями (W>1)
Рассмотрим простой двухподвижный манипулятор:
31

32.

Функция положения для выходного звена этого
механизма является функцией двух переменных
φ P(φ10, φ21),
и её производная определится как производная
функции двух переменных:
dφ2 [dP(φ10, φ21) / dφ10]dφ10 [dP(φ10, φ21) / dφ21]dφ21
q10 dφ10 q21 dφ21,
где q 1 0 и q 2 1 - частные производные по обобщённым координатам.
32
Конец ЛТММ3.