Кинематический анализ и синтез механизмов

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «Мехатронные системы»
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез
механизмов»
Автор Зубкова Ю.В., к.т.н., доцент кафедры «Мехатронные системы»
Ижевск
2017

2. Основные понятия и определения

Кинематический анализ механизма - исследование его основных параметров
с целью изучения законов изменения и на основе этого выбор из ряда
известных наилучшего механизма.
Целью кинематического анализа является определение кинематических
характеристик (траекторий, скоростей и ускорений характерных точек его
звеньев) без учёта сил, вызывающих это движение.
При этом решают в основном три задачи:
1) определение перемещений звеньев и траекторий заданных точек;
2) определение скоростей точек звеньев и угловых скоростей звеньев;
3) определение ускорений точек звеньев и угловых ускорений звеньев.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
2

3. Основные понятия и определения (продолжение)

Зависимость линейных координат в какой-либо точке механизма от
обобщенной координаты – линейная функция положения данной
точки в проекциях на соответствующие оси координат.
Хс= f( 1)
Зависимость угловой координаты какого-либо звена механизма от
обобщенной координаты – угловая функция положения данного
звена.
2= f( 1)
dt
dy c
v
cx
dx c
dx c
dx c dt
1
v
Vc
v
qcy
qcx
v qcx
v qcx
d
1
1
dt
dt 1
d 1
1
v
cx
1 vqcx
v
cy
1 vqcy
Полная скорость т. С будет
vc
vcx vcy
2
2
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
3

4. Основные понятия и определения (продолжение)

Первая производная угловой функции положения звена по обобщенной
координате – передаточное отношение
d 2
d 1 u 2 1
|
dt
dt
2
1 u 2 1
Вторая производная линейной функции положения по обобщенной координате
– аналог линейного ускорения точки в проекциях на
соответствующие оси
d2xc
d 12 a qcx
d 2 yc
a qcy
2
d 1
Задание: Запишите самостоятельно выражение аналога углового ускорения.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
4

5. Основные кинематические характеристики механизмов

1. Вид движения
2. Перемещение и траектория
- угловые, φ, рад
- линейные, S, м
3. Скорость (быстрота изменения перемещения во времени)
- угловая, ω = dφ/dt, рад/с = 1/с
- линейная, v = dS/dt, м/с
4. Ускорение (быстрота изменения скорости во времени)
- угловое, ε = dω/dt, рад/с2 = 1/с2
- линейное, a = dV/dt, м/с2
Движение любого звена может быть
периодическим и апериодическим
Время цикла Т = 60/n = 2π/ω, с,
где n – частота вращения кривошипа
ω – угловая скорость, 1/с
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
5

6. Кинематический анализ пространственного механизма

Первая и основная задача кинематики - определение функции положения.
Для пространственных механизмов наиболее эффективные методы решения:
- векторный метод (рычажные механизмы)
- метод преобразования координат (манипуляторы)
Кинематический анализ механизма проводят без учета сил, вызывающих его
движение, аналитическим или графическим методом.
Аналитический метод позволяет установить в виде математического
уравнения зависимость кинематических параметров механизма от
размеров звеньев.
Графический метод, более простой, основан на непосредственном
геометрическом построении планов положений механизма (наглядность).
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
6

7. Аналитический способ определения кинематических параметров рычажных механизмов

Пример: кривошипно-ползунный механизм
Дано: 1, lAB, lBS2, lBC, lAC
Определить: vi, ai, 2, 2.
Условие замкнутости данного контура:
(1)
l
l
AB
AB
l
BC
l
AC
cos 1 lBC cos 2 x C
(2)
sin 1 lBC sin 2 y
C
(3)
l
AB
0
sin 1
2 arc sin lAB
lBC
Из (3) следует, что
(4)
Продифференцируем (3) по обобщенной координате:
l
cos 1 lBC cos 2
AB
d 2
qcy
d 1 v
0
u 2 1
cos 1
u 2 1
cos 2
BC
l
l
AB
(5)
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
7

8. Аналитический способ определения кинематических параметров рычажных механизмов (продолжение)

Продифференцируем (2) по обобщенной координате:
lAB sin 1 lBC sin 21
d 2
d 1 vqcx
v v
v v
1
cx
1
cy
v
c
qcx
qcy
v
0
vcy
cx
2
2
Условие замкнутости данного векторного
контура имеет вид:
(6)
l
l
l
AB
l
l
BS 2
AS2
AB
cos 1 lBS cos 2 x S
AB
sin 1 lBS sin 2 y
2
2
(7)
S2
2
Продифференцировав (7) по обобщенной координате:
s2x
1 vqs
s2y
1 vqs
v
v
v
s2
v
2
s2
2x
(8)
2y
vs
x
2
2y
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
8

9. Кинематический анализ манипулятора

Целью кинематического анализа манипулятора
является определение положения, скорости и
ускорения произвольной точки звена исполнительного механизма - схвата - в различных
системах координат.
Прямая задача
Найти закон изменения абсолютных координат выходного звена по
заданным законам изменения относительных или абсолютных координат
звеньев.
Обратная задача
По заданному закону движения схвата найти законы изменения координат
звеньев, обычно, линейных или угловых перемещений в приводах.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
9

10. Задачи кинематики

Первая и основная задача кинематики - определение функции положения.
Методы решения для пространственных механизмов:
- векторный метод
- метод преобразования координат (метод Денавита и Хартенберга)
Два вида матриц:
- матрицы М, определяющие отношение между системами координат
соседних звеньев;
- матрицы Т, определяющие положение и ориентацию каждого звена
механизма в неподвижной или базовой системе координат.
Матрица перехода из i-ой системы координат в (i-1)-ю:
Mi
cos i
cos i sin i
sin i sin i
ai cos i
sin i
cos i cos i
cos i sin i
ai sin i
0
sin i
cos i
si
0
0
0
1
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
10

11. Метод Денавита и Хартенберга

Оси координат располагаются по следующим правилам:
• Для звена i ось zi направляется по оси кинематической пары, образуемой им
со звеном (i+1). Начало координат размещают в геометрическом центре
этой пары.
• Ось xi направляется по общему перпендикуляру к осям zi-1 и zi с
направлением от zi-1 к zi. Если оси zi-1 и zi совпадают, то xi перпендикулярна
к ним и направлена произвольно. Если они пересекаются в центре
кинематической пары, то начало координат располагается в точке
пересечения, а ось xi направляется по правилу векторного произведения
(кратчайший поворот оси zi до совмещения с zi-1 при наблюдении с конца xi
должен происходить против часовой стрелки).
• Ось yi направляется так, чтобы система координат была правой.
Прямая задача кинематики о положениях решается с помощью следующей
формулы:
R0 Tn Rn
где Tn - матрица, равная произведению матриц M i:
Tn M1M 2 ...M n
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
11

12. Метод Денавита и Хартенберга (продолжение)

Согласно принятому методу, каждый переход включает в себя
последовательность четырех движений: двух поворотов и двух
параллельных переносов, осуществляемых в указанной последовательности:
поворот вокруг оси zi-1 на угол , до тех пор, пока ось xi не станет
параллельной оси xi-1 (положительное направление поворота при
наблюдении с конца вектора zi-1 против часовой стрелки);
перенос вдоль оси xi на величину -ai до совмещения начала системы
координат Oi с точкой пересечения осей xi и zi-1 (отсчет по оси xi от точки
пересечения оси xi и оси zi-1);
перенос вдоль оси zi-1 на величину -si, после которого начало системы
координат Oi оказывается в начале координат Oi-1 системы (i-1)
(отсчитывается по оси zi-1 от ее начала координат Oi-1 до точки ее
пересечения с осью xi);
поворот i-ой системы вокруг оси xi на угол до параллельности осей zi и zi-1
(положительное направление поворота при наблюдении с конца вектора xi
против часовой стрелки).
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
12

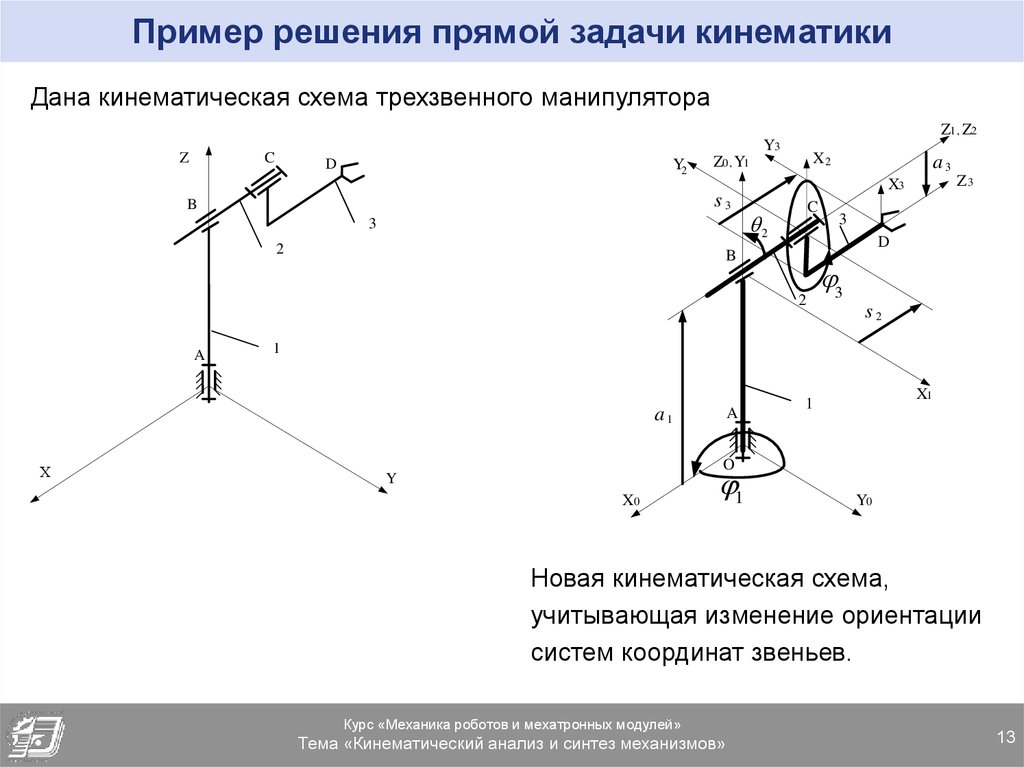
13. Пример решения прямой задачи кинематики

Дана кинематическая схема трехзвенного манипулятора
Z1 , Z2
Z
Y3
C
D
Y2
X2
Z0 , Y1
a3
Z3
X3
s3
B
3
2
C
2
D
B
2
A
3
s2
1
a1
Х
3
A
X1
1
O
Y
X0
1
Y0
Новая кинематическая схема,
учитывающая изменение ориентации
систем координат звеньев.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
13

14. Пример решения прямой задачи кинематики (продолжение)

Угол 1 = 90о
а1 = L1
S2 = L2 + r23
a3 L3'
s3 L3
Тип и параметры кинематических пар
Кинематическая
пара
Тип
пары
Номер
звена
Параметры
i , град
ai , м
i
-
L1
90
si , м
, град
0,1
В
1
01
1,2
П
2
-
L2 r23
-
-
2,3
В
3
23
L3
L3'
-
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
14

15. Пример решения прямой задачи кинематики (продолжение)

Матрицы перехода их системы Oi в систему Oi-1 (в общем виде):
- матрица поворота вокруг оси xi на угол -θi,
- матрица переноса вдоль оси xi на -ai,
- матрица переноса вдоль оси zi-1 на -si,
- матрица поворота вокруг оси zi-1 на угол -φi.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
15

16. Пример решения прямой задачи кинематики (продолжение)

Расширенные матрицы перехода для каждого из сочленений, с учетом
значений приведенных в таблице (слайд 14):
cos 01 0
M1
M3
sin 01
sin 01
L1 cos 01
0 cos 01
L1 sin 01
0
1
0
0
0
0
0
1
sin 23
0 L3' cos 23
sin 23
cos 23
0
L3' sin 23
0
0
0
L3
0
0
0
1
Вектор-столбец значений R3:
R3
L3' sin 01 sin 23
0
0 1 0
0
0 0 1 L2 +r23
0 0 0
cos 23
L1 L3' cos 23
M2
1 0 0
Координаты положения схвата
манипулятора для общего положения с учетом системы координат, м:
1,5
cos 01 ( L2 L3 r23 )
1
1
R3
0
4, 25
1
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
16

17. Пример решения прямой задачи кинематики (продолжение)

Положение некоторой произвольной точки М в системе координат звена i
определяется вектором rMi, а в системе координат звена (i-1) - вектором rMi-1.
,
где
- матрица перехода из i-ой
системы координат в (i-1)-ю
Шестизвенный манипулятор
в начальном положении
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
17

18. Пример решения прямой задачи кинематики (продолжение)

Положение выходного звена манипулятора определяется
матрицей Тn:
Углом подхода схвата α называется угол
между вектором подхода и базовым вектором
Тогда матрица Tn может быть представлена в виде:
В механизме с n - подвижностями в общем виде функцию положения схвата
можно записать так:
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
18

19. Кинематический анализ. Прямая задача

Необходимо определить линейные и угловые скорости и ускорения схвата при
заданных угловых и линейных обобщенных скоростях и ускорениях.
Решение прямой задачи кинематики для точки М схвата можно получить
продифференцировав четвертый столбец матрицы Тn по времени:
Угловая скорость схвата:
Дифференцируя это выражение по времени, получим формулу для
определения углового ускорения схвата:
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
19

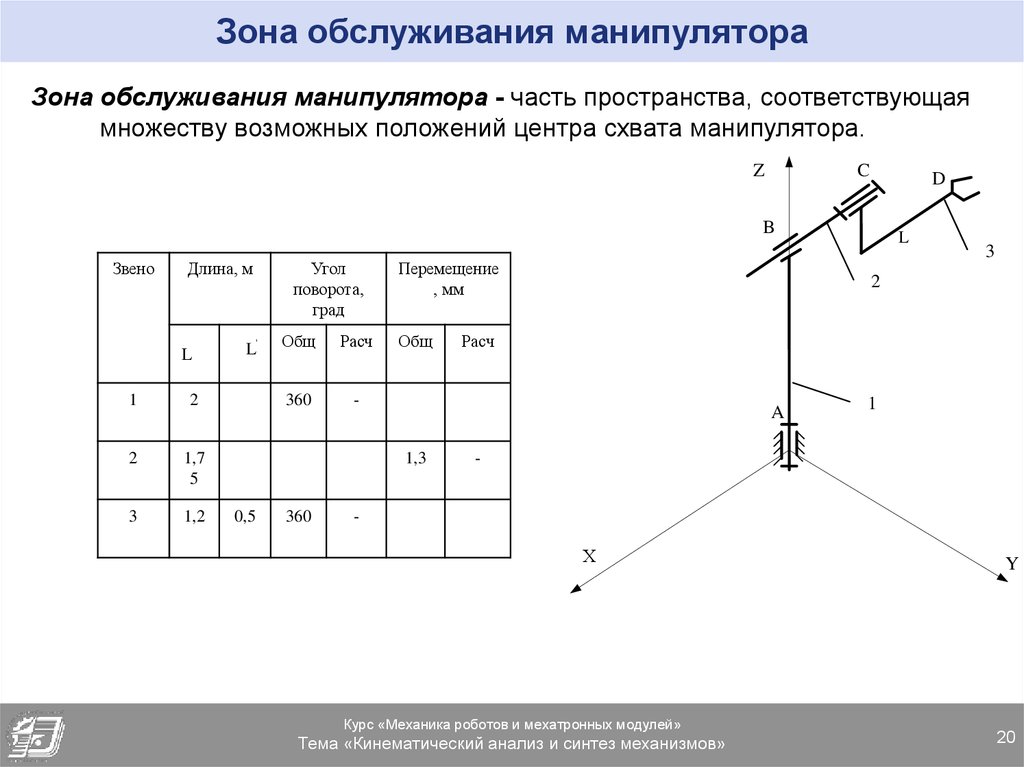
20. Зона обслуживания манипулятора

Зона обслуживания манипулятора - часть пространства, соответствующая
множеству возможных положений центра схвата манипулятора.
Z
C
D
B
Звено
Длина, м
L
1
2
2
1,7
5
3
1,2
L'
Угол
поворота,
град
Общ
Расч
360
-
Перемещение
, мм
Общ
0,5
360
3
2
Расч
A
1,3
L
1
-
-
Х
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
Y
20

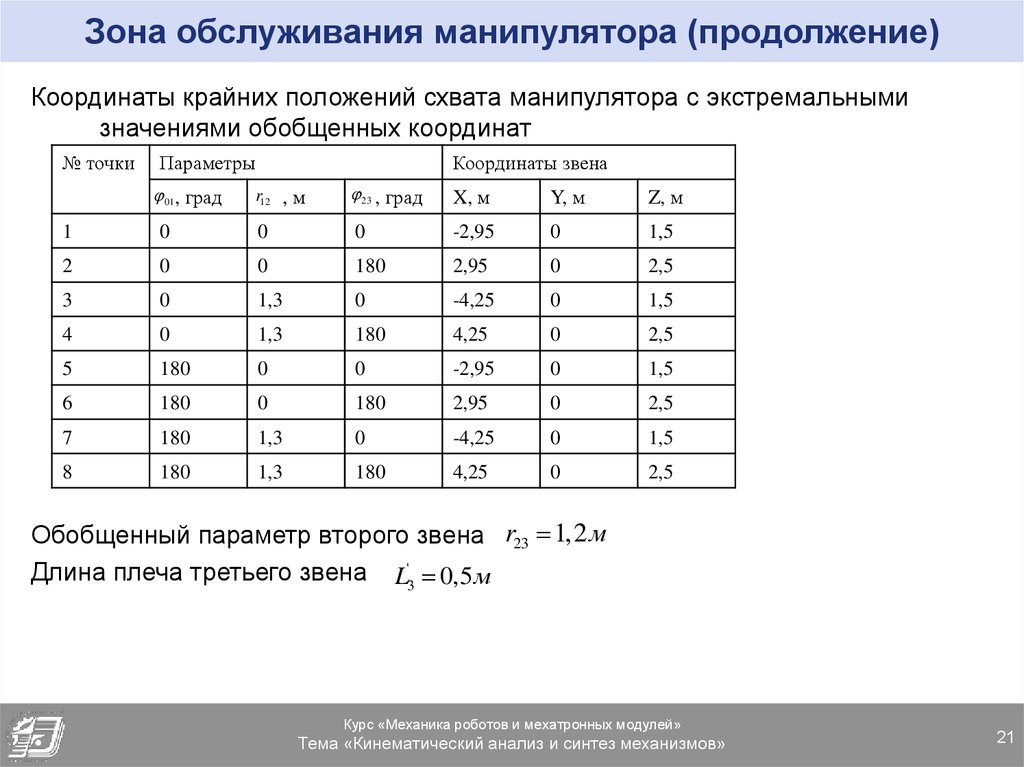
21. Зона обслуживания манипулятора (продолжение)

Координаты крайних положений схвата манипулятора с экстремальными
значениями обобщенных координат
№ точки
Параметры
01, град
Координаты звена
r12 , м
23 , град
X, м
Y, м
Z, м
1
0
0
0
-2,95
0
1,5
2
0
0
180
2,95
0
2,5
3
0
1,3
0
-4,25
0
1,5
4
0
1,3
180
4,25
0
2,5
5
180
0
0
-2,95
0
1,5
6
180
0
180
2,95
0
2,5
7
180
1,3
0
-4,25
0
1,5
8
180
1,3
180
4,25
0
2,5
Обобщенный параметр второго звена r23 1,2 м
Длина плеча третьего звена L'3 0,5 м
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
21

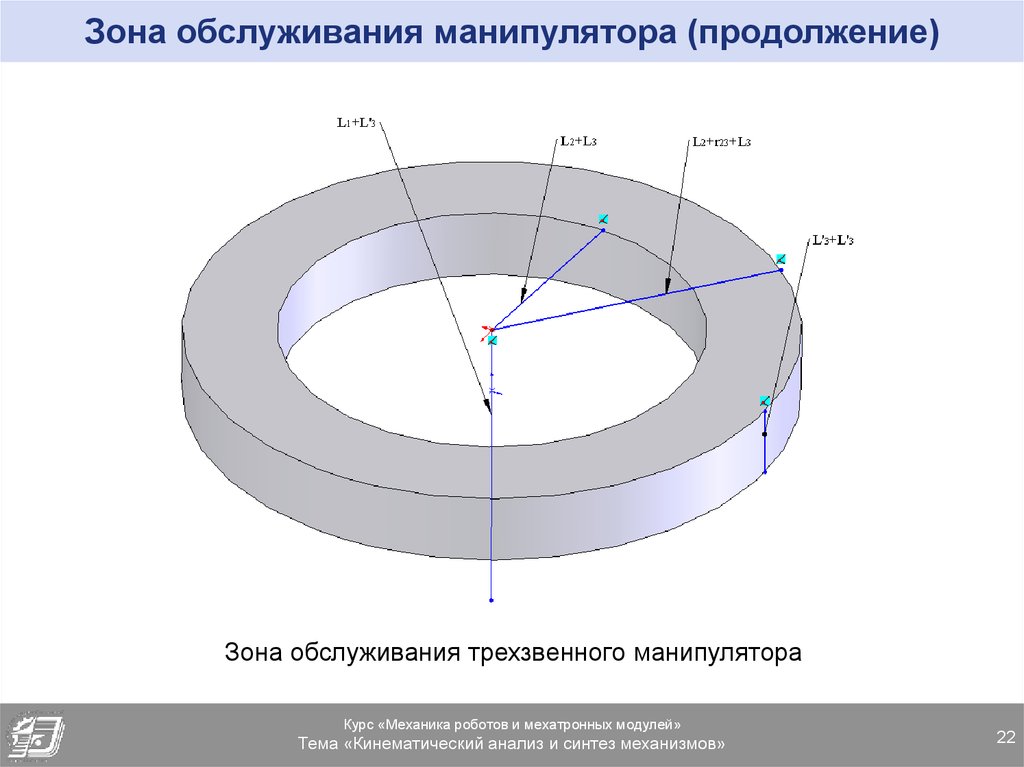
22. Зона обслуживания манипулятора (продолжение)

Зона обслуживания трехзвенного манипулятора
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
22

23. Графический метод решения задач кинематики

Графический метод основан на непосредственном геометрическом
построении планов положений (скоростей, ускорений) механизма.
Сущность метода:
Параметры движения и схемы механизмов изображаются на чертежах
условно при помощи масштабов.
Графически может быть отображена любая величина (длина, скорость,
ускорение, сила и т.д.).
Применяется так называемый вычислительный масштаб
Например, масштабный коэффициент длины АВ равен
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
23

24. Метод построения планов скоростей и ускорений

Метод построения планов скоростей и ускорений базируется на теоремах
Архимеда: скорость (ускорение) абсолютного движения точки представляют
собой геометрическую сумму переносного (поступательного) и относительного
(вращательного) движения:
V ABC VПЕР VОТН
n
а ABC а ПЕР аОТН а ПЕР аОТН
аОТН
Исходные данные для решения задачи:
- кинематическая схема манипулятора;
- размеры звеньев механизма;
- величина и направление скорости ведущего звена.
Допущения:
- звенья механизма считаем абсолютно жесткими;
- зазоры в кинематических парах отсутствуют.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
24

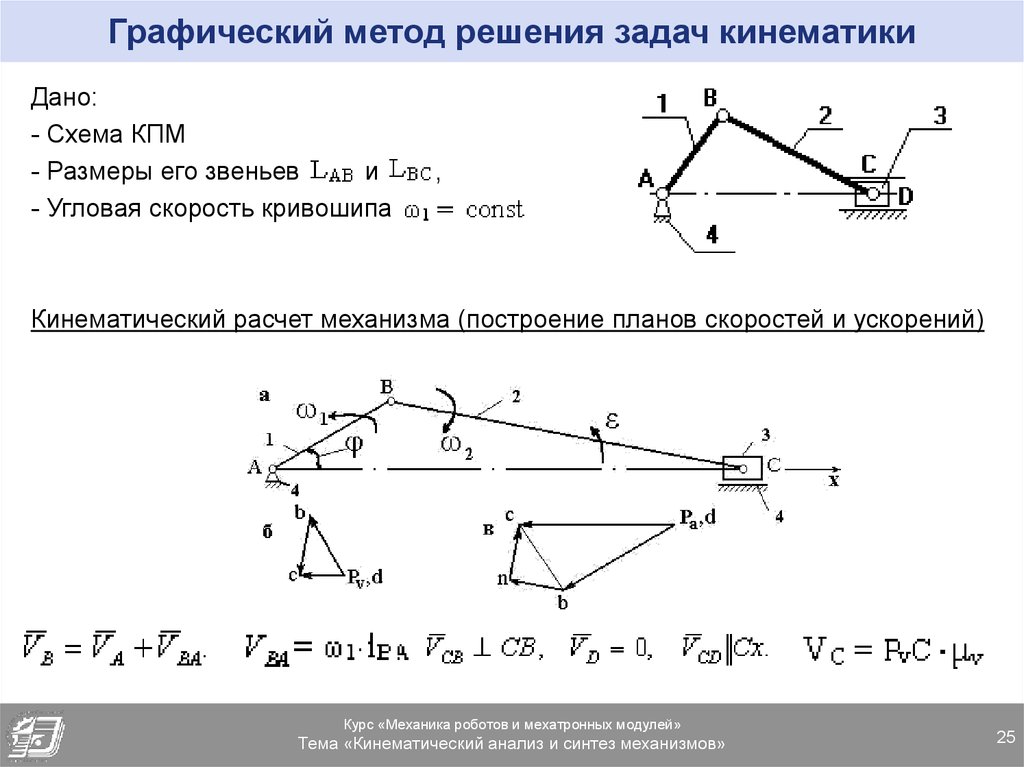
25. Графический метод решения задач кинематики

Дано:
- Схема КПМ
- Размеры его звеньев
и
- Угловая скорость кривошипа
,
.
Кинематический расчет механизма (построение планов скоростей и ускорений)
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
25

26. Графический метод решения задач кинематики (продолжение)

Векторное выражение ускорения точки В:
Ускорение точки С получим в результате графического решения следующих
векторных уравнений:
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
26

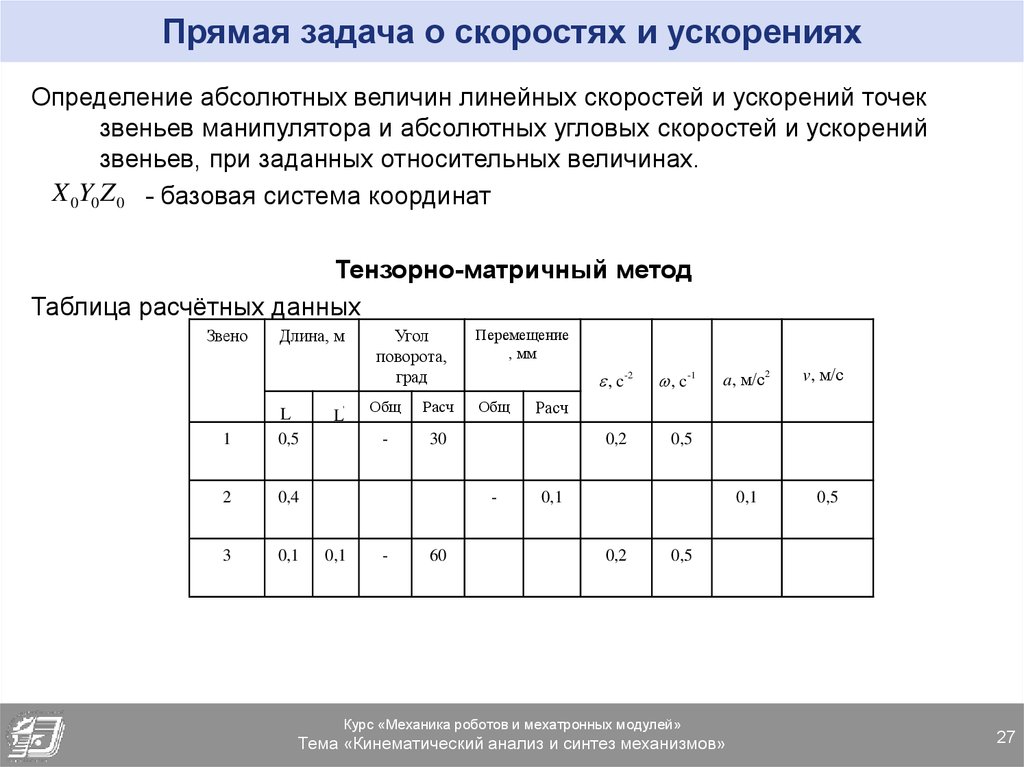
27. Прямая задача о скоростях и ускорениях

Определение абсолютных величин линейных скоростей и ускорений точек
звеньев манипулятора и абсолютных угловых скоростей и ускорений
звеньев, при заданных относительных величинах.
X 0Y0 Z 0 - базовая система координат
Тензорно-матричный метод
Таблица расчётных данных
Звено
Длина, м
1
L
0,5
2
0,4
3
0,1
L'
Угол
поворота,
град
Общ
Расч
-
30
Перемещение
, мм
, c-2
Общ
0,1
-
60
a, м/c2
v, м/c
0,1
0,5
Расч
0,2
-
, c-1
0,5
0,1
0,2
0,5
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
27

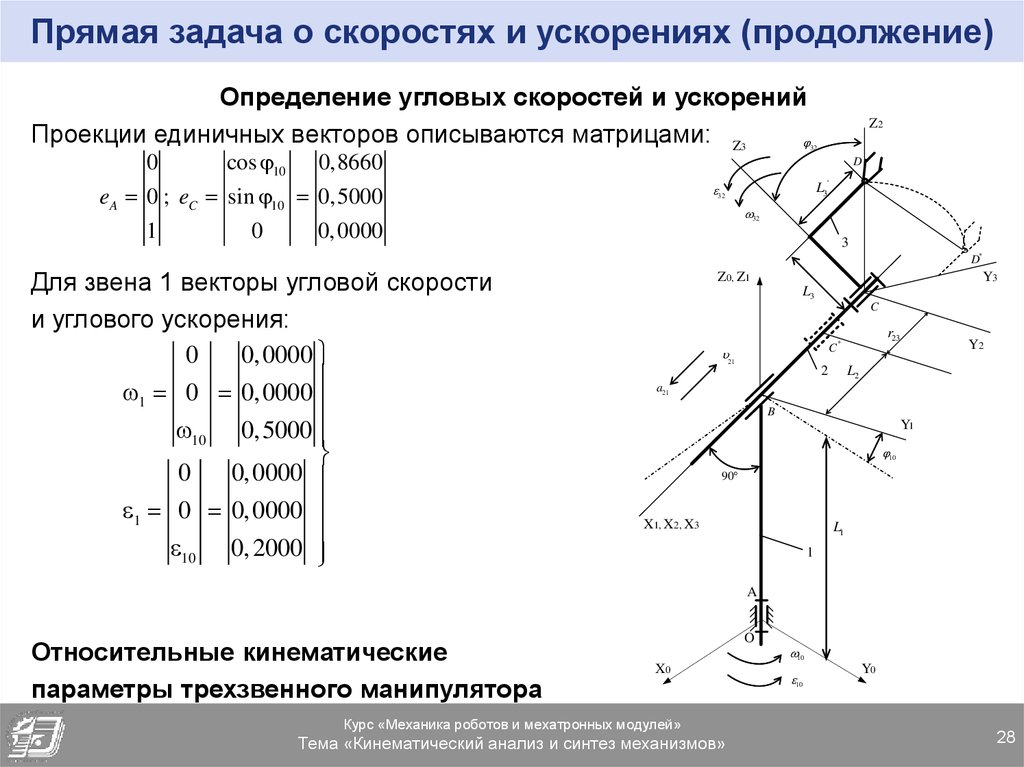
28. Прямая задача о скоростях и ускорениях (продолжение)

Определение угловых скоростей и ускорений
Проекции единичных векторов описываются матрицами: Z
0
cos 10
3
0
32
0,8660
D
eA 0 ; eC sin 10 0,5000
1
Z2
32
L3
'
32
0, 0000
3
D*
Для звена 1 векторы угловой скорости
и углового ускорения:
0
0, 0000
1 0 0, 0000
10 0,5000
0
0, 0000
1 0 0, 0000
10 0, 2000
Y3
Z0, Z1
L3
C
r23
C*
21
2
Y2
L2
a21
B
Y1
10
90
X1, X2, X3
L1
1
A
Относительные кинематические
параметры трехзвенного манипулятора
O
X0
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
10
10
Y0
28

29. Прямая задача о скоростях и ускорениях (продолжение)

Для звена 2 угловая скорость и ускорение:
2 1 21 ;
2 1 21 1 21 ,
а так как 21 0 и 21 0, то получим 2 1 , 2 1.
Векторы относительной угловой скорости и относительного углового ускорения
(закон вращения звена 3 относительно звена 2):
32 еС 32 ; 32 еС 32 ,
а соответствующие им матрицы записываются в виде:
32 cos 10
0, 4330
32 32 sin 10 0, 2500
0
0, 0000
.
32 cos 10 0,1730
32 32 sin 10 0,1000
0
0, 0000
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
29

30. Прямая задача о скоростях и ускорениях (продолжение)

Векторные уравнения угловой скорости и углового ускорения третьего звена:
3 2 32 1 32
3 2 32 2 32 1 32 2 32
В эти уравнения входит векторное произведение 2 32 , которое, как и
произведение любых двух векторов , описываемых матрицами
xn
xm
a n yn и am ym ,
zn
zm
в общем виде превращается в вектор с матрицей:
yn z m z n ym
an am zn xm xn zm
xn ym yn xm
10 32 sin 10
0,1250
Таким образом, матрица-столбец вектора: 2 32 10 32 cos 10 0, 2165
0
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
0
30

31. Прямая задача о скоростях и ускорениях (продолжение)

Матрицы угловой скорости и углового ускорения третьего звена:
32 cos 10
0, 4330
3 32 sin 10 0, 2550 ;
10
0,5000
32 cos 10 10 32 sin 10
3 32 sin 10 10 32 cos 10
10
0, 0482
0,3165
0, 2000
Модули векторов угловой скорости и углового ускорения:
3 0,7070 с 2 , 3 0,3775 с 2
Определение линейных скоростей и ускорений
Запишем матричные уравнения:
OB L01; BC A01L12 ; CD A01 A23rD3 ,
Столбец координат в системе X 3Y3 Z 3 , м;
xD3
L'3
1, 200
rD3 yD3 0 0, 0000 ,
zD3
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
L3
0,5000
31

32. Прямая задача о скоростях и ускорениях (продолжение)

Матрицы переноса соответственно от систем координат 1 к 0 и 2 к 1:
0
( L2 r23 )
0, 0000
L01 0 0, 0000 , L12
L1
0,5000
0,5000
0
0, 0000
0
0, 0000
Матрицы поворота при переходе, соответственно, от систем координат 1 к 0
и 3 к 2:
cos 10 sin 10 0 0,8660 0,5000 0, 0000
A01 sin 10 cos 10 0 0,5000 0,8660 0, 0000
0
1
0
0
1
0
A23 0 cos 32
sin 32
0 sin 32
cos 32
1, 0000
1, 0000 0, 0000 0, 0000
0, 0000 0,5000 0,8660
0, 0000 0,8660 0,5000
0, 0000
0, 0000
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
32

33. Прямая задача о скоростях и ускорениях (продолжение)

Таким образом, получаем матрицы:
0
0, 0000
OB 0 0, 0000 ;
L1
0,5000
L2 cos 10
0, 4330
BC L2 sin 10 0, 2500 ;
0
0, 0000
L'3 cos 10 L3 sin 10 sin 32
CD L'3 sin 10 L3 cos 10 sin 32
L3 cos 32
0, 0433
0,1250
0, 0500
Модули соответствующих векторов:
|OB|=0,5000 м; |BC|=0,5000 м; |CD|=0,1414 м.
Скорость точки В:
B 1 OB.
B 0
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
33

34. Прямая задача о скоростях и ускорениях (продолжение)

Векторное уравнение для определения скорости точки С:
C B CB 21 2 BC
Относительная скорость: 21 eC 21
21 cos 10
1,95
тогда в матричной форме: 21 sin 0, 2500
21
10
0
0, 0000
10 L2 sin 10
Элементы матрицы-вектора 2 BC :
2 BC 10 L2 cos 10 0, 2165
0
21 cos 10 10 L2 sin 10
Линейная скорость точки С:
0,1250
0
0,3080
C 21 sin 10 10 L2 cos 10 0, 4665 ,
0
0, 0000
Модуль скорости: |vc|=0,5990 м/с.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
34

35. Прямая задача о скоростях и ускорениях (продолжение)

Скорость точки D:
D C DC C 3 CD
Матрица-столбец вектора 3 CD :
L3 32 sin 10 cos 32 10 cos 10 sin 32 L'3 10 sin 10
0, 0750
L3 32 sin 32
0, 0433
3 CD L3 10 sin 10 sin 32 32 cos 10 cos 32 L'3 10 cos 10 0, 0433
0, 2330
Матрица вектора D : D 0,5098
0, 0433
D
= 0,5622 м/с.
Таким образом, определены значения линейных скоростей всех звеньев
манипулятора.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
35

36. Прямая задача о скоростях и ускорениях (продолжение)

Ускорение точки В:
a B 1 1 OB 1 OB
aB 0
Ускорение точки С:
aC aB aCB a21 2 2 BC 2 BC 2 2 21 .
где
a21 eC a21 ,
a21 cos 10
0, 0866
a 21 a21 sin 10 0, 0500
0
0, 0000
Матрица векторного произведения 2 2 BC :
2
10
L2 cos 10
0,1082
2
2 2 BC 10
L2 sin 10 0, 0625
0
0, 0000
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
36

37. Прямая задача о скоростях и ускорениях (продолжение)

Матрицы векторного произведения
10 L2 sin 10
2 BC 10 L2 cos 10
0
2 BC :
0, 0500
0, 0866
0, 0000
Матрица вектора ускорения Кориолиса:
2 10 21 sin 10
0, 2500
2 2 21 2 10 21 cos 10 0, 0433
0
0, 0000
Матрица вектора линейного ускорения точки С:
0, 4948
a C 0, 4071
0, 0000
2
Модуль вектора ускорения: aC 0,6407 м / с .
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
37

38. Прямая задача о скоростях и ускорениях (продолжение)

Ускорение точки D:
aD aC aDC aC 3 3 CD 3 CD,
0, 0108
3 3 CD 0, 0562
0, 0375
0, 0408
3 CD 0, 0111
0, 0077
Векторные произведения:
Матрица-столбец вектора линейного ускорения точки D:
0,5464
a D 0,3620
0, 0298
Модуль ускорения точки D:
aD 0,6561 м / с 2
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
38

39. Прямая задача о скоростях и ускорениях (продолжение)

Метод планов
Z
1. План угловых скоростей
32
c 1
Масштаб угловой скорости = 0, 01
мм
3
32 0,5c
2 1
1
Y
X
Z
2 1
2. План угловых ускорений
c 2
Масштаб углового ускорения = 0, 005
мм
1 0, 2(c 2 )
Угловое ускорение третьего звена:
32
2 32
3
3 2 32 2 32
X
Y
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
39

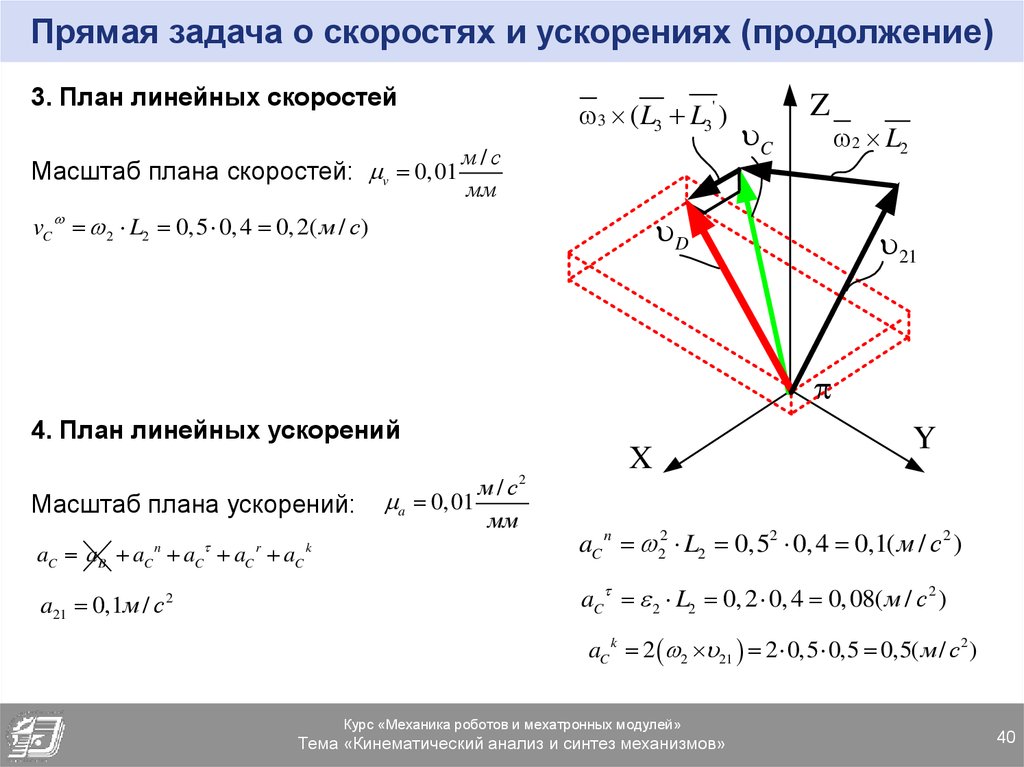
40. Прямая задача о скоростях и ускорениях (продолжение)

3. План линейных скоростей
3 ( L3 L3' )
м/с
Масштаб плана скоростей: v 0, 01
мм
C
Z
D
vC 2 L2 0,5 0, 4 0, 2( м / с)
2 L2
21
4. План линейных ускорений
Масштаб плана ускорений:
aC aB aC aC aC aC
n
a21 0,1м / с 2
r
k
a 0, 01
м/с
мм
2
X
Y
aC n 22 L2 0,52 0, 4 0,1( м / с 2 )
aC 2 L2 0, 2 0, 4 0, 08( м / с 2 )
aC k 2 2 21 2 0,5 0,5 0,5( м / с2 )
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
40

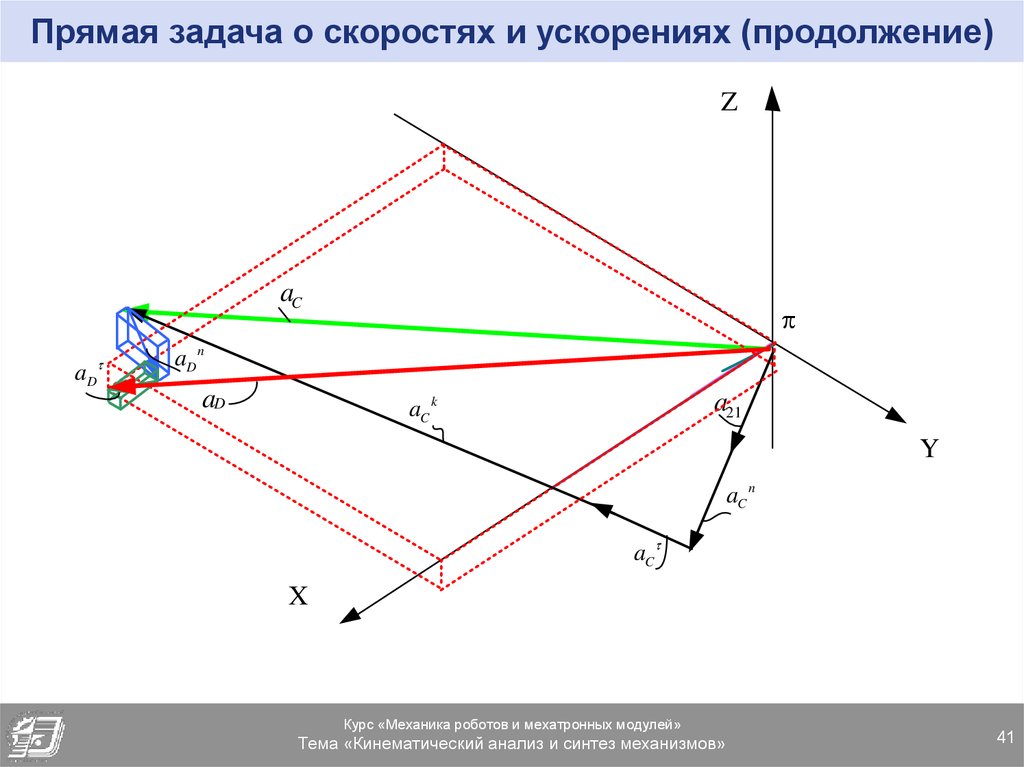
41. Прямая задача о скоростях и ускорениях (продолжение)

Z
aC
aD
aD n
aD
a21
aC k
Y
aC n
aC
X
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
41

42. Кинематический синтез механизмов

Кинематический синтез механизма – проектирование нового механизма.
Этапы кинематического синтеза:
1. Выбор схемы механизма в соответствии с заданными условиями и чаще
всего по аналогии с существующими механизмами.
2. Установление основные размеры механизма, наиболее полно
удовлетворяющие поставленным условиям.
3. Конструктивное оформление механизма, его кинематическое и силовое
исследование.
4. Расчет звеньев на прочность.
Синтез осуществляется при заданных скоростях, ускорениях, действующих
силах, напряжениях или деформациях.
При этом требуется определить необходимые размеры звеньев, их форму и
массу.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
42

43. Синтез механизмов

При синтезе часто решается задача оптимального проектирования
конструкции, когда находятся необходимые показатели работы машины
при наименьших затратах труда.
Основные этапы создания новой конструкции:
1) Разработка принципиальной схемы;
2) Проектирование и расчет машины и отдельных ее узлов;
3) Экспериментальные исследования и доводка опытного образца.
Основные этапы проектирования новой техники:
а) разработка технического задания, включающего основные исходные данные;
б) разработка эскизного проекта, включающего выбор схемы и компоновку
основных узлов конструкции;
в) разработка технического проекта, где осуществлены основные расчеты и
представлены сборочный чертеж и др. документация.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
43

44. Заключение

Кинематический анализ механизма - исследование его основных параметров
с целью изучения законов изменения перемещения, скорости и
ускорения.
Целью кинематического анализа является определение кинематических
характеристик механизма без учёта сил, вызывающих это движение.
При этом решаются прямая и обратная задачи кинематики (о положениях,
скоростях, ускорениях).
Два основных метода:
- аналитический;
- метод планов.
Зона обслуживания манипулятора - часть пространства, соответствующая
множеству возможных положений центра схвата манипулятора.
Кинематический синтез представляет собой метрический синтез. Здесь
определяются размеры звеньев механизма, при которых
удовлетворяются поставленные требования.
Курс «Механика роботов и мехатронных модулей»
Тема «Кинематический анализ и синтез механизмов»
44

45.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВО ИжГТУ имени М.Т. Калашникова, 2017
© Зубкова Юлия Валерьевна, 2017