Similar presentations:
Планы ускорений плоских механизмов
1. Тема 4.
4.4.2. Планы ускорений плоских механизмовПланом ускорений называется чертёж, на котором в
выбранном масштабе изображены векторы, равные по
модулю и направлению векторам ускорений различных
точек механизма.
При построении планов ускорений считается, что
линейные скорости всех точек и угловые скорости всех
звеньев механизма известны.
Для построения планов ускорений необходимо знать
формулы для определения ускорений точек при
различных движениях звеньев.
лекция № 5.
1
2. Тема 4.
а lOAп
А
2
a A lOA
лекция № 5
2
3. Тема 4.
аа
ВА
аВ а А а
n
2
a AB
AB
l AB
п
ВА
а ВА
п
ВА
а ВА
a BA AB l AB .
лекция № 5
AB
3
4. Тема 4.
4. Сложное движение.Это движение (движение кулисных механизмов) раскладывается на
переносное и относительное. Теорема о сложении ускорений для точки,
совершающей сложное движение, выглядит следующим образом:
а абс а пер а отн а кор ,
где а п ер
– ускорение переносного (вращательного) движения;
а отн - ускорение относительного движения; а кор - кориолисово ускорение.
Кориолисово
ускорение
характеризует
изменение
модуля
и
направления относительной скорости точки вследствие вращательного
переносного движения.
Кориолисово ускорение определяется векторным произведением:
а кор 2 пер V отн
Модуль этого ускорения:
акор 2 пер Vотн sin ,
α – угол между векторами переносной и относительной скоростей;
лекция № 5
4
5. Тема 4.
пер- вектор угловой скорости переносного движения; V отн-вектор относительной скорости.
В плоских механизмах угол α всегда равен 90°, т.к.
относительные скорости лежат в плоскости механизма, а оси
вращения перпендикулярны этой плоскости.
Направление кориолисова ускорения можно определить по
правилу Н.Е. Жуковского: для определения
направления ускорения Кориолиса
необходимо вектор относительной скорости
спроектировать на плоскость,
перпендикулярную оси переносного вращения,
и повернуть эту проекцию в направлении
вращения. В плоских механизмах вектор относительной
скорости уже лежит в плоскости вращения.
лекция № 5
5
6. Тема 4.
лекция № 56
7. Тема 4.
5. На основе зависимостей между ускорениями точек приразличных движениях звеньев определить величины и
направления составляющих абсолютных ускорений точек
механизма.
6. С помощью масштабного коэффициента найти длины
отрезков, изображающих составляющие абсолютных
ускорений точек механизма.
7. Показать векторы составляющих абсолютных
ускорений точек.
8. По длинам лучей, выходящих из полюса плана
ускорений, определить значения абсолютных ускорений
точек механизма.
лекция № 5
7
8. Тема 4.
Свойства плана ускорений:1. Отрезки планов ускорений проходящие через полюс изображают
абсолютные ускорения. Направление абсолютных ускорений всегда
получается от полюса. В конце векторов абсолютных ускорений
принято ставить малую букву той КП, которой обозначена
соответствующая точка на плане механизма;
2. Отрезки плана ускорений, соединяющие
концы векторов
абсолютных ускорений, обозначают относительные ускорения;
3. Векторы относительных ускорений точек жесткого звена
образуют на плане ускорений фигуру, подобную этому звену и
повернутую на угол (1800–φ) в сторону углового ускорения (здесь
φ – угол между нормальной составляющей относительного
ускорения и вектором полного относительного ускорения)
(принцип подобия);
4. Неподвижные точки механизма имеют соответствующие им точки
плана ускорений, расположенные в полюсе.
лекция № 5
8
9. Тема 4.
ABп
а В а А а ВА а ВА
n
2
a AB
AB
l AB
a BA AB l AB .
лекция № 5
9
10. Тема 4.
лекция № 510
11. Тема 4.
аС а А ап
СА
а СА
лекция № 5
11
12. Тема 4.
па С а А а СB а СB
лекция № 5
12
13. Тема 4.
Сравнивая треугольник abc планаускорений с треугольником ABC на
плане положений, можно сделать
вывод, что они подобны, так как
длины векторов относительных ускорений
ab, ac и bc пропорциональны длинам
отрезков AB, AC и BC жесткого звена,
а сами векторы повернуты на угол
(1800–φ) в сторону углового ускорения
(здесь φ – угол между нормальной
составляющей относительного ускорения
и вектором полного относительного
ускорения). Сказанное подтверждает
принцип подобия в плане ускорений.
лекция № 5
13
14. Тема 4.
Пример 2. Определение ускорений точек звена, входящего впоступательную пару.
Пусть известны длины звеньев, положение ведущего
звена, угловая скорость ( 1 ) и угловое ускорение ( 1) кулисы,
линейные скорость (V2) и ускорение (a2) движения ползуна
по кулисе. Требуется найти ускорение точки В ползуна.
Точка B, принадлежащая ползуну,
совершает сложное движение: она
вращается вместе с кулисой ОА и
движется по ней. За переносное
движение примем движение
точки B1, совпадающей с т. В ползуна и
вращающейся вместе с кулисой, а
относительное – движение точки В
ползуна относительно точки B1.
15. Тема 4.
а B а B1 а BB1 а ка B1
а BB1
ак
п
а B1 а В1 а В1
a Bn1 12 lOB
a B1 1 lOB .
а BB1
аk 2 1 V2 .
п
а В1
a Bn1
16. Тема 4.
а В1а2
ак
V2
1
лекция № 5
16
17. Тема 4.
После построения плана ускорений и определения значенийускорений
всех
характерных
точек
механизма
переходят
к
определению значений и направлений действия угловых ускорений
звеньев механизма, если они не были известны заранее.
Угловое ускорение – это отношение тангенциального (касательного)
ускорения звена механизма к действительной длине этого звена.
Направление
углового
ускорения
определяется
вектором
тангенциального ускорения, перенесенного с плана ускорений в точку
звена, совершающую вращательное движение. При этом разрывается
связь между этим звеном и остальными звеньями механизма. В этом
случае, рассматриваемая точка совместно со звеном, под действием
вектора тангенциального ускорения, получает возможность совершать
вращательное движение вокруг неподвижной точки этого звена
в направлении действия векторов тангенциального ускорения.
Полученное направление вращательного движения звена и является
направлением действия его углового ускорения.
Рассмотрим пример построения плана ускорений механизма.
лекция № 5
17
18. Тема 4.
Пример 3. Определение ускорений точек и угловыхускорений звеньев кулисного механизма
Пусть известны размеры звеньев, положение ведущего звена,
угловые скорости звеньев, скорость движения камня 3
относительно кулисы 2. Требуется определить составляющие
ускорения камня 3 механизма.
Точка A2, принадлежащая камню
3, совершает сложное движение: она
вращается вместе с кулисой 2 и движется
по ней. За переносное движение примем
движение т. A3, совпадающей с т. A2 камня
и вращающейся вместе с кулисой 2, а
за относительное – движение камня
по кулисе.
лекция № 5
18
19. Тема 4.
При этом вектор абсолютного ускорения т. А3, принадлежащейкулисе, будет равен:
п
А3
а А3 а
а
А3
где а = 22. lAB – нормальная составляющая ускорения переносного
движения (направлена параллельно АВ от т. А к т. В); а А3 –
тангенциальная составляющая ускорения (направлена
перпендикулярно AB, величина неизвестна).
п
А3
Вектор относительного ускорения т. А2 ( а А2 А3 ) неизвестен по
величине, но известен по направлению (параллелен АВ).
Появится и кориолисово ускорение т. А2, равное
а Акор2 2 2 VА2 А3
Здесь 2 – угловая скорость кулисы;
VA2 A3 – скорость движения камня 3 по кулисе.
Направление определяется по правилу Жуковского (см.рис.) путем
поворота вектора относительной скорости VA2 A3 на 90° в направлении 2 .
лекция № 5
19
20. Тема 4.
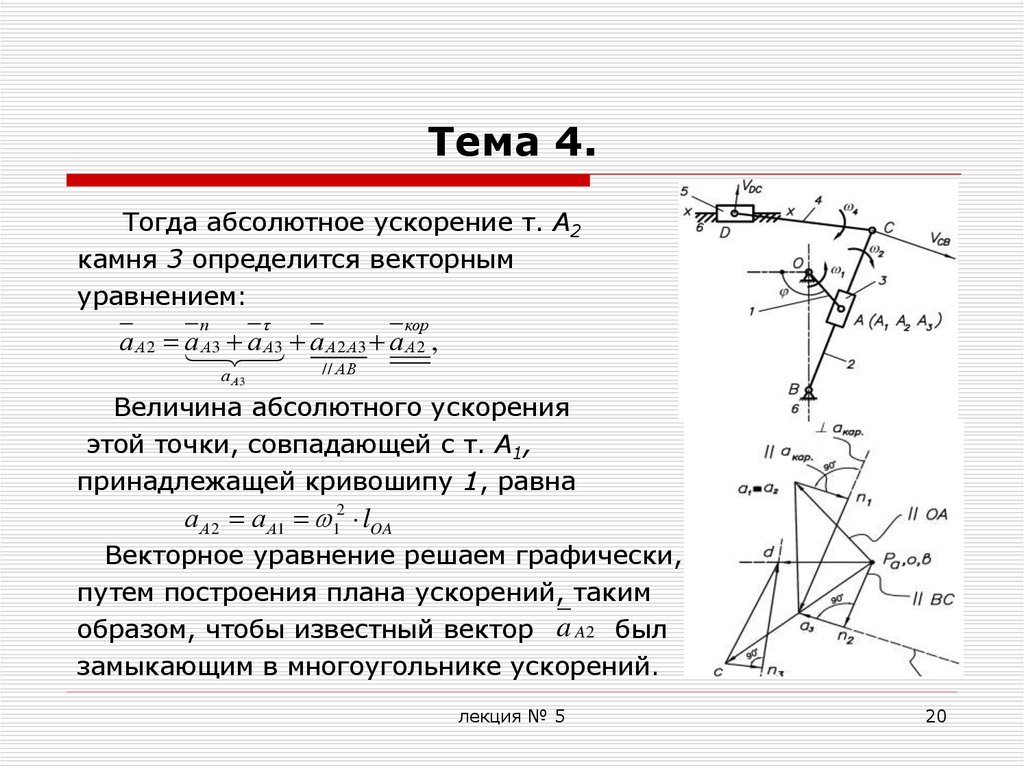
Тогда абсолютное ускорение т. А2камня 3 определится векторным
уравнением:
п
кор
а А2 а
А3 а А3 а А 2 А3 а А 2 ,
а А3
// АВ
Величина абсолютного ускорения
этой точки, совпадающей с т. А1,
принадлежащей кривошипу 1, равна
а А 2 а А1 12 lOA
Векторное уравнение решаем графически,
путем построения плана ускорений, таким
образом, чтобы известный вектор a A 2 был
замыкающим в многоугольнике ускорений.
лекция № 5
20
21. Тема 4.
22
а А2
акор
лекция № 5
21
22. Тема 4.
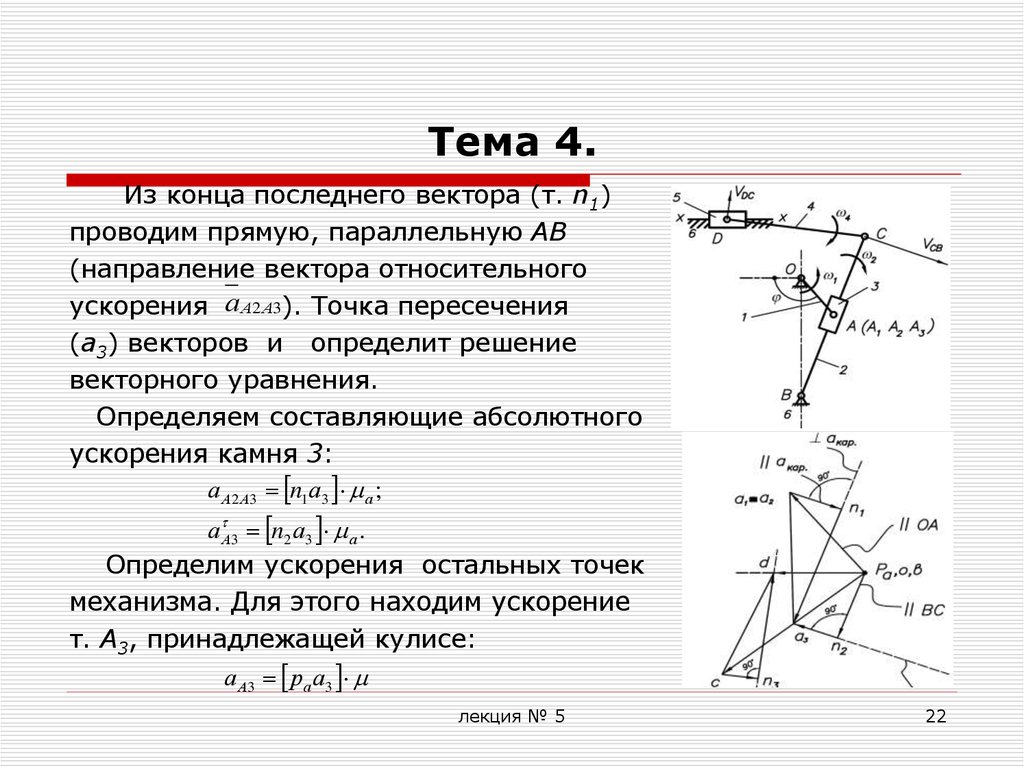
Из конца последнего вектора (т. n1)проводим прямую, параллельную АВ
(направление вектора относительного
ускорения а А2 А3). Точка пересечения
(a3) векторов и определит решение
векторного уравнения.
Определяем составляющие абсолютного
ускорения камня 3:
а А2 А3 n1а3 а ;
а А3 n2 а3 а .
Определим ускорения остальных точек
механизма. Для этого находим ускорение
т. А3, принадлежащей кулисе:
а А3 ра а3
лекция № 5
22
23. Тема 4.
АВ / ВС а3в / всра с
рс а аС
п
аD aC аDС
а DС
аС
// х х
DС
42 lСD
а DC
лекция № 5
23
24. Тема 4.
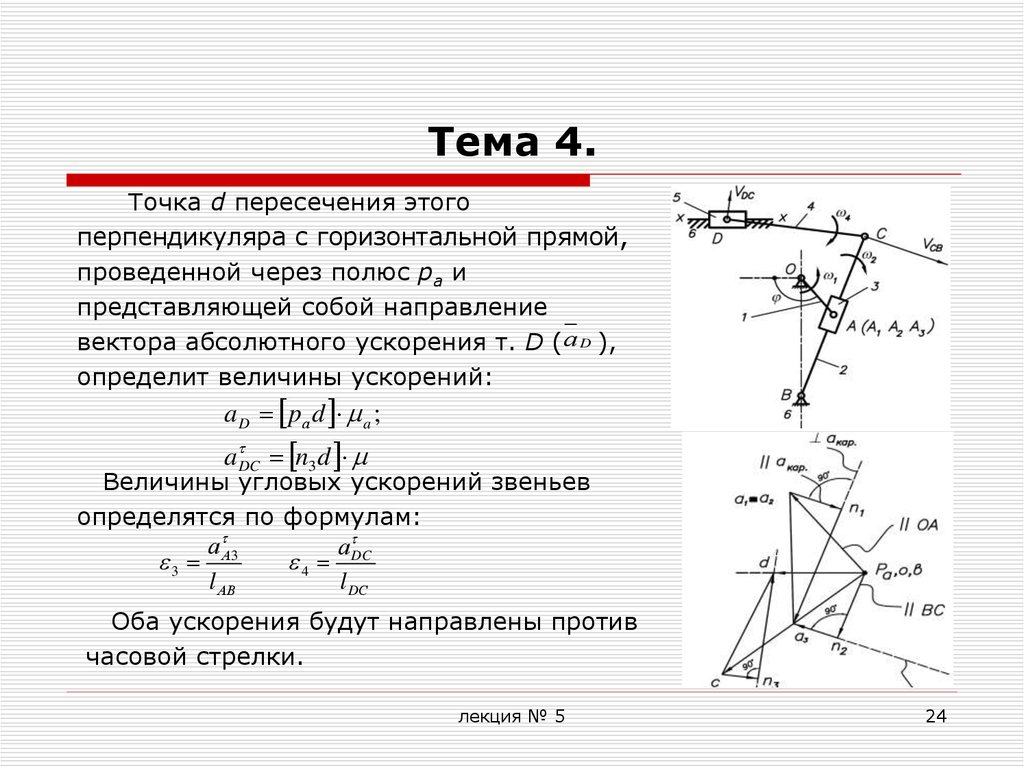
Точка d пересечения этогоперпендикуляра с горизонтальной прямой,
проведенной через полюс ра и
представляющей собой направление
вектора абсолютного ускорения т. D ( а D ),
определит величины ускорений:
a D p а d a ;
a DC n3 d
Величины угловых ускорений звеньев
определятся по формулам:
а А3
а DC
3
4
l АВ
l DС
Оба ускорения будут направлены против
часовой стрелки.
лекция № 5
24
25.
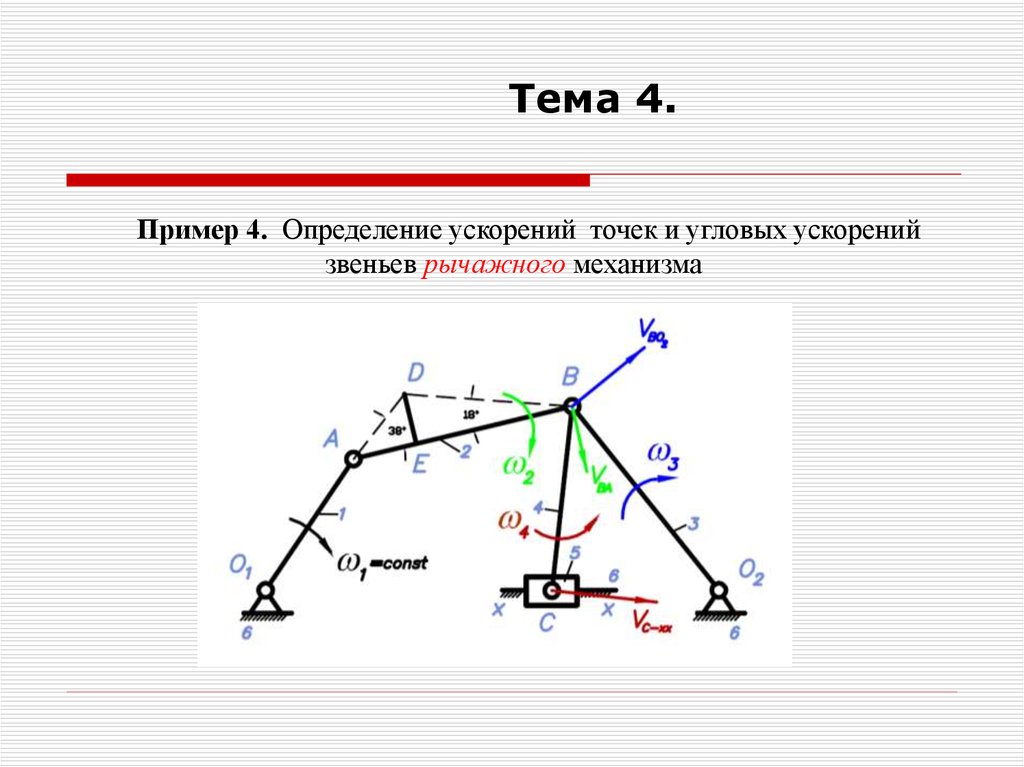
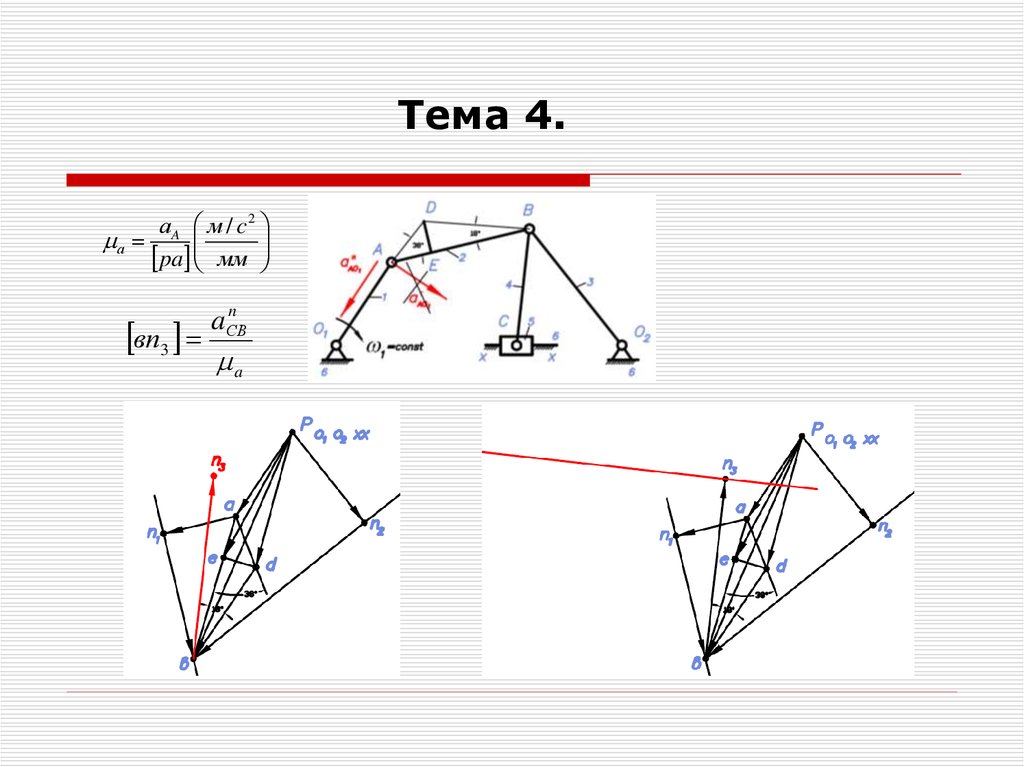
Тема 4.Пример 4. Определение ускорений точек и угловых ускорений
звеньев рычажного механизма
26.
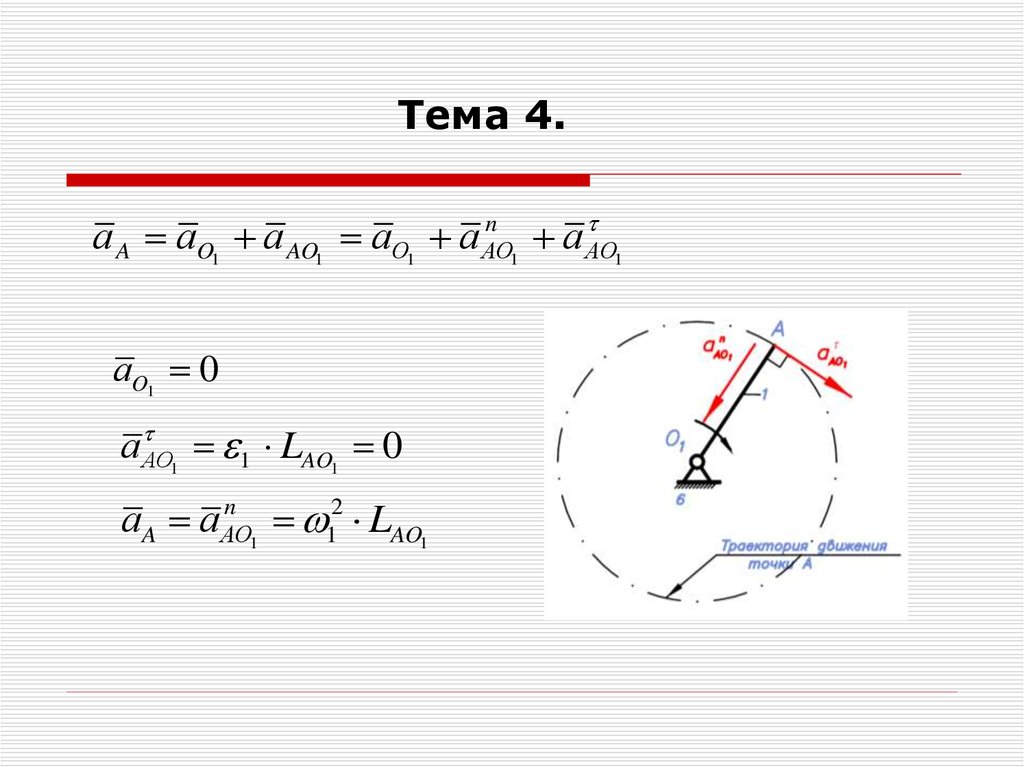
Тема 4.n
а A аO1 а AO1 аО1 а АО
а
АО1
1
аO1 0
аАО
1 LAO1 0
1
n
2
аA аАО
1 LAO1
1
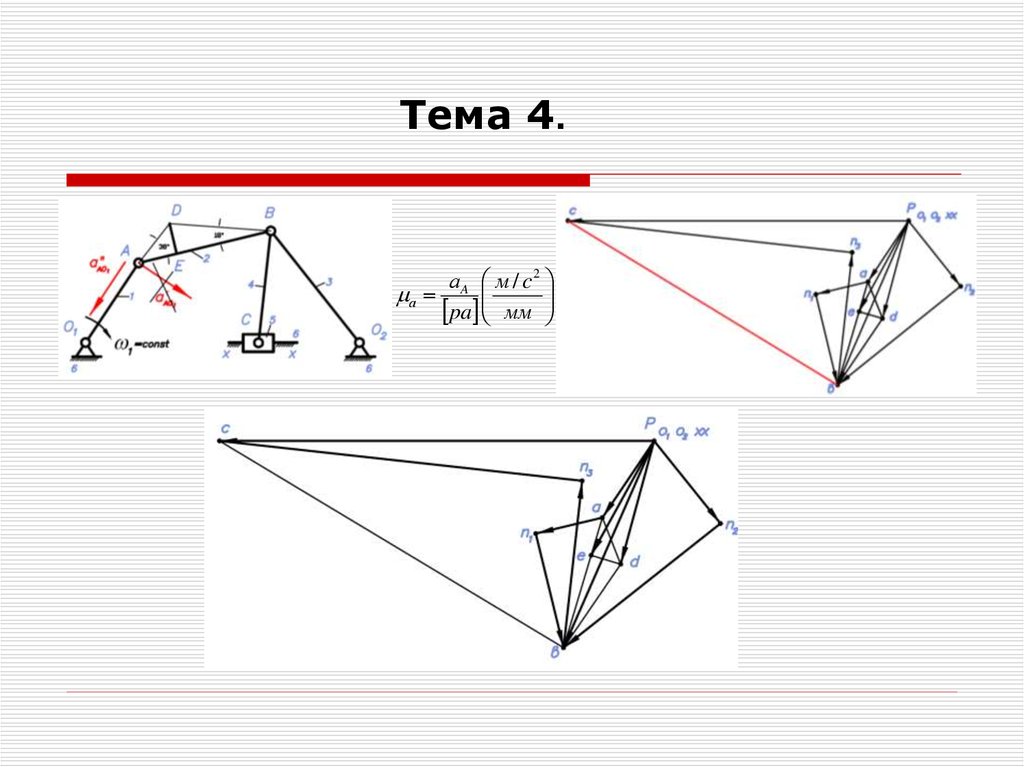
27.
Тема 4.n
aВ a А aBA
a
BA BA
IIВА
n
a
a
a
a
О2
BO2 IIBO
BO2 BO
В
2
2
n
2
a BA
BA
LBA
2
VBA
LBA
n
2
a BO
BO2 L BO2
2
2
V BO
2
LBO2
28.
Тема 4.n
a
a
a
a
B
CB IICВ
CB CB
C
aC axx aC xx( IIXX )
n
2
aCB
CB
LCB
2
VCB
LCB
29.
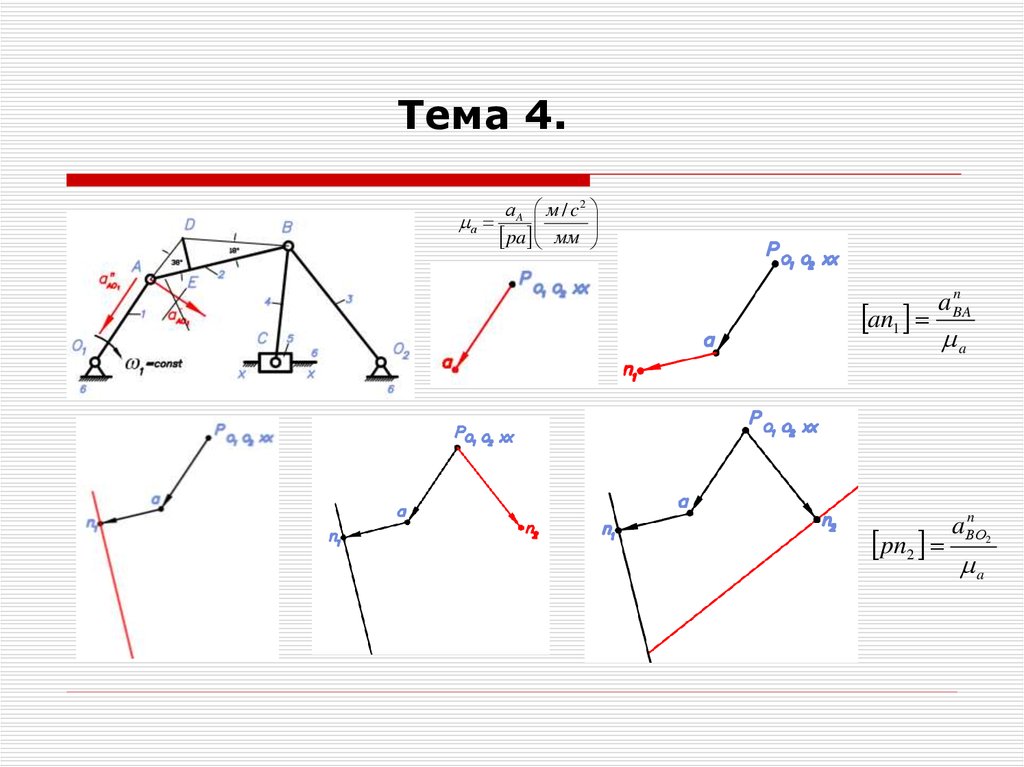
Тема 4.аA м / c2
а
pa мм
an1
n
a BA
a
pn2
n
a BО
2
a
30.
Тема 4.аA м / c2
а
pa мм
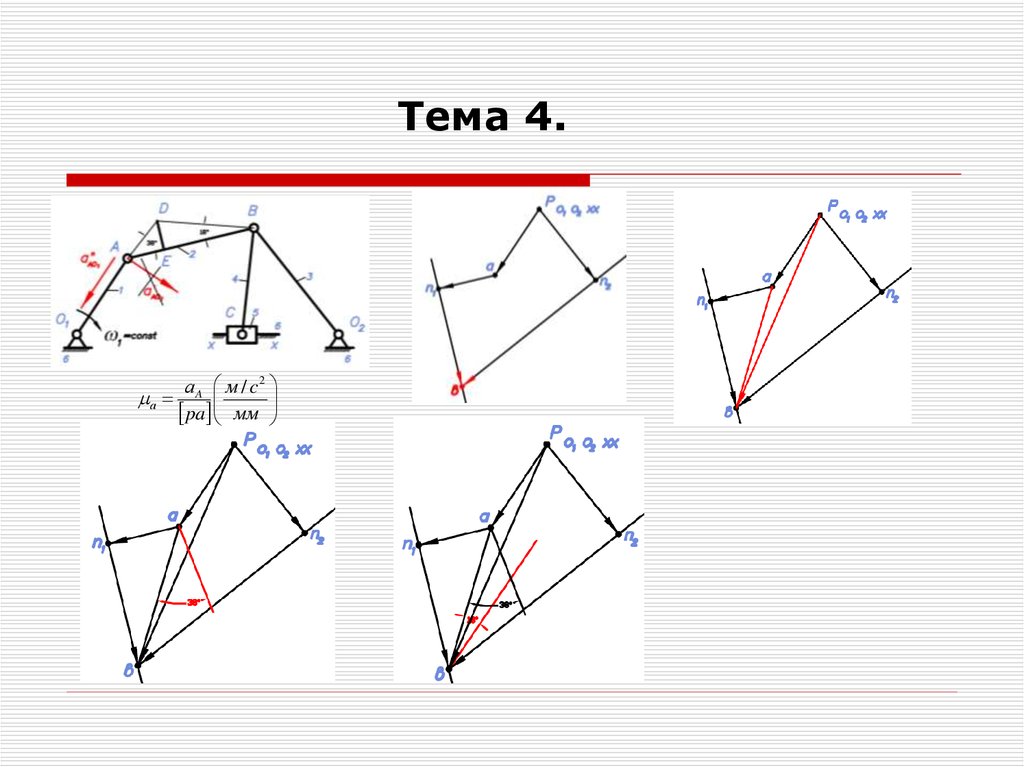
31.
Тема 4аA м / c2
а
pa мм
32.
Тема 4.аA м / c2
а
pa мм
вn3
n
aСB
a
33.
Тема 4.аA м / c2
а
pa мм
34.
Тема 4.аA м / c2
а
pa мм
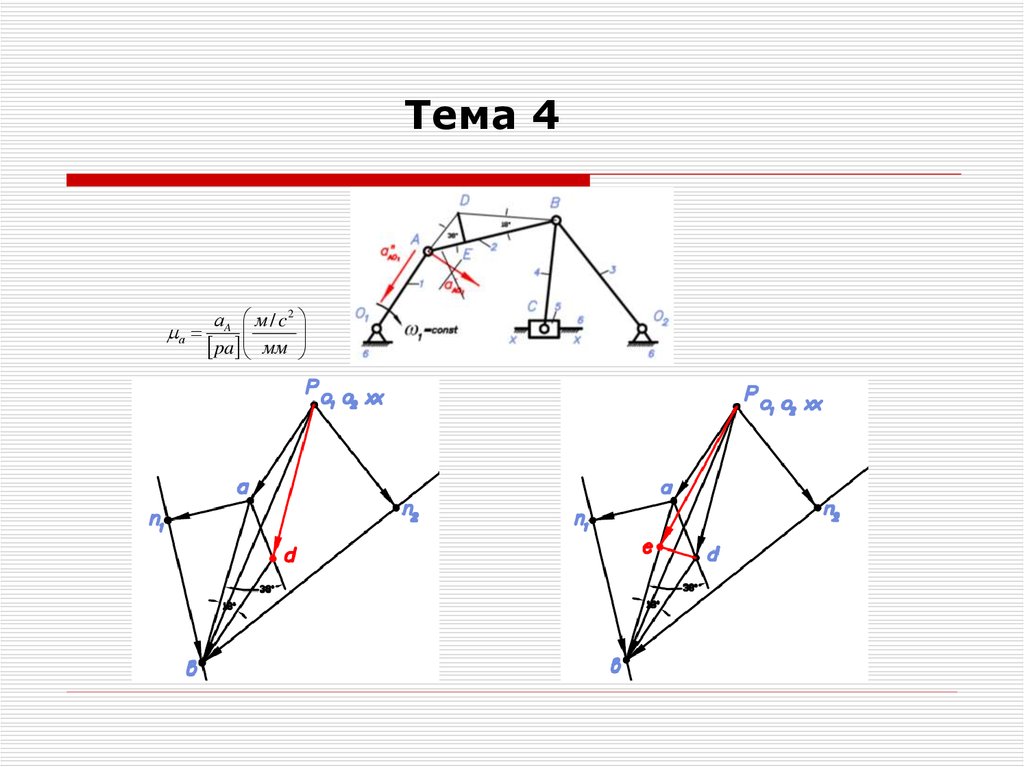
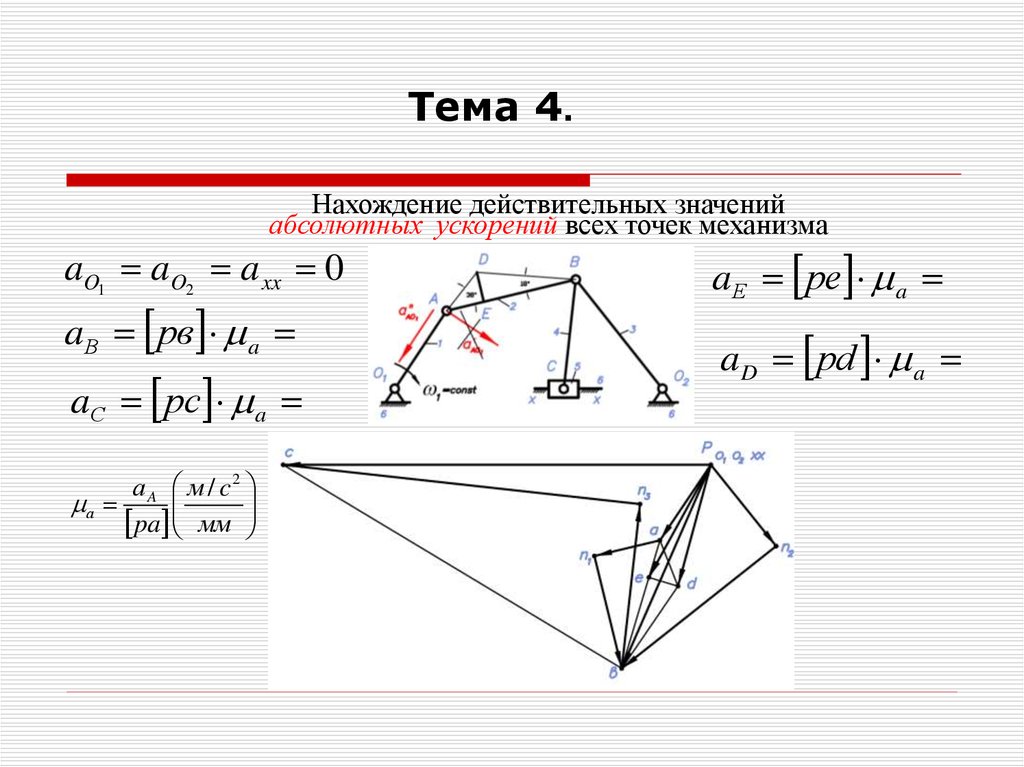
35.
Тема 4.Нахождение действительных значений
абсолютных ускорений всех точек механизма
aO1 aO2 a xx 0
a В рв a
aС рс a
аA м / c2
а
pa мм
a Е ре a
a D рd a
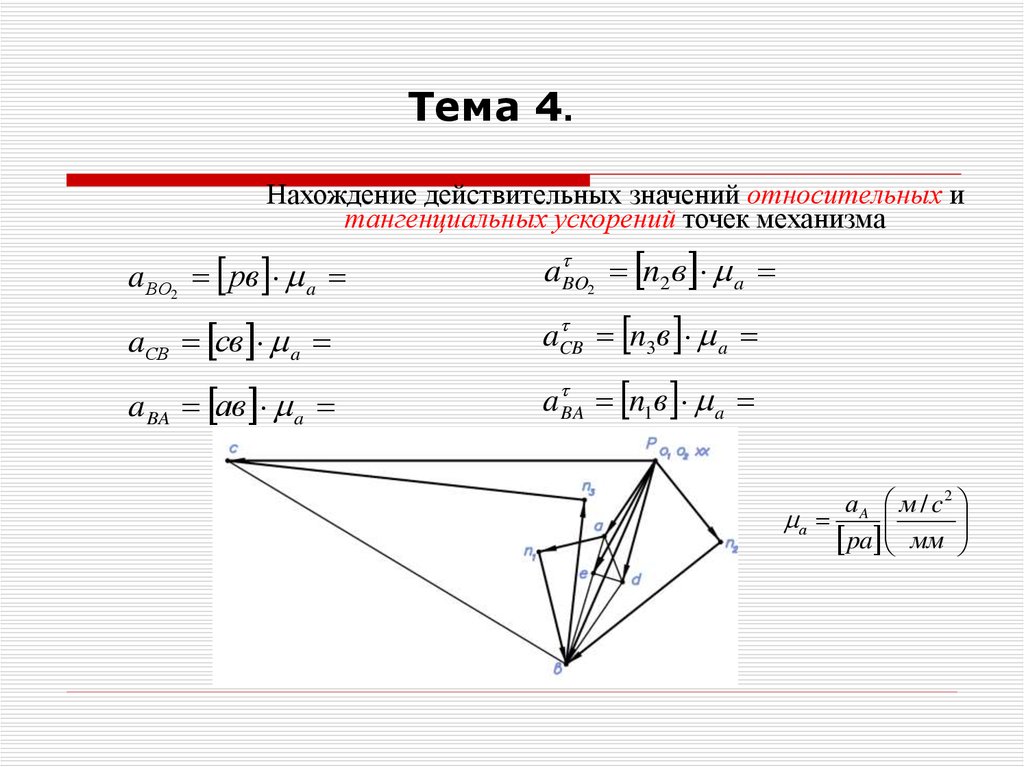
36.
Тема 4.Нахождение действительных значений относительных и
тангенциальных ускорений точек механизма
a ВО2 рв a
a BO2 n2 в a
aСB св a
aCB
n3 в a
a BA aв a
a BA n1в a
аA м / c2
а
pa мм
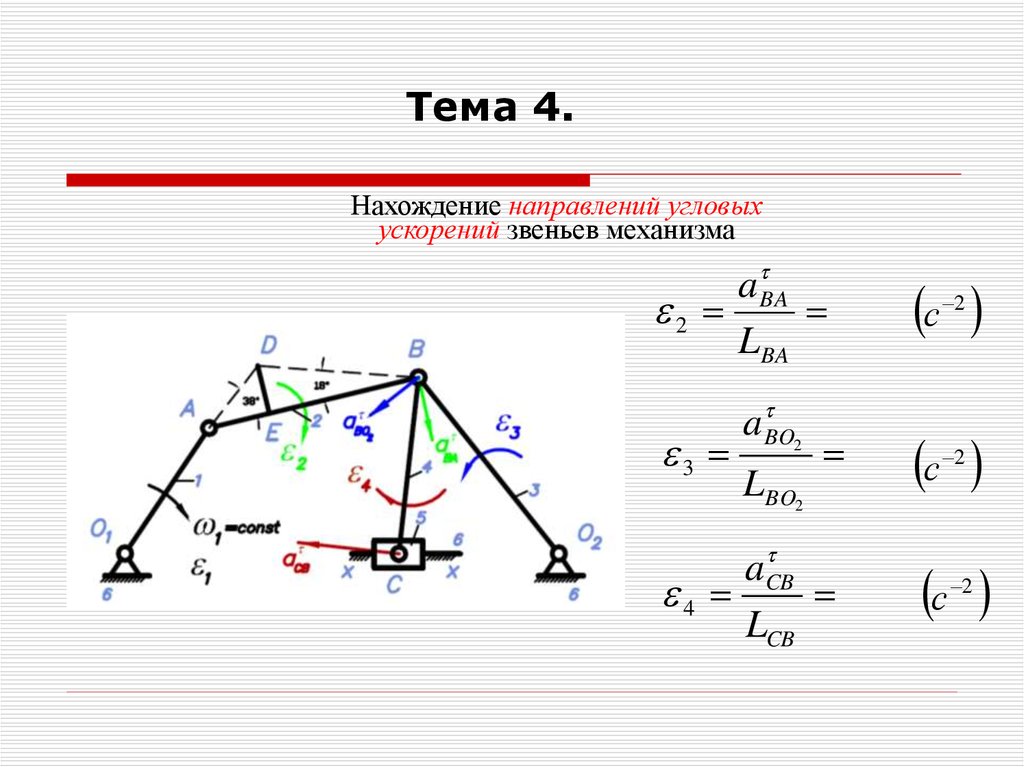
37.
Тема 4.Нахождение направлений угловых
ускорений звеньев механизма
a BA
2
LBA
3
a BO2
LBO2
aCB
4
LCB
с
2
с
2
с
2
























 mechanics
mechanics








