Similar presentations:
Прикладная механика. Схемный анализ и синтез механизмов и машин
1.
МИНОБРНАУКИ РОССИИФедеральное государственное бюджетное
образовательное учреждение высшего образования
«Омский государственный технический университет»
И. Л. Рязанцева
ПРИКЛАДНАЯ МЕХАНИКА
СХЕМНЫЙ АНАЛИЗ И СИНТЕЗ МЕХАНИЗМОВ
И МАШИН
Учебное пособие
Омск
Издательство ОмГТУ
2017
2.
УДК 621.01:531.8(075)ББК 34.412я73
Р99
Рецензенты:
В. Н. Тарасов, профессор кафедры механики ФГБОУ ВО «Сибирский
государственный автомобильно-дорожный университет (СибАДИ)»,
доктор технических наук;
Г. В. Редреев, заведующий кафедрой технического сервиса, механики
и электротехники ФГБОУ ВО «Омский государственный аграрный университет
им. П. А. Столыпина», кандидат технических наук, доцент
Рязанцева, И. Л.
Р99
Прикладная механика. Схемный анализ и синтез механизмов и машин :
учеб. пособие / И. Л. Рязанцева ; Минобрнауки России, ОмГТУ. – Омск :
Изд-во ОмГТУ, 2017. – 184 с. : ил.
ISBN 978-5-8149-2556-5
Подробно описаны методики кинематического анализа и синтеза сложных эпициклических зубчатых механизмов, метрического синтеза по заданным условиям рычажных механизмов, их кинематического, силового
расчетов и уравновешивания.
Учебное пособие содержит комплекты заданий для курсового проектирования по дисциплине «Прикладная механика» (раздел «Схемный анализ
и синтез механизмов») разных уровней сложности и комплект исходных данных для домашнего задания и расчетно-графической работы, предусмотренных учебными планами по специальностям и направлениям подготовки бакалавров кластера технических систем управления и жизнеобеспечения.
Предназначено для студентов специальностей 15.05.01; 20.05.01; 23.05.02;
24.05.01 и направлений подготовки бакалавров 15.03.01; 15.03.02; 15.03.03;
15.03.04; 15.03.05; 16.03.03; 22.03.01; 23.03.03; 24.03.01; 20.05.01; 20.03.01;
21.03.01; 27.03.01; 27.03.04.
УДК 621.01:531.8(075)
ББК 34.412я73
Печатается по решению редакционно-издательского совета
Омского государственного технического университета
© ОмГТУ, 2017
ISBN 978-5-8149-2556-5
2
3.
ОГЛАВЛЕНИЕПРЕДИСЛОВИЕ ........................................................................................................... 4
1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ И СИНТЕЗ ЗУБЧАТЫХ
МЕХАНИЗМОВ ........................................................................................................ 5
1.1. Кинематический анализ зубчатых механизмов ............................................. 5
1.2. Синтез планетарных зубчатых механизмов ................................................. 17
1.3. Методические указания к выполнению домашнего задания ..................... 24
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ И СИНТЕЗ ПЛОСКИХ РЫЧАЖНЫХ
МЕХАНИЗМОВ ......................................................................................................
2.1. Кинематический анализ плоских рычажных механизмов методом
планов ...............................................................................................................
2.2. Синтез плоских рычажных механизмов по заданным условиям ...............
2.2.1. Синтез четырехзвенных рычажных механизмов по двум
положениям их звеньев .......................................................................
2.2.2. Синтез четырехзвенных рычажных механизмов
по коэффициенту изменения средней скорости выходного
звена .......................................................................................................
2.3. Пример синтеза и кинематического анализа рычажного механизма ........
3. КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ МЕХАНИЗМОВ .......................................
3.1. Расчет сил инерции звеньев ...........................................................................
3.2. Кинетостатический расчет структурных групп II класса
2-го порядка методом планов ........................................................................
3.3. Кинетостатический расчет ведущего звена механизма ..............................
3.4. Кинетостатический расчет шестизвенного рычажного механизма
II класса ............................................................................................................
3.5. Расчет уравновешивающей силы методом Н. Е. Жуковского ...................
4. УРАВНОВЕШИВАНИЕ МЕХАНИЗМОВ ...........................................................
4.1. Статическое уравновешивание механизмов ................................................
4.2. Кинетостатический расчет кривошипно-ползунного механизма,
уравновешенного статически .........................................................................
4.3. Методические указания к выполнению курсового проекта .......................
31
32
48
48
53
55
62
62
65
73
75
84
87
88
94
96
5. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КУРСОВОГО ПРОЕКТА ......................... 98
ЗАКЛЮЧЕНИЕ ......................................................................................................... 102
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ..................................................................... 104
ПРИЛОЖЕНИЕ 1 ...................................................................................................... 105
ПРИЛОЖЕНИЕ 2 ...................................................................................................... 137
ПРИЛОЖЕНИЕ 3 ...................................................................................................... 149
ПРИЛОЖЕНИЕ 4 ...................................................................................................... 169
3
4.
ПРЕДИСЛОВИЕЗа время учебы в вузе студенты должны приобрести набор компетенций, установленных государственными образовательными стандартами.
Для достижения этой цели обучающимся нужно получить не только теоретические знания, но и сформировать умения и навыки (владения) использования полученных знаний для решения конкретных практических задач, которые могут возникнуть в их будущей профессиональной деятельности.
В связи с этим в учебных планах многих механико-машиностроительных
и других специальностей и направлений подготовки бакалавров, реализуемых
ОмГТУ, по дисциплине «Прикладная механика» в модуле «Схемный анализ
и синтез механизмов и машин» для разных направлений предусмотрены такие виды самостоятельной работы студентов, как курсовые проекты (КП)
и работы (КР), расчетно-графические работы (РГР), домашние задания (ДЗ).
Сложность состоит в том, что требования к освоению студентами основных образовательных программ из года в год возрастают, а объемы
аудиторной нагрузки, особенно лекционной, уменьшаются, поскольку образовательный процесс ориентирован на самостоятельную работу. Данное
учебное пособие разработано с целью улучшения методического обеспечения самостоятельной работы студентов и наиболее эффективного использования аудиторных занятий.
В отличие от уже имеющейся учебной литературы данное учебное пособие содержит теоретические сведения по таким разделам дисциплины «Прикладная механика», как кинематический анализ и синтез механизмов с высшими и низшими кинематическими парами, кинетостатический анализ
и уравновешивание механизмов, много примеров использования этих сведений для решения конкретных прикладных задач механики. Приведенные
в пособии рекомендации могут быть полезны студентам при выполнении ими
самостоятельной работы, а ссылки на литературные источники позволят более глубоко и детально изучить вопросы, которые у них могут возникнуть.
Кроме того, учебное пособие содержит комплекты заданий на КП (КР),
РГР, ДЗ, предусмотренные учебными планами соответствующих направлений подготовки специалистов и бакалавров по разделу «Схемный анализ и
синтез механизмов и машин» дисциплины «Прикладная механика». Задания
отличаются уровнем сложности, что позволит учесть мотивацию обучающихся при организации образовательного процесса.
4
5.
1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ И СИНТЕЗЗУБЧАТЫХ МЕХАНИЗМОВ
1.1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЗУБЧАТЫХ МЕХАНИЗМОВ
Задача кинематического анализа зубчатого механизма – определение
угловой скорости ω выходного звена механизма при известной скорости
входного движения или передаточного отношения i последнего.
Задачу кинематического анализа зубчатых механизмов можно решать
двумя методами: аналитическим и графическим [1–4].
Аналитическое решение задачи кинематики
Передаточное отношение i1,2 зубчатого механизма – отношение скоростей ω1 ведущего и ω2 ведомого колес:
i1, 2 = ω1 ω2 .
Передаточное отношение i1,2 есть кинематическая характеристика механизма, его можно выразить через геометрические параметры колес,
в частности через радиусы их начальных (rW1 и rW2) окружностей или числа
зубьев (z1 и z2).
i1,2 = w1 w2 = ± rw 2 rw1 = ± z2 z1 .
(1.1)
Знак минус в формуле (1.1) свидетельствует о том, что во внешнем зацеплении при передаче движения направление вращения колес изменяется.
На рис. 1.1 приведены кинематические схемы зубчатых механизмов
с неподвижными осями колес. В передаче с внешним зацеплением (рис. 1.1, а)
колеса вращаются в разных направлениях, что соответствует знаку «–»
в формуле (1.1). В передаче с внутренним зацеплением (рис. 1.1, б) колеса
вращаются в одном направлении. В связи с этим при расчете i1,2 в формуле (1.1) должен быть знак «+».
На рис. 1.1, в и г показаны кинематические схемы рядового и ступенчатого зубчатых механизмов. Передаточное отношение рядового механизма
(рис. 1.1, в,) состоящего из n одинарных колес, вычисляется по формуле
i1, n = ω1 ωn = (− 1) zn z1 ,
k
(1.2)
где 1 и n – номера ведущего и ведомого колес; k – количество пар с внешним зацеплением.
5
6.
аб
в
г
Рис. 1.1
Механизм, кинематическая схема которого приведена на рис. 1.1, в,
имеет две кинематические пары с внешним зацеплением. Его передаточное
отношение:
i1, 3 = ω1 ω3 = z3 z1 .
Колесо 2 является паразитным и на передаточное отношение не влияет.
Формула для расчета передаточного отношения ступенчатого механизма, состоящего из n подвижных звеньев, имеет вид
i1, n = ω1 ωn = (− 1)
k
Пzведомых
,
Пzведущих
(1.3)
где Пzведомых – произведение чисел зубьев ведомых колес; Пzведущих – произведение чисел зубьев ведущих колес.
Передаточное отношение i1,4 ступенчатого механизма (рис. 1.1, г), имеющего одну кинематическую пару с внешним зацеплением:
i1,4 =
ω1
z ⋅z
=− 2 4.
ω4
z1 ⋅ z3
Формула (1.3) универсальна. Ее можно использовать при расчете как
ступенчатого механизма, так и рядового.
Передаточное отношение i1,n многоступенчатого механизма с неподвижными осями колес можно определить как произведение передаточных
отношений отдельных ступеней:
i1, n = i1,2 ⋅ i2,3 ⋅ ... ⋅ in −1, n ,
(1.4)
где i1,2; i2,3; ... in–1,n – передаточные отношения отдельных ступеней, из которых состоит механизм.
6
7.
Воспользуемся формулой (1.4) для определения передаточного отношения i1,4 ступенчатого зубчатого механизма, кинематическая схема которого показана на рис. 1.1, г.i1, 4 = i1, 2 ⋅ i3, 4 = (− z2 z1 ) ⋅ (z4 z3 ) .
Механизмы с подвижными осями колес (рис. 1.2) называют эпициклическими. Их делят на планетарные (рис. 1.2, а) и дифференциальные
(рис. 1.2, б). Подвижность планетарного механизма равна единице, а подвижность дифференциального – двум.
На рис. 1.2, а, в–д показаны наиболее часто встречающиеся схемы механизмов планетарного типа.
а
б
г
в
д
Рис. 1.2
В основе кинематического анализа эпициклических механизмов лежит
метод Виллиса (метод обращения движения), суть которого состоит в том,
что относительное движение звеньев не изменится, если всему механизму,
включая стойку, мысленно сообщается дополнительное вращение вокруг
его геометрической оси с угловой скоростью, равной и противоположно
7
8.
направленной угловой скорости ωH водила. В результате сложения действительного и дополнительного движений водило останавливается и механизмпреобразуется в условный механизм с неподвижными осями колес, угловые
скорости которых отличаются от исходных на величину –ωH. Для преобразованного механизма составляется формула передаточного отношения.
Рассмотрим применение метода Виллиса на конкретном примере.
На рис. 1.2, а представлена кинематическая схема планетарного механизма,
состоящего из подвижного центрального (солнечного) колеса 1, неподвижного центрального колеса 3, называемого опорным, сателлита 2 и водила Н.
Сателлит 2 участвует в двух движениях. Он вращается вокруг собственной
оси O2, перемещающейся по дуге окружности, центр которой совпадает
с осью механизма, а радиус равен длине водила.
Для определения угловой скорости ωH водила воспользуемся методом
Виллиса. Составим таблицу (табл. 1.1), в которой обозначим номера звеньев
механизма, их угловые скорости до и после обращения движения. После
остановки водила механизм преобразуется в рядовой. Его кинематическая
схема приведена на рис. 1.3.
Таблица 1.1
№
звена
1
Угловая скорость звена
рассматриваемого механизма
ω1
Угловая скорость звена
преобразованного механизма
ω1 − ω Н
2
ω2
ω2 − ω Н
3
ω3 = 0
− ωН
Н
ωН
0
Рис. 1.3
8
9.
Для определения передаточного отношения i1(,H3 ) преобразованного механизма воспользуемся формулой (1.2), согласно которойi1(,H3 ) =
z
ω1 − ωН
= (− 1)1 3 .
− ωН
z1
(1.5)
Решаем уравнение относительно ωH и получаем
ωН =
ω1
1 + z3 z1
.
Этот метод расчета является универсальным и используется при расчете как планетарных, так и дифференциальных механизмов.
При определении передаточного отношения i1(,3H) любого планетарного
механизма можно использовать формулу
i1(,3H) = 1 − i1(,Н3 ) ,
(1.6)
где i1(,H3 ) – передаточное отношение преобразованного механизма.
Формула (1.6) плучена следующим образом. В соответствии с (1.5)
i1(,H3 ) =
ω1 − ωН
.
− ωН
Разделим почленно числитель на знаменатель и получим
i1(,H3 ) = −
ω1
+ 1.
ωН
Отношение ω1 ωН есть передаточное отношение i1(,3H) рассматриваемого планетарного механизма. Следовательно,
i1(,H3 ) = −i1(,3H) + 1
или
i1(,H3 ) + i1(,3H) = 1 .
Таким образом, в любом планетарном механизме сумма передаточных
отношений от центрального колеса к водилу и от этого же центрального
колеса к другому центральному колесу при условно неподвижном водиле
равна 1.
При кинематическом расчете сложного эпициклического механизма
аналитическим методом механизм делят на более простые составные части,
для каждой из которых составляется формула передаточного отношения.
9
10.
Искомые величины, в частности угловые скорости звеньев, определяютсяв ходе совместного решения этих уравнений.
Рассмотрим в качестве примера расчет сложного зубчатого эпициклического механизма привода барабана (рис. 1.4, а).
а
б
Рис. 1.4
Предположим, что угловая скорость ω1 колеса 1 составляет 100 1/с. Известны числа зубьев колес: z1 = 10 ; z2 = 20 ; z2 ′ = 11 ; z3 = 41 ; z3′ = 15 ;
z4 = 12 ; z5 = 39 и модуль m = 5 мм. Требуется определить угловую скорость ω5 барабана, жестко связанного с колесом 5.
Для решения задачи рассматриваемый механизм делим на две части.
Часть I механизма состоит из колес 3´, 4 и 5 с неподвижными осями. Передаточное отношение i3,5 этой части механизма определяется по формуле (1.2):
i3,5 =
ω3
z
= (− 1)1 5 .
ω5
z3′
(1.7)
Колесо 4 является паразитным.
Часть II механизма – эпициклическая. Роль водила играет барабан. Для
составления формулы передаточного отношения части II механизма воспользуемся методом Виллиса, в соответствии с которым всему механизму,
включая стойку, мысленно сообщается дополнительное вращение с угловой
скоростью –ω5. В результате водило (барабан) останавливается и механизм
из эпициклического преобразуется в ступенчатый (рис. 1.4, б).
10
11.
Угловые скорости звеньев рассматриваемой части действительногои преобразованного механизмов приведены в табл. 1.2.
Таблица 1.2
№
звена
1
Угловая скорость звена
рассматриваемого механизма
ω1
Угловая скорость звена
преобразованного механизма
ω1 − ω5
2
ω2
ω 2 − ω5
3
ω3
ω 3 − ω5
5
ω5
0
Передаточное отношение преобразованного механизма
i1(,53) =
ω1 − ω5
z ⋅z
= (− 1)1 2 3 .
ω3 − ω5
z1 ⋅ z2′
(1.8)
Уравнения (1.7) и (1.8) содержат два неизвестных, ω3 и ω5. Решаем их
совместно. Из уравнения (1.7) следует, что
39
ω3 = −ω5 ⋅ z5 z3′ = −ω5
= −2,6ω5 .
15
Значение ω3 подставляем в уравнение (1.8) и определяем ω5.
z ⋅z
ω1 − ω5 = (ω5 − ω3 ) 2 3 ;
z1 ⋅ z2 ′
ω1 = ω5 + (ω5 − ω3 )
z 2 ⋅ z3
;
z1 ⋅ z2 ′
ω1 = ω5 + (ω5 + 2,6ω5 ) ⋅
ω5 =
ω1
27,84
=
z 2 ⋅ z3
= 27,84ω5 .
z1 ⋅ z2 ′
100
= 3,59 1/с.
27,84
Графическое решение задачи кинематики
Графическое решение задачи кинематики основано на том, что начальные окружности колес, образующих зацепление, являются центроидами [1, 5],
т. е. окружные скорости зубьев этих колес в точке касания начальных
окружностей, называемой полюсом зацепления, равны по величине и совпадают по направлению. Во вращательной кинематической паре скорость
11
12.
точки, через которую проходит ее ось, является общей для звеньев, образующих эту пару. При вращении звена с угловой скоростью ω вокруг неподвижной оси скорость V любой его точки линейно зависит от ее расстояния r до оси вращения, т. е. V = ω ⋅ r .
Расчет кинематики зубчатого механизма выполняется в три этапа:
– в масштабе µl строится кинематическая схема механизма;
– в масштабе µV строится картина линейных скоростей;
– в масштабе µω строится картина угловых скоростей.
На рис. 1.5, а показана кинематическая схема зубчатого механизма
с внешним зацеплением колес. Кинематическая схема построена в масштабе µl. Радиусы начальных окружностей колес 1 и 2 обозначены как rW1
и rW2 соответственно. Точка А – точка касания начальных окружностей. Колеса вращаются вокруг неподвижных осей O1 и O2 в разных направлениях,
скорости точек зубьев, контактирующих в полюсе зацепления, совпадают
по направлению и равны V А .
б
а
в
Рис. 1.5
На втором этапе расчета на некотором расстоянии от кинематической
схемы (рис. 1.5, б) проводятся оси координат l и V. На размерную ось l про
ецируются точки А, O1 и O2. Скорость V А точки А направлена перпендикулярно O1O2. На картине линейных скоростей она изображается отрез12
13.
ком AA´ произвольной длины. Длина отрезка AA´ подбирается так, чтобымасштабный коэффициент µV оси скоростей (ось V) был целым числом или
простой десятичной дробью. µV = V A AA′ и измеряется в метрах в секунду,
деленных на миллиметр чертежа (м∙с–1/мм). Следует отметить, что
отрезок AA´ можно откладывать как влево, так и вправо от вертикальной
прямой. Направление отрезка AA´ на картине линейных скоростей на результаты расчета не влияет. Если соединить конец вектора скорости точки А
с точками О1 и О2, получим линии распределения скоростей точек колес 1 и 2.
Линии О1А´ и О2А´ распределения скоростей образуют с прямой О1О2 углы
φ1 и φ2 соответственно. Следует отметить, что картина скоростей дает
наглядное представление о характере изменения скоростей при переходе от
одного звена к другому и позволяет определить угловую скорость любого
звена рассматриваемого механизма.
Если перпендикулярно размерной оси l провести некоторую числовую
ось (рис. 1.5, в) и из произвольно выбранной на оси l точки p параллельно
О1А´ и О2А´ лучи, то последние пересекут числовую ось в точках a и b. Отрезки at и tb изображают в некотором масштабе µω угловые скорости колес
ω1 и ω2 соответственно, и отношение длин этих отрезков равно передаточному отношению механизма. Докажем это.
Согласно определению
i1, 2 =
ω1 VA rW 1
.
=
ω2 VA rW 2
(1.9)
Скорость точки А и радиусы rW1, rW2 выразим через длины отрезков картины скоростей:
V A = AA′ ⋅ µV ; rw1 = O1 A ⋅ µl ;
rw 2 = O2 A ⋅ µl .
С учетом этого формула (1.9) принимает вид
i1,2 =
AA′ O1 A tgϕ1
.
=
AA′ O2 A tgϕ 2
Из подобия треугольников О1AА´ и atp; О2AА´ и btp картин линейных
и угловых скоростей следует, что
i1, 2 =
ω1 tgϕ1 ta
=
= .
ω2 tgϕ 2 tb
13
14.
Осюда можно сделать вывод, что отрезки at и bt на картине угловыхскоростей (рис. 1.5, в) изображают угловые скорости колес. Поскольку точки a и b лежат по разные стороны от точки t, колеса 1 и 2 вращаются в разных направлениях.
Таким образом, для определения ω2 при известной величине ω1 надо
под картиной линейных скоростей построить картину угловых скоростей.
Для чего к размерной оси l проводится перпендикуляр и на нем откладывается отрезок at, изображающий ω1. Длина отрезка at выбирается произвольно, но так, чтобы масштабный коэффициент µω был целым числом или простой десятичной дробью. Величина µω вычисляется по формуле
µω = ω1 ta
и измеряется в радианах в секунду, деленных на миллиметр чертежа
(1·c–1/мм). Затем из точки a (рис. 1.5, в) на числовой оси проводится параллельно прямой О1А´ (рис. 1.5, б) луч, пересекающий размерную ось в точке р. Через точку р параллельно прямой О2А´ проводится луч до пересечения с числовой осью в точке b . ω2 = tb ⋅ µω .
Графический метод кинематического анализа прост, нагляден и может
быть использован при кинематическом анализе любого зубчатого механизма II класса. Чтобы метод распространить на механизмы высоких классов,
надо понизить их класс, например приняв ведомое звено в качестве ведущего и считая движение последнего условно известным. Покажем это на конкретном примере. Определим графически угловую скорость ω5 барабана
сложного эпициклического зубчатого механизма, кинематическая схема которого приведена на рис. 1.4.
Для решения задачи графическим методом надо определить радиусы
начальных окружностей всех колес. Рассмотрим случай, когда начальные
окружности зубчатых колес механизма совпадают с делительными, тогда
для расчета радиусов воспользуемся формулой [1–5]
ri = 0,5 ⋅ m ⋅ zi ,
где i = 1; 2; 2′ ; 3 . . . 5.
r1 = 0,5 ⋅ 5 ⋅ 10 = 25 мм;
r2 = 0,5 ⋅ 5 ⋅ 20 = 50 мм;
r2′ = 0,5 ⋅ 5 ⋅ 11 = 27,5 мм;
r3 = 0,5 ⋅ 5 ⋅ 41 = 102,5 мм;
r3′ = 0,5 ⋅ 5 ⋅ 15 = 37,5 мм;
r4 = 0,5 ⋅ 5 ⋅ 12 = 30 мм;
r5 = 0,5 ⋅ 5 ⋅ 39 = 97,5 мм.
14
(1.10)
15.
По этим размерам в масштабе строится кинематическая схема механизма (рис. 1.6, а). Осевые же размеры выбираются произвольно.б
а
в
Рис. 1.6
На рис. 1.6, а оси колес обозначены буквой О с индексом, совпадающим с номером колеса, а зацепления – буквами A, B, C, D. Для построения
картины скоростей справа от кинематической схемы проводятся оси координат l и V. На размерную ось l проецируются все характерные точки, обозначенные на кинематической схеме. Данный механизм при ведущем первом колесе является механизмом III класса. Поскольку область применения
графического метода ограниченна, надо понизить класс рассматриваемого
зубчатого механизма. Для этого примем в качестве ведущего звено 5. В свя
зи с этим при построении картины скоростей (рис. 1.6, б) скорость VD точки D колеса 5, жестко связанного с барабаном, будем считать известной
и изобразим отрезком произвольной длины DD´. Отрезок DD´ направлен
перпендикулярно к размерной оси l. Поскольку барабан вращается вокруг
неподвижной оси О5, точка О5 соединяется с точкой D´. Прямая D´O5 определяет закон распределения скоростей точек барабана, что позволяет найти
скорость любой его точки, в частности точки О2. Для этого из точки О2 про15
16.
водится перпендикуляр к размерной оси l до пересечения с прямой D´O5в точке О2′ . Точка D является общей для колес 5 и 4. Колесо 4 вращается вокруг неподвижной оси О4, что позволяет построить его линию распределения скоростей и определить скорость точки С. Для этого соединяем прямой
точки D´ и О4 и из точки С проводим перпендикуляр к оси l до пересечения
с прямой D´O4 в точке C´. Отрезок CC´ изображает в масштабе µV скоC
рость VC точки С колеса 3´, вращающегося вокруг неподвижной оси О3.
Точки C´ и О3 соединяются прямой линией. Для определения скорости VB
точки В колеса 3 через точку В проводится перпендикуляр к размерной оси l
до пересечения с прямой С´О3 в точке В´. Точка В является общей для колес 3 и 2. Поскольку скорости точек В и О2 известны, можно построить линию распределения скоростей точек блока сателлитов. Для этого точки В´
и О2′ картины скоростей соединяются прямой. Для определения скорости VA
из точки А восстанавливается перпендикуляр к оси l до пересечения с пря
мой В´О´2 в точке А´. Отрезок АА´ изображает в масштабе µV скорость V А
точки А блока сателлитов и колеса 1. Прямая, соединяющая точки А´ и О1,
определяет закон распределения скоростей точек первого колеса.
Масштабный коэффициент µV картины скоростей вычисляется по формуле
µV =
VA
.
AA′
(1.11)
Скорость точки А вычисляется по формуле
V A = ω1 ⋅ r1 = 100 ⋅ 0,025 = 2,5 м/с.
(1.12)
Длина отрезка АА´ измеряется в миллиметрах. В рассматриваемом примере она получилась равной 300 мм.
µV =
2,5
= 0,00833 (м/с)/мм.
300
Для определения ω5 строится картина (план) угловых скоростей
(рис. 1.6, в). Для ее построения под картиной скоростей на произвольном
расстоянии проводится числовая ось. Ее точка пересечения с размерной
осью обозначена буквой t. От точки t на числовой оси откладывается отре16
17.
зок tа, изображающий в масштабе µω угловую скорость ω1 колеса 1. Величина масштабного коэффициентв µω вычисляется по формулеµω =
ω1
ta
=
100
= 0,5 (1·с–1)/мм.
200
Из точки а на числовой оси параллельно О1А´ проводится луч до пересечения с размерной осью в точке p. Из точки p проводится луч параллельно D´O5 до пересечения с числовой осью в точке d. Отрезок td в масштабе µω изображает ω5.
ω5 = td ⋅ µω .
При td = 7 мм ω5 = 7 ⋅ 0,5 = 3,5 1/с.
Графический метод позволяет легко определить угловую скорость любого колеса рассматриваемого механизма. Предположим, что требуется
определить угловую скорость колеса 4. Для этого из точки p картины угловых скоростей надо провести прямую, параллельную линии распределения
скоростей колеса 4 (на картине скоростей это прямая C´D´), и найти точку
ее пересечения (пусть это будет точка c) с числовой осью. Отрезок tc изображает угловую скорость ω4 колеса 4.
ω4 = tc ⋅ µω .
1.2. СИНТЕЗ ПЛАНЕТАРНЫХ ЗУБЧАТЫХ МЕХАНИЗМОВ
При синтезе планетарных механизмов необходимо избрать принципиальную кинематическую схему механизма и определить числа зубьев колес.
Главным условием синтеза является обеспечение заданного передаточного отношения. Дополнительные условия синтеза – условия соосности; соседства; сборки.
Наибольшее распространение получили планетарные механизмы, кинематические схемы которых показаны на рис. 1.2, а, в–д. Передаточное отношение i1(,3H) этих механизмов вычисляется по формуле (1.6).
Возможности планетарного механизма зависят от знака передаточного
отношения i1(,H3 ) преобразованного механизма. По этому критерию планетар17
18.
ные механизмы делят на две группы: с положительным (рис. 1.2, в, д) и отрицательным (рис. 1.2, а, г) передаточным отношением i1(,H3 ) .В механизмах, относящихся к первой группе (рис. 1.2, в, д), ведущим,
как правило, является водило. Подбором чисел зубьев колес можно получить большое передаточное отношение iH(3,)1 . Его величина тем больше, чем
меньше i1(,H3 ) отличается от 1. Однако с увеличением iH(3,)1 коэффициент полезного действия (КПД) механизма уменьшается. В связи с этим механизмы
первой группы используют для передачи малых силовых потоков. Для
обеспечения приемлемого КПД передаточное отношение iH(3,)1 ограничивают
в диапазоне 30–100.
Механизмы, относящиеся ко второй группе (рис. 1.2, а, г), широко при(3 )
меняют в редукторах средней и большой мощности. Обычно i1,H = 3 − 15,
КПД = 0,96–0,98.
Использование в планетарных механизмах нескольких сателлитов позволяет разделить силовой поток и, как следствие, уменьшить его габаритные размеры и вес, уравновесить механизм, разгрузить опоры центрального
колеса и водила.
Условие соосности обеспечивает зацепление сателлитов с центральными колесами, при этом центральные зубчатые колеса и водило должны
иметь общую геометрическую ось вращения, т. е. быть соосными.
Для планетарных механизмов на рис. 1.2 условия соосности можно записать следующим образом:
или z1 + z2 = z3 − z2
(рис. 1.2, а);
r1 + r2 = r3 − r2
r1 + r2 = r3 + r2 ′
или z1 + z2 = z3 + z2 ′
(рис. 1.2, в);
r1 − r2 = r3 + r2 ′
или z1 − z2 = z3 + z2 ′
(рис. 1.2, г);
r1 − r2 = r3 − r2 ′
или z1 − z2 = z3 − z2 ′
(рис. 1.2, д).
Условие соседства – условие размещения соседних сателлитов при
многосателлитной конструкции. Числа зубьев колес надо подобрать так,
чтобы расстояние ac между осями соседних сателлитов 2 (рис. 1.7) было
больше диаметра da2 окружности вершин сателлитов. Если в механизме
используется сдвоенный сателлит, величина ac должна превышать диаметр d amax
2 окружности вершин большего из колес в блоке сателлитов.
18
19.
Рис. 1.7На рис. 1.7 показаны начальные окружности (совпадающие с делительными) центральных колес 1 и 3, начальные окружности и окружности вершин двух соседних сателлитов.
Расстояние C1C2 между центрами соседних сателлитов можно выразить
через межосевое расстояние C1О центрального колеса 1 и сателлита 2:
C1C2 = 2 ⋅ (r1 + r2 ) ⋅ sin θ 2 .
При равномерном расположении сателлитов θ =
2π
. В этой формуле K –
K
количество сателлитов, закрепленных на водиле.
Предположим, что начальные окружности являются делительными. Это
возможно, например, при нарезании колес без смещения. Тогда
С1С2 = m(z1 + z2 ) ⋅ sin θ 2 = m(z1 + z2 ) ⋅ sin π K .
Радиус окружности вершин сателлита
(
)
ra 2 = 0,5 ⋅ m z2 + 2ha* .
При ha* = 1 условие соседства выполняется, если
(z1 + z2 ) ⋅ sin π
19
K > ( z2 + 2 ) .
20.
После преобразования формула, описывающая условие соседства, принимает следующий вид:sin π K >
z2 + 2
.
z1 ± z2
(1.13)
Если в механизме используется сдвоенный сателлит, как на рис. 1.2, в–г,
то в числителе формулы (1.13) z2 принимается равным количеству зубьев z2max большего из колес в блоке сателлитов. При внешнем зацеплении колес 1 и 2 (рис. 1.2, а, в) в знаменателе принимают знак плюс, а при внутреннем зацеплении (рис. 1.2, г, д) – знак минус.
Если количество сателлитов кратно 2 или 3, то водило с равномерно
установленными на нем сателлитами будет уравновешено.
Условие сборки – условие собираемости механизма, если количество
сателлитов более одного. Согласно этому условию все сателлиты должны
одновременно зацепляться с центральными колесами.
Механизм, имеющий один сателлит, собирается легко. Проблема
сборки возникает только при многосателлитной конструкции механизма
(при K > 1 ).
Обычно сателлиты располагаются равномерно (ϴ = const). В этом случае первый установленный сателлит при сборке механизма полностью
определяет взаимное расположение центральных колес. Остальные же сателлиты можно ввести в зацепление только при определенном соотношении
между числами зубьев колес [2, 4].
Условимся устанавливать сателлит на водило в таком положении механизма, когда ось сателлита находится в вертикальной плоскости, проходящей через оси центральных колес и водила (рис. 1.8, а). При этом ось симметрии впадины опорного колеса 3 совпадает с вертикалью I-I и все сателлиты ориентированы при сборке одинаково.
Для установки сателлита необходимо, чтобы его зубья, расположенные
диаметрально, вошли во впадины центральных колес (рис. 1.8, б). Это имеет
место в тех случаях, когда у сателлита четное количество зубьев. При нечетном z2 во время сборки зуб сателлита входит во впадину опорного колеса
(колесо 3), а в диаметрально расположенную впадину колеса 2 входит зуб
центрального колеса 1 (рис. 1.8, в).
20
21.
аб
в
Рис. 1.8
При сборке многосателлитного зубчатого механизма первый сателлит
легко устанавливается на свое место. При этом центральное колесо 1, связанное с сателлитом и водилом, занимает вполне определенное положение.
Для установки следующего сателлита водило надо повернуть на угол
ϕ H = 2 ⋅ π K так, чтобы ось сателлита оказалась в вертикальной плоскости. Но при этом центральное колесо 1 тоже поворачивается на некоторый
угол φ1, связанный с φH следующей зависимостью:
ϕ1 = ϕ H ⋅ i1(,3H) .
(1.14)
Если в формулу (1.14) подставить значение ϕ H , то она примет вид
ϕ1 =
2 ⋅ π (3 )
⋅ i1, H .
K
(1.15)
Сателлит встанет на свое место, если угол φ1 будет равен некоторому
количеству целых угловых шагов. Угловой шаг колеса 1 обозначим как τ1.
Его величина вычисляется по формуле
τ 1 = 2 ⋅ π z1 .
21
22.
С учетом этогоϕ1 = τ 1 ⋅ Ц =
2 ⋅π
Ц,
z1
(1.16)
где Ц – целое количество шагов.
Поскольку в уравнениях (1.15) и (1.16) левые части равны, правые
можно приравнять.
2 ⋅ π (3 ) 2 ⋅ π
⋅ i1, H =
⋅Ц
K
z1
или
i1(,3H)
⋅ z1 = Ц .
K
(1.17)
Уравнение (1.17) описывает условие сборки, которое можно сформулировать следующим образом.
Выполнение условия сборки означает, что если первый сателлит установить на водило в выбранном вертикальном положении, то все остальные
сателлиты многосателлитной конструкции войдут в зацепление с центральными колесами (центральным колесом) в том же положении при повороте
водила на угол φН = 2·π/K. Следует отметить, что уравнение (1.17) описывает наиболее простой случай, когда все сателлиты устанавливаются за один
оборот водила.
При синтезе эпициклических механизмов кроме условий соосности, соседства, сборки должны выполняться и другие условия, обеспечивающие
качество зацепления. К ним относятся условия отсутствия подрезания, заострения зубьев колес и др. [1–5].
Рассмотрим на конкретном примере, как подобрать числа зубьев колес планетарного механизма, кинематическая схема которого приведена
на рис. 1.2, а, при следующих условиях: i1(,3H) = 4 ; K = 4 .
Главное условие синтеза – обеспечение заданного передаточного отно-
шения i1(,3H) . В соответствии с формулой (1.6)
i1(,3H) = 1 − i1(,H3 ) = 1 − (− z3 z1 ) = 1 + z3 z1 .
Отсюда следует, что
(
)
z3 = z1 ⋅ i1(,3H) − 1 .
22
(1.18)
23.
Если в уравнение подставить значение i1(,3H) , тоz3 = 3z1 .
(1.19)
Условие соосности для данного механизма описывается уравнением
z3 = z1 + 2 ⋅ z2 .
Это условие позволяет выразить z2 через z1 . Учитывая (1.19), получим
z2 = z1 .
(1.20)
i1(,3H)
По условию сборки
⋅ z1 должно быть целым числом. При заданных
K
значениях i1(,3H) и K условие (1.17) преобразуется к виду z1 = Ц .
Поскольку количество зубьев колеса всегда целое число, то условие
сборки выполняется при любом значении z1.
Учитывая условие отсутствия подрезания ножки зуба колеса, примем z1
равным 17. Тогда в соответствии с (1.19) и (1.20)
z3 = 51 .
z2 = 17 ,
Подбирая числа зубьев колес, необходимо учитывать следующее обстоятельство. При нарезании колеса с внутренними зубьями (таковым является колесо 3) может возникнуть радиальная интерференция, проявляющаяся в частичном срезании зубьев колеса зубьями долбяка. В рабочем зацеплении это может привести к заклиниванию передачи. Чтобы исключить последнее, целесообразно воспользоваться рекомендациями, приведенными
в табл. 1.3 [5].
Таблица 1.3
z1
20
21
22
23
24
25
26
z2
>60
>50
>44
>41
>38
>36
>35
В табл. 1.3 приняты следующие обозначения: z1 и z2 – количество зубьев колес с внешними и внутренними зубьями соответственно.
Учитывая эти рекомендации, назначим
z1 = 21,
z2 = 21,
z3 = 63.
23
24.
Проверим выполнение условия соседства. В соответствии с (1.13)180 z2 + 2
.
sin
>
K
z1 + z2
180 21 + 2
sin
>
4
21 + 21
или
sin 45 > 0,548 .
Условие соседства выполняется, поскольку sin 45 = 0,7071 .
1.3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
ДОМАШНЕГО ЗАДАНИЯ
Порядок выполнения домашнего задания или расчетно-графической работы:
1. По кинематической схеме изучается строение механизма.
2. Механизм условно делится на более простые составные части, для
каждой из которых записывается условие соосности и определяются недостающие числа зубьев колес.
3. Вычисляются радиусы делительных окружностей всех колес, выбирается масштабный коэффициент µl и на листе формата А3 строится в масштабе кинематическая схема механизма с соблюдением стандартных изображений звеньев и кинематических пар.
4. В соответствии с исходными данными вычисляются окружные скорости (скорость) точек звеньев (звена), угловые скорости (или частота вращения) которых заданы.
5. Выбираются масштабные коэффициенты µV и µω (или µn), строятся
картины линейных и угловых скоростей (или чисел оборотов), и определяется угловая скорость (или частота вращения) выходного звена механизма.
6. Выполняется аналитический расчет кинематики механизма. Для
каждой его составной части записывается формула передаточного отношения. Полученные уравнения решаются совместно.
7. На заключительном этапе выполнения задания производится сравнение результатов расчета, полученных разными методами. Расхождение
не должно превышать ±10.
24
25.
Выполним в качестве примера кинематический расчет сложного эпициклического механизма, кинематическая схема которого представленана рис. 1.9.
Рис. 1.9
Механизм состоит из центрального колеса 1, частота вращения которого n1 = 2000 об/мин; блока сателлитов 2 (2ꞌ); опорного колеса 3 с внутренними зубьями; водила Н, жестко связанного с колесом 4; блока колес 5 (5ꞌ),
вращающегося вокруг неподвижной оси О5; и одинарных колес 6 и 7, оси
которых неподвижны. Требуется определить аналитически и графически
частоту вращения n7 колеса 7 и количество K сателлитов. Известны модуль
(m = 10 мм) и числа зубьев колес: z1 = 20; z2 = 40; z3 = 77; z4 = 30; z5 = 49;
z5ꞌ = z6 = 15. Числа зубьев колес 2ꞌ и 7 не заданы, их надо определить.
Рассматриваемый механизм можно условно разделить на две составные
части – эпициклическую (часть I), состоящую из звеньев 1, 2 (2ꞌ), 3, Н,
и ступенчатую (часть II), в состав которой входят колесо 4, блок колес 5 (5ꞌ),
колеса 6 и 7.
Для определения z2´ и z7 воспользуемся условием соосности.
Колеса 1 и 3 будут соосны, если
z1 + z2 = z3 − z2 ′ .
Из этого уравнения следует, что z2 ′ = z3 − z1 − z2 = 77 − 20 − 40 = 17 .
25
26.
Для определения z7 воспользуемся условием соосности колес 4 и 7:z 4 + z5 = z5 ′ + 2 z 6 + z 7 .
Осюда следует, что z7 = z4 + z5 − z5′ − 2 z6 = 30 + 49 − 15 − 2 ⋅ 15 = 34 .
Для графического решения задачи кинематики надо в масштабе изобразить кинематическую схему механизма. В связи с этим вычислим радиусы
делительных окружностей ri всех колес механизма по формуле [1–5]
ri = 0,5 ⋅ m ⋅ zi ,
где i = 1; 2; 2′ ; 3; . . . 7.
Результаты расчета приведены в табл. 1.4.
Таблица 1.4
r1
r2
r2′
r3
r4
r5
r5′
r6
r7
245
75
75
170
мм
100
200
85
385
150
Для построения кинематической схемы механизма надо выбрать масштабный коэффициент µl. В соответствии с [1–4]
µl = ri ri ,
(1.21)
где ri – длина отрезка, изображающего ri на кинематической схеме.
Длина отрезка ri подбирается так, чтобы µl был целым числом или простой десятичной дробью. Округлять µl нельзя, поскольку это снижает точность расчета. При определении µl в рассматриваемом примере будем ориентироваться на размер r3, равный 385 мм. Если принять длину отрезка,
изображающего r3 на кинематической схеме, равной 128,33 мм, то
µl = 385 128,33 = 3 мм/мм.
По формуле (1.21) вычисляются длины отрезков, изображающих соответствующие размеры, и строится кинематическая схема.
На рис. 1.10, а изображена кинематическая схема рассматриваемого
механизма в масштабе. На этой схеме оси колес обозначены буквой О
с индексами, соответствующими их номеру, а зацепления – буквами A, B,
C, D, E.
26
27.
Для построения картины скоростей справа от кинематической схемы(рис. 1.10, б) проведем размерную ось l и спроецируем на нее все характерные точки схемы.
В соответствии с методикой графического решения для определения n7
надо построить картины линейных скоростей и чисел оборотов.
Вычисляем скорость VA точки А колеса 1 [1–4]:
V A = ω1 ⋅ r1 ,
где ω1 =
π ⋅ n1
π ⋅ 2000
= 209,3 1/с.
30
30
V A = 209,3 ⋅ 0,1 = 20,93 м/с.
=
На картине скоростей скорость точки А изображается отрезком AA´,
перпендикулярным оси l. Длина отрезка AA´ выбирается произвольно так,
чтобы масштабный коэффициент µV был целым числом или простой десям/с
тичной дробью. Например, при µV = 0,08
длина отрезка AA´ составляет
мм
261,63 мм.
Колесо 1 вращается вокруг неподвижной оси O1. Соединяем точки A´
и O1 прямой. Эта прямая определяет закон распределения линейных скоростей точек колеса 1.
Рис. 1.10
27
28.
Блок сателлитов 2 обкатывается по опорному колесу 3. Скорость VB еготочки В равна нулю. Для определения закона распределения скоротей блока
сателлитов 2 соединим точки A´ и В прямой линией и определим скорость
точки O2. Для этого через точку O2 проведем перпендикуляр к размерной
оси l до пересечения с прямой BA´ в точке O´2. Отрезок O2O´2 изображает
в масштабе µV скорость точки O2 водила Н, вращающегося вокруг неподвижной оси O4 и жестко связанного с колесом 4. Соединим прямой
точки O´2 и O4 и определим скорость VС точки С колеса 4. VС изображается
на картине скоростей отрезком CC´.
Для определения закона распределения скоростей колеса 5 соединяем
прямой точки C´ и O5. Точка D принадлежит колесу 5. Для определения ее
скорости VD проведем через точку D перпендикуляр к размерной оси l
до пересечения с прямой C´O5 в точке D´. Точка D является общей для колес 5 и 6. Колесо 6 вращается вокруг неподвижной оси O6. Если соединить
прямой точки D´ и O6, получим закон распределения скоростей точек колеса 6,
что позволит определить скорость точки E колес 6 и 7. Из точки E на картине скоростей восстановим перпендикуляр к оси l до пересечения с прямой
D´O6 в точке E´. Отрезок EE´ изображает в масштабе µV скорость точки E.
Если соединить прямой точки E´ и O7, получим закон распределения скоростей точек колеса 7.
Для определения n7 построим картину чисел оборотов. Для этого под
картиной линейных скоростей на произвольном расстоянии проведем числовую ось (см. рис. 1.10, б). Точку пересечения размерной и числовой осей
обозначим буквой t. От точки t на числовой оси откладываем отрезок ta,
длину которого выбираем произвольно, но так, чтобы масштабный коэффициент µn был целым числом или простой десятичной дробью. Пусть ta будет
равен 200 мм. Тогда
µn =
2000
= 10 (об/мин)/мм.
200
Из точки a на числовой оси проводим луч параллельно O1A´ до пересечения с вертикальной прямой в точке p. Из точки p проводим луч параллельно E´O7 до пересечения с числовой осью в точке e. Отрезок te в масштабе µn изображает n7.
n7 = te ⋅ µ n .
28
29.
Длина отрезка te получилась равной 5,5 мм, следовательноn7 = 5,5 ⋅ 10 = 55 об/мин.
При аналитическом определении частоты вращения n7 колеса 7 для
каждой из условных составных частей механизма составим формулу передаточного отношения.
Часть I – эпициклическая. Чтобы составить формулу передаточного отношения для этой части механизма, воспользумся методом Виллиса, в соответствии с которым всем звеньям мысленно сообщается дополнительное
вращение вокруг геометрической оси механизма с частотой –n4. В результате сложения действительного и дополнительного движений водило остановится и механизм преобразуется в ступенчатый, схема которого приведена
на рис. 1.11.
Рис. 1.11
В табл. 1.5 указана частота вращения звеньев части I механизма
до и после преобразования движения.
Таблица 1.5
№ звена
nдействит.
nпреобразов.
1
n1
n1 − n4
2
n2
n2 − n4
3
n3 = 0
− n4
Н(4)
n4
0
29
30.
Обозначим передаточное отношение преобразованного механизмакак i1(,43) .
i1(,43) =
n1 − n4
z ⋅z
= (− 1)1 2 3 .
z1 ⋅ z2′
− n4
(1.22)
Часть II состоит из колес с неподвижными осями. Ее передаточное отношение
i4,7 =
n4
z ⋅z ⋅z
= (− 1)3 5 6 7 .
n7
z4 ⋅ z5′ ⋅ z6
(1.23)
Используя уравнение (1.23), выразим n4 через n7.
n4 = −n7
z5 ⋅ z7
49 ⋅ 34
= −n7
= −3,7n7 .
z4 ⋅ z5′
30 ⋅ 15
Подставляем значение n4 в уравнение (1.22) и определяем n7.
z ⋅z
40 ⋅ 77
n1 = n4 1 + 2 3 = −3,7n7 1 +
= −37,22n7 ;
z1 ⋅ z2′
20 ⋅ 17
n7 = −
n1
2000
=−
− 53,73 об/мин.
37,22
37,22
Расхождение результатов, полученных графически и аналитически, составляет
n7анал − n7граф
53,73 − 55
∆n7 =
⋅100 % =
⋅100 % = 2,4%.
анал
57,73
n7
Количество сателлитов вычисляется по формуле (1.13). Блок сателлитов состоит из двух колес 2 и 2´. Большим из них является колесо 2, имеющее 40 зубьев. В связи с этим
180
40 + 2
sin
>
,
20 + 40
K
или
180
sin
> 0,7.
K
arcsin 0,7 = 45,5 .
180
, или K < 3,96 .
Следовательно, K <
45,5
Принимаем K = 3 .
30
31.
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ И СИНТЕЗ ПЛОСКИХРЫЧАЖНЫХ МЕХАНИЗМОВ
Целью кинематического анализа является изучение движения звеньев
механизма с учетом кинематических размеров звеньев и характера их связей.
В ходе кинематического исследования определяются кинематические
характеристики (перемещения, скорости, ускорения) звеньев и отдельных
их точек, например центров масс.
Данные кинематического анализа дают представление о движении звеньев конкретного механизма и, что очень важно, используются при его кинетостатическом и динамическом расчетах.
Задачи кинематического анализа можно решать разными методами [1–4]:
1) графическим, или методом кинематических диаграмм;
2) графоаналитическим, или методом планов;
3) аналитическим.
Метод кинематических диаграмм прост и нагляден. Он позволяет получить представление об изменении кинематических характеристик звена механизма (или точки звена) за цикл его движения и легко определить вели
чину перемещения S, скорости V и усколения a в любой момент времени
или в любом заданном положении механизма. Суть метода состоит в том,
что по тем или иным данным строится исходная кинематическая диаграмма
(например, диаграмма перемещения или ускорения) и по ней методами графического дифференцирования или интегрирования строятся остальные
диаграммы [1, 2, 4].
Метод планов прост, нагляден и обеспечивает высокую точность получаемых результатов, благодаря чему он широко применяется в инженерной
практике. Суть метода заключается в том, что связи между кинематическими характеристиками описываются векторными уравнениями, решаемыми
графически.
Аналитические методы (например, метод преобразования координат,
метод векторных замкнутых контуров) отличаются точностью и сложностью. При их использовании связь между входными и выходными кинематическими параметрами механизма описывается математическими уравнениями, решить которые нередко можно только численными методами.
Познакомимся более подробно с графоаналитическим методом кинематического анализа рычажных механизмов.
31
32.
2.1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВМЕТОДОМ ПЛАНОВ
Как уже отмечалось, при использовании этого метода связи между скоростями и ускорениями точек звеньев механизма описываются векторными
уравнениями. Графическое решение векторного уравнения называют
планом. Если векторное уравнение описывает связь между скоростями точек звеньев, то его графическое решение называют планом скоростей. Если
же оно описывает связь между ускорениями, то графическое решение является планом ускорений.
При построении планов скоростей и ускорений необходимо помнить:
1. Точку плана скоростей (или ускорений), скорость (ускорение) которой равна нулю, называют полюсом и обозначают pV на плане скоростей
или pa на плане ускорений.
2. Векторы абсолютных скоростей (ускорений) выходят из полюса pV (pa)
плана скоростей (ускорений).
3. Векторы относительных скоростей (ускорений) проходят через концы векторов абсолютных скоростей (ускорений).
4. План скоростей (ускорений) обладает свойством подобия.
Кинематический анализ любого рычажного механизма начинают
с расчета исходного механизма. Затем выполняется кинематический расчет структурных групп в порядке их присоединения к исходному механизму,
т. е. в соответствии с формулой строения механизма.
Строение исходного механизма зависит от его подвижности W. Большая часть механизмов имеет W = 1. Рассмотрим кинематический расчет исходного механизма, подвижность которого равна 1. Его кинематическая
схема приведена на рис. 2.1. Исходный механизм состоит из стойки 0 и кривошипа 1, вращающегося вокруг неподвижной оси, проходящей через геометрическую ось шарнира О, с постоянной угловой скоростью ω1. Ско
рость V A и ускорение a A точки А кривошипа вычисляются по формулам
[1–6]:
V A = ω1 ⋅ lOA ;
a A = ω12 ⋅ lOA ,
где lOA – длина кривошипа, м.
32
33.
Скорость V A направлена перпендикулярно звену в сторону его вращения (рис. 2.1), а ускорение a A – параллельно кривошипу, от точки А к цен-
тру вращения.
Рис. 2.1
Поскольку в основном используются механизмы II класса, рассмотрим
расчетные модели, применяемые при кинематическом анализе структурных
групп II класса 2-го прорядка всех пяти видов (модификаций).
Кинематический анализ структурной группы
II класса 2-го порядка первого вида
Структурная группа II класса 2-го прорядка первого вида, называемая
двухповодковой, изображена на рис. 2.2, а. Известны: положение звеньев,
их кинематические размеры, скорости и ускорения точек А и С поводков.
В ходе кинематического анализа должны быть определены: скорость
и ускорение точки В (шарнира В), угловые скорости и ускорения звеньев 2 и 3.
Каждое звено рассматриваемой структурной группы в общем случае
совершает плоскопараллельное движение, которое можно представить состоящим из двух простых движений: переносного поступательного и относительного вращательного. В относительном движении звено АВ вращается
вокруг мгновенно неподвижной точки А, а звено ВС – вокруг точки С. В со
ответствии с теоремой о скоростях точек плоской фигуры [6] скорости V A
и VB точек А и В звена 2 связаны зависимостью [1, 2, 4]
(2.1)
VB = V A + VBA ,
где V A – переносная скорость точки В; VBA – относительная скорость точки В.
33
34.
ав
б
Рис. 2.2
Линия действия скорости VBA направлена перпендикулярно звену АВ
в рассматриваемом положении.
Скорости VС и VB точек С и В звена 3 связаны зависимостью
(2.2)
VB = VС + VBС ,
где VС – переносная скорость точки В; VBС – относительная скорость точки В.
Линия действия скорости VBС направлена перпендикулярно звену ВС.
Левые части уравнений (2.1) и (2.2) равны, следовательно правые можно приравнять. Получим векторное уравнение
C
C
C
C
(2.3)
V A + VBA = VC + VDC .
34
35.
Уравнение (2.3) содержит два неизвестных и имеет графическое решение. Для его решения подбирается масштабный коэффициент µV, величинукоторого можно вычислить, например, через скорость точки А.
м/с
.
мм
µV = VA pv a
(2.4)
В этой формуле pVa – длина отрезка, изображающего V A на плане ско-
ростей. Длина отрезка подбирается так, чтобы масштабный коэффициент µV
был простой десятичной дробью или целым числом.
Для решения уравнения (2.3) на поле чертежа выбирается произвольно
положение полюса плана скоростей (точка pV) и из него проводится прямая,
параллельная линии действия V A (рис. 2.2, б). На этой прямой из точки pV
откладывается отрезок pVa так, чтобы вектор скорости точки А выходил
из полюса и сохранял заданное направление. Из точки а плана скоростей
проводится луч, перпендикулярный звену АВ. Чтобы изобразить ско
рость VС , из точки pV параллельно линии действия скорости точки С проводится прямая, на которой откладывается отрезок pVc, длина которого вычисляется по формуле
pV c = VC µV .
Вектор, соединяющий на плане скоростей точки pV и c, должен совпа
дать по направлению с вектором скорости VС . Поскольку скорости VС и VBС
суммируются, из точки c плана скоростей проводится луч, перпендикулярный звену ВС, до пересечения с лучом, выходящим из точки а. Точка пересечения этих лучей есть точка b. Отрезок pVb изображает в масштабе иско
мую скорость VB , а отрезки ab и cb – относительные скорости VBA и VBС соответственно. Модули линейных и угловых скоростей вычисляются
по формулам:
VB = pV b ⋅ µV ;
VBA = ab ⋅ µV ;
ω2 = VBA l AB ;
VBC = cb ⋅ µV ;
ω3 = VBC lCB .
Следует отметить, что в этих формулах длины отрезков pVb, ab, cb плана скоростей измеряются в миллиметрах.
35
36.
Направление вращения звеньев рассматриваемой структурной группыв заданном положении показано на рис. 2.2, а.
При расчете ускорений используется теорема об ускорениях точек
плоской фигуры [6], согласно которой ускорения a A и a B точек А и В звена 2 связаны уравнением
n
a B = a A + a BA
+ a τBA ,
(2.5)
n
где a A – переносное ускорение точки В; a BA
и a τBA – нормальная и тангенциальная составляющие относительного ускорения точки В.
n
направлена параллельно звену АВ,
Линия действия ускорения a BA
а ускорения a τBA – перпендикулярно АВ. Поскольку в относительном движении шатун 2 вращается вокруг мгновенно неподвижной точки А, вектор
n
ускорения a BA
направлен из точки В в сторону точки А звена АВ. Мо n
дуль a BA
вычисляется по формуле
n
a BA
= ω22 ⋅ l AB .
Ускорения aС и a B точек С и В звена 3 связаны уравнением
n
a B = aС + a BС
+ a τBС ,
(2.6)
n
где aС – переносное ускорение точки В; a BС
и a τBС – нормальная и тангенциальная составляющие относительного ускорения точки В.
n
Линии действия ускорений a BС
и a τBС направлены параллельно и пер n
пендикулярно звену СВ соответственно. Причем вектор ускорения a BС
n
направлен из точки В в сторону точки С шатуна 3. Модуль a BС
вычисляется
по формуле
n
a BС
= ω32 ⋅ lСB .
Левые части уравнений (2.5) и (2.6) равны, следовательно правые можно приравнять.
C
Cn
C
C
Cn
C
(2.7)
a A + a BA
+ a τBA = aC + a BC
+ a τBC .
36
37.
Уравнение (2.7) содержит два неизвестных. Для его графического решения надо подобрать масштабный коэффициент µa. Значение µa можно задать, ориентируясь на величину одного из ускорений a A или aС . Например,
µ a = a A pа a ,
(2.8)
где paa – длина отрезка, изображающего a A на плане ускорений.
Длина отрезка paa задается произвольно, но подбирается так, чтобы
масштабный коэффициент µa был простой десятичной дробью или целым
числом. Масштабный коэффициент µa измеряется в метрах в секунду за се м с2
. Длины отрезков pac, an, cm,
кунду, деленных на миллиметр чертежа
мм
n n
которые на плане ускорений будут изображать ускорения aС , a BA
, a BС , вычисляются по формулам:
p a c = aC µ a ,
n
µa ,
an = a BA
n
cm = a BC
ma .
Их длина измеряется в миллиметрах.
Решение уравнения (2.7) начинается с выбора положения полюса плана
ускорений pa (рис. 2.2, в). Из этой точки проводится прямая, параллельная
линии действия ускорения a A , и откладывается отрезок paa так, чтобы вектор ускорения точки А сохранял заданное направление. Из точки a плана
ускорений проводится прямая, параллельная звену АВ, и на ней откладывается отрезок an, через конец которого (точка n) проводится перпендикуляр,
являющийся линией действия ускорения a τBA . Следует отметить, что вектор,
соединяющий точки a и n плана ускорений, при переносе его в точку В звена АВ должен быть направлен в сторону точки А.
Из точки pa плана ускорений проводится прямая, параллельная линии
действия ускорения aС , и откладывается отрезок pac (рис. 2.2, в) так, чтобы
вектор ускорения точки С сохранял заданное направление. Из точки c плана ускорений параллельно звену ВС проводится луч, на котором откладывается отрезок cm так, чтобы вектор, соединяющий точки c и m плана ускорений, при переносе его в точку В звена СВ был направлен в сторону точки С.
Через точку m проводится перпендикуляр, являющийся линией действия
ускорения a τBС . Точка пересечения перпендикуляров есть точка b. Отре
зок pab, соединяющий точку b с полюсом pa, изображает ускорение a B
37
38.
в масштабе µa. Отрезки ab и bc изображают в масштабе относительныеC
ускорения a BA и a BC соответственно.
Линейные и угловые ускорения вычисляются по формулам:
a B = pa b ⋅ µ a ;
a BC = cb ⋅ µ a ;
a BA = ab ⋅ µ a ;
aτBC = mb ⋅ m a ;
ε 2 = aτBA l AB ;
aτBA = nb ⋅ µ a ;
ε 3 = aτBC l BC .
В этих формулах длины отрезков pVb, ab, cb, nb, mb измеряются в миллиметрах.
Направление углового ускорения шатунов показано на рис. 2.2, а.
Кинематический анализ структурной группы
II класса 2-го порядка второго вида
Структурная группа II класса 2-го порядка второго вида показана
на рис. 2.3, а. Она состоит из шатуна 2 и ползуна 3. Ось направляющей пол
зуна обозначена как x–x. Скорость V A и ускорение a A точки А шатуна в заданном положении структурной группы известны по величине и направлению. Требуется методом планов определить скорость и ускорение ползуна
(точки В), угловые скорость и ускорение шатуна.
а
в
б
Рис. 2.3
38
39.
Скорости VB и V A точек В и А звена 2 связаны уравнением [1, 3, 4](2.9)
VB = V A + VBA ,
в котором вектор относительной скорости VBA направлен перпендикулярно
шатуну в рассматриваемом положении, а вектор VB – параллельно x–x.
Уравнение содержит две неизвестных и может быть решено.
Для графического решения уравнения (2.9) выбирается масштабный
коэффициент µV и по формуле (2.4) вычисляется длина отрезка pVa, которым
скороть V A будет изображена на плане скоростей.
pV a = V A µV .
Для решения уравнения (2.9) выбирается положение полюса pV плана
скоростей (рис. 2.3, б). Из точки pV параллельно линии действия скоро
сти V A проводится прямая, и на ней откладывается отрезок длиной pVa.
Из точки a плана скоростей проводится луч, перпендикулярный звену АВ,
до пересечения в точке b с прямой, параллельной x–x и проходящей через
полюс pV плана скоростей. Отрезок pVb изображает в масштабе скорость
точки В (ползуна), а отрезок ab – относительную скорость этой точки. Длины отрезков измеряются в миллиметрах.
Модули скоростей вычисляются по формулам:
VB = pV b ⋅ µV ;
VBA = ab ⋅ µV ;
ω2 = VBA l AB .
При прохождении через заданное положение шатун в относительном
движении вращается по ходу часовой стрелки (рис. 2.3, а).
Для определения ускорения a B ползуна используется векторное уравнение
n
(2.10)
+ a τBA .
a B = a A + a BA
В уравнении (2.10) ускорение a A известно по величине и направлению.
n
Нормальная составляющая a BA
относительного ускорения точки В направлена параллельно шатуну 2 от точки В в сторону точки А, и ее модуль вычисляется по формуле
n
a BA
= ω22 ⋅ l AB .
39
40.
Тангенциальная составляющая a τBA относительного ускорения точки Внаправлена перпендикулярно звену АВ.
Для графического решения уравнения (2.10) (рис. 2.3, в) выбирается
масштабный коэффициент µa и по формуле (2.8) вычисляются длины отрез
n
ков paa и an, которыми ускорения a A и a BA
будут изображаться на плане
ускорений.
pa a = a A µ a ;
n
an = a BA
µa .
Из произвольно выбранной точки pa плана ускорений параллельно линии действия ускорения точки А проводится прямая, на которой откладыва
ется отрезок длиной paa (рис. 2.3, в) так, чтобы вектор a A выходил из полюса и сохранял заданное направление. Из точки a плана ускорений параллельно звену АВ проводится прямая, и на ней откладывается отрезок длиной
n
an, изображающий ускорение a BA
. Через точку n проводится перпендикуляр
к an до пересечения в точке b с прямой, параллельной x–x и проходящей
через полюс pa. Отрезок pab плана ускорений изображает искомое ускоре
ние a B .
Относительное ускорение a BA определяется решением векторного
n
уравнения a BA = a BA
+ a τBA . Точки a и b плана ускорений соединяются пря
n
мой. Вектор a BA направлен навстречу векторам a BA
и a τBA .
Модули ускорений вычисляются по формулам:
a B = pa b ⋅ µ a ;
aτBA = nb ⋅ µ a ;
a BA = ab ⋅ µ a ;
ε 2 = aτBA l AB .
Направление ε2 показано на рис. 2.3, а.
Кинематический анализ структурной группы
II класса 2-го порядка третьего вида
Кинематическая схема рассматриваемой структурной группы изображена на рис. 2.4, а в масштабе µl. Она состоит из кулисы 3, вращающейся
вокруг неподвижной оси, проходящей через геометрическую ось шарнара О,
и камня кулисы 2. Шарнир А соединяет камень кулисы с некоторым звеном 1 (например, кривошипом), не входящим в структурную группу.
40
41.
Обозначим буквой А1 конец звена 1, буквой А2 точку А камня кулисы и буквой А3 точку А кулисы, совпадающую в рассматриваемый момент с точкой А2.а
б
в
Рис. 2.4
На данном этапе расчета скорость V А1 и ускорение а А1 точки А звена 1
известны по величине и направлению (рис. 2.4, а). Поскольку звенья 1 и 2
связаны шарнирно, скорости и ускорения точек А1 и А2 геометрически
равны.
a A1 = a A2 .
V A1 = V A2 ;
Скорости V А3 и V А2 точек А3 и А2 связаны зависимостью [1, 2, 4]
(2.11)
V А3 = V А 2 + V А3 А 2 ,
где V А2 и V А3А2 – переносная и относительная скорости точки А кулисы соответственно.
Скорость V А3А2 направлена параллельно ОА, а абсолютная скорость V А3
точки А3 – перпендикулярно кулисе.
Для графического решения уравнения (2.11) выбирается масштабный
коэффициент µV и по формуле (2.4) вычисляется длина отрезка pVa, которым
скороть V А2 будет изображаться на плане скоростей.
Из полюса pV, произвольно выбранного на свободном поле чертежа
(рис. 2.4, б), параллельно линии действия вектора V А1 проводится прямая,
41
42.
на которой в миллиметрах чертежа откладывается отрезок pVa1. Из точки a1(или a2) проводится луч, параллельный ОА, а из полюса pV – луч, перпендикулярный ОА. Точка пересечения этих лучей и есть искомая точка a3, определяющая длины отрезков, изображающих на плане скоростей искомые
скорости V А3А2 и V А3 . Величины этих скоростей вычисляются по формулам:
V A3 = pV a3 ⋅ µV ;
V A3 A2 = a2 a3 ⋅ µV .
Угловая скорость ω3 кулисы определяется по формуле
ω3 = V A3 lOA .
Кинематический размер lOA зависит от положения звеньев и вычисляется следующим образом:
lOA = OA ⋅ µl .
Для расчета ускорений используется уравнение [1, 2, 4]
(2.12)
a A3 = a A2 + a Ak 3 A2 + a Ar 3 A2 ,
где a A3 – абсолютное ускорение точки А3; a A2 – переносное ускорение точ
ки А3; a Ak 3 A2 – ускорение Кориолиса; a Ar 3 A2 – относительное ускорение точки А3.
Модуль ускорения a Ak 3 A2 вычисляется по формуле [6]
а Ak 3 A2 = 2 ⋅ VA3 A2 ⋅ ω3 .
Направление ускорения a Ak 3 A2 определяется поворотом вектора V А3А2
вокруг его начала на угол 90о в направлении переносной угловой скорости,
совпадающей с ω3 (рис. 2.4, б).
Вектор a Ar 3 A2 направлен параллельно кулисе (параллельно ОА).
Поскольку кулиса вращается вокруг оси О, ускорение a A3 ее точки А
можно разложить на составляющие a An 3 и a τA3 . Тогда
a A3 = a An 3 + a τA3 .
(2.13)
Нормальная составляющая a An 3 ускорения точки А3 направлена параллельно кулисе, из точки А в сторону точки О (рис. 2.4, в), а тангенциаль42
43.
ная – перпендикулярно ОА. Величина ускорения a An 3 вычисляется по формулеa nA3 = ω32 ⋅ lOA .
Модуль ускорения a τA3 подлежит определению.
Левые части уравнений (2.12) и (2.13) равны, следовательно правые
можно приравнять. Получится новое векторное уравнение с двумя неизвестными:
(2.14)
a A2 + a Ak 3 A2 + a Ar 3 A2 = a An 3 + a τA3 .
Уравнение (2.14) решается графически. Для его решения выбирается
масштабный коэффициент µa и по формуле (2.8) вычисляются длины отрезков, которыми будут изображаться на плане ускорений известные ускоре
ния. Длина отрезка paa2, изображающего ускорения a A1 и a A2 :
p a a 2 = a A2 µ a .
Длина отрезка a2k, изображающего ускорение Кориолиса a Ak 3 A2 :
a 2 k = a kA3 A2 µ a .
Длина отрезка pan, изображающего ускорение a An 3 :
pa n = a nA3 µ a .
Графическое решение уравнения (2.14) приведено на рис. 2.4, в. План
ускорений строится следующим образом. Из произвольно выбранного по
люса pa параллельно линии действия ускорения a A2 проводится прямая,
и на ней в миллиметрах чертежа откладывается отрезок paa2. Точки a1 и a2
на плане ускорений совпадают из-за равенства ускорений точек А1 и А2.
Из точки a2 параллельно линии действия ускорения a Ak 3 A2 проводится прямая, на которой откладывается отрезок a2k, и через точку k проводится перпендикуляр к a2k.
Из полюса pa параллельно ОА проводится прямая, на которой откладывается отрезок pan. Через точку n проводится перпендикуляр к pan. Точка
43
44.
пересечения перпендикуляров – искомая точка a3 плана ускорений. Точка a3соединяется с полюсом pa. Отрезок paa3 в масштабе µa изображает ускорение точки А кулисы. Модули ускорений вычисляются по формулам:
a Ar 3 A2 = ka3 ⋅ µ a ;
aτA3 = na3 ⋅ µ a ;
a A3 = p a a 3 ⋅ µ a ;
ε 3 = aτA3 lOA .
Кинематический анализ структурной группы
II класса 2-го порядка четвертого вида
Структурная группа состоит из камня кулисы 2 и ползуна 3 (рис. 2.5, а).
а
б
в
Рис. 2.5
Звенья 2 и 3 соединены простым шарниром А и образуют поступательные пары со звеном 1 и стойкой 0 соответственно. Обозначим точку А звена 1
буквой А1, точку А звена 2 – буквой А2 и точку А звена 3 – буквой А3.
На данном этапе расчета скорость V A1 и ускорение a A1 точки А звена 1 из
вестны. Скорость V A2 точки А звена 2 определяется по уравнению [1, 2, 4]
(2.15)
V А2 = V А1 + V А2 А1 ,
где V A1 и V A2 A1 – переносная и относительная скорости точки А2.
Скорость V A2 A1 направлена параллельно t–t. Звено 3 перемещается па
раллельно направляющей x–x, следовательно скорость VA3 направлена параллельно x–x. Звенья 2 и 3 соединены шарнирно. При таком соединении
скорости и ускорения точек А2 и А3 связаны соотношениями:
a A 2 = a A3 .
V A 2 = V A3 ;
Таким образом, скорость VA2 известна по направлению.
44
45.
Для графического решения уравнения (2.15) выбирается масштабныйкоэффициент µV и по формуле (2.4) вычисляется длина отрезка pVa1, кото
рым скороть V А1 будет изображаться на плане скоростей (рис. 2.5, б). План
скоростей строится следующим образом.
Из произвольно выбранного полюса pV проводится прямая, параллель
ная линии действия скорости V А1 , и на ней откладывается отрезок длиной
pVa1. Из точки a1 проводится луч, параллельный t–t, а из полюса – луч, параллельный x–x. Точка a2 есть точка пересечения лучей. Точка a3 плана скоростей совпадает с точкой a2. Отрезок pVa2 изображает в масштабе µV скоро
сти точек А2 и А3, отрезок a1a2 – относительную скорость V A2 A1 . Модули
скоростей вычисляются по формулам:
V A2 A1 = a1a 2 ⋅ µV .
V A2 = V A3 = pV a 2 ⋅ µV ;
Для расчета ускорения а А2 точки звена 2 используется уравнение
a A2 = a A1 + a Ak 2 A1 + a Ar 2 A1 ,
(2.16)
где а А1 и a Ar 2 A1 – переносное и относительное ускорения точки А2; a Ak 2 A1 –
ускорение Кориолиса.
Ускорение a Ar 2 A1 направлено параллельно t–t, а ускорение а А2 – параллельно x–x. Модули этих ускорений подлежат определению. Величина
ускорения a Ak 2 A1 вычисляется по формуле
a kA2 A1 = 2 ⋅ V A2 A1 ⋅ ω1 .
Направление ускорения Кориолиса определяется поворотом векто
ра V A2 A1 относительно его начала на угол 90о в направлении ω1 (ее величина
и направление заданы).
Для графического решения уравнения (2.16) выбирается масштабный
коэффициент µa и по формуле (2.8) вычисляется длина отрезка paa1, кото
рым ускорение а А1 будет изображаться на плане ускорений (рис. 2.5, в).
pa a1 = a A1 µ a .
Длина отрезка a1k, изображающего ускорение Кориолиса a Ak 2 A1 :
a1k = a kA2 A1 µ a .
45
46.
Для решения уравнения (2.16) из произвольно выбранной точки pa плана ускорений параллельно линии действия ускорения а А1 проводится пря
мая, на которой в направлении вектора а А1 откладывается отрезок paa1 (его
длина измеряется в миллиметрах). Из точки a1 плана ускорений перпенди
кулярно t–t проводится луч, на котором в направлении a Ak 2 A1 откладывается
отрезок a1k. Из точки k параллельно t–t проводится луч. Из полюса pa проводится луч, параллельный x–x. Точка пересечения этих лучей – точка a2.
Отрезок ad изображает относительное ускорение a Ar 2 A1 , отрезок paa2 – уско
рения а А2 и а А3 .
Модули ускорений вычисляются по формулам:
a Ar 2 A1 = ka 2 ⋅ µ a ;
а А 2 = a A3 = p a a 2 ⋅ µ a .
Кинематический анализ структурной группы
II класса 2-го порядка пятого вида
Структурная группа состоит из камня 2 кулисы и кулисы 3, совершающей поступательное движение вдоль направляющей x–x (рис. 2.6, а). Камень кулисы соединен простым шарниром со звеном 1, например с кривошипом. Обозначим точку А звена 1 буквой А1, точку А звена 2 – буквой А2
и точку А звена 3 – буквой А3. Поскольку звенья 1 и 2 связаны шарнирно,
скорости и ускорения точек А1 и А2 равны по величине и совпадают
по направлению. На данном этапе расчета скорость V A1 и ускорение a A1 из
вестны. Следовательно, известны скорость V A2 и ускорение a A2 точки А
камня. Скорость V A3 точки А кулисы определяется в ходе решения уравнения
V А3 = V А 2 + V А3 А 2 ,
(2.17)
где V А2 и V А3А2 – переносная и относительная скорости точки А кулисы со-
ответственно.
Скорость V А3А2 направлена параллельно y–y, а абсолютная скорость V A3 –
параллельно x–x (рис. 2.6, а).
46
47.
аб
в
Рис. 2.6
Для решения уравнения (2.17) выбирается масштабный коэффициент µV
и по формуле (2.4) вычисляется длина отрезка pVa1, изображающего ско
рость V А1 на плане скоростей (рис. 2.6, б). Из произвольно выбранного по
люса pV проводится прямая, параллельная линии действия скорости V А1 ,
и на ней откладывается отрезок длиной pVa1. Из точки a2, совпадающей
с точкой a1, проводится луч, параллельный y–y, а из полюса pV – луч, параллельный x–x. Точка пересечения лучей есть точка a3, определяющая длины
отрезков, изображающих на плане скоростей искомые скорости V А3 и V А3А2 .
Их модули вычисляются по формулам:
V А3 А2 = a 2 a3 ⋅ µV ;
V А3 = pV a3 ⋅ µV .
Ускорение а А3 кулисы определяется в ходе решения векторного уравнения
a A3 = a A2 + a Ar 3 A2 ,
(2.18)
где а А2 и a Ar 3 A2 – переносное и относительное ускорения точки А кулисы
соответственно.
Ускорение a Ar 3 A2 направлено параллельно y–y, а абсолютное ускорение
а А3 – параллельно x–x.
Для графического решения уравнения (2.18) подбирается масштабный
коэффициент µa и по формуле (2.8) вычисляется длина отрезка paa2, кото
рым ускорение а А2 будет изображаться на плане ускорений (рис. 2.6, в). За47
48.
тем из произвольно выбранной точки pa плана ускорений параллельно линии действия ускорения а А2 проводится прямая, на которой в направлении
вектора а А1 откладывается отрезок paa2 (его длина измеряется в миллиметрах). Из точки a2, совпадающей с точкой a1, параллельно y–y и из полюса pa
параллельно x–x проводятся лучи. Точка их пересечения есть точка a3,
определяющая длины отрезков, изображающих на плане ускорений иско
мые ускорения а А3 и a Ar 3 A2 . Их модули вычисляются по формулам:
a A 3 A 2 = a 2 a3 ⋅ µ a ;
a А3 = pа a3 ⋅ µ a .
При решении задач кинематики следует помнить, что на планах скоростей и ускорений длины отрезков, их изображающих, измеряются в миллиметрах (мм), длины звеньев – в метрах (м), линейные скорости – метрах
в секунду (м/с), а линейные ускорения – метрах в секунду за секунду (м/с2).
Угловые скорости имеют размерность – радиан в секунду (1/с), а угловые
ускорения – радиан в секунду за секунду (1/с2).
2.2. СИНТЕЗ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ
ПО ЗАДАННЫМ УСЛОВИЯМ
При синтезе механизма определяются кинематические размеры звеньев,
обеспечивающие требуемое движение заданного звена или его точки. Условия синтеза могут быть различны. Ознакомимся с некоторыми расчетными
моделями, применяемыми при синтезе рычажных механизмов по заданным
условиям.
2.2.1. Синтез четырехзвенных рычажных механизмов
по двум положениям их звеньев
Центральный кривошипно-ползунный механизм
Кинематическая схема центрального кривошипно-ползунного механизма приведена на рис. 2.7. Механизм состоит из стойки 0, кривошипа 1,
шатуна 2 и ползуна 3. У центрального механизма ось направляющей ползуна проходит через ось вращения кривошипа (геометрическую ось шарнира О). Известен ход H ползуна, по величине которого определяются длины lOA и lAB звеньев 1 и 2 соответственно.
48
49.
Ход ползуна – максимальное его перемещение за цикл. Ход ползуна равен удвоенной длине (lOA) кривошипа, т. е.lOA = H 2 .
(2.19)
Работоспособность рассматриваемого механизма зависит от величины
угла давления [2].
Угол давления β – угол между вектором силы давления на данное звено
со стороны другого звена и вектором скорости точки приложения движущей силы.
Рис. 2.7
Если массами звеньев пренебречь, то при ведущем кривошипе сила R32 ,
с которой ползун действует на шатун, будет направлена по звену АВ, как
показано на рис. 2.7. Угол давления β – это угол наклона шатуна к оси x–x.
В течение цикла величина угла давления изменяется, достигая максимального значения при φ1, равном 90о и 270о. Чем больше угол β, тем больше силовое воздействие со стороны ползуна на стойку. В связи с этим величину
угла β ограничивают. Условие нормальной работы механизма:
β max ≤ [β ],
где βmax – максимальное значение угла давления; [β] – допускаемое значение
угла давления.
Очевидно, чем длина lAB шатуна больше длины lOA кривошипа, тем
меньше βmax. В [2] приведена рекомендация, согласно которой у двигателей
внутреннего сгорания lAB = (3–5)lOA. При таком соотношении длин кривошипа и шатуна βmax находится в интервале 11–19о.
49
50.
Дезаксиальный (внеосный) кривошипно-ползунный механизмКинематическая схема механизма показана на рис. 2.8. Направляющая x–x ползуна смещена относительно оси вращения кривошипа на величину e . Заданы: ход H ползуна; соотношения l AB lOA = n и e lOA = m . По заданным условиям надо определить длину кривошипа lOA, длину шатуна lAB,
дезаксиал e. На рис. 2.8 крайние положения механизма обозначены как первое и второе. В первом положении кривошип и шатун вытянуты в одну линию OB1 и ползун наиболее удален от оси вращения кривошипа. Во втором
положении звенья 1 и 2 сложились в линию A2B2 и ползун максимально
приблизился к оси вращения кривошипа. В связи с этим
и
OB1 = lОА + l АВ
OB2 = l АВ − lОА .
Рис. 2.8
Рассмотрим треугольник ОКВ1. По теореме Пифагора
(OB1 )2 = (OK )2 + (KB1 )2 ,
(2.20)
где OK = e ; KB1 = KB2 + H .
KB2 – катет треугольника ОКВ2. KB2 =
KB2 =
(OB2 )2 − (OK )2
или
(l AB − lOA )2 − e2 .
После подстановки значений уравнение (2.20) преобразуется к виду
(lOA + l AB )
2
=e +
2
( (l
AB
50
)
2
− lOA ) − e + H .
2
2
51.
Если lAB и e выразить через lOA, то после преобразования уравнениепримет вид
2
− 2 ⋅ H ⋅ lOA
4 ⋅ n ⋅ lOA
(n − 1)2 − m 2 − H 2 = 0 .
(2.21)
Уравнение (2.21) алгебраическое квадратное с одним неизвестным.
Значение lOA определяется в ходе его решения, а значения lAB и e вычисляются по формулам:
l AB = lOA ⋅ n ;
e = lOA ⋅ m .
Данная расчетная модель является универсальной и может быть использована при синтезе механизмов с положительным дезаксиалом (рис. 2.9, а)
и дезаксиальных механизмов, у которых ось направляющей ползуна расположена под углом γ (рис. 2.9, б).
а
б
Рис. 2.9
Кривошипно-коромысловый механизм
Кинематическая схема механизма показана на рис. 2.10. Рассмотрим
случай, когда оси шарниров О и С, соединяющих кривошип 1 и коромысло 3 со стойкой 0, расположены на одной оси в горизонтальной плоскости.
Расстояние lOC между ними задано. Положение коромысла в крайних положениях механизма определяется значениями углов ψ1 и ψ2, величины которых заданы. Требуется подобрать длины lOA, lAB и lBC кривошипа 1, шатуна 2
и коромысла 3 соответственно.
При таких условиях возможно множество решений. Рассмотрим графическое решение задачи, как наиболее простое. Все построения выполняются
в масштабе. Масштабный коэффициент µℓ выбирается произвольно.
51
52.
Рис. 2.10Задается положение точки О кривошипа (рис. 2.10), и от нее по горизонтальной прямой откладывается отрезок ОС, изображающий в масштабе µl кинематический размер lOC.
ОС = lOC µl .
Длина отрезка ОС измеряется в миллиметрах. Из точки С проводятся
лучи, составляющие с прямой ОС углы ψ1 и ψ2. Если задаться длиной lBC коромысла, то размеры lOA и lAB определяются легко, а именно: из точки С, как
из центра, проводится окружность радиусом СВ = lBC µl и определяется
положение точек пересечения этой окружности с лучами, образующими углы ψ1 и ψ2 с горизонтальной прямой ОС. Точки пересечения на рис. 2.10
обозначены буквами B1 и B2. Отрезки CB1 и CB2 изображают крайние положения коромысла. Коромысло занимает положение CB1, когда кривошип
и шатун вытянуты в одну прямую OB1, а положение CB2, когда звенья 1 и 2
складываются. Отрезок ОВ2 = АВ − ОА . Таким образом, 2 ⋅ ОА = ОВ1 − ОВ2 .
Длина кривошипа
lOA = OA ⋅ µl = 0,5 ⋅ (OB1 − OB2 ) ⋅ µl .
Тогда l AB = (OB1 − OA) ⋅ µl .
Если при синтезе кривошипно-коромыслового механизма длина lBC коромысла задана, то задача имеет однозначное решение.
52
53.
2.2.2. Синтез четырехзвенных рычажных механизмовпо коэффициенту изменения средней скорости
выходного звена
В некоторых механизмах циклического действия выходное звено перемещается из одного крайнего положения в другое и часто технологическая
операция совершается при его движении в одну сторону (например, строгальные, зубодолбежные станки).
Движение, при котором совершается технологическая операция (совершается полезная работа), называется рабочим ходом, а движение в обратном направлении – холостым ходом. Обычно холостой ход совершается
быстрее рабочего.
Отношение средних скоростей выходного звена во время холостого
и рабочего ходов называют коэффициентом изменения его средней скорости и обозначают буквой K .
При поступательном движении выходного звена
СР
СР
,
VРХ
K = V ХХ
СР
СР
где V ХХ
и VРХ
– средняя скорость холостого и рабочего ходов соответст-
венно.
При вращении выходного звена
СР
СР
,
K = ω ХХ
ωРХ
СР
СР
где ω ХХ
и ω РХ
– средняя угловая скорость холостого и рабочего хода соот-
ветственно.
Коэффициент изменения средней скорости выходного звена можно выразить через углы φXX и φPX холостого и рабочего хода входного звена механизма (рис. 2.11).
K = ϕ РХ ϕ ХХ .
(2.22)
Вывод формулы (2.22) приведен в [3].
Рассмотрим расчетную модель, позволяющую определить кинематические размеры дезаксиального кривошипно-ползунного маханизма (рис. 2.11)
по коэффициенту изменения средней скорости ползуна.
53
54.
Рис. 2.11Пусть заданы: ход H ползуна; коэффициент K; отношение длины lAB
шатуна к длине lOA кривошипа ( l AB lOA = n ). В ходе синтеза должны быть
определены кинематические размеры lOA, lAB и дезаксиал e. На рис. 2.11 показана кинематическая схема рассматриваемого механизма в крайних его
положениях. Индексом «1» обозначено положение, в котором кривошип
и шатун вытянуты в одну прямую и ползун наиболее удален от точки О
кривошипа, а индексом «2» – положение, в котором звенья 1 и 2 сложились
и ползун 3 максимально приблизился к точке О.
Рассмотрим последовательность решения задачи.
Определяются величины углов φXX и φPX холостого и рабочего хода. Для
этого используются уравнения:
K = ϕ РХ ϕ ХХ ,
(2.23)
ϕ РХ + ϕ ХХ = 360 .
(2.24)
Уравнения (2.23) и (2.24) решаются совместно. В результате
ϕ ХХ = 360 (K + 1) ;
ϕ РХ = 360 − ϕ ХХ .
Определяется угол В2ОВ1, обозначенный на рисунке буквой β.
β = ϕ РХ − 180 .
В треугольнике ОВ2В1 сторона ОВ1 = lOA + l AB = lOA ⋅ (n + 1) , а сторона
ОВ2 = l AB − lOA = lOA ⋅ (n − 1) .
54
55.
Согласно теореме косинусов(B2 B1 )2 = (OB1 )2 + (OB2 )2 − 2(OB1 ) ⋅ (OB2 ) ⋅ cos β
или
2
2
2
H 2 = lOA
⋅ (n + 1)2 + lOA
⋅ (n − 1)2 − 2 ⋅ lOA
⋅ (n + 1) ⋅ (n − 1) ⋅ cos β .
[(
) (
)
]
2
После преобразования получим H 2 = 2 ⋅ lOA
⋅ n 2 + 1 − n 2 − 1 ⋅ cos β . От-
куда
H2
.
lOA =
2 ⋅ n 2 + 1 − n 2 − 1 ⋅ cos β
[(
) (
)
]
(2.25)
По формуле (2.25) вычисляется кинематический размер lOA, затем размер lAB.
l AB = n ⋅ lOA .
Для определения размера e надо знать величину угла α. Согласно теореме косинусов
(OB2 )2 = (OB1 )2 + (B2 B1 )2 − 2 ⋅ (OB1 ) ⋅ (B2 B1 ) ⋅ cos α
или
(l AB − lOA )2 = (lOA + l AB )2 + H 2 − 2 ⋅ (lOA + l AB ) ⋅ H ⋅ cosα .
(
l AB + lOA )2 − (l AB − lOA )2 + H 2
.
cos α =
2 ⋅ (l AB + lOA ) ⋅ H
(2.26)
По значению косинуса определяется величина угла α и размер e .
e = (l AB + lOA ) ⋅ sin α .
(2.27)
В формулах (2.25)–(2.27) все линейные размеры (lOA, lAB, e, H) измеряются в миллиметрах или метрах.
2.3. ПРИМЕР СИНТЕЗА И КИНЕМАТИЧЕСКОГО АНАЛИЗА
РЫЧАЖНОГО МЕХАНИЗМА
Покажем на примере, как используются расчетные модели, описанные
в подразделах 2.2.1 и 2.2.2, при решении конкретных задач.
Предположим, что требуется определить длину lOA кривошипа 1,
длину lAB шатуна 2, дезаксиал e кривошипно-ползунного механизма, кине55
56.
матическая схема которого показана на рис. 2.12; рассчитать скорость VBи ускорение a B ползуна, угловые скорость ω2 и ускорение ε2 шатуна в за-
данном положении механизма. Известны: ход ползуна H = 100 мм; угол
наклона направляющей ползуна γ = 20°; l AB lOA = 5 ; e lOA = 0,4 ; средняя
скорость ползуна VBСР = 1,27 м/с.
Рис. 2.12
Для расчета кинематических размеров воспользуемся формулой (2.21),
согласно которой
2
4 ⋅ n ⋅ lOA
− 2 ⋅ H ⋅ lOA
(n − 1)2 − m 2 − H 2 = 0 .
Согласно исходным данным в этом уравнении n = 5; m = 0,4
и H = 100 мм. После подстановки значений n, m, H и преобразований получаем уравнение вида
2
lOA
− 39,8lOA − 500 = 0 .
(2.28)
′′ = −10,03. Поскольку
′ = 49,83 и lOA
Уравнение (2.28) имеет два корня: lOA
длина кривошипа не может быть отрицательной, принимаем l1OA = 49,83 мм.
l AB = n ⋅ lOA = 5 ⋅ 49,83 = 249,17 мм,
e = m ⋅ lOA = 0,4 ⋅ 49,83 = 19,93 мм.
Кинематический расчет выполняется в несколько этапов. На первом
этапе определяется угловая скорость ω1 кривошипа. За один оборот кривошипа (за один цикл движения) ползун совершает один двойной ход, т. е. перемещается из нулевого положения в шестое и возвращается из шестого по56
57.
ложения в нулевое. Обозначим время одного полного оборота кривошипакак tЦ (время цикла). Зная среднюю скорость VBСР движения ползуна, время
цикла можно вычислить по формуле
t Ц = 2 ⋅ H VВСР .
(2.29)
СР
В формуле (2.29) ход H измеряется в метрах, скорость VВ
– в метрах
в секунду, время цикла tЦ – в секундах.
t Ц = 2 ⋅ 0,1 1,27 = 0,157 с.
При кинематическом исследовании механизмов считается, что кривошип вращается с постоянной угловой скоростью. За цикл он поворачивается на угол 2π. Следовательно:
ω1 = 2π t Ц =
2 ⋅ 3,14
= 40 1/с.
0,157
Поскольку кинематический расчет выполняется методом планов, надо
построить разметку механизма. Разметка механизма – ряд последовательных положений звеньев механизма за цикл его движения.
Разметка строится в масштабе. Масштабный коэффициент µl выбирается произвольно. Он связан с размером lOA следующим образом:
µl = lOA ( м ) OA(мм ) ,
(2.30)
где ОА – длина отрезка, изображающего кривошип на разметке. Длина отрезка ОА подбирается так, чтобы масштабный коэффициент был целым числом или простой десятичной дробью.
Примем OA = 24,915 мм, тогда µl = 0,04983 24,915 = 0,002 м/мм.
Построение разметки начинается с выбора положения точки О
(рис. 2.13, а). Из нее под углом γ = 20 к горизонтальной прямой x–x проводится прямая Т–Т. Параллельно ей на расстоянии e проводится прямая t–t, по которой перемещается точка В ползуна и шатуна.
e = e µ l = 0,01993 0,002 = 9,965 мм.
Длина АВ отрезка, которым на разметке изображается шатун, составляет
AB = l AB µl = 0,2492 0,002 = 124,6 мм.
57
58.
Из точки О раствором циркуля, равным ОА, проводится окружность(траектория движения конца А кривошипа). Для определения одного
из крайних положений механизма из точки О раствором циркуля, равным
ОА + АВ = 24,92 + 124,6 = 149,5 мм, на прямой t–t делаем засечку, получаем
точку B0, соединяем ее с точкой О и находим точку A0, как точку пересечения прямой OB0 с траекторией движения конца А кривошипа.
а
б
в
Рис. 2.13
Для определения второго крайнего положения механизма из точки О
раствором циркуля, равным АB − OА = 124,6 − 24,92 = 99,68 мм, на прямой t–t делаем засечку, получаем точку B6. Соединяем ее с точкой О и продолжаем прямую OB6 до пересечения с траекторией движения конца А кривошипа в точке A6. Расстояние между точками B0 и B6 – ход H ползуна.
Угол между нулевым и шестым положениями кривошипа, измеренный
в направлении его вращения, – угол рабочего хода (φPX). Угол φXX, дополня58
59.
ющий угол рабочего хода до 360о, называют углом холостого хода. Каждыйиз этих углов делим на 6 равных частей и получаем 12 положений кривошипа. Нумеруются положения в направлении вращения звена 1, начиная
с нулевого. Двенадцатое положение совпадает с нулевым.
Чтобы определить соответствующие положения шатуна и ползуна, надо
из точек A1, A2, A3 ... A11 на прямой t–t сделать засечки раствором циркуля
AB = 124,6 мм. Получим положения точки B шатуна в соответствующих
положениях механизма. Точки A и B с одинаковыми индексами соединяем
прямыми линиями, которые изображают шатун в соответствующих положениях механизма.
Для расчета скоростей и ускорений используем метод планов. Рассматриваемый механизм состоит из исходного механизма, включающего стойку 0
и кривошип 1, и структурной группы (шатун – ползун) II класса 2-го порядка второго вида.
Выполним расчет скоростей и ускорений для 1-го положения механизма.
Расчет скоростей начинается с определения скорости V A точки А кривошипа.
V A = ω1 ⋅ lOA = 40 ⋅ 0,04983 = 1,993 м/с.
Направлен вектор скорости V A перпендикулярно кривошипу в первом
его положении (перпендикулярно ОА1) в сторону его вращения.
Скорости точек А и B шатуна связаны уравнением (2.9), согласно которому
(2.31)
VB = V A + VBA .
В уравнении (2.31) линия действия скорости VВ направлена параллель
но t–t, а относительной скорости VВА – перпендикулярно A1B1. Для графического решения уравнения (2.31) определяется масштабный коэффициент µV.
Примем длину отрезка pVa, которым скороть V А будет изображаться
на плане скоростей, равной 66,43 мм. Тогда в соответствии с формулой (2.4)
µV = V A pv a = 1,993 66,43 = 0,03 (м/с)/мм.
Из точки pV плана скоростей (рис. 2.13, б) проводится прямая, перпендикулярная ОА1, на которой откладывается отрезок pVa1 = 66,43 мм. Конец
59
60.
отрезка обозначается буквой а1, индекс которой соответствует номеру положения механизма. Из точки а1 перпендикулярно A1B1 проводится луч.Из полюса pV плана скоростей параллельно t–t тоже проводится луч. Точка
пересечения этих лучей есть искомая точка b1 плана скоростей. Отрезки a1b1
и pVb1 изображают в масштабе µV скорости VВА и VВ соответственно. Их модули вычисляются по формулам:
VВА = a1b1 ⋅ µV = 58 ⋅ 0,03 = 1,74 м/с;
VВ = pV b1 ⋅ µV = 38 ⋅ 0,03 = 1,14 м/с.
Угловая скорость ω2 шатуна:
ω2 = VBA l AB = 1,74 0,2492 = 6,98 1/с.
Для определения скорости VS 2 шатуна воспользуемся свойством подо-
бия плана скоростей [6], согласно которому
l AS 2 l AB = a1s2 a1b1 ,
откуда a1s2 = a1b1 ⋅ l AS 2 l AB = 58 ⋅ 0,1246 0,2492 = 29 мм.
На плане скоростей от точки а1 на прямой a1b1 откладываем отрезок a2s2
и точку s2 соединяем прямой линией с полюсом pV.
VS 2 = pV s2 ⋅ µV = 44 ⋅ 0,03 = 1,32 м/с.
Расчет ускорений начинается с определения ускорения a A точки А
кривошипа. Поскольку ω1 = const , значение a A вычисляется по формуле
a A = ω12 ⋅ lOA = 402 ⋅ 0,04983 = 79,73 м/с2.
Направлено ускорение a A параллельно кривошипу, из точки А в точку О
в рассматриваемом положении.
Ускорения точек A и B шатуна связаны уравнением (2.10), согласно которому
n
(2.32)
a B = a A + a BA
+ aτBA ,
n
где aBA
= ω22 ⋅ l AB = 6,982 ⋅ 0,2492 = 12,15 м/с2.
n
Ускорение a BA
направлено параллельно А1В1, из точки В1 в точку А1.
Ускорение a τBA направлено перпендикулярно А1В1, а ускорение a В – парал-
60
61.
лельно t–t. Уравнение (2.32) решается графически. Масштабный коэффициент плана ускорений:µ a = a A pa a = 79,73 79,73 = 1,0 (м/с2) мм.
Из точки pa плана ускорений (рис. 2.13, в) параллельно ОА1 проводится
прямая, и на ней откладывается отрезок paa1 длиной 79,73 мм. Через точку a1
проводится прямая, параллельная А1В1, на которой откладывается отрезок a1n1. Его длина вычисляется по формуле
n
a1n1 = a BA
µ a = 12,15/1 = 12,15 мм.
Через точку n1 проводится перпендикуляр к a1n1, а из полюса pa – луч,
параллельный t–t, до пересечения с перпендикуляром в точке b1. Отрез
ки n1b1 и pab1 изображают ускорения a τBA и a В соответственно. Соединив
прямой точки a1 и b1 плана ускорений, получим отрезок, изображающий
в масштабе µa ускорение a BA .
Значения искомых ускорений вычисляются по формулам:
a В = pa b1 ⋅ µa = 76 ⋅ 1 = 76 м/с2;
aτBA = n1b1 ⋅ µa = 43,5 ⋅ 1 = 43,5 м/с2;
a BA = a1b1 ⋅ µ a = 45 ⋅ 1 = 45 м/с2;
ε 2 = aτBA l2 = 43,5 0,2492 = 174,6 1/с2.
Для расчета ускорения aS 2 центра масс шатуна используем свойство
подобия плана ускорений. Составим пропорцию l AS 2 l AB = a1s2 a1b1 . В ней
a1s2 и a1b1 длины отрезков плана ускорений. Из этой пропорции следует, что
a1s2 = a1b1 ⋅ l AS 2 l AB = 45 ⋅ 0,1246 0,2492 = 22,5 мм. Отрезок a1s2 откладываем
на плане ускорений на прямой a1b1 от точки a1 в сторону точки b1, получаем
точку s2, которую соединяем с полюсом pa.
aS 2 = pa s2 ⋅ µa = 74 ⋅ 1 = 74 м/с2.
61
62.
3. КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ МЕХАНИЗМОВЧтобы выбрать рациональную форму, размеры деталей, подобрать материалы, обеспечить прочность, работоспособность механизма и требуемый
ресурс его работы, надо знать силы, действующие на звенья механизма
и в его подвижных соединениях. Следует помнить, что силы эти при работе
механизма изменяются как по величине, так и по направлению.
Раздел прикладной механики, изучающий силы, действующие в механизмах, называется «Кинетостатика механизмов». Кинетостатика базируется на принципах механики, в частности на принципе Даламбера и принципе
освобождаемости от связей [1–4].
В соответствии с принципом Даламбера, если в любой момент времени
к каждой точке подвижной механической системы кроме действующих
на нее внешних и внутренних сил добавить силы инерции, то система будет находиться в мгновенном равновесии и к ней применимы все положения
статики.
Согласно принципу освобождаемости от связей состояние механической системы не изменится, если связи отбросить, а их действие заменить
реакциями.
В ходе кинетостатического (силового) расчета определяются реакции
в кинематических парах и уравновешивающая сила Pур (или момент сил Мур),
приложенные к ведущему звену и обеспечивающие выполнение технологического процесса.
Силы можно определить разными методами: методом непосредственного разложения сил (графический метод); методом планов (графоаналитический метод); аналитическим методом [1–4, 6]. В инженерной практике
получил распространение метод планов.
3.1. РАСЧЕТ СИЛ ИНЕРЦИИ ЗВЕНЬЕВ
Для расчета сил, действующих в механизме, необходимо в каждом
из рассматриваемых его положений определить силы инерции.
Если звено совершает плоскопараллельное движение (например, ша
тун), то все силы инерции приводятся к главному вектору PИ и главно62
63.
му моменту МИ (рис. 3.1, а), для расчета которых используются формулы[1–4, 6]:
(3.1)
PИ = −m ⋅ aS ,
(3.2)
M И = −J S ⋅ ε .
В формулах (3.1) и (3.2) приняты следующие обозначения: m – масса
звена; JS – момент инерции звена относительно оси, проходящей через его
центр масс; aS – ускорение центра масс звена; ε – угловое ускорение звена.
а
б
в
Рис. 3.1
Величины aS и ε вычисляются в ходе кинематичекого анализа меха-
низма. При поступательном движении звена (рис. 3.1, б) его силы инерции
приводятся к главному вектору PИ сил инерции, вычисляемому по формуле
(3.3)
PИ = − m ⋅ a А ,
где a А – ускорение ползуна.
Главный момент МИ сил инерции в этом случае равен нулю. Если ползун перемещается с постоянной скоростью, то РИ = 0.
При вращении звена вокруг неподвижной оси, проходящей через его
центр масс (рис. 3.1, в), главный вектор PИ сил инерции равен нулю, а главный момент МИ вычисляется по формуле (3.2). В случае, когда звено вращается с постоянной угловой скоростью, МИ = 0.
Если ось вращения звена не проходит через его центр масс, главный
вектор PИ и главный момент МИ не равны нулю и вычисляются по формулам (3.1) и (3.2) соответственно.
63
64.
При решении прикладных задач нередко используют более простойинженерный метод расчета сил инерции, называемый методом замещающих точечных масс.
Идея расчета состоит в том, что звено заменяют системой точечных
масс. Силы инерции звена определяют как силы инерции масс, расположенных в замещающих точках. Очевидно, что звено и замещающая его система
точечных масс должны быть эквивалентны.
Условия эквивалентности:
1. Масса звена должна быть равна сумме замещающих масс.
2. Общий центр масс замещающей системы точечных масс должен
совпадать с центром масс звена.
3. Момент инерции масс, находящихся в замещающих точках, относительно оси, проходящей через их общий центр масс, должен быть равен моменту инерции звена относительно этой же оси.
Если при замене выполняются только первые два условия, то замена
приближенная (статическая), при выполнении трех условий – точная (динамическая).
На определенных этапах силового расчета целесообразно применять
статическую замену звена точечными массами. Это позволяет значительно
упростить расчетную модель.
Если звено симметричное (рис. 3.2), то при статической замене точечные массы mA и mB размещают в точки А и В (в центры шарниров).
Рис. 3.2
Условия эквивалентности замены:
m A + mB = m ;
m A ⋅ a = mB ⋅ b .
64
65.
После совместного решения уравненийmB = m ⋅ a (a + b ) ,
m A = m ⋅ b (a + b ) ;
где m – масса звена; a и b – размеры.
Силы инерции точечных масс:
PИA = − m A ⋅ a A ;
(3.4)
PИB = − mB ⋅ a B .
3.2. КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ СТРУКТУРНЫХ ГРУПП
II КЛАССА 2-ГО ПОРЯДКА МЕТОДОМ ПЛАНОВ
Порядок силового расчета механизмов обусловлен статической определимостью структурных групп. Начинают его с расчета структурной группы,
наиболее удаленной от исходного механизма. Структурные группы рассчитывают в порядке, обратном их присоединению. Исходный механизм рассматривается последним.
Ознакомимся более подробно с расчетными моделями структурных
групп II класса 2-го порядка, как наиболее распространенными.
Структурная группа II класса 2-го порядка первого вида
На рис. 3.3, а показана схема нагружения этой структурной группы. Все
внешние силы, действующие на звенья 2 и 3, приведены к равнодействую
щим P2 и P3 и парам сил с моментами М2 и М3 соответственно. Силы P2 , P3
и моменты сил М2 и М3 известны по величине и направлению. Определению
подлежат реакции R12 и R43 , действующие в шарнирах А и С, и реакция R32
или R23 , действующая в шарнире В. Линии действия этих сил проходят через центры шарниров, но они неизвестны по величине и направлению.
Для решения задачи реакции в шарнирах А и С раскладываются на со n
n
ставляющие. Нормальные составляющие реакций R12
и R43
направлены
τ
τ
по звеньям 2 и 3 соответственно, а тангенциальные составляющие R12
и R43
–
перпендикулярно им.
65
66.
аб
Рис. 3.3
Поскольку структурная группа находится в мгновенном равновесии,
то и каждое ее звено находится в равновесии. В связи с этим можно записать:
τ
− R12
⋅ l АВ + M 2 + P2 ⋅ h2 = 0 ;
(3.5)
τ
(3.6)
R43
⋅ lВС − M 3 − P3 ⋅ h3 = 0 .
n τ
τ
n
(3.7)
R12
+ R12 + P2 + P3 + R43
+ R43
= 0.
В уравнениях (3.5) и (3.6) h2 и h3 – плечи сил P2 и P3 соответственно.
τ
τ
По этим уравнениям вычисляются значения R12
и R43
тангенциальных со-
ставляющих реакций, уточняется их направление. Если при решении уравнений (3.5) и (3.6) значение какой-либо из искомых реакций получилось отрицательным, то она направлена противоположно указанному на схеме
нагружения направлению.
Нормальные составляющие реакций определяются в ходе решения векторного уравнения (3.7).
Графическое решение векторного уравнения называется планом сил.
План сил строится в масштабе µp. Значение µp выбирается произвольно
с учетом модулей сил. На рис. 3.3, б приведено графическое решение векторного уравнения (3.7).
66
67.
Для построения плана сил определяются длины отрезков, которые будут изображать в принятом масштабе известные по величине силы. Так,τ
ab = R12
µP ;
bc = P2 µ P ;
cd = P3 µ P ;
τ
de = R43
µP .
Все известные силы последовательно изображаются на чертеже. Для
определения нормальных составляющих искомых реакций через точку а
τ
плана сил проводится перпендикуляр к линии действия силы R12
, а через
τ
точку е – перпендикуляр к линии действия реакции R43 . В точке пересечения перпендикуляров силовой многоугольник замыкается. Отрезок af изоб n
n
R
ражает 12 , а отрезок ef ̶ R43
.
Реакции R12 и R43 определяются в ходе решения следующих векторных
уравнений:
n τ
+ R12
R12 = R12
и
n τ
+ R43 .
R43 = R43
На плане сил они изображены отрезками fb и df соответственно.
Для определения реакции в шарнире В надо рассмотреть равновесие
системы сил, действующих на одно из звеньев структурной группы. Равновесие системы сил, действующих на звено 2, описывается уравнением
(3.8)
R12 + P2 + R32 = 0 ,
а равновесие системы сил, действующих на звено 3, уравнением
R43 + P3 + R23 = 0 .
(3.9)
На рис. 3.3, б показано решение уравнения (3.9).
При построении плана сил надо иметь в виду, что порядок сложения
сил на конечный результат не влияет.
n
n
Модули сил вычисляются по формулам: R12 = af ⋅ µ P ; R43 = ef ⋅ µ P ;
R12 = fb ⋅ µ P ; R23 = R32 = fc ⋅ µ P .
Структурная группа II класса 2-го порядка второго вида
Схема нагружения рассматриваемой структурной группы приведена
на рис. 3.4, а.
Все внешние силы, действующие на шатун 2, включая силы инерции,
приведены к силе P2 и паре сил с моментом M2, а силы, действующие
67
68.
на ползун 3, к равнодействующей P3 . Силы P2 и P3 , момент M2 заданы.Требуется определить реакции R12 , R32 (или R23 ) в шарнирах А, В и реак
цию R03 , с которой стойка действует на ползун.
а
б
Рис. 3.4
Поскольку величина и направление реакции R12 не известны, она пред n
τ
ставлена в виде составляющих R12
и R12
. Реакция в поступательной паре
всегда направлена по нормали к направляющей. Не известны ее величина
и точка приложения. На схеме нагружения положение реакции R03 по отношению к точке В задано размером X, подлежащим определению. Под
действием заданной системы сил кинематическая цепь находится в равновесии. Условия равновесия:
τ
(3.10)
R12
⋅ l AB − M 2 − P2 ⋅ h2 = 0 ;
n τ
(3.11)
R12
+ R12 + P2 + P3 + R03 = 0 ,
где l2AB – длина шатуна; h2 – плечо силы P2 .
τ
Модуль реакции R12
определяется решением уравнения (3.10). Если зна-
чение реакции получается отрицательным, то она имеет направление, противоположное обозначенному на схеме нагружения. Величина и направление
68
69.
nсил R12
и R03 определяются при решении уравнения (3.11). Графическое его
решение показано на рис. 3.4, б. Построения выполнены в масштабе µp.
Реакция R23 определяется по уравнению равновесия системы сил, действующих на ползун:
R23 + P3 + R03 = 0 .
(3.12)
Решение уравнения (3.12) показано на рис. 3.4, б.
Модули искомых сил вычисляются следующим образом:
R23 = ec ⋅ µ P .
Для определения положения точки приложения реакции R03 (размера Х)
n
R12
= ea ⋅ µ P ;
R03 = ed ⋅ µ P ;
R12 = eb ⋅ µ P ;
составляется уравнение моментов сил, действующих на ползун, относительно точки В. R03 ⋅ X = 0. Поскольку R03 ≠ 0, X = 0. Следовательно, линия
действия реакции R03 проходит через ось шарнира В.
Структурная группа II класса 2-го порядка третьего вида
Структурная группа состоит из кулисы 3 и камня кулисы 2. Схема ее
нагружения приведена на рис. 3.5, а. Известны сила P3 и момент M3, действующие на кулису 3. Пусть камень кулисы не нагружен. Требуется опре
делить силу R12 , с которой звено 1 действует на звено 2, реакцию R03
в шарнире О и реакцию R32 (или R23 ) в соединении кулисы с камнем.
Под действием указанной на рис. 3.5, а системы сил структурная группа находится в равновесии. Следовательно, каждое ее звено тоже находится
в равновесии. На камень кулисы действуют только две силы (рис. 3.5, б) –
R12 и R32 (сила, с которой кулиса действует на камень).
Реакция R32 направлена перпендикулярно ОА, но точка ее приложения
неизвестна. Направление реакции R12 неизвестно, но линия ее действия
проходит через ось шарнира А. По аксиоме статики [6], если тело находится
в равновесии под действием двух сил, то эти силы должны быть равны по
величине и направлены по одной прямой в противоположные стороны. Та
ким образом, реакция R12 направлена перпендикулярно ОА, а линия дей
ствия реакции R32 проходит через точку А.
69
70.
ба
в
г
Рис. 3.5
R
На рис. 3.5, в показана схема нагружения кулисы. Реакция 23 , обра
зующая с R32 уравновешенную систему сил, проходит через точку А кулисы
перпендикулярно ОА. Ее величина вычисляется по уравнению
R23 ⋅ lOA − P3 ⋅ h3 − M 3 = 0 .
(3.13)
В уравнении (3.13) lOA = OA ⋅ µl , а h3 – плечо силы P3 .
Величина и направление реакции R03 определяются при решении уравнения
R23 + P3 + R03 = 0 .
Графическое его решение показано на рис. 3.5, г. План сил построен
в масштабе µp.
Модули сил: R12 = R23 = R32 = bc ⋅ µ P ; R03 = ca ⋅ µ P .
Структурная группа II класса 2-го порядка четвертого вида
Кинематическая схема структурной группы, состоящей из камня кулисы 2 и ползуна 3, перемещающегося параллельно x–x, показана на рис. 3.6, а.
Звено 2 не нагружено. На звено 3 действует известная по величине
и направлению внешняя сила P3 . Надо определить силу R12 , с которой
кулиса 1 действует на камень 2, и реакцию R03 в соединении ползуна
со стойкой.
70
71.
ва
б
г
Рис. 3.6
На камень кулисы действует уравновешенная система сил (рис. 3.6, б),
следовательно R12 = − R32 . Линия действия этих сил проходит через центр
шарнира А перпендикулярно t–t. Поскольку R23 = − R32 , то и реакция R23
перпендикулярна t–t. На рис. 3.6, в показана схема нагружения ползуна 3.
Реакция R03 направлена перпендикулярно x–x, и ее положение относительно
шарнира А определяется линейным размером X.
Уравнение равновесия системы сил, действующих на ползун:
R23 + P3 + R03 = 0 .
Его графическое решение в масштабе µ P показано на рис. 3.6, г. Раз
мер X, определяющий положение точки приложения реакции R03 , вычисляется по уравнению моментов сил, действующих на звено 3, относительно
центра шарнира А. В данном случае X = 0.
Значения искомых сил:
R12 = R23 = R32 = bc ⋅ µ P ;
71
R03 = ca ⋅ µ P .
72.
Структурная группа II класса 2-го порядка пятого видаСтруктурная группа (рис. 3.7, а) состоит из кулисного камня 2 и посту
пательно движущийся кулисы 3, на которую действует внешняя сила P3 .
Последняя известна по величине, направлению и приложена в точке S3. Камень кулисы внешними силами не нагружен. Определению подлежат реак
ция R12 , с которой звено 1 действует на звено 2, реакция R03 и реакция R32
(или R23 ) в соединении камня и кулисы. R23 = − R32 .
в
а
г
б
Рис. 3.7
На рис. 3.7, б показана схема нагружения камня кулисы. По условию
его равновесия R12 = − R32 . Следовательно, реакция R32 проходит через
центр шарнира А перпендикулярно y–y. Реакция R23 проходит через точку
А кулисы (рис. 3.7, в).
R
+
P
Уравнение равновесия кулисы: 23
3 + R03 = 0. Графическое его ре-
шение показано на рис. 3.7, г. План сил построен в масштабе µp.
Модули искомых реакций:
R12 = R23 = R32 = ac ⋅ µ P ; R03 = cb ⋅ µ P .
72
73.
Положение точки приложения реакции R03 (размер X) определяетсяпо уравнению моментов сил, действующих на кулису, относительно точки S3.
R23 ⋅ lS 3 A − R03 ⋅ X = 0 ,
где lS 3 A = S3 A ⋅ µl .
Отсюда X = R23 ⋅ lS 3 A R03 .
3.3. КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ ВЕДУЩЕГО ЗВЕНА
МЕХАНИЗМА
Особенность силового расчета ведущего звена механизма состоит в том,
что система сил, действующих на него, без учета движущей силы не находится в равновесии. Для обеспечения равновесия к звену дополнительно
прикладывают силу Pур или пару сил с моментом Myp, которые называют
уравновешивающими.
Схема нагружения кривошипа зависит от типа привода механизма.
Наиболее часто привод осуществляется через муфту. Возможен привод через редуктор или ременную передачу.
Рассмотрим случай, когда привод механизма осуществляется от двигателя через муфту.
б
а
Рис. 3.8
На рис. 3.8, а показана схема нагружения кривошипа. Внешняя сила P1
и пара сил с моментом M1 являются результирующими внешних нагрузок
73
74.
и сил инерции и на данном этапе расчета известны. Реакция R21 известнапо величине и направлению, поскольку R21 = − R12 . Сила R01 , с которой
стойка действует на кривошип, подлежит определению. Чтобы обеспечить
равновесие кривошипа, к нему прикладывается уравновешивающий момент Myp, величина которого определяется по уравнению
M ур − R21 ⋅ H 2 − P1 ⋅ H 1 − М 1 = 0.
(3.14)
В уравнении (3.14) H1 и H2 – плечи сил P1 и R21 соответственно.
Реакция R01 вычисляется в ходе решения векторного уравнения:
(3.15)
R21 + P1 + R01 = 0 .
Графическое решение уравнения (3.15) дано на рис. 3.8, б. План сил построен в масштабе µp.
Длины отрезков, изображающих силы R21 и P1 :
ab = R21 µ P ;
bc = P1 µ P .
Модуль реакции R01 вычисляется по формуле
R01 = ac ⋅ µ P .
Если привод механизма осуществляется через зубчатую передачу,
система сил, действующих на кривошип, уравновешивается уравновешива
ющей силой Pур (рис. 3.9, а).
а
б
Рис. 3.9
74
75.
Кривошип жестко связан с зубчатым колесом 1´, образующим зацепление с ведушей шестерней 2. Центр масс звена 1 находится в точке О.На кривошип действуют силы: тяжести G1 , реакции R21 и R01 и уравнове
шивающая сила Pур , направленная по нормали к контактирующим поверхностям зубьев колес 1´ и 2. В эвольвентном зацеплении нормаль к контактирующим поверхностям зубьев касается основных окружностей, радиусы
которых обозначены rb1´ и rb2 соответственно. Главный вектор и главный
момент сил инерции кривошипа в этом случае равны нулю.
Уравновешивающая сила вычисляется по уравнению
Pур ⋅ rb1′ − R21 ⋅ H = 0,
а реакция R01 определяется при решении векторного уравнения
Pур + G1 + R21 + R01 = 0.
(3.16)
Графическое решение уравнения (3.16) приведено на рис. 3.9, б. Мо
дуль реакции R01 :
R01 = ad ⋅ µ P .
3.4. КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТ ШЕСТИЗВЕННОГО
РЫЧАЖНОГО МЕХАНИЗМА II КЛАССА
Рассмотрим конкретный пример кинетостатического расчета многозвенного рычажного механизма.
Пусть требуется выполнить силовой расчет шестизвенного кривошипно-ползунного механизма, кинематическая схема которого приведена
на рис. 3.10, а. Механизм состоит из стойки 0, кривошипа 1, шатунов 2 и 4,
коромысла 3 и ползуна 5. Кривошип вращается с постоянной угловой скоростью ω1 вокруг оси О. На ползун (выходное звено) действует сила полез
ного сопротивления ( PПС ), известная по величине и направлению. Заданы
массы звеньев (m1, m2, m3, m4, m5) и положения их центров масс, обозначенные на кинематической схеме буквами S1, S2, S3, S4, S5 соответственно.
Центр масс ползуна совпадает с точкой D. Известны все кинематические
75
76.
размеры. Требуется определить реакции во всех кинематических парахи уравновешивающий момент Myp, действующий на кривошип.
а
б
в
Рис. 3.10
Алгоритм силового расчета определяется формулой строения механизма, имеющей вид
0;1
2;3
4;5
.
→
→
и. м.
II ;2
II ;2
Механизм состоит из исходного механизма и двух последовательно соединенных структурных групп II класса 2-го порядка первого и второго вида соответственно.
Чтобы определить силы, действующие в механизме, необходимо иметь
данные кинематического расчета. В связи с этим методом планов выполним
кинематический расчет механизма в заданном его положении. Используем
расчетную модель, описанную в подразделе 2.1 данного учебного пособия.
76
77.
Алгоритм расчета скоростейСкорость V A точки A кривошипа: VA = ω1 ⋅ lOA . Вектор скорости V A
направлен перпендикулярно звену 1 в сторону вращения.
Скорость VB точки B шатуна 2 вычисляется при решении уравнения
(3.17)
VB = V A + VBA .
В уравнении (3.17) вектор VBA направлен перпендикулярно шатуну 2,
а вектор VB – перпендикулярно коромыслу BC в заданном его положении.
Уравнение (3.17) решается путем построения плана скоростей (рис. 3.10, б).
Масштабный коэффициент плана скоростей – µV.
Скорость VD ползуна определяется по уравнению
(3.18)
VD = VB + VDB .
Скорость VB точки B шатуна изображена на плане скоростей отрез
ком pVb, т. е. известна по величине и направлению. Скорость VDB направлена перпендикулярно шатуну 4, а абсолютная скорость точки D направлена
параллельно x–x. Графическое решение уравнения (3.18) – на рис. 3.10, б.
Модули линейных и угловых скоростей вычисляются по формулам:
VB = pV b ⋅ µV ;
VBA = ab ⋅ µV ;
ω2 = VBA l AB ;
VD = pV d ⋅ µV ;
ω3 = VB lBC ;
VDB = bd ⋅ µV ;
ω4 = VDB lDB .
Скорости центров масс звеньев определяются по свойству подобия
планов скоростей (см. подраздел 2.2.3 данного учебного пособия).
Для определения скорости VS1 центра масс кривошипа составляется
пропорция AO OS1 = pV a pV s1 , откуда pV s1 = apV ⋅ OS1 AO . Отрезок pVs1
откладывается на отрезке pVa плана скоростей. Он изображает в масшта
бе µV скорость VS1 .
Для расчета скорости VS 2 центра масс шатуна используется пропорция
AS2 AB = as2 ab , из которой следует as2 = ab ⋅ AS2 AB . На плане скоростей
определяется положение точки s2. Последняя соединяется с полюсом pV.
77
78.
Скорость VS 3 центра масс коромысла вычисляется по пропорцииCS3 CB = pV s3 pV b , откуда pV s3 = pV b ⋅ CS3 CB . Отрезок pVs3 откладывается на отрезке pVb плана скоростей.
Скорость VS 4 центра масс шатуна 4 вычисляется с использованием
пропорции BS4 BD = bs4 bd , из которой следует bs4 = bd ⋅ BS4 BD . Отрезок bs4 откладывается от точки b на отрезке bd плана скоростей, затем точка s4 соединяется с полюсом pV.
Скорости центров масс звеньев вычисляются по формулам:
VS1 = pV s1 ⋅ µV ; VS 2 = pV s2 ⋅ µV ; VS 3 = pV s3 ⋅ µV ; VS 4 = pV s4 ⋅ µV .
Алгоритм расчета ускорений
При кинематическом расчете угловую скорость кривошипа считают по
стоянной. В связи с этим ускорение a A конца A кривошипа вычисляется по
формуле a A = ω12 ⋅ lOA . Вектор a A направлен параллельно кривошипу в рассматриваемом его положении от точки A в сторону точки О.
Ускорение a B точки В шатуна 2 определяется по уравнению (2.7),
согласно которому
C
Cn
C
Cn
C
+ aτBA = a BC
+ aτBC .
a A + a BA
(3.19)
n
относительного ускорения точки В
Нормальная составляющая a BA
направлена параллельно звену 2 от точки В в сторону точки A, и ее модуль
Cn
n
определяется по формуле a BA
направлено парал= ω22 ⋅ l AB . Ускорение a BC
n
лельно коромыслу и составляет a BC
= ω32 ⋅ lBC .
C
Тангенциальные составляющие aτBA и aτBC ускорений направлены пер-
пендикулярно шатуну 2 и коромыслу 3 соответственно. Если принять масштабный коэффициент плана ускорений равным µa, то длины отрезков
(см. рис. 3.10, в), которыми должны быть изображены известные по величине ускорения, составят:
pa a = a A µa ;
n
an = a BA
µa ;
n
pa m = a BC
ma .
Графическое решение уравнения (3.19) показано на рис. 3.10, в.
78
79.
Ускорение a D ползуна 5 вычисляется по уравнению (2.10), в соответствии с которымn
(3.20)
a D = a B + a DB
+ aτDB .
В этом уравнении ускорение a B определено и на плане ускорений
n
изображается отрезком pab. Нормальная составляющая a DB
относительного
ускорения точки D направлена параллельно шатуну 4 от точки D в сторону
n
точки B. a DB
= ω42 ⋅ lDB . Тангенциальная составляющая aτDB направлена пер
пендикулярно звену 4, а абсолютное ускорение a D – параллельно направляющей x–x.
Для решения уравнения (3.20) вычисляется длина отрезка bk, изобра n
n
жающего на плане ускорений a DB
. bk = a DB
µa . Решение уравнения (3.20)
показано на рис. 3.10, в.
Линейные и угловые ускорения вычисляются по формулам:
aτBA = nb ⋅ µa ;
a BA = ab ⋅ µa ;
a B = pa b ⋅ µa ;
aτBC = mb ⋅ ma ;
aτDB = kd ⋅ µa ;
a D = pa d ⋅ µa ;
ε 2 = aτBA l AB ;
ε 3 = aτBC lBC ;
ε 4 = aτDB lBD .
Ускорения центров масс звеньев определены по свойству подобия планов ускорений (см. подраздел 2.2.3 данного учебного пособия).
AO OS1 = pa a pa s1 , откуда pa s1 = apa ⋅ OS1 AO . На плане ускорений
откладывается отрезок pas1, который и изображает в масштабе µa ускорение
aS1 . aS1 = pa s1 ⋅ µa .
По пропорции AS2 AB = as2 ab вычисляется длина отрезка as2, определяющего на плане ускорений положение точки s2 (см. рис. 3.10, в). Точка s2
соединяется с полюсом плана ускорений. aS 2 = pa s2 ⋅ µa .
Для определения ускорения aS 3 центра масс коромысла вычисляется длина отрезка, pas3. По свойству подобия CS3 CB = pa s3 pa b , откуда
pa s3 = pa b ⋅ CS3 CB . aS 3 = pa s3 ⋅ µa .
79
80.
Пропорцию BS4 BD = bs4 bd решаем относительно bs4. Получаемbs4 = bd ⋅ BS4 BD . Отрезок bs4 откладываем на отрезке bd плана ускорений
от точки b. Точку s4 соединяем с полюсом плана ускорений.
aS 4 = pa s4 ⋅ µa .
Теперь переходим непосредственно к силовому расчету механизма.
Начинается он с расчета структурной группы, состоящей из шатуна 4 и ползуна 5. Результаты этого расчета используются при кинетостатическом расчете структурной группы, состоящей из шатуна 2 и коромысла 3. В последнюю очередь вычисляются силы, действующие на кривошип.
Силовой расчет структурной группы,
состоящей из звеньев 4 и 5
Для обеспечения ее равновесия, в соответствии с принципом Даламбера,
надо определить силы инерции шатуна и ползуна. Воспользуемся инженерным методом расчета сил инерции, упрощающим расчетную модель.
Массу шатуна 4 разнесем в центры шарниров B и D и обозначим их
буквами mB4 и mD4 соответственно (рис. 3.11, а).
mD 4 = m4 ⋅ lS 4 B lBD ,
mB 4 = m4 ⋅ lS 4 D lBD ;
где lBD – длина шатуна; lS 4 D и lS 4 B – кинематические размеры.
Силы инерции этих масс:
PИB 4 = mB 4 ⋅ a B ; PИD 4 = mD 4 ⋅ a D .
Сила инерции ползуна: PИ 5 = m5 ⋅ a D .
Направление сил инерции обозначено на рис. 3.11, а. Силы тяжести,
действующие на звенья, вычисляются по формуле
Gi = mi ⋅ q ,
(3.21)
где mi – масса i-го звена; q – ускорение свободного падения.
В соответствии с принципом освобождаемости от связей действие от
брошенных звеньев заменяется реакциями. Реакция R34 в шарнире В рас τ
n
кладывается на составляющие R34
и R34
. Реакция R05 (действующая на ползун со стороны стойки) направлена перпендикулярно направляющей (перпендикулярно x–x).
80
81.
аб
Рис. 3.11
Уравнения равновесия системы сил, действующих на структурную
группу:
τ
− R34
⋅ BD + PИB 4 ⋅ h1 + G4 ⋅ h2 = 0 ;
n
τ
G
R34
+ R34
+ G4 + PИB 4 + PИD 4 + G5 + PИ 5 + PПС + R05 = 0 .
(3.22)
(3.23)
В уравнении (3.22) h1 и h2 – длины отрезков (в мм), изображающих
плечи сил на схеме нагружения структурной группы (рис. 3.11, а). Реакция
τ
n
определяется при решении уравнения (3.23), а реакции R34
и R05 – при
R34
решении векторного уравнения. Его решение в графической форме представлено на рис. 3.11, б. Масштабный коэффициент плана сил – µp.
Реакция R45 в шарнире D определяется при решении уравнения
G
G5 + PИ 5 + PПС + R05 + R45 = 0 .
81
82.
Определение реакций в кинематических парах структурной группы,состоящей из звеньев 2 и 3
Схема ее нагружения приведена на рис. 3.12, а. Для расчета сил
инерции шатуна 2 и коромысла 3 массы этих звеньев разносим в центры
шарниров А, В и С соответственно. Обозначим точечные массы, заменяющие шатун, – mB2 и mA2, а точечные массы, заменяющие коромысло, –
mB3 и mC3.
mB 2 = m2 ⋅ lS 2 A l AB ;
m A2 = m2 ⋅ lS 2 B l AB ;
mB 3 = m3 ⋅ lS 3C lBC ;
mC 3 = m3 ⋅ lS 3 B lBC .
а
б
Рис. 3.12
82
83.
Силы инерции этих масс:PИB 2 = mB 2 ⋅ a B ;
PИA2 = m A2 ⋅ a A ;
PИB 3 = mB 3 ⋅ a B ;
PИC 3 = 0 .
Силы тяжести звеньев 2 и 3 вычисляются по формуле (3.21).
Уравнения равновесия системы сил, действующих на структурную
группу:
τ
− R12
⋅ AB + PИA2 ⋅ h4 + G2 ⋅ h3 = 0 ;
τ
R03
⋅ BC − G3 ⋅ h5 = 0 ;
n τ
τ
n
R12
+ R12 + G2 + PИA2 + PИB 2 + PИB 3 + G3 + R43 + R03
+ R03
= 0.
(3.24)
(3.25)
(3.26)
В уравнениях (3.24) и (3.25) h3 , h4 , h5 – длины отрезков (в мм), изобра τ
τ
и R03
определяются при решении уравнежающих плечи сил. Реакции R12
n
n
ний (3.24) и (3.25), реакции R12
и R03
– по уравнению (3.26), графическое
решение которого дано на рис. 3.12, б. Реакцию R23 или R32 можно определить по уравнению равновесия системы сил, действующих на шатун 2 или
коромысло 3. Уравнение равновесия шатуна 2:
R12 + G2 + PИA2 + PИB 2 + R32 = 0 .
Завершающий этап силового расчета – определение уравновешивающе
го момента Myp и реакции R01 в шарнире О.
Расчет сил, действующих на кривошип
На рис. 3.13, а показана схема нагружения кривошипа. На него дей
ствуют силы: R21 , G1 ; PИA1 ; R01 и Myp.
В соответствии с методом замещающих точечных масс кривошип заменяем двумя точечными массами mA1 и mO1.
m А1 = m1 ⋅ lOS1 lOA ,
mO1 = m1 ⋅ l AS1 lOA .
Силы инерции точечных масс:
PИA1 = m A1 ⋅ a A , PИO1 = 0 .
Реакция R21 известна по величине и направлению, поскольку R21 = − R12 .
83
84.
аб
Рис. 3.13
Уравнения равновесия системы сил, действующих на кривошип:
M ур + G1 ⋅ H 1 − R21 ⋅ H 2 = 0.
R21 + PИA1 + G1 + R01 = 0 .
(3.27)
(3.28)
В уравнении (3.27) H1 и H2 – действительные плечи сил, измеряемые
в метрах. Графическое решение уравнения (3.28) показано на рис. 3.13, б.
Масштабный коэффициент плана сил – µp.
3.5. РАСЧЕТ УРАВНОВЕШИВАЮЩЕЙ СИЛЫ
МЕТОДОМ Н. Е. ЖУКОВСКОГО
Метод расчета уравновешивающей силы Pур (или уравновешивающего
момента), предложенный Н. Е. Жуковским, основывается на принципе возможных перемещений [1, 4].
В соответствии с этим методом для определения уравновешивающей
силы надо построить повернутый на 90о план скоростей, к соответствующим точкам которого приложить все внешние силы, включая силы инерции
и уравновешивающие силы. Под действием этой системы сил план скоростей, получивший название рычага Жуковского, находится в равновесии
84
85.
и сумма моментов сил относительно точки pV равна нулю. По сути такаясумма моментов физически представляет собой равенство нулю мгновенных
мощностей сил, действующих в механической системе в ее установившемся
движении. Уравнение содержит только одно неизвестное Pур . Следует
отметить, что план скоростей можно поворачивать в любую сторону, поскольку это не влияет на конечный результат. Если на звено действует момент M (рис. 3.14, а), то его заменяют эквивалентной парой (рис. 3.14, б),
момент которой равен M, а плечо пары равно длине звена. Модуль сил, образующих пару, вычисляется по формуле
P′ = P′′ = M l AB .
а
б
в
Рис. 3.14
При составлении схемы нагружения рычага Жуковского силы P′ и P′′
помещаются в точки a и b соответственно (рис. 3.14, в). Направление их
не меняется.
Рассмотрим конкретный пример расчета уравновешивающего момента
методом рычага Жуковского. Определим уравновешивающий момент Myp,
действующий на кривошип кривошипно-ползунного механизма в положении, изображенном на рис. 3.10, а. План скоростей механизма показан
на рис. 3.10, б.
Повернем план скоростей на угол 90о против хода часовой стрелки
и в точки a, b, d, s1, s2, s3, s4, s5 (рис. 3.15) параллельно самим себе со схем
нагружения структурных групп (рис. 3.11, а и 3.12, а) и кривошипа
(рис. 3.13, а) перенесем силу полезного сопротивления, силы тяжести
и инерции, сохраняя их направление. Уравновешивающий момент представим
85
86.
′′
′
′
в виде пары сил Pур и Pур с плечом, равным lOA. Силы Pур и Pур′′ приложим
в точках a и pV , как показано на рис. 3.15. Под действием системы сил рычаг Жуковского находится в равновесии. Условие равновесия описывается
уравнением
− PУР ⋅ pV a − G1 ⋅ h1 − G2 ⋅ h2 + (PПС + PИD 4 + PИ 5 ) ⋅ pV d +
+ G3 ⋅ h3 + G4 ⋅ h4 + (PИB 2 + PИB 3 + PИB 4 ) ⋅ h5 = 0.
(3.29)
Рис. 3.15
В уравнении (3.29) плечи сил измеряются на схеме нагружения рычага
Жуковского в миллиметрах чертежа. Если при решении уравнения (3.29)
значение уравновешивающей силы получилось отрицательным, то она имеет направление, противоположное указанному на схеме нагружения.
Уравновешивающий момент вычисляется по формуле
M ур = Pур ⋅ lOA .
(3.30)
В уравнении (3.30) lOA – длина кривошипа (м).
Метод Жуковского является универсальным и может быть использован
для расчета уравновешивающей силы или уравновешивающего момента
механизма любой сложности.
86
87.
4. УРАВНОВЕШИВАНИЕ МЕХАНИЗМОВПри работе механизма его подвижные звенья оказывают нежелательное
переменное силовое воздействие на стойку и, как следствие, на фундамент.
На рис. 4.1, а показан кривошипно-ползунный механизм, состоящий из
стойки 0, кривошипа 1, шатуна 2 и ползуна 3. Механизм закреплен на фундаменте 4. В рассматриваемом положении на стойку действует внешняя
сила P , реакции R10 и R30 . Они известны, поскольку R10 = − R01 и R30 = − R03 .
Реакции R01 и R03 определяются в ходе силового расчета механизма. Кроме
того, на стойку со стороны фундамента 4 действуют силы, которые можно
привести к главному вектору R40 и главному моменту M40. Главный вектор
проходит через ось O вращения кривошипа.
Система сил, действующих на стойку, находится в равновесии. Уравнения равновесия системы сил:
(4.1)
P + R10 + R30 + R40 = 0 ,
M 40 − R30 ⋅ l = 0 .
(4.2)
Графическое решение уравнения (4.1) приведено на рис. 4.1, б. В урав
нении (4.2) буквой l обозначено плечо силы R30 . Величина l зависит от положения ползуна, т. е. является переменной.
б
а
Рис. 4.1
87
88.
Обозначим главный вектор сил, действующих на фундамент, как R04 ,а главный момент – M04. Тогда R04 = − R40 и M 04 = − M 40 .
Главный вектор R04 и главный момент M04 зависят от внешних сил, сил
инерции и сил тяжести (последние постоянны). Они содержат две переменные составляющие, одна из которых обусловлена движением звеньев
с ускорением (это силы инерции), другая – действием активных сил и моментов.
Уравновешиванием называют устранение переменного воздействия
на фундамент со стороны стойки механизма. Механизм считается уравновешенным, если главный вектор и главный момент сил, действующих
со стороны его стойки на фундамент, остаются постоянными при заданном
движении начальных звеньев. Выполнение этих условий обеспечить крайне
сложно. Обычно ограничиваются частичным уменьшением инерционного
воздействия звеньев.
Уравновешивание путем распределения масс звеньев по условию минимизации инерционного воздействия на фундамент называют уравновешиванием масс механизма.
Обозначим главный вектор и главный момент сил инерции механизма
буквами PИΣ , M ИΣ соответственно. Тогда условия уравновешивания масс
механизма будут описываться уравнениями:
PИΣ = 0 ;
M ИΣ = 0 .
(4.3)
(4.4)
При выполнении всех условий уравновешивание называют динамическим. При выполнении только условия (4.3) – статическим, а при выполнении только условия (4.4) – моментным.
4.1. СТАТИЧЕСКОЕ УРАВНОВЕШИВАНИЕ МЕХАНИЗМОВ
При статическом уравновешивании массы звеньев распределяют так,
чтобы общий центр масс механизма был неподвижен. Задачу статического
уравновешивания решают обычно методом замещающих точечных масс,
в соответствии с которым каждое звено заменяют двумя точечными масса88
89.
ми, находящимися в центрах шарниров. Условия замены звена точечнымимассами, формулы для расчета последних приведены в подразделе 3.1 данного учебного пособия.
Статическое уравновешивание
кривошипно-коромыслового механизма
Кинематическая схема кривошипно-коромыслового механизма показана на рис. 4.2, а.
б
а
в
Рис. 4.2
Каждое из подвижных звеньев рассматриваемого механизма заменяем
двумя точечными массами, находящимися в центрах шарниров, соединяющих данное звено с другими звеньями. В частности, кривошип заменяется
массами mA1 и mO1, шатун – массами mA2 и mB2, а коромысло – массами mB3
и mC3, величины которых вычисляются по формулам:
m A1 = m1 ⋅
lOS1
lOA
mО1 = m1 ⋅
;
89
l AS
1
lOA
;
(4.5)
90.
m A2 = m2 ⋅lBS 2
mB 3 = m3 ⋅
lCS 3
l AB
lBC
;
mB 2 = m2 ⋅
l AS 2
;
mC 3 = m3 ⋅
lBS 3
l AB
lBC
;
(4.6)
.
(4.7)
В формулах (4.5)–(4.7) m1, m2, m3 – массы подвижных звеньев.
Массы mO1 и mC3 неподвижны. Подвижные массы mA и mB сосредоточены в точках А и В.
mB = mB 2 + mB 3 .
m A = m A1 + m A2 ;
Для их уравновешивания на кривошип и коромысло устанавливаются
противовесы, массы mП1 и mП2 которых подбираются по условиям:
mП 1 ⋅ lOD = m A ⋅ lOA ;
mП 2 ⋅ lCE = mB ⋅ lBC .
(4.8)
В формулах (4.8) lOD и lCE – радиусы установки противовесов. Они подбираются по конструктивным соображениям.
В заключение следует отметить, что двумя противовесами можно обеспечить полное статическое уравновешивание кривошипно-коромыслового
механизма. Сложнее решить эту задачу, если механизм содержит поступательно движущиеся звенья.
Статическое уравновешивание
кривошипно-ползунного механизма
Кинематическая схема механизма показана на рис. 4.2, б. Его полное
статическое уравновешивание обеспечивается установкой противовесов на
шатун и кривошип.
Для определения параметров противовесов кривошип заменяют точечными массами mA1 и mO1, а шатун – массами mA2 и mB2. Массы mA1 и mO1
определяются по формулам (4.5), а массы mA2 и mB2 – по формулам (4.6).
Масса mO1 неподвижна. Обозначим подвижную массу в точке В как mB.
mB = mB 2 + m3 .
Статический момент противовеса массой mП1, устанавливаемого в точке С шатуна, определяется по условию
mП 1 ⋅ l AC = mB ⋅ l AB .
90
91.
После установки этого противовеса в точке А будет сосредочена значительная масса mA, для уравновешивания которой на кривошип устанавливается второй противовес массой mП2.mП 2 ⋅ lOD = m A ⋅ lOA ,
где m A = m A1 + m A2 + mП 1 + mB .
Следует отметить, что радиусы lAC и lOD установки противовесов подбираются с учетом конструктивных особенностей механизма и возможных
конструктивных или иных ограничений.
При полном статическом уравновешивании кривошипно-ползунного
механизма заметно возрастают масса механизма и его габаритные размеры.
При ограничении габаритов масса механизма может увеличиваться кратно.
Кроме того, значительно увеличивается момент инерции шатуна и, как
следствие, главный момент сил инерции механизма, что приводит к увеличению его моментной неуравновешенности. Перечисленные недостатки
ограничивают использование полного статического уравновешивания.
На практике чаще используют частичное статическое уравновешивание
кривошипно-ползунных механизмов.
Частичное статическое уравновешивание
кривошипно-ползунного механизма
При частичном статическом уравновешивании для уменьшения главного вектора сил инерции кривошипно-ползунного механизма используют
один противовес, устанавливаемый на кривошип 1 (рис. 4.2, в). Статический
момент противовеса определяют по условию
mП ⋅ lOC = m A ⋅ lOA ,
где m A = m A1 + m A2 ,
m A1 = m1 ⋅
lОS
1
lOA
,
m A2 = m2 ⋅
(4.9)
lBS 2
l AB
.
Центр масс кривошипно-ползунного механизма, уравновешенного одним противовесом, не будет неподвижным. Он перемещается вдоль направляющей ползуна, т. е. механизм имеет неуравновешенные силы инерции.
Противовес устраняет вертикальное динамическое воздействие на стойку,
а горизонтальное динамическое воздействие остается неуравновешенным.
91
92.
Тем не менее, частичное статическое уравновешивание получило широкоеприменение, например, в двигателях внутреннего сгорания, криогенных
и сельскохозяйственных машинах.
Существуют и другие способы частичного или полного уравновешивания сил инерции звеньев. На рис. 4.3 показан кривошипно-ползунный механизм, уравновешивание которого осуществляется посредством установки
дполнительной кинематической цепи. К кривошипу в точке A´ прикреплен
шатун A´B´, связанный вращательной кинематической парой с ползуном 3´.
При равенстве кинематических размеров lOA и lOA´, lAB и lA´B´, равенстве масс
звеньев (кривошипов, шатунов и ползунов) основной и дополнительной цепей механизмы симметричны относительно оси вращения и не требуют дополнительного уравновешивания. Механизм на рис. 4.3 называют самоуравновешенным.
Рис. 4.3
На рис. 4.4 показана кинематическая схема кривошипно-ползунного
механизма, у которого для уравновешивания силы инерции ползуна на валах О и Оʹ установлены одинаковые зубчатые колеса, жестко связанные
с кривошипами. Колеса образуют внешнее зацепление и вращаются с одинаковой угловой скоростью ω1 в разных направлениях. На колесах закреплены противовесы массой mП. Радиусы их установки ρП.
При работе механизма на противовесы действуют равные по величине
силы инерции PИП . PИП = mП ⋅ ρ П ⋅ ω12 .
Y
Вертикальные составляющие PИП
этих сил уравновешивают друг друга,
X
а горизонтальные PИП
– частично поступательно движущиеся массы.
92
93.
Рис. 4.4При решении некоторых инженерных задач для определения кинематических характеристик механизмов используют приближенные расчетные
зависимости [1]. Так, при расчете ускорения ползуна центрального кривошипно-ползунного механизма, у которого длина шатуна больше длины кривошипа (более чем в 3 раза), используется формула
l
a B = ω12 ⋅ lOA ⋅ cosϕ1 + OA cos 2ϕ1 ,
l AB
где φ1 – угол поворота кривошипа.
С учетом этого сила инерции ползуна массой m3
l
PИB = m3 ⋅ ω12 ⋅ lOA ⋅ cosϕ1 + OA cos 2ϕ1 .
l AB
Сумма проекций сил инерции противовесов на горизонтальную ось:
X
2 PИП
= 2mП ⋅ ρ П ⋅ ω12 ⋅ cosϕ1 .
Параметры противовесов подбираются так, чтобы выполнялось условие
mП ⋅ ρ П = 0,5 ⋅ m3 ⋅ lOA .
В этом случае горизонтальные составляющие сил инерции противовесов уравновесят силу инерции первого порядка, действующую на ползун.
Для уравновешивания силы инерции второго порядка надо встроить в механизм дополнительные колеса, вращающиеся с угловой скоростью, в два раза
превышающей ω1, и на них установить противовесы.
93
94.
4.2. КИНЕТОСТАТИЧЕСКИЙ РАСЧЕТКРИВОШИПНО-ПОЛЗУННОГО МЕХАНИЗМА,
УРАВНОВЕШЕННОГО СТАТИЧЕСКИ
На рис. 4.5, а показана кинематическая схема четырехзвенного кривошипно-ползунного механизма, для частичного статического уравновешивания которого на кривошипе установлен противовес 4 массой mП. Его статический момент вычисляется по формуле (4.9). Противовес не влияет на систему сил, действующих на структурную группу, в частности на величину
и направление реакций R12 , R03 , R23 (или R32 ). Схема нагружения структурной группы приведена на рис. 4.5, б.
а
в
б
Рис. 4.5
В соответствии с формулой (3.21) силы тяжести шатуна и ползуна:
G2 = m2 ⋅ g ;
G3 = m3 ⋅ g .
В соответствии с формулами (3.1) и (3.2) силы инерции звеньев:
PИ 2 = m2 ⋅ aS 2 ;
M И 2 = J S 2 ⋅ ε 2 ; PИ 3 = m3 ⋅ a B .
94
95.
Условие равновесия системы сил, действующих на шатун:τ
(4.10)
R12
⋅ l AB + G2 ⋅ h2 − PИ 2 ⋅ h1 − M И 2 = 0 ,
где h1 и h2 натуральные плечи сил G2 и PИ 2 соответственно.
n
τ
Реакция R12
определяется при решении уравнения (4.10). Силы R12
и R03 определяются при решении векторного уравнения
n τ
(4.11)
R12
+ R12 + G2 + PИ 2 + G3 + PИ 3 + PПС + R03 = 0 .
Графическое решение уравнения (4.11) показано на рис. 4.5, в. План сил
построен в масштабе µp.
Схема нагружения кривошипа показана на рис. 4.6, а. Противовес рассматривается как точечная масса. Силы тяжести кривошипа и противовеса:
G1 = m1 ⋅ g ;
GП = mП ⋅ g .
R21
б
а
Рис. 4.6
Силы инерции кривошипа и противовеса:
PИ 1 = m1 ⋅ aS1 ;
PИП = mП ⋅ aС ,
где aС – ускорение точки С кривошипа.
аС = ω12 ⋅ lOC .
95
96.
Уравнения равновесия кривошипа:По
− M ур + R21 ⋅ H + G1 ⋅ H 1 − GП ⋅ H 2 = 0.
(4.12)
R21 + PИ 1 + G1 + GП + PИП + R01 = 0 .
(4.13)
уравнению
(4.12)
вычисляется уравновешивающий момент,
а по уравнению (4.13) – реакция R01 . Графическое решение уравнения (4.13)
приведено на рис. 4.6, б. R01 = af ⋅ µ P . Если бы механизм не был уравнове
′ в шарнире О на плане сил (рис. 4.6, б) изображалась бы
шен, реакция R01
′ = ad ⋅ µ P . Расчет показал, что после установки противовеотрезком ad . R01
са на кривошип величина реакции R01 уменьшилась.
4.3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ
КУРСОВОГО ПРОЕКТА
Задания на курсовой проект (КП) содержатся в приложениях 2–4. Они
отличаются уровнем сложности кинематических схем механизмов и набором задач, которые должны быть решены студентом в ходе курсового проектирования.
Так, при выполнении задания типа С4 (прил. 2) студент должен провести метрический синтез четырехзвенного кривошипно-ползунного механизма, его структурный, кинематический, силовой расчет и частичное статическое уравновешивание.
В заданиях типа У4 (прил. 4) кинематические размеры кривошипноползунного механизма заданы. В ходе курсового проектирования обучающийся решает задачи структурного, кинематического и силового анализа.
По желанию для увеличения рейтинга он может выполнить частичное статическое уравновешивание с последующим силовым расчетом уравновешенного механизма.
Наиболее сложные задания на КП содержатся в приложении 3 (задания
с номерами 6-1–6-18). Они предусматривают структурный, кинематический
и кинетостатический анализ сложного шестизвенного рычажного механизма, содержащего структурные группы II класса 2-го порядка разных видов.
96
97.
Независимо от сложности задания целесообразно придерживаться следующего алгоритма выполнения КП.1. Изучаются исходные данные, и в случае отсутствия кинематических
размеров производится метрический синтез механизма (подраздел 2.2 данного учебного пособия).
2. Выполняется структурный анализ механизма, результат которого используется на последующих этапах расчета.
3. В соответствии с формулой строения механизма методом планов выполняется его кинематический расчет:
– в масштабе строится разметка механизма для 12 положений и определяются его крайние положения (подраздел 2.3 учебного пособия);
– для 12 положений механизма методом планов определяются линейные и угловые скорости звеньев и отдельных их точек, в частности центров
масс. Расчетные модели описаны в подразделе 2.1, пример их использования – в подразделах 2.3 и 3.4;
– для двух положений механизма (по согласованию с преподавателем)
выполняется расчет ускорений, соответствующие расчетные модели описаны в подразделах 2.1, 2.3 и 3.4.
4. Кинетостатический расчет механизма методом планов выполняется
для двух его положений. Расчетные модели структурных групп и исходного
механизма, последовательность расчета приведены в подразделах 3.2–3.4
учебного пособия. Метод определения сил инерции (подраздел 3.1) согласуется с преподавателем.
5. Уравновешивающий момент Myp вычисляется методом Н. Е. Жуковского для двух положений механизма. Методика расчета приведена в подразделе 3.5. На этом этапе выполнения КП оценивается (в процентах) расхождение результатов расчета Myp, полученных разными методами.
6. Определяются параметры противовеса, устанавливаемого в плоскости движения кривошипа, и для двух положений методом планов выполняется силовой расчет уравновешенного механизма (подраздел 4.2).
При исследовании сложного рычажного механизма (прил. 3) пункты 1
и 6 данного алгоритма не выполняются.
Пояснительная записка формируется параллельно с выполнением расчетов. Требования к ее оформлению будут сформулированы в следующем
разделе данного учебного пособия.
97
98.
5. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮКУРСОВОГО ПРОЕКТА
Требования к оформлению графической части проекта
При оформлении курсового проекта все графические построения выполняются на листе (листах) формата А1 (594 × 841 мм).
Все построения на листе, а именно: планы положений (разметка механизма), скоростей, ускорений и сил, диаграммы, схемы нагружения – должны иметь названия и масштабные коэффициенты с обязательным указанием размерности последних.
Масштабный коэффициент должен быть целым числом или простой
десятичной дробью. При построении планов сил предпочтительными являются следующие масштабные коэффициенты: 1; 2; 4; 5; 10; 20; 25; 50;
100 Н/мм.
Масштабные коэффициенты графических построений должны быть такими, чтобы лист был заполнен равномерно.
Планы скоростей, ускорений и сил должны быть снабжены векторными уравнениями, решением которых они и являются.
Надписи выполняются шрифтом, размер которого студент подбирает
по своему усмотрению. Все надписи должны легко читаться.
На разметке и схемах нагружения звенья и кинематические пары изображаются сплошными основными линиями толщиной 0,8–1,2 мм.
Векторы скоростей и ускорений на планах соответственно скоростей
и ускорений, векторы сил на схемах нагружения и на планах сил, траектории движения точек звеньев изображаются сплошнами линиями толщиной
0,4–0,6 мм.
Все вспомогательные построения выполняются сплошными тонкими
линиями толщиной 0,2–0,4 мм и на чертеже сохраняются.
На разметке механизма и на схемах нагружения все вращательные кинематические пары должны изображаться одинаково – окружностями диаметра 1,5–2 мм. Линий внутри этих окружностей не должно быть.
Результаты силового расчета механизма должны быть представлены
на листе в табличной форме с обязательным указанием номеров положений,
для которых выполнен расчет, и единиц измерения сил и моментов сил.
При построении графиков должны соблюдаться следующие требования:
оси координат и линии графиков изображаются сплошными основными ли98
99.
ниями толщиной 0,8–1,2 мм. Оси координат должны иметь название и равномерную шкалу. На графиках должны быть указаны масштабные коэффициенты осей координат.Требования к оформлению пояснительной записки
Пояснительная записка (ПЗ) оформляется на одной стороне белой бумаги формата А4 (210 × 297 мм). Кроме основного содержания она включает: титульный лист; аннотацию; задание на КП; оглавление; введение; заключение; библиографический список.
Нумерация страниц начинается с титульного листа, но номер страницы
на нем не проставляется.
Аннотация – краткое содержание пояснительной записки. Она дает
представление об основных результатах работы, ее объеме и располагается
на отдельном листе.
Заключение содержит описание результатов выполненной работы
и размещается на отдельном листе.
В основную часть записки входит описание всех расчетов и построений.
Изложение ведется в безличной форме или от первого лица множественного
числа, например: «… расчет выполняется по формуле …» или «… расчет
выполняем по формуле …».
В тексте обязательно должны быть ссылки на литературные источники,
рисунки, таблицы, формулы.
Ссылки на литературные источники заключаются в квадратные скобки,
например: «…используется формула, приведенная в [1, 3]…», где цифрами
обозначаются номера источников в библиографическом списке.
Текст записки набирается в текстовом редакторе Word, шрифт – Times
New Roman Cyr, 14 пт; абзацный отступ – 5 мм; межстрочный интервал –
полуторный. Поля, мм: сверху и снизу – 20–25, слева – 25, справа – 10.
Названия разделов и подразделов выравниваются по центру и выделяются пропуском строки сверху и снизу. После номера раздела ставится точка, затем следуют пробел и название. В конце названия точка не ставится.
Например: « 2.2. Расчет скоростей ».
Текст ПЗ выравнивается по ширине страницы.
Рисунок размещается после первой ссылки на него. Рисунки могут
иметь сквозную нумерацию по всему тексту или в пределах одного раздела.
В первом случае номер рисунка обозначается, например: «Рис. 10».
99
100.
Во втором случае (когда нумерация в пределах одного раздела) номеррисунка состоит из двух частей, включающих номер раздела и номер рисунка в этом разделе. Например: «Рис. 4.2» – второй рисунок в разделе 4,
«Рис. 3.11» – одиннадцатый рисунок в разделе 3.
Номер рисунка проставляется под рисунком с выравниванием по центру. Если рисунок имеет название, то оно следует за номером рисунка с выравниванием по центру. Например: «Рис. 3.2. Схема нагружения структурной группы». Точка после названия не ставится.
В тексте при ссылке на рисунки используют сокращения типа:
«На рис. 2 . . .» или « . . . на рис. 4.2, а . . . ».
Нумерация таблиц, как и нумерация рисунков, может быть сквозной по
всему тексту или в пределах одного раздела. Номер проставляется над таблицей с выравниванием по левому краю. Если у таблицы есть название, то
оно набирается на следующей после номера таблицы строке с выравниванием по центру. В тексте ссылку на таблицу можно сделать следующим образом: « . . . в табл. 1 » или « . . . в табл. 2.1 ».
Формулы набираются в редакторе формул. Формулы нумеруют в тех
случаях, когда в тексте есть ссылки на них. Формулы могут иметь сквозную
нумерацию по всему тексту или в пределах одного раздела. Последнее
наиболее целесообразно. Номер формулы проставляется в конце строки,
в которой она расположена, в круглых скобках. Например: (13) или (3.11).
При описании расчета какой-либо физической величины сначала записывается формула, по которой эта величина вычисляется, и расшифровываются все впервые встречающиеся обозначения, затем в формулу подставляются значения и приводится конечный результат. Например:
µt = TЦ L ,
где ТЦ – время цикла, с; L – длина отрезка, которым время цикла изображается на графике, мм.
µt = 0,9 180 = 0,005 с/мм.
В основном содержании результаты расчетов должны быть представлены в табличной форме. Так, результаты расчета скоростей можно представить в виде табл. 1, а ускорений – в виде табл. 2.
Результаты силового расчета целесообразно представить в таблице,
имеющей, например, такую форму (см. табл. 3).
100
101.
Таблица 1VA
№ полож.
ω2
VS 2
VS1
VBA
VB
м/с
1/с
0
1
2
...
...
11
Таблица 2
№
полож.
aA
aτBA
n
a BA
aB
a BA
a S1
м/с2
ε2
aS 2
1/с2
Таблица 3
№
полож.
РИ 1
РИ 2
РИ 3
РПС
τ
R12
Н
n
R12
R12
R03
R01
MИ2
M ур
Нм
Введение и заключение печатаются на отдельных страницах. Эти разделы пояснительной записки не нумеруются.
Библиографический список помещается на отдельной странице. Заглавие «Библиографический список» выравнивается по центру, через строку
от него помещается пронумерованный список литературных источников,
которые использовались студентом при выполнении КП. Нумерация литературных источников осуществляется в порядке ссылок на них в тексте или
по алфавиту.
Библиографические описания источников приводятся в соответствии
с ГОСТ 7.1–2003. Например: «1. Теория механизмов и машин : учеб. для вузов / К. В. Фролов, С. А. Попов, А. К. Мусатов [и др.] ; под ред. К. В. Фролова. – М. : Высш. шк., 1987. – 496 с.».
101
102.
ЗАКЛЮЧЕНИЕПрикладная механика – одна из дисциплин, формирующих техническое
мировоззрение будущих бакалавров, специалистов и магистров. При изучении раздела «Схемный анализ и синтез механизмов и машин» этой дисциплины студенты знакомятся с общими методами и принципами расчета механизмов на уровне схем, т. е. выполняют этап разработки эскизного проекта, и формируют системный подход к решению задач механики.
Прикладная механика решает задачи исследования и синтеза движения
механических систем. В первом приближении задача о движении решается
в кинематической постановке, при которой объект идеализируется, в частности, в кинематической модели движения не учитываются силы, инерционные характеристики объектов и многие реальные параметры: первичные
погрешности, силовые и температурные деформации, трение, изменение
геометрии связей в ходе эксплуатации и др.
В учебном пособии описано решение задачи кинематики наиболее распространенным графоаналитическим методом, в основу которого положено
графическое решение векторных уравнений, полученных из разложения
движения на более простые составляющие.
Результаты кинематического расчета используются для определения
сил, действующих в механизме, и решения задач динамического анализа
и синтеза.
Расчет сил, действующих в механизме при его движении, – задача динамики. Использование принципа Даламбера позволяет составить силовую
модель по форме уравнений статики.
В настоящем пособии показано, что все механизмы устроены одинаково. Любой механизм можно разделить на простейшие кинематические цепи,
одна из которых имеет подвижность, равную подвижности механизма,
а остальные, называемые структурными группами, имеют подвижность,
равную нулю. Структурные группы статически определимы. Использование
этого положения позволяет унифицировать решение задач кинематики
и кинетостатики.
В издании большое внимание уделено зубчатым механизмам, в частности планетарным, получившим широкое применение в силовых приводах.
Используя многосателлитную конструкцию, можно за счет разделения си102
103.
лового потока кратно уменьшить нагрузку, передаваемую каждым зацеплением, и за счет этого сделать механизм более компактным. Однако у механизма в этом случае появляются избыточные связи, следствием которых является неопределенность в распределении нагрузки между сателлитами.Для выравнивания нагрузки надо устранить или ослабить избыточные связи.
Для этого жестким делают водило только одного из сателлитов, у остальных изгибную податливость водила увеличивают, обеспечивая самоустановку сателлитов.
Задача выравнивания нагрузки между сателлитами при разделении силового потока, уменьшение ее концентрации по ширине зубчатого венца,
исключение кромочного контакта зубьев при пересопряжении – актуальные,
сложные и важные инженерные задачи, для решения которых надо иметь
определенный уровень знаний, умений и навыков.
В условиях непрерывного роста рабочих скоростей и нагрузок при проектировании машин и механизмов надо учитывать их реальные свойства.
Исследование и проектирование схем реальных механизмов базируется
как на идеализированных моделях, так и моделях высокой степени достоверности, для которых характерен исследовательский этап по оценке влияния реальных параметров систем на их работоспособность. В связи с этим
знания, умения и навыки, приобретенные студентами в ходе изучения раздела «Схемый анализ и синтез механизмов и машин», будут востребованы
при дальнейшем изучении дисциплины «Прикладная механика», многих
специальных дисциплин и, конечно, в их инженерной практике.
103
104.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК1. Артоболевский, И. И. Теория механизмов и машин / И. И. Артоболевский. – М. : Наука, 1975. – 640 с.
2. Теория механизмов и машин : учеб. для втузов / К. В. Фролов,
С. А. Попов, А. К. Мусатов [и др.] ; под ред. К. В. Фролова. – М. : Высш.
шк., 1987. – 496 с.
3. Рязанцева, И. Л. Теория механизмов и машин в вопросах и ответах /
И. Л. Рязанцева. – Омск : Изд-во ОмГТУ, 2013. – 130 с.
4. Федоров, Н. Н. Теория механизмов и машин : учеб. для вузов /
Н. Н. Федоров. – Омск : Изд-во ОмГТУ, 2008. – 224 с.
5. Рязанцева, И. Л. Теория и синтез передач зацеплением : учеб. пособие / И. Л. Рязанцева. – Омск : Изд-во ОмГТУ, 2011. – 82 с.
6. Яблонский, А. А. Курс теоретической механики : в 2 т. / А. А. Яблонский, В. М. Никифоров. – М. : Высш. шк., 1964. – Т. 1. – 434 с.
104
105.
ПРИЛОЖЕНИЕ 1КИНЕМАТИЧЕСКИЙ РАСЧЕТ СЛОЖНОГО
ЗУБЧАТОГО МЕХАНИЗМА
105
106.
106107.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 1
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n звена механизма, отмеченного в таблице вопросительным знаком.
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
n6 , об/мин
z
z2
z2ʹ
z3
z4
z5
z5ʹ
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
600
?
13
42
9
?
35
10
12
?
1000
?
20
?
18
80
?
12
20
22
?
800
15
30
?
60
29
?
10
32
?
1100
17
34
14
?
39
11
?
33
900
?
14
28
?
56
40
?
18
32
?
1600
21
42
15
?
32
14
16
?
?
2000
9
30
19
?
38
?
16
37
1800
?
11
?
21
69
40
?
18
36
1500
?
21
36
?
70
33
21
?
34
?
700
?
40
18
71
45
19
24
?
10
5
8
16
12
5
10
8
12
16
107
108.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 2
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n звена механизма, отмеченного в таблице вопросительным знаком.
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n Н , об/мин
n5 , об/мин
z1
z2
z2ʹ
z3
z3ʹ
z4
z4ʹ
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
800
?
64
?
17
70
?
27
16
29
1200
?
?
25
20
67
23
?
17
36
?
900
67
26
?
59
17
43
?
37
1700
?
80
27
30
?
25
50
34
?
950
?
78
?
22
75
20
?
33
35
?
1600
70
17
?
80
28
30
?
40
1800
?
?
20
11
66
27
32
23
?
?
1300
82
30
18
?
?
35
30
32
2000
?
90
?
25
80
19
?
17
47
?
2200
96
29
?
100
21
40
20
?
14
10
5
8
12
10
5
12
14
8
108
109.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 3
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n звена механизма, отмеченного в таблице вопросительным знаком.
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
n5 , об/мин
n Н , об/мин
z1
z2
z2ʹ
z3
z3ʹ
z4
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
500
500
?
12
30
10
?
75
?
25
500
500
?
?
38
24
24
?
30
20
1000
1500
?
12
?
20
22
72
26
?
–500
?
500
40
10
26
?
?
33
24
?
200
–500
51
9
?
45
70
?
30
500
?
–100
38
12
?
35
80
25
?
?
450
300
?
11
22
34
88
?
24
?
300
500
38
?
15
35
?
20
30
?
1000
400
10
40
20
?
72
26
?
500
400
?
?
34
12
33
75
?
25
6
10
5
8
12
10
5
12
6
8
109
110.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 4
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n5 барабана (звено 5).
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z3ʹ
z4
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
3000
9
30
?
49
?
12
41
3000
12
?
16
61
20
12
?
2500
?
34
18
65
21
?
45
2500
17
38
26
?
25
12
?
2000
20
?
32
93
28
?
52
2000
?
44
38
105
?
12
55
1500
26
47
?
117
34
12
?
1500
30
51
52
?
38
?
62
1000
34
55
?
109
28
?
76
1000
25
?
42
113
?
12
57
16
10
5
8
12
10
5
12
16
8
110
111.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 5
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n3 барабана (звено 3).
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z3
z3ʹ
z4
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1500
?
30
100
?
70
10
3000
18
?
98
82
50
?
2500
?
30
95
72
40
?
1700
20
40
?
94
?
12
1800
30
50
?
90
?
9
2200
20
?
90
?
78
10
1400
25
?
105
88
?
11
1550
?
40
107
78
50
?
2000
33
20
?
98
72
?
2500
45
20
?
?
75
10
16
10
5
8
12
5
10
16
8
12
111
112.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 6
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n7 водила 7.
3. По условию соседства определить количество сателлитов 2 и 5.
Условное
обозначение
n1 , об/мин
n6 , об/мин
z1
z2
z3
z4
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
2500
0
9
?
73
?
14
56
2000
0
?
27
64
20
?
70
3000
0
11
?
83
?
24
72
2000
200
?
30
72
?
16
54
1200
–250
12
18
?
18
16
?
1800
–200
12
?
52
24
?
72
1600
–200
9
27
?
28
14
?
1550
–220
11
?
83
?
18
60
2200
0
10
?
54
20
25
?
1600
0
?
21
53
20
?
72
10
5
10
8
12
16
10
16
8
12
Примечание. Знак «–» означает, что колеса 1 и 6 вращаются в разных направлениях.
112
113.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 7
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n4 колеса 4 сложного зубчатого механизма.
3. По условию соседства определить количество сателлитов 2 и 5.
Условное
обозначение
n1 , об/мин
n6 , об/мин
z1
z2
z3
z4
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1200
0
?
25
59
52
?
24
1000
0
10
18
?
62
24
?
1500
0
11
?
79
?
32
26
2000
100
10
?
80
90
?
38
1200
250
?
20
52
80
16
?
1800
–200
9
25
?
85
10
?
1600
–250
12
?
52
?
30
40
1550
220
?
18
46
?
16
40
2200
300
11
34
?
95
?
35
1600
350
?
35
80
?
26
38
5
12
10
8
10
16
12
5
8
12
Примечание. Знак «–» означает, что колеса 1 и 6 вращаются в разных направлениях.
113
114.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 8
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n6 колеса 6 зубчатого механизма.
3. По условию соседства определить количество сателлитов 2 и 4.
Условное
обозначение
n1 , об/мин
z1
z2
z3
z4
z4ʹ
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1200
?
13
38
23
18
?
58
1000
13
14
?
24
?
64
59
1500
14
?
44
25
10
65
?
2000
?
16
47
?
21
66
61
1200
16
?
50
22
?
60
62
1800
17
18
?
28
23
68
?
1600
?
21
62
31
26
?
66
1550
23
24
?
34
28
?
68
2200
26
?
80
?
32
77
72
1600
?
32
95
42
?
82
77
5
8
10
12
15
5
8
10
12
15
114
115.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 9
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n6 колеса 6 зубчатого механизма.
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z4
z4ʹ
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1200
?
42
11
12
17
?
19
33
1000
12
46
?
12
21
73
?
33
1500
13
?
14
12
23
76
21
?
1800
14
50
15
?
25
75
20
?
2000
17
56
18
12
?
?
19
40
2200
21
64
22
?
39
82
?
40
1800
25
72
26
12
?
?
15
56
2000
?
80
50
22
35
90
?
54
2100
33
?
34
12
63
94
20
?
1400
37
96
?
12
71
98
20
?
5
8
10
12
15
5
8
10
12
15
115
116.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 10
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n звена механизма, отмеченного в таблице вопросительным знаком.
3. По условию соседства определить количество сателлитов 2 и 5.
Условное
обозначение
n1 , об/мин
n Н , об/мин
n6 , об/мин
z1
z2
z3
z4
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
?
600
500
?
20
66
28
?
52
?
750
650
32
23
?
31
11
?
?
500
400
38
?
90
34
?
60
?
400
500
?
28
98
36
12
?
?
250
500
46
25
?
?
14
66
1000
250
?
18
?
38
?
11
43
1500
300
?
?
14
42
22
15
?
3000
450
?
20
?
54
25
?
57
2000
350
?
16
?
46
?
10
43
2500
400
?
18
?
50
24
?
48
5
8
10
12
15
5
8
10
12
15
116
117.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 11
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения nН водила Н.
3. По условию соседства определить количество сателлитов 2 и 5.
Условное
обозначение
n1 , об/мин
n3 , об/мин
z1
z2
z3
z4
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
800
400
12
?
42
42
?
18
900
500
?
16
45
40
10
?
1000
600
14
17
?
42
?
22
1100
700
15
?
51
?
11
24
1000
500
17
20
?
54
13
?
1200
0
?
25
72
?
10
38
500
0
25
?
81
68
?
44
600
0
?
31
90
78
14
?
400
0
31
34
?
?
15
56
1000
0
19
?
63
52
?
32
5
8
10
12
15
5
8
10
12
15
117
118.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 12
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n6 барабана (колесо 6).
3. По условию соседства определить количество сателлитов 2.
Условное
обозначение
n1 , об/мин
z1
z2
z3
z4
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1000
?
16
47
20
12
?
1100
?
18
52
22
?
48
1500
18
?
56
?
12
50
1400
20
?
56
30
?
58
2000
22
15
?
34
12
?
2100
?
16
56
38
?
62
2500
26
15
?
42
13
?
2600
28
?
54
?
14
74
2000
?
17
64
?
11
72
1800
34
?
62
58
?
80
5
8
10
12
10
5
8
10
12
5
118
119.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 13
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n1 колеса 1.
3. По условию соседства определить количество сателлитов 2 (2ʹ)
и 5 (5ʹ).
Условное
обозначение
n Н , об/мин
z1
z2
z2ʹ
z3
z4
z5
z5ʹ
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
800
95
?
20
100
55
?
10
30
900
?
15
21
102
?
16
10
31
1000
97
15
22
?
59
17
10
?
1100
94
15
?
98
53
14
?
29
1000
?
15
18
96
?
13
10
28
1200
92
15
17
?
49
12
10
?
500
91
?
16
92
47
?
10
26
600
90
15
?
88
45
11
?
24
400
89
?
12
86
45
10
10
?
1000
87
15
12
?
4?3
?
10
24
5
8
10
12
10
5
8
10
12
12
119
120.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 14
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n8 барабана (колесо 8).
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z3
z4
z5
z6
z7
z8
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
800
?
40
10
39
?
20
12
72
900
10
41
?
41
82
?
12
73
1000
11
?
10
43
84
22
?
74
1100
14
45
10
?
90
25
12
?
1000
15
46
10
?
92
?
12
78
1200
16
46
?
52
?
27
12
79
1500
18
32
16
?
98
29
?
81
1600
?
51
10
61
102
31
12
?
1400
12
?
10
44
86
23
12
?
1000
13
44
?
47
?
24
12
76
12
10
8
15
5
15
10
12
8
5
120
121.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 15
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n5 колеса 5.
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z4
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1800
9
30
?
54
?
20
40
1900
?
31
15
56
11
21
?
2000
11
?
15
58
10
?
50
2100
12
34
15
?
10
?
52
1800
?
38
15
66
?
34
54
1900
15
?
15
72
10
38
?
1500
17
46
?
78
10
?
62
1600
20
50
15
?
10
50
?
1400
22
54
?
91
?
56
76
2000
?
60
15
100
10
60
?
12
10
8
15
5
15
10
12
8
5
121
122.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 16
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n3 барабана (колеса 3, 3ʹ, 3ʹʹ).
3. По условию соседства определить количество сателлитов 2 и 4.
Условное
обозначение
n1 , об/мин
z1
z2
z3
z3ʹ
z3ʹʹ
z4
z5
z6
z7
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1500
?
20
58
?
44
21
21
?
24
1750
20
22
?
69
50
?
23
10
?
1800
19
?
61
66
?
22
?
10
27
2000
22
24
?
?
?
25
25
10
26
2250
?
27
79
84
65
?
28
10
?
2500
28
?
88
93
74
31
?
?
54
2750
31
?
97
?
83
34
34
10
?
3000
?
41
121
?
107
42
42
?
87
1400
47
46
?
150
?
50
?
10
111
1900
34
36
?
111
92
?
37
?
72
5
8
10
15
12
5
8
10
15
12
122
123.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 17
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n3 барабана (колесо 3(3ʹ)).
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z3
z3ʹ
z4
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1800
?
42
99
63
27
?
1900
22
?
120
77
?
9
2400
24
51
?
?
36
9
2500
18
45
?
?
30
9
2700
20
?
114
73
?
9
2750
?
53
132
85
38
?
3000
28
?
138
89
?
9
3100
?
57
144
?
42
9
3200
32
59
?
97
44
?
3400
34
?
156
101
?
9
12
10
8
15
5
15
10
12
8
5
123
124.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 18
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n3 барабана (колеса 3 и 3ʹ).
3. По условию соседства определить количество сателлитов 2.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z3ʹ
z4
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
2500
11
27
?
53
?
18
20
2400
11
29
17
?
62
?
22
2300
?
31
19
61
68
22
?
2200
11
?
21
65
?
24
26
2000
?
35
23
69
80
26
?
2750
11
?
25
73
86
?
30
3000
11
39
27
?
92
30
?
3100
11
41
?
81
?
32
34
2250
11
43
31
?
104
?
36
1800
?
45
33
89
110
36
?
5
8
10
12
15
15
12
10
8
5
124
125.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 19
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения nН водила Н зубчатого механизма.
3. По условию соседства определить количество сателлитов 4.
Условное
обозначение
n1 , об/мин
z1
z1ʹ
z2
z2ʹ
z3
z3ʹ
z4
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1200
?
11
45
12
48
?
32
1500
10
20
38
?
36
72
?
1000
11
?
?
12
47
74
29
1800
9
14
48
10
?
?
28
2000
13
12
48
?
49
74
?
1200
?
?
45
12
43
88
34
1700
10
25
52
9
?
75
?
1800
11
20
?
11
44
?
25
1100
12
?
48
15
?
62
20
1400
?
28
38
10
40
72
?
5
8
10
12
15
5
8
10
12
15
125
126.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 20
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n5 колеса 5 зубчатого механизма.
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z1ʹ
z2
z2ʹ
z3
z4
z4ʹ
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
600
?
46
27
9
27
20
?
47
700
10
42
30
?
30
20
15
?
900
11
?
?
11
44
19
12
49
1000
12
46
48
12
?
?
10
53
1200
9
49
?
9
45
?
13
56
1100
?
50
50
10
50
20
?
60
1400
14
?
63
?
66
20
12
60
1500
12
46
60
12
?
?
10
58
1700
9
60
?
9
54
25
20
?
1600
10
42
50
?
50
28
?
60
5
8
10
12
15
15
12
10
8
5
126
127.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 21
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения nН водила Н.
3. По условию соседства определить количество сателлитов 2 и 4.
Условное
обозначение
n1 , об/мин
n3 , об/мин
z1
z2
z3
z4
z4ʹ
z5
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1000 1100 1400 1600 1800 2000 2200 2700 2900 3000
–1200 –1300 –1600 –1800 –2000 –2200 –2400 –2900 –3100 –3300
18
?
22
?
26
28
?
?
27
29
?
29
32
34
36
?
40
35
?
39
74
77
?
92
?
104
110
95
101
?
?
50
56
60
64
68
?
82
86
90
11
?
11
11
11
?
11
?
11
11
18
19
22
?
26
28
30
35
?
39
55
58
?
73
?
85
91
106
112
?
8
5
10
12
15
5
8
10
12
Примечание. Знак «–» означает, что звенья 1 и 3 вращаются в разных направлениях.
127
15
128.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 22
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n4 барабана (звено 4).
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z3ʹ
z4
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1300
17
28
13
?
?
42
16
1000
?
29
14
34
10
?
17
1500
23
31
?
38
10
48
?
1700
27
?
18
42
10
?
21
2000
?
35
20
46
?
56
23
2100
35
?
22
50
10
?
25
2400
41
40
25
?
10
66
?
2500
45
42
?
60
10
?
30
2700
?
44
29
64
?
74
32
3000
53
46
31
?
10
78
?
5
8
10
12
16
5
8
10
12
16
128
129.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 23
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n3 барабана (звено 3).
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z3ʹ
z4
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1300
?
31
12
60
?
14
11
1200
20
34
15
?
45
17
?
1500
22
?
17
75
49
?
11
1750
24
38
?
81
53
?
11
2000
?
40
21
87
67
28
?
2150
28
?
23
93
?
25
11
2400
30
44
?
99
65
27
?
2500
32
46
27
?
?
29
11
2700
34
?
29
111
73
?
11
3000
?
50
31
117
77
33
?
5
8
10
12
16
5
8
10
12
16
129
130.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 24
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n3 барабана (звено 3).
3. По условию соседства определить количество сателлитов.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z4
z5
z5ʹ
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1250
?
18
10
80
?
17
12
1500
9
?
13
89
37
?
15
1750
9
26
?
92
38
21
?
2000
9
28
?
95
?
22
17
2250
9
34
18
?
41
?
20
2500
9
?
22
116
46
29
?
2750
?
46
29
122
?
31
26
3000
9
?
26
?
50
33
28
1250
9
54
28
134
52
?
?
1500
9
58
?
140
?
37
32
5
8
10
12
16
5
8
10
12
16
130
131.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 25
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n5 колеса 5.
3. По условию соседства определить количество сателлитов 2 и 4.
Условное
обозначение
n Н , об/мин
n1 , об/мин
z1
z2
z2ʹ
z3
z3ʹ
z4
z4ʹ
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1000
2000
78
22
?
31
?
46
20
48
1100
2000
80
28
22
?
25
?
17
50
1000
2250
?
24
20
38
28
50
26
?
1000
2250
85
?
23
40
31
65
?
54
1000
1800
?
18
26
42
?
65
43
56
1000
1800
80
22
12
?
36
?
48
58
1000
1500
82
22
?
50
34
50
24
?
1000
1500
?
22
13
50
31
46
?
62
1000
2100
98
?
12
65
28
42
?
54
1000
2100
99
22
13
?
25
38
17
?
5
8
10
12
15
5
8
10
12
15
Примечание. Знак «–» означает, что колесо 1 и водило Н вращаются в разных направлениях.
131
132.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 26
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения nН водила Н.
3. По условию соседства определить количество сателлитов 2 и 4.
Условное
обозначение
n1 , об/мин
n3 , об/мин
z1
z2
z3
z4
z4ʹ
z5
z6
Модуль
мм
Варианты
А
Б
В
3000 3000 2500
–2000 –2000 –500
?
10
11
9
10
?
27
?
33
28
?
31
18
14
20
?
17
18
61
62
?
5
8
10
Г
Д
Е
Ж
З
И
К
2500 3000 3000 2500 2500 3000 3000
–500 –1500 –1500 –1000 –1000 –1500 –1500
12
9
?
11
12
?
10
12
?
13
15
?
13
13
?
33
36
?
42
35
?
34
34
34
?
38
34
31
?
17
12
20
?
14
13
20
25
?
20
18
22
?
70
?
74
71
74
?
66
12
15
5
8
10
12
Примечание. Знак «–» означает, что колеса 1 и 3 вращаются в разных направлениях.
132
15
133.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 27
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n5 барабана (звено 5).
3. По условию соседства определить количество сателлитов 2.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z3ʹ
z4
z5
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1300
?
25
31
68
?
10
66
1400
12
?
34
74
49
13
?
1500
12
31
37
?
52
?
84
1700
12
34
?
86
55
?
93
2000
?
36
42
90
?
21
99
2100
12
?
44
94
54
23
?
2400
12
40
46
?
?
25
111
2500
12
42
?
102
63
?
117
2700
12
46
52
?
67
31
?
3000
12
?
56
118
71
?
141
5
8
10
12
16
5
8
10
12
16
133
134.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 28
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения nН водила H.
3. По условию соседства определить количество сателлитов 2.
Условное
обозначение
n1 , об/мин
z1
z2
z2ʹ
z3
z4
z5
z5ʹ
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
1100
?
39
11
41
?
50
10
80
1200
11
44
?
45
21
?
10
73
1300
12
?
37
37
20
50
?
81
1400
10
40
20
?
22
44
?
78
1600
14
52
?
48
19
40
11
?
1500
20
?
44
65
16
52
?
80
1700
?
60
36
41
20
50
10
?
2000
16
50
?
52
22
48
?
82
1900
15
?
52
48
20
?
11
65
1750
?
68
56
70
?
50
10
80
10
12
15
5
8
10
12
15
5
8
134
135.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 29
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения nН водила H.
3. По условию соседства определить количество сателлитов 2 и 5.
Условное
обозначение
n1 , об/мин
z1
z2
z3
z4
z5
z5′
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
2000
?
13
48
?
30
15
60
1900
20
?
60
16
?
16
64
2000
24
12
?
16
34
?
64
1800
26
?
52
20
40
16
?
1700
?
14
48
13
26
13
?
1600
22
15
?
14
28
?
56
1900
26
14
?
15
?
14
59
1500
24
?
50
?
30
12
54
1200
?
15
60
20
?
15
75
1400
18
?
42
11
33
?
60
5
8
10
12
15
5
8
10
12
15
135
136.
ОмГТУКафедра «Машиноведение»
Кинематический расчет сложного зубчатого механизма
Задание 30
1. По условию соосности определить числа зубьев колес, отмеченных
в таблице вопросительным знаком.
2. Графическим и аналитическим методами вычислить частоту вращения n1 колеса 1.
3. По условию соседства определить количество сателлитов 2 и 5.
Условное
обозначение
n Н , об/мин
z1
z2
z 2′
z3
z4
z5
z5′
z6
Модуль
мм
Варианты
А
Б
В
Г
Д
Е
Ж
З
И
К
200
60
?
14
26
20
50
?
85
220
?
22
18
22
?
32
14
72
180
64
18
?
24
21
50
15
?
210
60
16
20
?
20
60
?
93
240
70
14
?
38
30
?
12
102
160
68
?
15
33
?
56
12
96
210
?
22
16
34
30
?
13
105
175
66
?
14
28
25
50
?
89
190
74
18
?
34
27
60
15
?
250
80
16
21
?
30
70
14
?
15
10
12
8
5
15
12
8
10
5
136
137.
ПРИЛОЖЕНИЕ 2ПРОЕКТИРОВАНИЕ И ИССЛЕДОВАНИЕ
РЫЧАЖНОГО МЕХАНИЗМА РАБОЧЕЙ МАШИНЫ
137
138.
138139.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-1
5–7
1.
2.
3.
4.
Выполнить метрический синтез механизма.
Провести структурный анализ механизма.
Выполнить кинематический и силовой расчеты.
Уравновесить механизм.
Условное
обозначение
ω1, рад/с
К
H, м
l AB lOA
lOS1 lOA
l AS2 l AB
m1, кг
m2, кг
m3, кг
Р, Н
δ
Варианты
1
27
1,08
0,25
4
0,5
0,5
3,5
10
13
1500
0,05
2
29
1,03
0,23
4,5
0,4
0,5
2,4
9
12
1600
0,04
3
30
1,02
0,24
5
0,5
0,5
2,2
11
10
1400
0,03
4
31
1,04
0,2
3,5
0,5
0,4
2,0
8
12,5
1250
0,04
Примечание. Н – ход ползуна.
139
5
25
1,07
0,22
4,1
0,5
0,5
3,0
10,5
13
1650
0,06
6
28
1,03
0,18
3,6
0,5
0,4
1,8
8
7
1300
0,05
7
23
1,05
0,1
5
0,4
0,5
1,5
6,5
5
900
0,035
8
21
1,06
0,15
5,5
0,5
0,4
1,3
7
9,5
1100
0,025
140.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-2
3–5
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
Варианты
l AS2 l AB
1
95
0,10
4
0,2
0,5
0,5
2
70
0,12
3,5
–0,25
0,5
0,5
3
80
0,15
5
–0,28
0,5
0,5
4
90
0,2
3,2
0,19
0,5
0,5
5
82
0,18
4,5
0,3
0,5
0,5
6
87
0,08
5,5
–0,35
0,5
0,5
7
75
0,14
4,7
0,45
0,5
0,5
8
73
0,09
3,9
–0,4
0,5
0,5
γ, град
m1, кг
m2, кг
m3, кг
Р, Н
δ
70
1,5
7,0
3,0
750
0,06
75
1,2
6,0
2,5
800
0,05
80
2,0
10
5,0
700
0,04
82
1,80
7,0
4,5
850
0,062
65
2,5
13
7,0
900
0,055
73
1,3
6,5
4,0
650
0,03
79
2,5
10
5,5
840
0,035
68
1,2
4,5
3,5
500
0,04
ω1, рад/с
H, м
l AB lOA
e lOA
lOS1 lOA
Примечание. Н – ход ползуна.
140
141.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-3
5–7
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
VBср , м/с
H, м
l AB lOA
lOS1 lOA
l AS2 l AB
γ, град
m1, кг
m2, кг
m3, кг
Р, Н
δ
Варианты
1
2
3
4
5
6
7
8
3,15
0,15
5
0,3
2,78
0,13
5,5
0,33
2,45
0,16
6
0,3
2,95
0,2
4,5
0,4
3,38
0,18
5,3
0,4
3,49
0,17
4,9
0,35
4,05
0,21
3,5
0,33
1,9
0,14
4,79
0,3
0,35
90
1,5
5,6
2,7
1750
0,06
0,4
80
2,35
6,8
2,5
1500
0,05
0,3
70
1,6
5,5
2,8
2000
0,04
0,35
50
1,9
5,2
3,0
3000
0,062
0,3
60
1,8
6,0
3,2
2800
0,055
0,4
45
1,7
4,7
3,4
2500
0,03
0,33
30
2,0
7,5
3,5
2400
0,035
0,33
20
1,75
6,3
3,05
1900
0,04
Примечание. Н – ход ползуна.
141
142.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-4
5–7
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
К
H, м
l AB lOA
lOS1 lOA
l AS2 l AB
m1, кг
m2, кг
m3, кг
Р, Н
δ
Варианты
1
43,5
1,05
0,12
6,1
0,35
2
39
1,04
0,14
7,3
0,33
3
37
1,03
0,15
6,5
0,3
4
29
1,02
0,18
8,0
0,35
5
35
1,01
0,13
8,2
0,33
6
41
1,1
0,19
6,5
0,3
7
32
1,07
0,16
7,5
0,33
8
45,5
1,06
0,25
5,9
0,35
0,3
2,0
6,5
20
3000
0,03
0,33
2,2
8,1
25
4000
0,02
0,33
1,9
6,0
19
2800
0,03
0,3
1,8
6,4
18
2500
0,025
0,33
1,7
5,9
15
2700
0,04
0,4
2,05
6,5
21
3500
0,05
0,3
1,75
5,3
16
2400
0,04
0,33
2,3
8,0
27
4500
0,05
Примечание. Н – ход ползуна.
142
143.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-5
5–7
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
H, м
l AB lOA
e lOA
lOS1 lOA
l AS2 l AB
γ, град
m1, кг
m2, кг
m3, кг
Р, Н
δ
Варианты
1
64
0,12
4,5
0,25
0,4
2
45
0,20
4,0
0,2
0,5
3
41
0,11
5
0,27
0,3
4
39
0,17
3,5
0,24
0,35
5
37
0,13
4,4
0,4
0,4
6
35
0,09
3,8
0,3
0,5
7
53
0,15
4,6
0,25
0,45
8
58
0,12
5,0
0,32
0,33
0,33
20
0,5
1,3
0,95
400
0,02
0,4
10
0,85
1,5
2,0
450
0,025
0,3
15
0,9
1,7
1,4
500
0,03
0,35
21
1,10
2,1
1,9
600
0,02
0,5
17
0,7
2,5
1,8
750
0,03
0,33
25
0,6
3,0
0,9
650
0,025
0,4
30
1,2
2,7
2,35
800
0,04
0,5
22
1,3
3,2
2,6
690
0,045
Примечание. Н – ход ползуна.
143
144.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-6
5–7
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
К
H, м
l AB lOA
lOS1 lOA
l AS2 l AB
γ, град
m1, кг
m2, кг
m3, кг
Р, Н
δ
Варианты
1
46
1,08
0,11
3,5
0,33
2
74
1,03
0,12
4,0
0,4
3
53
1,06
0,2
4,2
0,5
4
49
1,04
0,13
5,0
0,4
5
62,5
1,02
0,14
3,8
0,5
6
57
1,07
0,15
4,5
0,33
7
64,5
1,03
0,16
5,3
0,5
8
79
1,025
0,1
3,9
0,4
0,3
20
0,7
2,4
1,0
400
0,02
0,4
15
0,8
3,0
1,1
450
0,03
0,33
10
1,2
3,5
1,4
500
0,04
0,33
12
0,6
2,8
0,8
490
0,035
0,3
16
1,0
3,6
1,5
550
0,025
0,4
25
1,1
4,5
1,5
600
0,04
0,33
30
1,25
5,4
1,6
580
0,03
0,33
18
0,75
3,1
1,3
610
0,025
Примечание. Н – ход ползуна.
144
145.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-7
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
VBср , м/с
H, м
l AB lOA
lOS1 lOA
l AS2 l AB
m1, кг
m2, кг
m3, кг
Р, Н
SН/Н
δ
Варианты
1
2
3
4
5
6
7
8
2,1
0,2
9
0,35
0,3
2,5
0,22
8
0,4
0,3
3,0
0,24
7
0,33
0,35
2,2
0,19
10
0,5
0,4
2,8
0,25
8,5
0,45
0,3
1,9
0,21
9,5
0,33
0,3
3,1
0,27
7,5
0,3
0,4
2,4
0,28
10
0,4
0,35
50
11
110
52
10
120
55
9,5
115
45
15
125
53
14
116
48
13
126
50
12
130
49
16
118
20 ⋅ 105
18 ⋅ 105
19 ⋅ 105
16 ⋅ 105
17 ⋅ 105
18,5 ⋅ 105
17,5 ⋅ 105
25 ⋅ 105
0,4
0,06
0,3
0,05
0,6
0,04
0,5
0,062
0,45
0,055
0,35
0,03
0,55
0,035
0,47
0,04
Примечание. Н – ход ползуна.
145
146.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-8
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
H, м
l AB lOA
e lOA
S пр H
lOS1 lOA
l AS2 l AB
m1, кг
m2, кг
m3, кг
Р, Н
δ
Варианты
1
1,6
0,12
10
0,15
0,8
0,35
2
1,9
0,10
8,5
0,17
0,9
0,4
3
2,1
0,16
7,5
0,2
0,7
0,33
4
1,5
0,09
6,0
0,12
0,75
0,3
5
2,7
0,13
9,5
0,1
0,6
0,35
6
2,5
0,15
6,6
0,21
0,75
0,3
7
1,4
0,11
7,2
0,18
0,65
0,4
8
3,0
0,14
9
0,23
0,55
0,4
0,33
10
15
45
0,3
25
16
50
0,33
30
20
60
0,3
19
11
34
0,4
30
15
45
0,4
38
22
65
0,3
25
12,5
38
0,35
29
17
80
3 ⋅ 105
4 ⋅ 105
2 ⋅ 105
5 ⋅ 105
3,2 ⋅ 105
6 ⋅ 105
2,7 ⋅ 105
4,2 ⋅ 105
0,06
0,05
0,04
0,062
0,055
0,03
0,035
0,04
Примечание. Н – ход ползуна.
146
147.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-9
5–7
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
К
H, м
l AB lOA
lOS1 lOA
l AS2 l AB
m1, кг
m2, кг
m3, кг
Р, Н
δ
Варианты
1
29
1,02
0,24
5
0,3
0,4
5
13
20
3600
0,025
2
19
1,03
0,15
3,5
0,33
0,4
4
11
19
3200
0,03
3
17
1,04
0,26
4,0
0,35
0,3
5,5
10
18
3000
0,04
4
23
1,025
0,17
3,2
0,3
0,33
4,2
9
21
3300
0,03
Примечание. Н – ход ползуна.
147
5
15
1,05
0,14
4,5
0,35
0,3
3,5
7
23
3700
0,02
6
27
1,035
0,11
4,2
0,4
0,4
2,5
6
15
3500
0,045
7
25
1,04
0,18
4,7
0,3
0,33
4,5
10
17
4000
0,035
8
20
1,02
0,13
5,5
0,4
0,33
3,5
8
14
2800
0,06
148.
ОмГТУКафедра «Машиноведение»
Проектирование и исследование рычажного механизма рабочей машины
Задание С4-10
5–7
1. Выполнить метрический синтез механизма.
2. Провести структурный анализ механизма.
3. Выполнить кинематический и силовой расчеты.
4. Уравновесить механизм.
Условное
обозначение
Варианты
1
2
3
4
5
6
7
8
VBср , м/с
2,5
1,7
1,5
1,2
1,4
2,4
3,9
4,0
H, м
0,3
0,21
0,20
0,18
0,12
0,19
0,3
0,28
l AB lOA
4
3,5
4,5
5
5,2
4,3
3,8
3,9
lOS1 lOA
0,3
0,35
0,36
0,37
0,33
0,4
0,35
0,3
l AS2 l AB
0,3
0,35
0,4
0,33
0,36
0,37
0,3
0,35
5
11
16
1000
0,03
4
8
10,5
900
0,05
3
9
9
950
0,04
6
9
7,5
850
0,025
7
10,5
5,5
1100
0,02
4
8
8,6
1150
0,02
7
9,5
17,5
1050
0,03
6
9,5
13
1200
0,025
m1, кг
m2, кг
m3, кг
Р, Н
δ
Примечание. Н – ход ползуна.
148
149.
ПРИЛОЖЕНИЕ 3ИССЛЕДОВАНИЕ СЛОЖНОГО
РЫЧАЖНОГО МЕХАНИЗМА
149
150.
150151.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма транспортной машины
Задание 6-1
Н – ход кулисы
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
Y1, мм
Y2, мм
lO1A, мм
lАВ, мм
lAS2, мм
lBO2, мм
lBC, мм
n, об/мин
G1 , Н
1
190
100
160
80
200
120
170
90
160
300
Варианты
2
3
4
210 300 270
100 170 190
190 270 290
90 105 90
230 300 320
130 150 200
180 230 270
80 130 150
170 180 190
240 250 200
5
205
110
220
60
200
100
200
100
200
329
Условное
обозначение
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
PMAX, Н
δ
151
Варианты
1
2
3
4
5
80
90
120 140
80
120 150 220 250
200
30
37
43
50
60
300 280 320 350
370
1,7
1,5
1,5
1,2
1,8
0,7
0,8 0,95 1,05
0,7
0,2 0,24 0,28 0,3
0,35
1500 1700 1800 1600 1900
0,05 0,056 0,04 0,033 0,029
152.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма транспортной машины
Задание 6-2
Н – ход кулисы
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
Y1, мм
Y2, мм
lO1A, мм
lO1S1, мм
lАВ, мм
lAS2, мм
lBO2, мм
lO2C, мм
n, об/мин
1
190
100
300
60
20
190
95
140
250
250
Варианты
2
3
4
230 160 190
140 170 120
290 280 240
90 50 80
30
0
35
230 170 190
115 85 95
180 130 150
260 250 210
220 200 210
5
150
70
260
47
0
154
77
100
245
180
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
PMAX, Н
δ
152
1
450
120
180
50
360
1,9
0,12
0,35
1000
0,04
Варианты
2
3
4
5
470 490 420
445
160 180 190
150
116 200 180
160
60
70
40
45
365 345 350
380
1,8
2,0
1,6
1,95
0,11 0,13 0,18 0,15
0,45 0,55 0,40 0,50
800 900 1100 950
0,029 0,022 0,033 0,025
153.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма транспортной машины
Задание 6-3
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
Y1, мм
Y2, мм
lO1A, мм
lАВ, мм
lAS2, мм
lBO2, мм
n, об/мин
G1 , Н
1
1300
1200
2700
360
1700
750
1500
140
1300
Варианты
2
3
4
1400 1400 1260
1200 1360 1300
2800 2600 2500
300 440 360
1700 1850 1600
850 900 800
1200 1360 1400
160 170 160
1200 1450 1300
5
1400
1300
2600
400
1760
900
1300
185
1400
Условное
обозначение
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
PMAX, Н
δ
153
1
550
700
0
300
6,5
2,5
2,2
5000
0,067
Варианты
2
3
4
550 600 500
750 720 740
0
0
0
350 380 330
6,2 6,7 7,0
2,7 2,3 2,4
2,0 2,5 2,7
5500 6000 6500
0,05 0,04 0,033
5
580
690
0
340
7,5
2,8
2,0
6200
0,029
154.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма транспортной машины
Задание 6-4
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
Y, мм
lO1A, мм
lO1S1, мм
lАВ, мм
lAS2, мм
lBO2, мм
lВC, мм
lВS3, мм
lВS4, мм
n, об/мин
Варианты
1
2
3
4
200 310 800 800
260 950 900 1050
170 350 300 400
50 60 55
70
580 800 750 950
390 400 370 475
570 850 900 900
1000 1250 1270 1200
285 425 500 450
650 625 635 600
180 200 220 140
5
800
1260
450
75
1100
550
1050
1200
525
600
150
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
J4, кг·м2
PMAX, Н
δ
154
1
300
200
300
300
550
5,5
2,2
1,2
1,3
4500
0,05
Варианты
2
3
4
420 450 500
320 280 350
320 280 350
350 390 330
450 520 530
6,0
5,7
6,5
2,5
2,2
2,7
1,5
1,7
1,5
1,2
1,3 1,15
5000 3000 5500
0,033 0,020 0,029
5
550
380
380
330
550
7,0
3,0
2,0
1,1
4000
0,040
155.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-5
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X1, мм
X2, мм
lO1A, мм
lO1S1, мм
lBO2, мм
lО2S3, мм
lВC, мм
lВS4, мм
n, об/мин
G1 , Н
1
240
240
90
45
135
10
210
105
220
400
Варианты
2
3
4
180 165 200
165 195 240
80 100 110
0
40
50
150 160 170
15 15
10
170 150 170
85 75
85
250 200 175
350 450 500
5
285
270
120
60
240
20
210
105
160
500
Условное
обозначение
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J3, кг·м2
J4, кг·м2
PMAX, Н
δ
155
1
0
320
200
150
2,0
0,5
0,4
2500
0,02
Варианты
2
3
4
0
0
0
300 280 300
180 160 180
110 120 150
2,0
3,0
4,0
0,6
0,5
0,7
0,3 0,25 0,3
3000 3500 4000
0,017 0,020 0,021
5
0
350
200
160
4,0
0,8
0,4
4500
0,015
156.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-6
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X1, мм
X2, мм
lO1A, мм
lO1S1, мм
lАВ, мм
lАC, мм
lАS2, мм
lCD, мм
lCS4, мм
θ, град
n, об/мин
1
140
345
90
10
240
370
180
170
75
20
150
Варианты
2
3
4
130 100 195
240 220 260
60 90
70
20
5
10
210 170 240
270 250 300
135 125 150
180 190 200
80 80
90
30 35
40
180 200 175
5
230
380
90
15
270
370
190
240
120
25
225
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J4, кг·м2
PMAX, Н
δ
156
1
300
350
200
150
160
2,5
0,5
0,08
1200
0,033
Варианты
2
3
4
350 320 280
250 220 240
150 150 200
150 160 200
200 190 200
1,8
1,6
2,0
0,5
0,4
0,5
0,08 0,09 0,09
1400 1300 1500
0,029 0,025 0,022
5
400
350
220
220
250
2,5
0,65
0,1
1600
0,020
157.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
Y, мм
lO1A, мм
lАВ, мм
lВC, мм
lАC, мм
l CD, мм
l CS4, мм
n, об/мин
PMAX, Н
1
230
50
50
190
130
170
180
90
240
1500
Варианты
2
3
4
5
200 200 170 240
40
50
30
40
60 75
50
70
190 200 165 210
140 150 165 160
130 120 130 180
190 200 170 180
95 70
65
90
260 205 220 180
2000 1600 2200 1800
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J4, кг·м2
δ
157
1
420
375
40
100
110
1,9
0,5
0,25
0,04
Варианты
2
3
4
400 380 350
350 360 320
35
50
25
80
75
120
120 115 100
1,7
1,5
1,4
0,4 0,35 0,38
0,28 0,24 0,22
0,033 0,029 0,025
5
325
280
30
110
105
1,2
0,41
0,27
0,022
158.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-8
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X1, мм
X2, мм
Y, мм
lO1A, мм
lАВ, мм
lAS2, мм
lBO2, мм
n, об/мин
G1 , Н
1
100
200
300
100
450
240
360
200
350
Варианты
2
3
4
160 70
40
120 260 140
260 270 1280
120 100 100
340 390 340
170 200 170
280 320 240
175 160 180
360 380 400
5
200
240
220
120
360
180
340
190
370
Условное
обозначение
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
PMAX, Н
δ
158
1
150
150
0
500
1,5
0,40
0,60
3200
0,018
Варианты
2
3
4
110 140 110
140 220 130
0
0
0
450 520 530
1,7
1,9
2,1
0,25 0,32 0,25
0,55 0,52 0,48
3500 3800 4200
0,013 0,012 0,011
5
120
230
0
380
1,9
0,30
0,50
5000
0,011
159.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-9
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X1, мм
X2, мм
Y, мм
lO1A, мм
lBO2, мм
lВC, мм
lВS4, мм
θ, град.
n, об/мин
G1 , Н
1
550
400
270
200
500
150
75
140
120
290
Варианты
2
3
4
400 430 470
425 500 425
200 200 275
175 225 200
325 350 350
125 150 125
60 75
65
150 130 135
190 170 160
270 320 295
5
425
200
350
190
360
125
70
120
180
280
Условное
обозначение
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J3, кг·м2
J4, кг·м2
PMAX, Н
δ
159
1
100
200
0
145
2,8
0,95
0,6
2200
0,015
Варианты
2
3
4
120 130 150
220 230 250
0
0
0
135 160 145
2,5
3,1 2,85
1,05 0,85 1,20
0,5
0,6
0,5
2000 2500 3000
0,014 0,013 0,012
5
110
210
0
140
2,7
0,98
0,5
3500
0,017
160.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-10
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
lO1A, мм
lАВ, мм
lВC, мм
lAS2, мм
lCD, мм
lCS4, мм
n, об/мин
PMAX, Н
1
440
80
240
120
180
160
80
150
4000
Варианты
2
3
4
480 420 310
105 90 105
270 240 260
75 90 180
180 170 270
240 180 220
120 90 110
160 170 165
5000 5250 4500
5
250
75
180
160
190
200
100
140
4200
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J4, кг·м2
δ
160
1
400
400
220
100
50
1,1
0,6
0,4
0,017
Варианты
2
3
4
500 480 520
390 370 450
150 200 150
140 110 130
70
55
65
1,7
1,2
1,7
0,5
0,4 0,55
0,3
0,2 0,25
0,015 0,020 0,022
5
380
350
120
120
60
1,0
0,7
0,35
0,025
161.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-11
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
lO1A, мм
lBO2, мм
lАВ, мм
lВC, мм
l O2C, мм
lCD, мм
lO1S1, мм
lAS2, мм
lCS4, мм
n, об/мин
1
400
90
175
450
200
140
370
40
200
160
20
Варианты
2
3
4
430 470 460
100 110 120
190 200 210
500 550 520
240 250 220
150 170 160
380 390 400
50 30 60
210 300 310
170 180 200
25 30 35
5
440
130
220
510
210
180
410
70
260
220
40
Условное
обозначение
PMAX, Н
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
J4, кг·м2
δ
161
Варианты
1
2
3
4
8000 9000 10000 12000
1800 2500 2200 3000
400 450 500 550
350 300 450 500
250 300 600 750
700 750 900 1000
5
6
7
8
0,4
0,5
0,6
0,9
1
1,2
1,3
1,4
0,8
0,9
0,8
1,0
0,05 0,04 0,055 0,067
5
11000
2700
600
550
550
1100
7,5
1,0
1,5
0,9
0,05
162.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма транспортной машины
Задание 6-12
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
Y1, мм
Y2, мм
lO1A, мм
lBO2, мм
lАВ, мм
lO1S1, мм
lAS2, мм
lCS5, мм
n, об/мин
Варианты
1
2
3
4
180 190 200 210
25 35 30 40
50 55 45 50
40 30 35 45
90 75 85 95
210 220 230 235
20 10 15 25
80 90 100 75
40 45 50 55
400 420 430 450
5
220
20
55
30
100
280
0
110
35
440
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
PMAX, Н
δ
162
1
25
4
2
0
1,3
0,15
0,02
0,015
20
0,025
Варианты
2
3
4
30
40
50
5
6
7
3
4
5
0
0
0
1,5
2,0
2,5
0,18 0,2 0,25
0,03 0,04 0,05
0,018 0,02 0,025
30
40
50
0,022 0,02 0,018
5
42
6,5
4,5
0
2,7
0,17
0,045
0,03
45
0,02
163.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма транспортной машины
Задание 6-13
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
Y1, мм
Y2, мм
lO1A, мм
lАВ, мм
lBO2, мм
lВC, мм
lCD, мм
lO1S1, мм
lAS2, мм
lCS4, мм
n, об/мин
1
280
120
180
55
300
310
210
280
20
100
120
110
Варианты
2
3
4
290 300 310
130 140 150
190 200 210
60 65 70
310 320 330
315 320 325
235 220 245
290 300 310
25 30 35
110 120 130
125 130 135
120 115 125
5
320
160
220
75
340
330
260
320
20
125
125
118
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
J4, кг·м2
PMAX, Н
δ
163
1
150
70
80
85
6
1,2
0,1
0,5
0,2
500
0,05
Варианты
2
3
4
160 170 180
75
80
85
85
90
110
85
90
95
7
10
9
1,3
1,4
1,5
0,15 0,2 0,25
0,6
0,7
0,8
0,25 0,3 0,35
550 600 650
0,04 0,033 0,045
5
190
100
120
92
8
1,6
0,22
0,75
0,32
700
0,036
164.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-14
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
Y, мм
lO1A, мм
lАВ, мм
lВC, мм
lBO2, мм
lO1S1, мм
lAS2, мм
lВS3, мм
lВS4, мм
n, об/мин
1
275
215
70
200
220
220
30
70
75
75
140
Варианты
2
3
4
260 245 255
195 255 235
65 60 65
190 180 185
210 230 240
210 230 240
20
0 15
65 75 70
70 80 100
70 80 100
160 130 150
5
215
175
50
160
180
180
10
50
75
75
145
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
J4, кг·м2
PMAX, Н
δ
164
1
150
30
40
40
200
1,0
0,04
0,06
0,06
7500
0,067
Варианты
2
3
4
180 170 180
40
32
35
45
42
38
45
42
38
220 210 190
1,2
1,1 0,95
0,05 0,045 0,038
0,075 0,07 0,065
0,075 0,07 0,065
8000 7000 6500
0,056 0,083 0,100
5
155
28
35
35
180
0,9
0,03
0,05
0,05
5700
0,050
165.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-15
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X1, мм
X2, мм
Y, мм
lO1A, мм
lАВ, мм
lBO2, мм
lСO2, мм
lCD, мм
lAS2, мм
lСS4, мм
n, об/мин
1
120
650
280
100
300
325
650
400
100
150
180
Варианты
2
3
4
100 80 0
600 700 750
340 310 290
120 110 90
350 320 380
315 370 395
630 740 790
380 380 370
120 105 90
160 155 165
190 185 195
5
50
800
270
85
310
420
840
390
85
180
170
Условное
обозначение
G1 , Н
G2 , Н
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J2, кг·м2
J3, кг·м2
J4, кг·м2
PMAX, Н
δ
165
1
400
100
180
120
500
2,0
0,08
0,4
0,03
9000
0,05
Варианты
2
3
4
450 425 375
110 105
90
200 190 185
130 125 115
600 550 475
3,0
2,5 1,75
0,09 0,05 0,075
0,5 0,45 0,37
0,04 0,035 0,032
9500 10000 8500
0,04 0,033 0,056
5
350
95
175
110
450
1,5
0,07
0,35
0,028
8000
0,045
166.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-16
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
lO1A, мм
lBO2, мм
lВC, мм
lВS4, мм
n, об/мин
G1 , Н
G2 , Н
1
50
100
100
300
120
100
500
0
Варианты
2
3
4
60 70 55
140 90 100
150 75 90
500 250 280
150 80 90
120 110 130
700 480 530
0
0
0
5
65
110
75
270
120
125
600
0
Условное
обозначение
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J3, кг·м2
J4, кг·м2
PMAX, Н
δ
166
1
150
35
300
0,4
0,5
0,03
2000
0,033
Варианты
2
3
4
5
200 180 140 190
50
40
38
45
400 260 280 320
0,8
0,3
0,4
0,6
0,3
0,4 0,45 0,2
0,05 0,02 0,03 0,02
1750 1500 1800 1400
0,025 0,05 0,029 0,025
167.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма транспортной машины
Задание 6-17
Н – ход кулисы
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
Y1, мм
Y2, мм
lO1A, мм
lBO2, мм
lО2S4, мм
n, об/мин
G1 , Н
G2 , Н
1
1000
1500
340
2200
1000
40
350
0
Варианты
Условное
2
3
4
5 обозначение
1100 900 1200 1050 G3, Н
1600 1400 1750 1550 G4, Н
350 300 400 320 G5, Н
2300 2000 2500 2100 J1, кг·м2
1050 900 1200 950 J3, кг·м2
35
60
50
25 PMAX, Н
400 375 410 425 δ
0
0
0
0
167
1
100
0
500
1,5
0,1
70
0,05
Варианты
2
3
4
110 105 120
0
0
0
600 700 560
2,0 1,75 2,1
0,2 0,25 0,3
80
90 100
0,067 0,04 0,045
5
125
0
650
2,3
0,27
85
0,067
168.
ОмГТУКафедра «Машиноведение»
Исследование сложного рычажного механизма технологической машины
Задание 6-18
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
Условное
обозначение
X, мм
lO1A, мм
lBO2, мм
lВC, мм
lВS4, мм
n, об/мин
G1 , Н
G2 , Н
1
50
100
140
420
150
100
500
0
Варианты
2
3
4
60 70 65
105 110 120
100 125 150
300 350 450
130 140 170
110 120 125
550 650 675
0
0
0
5
55
100
100
280
90
105
520
0
Условное
обозначение
G3 , Н
G4 , Н
G5 , Н
J1, кг·м2
J3, кг·м2
J4, кг·м2
PMAX, Н
δ
168
Варианты
1
2
3
4
150 140 130 180
100 125 130 107
500 400 450 550
2,0
1,8
2,1 1,75
0,2 0,18 0,22 0,15
0,3
0,2 0,25 0,45
2500 2200 2400 2300
0,033 0,05 0,04 0,029
5
170
120
380
1,6
0,16
0,15
2000
0,036
169.
ПРИЛОЖЕНИЕ 4ИССЛЕДОВАНИЕ РЫЧАЖНОГО МЕХАНИЗМА
РАБОЧЕЙ МАШИНЫ
169
170.
170171.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-1
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
32
0,110
0,055
0,370
0,120
+0,020
4,7
11,2
10,5
0,01
0,13
1300
1/20
2
28
0,120
0,060
0,410
0,140
+0,040
5,1
12,3
11,2
0,012
0,6
1450
1/25
3
25
0,135
0,067
0,430
0,150
+0,030
5,3
13,7
11,9
0,015
0,21
1500
1/23
171
4
30
0,150
0,075
0,450
0,160
–0,03
5,8
14,9
12,3
0,018
0,25
1570
1/26
5
15
0,180
0,090
0,615
0,200
–0,050
6,3
15,8
13,4
0,02
0,5
1680
1/28
6
20
0,200
0,100
0,710
0,230
+0,05
7,1
17,4
14,5
0,04
0,73
1920
1/21
7
17
0,210
0,110
0,730
0,280
–0,060
7,6
19,3
15,1
0,09
0,9
2150
1/22
172.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-2
3–5
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
γ, град
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
100
0,02
0,01
0,065
0,018
–0,005
20
0,14
0,39
0,16
0,00011
0,00012
210
1/15
2
90
0,025
0,0125
0,075
0,025
+0,006
40
0,15
0,42
0,17
0,00012
0,0002
220
1/18
3
75
0,028
0,014
0,085
0,028
–0,008
60
0,16
0,44
0,18
0,00013
0,0003
230
1/17
172
4
50
0,030
0,015
0,12
0,030
+0,01
30
0,17
0,46
0,19
0,00014
0,0006
240
1/20
5
40
0,035
0,0175
0,125
0,030
–0,01
50
0,18
0,48
0,21
0,00016
0,0006
250
1/23
6
32
0,040
0,02
0,13
0,040
–0,012
40
0,19
0,51
0,23
0,00017
0,00075
260
1/25
7
25
0,050
0,025
0,18
0,060
+0,008
60
0,20
0,56
0,27
0,00018
0,0015
270
1/21
173.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-3
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
γ, град
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
65
0,05
0,025
0,16
0,08
–0,01
40
0,65
0,9
0,46
0,0011
0,0020
240
1/17
2
72
0,06
0,03
0,18
0,06
+0,012
30
0,75
1,42
0,75
0,0022
0,0050
200
1/13
3
55
0,07
0,035
0,22
0,08
–0,020
50
0,96
2,44
0,88
0,0053
0,01
220
1/11
173
4
35
0,08
0,04
0,28
0,09
+0,025
35
1,17
2,6
0,95
0,0084
0,018
210
1/23
5
23
0,09
0,045
0,32
0,13
–0,03
50
1,38
2,8
1,21
0,0120
0,025
270
1/22
6
47
0,1
0,05
0,35
0,12
–0,016
60
1,85
3,51
1,40
0,0170
0,040
250
1/18
7
84
0,15
0,075
0,45
0,15
+0,040
45
2,5
3,8
2,10
0,0218
0,070
230
1/20
174.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-4
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
37
0,06
0,03
0,2
0,075
–0,016
0,55
1,2
0,86
0,041
0,005
210
1/19
2
45
0,064
0,032
0,22
0,08
+0,015
0,75
1,42
1,25
0,052
0,007
220
1/21
3
26
0,08
0,04
0,25
0,09
–0,022
0,80
2,44
1,9
0,063
0,015
230
1/23
174
4
23
0,09
0,045
0,29
0,10
–0,025
1,27
2,6
1,9
0,084
0,025
250
1/25
5
21
0,1
0,05
0,33
0,11
+0,03
1,58
2,8
2,2
0,096
0,035
240
1/18
6
51
0,12
0,06
0,37
0,14
–0,035
1,8
3,51
2,8
0,107
0,040
260
1/21
7
42
0,09
0,045
0,30
0,095
–0,021
2,4
3,8
2,4
0,078
0,030
270
1/22
175.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-5
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
γ, град
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
70
0,041
0,02
0,15
0,050
–0,01
20
0,45
0,9
0,46
0,0011
0,002
215
1/30
2
80
0,045
0,022
0,16
0,060
–0,016
15
0,55
1,42
0,75
0,0012
0,003
230
1/28
3
90
0,05
0,025
0,14
0,070
+0,018
30
0,66
2,44
0,88
0,0013
0,001
245
1/20
175
4
60
0,055
0,028
0,175
0,080
+0,007
25
0, 87
2,6
0,95
0,0014
0,007
250
1/23
5
75
0,065
0,032
0,21
0,070
–0,015
30
1,08
2,8
1,21
0,0016
0,01
275
1/25
6
30
0,08
0,04
0,28
0,090
+0,016
10
1,80
3,51
2,4
0,0017
0,023
290
1/11
7
45
0,1
0,05
0,30
0,10
–0,023
40
2,2
3,8
2,1
0,0018
0,029
310
1/18
176.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-6
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
γ, град
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
100
0,060
0,030
0,24
0,110
–0,012
80
0,21
0,63
0,25
0,0019
0,003
155
1/20
2
90
0,065
0,032
0,26
0,125
+0,011
70
0,22
0,69
0,26
0,0021
0,004
175
1/21
3
70
0,070
0,035
0,28
0,135
–0,019
50
0,24
0,79
0,27
0,0025
0,005
195
1/18
176
4
65
0,075
0,038
0,32
0,165
–0,008
65
0,25
0,81
0,28
0,0028
0,007
215
1/19
5
50
0,080
0,040
0,34
0,17
+0,024
75
0,27
0,85
0,29
0,0031
0,008
240
1/21
6
75
0,085
0,042
0,36
0,180
–0,015
62
0,29
0,95
0,32
0,0036
0,010
260
1/24
7
40
0,090
0,045
0,39
0,185
–0,030
58
0,31
0,98
0,35
0,0039
0,012
280
1/25
177.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS5, м
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р/105, Н
δ
Варианты
1
32
0,08
0,04
0,65
0,22
49
9,6
124
20
0,38
16,0
0,1
2
35
0,085
0,042
0,68
0,23
50
10,0
125
22
0,56
16,5
0,08
3
38
0,09
0,045
0,72
0,24
51
11
126
24
0,42
17,0
0,07
177
4
30
0,095
0,047
0,76
0,25
52
11,5
127
26
0,53
17,5
0,08
5
33
0,1
0,05
0,8
0,26
53
12
128
30
0,60
18,0
0,09
6
34
0,087
0,044
0,7
0,23
52,5
10,5
129
28
0,47
18,5
0,10
7
39
0,092
0,046
0,74
0,25
53,5
11,2
130
32
0,55
19,0
0,08
178.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-8
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS5, м
lАВ, м
lАS5, м
e, м
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р/105, Н
Sпр, м
δ
Варианты
1
18
0,055
0,028
0,3
0,12
0,01
20
60
220
3
0,5
4
0,05
0,1
2
20
0,085
0,042
0,5
0,25
0,02
30
70
250
6
1,5
5
0,07
0,09
3
15
0,075
0,038
0,4
0,2
0,015
35
90
300
5
1,2
6
0,06
0,08
178
4
17
0,056
0,028
0,3
0,15
0,012
40
110
350
6
0,82
7
0,04
0,07
5
22
0,095
0,047
0,5
0,25
0,025
17
50
200
4
1,05
3
0,06
0,05
6
13
0,054
0,027
0,25
0,10
0,008
30
80
240
3,5
0,42
4,5
0,03
0,06
7
16
0,07
0,035
0,35
0,14
0,012
35
100
260
5
1,1
5,5
0,05
0,07
179.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-9
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
14
0,09
0,045
0,27
0,16
+0,024
25
11
31
0,17
0,065
3000
1/20
2
17
0,11
0,055
0,33
0,20
–0,035
30
13
29
0,15
0,12
1750
1/25
3
22
0,125
0,065
0,4
0,24
+0,03
40
20
23
0,2
0,3
2500
1/19
179
4
24
0,08
0,04
0,26
0,18
+0,02
23
15
19
0,18
0,08
2200
1/30
5
20
0,12
0,06
0,45
0,27
–0,025
37
50
25
0,2
0,84
4000
1/35
6
18
0,075
0,037
0,24
0,14
+0,015
28
14
17
0,15
0,06
1600
1/40
7
26
0,13
0,065
0,52
0,3
–0,034
45
55
35
0,22
1,14
4500
1/32
180.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-10
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
15
0,1
0,05
0,35
0,175
–0,014
40
25
15
0,6
0,25
3500
1/25
2
18
0,09
0,045
0,4
0,2
+0,023
38
27
16
0,8
0,36
3300
1/20
3
19,5
0,075
0,038
0,31
0,15
+0,021
33
23
20
0,4
0,18
3000
1/30
180
4
22,5
0,08
0,04
0,25
0,125
–0,017
35
19
17
0,25
0,1
3200
1/19
5
17,5
0,065
0,032
0,2
0,1
+0,016
30
17
14
0,17
0,06
2500
1/32
6
23
0,05
0,025
0,17
0,085
–0,011
28
15
13
0,8
0,036
2500
1/35
7
27
0,11
0,055
0,36
0,18
+0,023
45
26
22
0,5
0,28
4000
1/40
181.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-11
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
24
0,05
0,025
0,2
0,08
–0,013
20
15
23
0,15
0,05
2000
1/22
2
25
0,06
0,03
0,22
0,085
+0,015
22
16
19
0,16
0,065
2100
1/20
3
27
0,075
0,04
0,3
0,11
+0,021
27
20
25
1,75
0,15
2200
1/30
181
4
22
0,08
0,04
0,28
0,1
–0,02
30
19
24
1,8
0,12
1900
1/35
5
19
0,09
0,045
0,3
0,12
+0,013
35
21
30
2,0
0,16
2400
1/40
6
21
0,12
0,06
0,4
0,12
–0,025
50
30
28
2,1
0,4
2500
1/35
7
32
0,14
0,07
0,45
0,15
–0,04
55
32
34
2,2
0,54
2700
1/45
182.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-12
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
25
0,14
0,07
0,52
0,17
+0,03
13
4
17
0,53
0,0085
450
1/30
2
23
0,08
0,04
0,32
0,11
–0,02
9
3
10
0,56
0,026
500
1/20
3
17
0,055
0,027
0,17
0,07
–0,011
17
5
10
0,6
0,012
500
1/25
182
4
13
0,065
0,0325
0,2
0,06
+0,02
19
7
15
0,65
0,023
600
1/40
5
33
0,09
0,045
0,31
0,1
–0,018
25
8
10
0,8
0,064
700
1/45
6
36,5
0,1
0,05
0,37
0,12
+0,025
20
6
15
0,85
0,07
1200
1/50
7
40
0,076
0,013
0,11
0,04
+0,01
5
8
12
0,12
0,008
110
1/35
183.
ОмГТУКафедра «Машиноведение»
Исследование рычажного механизма рабочей машины
Задание У4-13
5–7
Н – ход ползуна
1. Провести структурный анализ механизма.
2. Выполнить кинематический и силовой расчеты.
3. Уравновесить механизм.
Условное
обозначение
ω1, рад/с
lОА, м
lОS1, м
lАВ, м
lАS2, м
e, м
γ, град
m1, кг
m2, кг
m3, кг
IS1, кг·м2
IS2, кг·м2
Р, Н
δ
Варианты
1
81
0,05
0,025
0,16
0,05
+0,01
10
0,65
0,9
0,46
0,0011
0,0020
240
1/17
2
73
0,06
0,03
0,18
0,06
–0,01
13
0,75
1,42
0,75
0,0022
0,0050
250
1/13
3
27
0,07
0,035
0,22
0,07
–0,012
15
0,96
2,44
0,88
0,0053
0,01
2 70
1/11
183
4
45
0,08
0,04
0,28
0,08
–0,014
17
1,17
2,6
0,95
0,0084
0,018
285
1/23
5
62
0,09
0,045
0,32
0,13
+0,013
12
1,38
2,8
1,21
0,0120
0,025
260
1/22
6
58
0,1
0,05
0,35
0,12
–0,016
20
1,85
3,51
1,40
0,0170
0,040
320
1/18
7
35
0,15
0,075
0,45
0,15
+0,015
16
2,5
3,8
2,10
0,0218
0,070
340
1/20
184.
Учебное изданиеРязанцева Ирина Леонидовна
ПРИКЛАДНАЯ МЕХАНИКА
СХЕМНЫЙ АНАЛИЗ И СИНТЕЗ МЕХАНИЗМОВ
И МАШИН
Учебное пособие
Редактор М. А. Болдырева
Компьютерная верстка Е. В. Беспаловой
Сводный темплан 2017 г.
Подписано в печать 10.11.17. Формат 60×841/16. Отпечатано на дупликаторе.
Бумага офсетная. Усл. печ. л. 11,5. Уч.-изд. л. 11,5.
Тираж 70 экз. Заказ 687.
Издательство ОмГТУ. 644050, г. Омск, пр. Мира, 11; т. 23-02-12.
Типография ОмГТУ.
184

































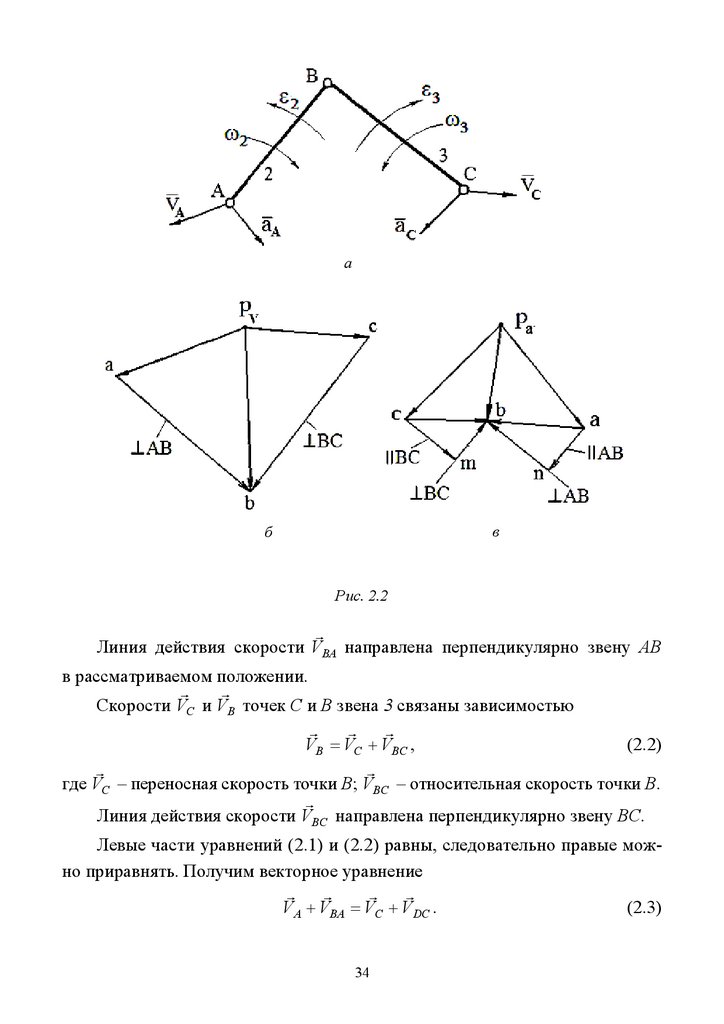























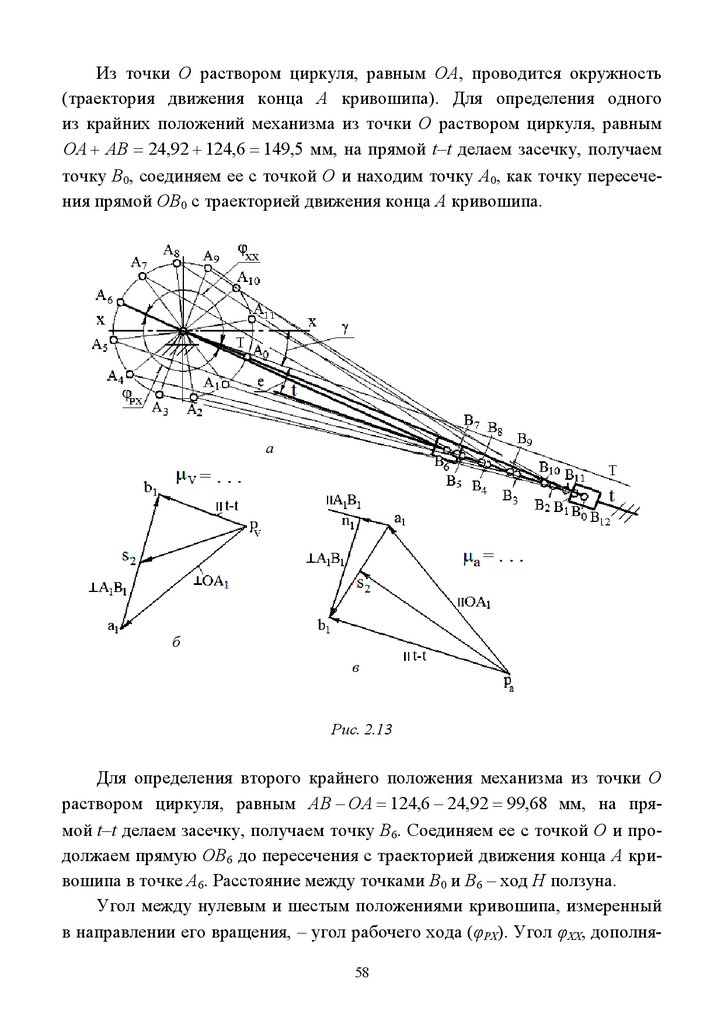












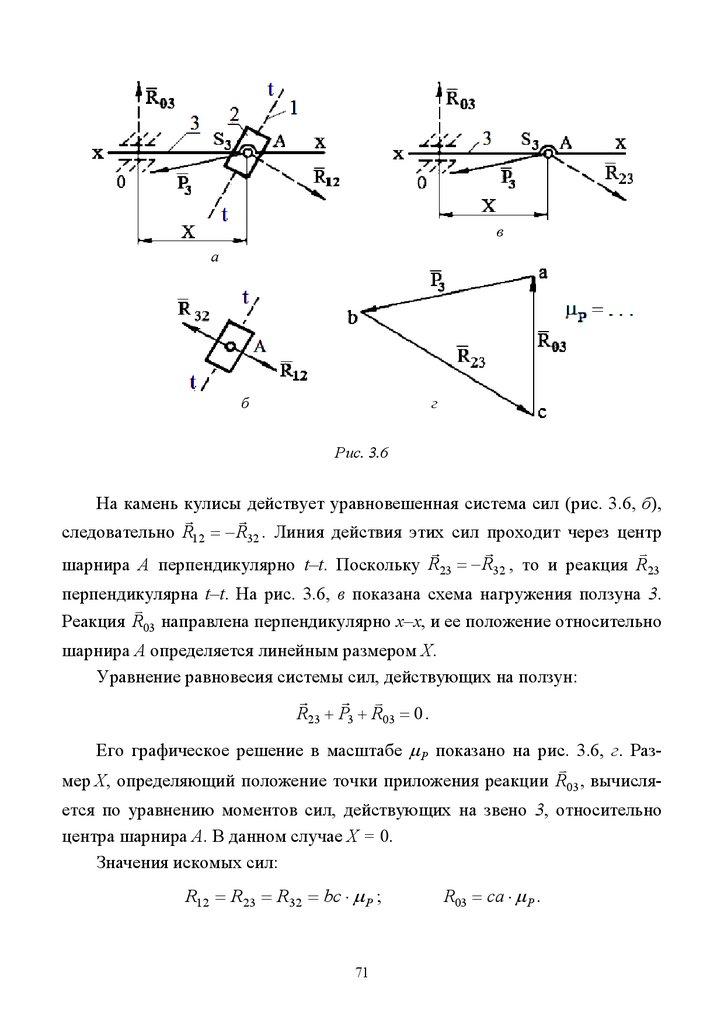




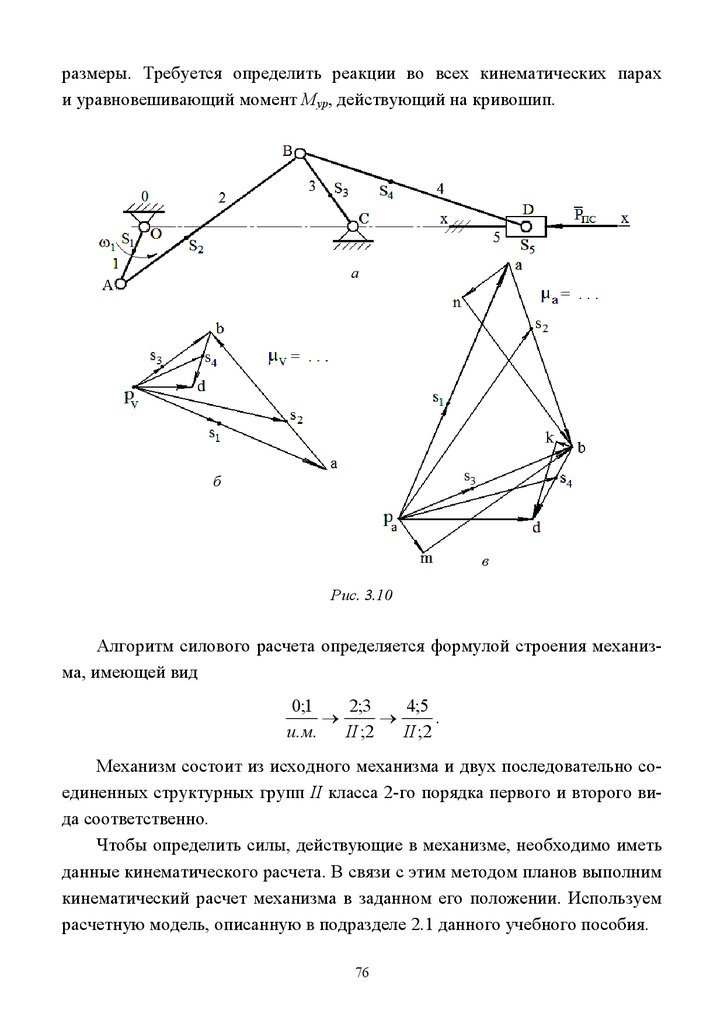





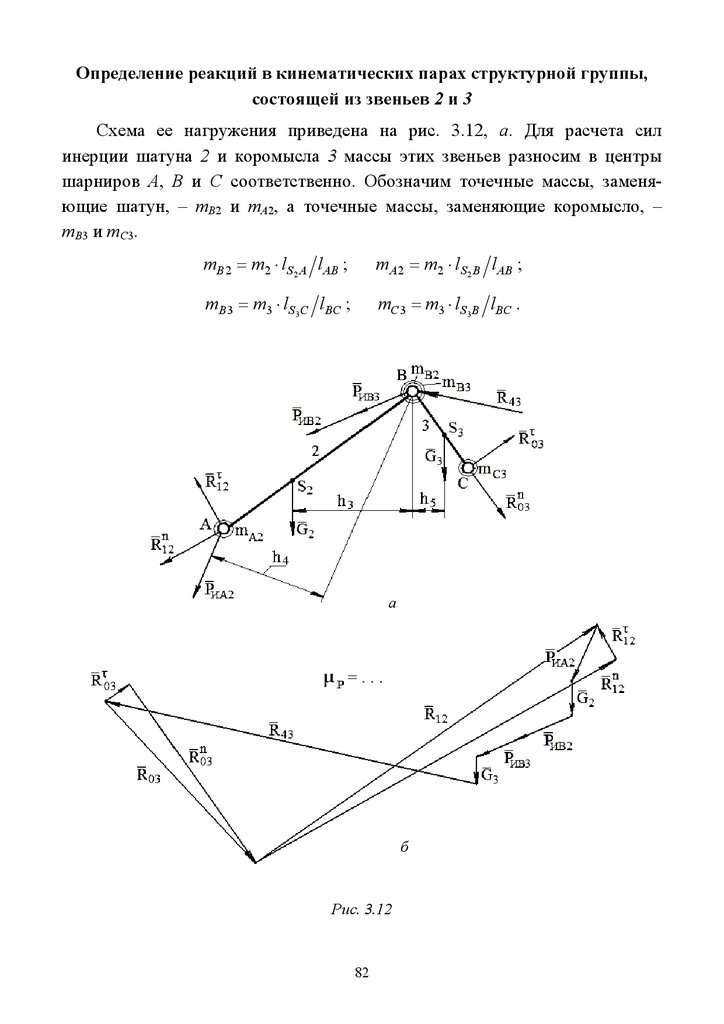






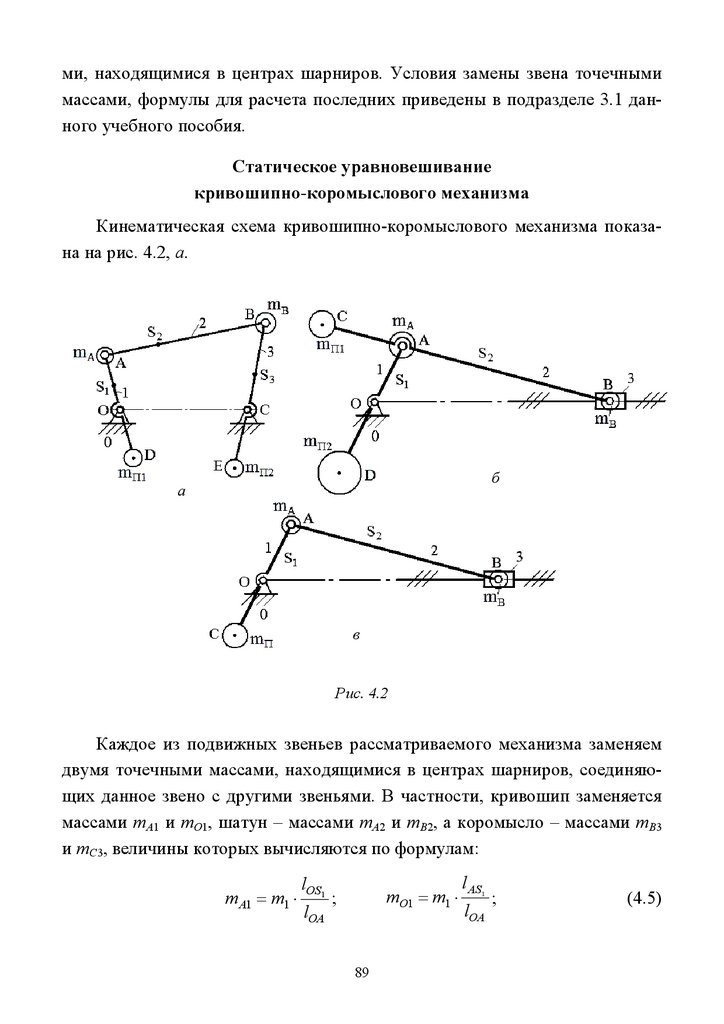




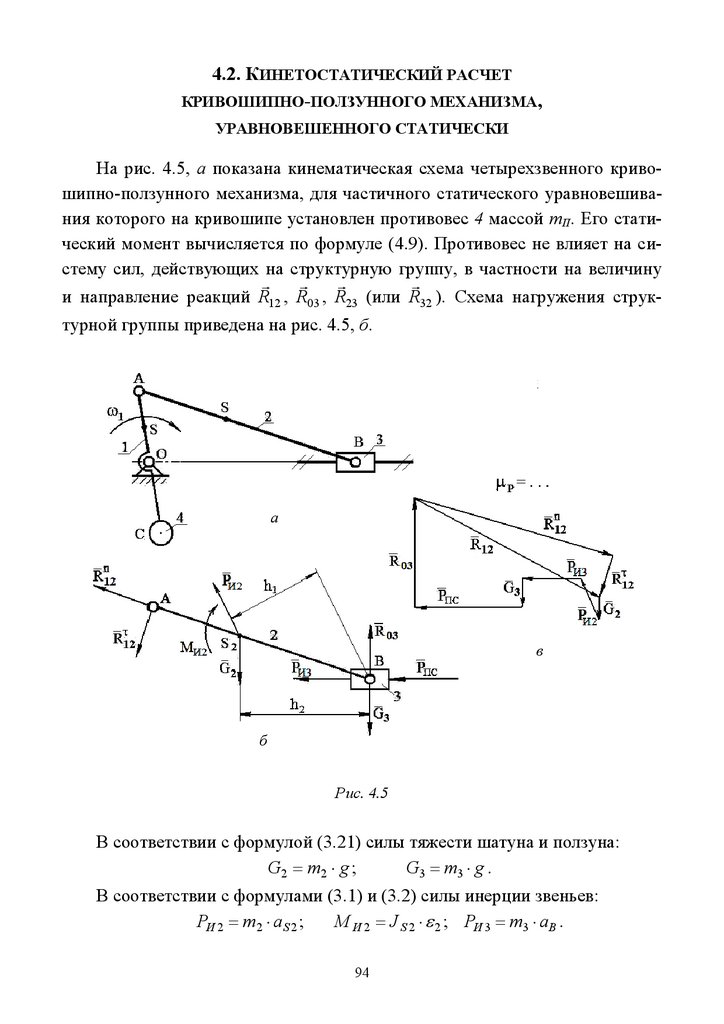






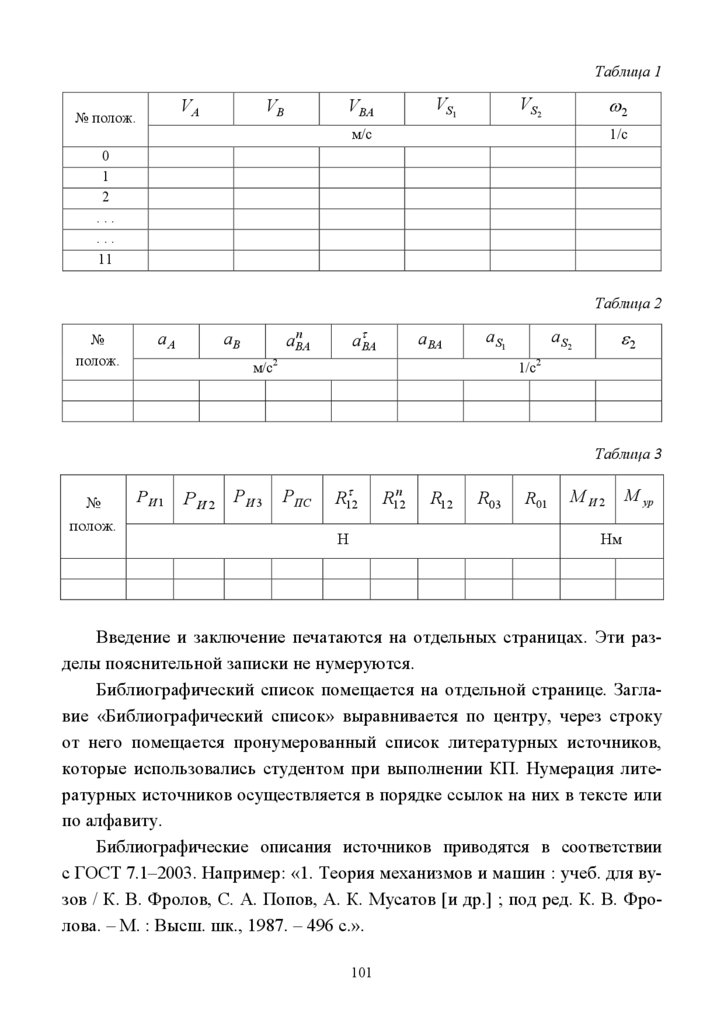













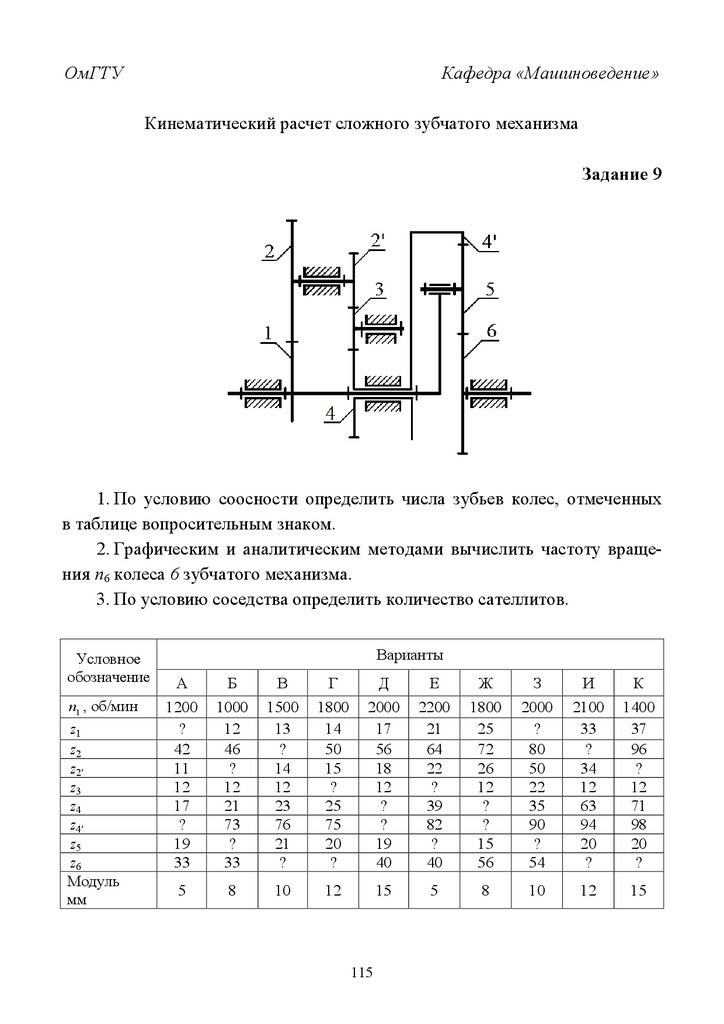


















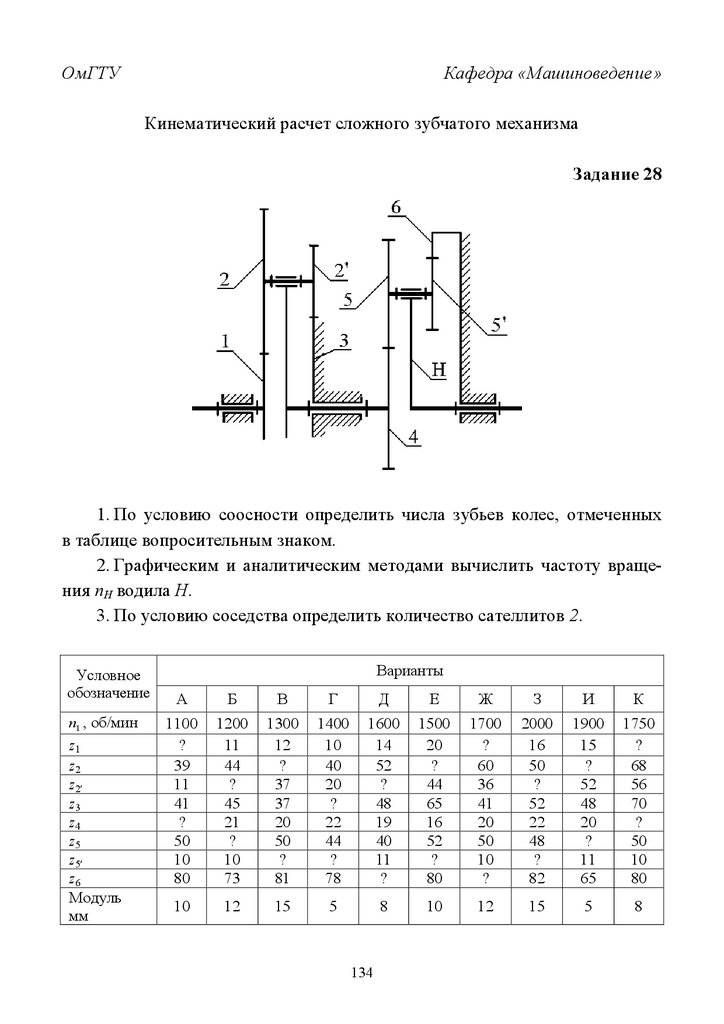





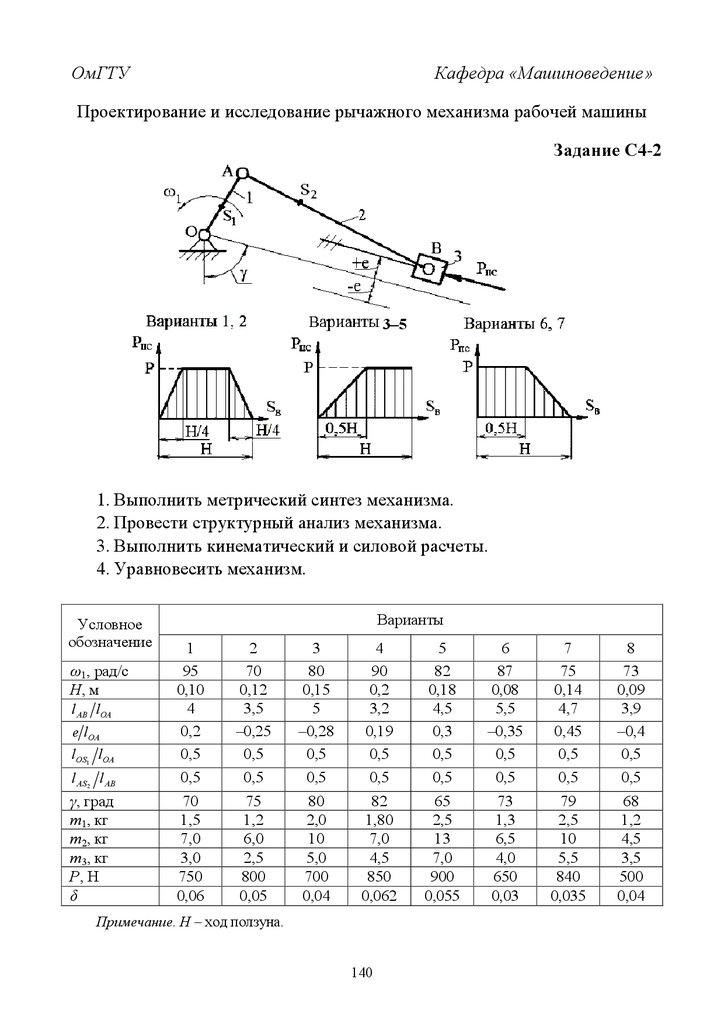




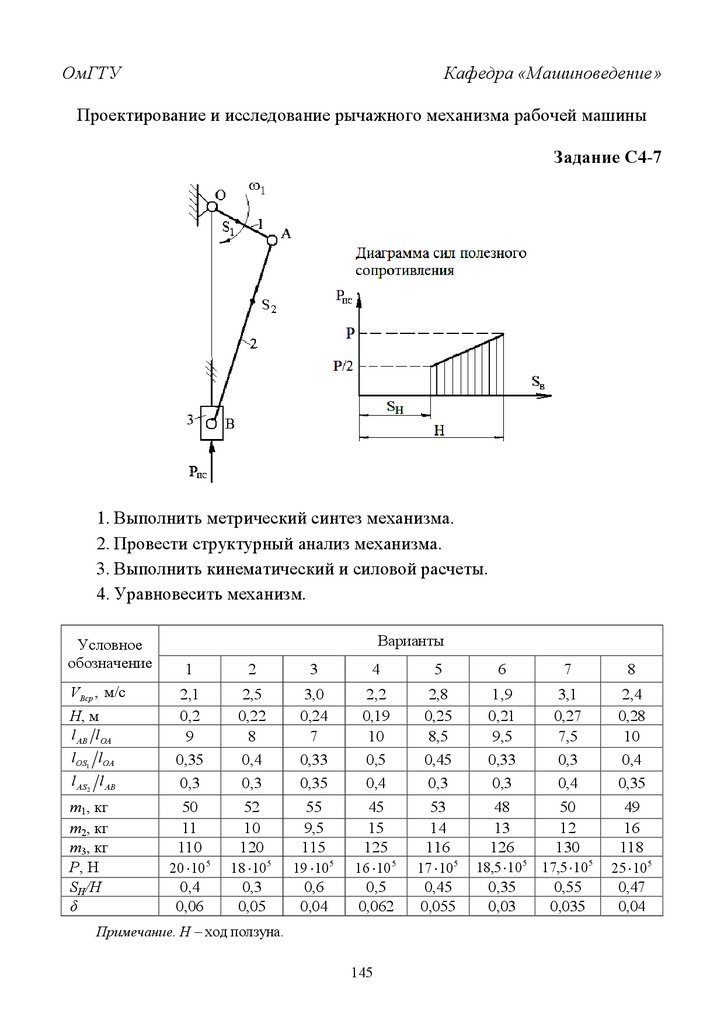

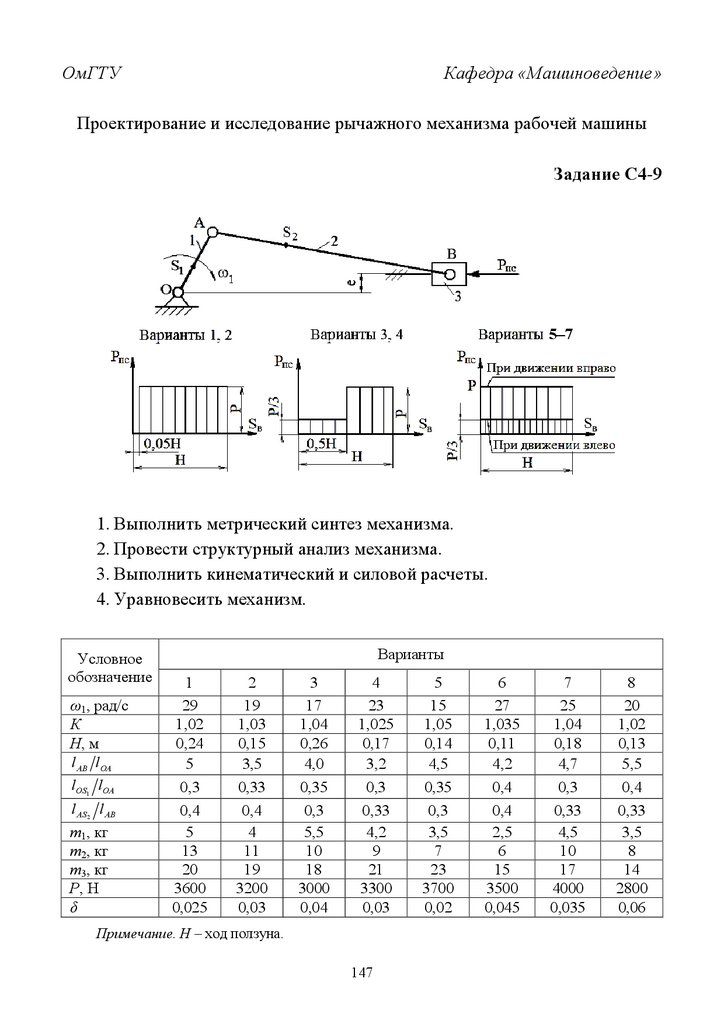





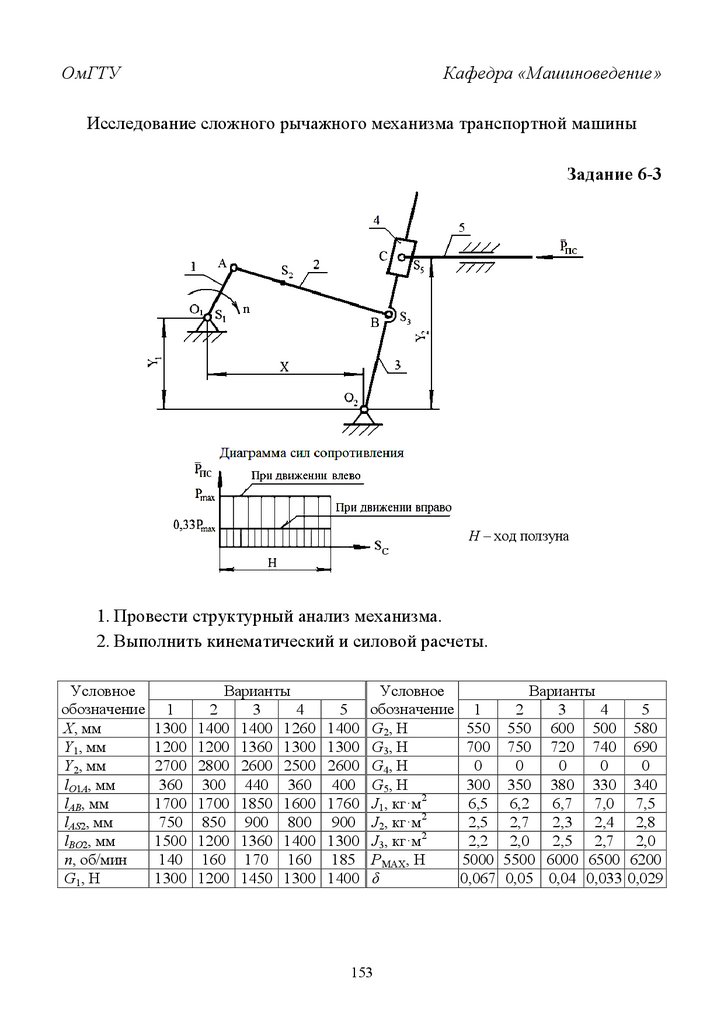
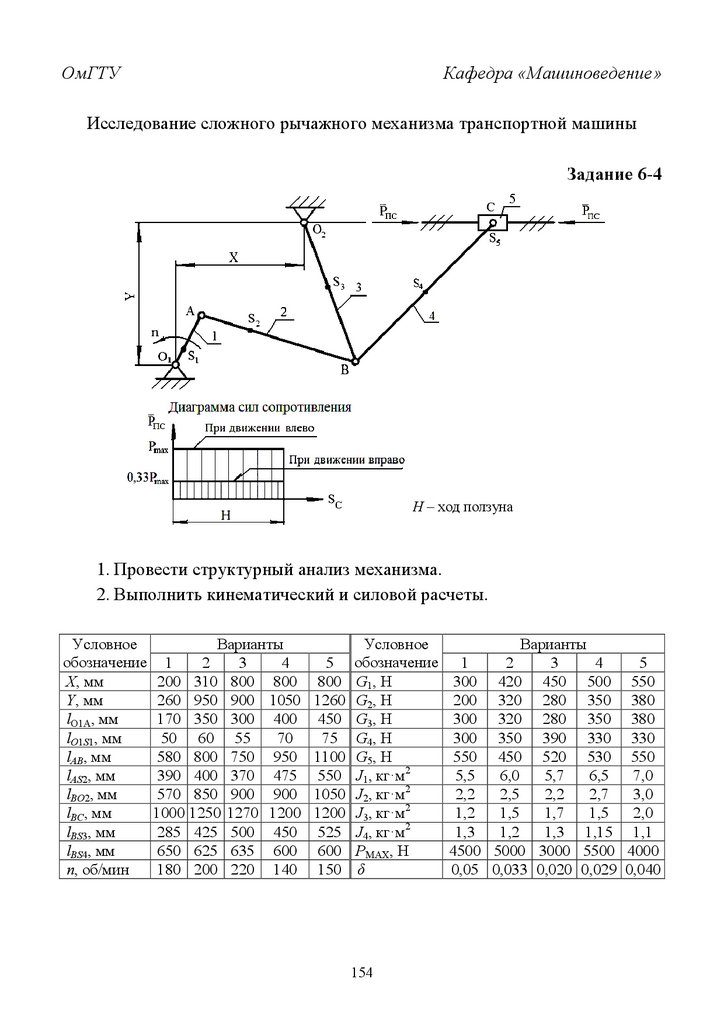
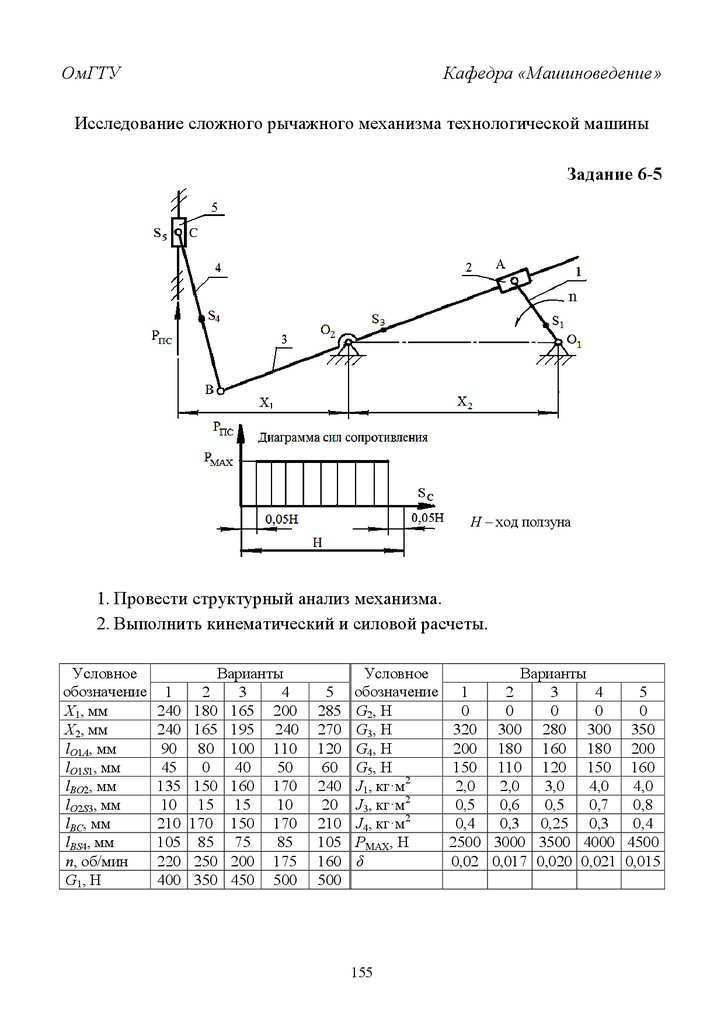
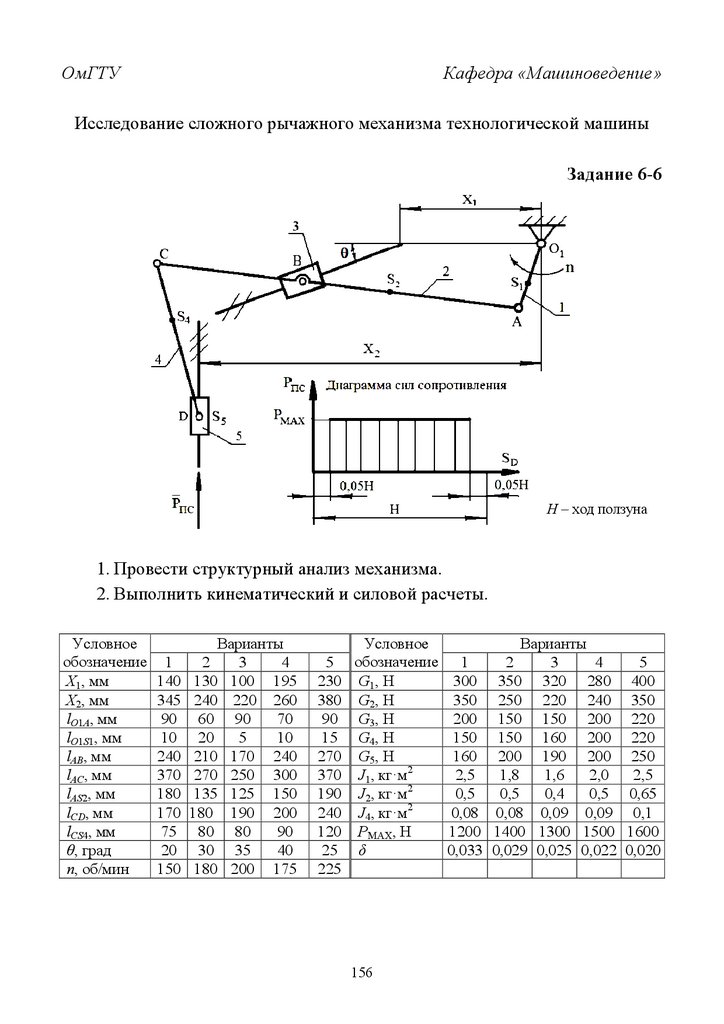
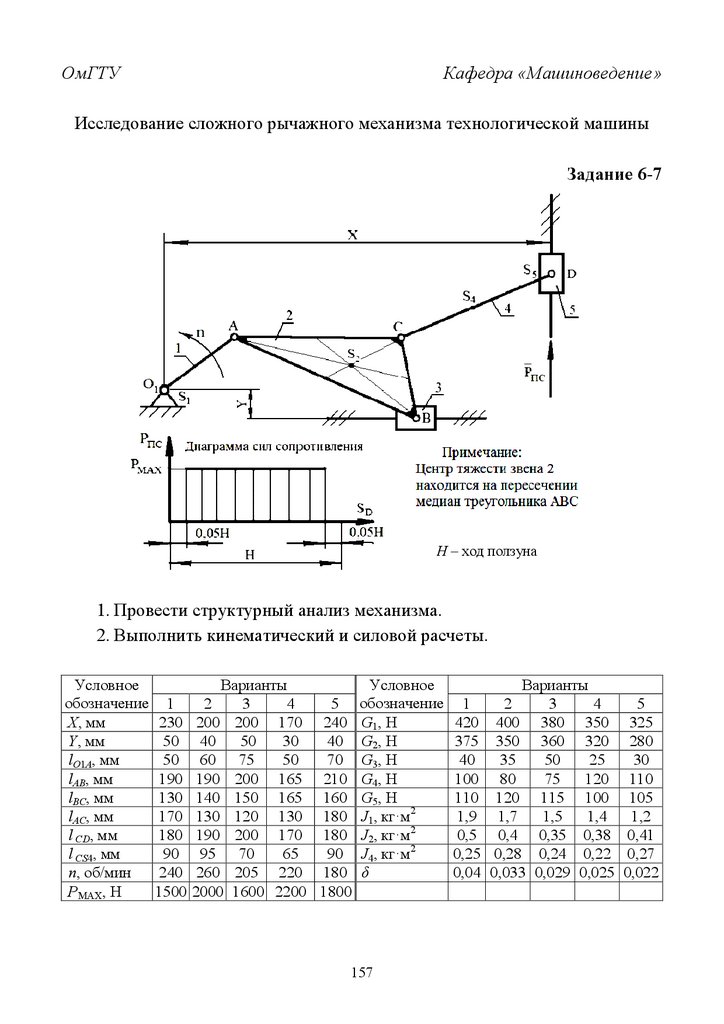


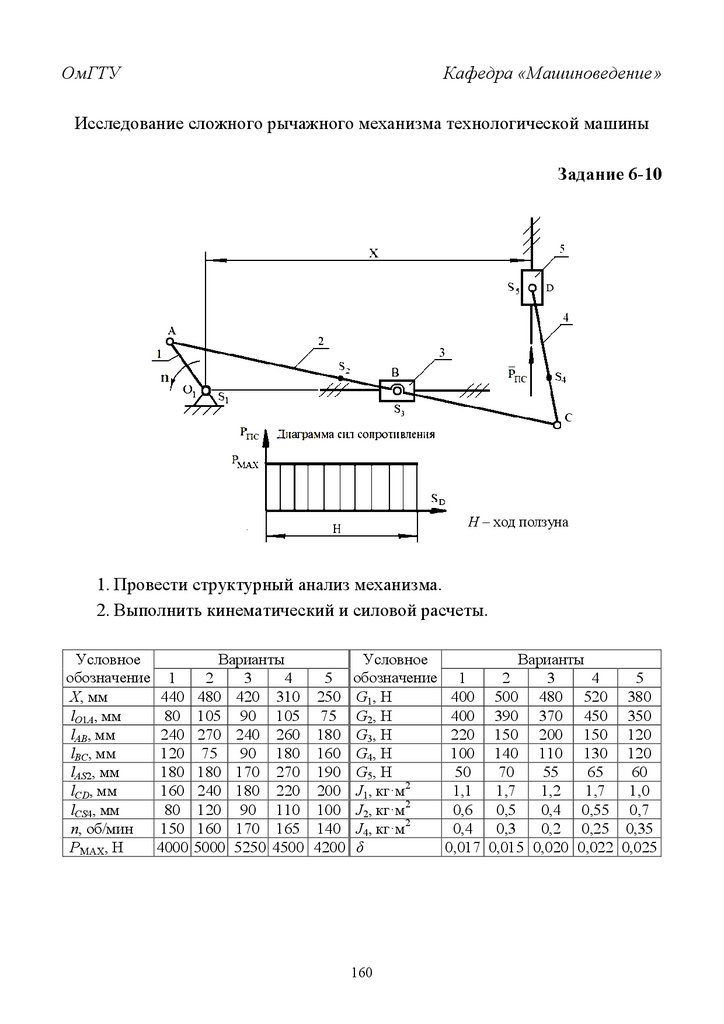
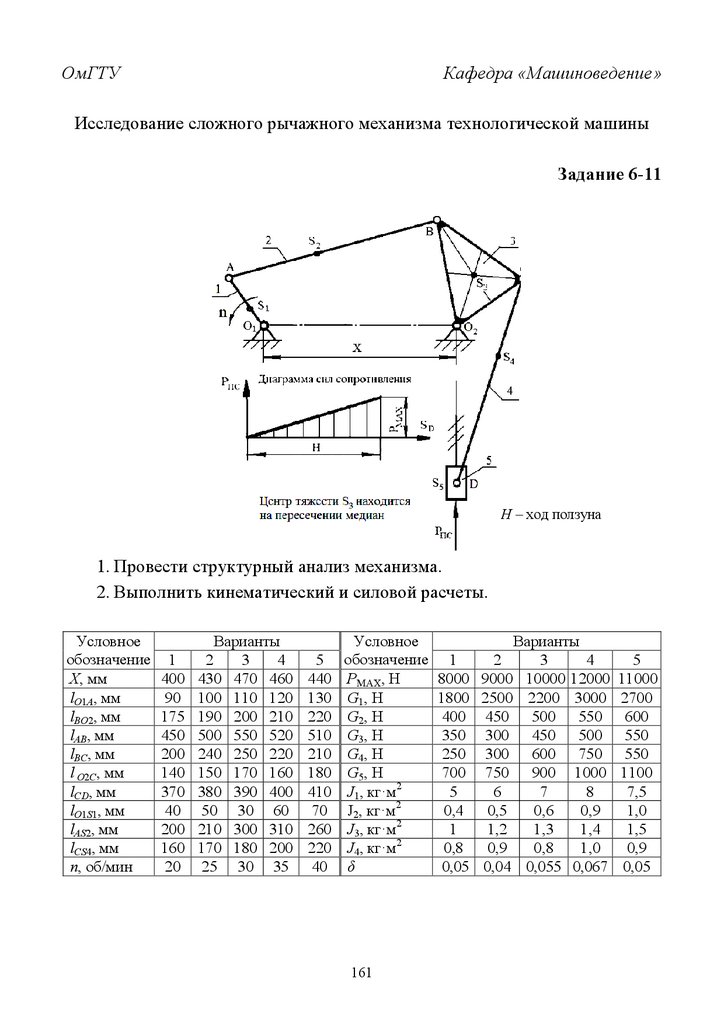
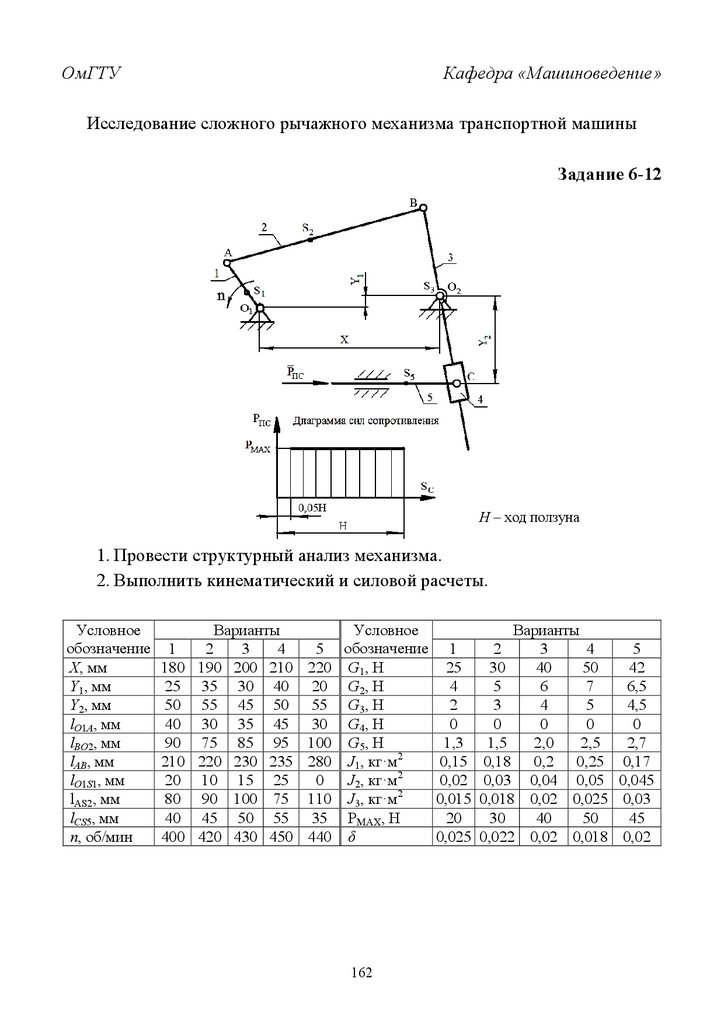
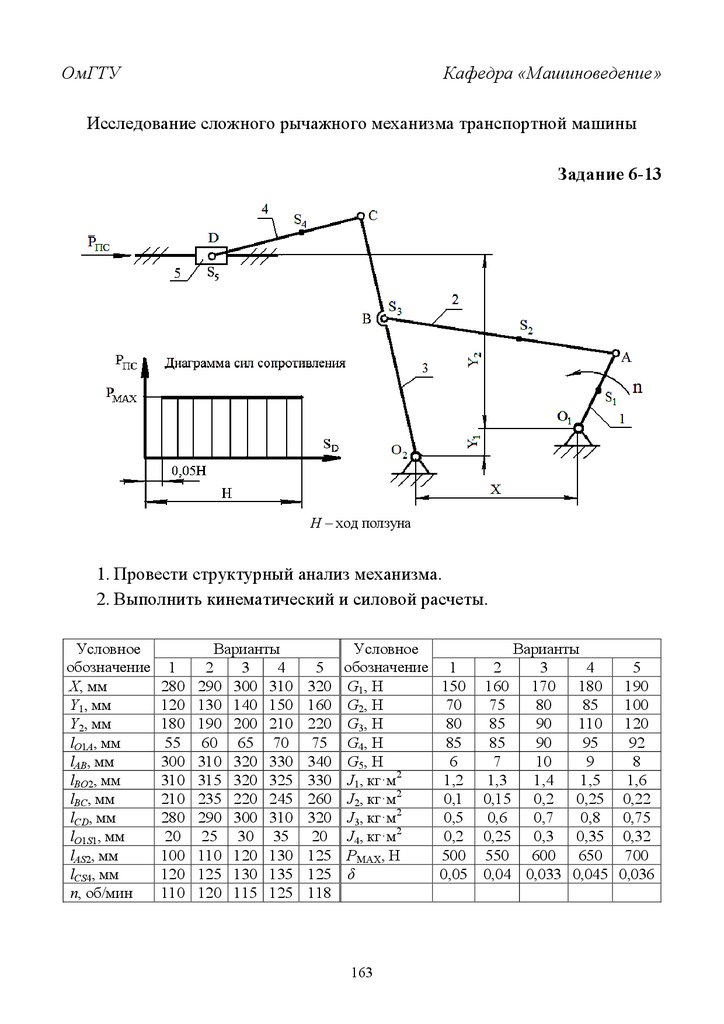

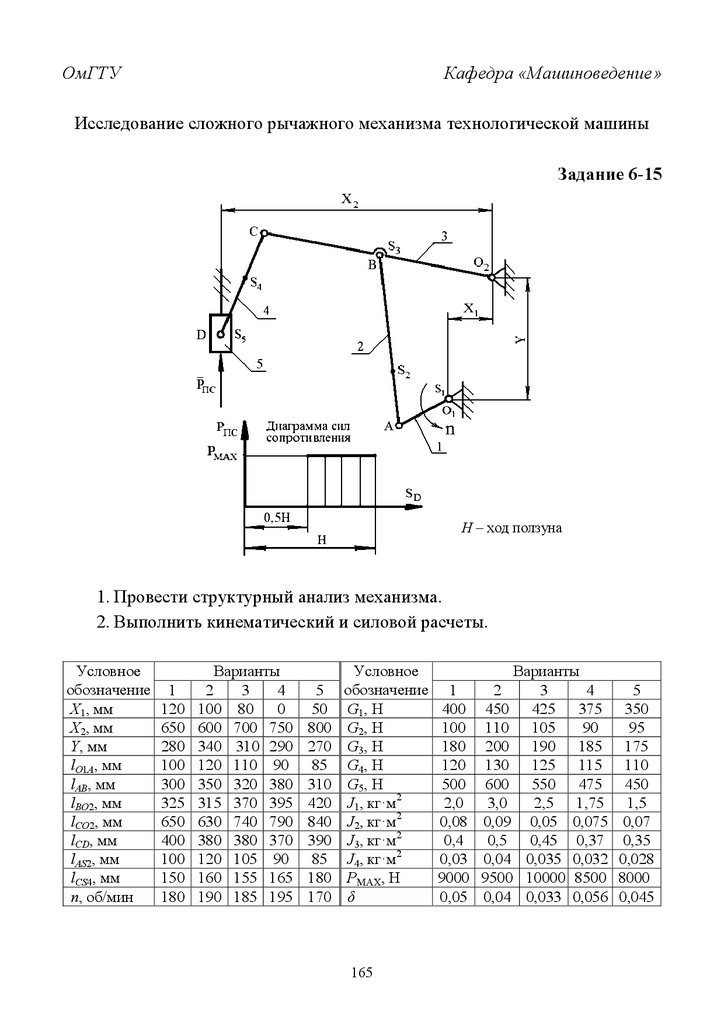
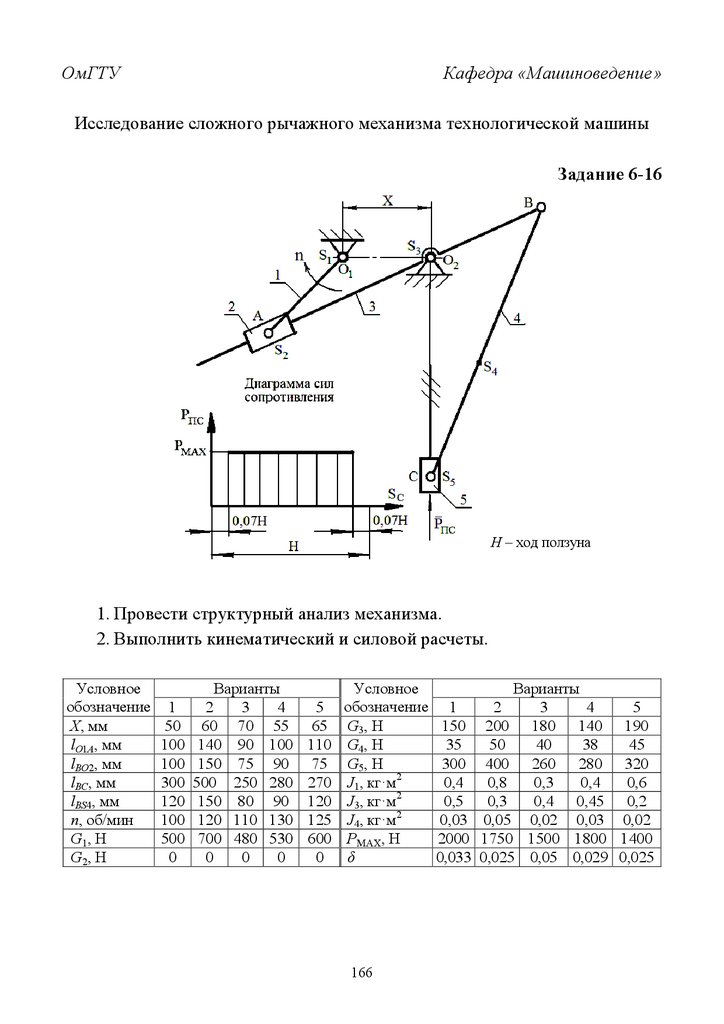
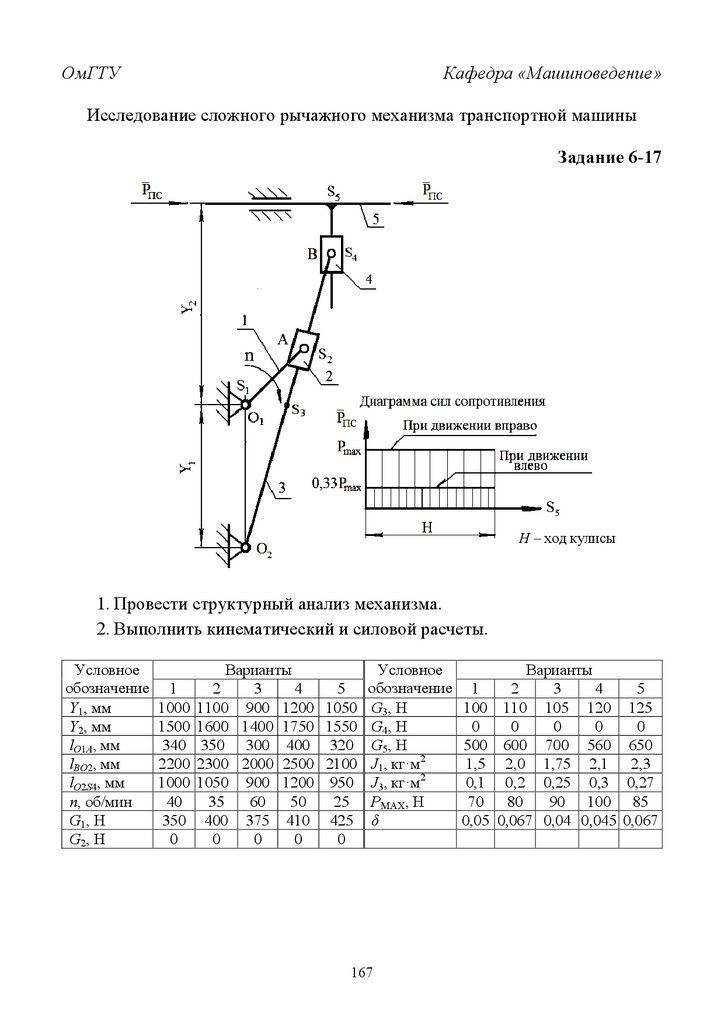
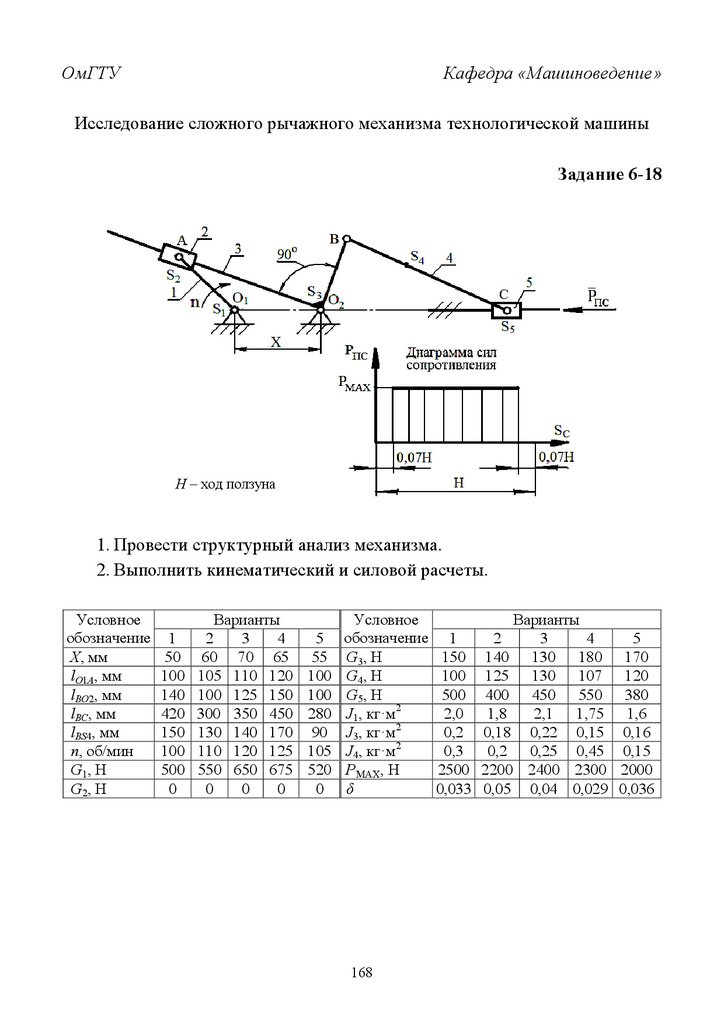








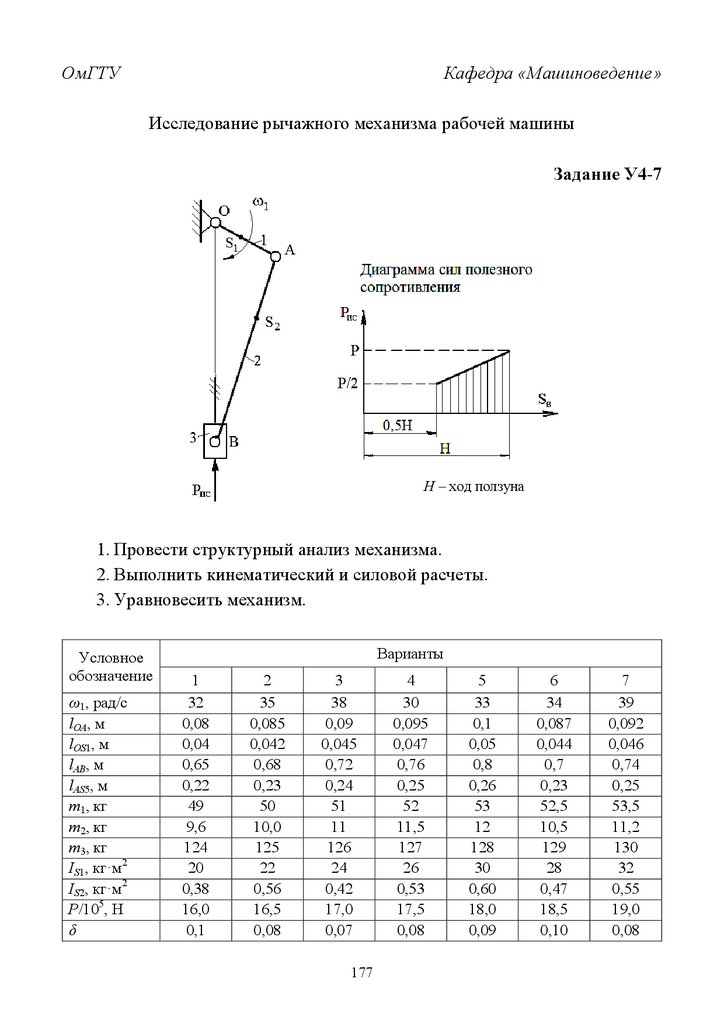




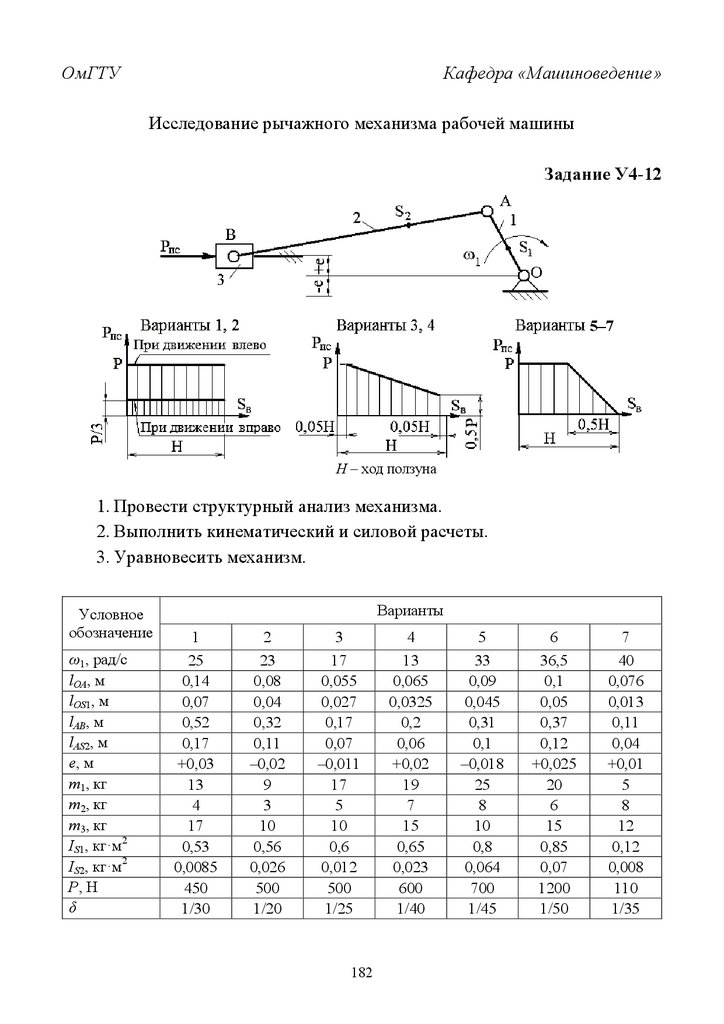


 mechanics
mechanics








