Кинематический анализ плоских рычажных механизмов. Построение плана ускорений

1.

Тема: Кинематический анализ плоских рычажных механизмов.
Построение плана ускорений
Определение величин и направлений действия абсолютных и относительных
ускорений характерных точек
Дано:
lOA
l AB
1
2 О
А
l
2
1
В
А
В 3
а l м 2
с
n
i
О
С
0
lOA
l AB
l BС
2 3
1
2
i i
0
0
Дано:
l
1
2
3
1. Рассчитывают величины нормальных ускорений звеньев, совершающих вращательное и сложное движения
(кривошип, коромысло, шатун)
n
кривошип : а АО
21 lOA const;
2. Рассчитывают значение масштабного коэффициента ускорений
где
n
коромысло : аВС
23 lBС
n
шатун : аВА
22 l AB
n
м / с2
а АО
а
pа мм
pа – отрезок произвольной длины (мм), который определяет модуль вектора нормального
ускорения кривошипа.
3. Переводят значения нормальных ускорений ведомых звеньев из
действительных величин (м / с2 ) в мм., используя масштабный
коэффициент а :
n
BA
n
aBA
мм.
а
n
BС
n
aBС
мм.
а
a
a

2.

Тема: Кинематический анализ плоских рычажных механизмов.
Построение плана ускорений
Определение величин и направлений действия абсолютных и относительных
ускорений характерных точек
Дано:
l
Дано:
lOA
l AB
1
2 О
А
В
А
2
1
В 3
О
0
0
l AB
l BС
2 3
1
lOA
С
0
1
2
3
4. Составляются уравнения распределения векторов ускорений для характерных точек механизма
точка О
аO 0
точка А
а A аО а АО
Вектор относительного ускорения звена раскладывается на два вектора – нормального и тангенциального ускорений
n
τ
а АО а АО
а AO
;
получаем
n
τ
а A аО а АО
а AO
// OA OA
Вектор нормального а
и направлен к центру его вращения (от первой буквы в индексе, при векторе, ко второй букве на плане положения)
n
i (центростремительного) ускорения лежит на линии вдоль (параллельной) оси звена
τ
Вектор тангенциального аi (касательного) ускорения лежит на линии перпендикулярной оси звена
(касательная к окружности его вращения)
ТОЛЬКО у кривошипа
а
τ
АО
0, т. к. 1 const ,
следовательно
1
а АО
0
lОA

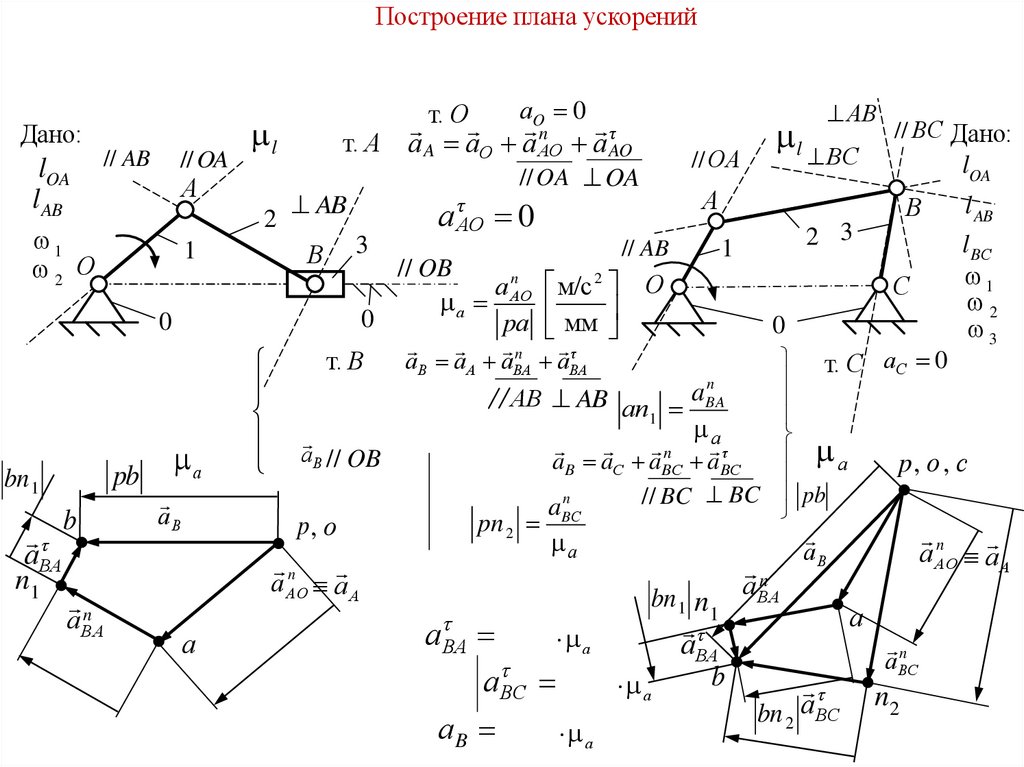
3.

Построение плана ускорений
Дано:
lOA // AB
l AB
1
2 О
// OA
l
А
2
0
bn 1
аВA
n1
b
n
а ВA
аВ
3
// OB
n
м/с 2 О
а АО
а
0
pаа мм
n
τ
аВ а А аВА
аВA
т. В
n
АВ AB аn a BA
11
а
τ
n
а В // OB
aB aС aBС
aBС
n
а АО
аА
а
ВС
// ВС Дано:
lOA
В
2 3
1
// AB
p, о
АВ
А
τ
а АО
0
n
aBС
ppnn22
а
l
// ОА
// OA OA
AB
В
1
а
pb
а 0
т. О
On
τ
т. А а A аО а АО а AO
0
// BC BC
bn 1 n
аВА
а
а ВС
а
аB
а
аС 0
n
а АО
аА
а
1
а
bn ВС
2
1
2
3
p, о , с
аВ
n
а ВA
а ВA
b
l BС
С
т. С
а
pb
l AB
n
а ВС
n2

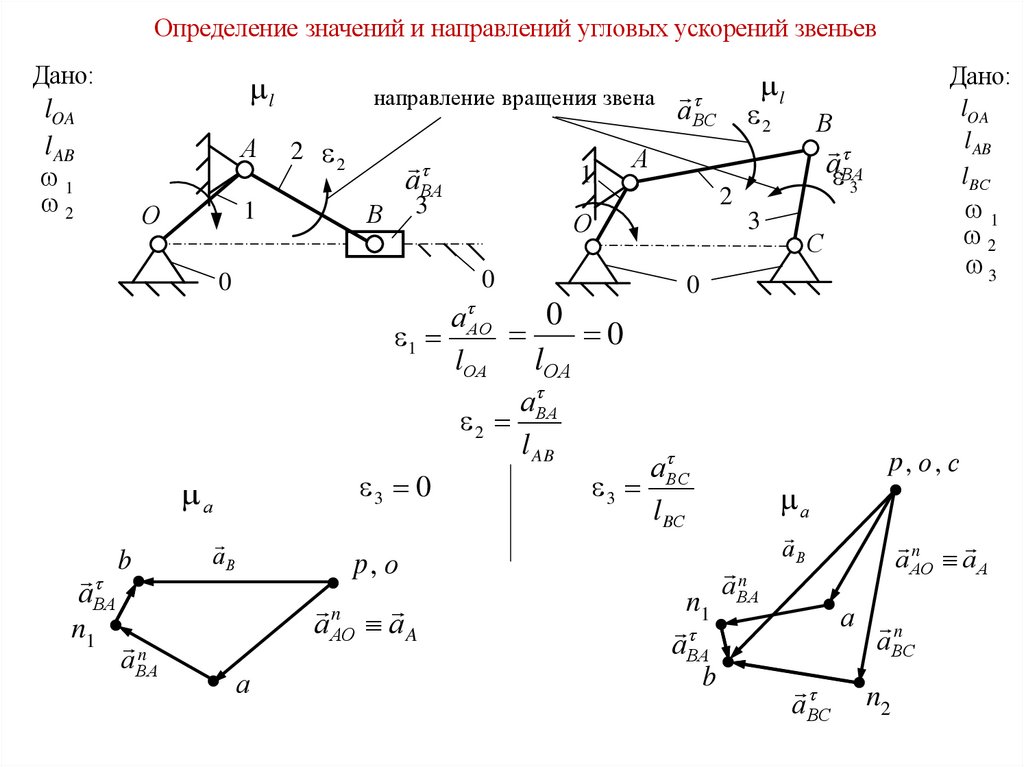
4.

Определение значений и направлений угловых ускорений звеньев
Дано:
l
lOA
l AB
А
1
2
1
О
В
а ВA
1
3
l
2
а ВС
аВ
p, о
n
а АО а A
а
а ВA
3
2
О
Дано:
lOA
l AB
l BС
В
А
3
1
2
3
С
0
0
а АО
0
1
lОA
lОA
а ВА
2
l AB
а ВС
3 0
3
l BС
а
а ВA
n1
n
а ВA
2 2
0
0
b
направление вращения звена
n1
а ВA
b
а
n
а ВA
p, о , с
аВ
n
а АО
аА
а n
а ВС
а ВС
n2

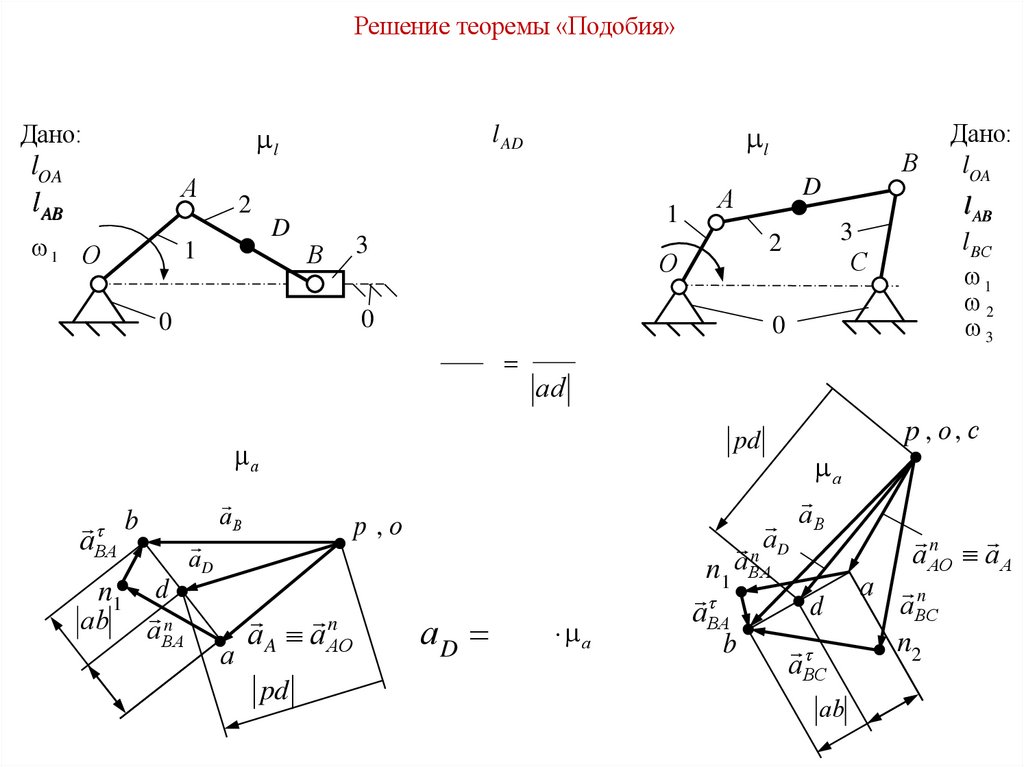
5.

Решение теоремы «Подобия»
l
Дано:
lOA
l AB
А
1 О
1
l
l AD
2
D
1
В
3
0
а
n1 d
аb а n
ВA
аD
p , о, с
а
а
В
а
n D
а
n ВA
p ,о
1
а
n
а A а АО
pd
аD
l AB
l BС
1
2
3
аd
pd
аВ
3
С
2
О
b
аВA
D
А
0
0
В
Дано:
lOA
а
а ВA
b
d
а ВС
аb
n
а АО а А
а n
а ВС
n2