Similar presentations:
Проверка передаточных функций кулачкового механизма методом планов скоростей и ускорений
1. Проверка передаточных функций кулачкового механизма методом планов скоростей и ускорений
И.И. Сорокинак.т.н., доцент
Высшая кинематическая пара (ВКП) в кулачковом механизме
заменяется двумя низшими и дополнительным звеном,
полученный при этом механизм носит название заменяющий
и будет иметь различные геометрические параметры в
зависимости от положения в котором такая замена была
произведена.
Планы скоростей и ускорений строятся для заменяющего
механизма.
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
2.
1. На центровом профиле кулачка выбирают такоеположение для которого ПФ определены однозначно и не
равны нулю.
Рассмотрим на примере
• для ПФ скорости не подходят
положения: 0, 7-8, 13; (в них
ПФ скорости равна нулю)
• для ПФ ускорения не подходят
положения: 0, 3, 6-7, 10, 13; (в
них ПФ ускорения не
определена однозначно).
Могут быть выбраны
положения:
1, 2, 4, 5, 8, 9 , 11 ,12
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
3.
2. Построение заменяющего механизма (заменаВКП 2 низшими и звеном) Для выбранного положения
механизма находим центр кривизны траектории движения
центра толкателя, точка А.
1. Заменяем хордами участки
центрового профиля, соседние
с выбранным.
Выбрано положение 2.
Хорды 1-2 и 2-3
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
4.
2. Построение заменяющего механизма (заменаВКП 2 низшими и звеном) Для выбранного положения
механизма находим центр кривизны траектории движения
центра толкателя, точка А.
2. В середине каждой хорды
восстанавливаем перпендикуляр.
Точка их пересечения и
будет центром кривизны
траектории движения
ролика толкателя А.
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
5.
2. Построение заменяющего механизма (заменаВКП 2 низшими и звеном) т. А центр кривизны
траектории движения толкателя в выбранном положении
Для плоского кулачкового
механизма с поступательно
движущимся толкателем
заменяющий механизм –
кривошипно-ползунный, где
ОА – кривошип,
АВ – шатун,
в роли ползуна выступает
ролик.
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
6.
2. Построение заменяющего механизма (заменаВКП 2 низшими и звеном)
Для плоского кулачкового
механизма с коромысловым
толкателем заменяющий
механизм – шарнирный
четырехзвенник, где
ОА – кривошип,
АВ – шатун,
ВN - кооромысло
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
7.
3. Определение ПФ кулачкового механизма методомпланов скоростей и ускорений
Для сравнения передаточных функций можно воспользоваться
сравнением соответствующих отрезков с планов скоростей и
ускорений и диаграмм соответствующих передаточных функций.
Строим планы скоростей и ускорений для заменяющего
механизма в вынужденном масштабе
pa qa OA
В этом случае масштабы определения ПФ совпадают с масштабом
построения кулачкового механизма, и, в большинстве случаев, с
масштабами построения диаграмм ПФ.
мм
V qB а qB l ,
м
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
8.
3.1. Определение ПФ скорости кулачковогомеханизма с поступательно движущимся
толкателем
1. Кривошип совершает вращательное движение с
постоянной угловой скоростью. Найдем скорость т. А:
V A k lOA
k lOA OA
VqA
k
k
l
VA
V qB l ,
мм
м
2. Шатун совершает плоское движение
VВ VА VВА
pb pa ab
При повороте плана скоростей на 90 градусов в сторону
противоположную направлению угловой скорости кулачка ПФ
скорости определяется непосредственно с плана механизма
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
9.
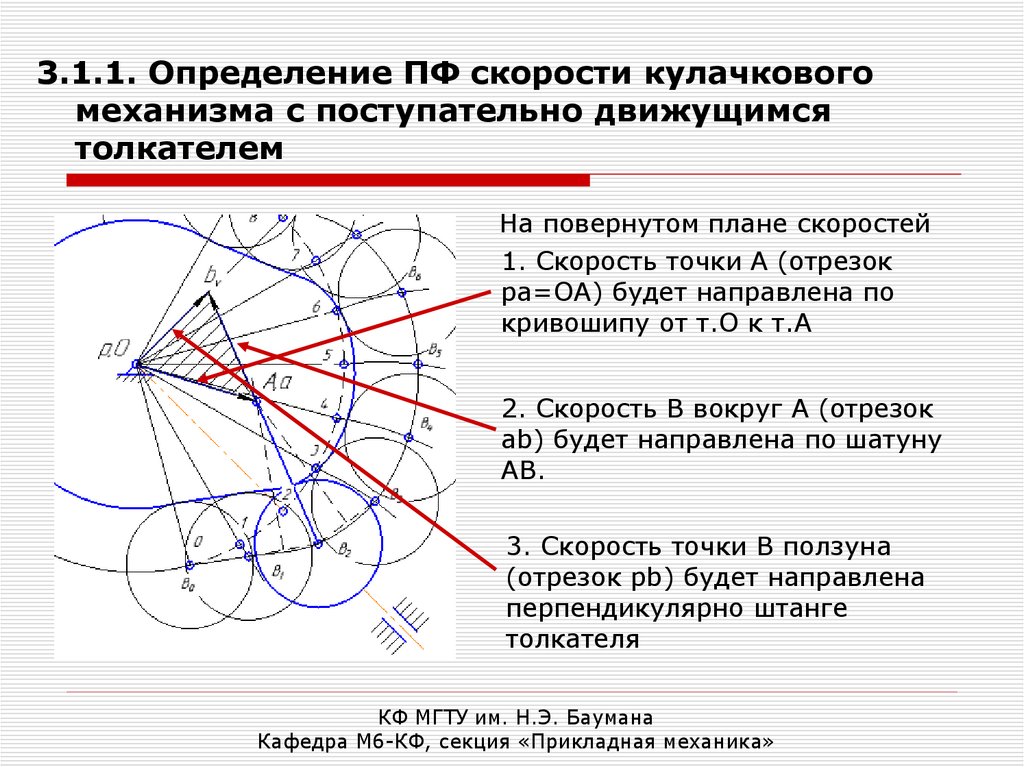
3.1.1. Определение ПФ скорости кулачковогомеханизма с поступательно движущимся
толкателем
На повернутом плане скоростей
1. Скорость точки А (отрезок
ра=ОА) будет направлена по
кривошипу от т.О к т.А
2. Скорость В вокруг А (отрезок
аb) будет направлена по шатуну
АВ.
3. Скорость точки В ползуна
(отрезок pb) будет направлена
перпендикулярно штанге
толкателя
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
10.
3.1.1. Определение ПФ скорости кулачковогомеханизма с поступательно движущимся
толкателем
Таким
образом,
ПФ
скорости
непосредственно с плана скоростей.
толкателя
определяется
Если построения велись в одинаковом масштабе, то она
сравнивается с ординатой снятой с диаграммы ПФ скорости в
соответствующем положении толкателя
V
pbv y VqB
max
100%
В противном случае перед сравнением необходимо перевести
полученные значения через масштабы построений и сравнивать
ДЕЙСТВИТЕЛЬНЫЕ значения ПФ.
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
11.
3.1.2. Определение ПФ ускорения кулачковогомеханизма с поступательно движущимся
толкателем
1. Кривошип совершает вращательное движение с
постоянной угловой скоростью. Найдем ускорение т. А:
a A lOA
2
k
a A 2k lOA OA
aqA 2
2
k
k
l
aA a
a qB l ,
мм
м
2. Шатун совершает плоское движение
n
aB aA aBA
aBA
n
qb qa ab b nb
2
2
2
2
2
2
2
V
ab
ab
ab
ab
1
n
aBA
l AB 12 BA 2 l
l 21
1
l AB V AB AB l
AB l
AB aq
При повороте плана ускорений на 180 градусов ПФ ускорения
определяется непосредственно с плана механизма
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
n
A
12.
3.1.2. Определение ПФ ускорения кулачковогомеханизма с поступательно движущимся
толкателем
На повернутом плане ускорений
1. Ускорение точки А (отрезок
qа=ОА) будет направлена по
кривошипу от т.О к т.А
ab 2
ab
AB
n
2. Нормальная составляющая
ускорения В вокруг А (отрезок аbn)
будет направлена по шатуну АВ от
т.А к т.В.
3. Тангенциальная составляющая
ускорения В вокруг А (отрезок bnb)
будет направлена перпендикулярно
шатуну АВ.
4. Ускорение точки В ползуна
(отрезок qb) будет направлено
параллельно штанге толкателя
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
13.
3.1.2. Определение ПФ ускорения кулачковогомеханизма с поступательно движущимся
толкателем
Таким
образом,
ПФ
ускорения
непосредственно с плана скоростей.
толкателя
определяется
Если построения велись в одинаковом масштабе, то она
сравнивается с ординатой снятой с диаграммы ПФ скорости в
соответствующем положении толкателя
a
qb y aqB
max
100%
В противном случае перед сравнением необходимо перевести
полученные значения через масштабы построений и сравнивать
ДЕЙСТВИТЕЛЬНЫЕ значения ПФ.
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
14.
3.2. Определение ПФ скорости кулачковогомеханизма с коромысловым толкателем
1. Кривошип совершает вращательное движение с постоянной
угловой скоростью. Найдем скорость т. А:
V A k lOA
k lOA OA
VqA
k
k
l
VA
V qB l ,
мм
м
2. Шатун совершает плоское движение, а коромысло вращательное
VВ VА VВА
pb pa ab
При повороте плана скоростей на 90 градусов в сторону
противоположную направлению угловой скорости кулачка ПФ
скорости определяется непосредственно с плана механизма
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
15.
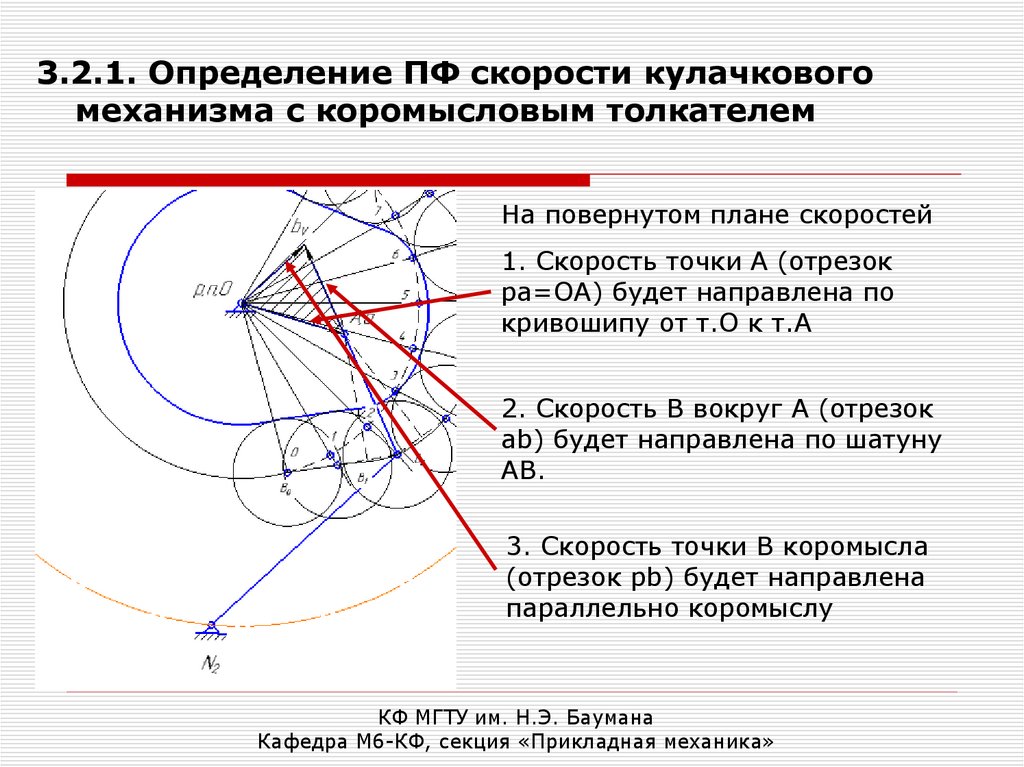
3.2.1. Определение ПФ скорости кулачковогомеханизма с коромысловым толкателем
На повернутом плане скоростей
1. Скорость точки А (отрезок
ра=ОА) будет направлена по
кривошипу от т.О к т.А
2. Скорость В вокруг А (отрезок
аb) будет направлена по шатуну
АВ.
3. Скорость точки В коромысла
(отрезок pb) будет направлена
параллельно коромыслу
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
16.
3.2.1. Определение ПФ скорости кулачковогомеханизма с коромысловым толкателем
Таким
образом,
ПФ
скорости
непосредственно с плана скоростей.
толкателя
определяется
Если построения велись в одинаковом масштабе, то она
сравнивается с ординатой снятой с диаграммы ПФ скорости в
соответствующем положении толкателя
V
pbv y VqB
max
100%
В противном случае перед сравнением необходимо перевести
полученные значения через масштабы построений и сравнивать
ДЕЙСТВИТЕЛЬНЫЕ значения ПФ.
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
17.
3.2.2. Определение ПФ ускорения кулачковогомеханизма с коромысловым толкателем
1. Кривошип совершает вращательное движение с
постоянной угловой скоростью. Найдем ускорение т. А:
мм
a qB l ,
м
a A 2k lOA OA
aqA 2
2
k
k
l
a A lOA
2
k
aA a
n
A
2. Шатун совершает плоское движение, а коромысло вращательное
n
aB aBn aB aA aBA
aBA
n
3
n
qb ab b b qa ab bnb
n
BA
a
n
3
2
VBA
ab2 l
ab2 l 12 ab2 12 ab2 1
l AB
2
2
l AB
V AB AB l
AB l
AB aq
2
1
2
2
2
2
2
2
2
V
pb
pb
pb
pb
1
aBn lNB 32 B 2 l
l 21
1
lNB V NB NB l
NB l
NB aq
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
18.
3.2.2. Определение ПФ ускорения кулачковогомеханизма с коромысловым толкателем
На повернутом плане ускорений
1. Ускорение точки А (отрезок qа=ОА)
будет направлена по кривошипу от т.О к
т.А
2. Нормальная составляющая ускорения В
вокруг А (отрезок аbn) будет направлена
по шатуну АВ от т.А к т.В.
3. Тангенциальная составляющая
ускорения В вокруг А (отрезок bnb) будет
направлена перпендикулярно шатуну АВ.
Ускорение точки
В (отрезок qb)
2
ab
ab
AB
n
2
pb
qb2n
NB
4. Нормальная составляющая ускорения
точки В коромысла (отрезок qb2n) будет
направлена по коромыслу BN.
5. Тангенциальная составляющая
ускорения точки В коромысла (отрезок
b2nb) будет направлена перпендикулярно
коромыслу BN.
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
19.
3.2.2. Определение ПФ ускорения кулачковогомеханизма с коромысловым толкателем
Таким
образом,
ПФ
ускорения
непосредственно с плана скоростей.
толкателя
определяется
Если построения велись в одинаковом масштабе, то она
сравнивается с ординатой снятой с диаграммы ПФ скорости в
соответствующем положении толкателя
a
qb y aqB
max
100%
В противном случае перед сравнением необходимо перевести
полученные значения через масштабы построений и сравнивать
ДЕЙСТВИТЕЛЬНЫЕ значения ПФ.
КФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»
20.
СПАСИБО ЗА ВНИМАНИЕКФ МГТУ им. Н.Э. Баумана
Кафедра М6-КФ, секция «Прикладная механика»


















 mechanics
mechanics








