Similar presentations:
Понятие функции. Область определения и множество значений функции
1.
yy = f(x)
0
x
2.
ОпределениеЕсли каждому значению х из некоторого
множества чисел Х в силу некоторого (вполне
определённого) закона поставлено в соответствие
(одно) число у, то говорят, что на множестве Х
задана функция у(х).
При этом х называют независимой переменной
или аргументом, а у – зависимой переменной или
функцией.
Чтобы указать, что у есть функция от х, пишут
у = f (х), где буква f характеризует то правило, по
которому получаются значения у,
соответствующие данным х
3. Число, соответствующее числу х0 , для данной функции у(х), называют значением этой функции в точке х0 и обозначают у(х0). Если
функция записанав виде у = f(х), то это число обозначают f(х0)
Например, для функции у = 3х пишут
У(1) = 3,
у(2) = 6,
у(-3) = -9
Или
f(1) = 3,
f (2) = 6,
f(-3) = -9
При этом говорят, например, что значение данной
функции в точке 1 равно 3 или «игрек от 1 равен
3», или «эф от 1 равно 3»
4.
Область определения имножество значений функции
Областью
определения
функции
называют
множество всех значений, которые может принимать
ее аргумент (т.е. независимая переменная х )
Обозначается D(y)
Множество значений (или область значений)
функции –это множество всех значений, которые
может принимать зависимая переменная у.
Обозначается E(y)
5.
Способы задания функции:• аналитический ( с помощью формулы );
• графический ( с помощью графика );
• табличный ( с помощью таблицы значений );
• словесный ( правило задания функции
описывается
словами ).
6.
хх
х
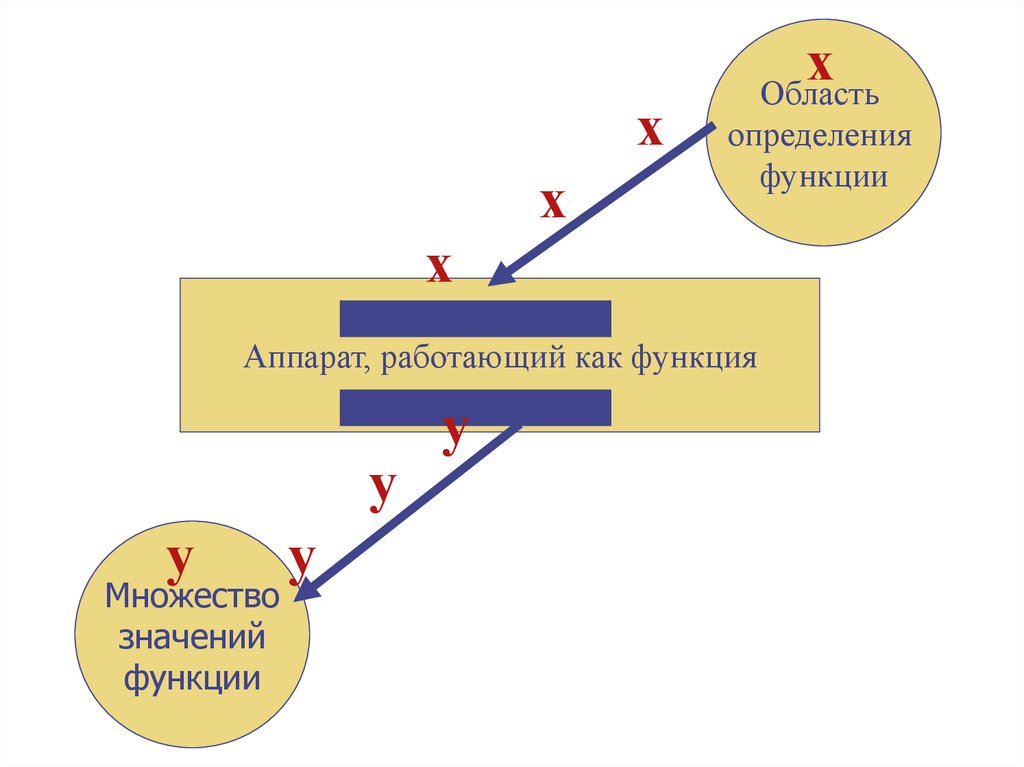
Область
определения
функции
х
Аппарат, работающий как функция
у
у
Множество
значений
функции
у
у
7. Задание 1
Пусть дана функция у = f(х). Что называют:а) независимой переменной или аргументом;
б) зависимой переменной или функцией;
в) областью определения функции;
г) множеством значений функции?
8. Задание 2
а) у = 2хх + 7. Назовите независимую и зависимую
переменные. Вычислите: у(3), у(-2), у(0), у(4).
Результаты запишите в таблицу
х
3
-2
0
-4
у
13
3
7
-1
9.
Функции и их графикиy
y = f(x)
0
x
10.
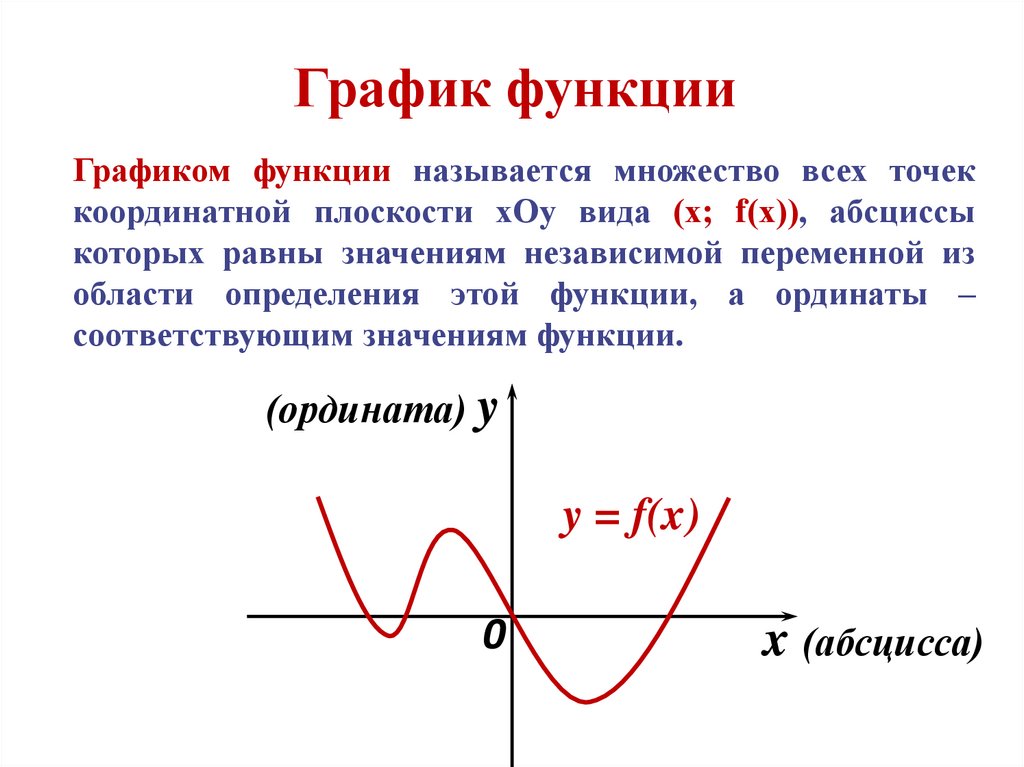
График функцииГрафиком функции называется множество всех точек
координатной плоскости хОу вида (х; f(х)), абсциссы
которых равны значениям независимой переменной из
области определения этой функции, а ординаты –
соответствующим значениям функции.
(ордината) y
y = f(x)
0
x (абсцисса)
11.
График непрерывной функцииy
y = f(x)
0
x
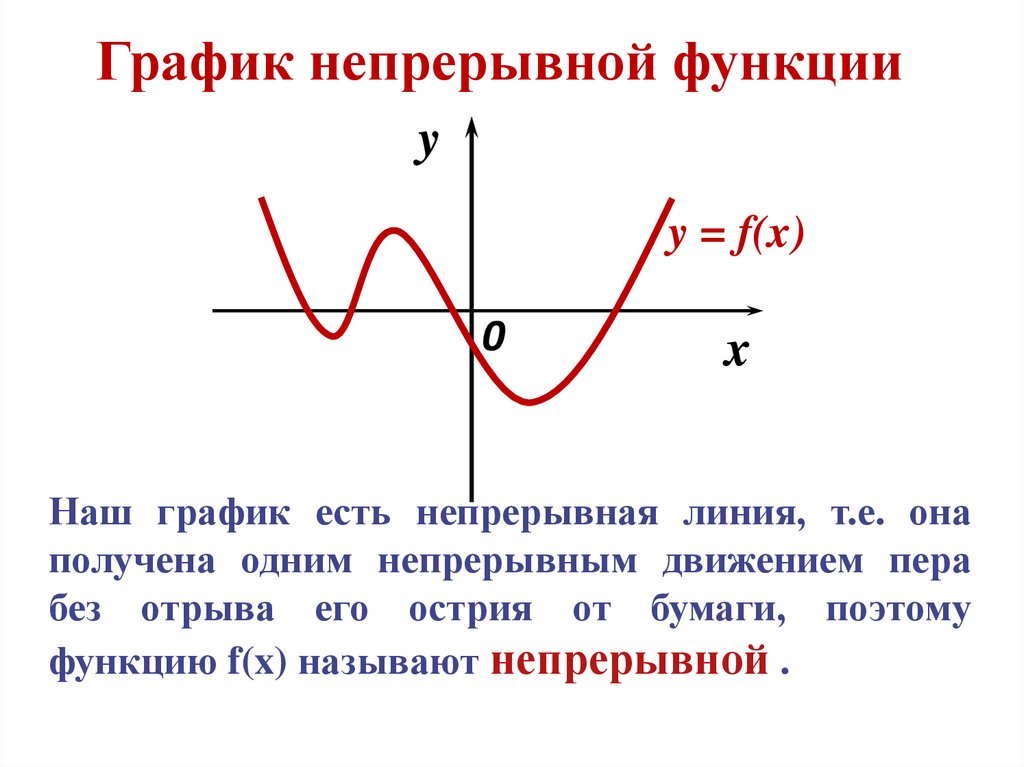
Наш график есть непрерывная линия, т.е. она
получена одним непрерывным движением пера
без отрыва его острия от бумаги, поэтому
функцию f(x) называют непрерывной .
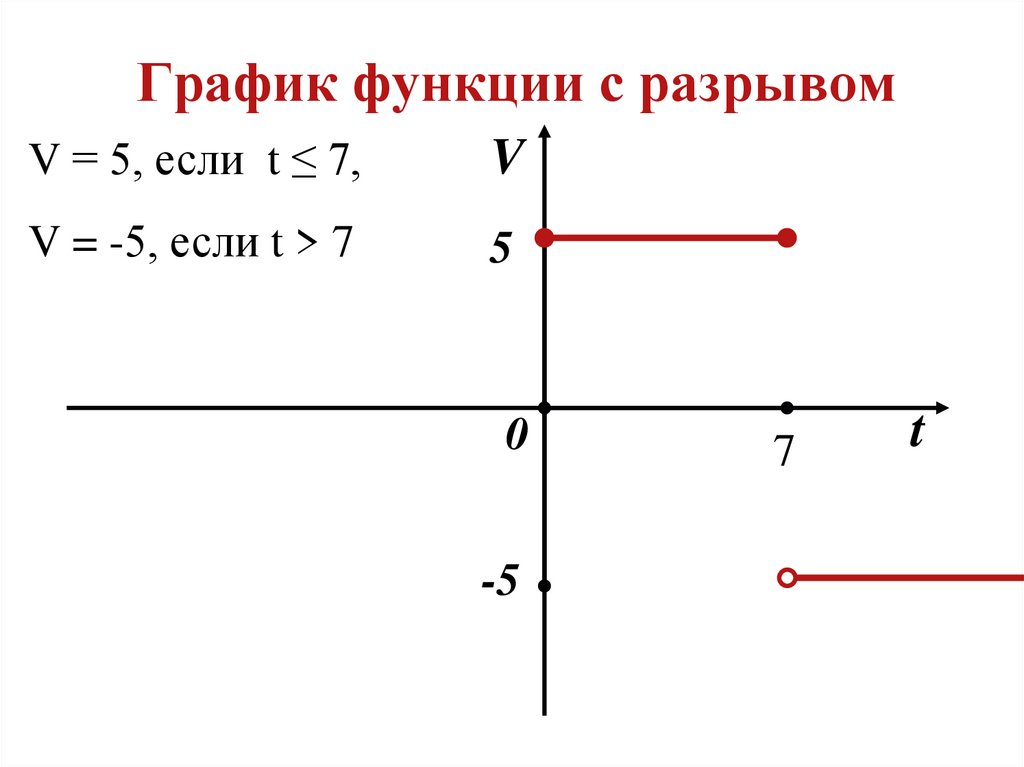
12. График функции с разрывом
V = 5, если t ≤ 7,V
V = -5, если t > 7
5
0
-5
7
t






 mathematics
mathematics








